Improved War Strategy Optimization with Extreme Learning Machine for Health Data Classification
Abstract
1. Introduction
2. Literature Review
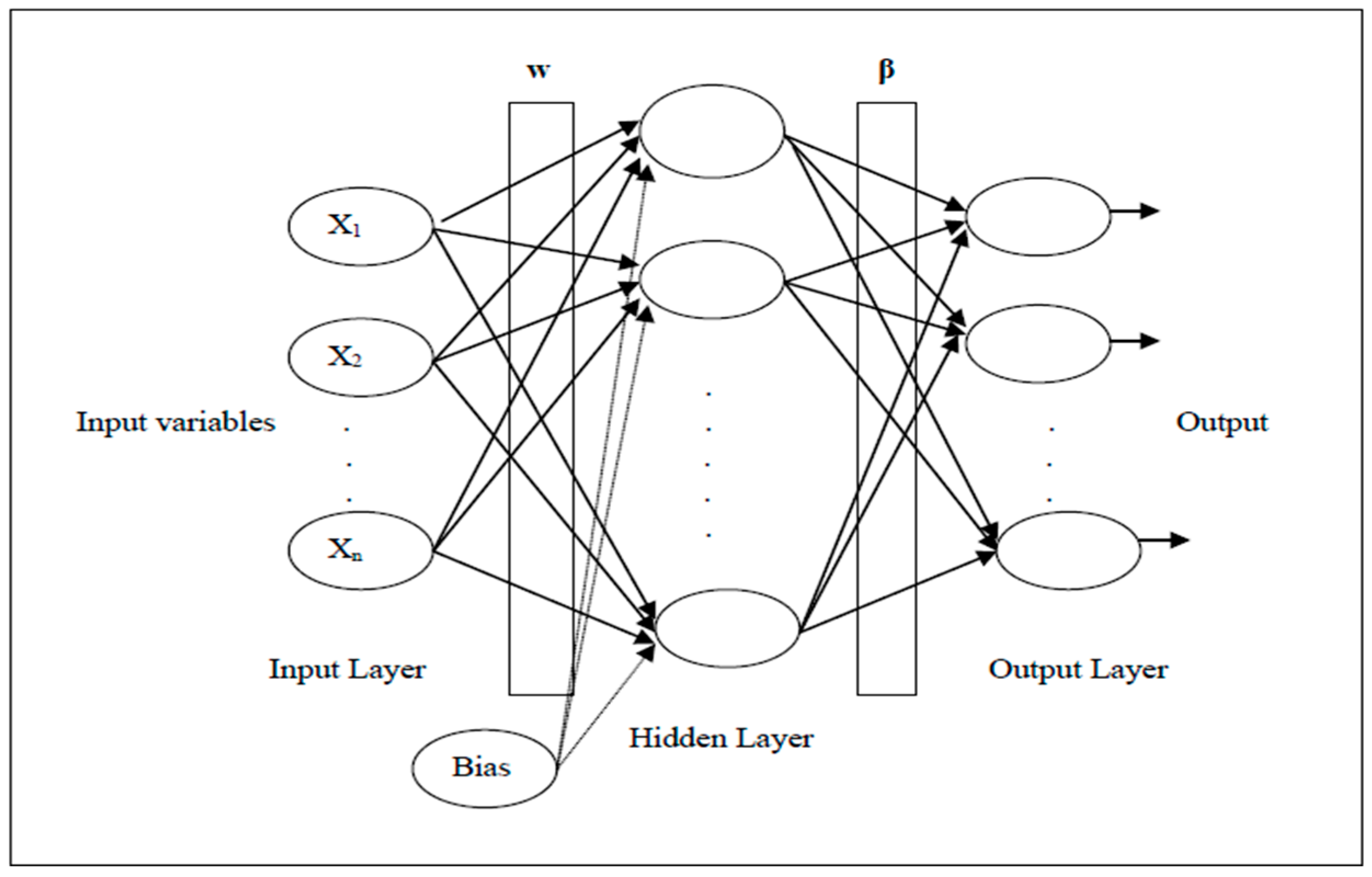
3. Extreme Learning Machine (ELM)
4. War Strategy Optimization (WSO) Algorithm
4.1. Attack Strategy
4.2. Updating Weight and Rank
4.3. Defensive Strategy
4.4. Replacing Weak Soldiers
5. Opposition-Based Learning (OBL)—OWSO
6. Proposed Improved Random Opposition-Based Learning (IROBL)—IWSO
| Algorithm 1. Improved War Strategy Optimization’s Pseudocode | ||||
| Input: Number of soldier, maximum iteration (Maxiter), lower bound, upper bound, dimension of search space, fitness function, R = 0.1 | ||||
| Output: best fitness, king position | ||||
| Begin | ||||
| Randomly initialize the soldiers’ positions in the search space | ||||
| Calculate fitness of each soldier | ||||
| Select best soldier as King and second as a Commander | ||||
| Main loop: while t < Maxiter | ||||
| For 1: Number of Soldiers | ||||
| RR = rand () | ||||
| if RR < R | ||||
| (Exploration) Update position of soldiers according to Equation (13) | ||||
| else: | ||||
| (Exploitation) Update position of soldiers according to Equation (9) | ||||
| end if | ||||
| Ensure position is within bounds | ||||
| Calculate Fitness | ||||
| if fitness better than previous | ||||
| Update soldier position using Equation (10) | ||||
| Update soldier rank and weight using Equation (11) | ||||
| end if | ||||
| (Random Opposition) Find random opposition position of soldier using Equation (16) | ||||
| if fitness of opposition better than previous | ||||
| Update soldier position using Equation (10) | ||||
| Update soldier rank and weight using Equation (11) | ||||
| end if | ||||
| end for | ||||
| Find the lowest fitness score as weakest | ||||
| Randomly relocate the weakest soldier using Equation (14) | ||||
| Update King and Commander | ||||
| t = t+1 | ||||
| end while | ||||
| end | ||||
7. Performance Evaluation
8. Health Datasets Used
9. Studied Metaheuristic Algorithms
10. Results and Discussion
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Results of Classification Precision, Sensitivity, Specificity, F1 Score Values
| Methods | Breast | Bupa | Dermatology | Diabetes | Hepatitis | Lymphography | Parkinsons | SAheart | SPECTF | Vertebral | WDBC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ELM | 98.32 [10] | 78.70 [11] 71.30 [11] 88.36 [15] | * 100.00 [14] 53.67 [15] | * 79.69 [10] | 84.00 [13] 63.54 [15] | 65.24 [15] | 91.05 [10] 86.15 [12] | * 77.85 [10] | 79.12 [10] | N/A | 97.42 [10] 96.13 [12] |
| FPA | 97.81 [8] | N/A | N/A | 76.71 [8] | N/A | N/A | N/A | 74.05 [8] | 80.21 [8] | 87.73 [8] | 94.84 [8] |
| BAT | 91.31 [8] | N/A | N/A | 77.09 [8] | N/A | N/A | N/A | 72.78 [8] | 78.02 [8] | 83.96 [8] | 89.69 [8] |
| SSA | 97.47 [8] | N/A | N/A | 75.19 [8] | N/A | N/A | N/A | 76.58 [8] | 78.02 [8] | 82.07 [8] | 95.36 [8] |
| HHO | 96.57 [8] | N/A | N/A | 71.37 [8] | N/A | N/A | N/A | 75.31 [8] | 78.02 [8] | 87.73 [8] | 91.75 [8] |
| GWO | 97.81 [8] | N/A | N/A | 77.86 [8] | N/A | N/A | N/A | 74.68 [8] | * 83.51 [8] | * 91.50 [8] | 95.36 [8] |
| PSO | 97.19 [8] 98.32 [10] | 71.54 [12] | N/A | 78.62 [8] 79.17 [10] | N/A | N/A | 92.54 [10] 87.59 [12] | 74.05 [8] 77.22 [10] | 82.41 [8] 80.22 [10] | 86.79 [8] | 96.39 [8] * 98.45 [10] 96.28 [12] |
| DE | 97.19 [8] | N/A | N/A | 77.48 [8] | N/A | N/A | N/A | 77.84 [8] | 78.02 [8] | 88.67 [8] | 95.87 [8] |
| MNHO | 97.51 [8] | N/A | N/A | 77.86 [8] | N/A | N/A | N/A | 77.84 [8] | 81.31 [8] | 89.62 [8] | 96.90 [14] |
| RBFs | 97.38 [9] | N/A | N/A | 77.61 [9] | 87.10 [9] | N/A | * 92.62 [9] | N/A | N/A | N/A | N/A |
| RBFNN-ELM-GA | 97.38 [9] | N/A | N/A | 77.61 [9] | 87.10 [9] | N/A | * 92.62 [9] | N/A | N/A | N/A | N/A |
| DE | * 98.74 [10] | 76.26 [12] | N/A | 78.65 [10] | N/A | N/A | 89.55 [10] 87.08 [12] | 77.22 [10] | 81.32 [10] | N/A | 97.42 [10] 96.10 [12] |
| CSO-RELM | 96.64 [10] | N/A | N/A | 73.66 [10] | N/A | N/A | 91.05 [10] | 75.95 [10] | 79.12 [10] | N/A | 95.88 [10] |
| CSO-ELM | 97.90 [10] | N/A | N/A | 78.13 [10] | N/A | N/A | 92.54 [10] | 76.58 [10] | 79.12 [10] | N/A | 97.42 [10] |
| HAELM | N/A | * 88.90 [11] | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A |
| ABC | N/A | 76.75 [12] | N/A | N/A | N/A | N/A | 88.31 [12] | N/A | N/A | N/A | 96.42 [12] |
| OSELM | N/A | 63.29 [13] | N/A | N/A | 81.20 [13] | N/A | N/A | N/A | N/A | N/A | N/A |
| CSELM | N/A | 73.08 [13] | N/A | N/A | 86.80 [13] | N/A | N/A | N/A | N/A | N/A | N/A |
| ICSELM | N/A | 75.83 [13] | N/A | N/A | * 100.00 [13] | N/A | N/A | N/A | N/A | N/A | N/A |
| FA | N/A | N/A | * 100.00 [14] | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A |
| BP | N/A | N/A | 83.52 [15] | N/A | 69.23 [15] | 83.78 [15] | N/A | N/A | N/A | N/A | N/A |
| NEURO-FUZZY | N/A | N/A | 82.42 [15] | N/A | 69.23 [15] | * 89.19 [15] | N/A | N/A | N/A | N/A | N/A |
| PCA | N/A | N/A | 53.30 [15] | N/A | 75.44 [15] | 65.41 [15] | N/A | N/A | N/A | N/A | N/A |
| KELM | N/A | N/A | 89.01 [15] | N/A | 64.10 [15] | 83.78 [15] | N/A | N/A | N/A | N/A | N/A |
| PCA-KELM | N/A | N/A | 95.60 [15] | N/A | 76.92 [15] | 86.49 [15] | N/A | N/A | N/A | N/A | N/A |
| Breast | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 98.92 | 1.32 | 99.67 | 0.73 | 100.00 | 0.00 | 99.79 | 0.50 | 99.67 | 0.71 | 99.86 | 0.43 | 99.81 | 0.49 |
| Sensitivity | 93.88 | 2.41 | 95.64 | 2.20 | 96.29 | 2.01 | 96.21 | 2.27 | 95.97 | 1.90 | 96.20 | 1.98 | 96.63 | 1.74 |
| Specificity | 99.41 | 0.71 | 99.69 | 0.99 | 100.00 | 0.00 | 99.85 | 0.35 | 99.82 | 0.38 | 99.92 | 0.23 | 99.90 | 0.26 |
| F1 Score | 96.31 | 1.32 | 97.60 | 1.16 | 98.10 | 1.05 | 97.95 | 1.21 | 97.77 | 1.05 | 97.98 | 1.09 | 98.18 | 0.86 |
| Bupa | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 86.60 | 9.82 | 78.54 | 14.64 | 81.72 | 13.63 | 85.38 | 11.45 | 83.37 | 10.99 | 82.60 | 13.61 | 81.13 | 11.04 |
| Sensitivity | 77.76 | 4.68 | 81.44 | 5.80 | 79.25 | 4.34 | 80.18 | 4.63 | 78.44 | 4.21 | 78.16 | 5.00 | 81.73 | 5.41 |
| Specificity | 82.72 | 6.73 | 80.63 | 4.96 | 80.69 | 6.44 | 84.70 | 6.07 | 81.07 | 5.93 | 82.01 | 7.46 | 82.89 | 5.03 |
| F1 Score | 81.45 | 4.22 | 78.84 | 7.06 | 79.63 | 7.03 | 82.17 | 5.70 | 80.31 | 5.27 | 79.48 | 6.58 | 80.79 | 4.92 |
| Dermatology | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 97.19 | 5.73 | 98.92 | 1.74 | 98.77 | 4.06 | 99.76 | 1.30 | 99.46 | 1.72 | 99.76 | 1.30 | 100.00 | 0.00 |
| Sensitivity | 95.35 | 6.53 | 97.57 | 4.41 | 99.36 | 1.32 | 100.00 | 0.00 | 99.13 | 2.20 | 100.00 | 0.00 | 100.00 | 0.00 |
| Specificity | 99.05 | 1.47 | 99.61 | 0.60 | 99.73 | 0.69 | 99.96 | 0.19 | 99.83 | 0.56 | 99.96 | 0.19 | 100.00 | 0.00 |
| F1 Score | 96.16 | 5.43 | 98.18 | 2.48 | 99.01 | 2.26 | 99.88 | 0.68 | 99.28 | 1.68 | 99.88 | 0.68 | 100.00 | 0.00 |
| Diabetes | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 87.05 | 15.20 | 85.06 | 17.12 | 86.38 | 12.80 | 85.04 | 15.51 | 85.13 | 17.29 | 90.38 | 4.91 | 90.86 | 7.28 |
| Sensitivity | 74.99 | 2.93 | 75.82 | 2.99 | 75.59 | 2.65 | 78.65 | 3.94 | 75.08 | 2.79 | 80.04 | 2.84 | 81.18 | 2.07 |
| Specificity | 76.01 | 3.74 | 76.33 | 4.20 | 73.17 | 4.84 | 77.79 | 5.32 | 74.01 | 4.17 | 77.91 | 6.07 | 80.40 | 4.04 |
| F1 Score | 79.80 | 8.43 | 79.12 | 9.69 | 80.20 | 7.77 | 80.97 | 9.36 | 78.71 | 9.93 | 84.84 | 3.26 | 85.59 | 4.36 |
| Hepatitis | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 92.84 | 16.44 | 92.06 | 14.77 | 94.11 | 11.34 | 88.89 | 17.82 | 93.61 | 13.61 | 92.72 | 12.84 | 98.83 | 4.68 |
| Sensitivity | 96.51 | 6.48 | 97.36 | 6.30 | 99.03 | 3.77 | 98.41 | 3.95 | 98.61 | 2.44 | 97.59 | 7.01 | 98.86 | 3.84 |
| Specificity | 96.76 | 6.79 | 98.11 | 4.17 | 97.73 | 5.18 | 98.15 | 2.84 | 98.92 | 2.33 | 97.58 | 5.17 | 98.51 | 5.11 |
| F1 Score | 93.58 | 11.62 | 93.73 | 9.12 | 96.07 | 6.69 | 92.19 | 11.69 | 95.41 | 8.21 | 94.60 | 8.72 | 98.74 | 3.27 |
| Lymphography | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 93.56 | 5.94 | 94.72 | 5.86 | 97.69 | 2.79 | 96.16 | 4.39 | 94.03 | 5.45 | 94.17 | 4.84 | 94.77 | 4.82 |
| Sensitivity | 91.86 | 4.49 | 94.22 | 4.39 | 96.49 | 3.21 | 94.95 | 3.81 | 94.17 | 4.72 | 94.59 | 3.99 | 94.36 | 3.73 |
| Specificity | 94.49 | 4.30 | 96.08 | 3.68 | 98.00 | 2.54 | 96.75 | 3.66 | 94.73 | 4.12 | 94.91 | 3.94 | 95.68 | 3.49 |
| F1 Score | 92.52 | 3.39 | 94.29 | 3.27 | 97.04 | 2.19 | 95.48 | 3.28 | 93.90 | 2.87 | 94.23 | 2.48 | 94.44 | 2.60 |
| Parkinsons | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 90.29 | 18.13 | 88.85 | 17.67 | 87.76 | 19.81 | 91.47 | 15.84 | 93.70 | 14.33 | 94.81 | 11.58 | 84.63 | 15.12 |
| Sensitivity | 88.12 | 5.29 | 89.93 | 5.76 | 89.93 | 4.36 | 88.06 | 4.08 | 88.60 | 4.24 | 88.02 | 4.49 | 95.17 | 4.03 |
| Specificity | 92.06 | 7.34 | 92.82 | 6.40 | 92.02 | 7.17 | 93.77 | 5.83 | 93.82 | 7.30 | 94.85 | 6.58 | 93.40 | 3.91 |
| F1 Score | 87.79 | 10.80 | 87.85 | 9.17 | 87.46 | 12.14 | 88.95 | 9.43 | 90.19 | 8.61 | 90.69 | 6.11 | 88.62 | 7.66 |
| SAheart | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 81.47 | 25.88 | 76.77 | 25.99 | 71.69 | 26.09 | 77.75 | 24.77 | 83.35 | 23.50 | 76.59 | 26.70 | 75.50 | 18.41 |
| Sensitivity | 74.49 | 3.91 | 77.59 | 5.96 | 77.33 | 3.94 | 78.54 | 5.00 | 74.49 | 3.14 | 77.04 | 5.77 | 77.95 | 3.86 |
| Specificity | 83.11 | 8.92 | 78.11 | 6.65 | 78.09 | 6.02 | 82.79 | 7.54 | 82.30 | 9.13 | 78.99 | 5.98 | 79.95 | 4.71 |
| F1 Score | 74.90 | 14.42 | 73.69 | 14.58 | 71.39 | 14.84 | 75.61 | 14.08 | 76.49 | 12.77 | 73.29 | 14.80 | 75.55 | 10.49 |
| SPECTF | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 96.19 | 11.32 | 81.44 | 29.89 | 89.34 | 23.22 | 91.40 | 20.78 | 83.95 | 24.17 | 90.68 | 18.32 | 93.77 | 17.62 |
| Sensitivity | 84.95 | 3.25 | 86.09 | 6.06 | 85.32 | 3.74 | 84.72 | 5.30 | 87.73 | 6.21 | 87.51 | 4.66 | 88.56 | 4.74 |
| Specificity | 86.64 | 13.13 | 89.61 | 9.49 | 85.59 | 11.49 | 91.35 | 10.14 | 86.84 | 10.84 | 87.05 | 12.51 | 90.88 | 10.46 |
| F1 Score | 89.72 | 7.24 | 79.52 | 19.97 | 85.12 | 16.08 | 86.17 | 14.33 | 83.11 | 16.30 | 87.66 | 11.13 | 89.53 | 12.08 |
| Vertebral | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 85.96 | 8.68 | 86.26 | 6.66 | 88.15 | 6.72 | 88.89 | 6.21 | 87.33 | 4.91 | 86.89 | 6.66 | 88.52 | 5.00 |
| Sensitivity | 80.20 | 6.53 | 81.92 | 5.85 | 79.66 | 4.90 | 82.80 | 6.42 | 78.53 | 4.73 | 81.60 | 6.10 | 83.59 | 3.79 |
| Specificity | 93.56 | 2.92 | 93.59 | 2.86 | 94.43 | 2.09 | 94.72 | 2.84 | 93.69 | 2.24 | 93.65 | 2.96 | 94.52 | 2.35 |
| F1 Score | 82.39 | 3.50 | 83.72 | 3.33 | 83.37 | 3.03 | 85.52 | 4.57 | 82.54 | 3.04 | 83.90 | 4.30 | 85.87 | 3.07 |
| WDBC | ALO | DA | PSO | GWO | WSO | OWSO | IWSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Precision | 94.97 | 4.97 | 94.28 | 4.31 | 95.78 | 3.88 | 94.69 | 3.97 | 94.22 | 4.01 | 94.75 | 4.62 | 98.34 | 2.49 |
| Sensitivity | 93.69 | 3.18 | 95.10 | 2.60 | 94.45 | 3.03 | 95.38 | 2.70 | 95.04 | 2.27 | 94.23 | 2.44 | 98.09 | 1.77 |
| Specificity | 95.28 | 3.29 | 94.65 | 3.05 | 95.99 | 2.14 | 94.96 | 2.35 | 94.37 | 2.55 | 95.36 | 2.54 | 98.90 | 1.42 |
| F1 Score | 94.20 | 2.38 | 94.59 | 1.96 | 95.01 | 1.74 | 94.95 | 1.85 | 94.56 | 2.06 | 94.39 | 2.09 | 98.18 | 1.12 |
References
- Polatlı, L.Ö.; Karadayı, M.A. Sağlık hizmetlerinde güncel makine öğrenmesi algoritmaları. Eurasian J. Health Technol. Assess. 2022, 6, 117–143. [Google Scholar] [CrossRef]
- World Health Organization. International Classification of Diseases Eleventh Revision (ICD-11). Geneva 2022. Available online: https://icdcdn.who.int/icd11referenceguide/en/html/index.html (accessed on 9 May 2025).
- World Health Organization. Noncommunicable Diseases. 2023. Available online: https://www.who.int/news-room/fact-sheets/detail/noncommunicable-diseases (accessed on 9 May 2025).
- Escobar, E.; Cuevas, H.E. Implementation of Metaheuristics with Extreme Learning Machines, Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Ayyarao, T.S.; Ramakrishna, N.; Elavarasan, R.M.; Polumahanthi, N.; Rambabu, M.; Saini, G.; Khan, B.; Alatas, B. War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization. IEEE Access 2022, 10, 25073–25105. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; IEEE: New York, NY, USA, 2005; pp. 695–701. [Google Scholar] [CrossRef]
- Al Bataineh, A.; Jalali, S.M.J.; Mousavirad, S.J.; Yazdani, A.; Islam, S.M.S.; Khosravi, A. An efficient hybrid extreme learning machine and evolutionary framework with applications for medical diagnosis. Expert Syst. 2024, 41, e13532. [Google Scholar] [CrossRef]
- Siouda, R.; Nemissi, M.; Seridi, H. Diverse activation functions based-hybrid RBF-ELM neural network for medical classification. Evol. Intell. 2024, 17, 829–845. [Google Scholar] [CrossRef]
- Eshtay, M.; Faris, H.; Obeid, N. Improving extreme learning machine by competitive swarm optimization and its application for medical diagnosis problems. Expert Syst. Appl. 2018, 104, 134–152. [Google Scholar] [CrossRef]
- Raja, G.; Reka, K.; Murugesan, P.; Meenakshi Sundaram, S. Predicting Liver Disorders Using an Extreme Learning Machine. SN Comput. Sci. 2024, 5, 677. [Google Scholar] [CrossRef]
- Ma, C. An efficient optimization method for extreme learning machine using artificial bee colony. J. Digit. Inf. Manag. 2017, 15, 135–147. [Google Scholar]
- Mohapatra, P.; Chakravarty, S.; Dash, P.K. An improved cuckoo search based extreme learning machine for medical data classification. Swarm Evol. Comput. 2015, 24, 25–49. [Google Scholar] [CrossRef]
- Kaya, Y.; Kuncan, F. A hybrid model for classification of medical data set based on factor analysis and extreme learning machine: FA + ELM. Biomed. Signal Process. Control 2022, 78, 104023. [Google Scholar] [CrossRef]
- Goel, T.; Nehra, V.; Vishwakarma, V.P. An efficient classification based on genetically optimised hybrid PCA-Kernel ELM learning. Int. J. Appl. Pattern Recognit. 2016, 3, 241–258. [Google Scholar] [CrossRef]
- Al Bataineh, A.; Manacek, S. MLP-PSO hybrid algorithm for heart disease prediction. J. Pers. Med. 2022, 12, 1208. [Google Scholar] [CrossRef] [PubMed]
- Albadr, M.A.A.; Ayob, M.; Tiun, S.; AL-Dhief, F.T.; Hasan, M.K. Gray wolf optimization-extreme learning machine approach for diabetic retinopathy detection. Front. Public Health 2022, 10, 925901. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, C.; Peng, T.; Pan, Y.; Liu, J. A medical disease assisted diagnosis method based on lightweight fuzzy SZGWO-ELM neural network model. Sci. Rep. 2024, 14, 27568. [Google Scholar] [CrossRef] [PubMed]
- Bacanin, N.; Stoean, C.; Markovic, D.; Zivkovic, M.; Rashid, T.A.; Chhabra, A.; Sarac, M. Improving performance of extreme learning machine for classification challenges by modified firefly algorithm and validation on medical benchmark datasets. Multimed. Tools Appl. 2024, 83, 76035–76075. [Google Scholar] [CrossRef]
- Lahoura, V.; Singh, H.; Aggarwal, A.; Sharma, B.; Mohammed, M.A.; Damaševičius, R.; Kadry, S.; Cengiz, K. Cloud computing-based framework for breast cancer diagnosis using extreme learning machine. Diagnostics 2021, 11, 241. [Google Scholar] [CrossRef]
- Kuang, X.; Hou, J.; Liu, X.; Lin, C.; Wang, Z.; Wang, T. Improved African Vulture Optimization Algorithm Based on Random Opposition-Based Learning Strategy. Electronics 2024, 13, 3329. [Google Scholar] [CrossRef]
- Ma, M.; Wu, J.; Shi, Y.; Yue, L.; Yang, C.; Chen, X. Chaotic Random Opposition-Based Learning and Cauchy Mutation Improved Moth-Flame Optimization Algorithm for Intelligent Route Planning of Multiple UAVs. IEEE Access 2022, 10, 49385–49397. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Cai, S.; Xu, M. A Random Opposition-Based Learning Grey Wolf Optimizer. IEEE Access 2019, 7, 113810–113825. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Mahdavi, S.; Rahnamayan, S.; Deb, K. Opposition based learning: A literature review. Swarm Evol. Comput. 2018, 39, 1–23. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. Topics: Statistical Theory and Methods, Statistics and Computing/Statistics Programs, Applied Statistics. In An Introduction to Statistical Learning; Springer Texts in Statistics; Springer: Cham, Switzerland, 2023; ISBN 978-3-031-38747-0. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. In Breakthroughs in Statistics: Methodology and Distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 196–202. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Wolberg, W. Breast Cancer Wisconsin (Original); UCI Machine Learning Repository: Irvine, CA, USA, 1990. [Google Scholar] [CrossRef]
- Liver Disorders; UCI Machine Learning Repository: Irvine, CA, USA, 2016. [CrossRef]
- Ilter, N.; Guvenir, H. Dermatology; UCI Machine Learning Repository: Irvine, CA, USA, 1998. [Google Scholar] [CrossRef]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Proceedings of the Symposium on Computer Applications and Medical Care, Minneapolis, MN, USA, 8–10 June 1988; IEEE Computer Society Press: Washington, DC, USA, 1988; pp. 261–265. [Google Scholar]
- Hepatitis; UCI Machine Learning Repository: Irvine, CA, USA, 1938. [CrossRef]
- Zwitter, M.; Soklic, M. Lymphography; UCI Machine Learning Repository: Irvine, CA, USA, 1988. [Google Scholar] [CrossRef]
- Little, M. Parkinsons; UCI Machine Learning Repository: Irvine, CA, USA, 2007. [Google Scholar] [CrossRef]
- South African Heart. Knowledge Extraction based on Evolutionary Learning (2004–2018). 2004–2018. Available online: https://sci2s.ugr.es/keel/dataset.php?cod=184 (accessed on 9 May 2025).
- Cios, K.; Kurgan, L.; Goodenday, L. SPECTF Heart; UCI Machine Learning Repository: Irvine, CA, USA, 2001. [Google Scholar] [CrossRef]
- Barreto, G.; Neto, A. Vertebral Column; UCI Machine Learning Repository: Irvine, CA, USA, 2005. [Google Scholar] [CrossRef]
- Wolberg, W.; Mangasarian, O.; Street, N.; Street, W. Breast Cancer Wisconsin (Diagnostic); UCI Machine Learning Repository: Irvine, CA, USA, 1993. [Google Scholar] [CrossRef]
- Mirjalili, S. A New MATLAB Optimization Toolbox. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/55980-a-new-matlab-optimization-toolbox (accessed on 9 May 2025).
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. MHS’95. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: New York, NY, USA, 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]




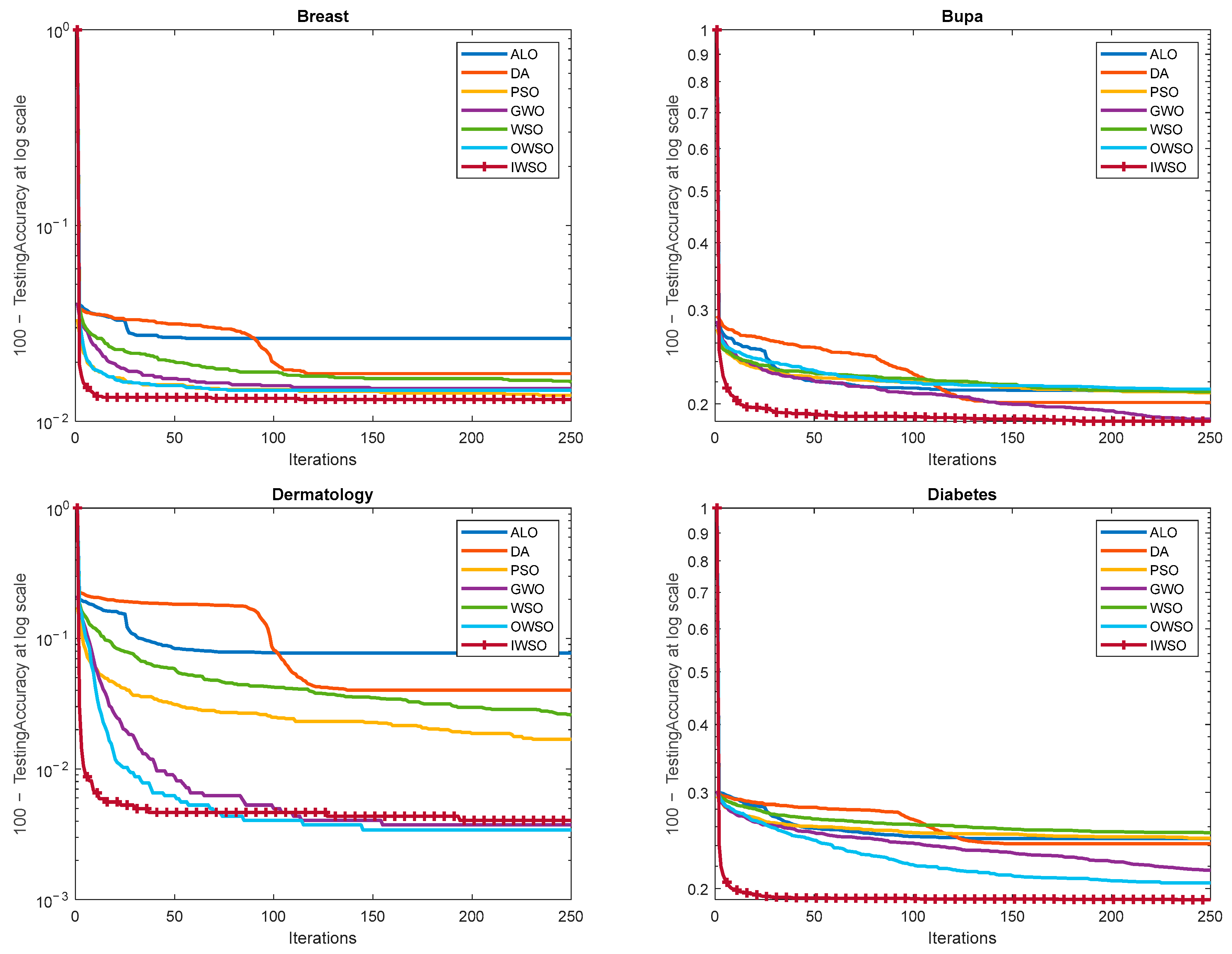
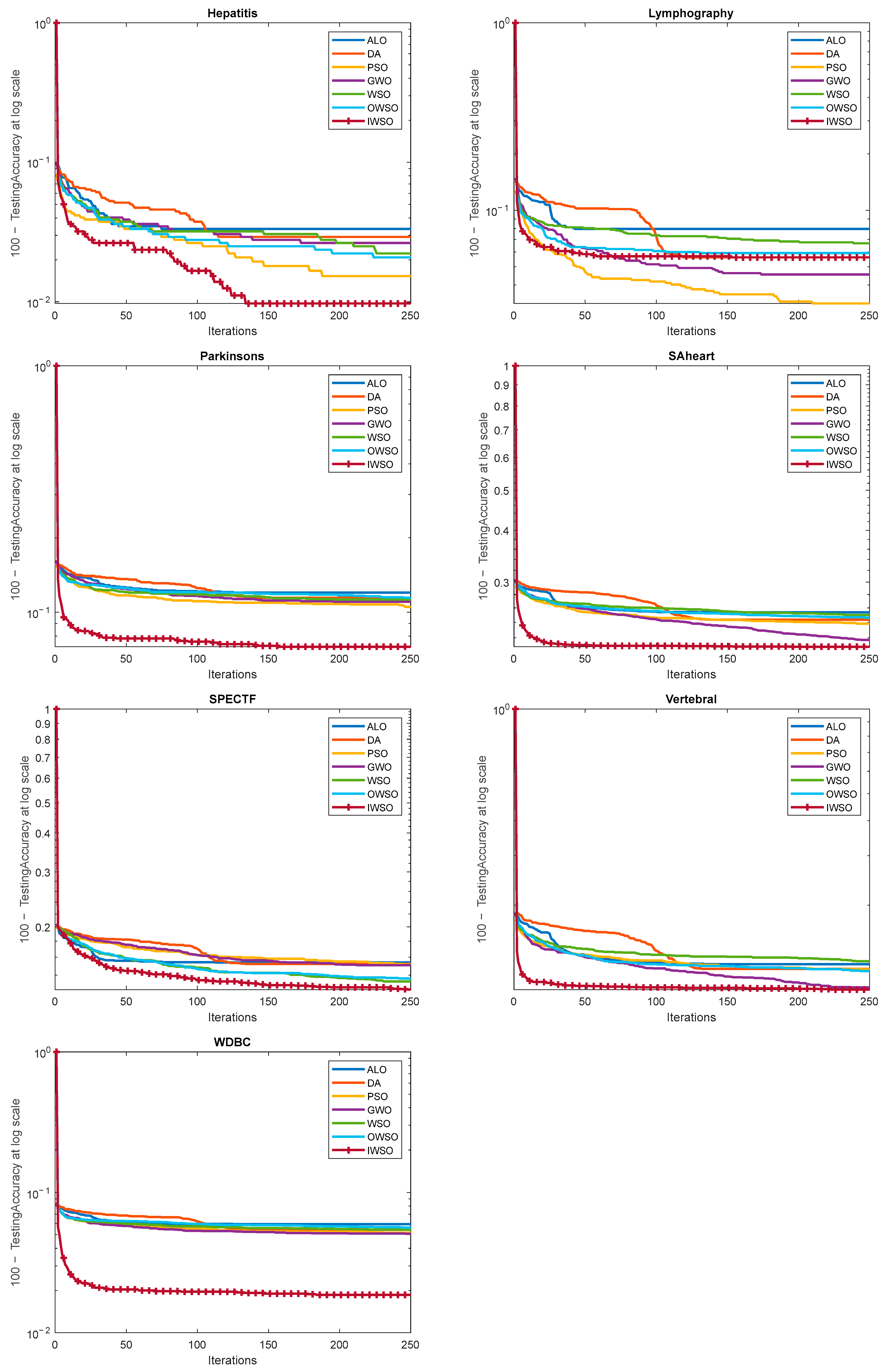
| No | Dataset | Features | Records | Classes | Ref. |
|---|---|---|---|---|---|
| 1 | Breast | 9 | 699 | 2 | [30] |
| 2 | Bupa | 5 | 345 | 2 | [31] |
| 3 | Dermatology | 34 | 366 | 6 | [32] |
| 4 | Diabetes | 9 | 768 | 2 | [33] |
| 5 | Hepatitis | 19 | 155 | 2 | [34] |
| 6 | Lymphography | 19 | 148 | 4 | [35] |
| 7 | Parkinsons | 22 | 197 | 2 | [36] |
| 8 | SAheart | 10 | 462 | 2 | [37] |
| 9 | SPECTF | 44 | 267 | 2 | [38] |
| 10 | Vertebral | 6 | 310 | 3 | [39] |
| 11 | WDBC | 30 | 569 | 2 | [40] |
| Dataset | WSO | OWSO | IWSO | |||
|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | |
| Breast | 98.42 | 0.76 | 98.56 | 0.79 | * 98.71 | 0.62 |
| Bupa | 78.93 | 3.60 | 78.67 | 3.34 | * 81.42 | 3.24 |
| Dermatology | 97.41 | 2.22 | * 99.66 | 0.52 | 99.60 | 0.59 |
| Diabetes | 74.67 | 1.82 | 79.52 | 3.28 | * 80.91 | 2.04 |
| Hepatitis | 97.78 | 2.62 | 97.92 | 2.38 | * 99.03 | 1.79 |
| Lymphography | 93.33 | 2.73 | 94.09 | 2.20 | * 94.39 | 2.51 |
| Parkinsons | 88.74 | 2.67 | 88.56 | 2.85 | * 92.76 | 1.72 |
| SAheart | 75.02 | 2.09 | 75.39 | 2.05 | * 79.06 | 2.60 |
| SPECTF | 86.63 | 2.83 | 86.33 | 2.27 | * 87.42 | 2.95 |
| Vertebral | 87.38 | 2.07 | 88.35 | 2.98 | * 90.00 | 2.04 |
| WDBC | 94.59 | 1.48 | 94.39 | 1.37 | * 98.14 | 1.05 |
| Overall Mean | 88.45 | 89.22 | * 91.04 | |||
| Overall Rank | 3 | 2 | 1 | |||
| Dataset | ALO | DA | PSO | GWO | IWSO | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| Breast | 97.35 | 0.97 | 98.25 | 0.83 | 98.64 | 0.76 | 98.53 | 0.86 | * 98.71 | 0.62 |
| Bupa | 78.83 | 3.70 | 79.87 | 3.10 | 79.00 | 3.45 | 81.26 | 3.82 | * 81.42 | 3.24 |
| Dermatology | 92.27 | 3.58 | 95.98 | 2.77 | 98.32 | 1.14 | 99.63 | 0.63 | * 99.60 | 0.59 |
| Diabetes | 75.28 | 2.33 | 75.83 | 1.99 | 75.26 | 1.72 | 78.38 | 3.04 | * 80.91 | 2.04 |
| Hepatitis | 96.67 | 2.98 | 97.08 | 2.71 | 98.47 | 2.04 | 97.36 | 2.56 | * 99.03 | 1.79 |
| Lymphography | 92.05 | 3.03 | 94.39 | 2.51 | * 96.82 | 2.28 | 95.45 | 3.16 | 94.39 | 2.51 |
| Parkinsons | 87.99 | 2.62 | 88.56 | 2.92 | 89.48 | 2.65 | 88.97 | 2.25 | * 92.76 | 1.72 |
| SAheart | 74.64 | 1.56 | 75.65 | 2.46 | 76.18 | 1.83 | 78.26 | 3.54 | * 79.06 | 2.60 |
| SPECTF | 84.63 | 2.75 | 84.79 | 1.89 | 84.83 | 1.79 | 84.92 | 2.95 | * 87.42 | 2.95 |
| Vertebral | 87.67 | 2.24 | 88.14 | 1.97 | 88.17 | 2.00 | 89.82 | 3.25 | * 90.00 | 2.04 |
| WDBC | 94.06 | 1.64 | 94.59 | 1.60 | 94.84 | 1.38 | 94.92 | 1.46 | * 98.14 | 1.05 |
| Overall Mean | 87.40 | 88.47 | 89.09 | 89.77 | * 91.04 | |||||
| Overall Rank | 5 | 4 | 3 | 2 | 1 | |||||
| IWSO vs. ALO | IWSO vs. DA | IWSO vs. PSO | IWSO vs. GWO | IWSO vs. WSO | IWSO vs. OWSO | |
|---|---|---|---|---|---|---|
| p value | 2.08 × 10−38 | 1.40 × 10−29 | 6.95 × 10−20 | 1.98 × 10−10 | 1.68 × 10−28 | 2.10 × 10−17 |
| h | + | + | + | + | + | + |
| Dataset | ALO | DA | PSO | GWO | WSO | OWSO | IWSO |
|---|---|---|---|---|---|---|---|
| Breast | 7 | 6 | 2 | 4 | 5 | 3 | * 1 |
| Bupa | 6 | 3 | 4 | 2 | 5 | 7 | * 1 |
| Dermatology | 7 | 6 | 4 | 2 | 5 | * 1 | 3 |
| Diabetes | 5 | 4 | 6 | 3 | 7 | 2 | * 1 |
| Hepatitis | 7 | 6 | 2 | 5 | 4 | 3 | * 1 |
| Lymphography | 7 | 3 | * 1 | 2 | 6 | 5 | 4 |
| Parkinsons | 7 | 6 | 2 | 3 | 4 | 5 | * 1 |
| SAheart | 7 | 4 | 3 | 2 | 6 | 5 | * 1 |
| SPECTF | 7 | 6 | 5 | 4 | 2 | 3 | * 1 |
| Vertebral | 6 | 5 | 4 | 2 | 7 | 3 | * 1 |
| WDBC | 7 | 4 | 3 | 2 | 5 | 6 | * 1 |
| Sum of ranks | 73 | 53 | 36 | 31 | 56 | 43 | 16 |
| Mean of ranks | 6.64 | 4.82 | 3.27 | 2.82 | 5.09 | 3.91 | 1.45 |
| Overall ranks | 7 | 5 | 3 | 2 | 6 | 4 | * 1 |
| Dataset | LightGBM | XGBoost | SVM | Neural Network (MLP) | CNN | IWSO |
|---|---|---|---|---|---|---|
| Breast | 96.72 | 96.26 | 97.02 | 95.45 | 96.08 | * 98.71 |
| Bupa | 68.88 | 68.46 | 68.37 | 68.27 | 68.11 | * 81.42 |
| Dermatology | 96.57 | 96.30 | 69.51 | 96.91 | 31.48 | * 99.60 |
| Diabetes | 74.29 | 73.19 | 75.09 | 67.95 | 66.67 | * 80.91 |
| Hepatitis | 87.64 | 85.97 | 83.33 | 79.58 | 80.14 | * 99.03 |
| Lymphography | 82.67 | 84.44 | 78.00 | 81.78 | 75.33 | * 94.39 |
| Parkinsons | 90.90 | 88.70 | 79.72 | 78.47 | 79.66 | * 92.76 |
| SAheart | 67.34 | 66.69 | 65.78 | 68.51 | 63.62 | * 79.06 |
| SPECTF | 78.72 | 79.96 | 79.14 | 77.45 | 78.68 | * 87.42 |
| Vertebral | 83.55 | 83.05 | 85.66 | 79.68 | 48.39 | * 90.00 |
| WDBC | 96.41 | 96.34 | 91.83 | 92.34 | 88.64 | * 98.14 |
| Mean of Acc. | 83.97 | 83.58 | 79.40 | 80.58 | 70.62 | * 91.04 |
| Rank | 2 | 3 | 5 | 4 | 6 | * 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydilek, İ.B.; Uslu, A.; Kına, C. Improved War Strategy Optimization with Extreme Learning Machine for Health Data Classification. Appl. Sci. 2025, 15, 5435. https://doi.org/10.3390/app15105435
Aydilek İB, Uslu A, Kına C. Improved War Strategy Optimization with Extreme Learning Machine for Health Data Classification. Applied Sciences. 2025; 15(10):5435. https://doi.org/10.3390/app15105435
Chicago/Turabian StyleAydilek, İbrahim Berkan, Arzu Uslu, and Cengiz Kına. 2025. "Improved War Strategy Optimization with Extreme Learning Machine for Health Data Classification" Applied Sciences 15, no. 10: 5435. https://doi.org/10.3390/app15105435
APA StyleAydilek, İ. B., Uslu, A., & Kına, C. (2025). Improved War Strategy Optimization with Extreme Learning Machine for Health Data Classification. Applied Sciences, 15(10), 5435. https://doi.org/10.3390/app15105435








