Complex Network Modeling and Analysis of Microfracture Activity in Rock Mechanics
Abstract
1. Introduction
2. Experimental Methods and Testing Procedures
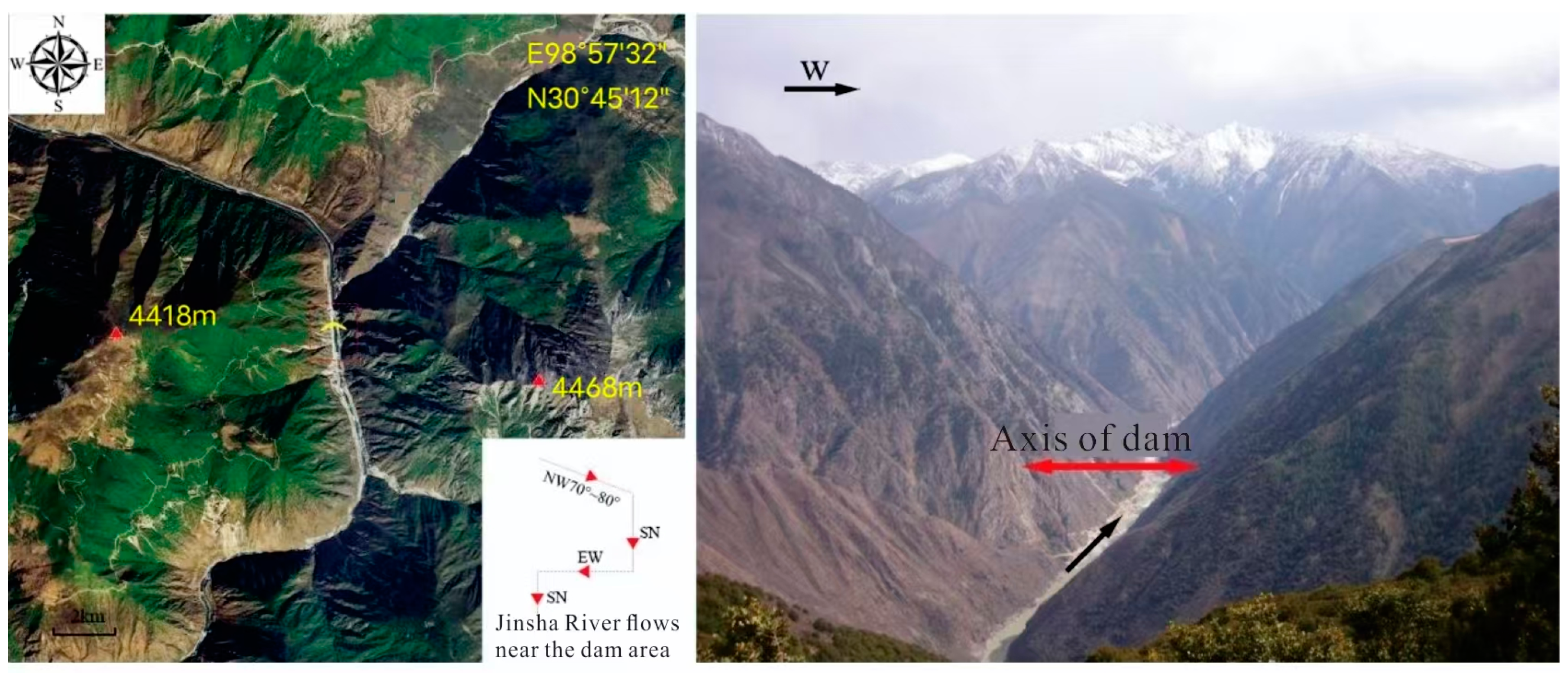
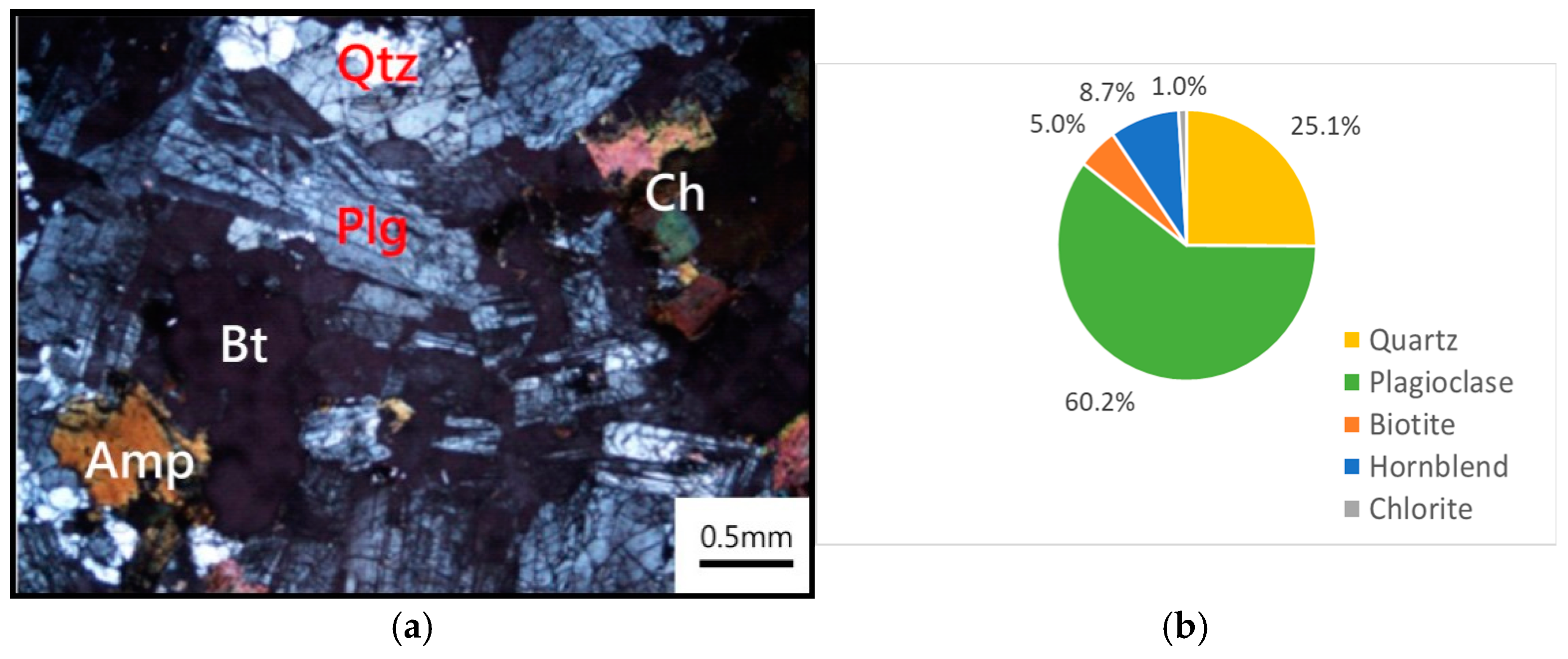
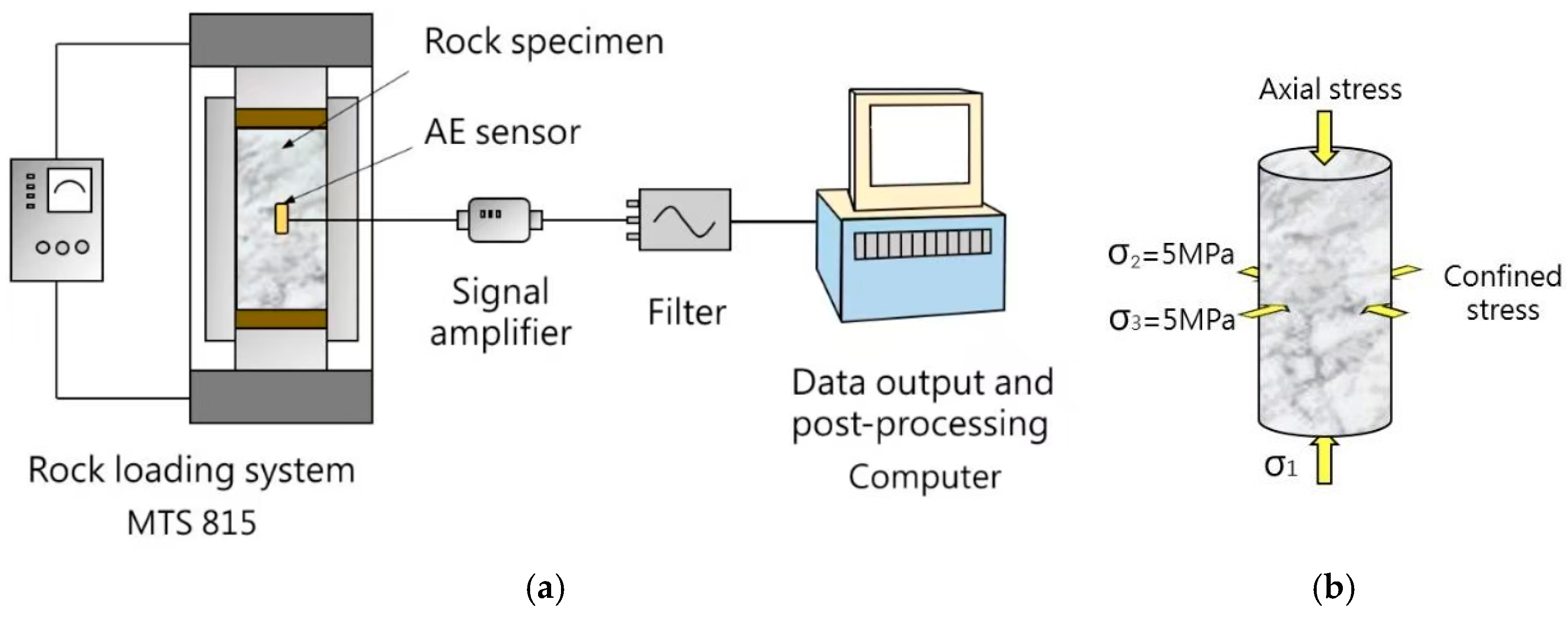
2.1. Samples and Test Equipment
2.2. Testing Program
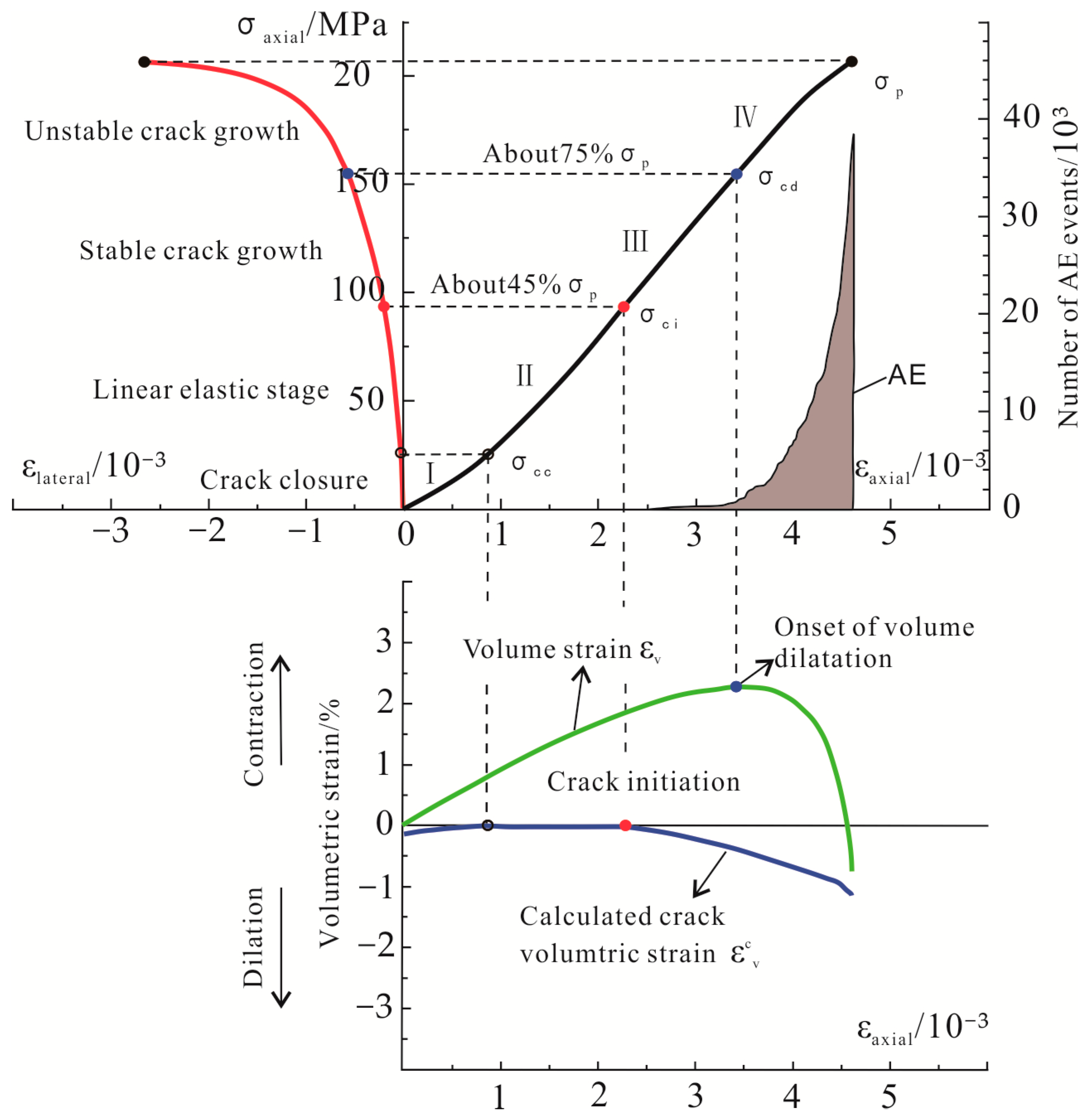
2.3. Test Results and Preliminary Analysis
3. Construction of the Rock Microfracture Network
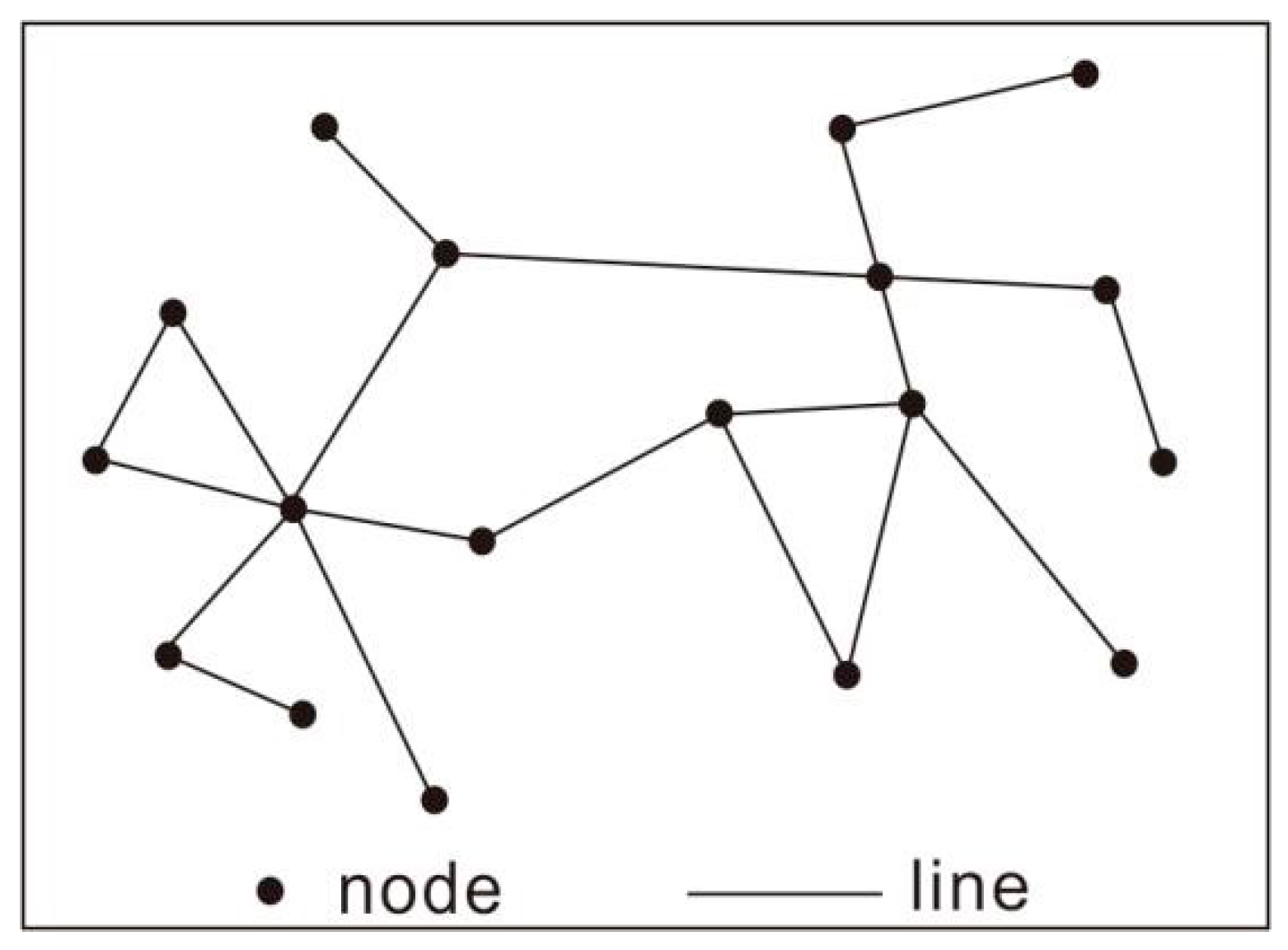
3.1. Introduction to Graph Theory and Complex Networks
3.2. Basic Parameters of Complex Networks
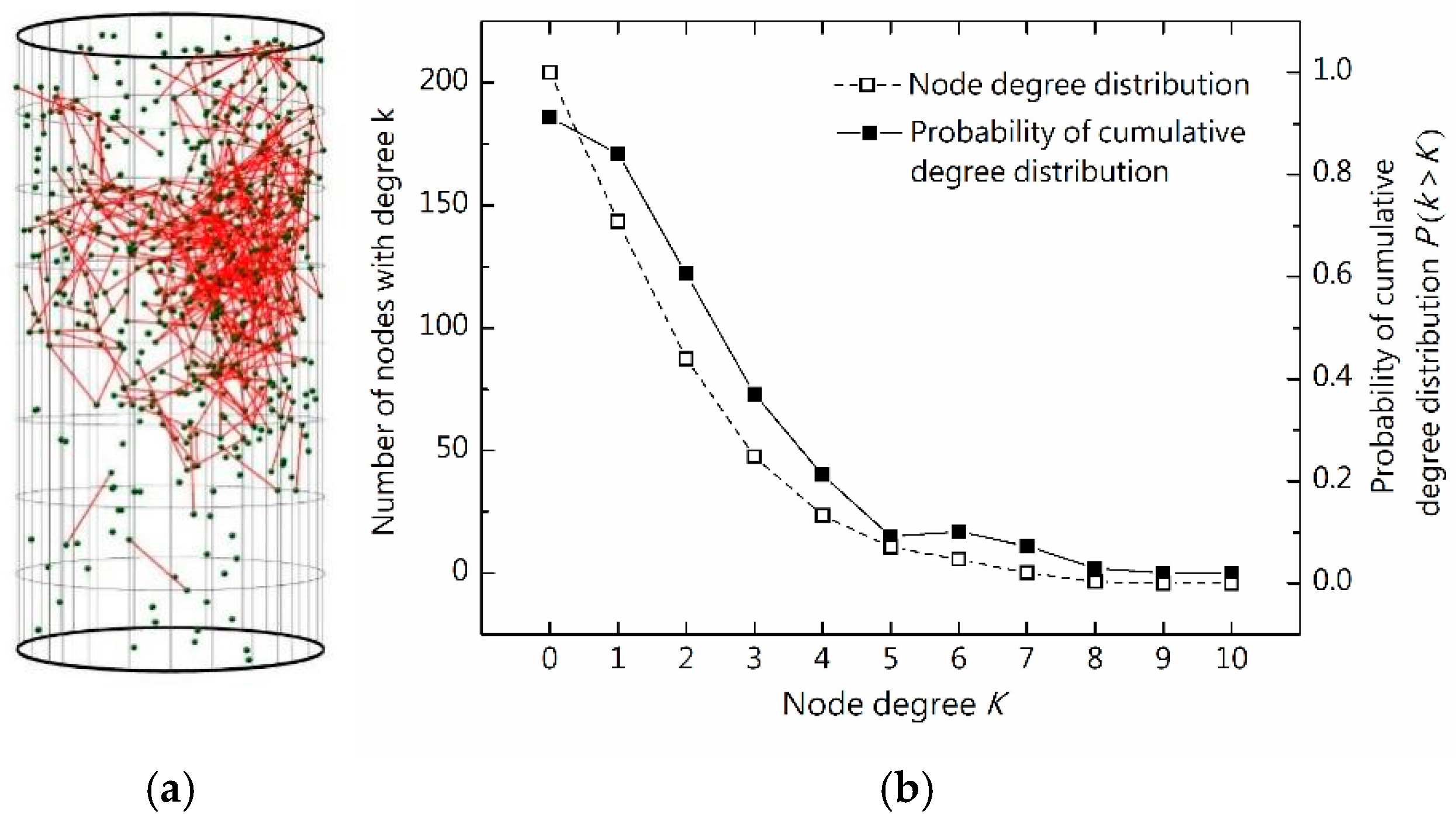
3.2.1. Degree and Degree Distributions
3.2.2. Shortest Path
3.2.3. Clustering Efficiency
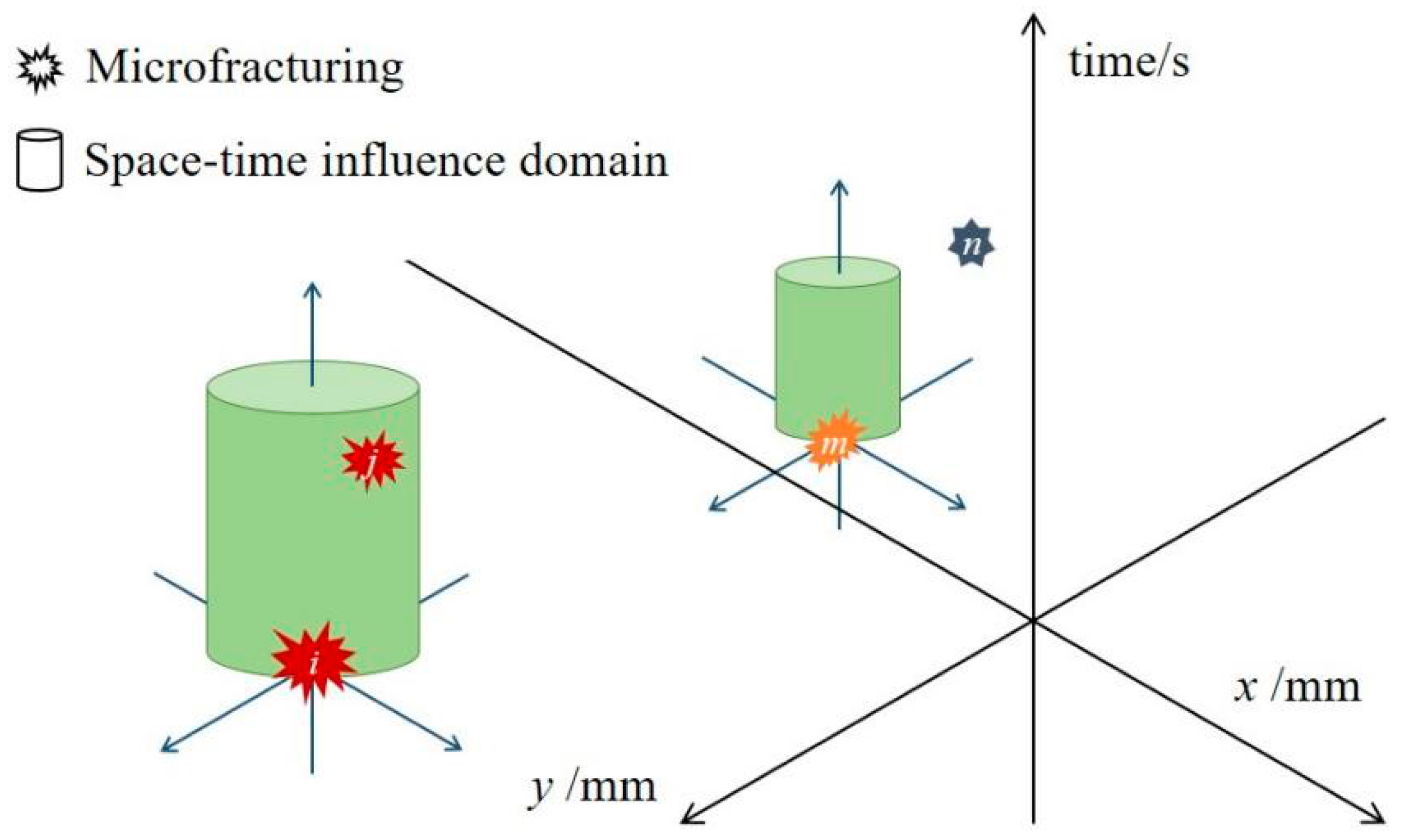
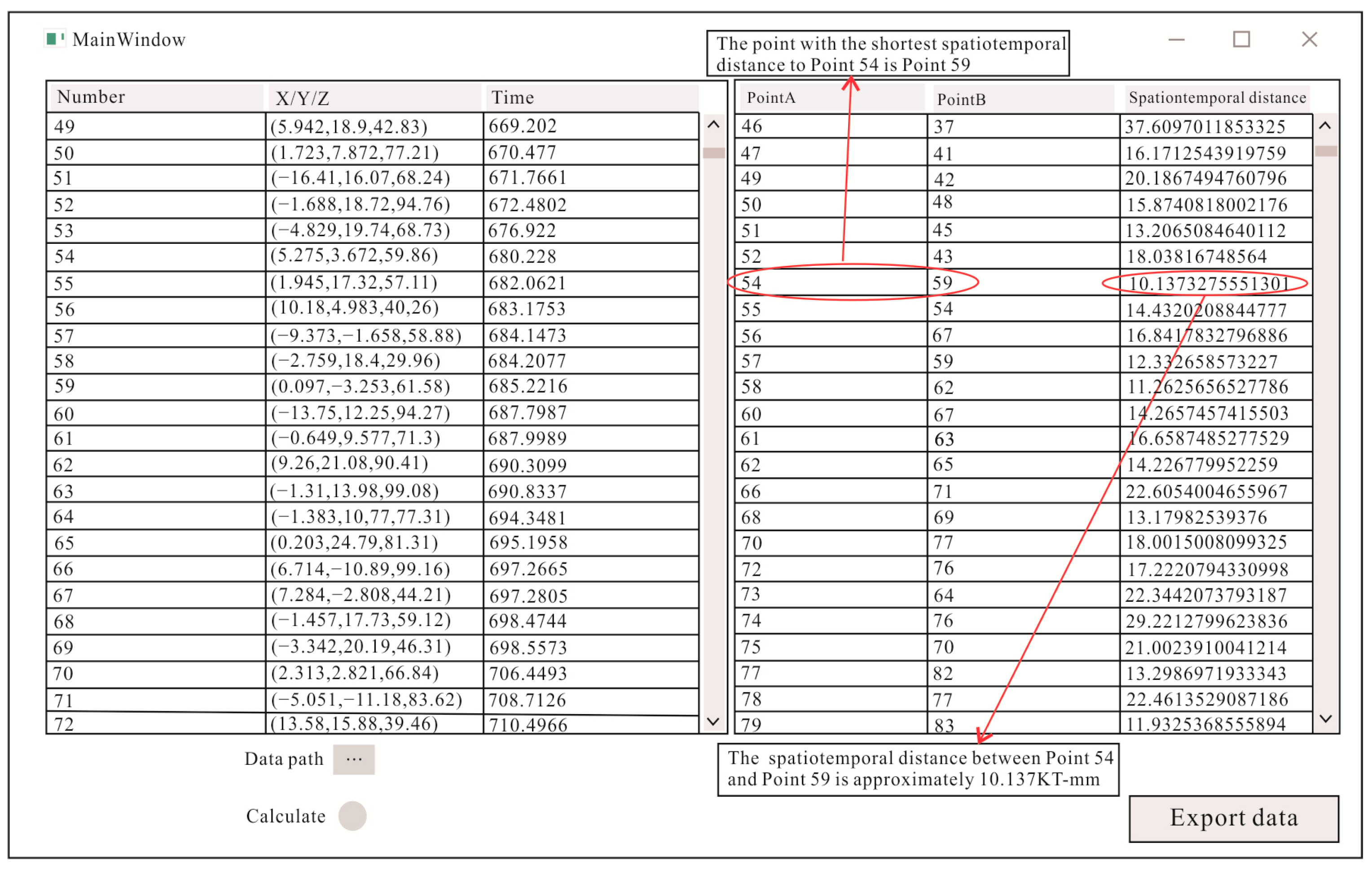
3.3. Space–Time Single-Link Cluster
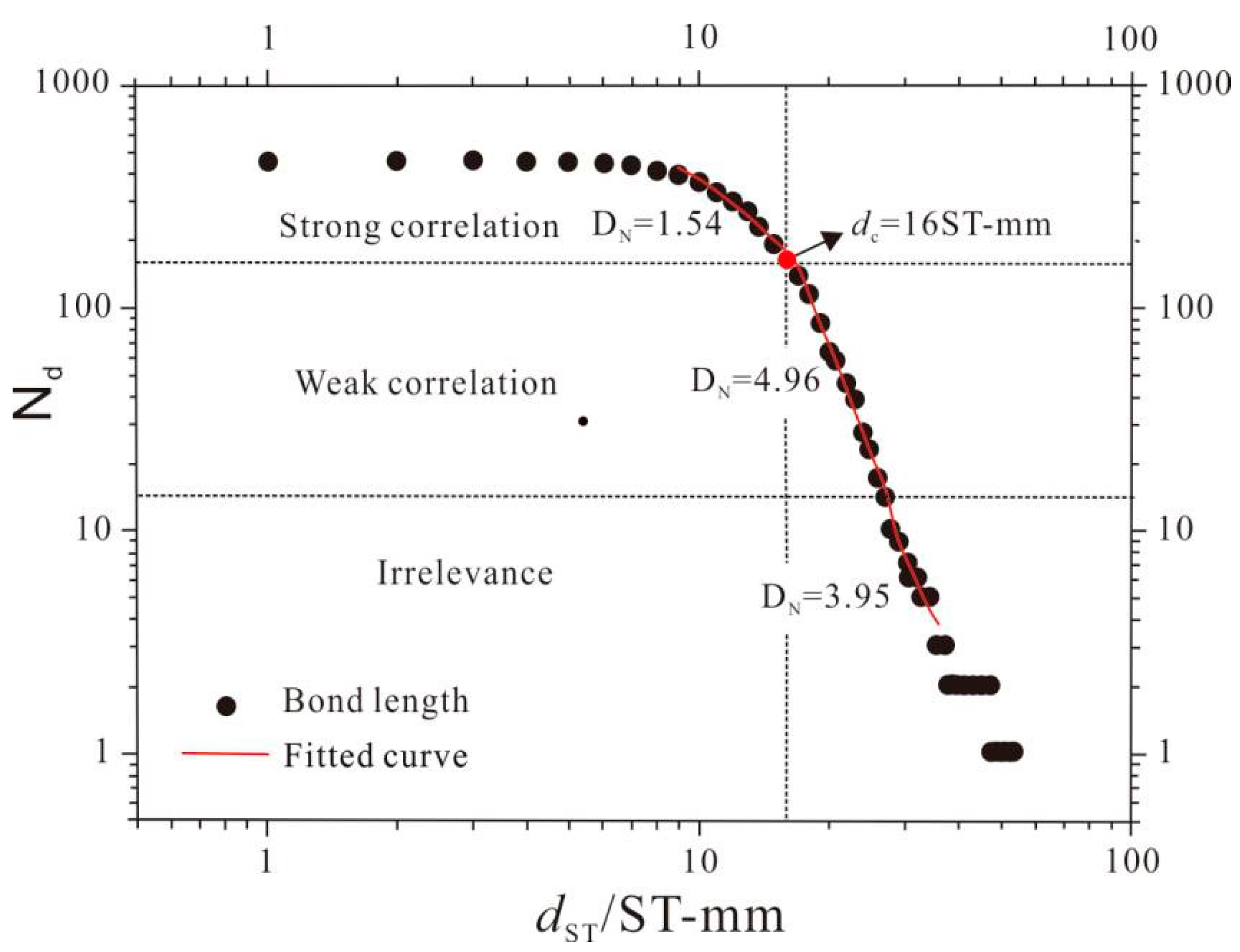
3.4. Solution of the Characteristic Bond Length dc
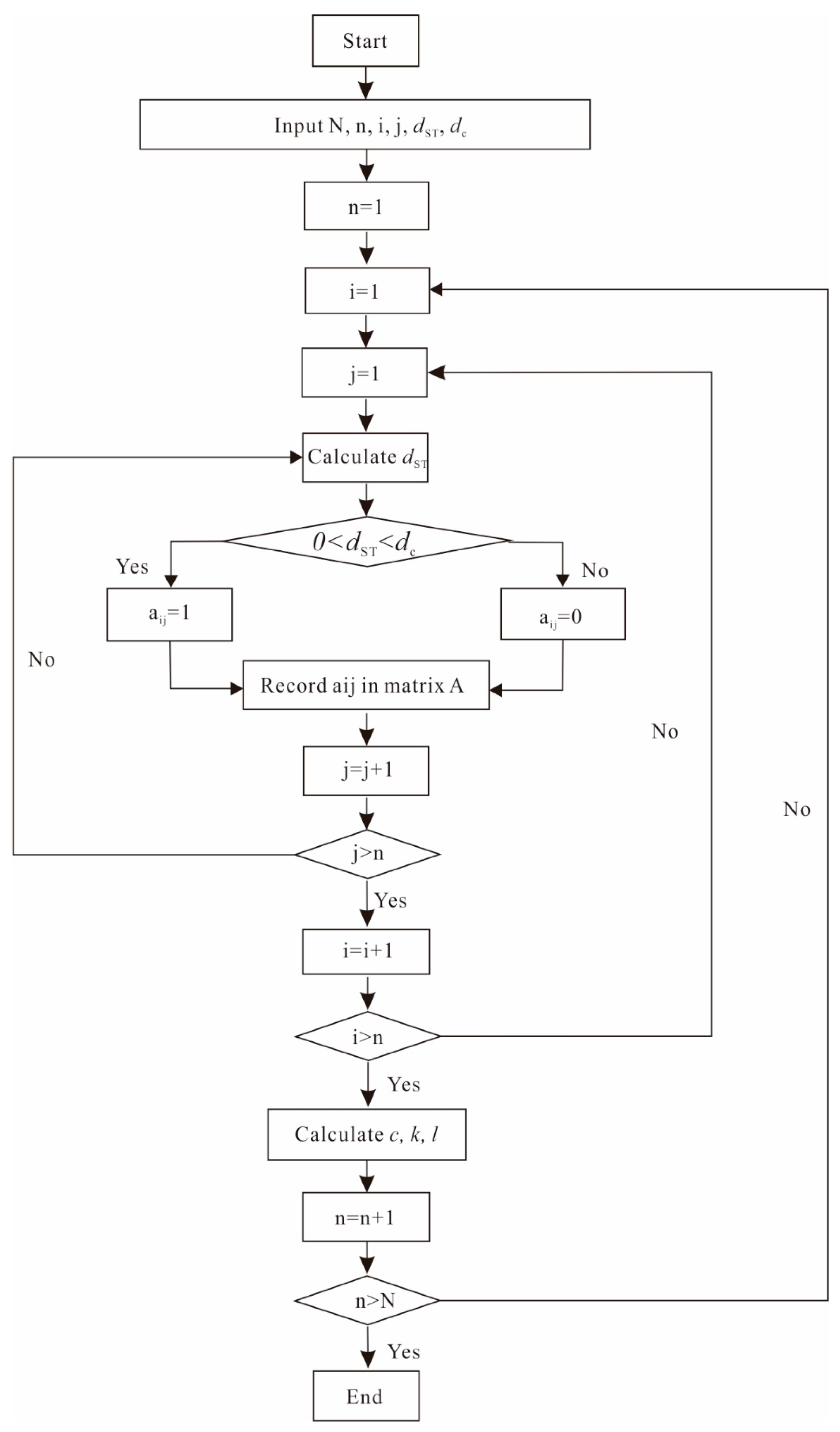
3.5. Construction Method of the Rock Microfracture Network
4. Results and Discussion
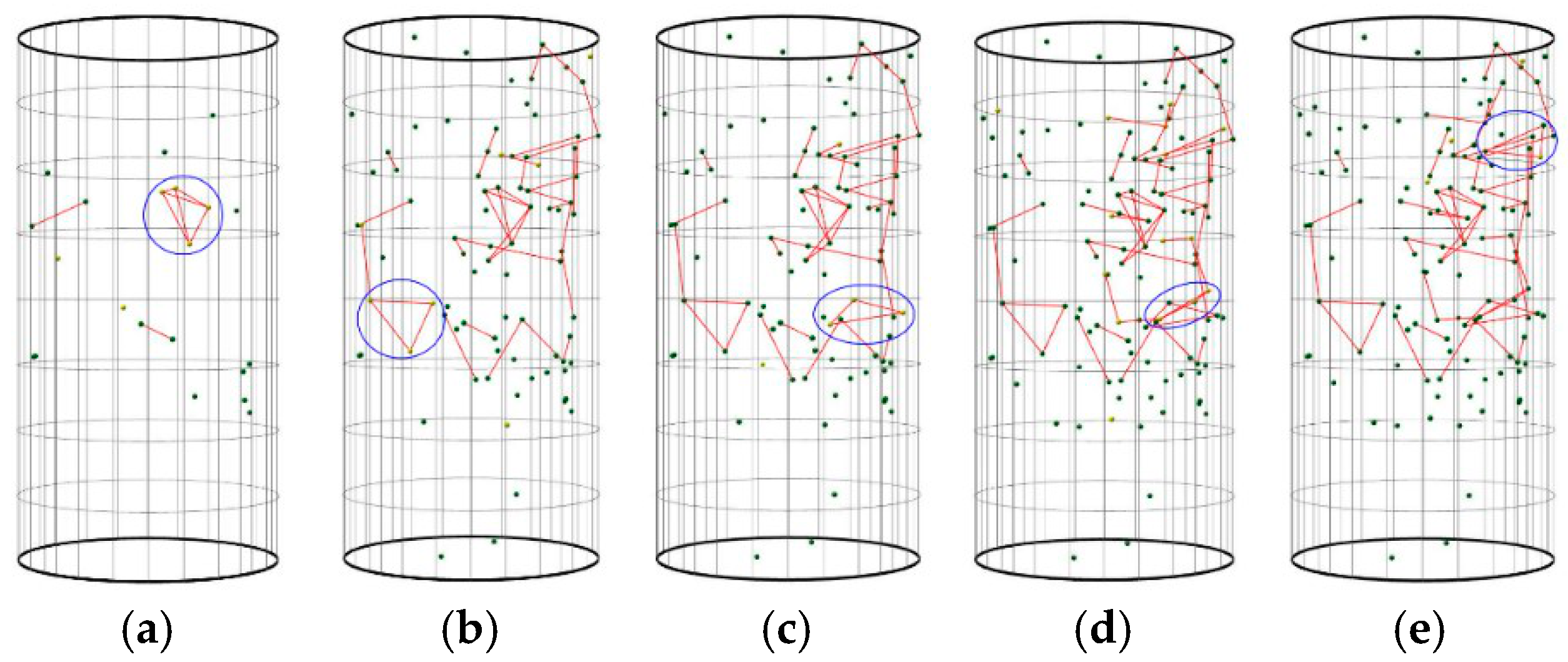
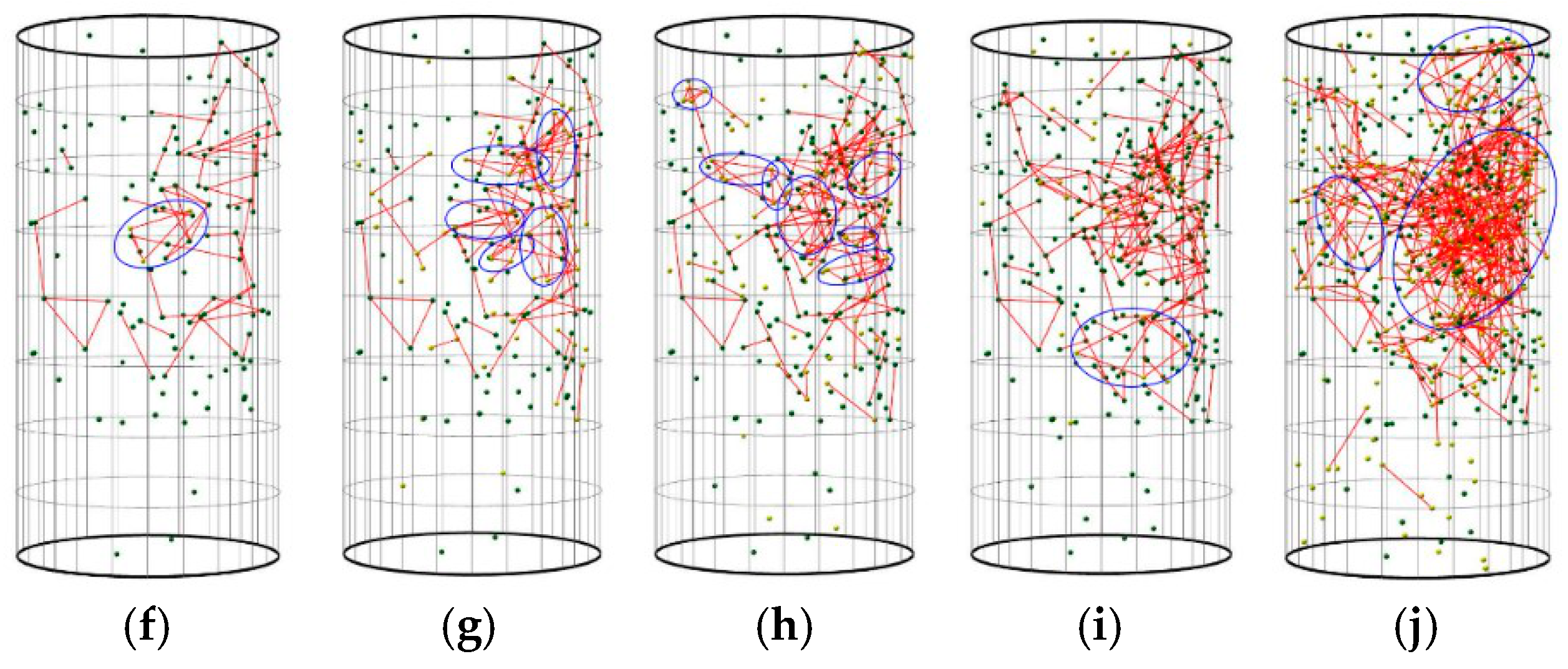
4.1. Characteristics of Rock Microfracture Networks
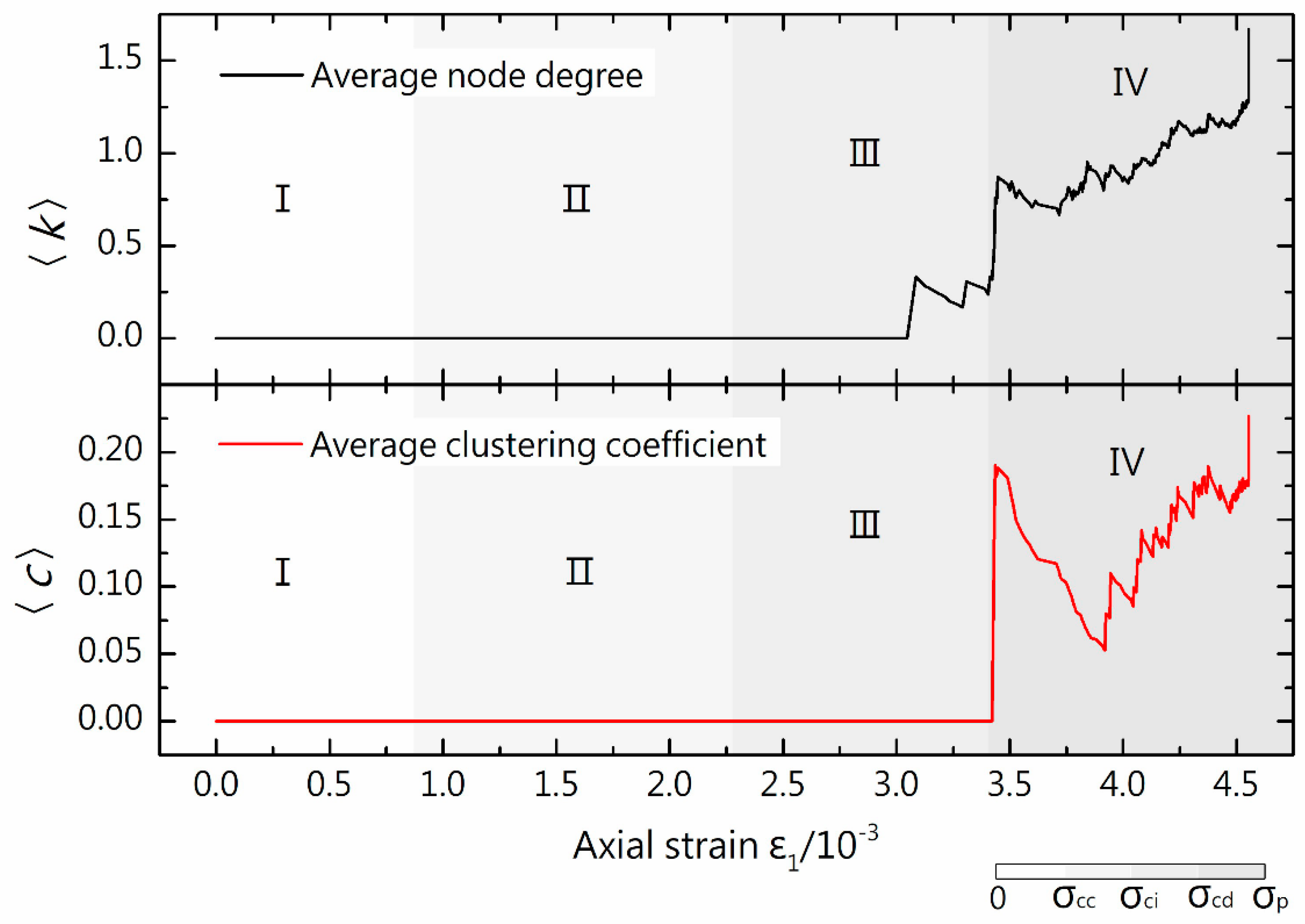
4.2. Dynamic Evolution Characteristics of the Rock Microfracture Network
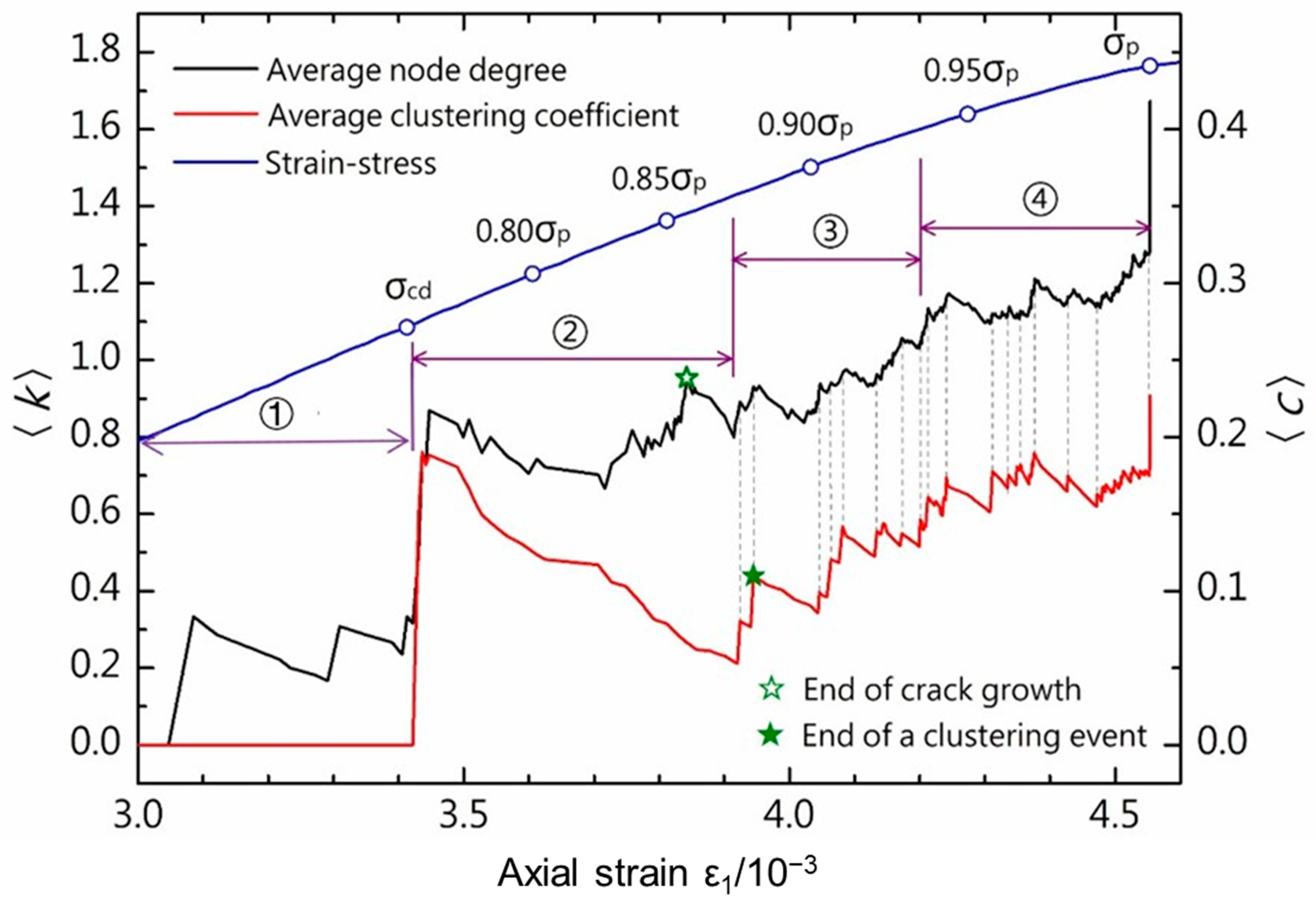
4.3. Analysis of Microfracture Activity
4.4. Limitations and Uncertainties
4.4.1. Limitations
4.4.2. Uncertainties
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Griffith, A.A. VI. The phenomena of rupture and flow in solids. Philosophical transactions of the royal society of London. Ser. A Contain. Pap. A Math. Or Phys. Character 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Part I—Theory of the fracture process. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1967, 4, 395–406. [Google Scholar] [CrossRef]
- Brace, W.F.; Paulding, B.W., Jr.; Scholz, C.H. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Hoek, E.; Bieniawski, Z.T. Brittle fracture propagation in rock under compression. Int. J. Fract. Mech. 1965, 1, 137–155. [Google Scholar] [CrossRef]
- Lajtai, E.Z. Brittle fracture in compression. Int. J. Fract. 1974, 10, 525–536. [Google Scholar] [CrossRef]
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Rudajev, V.; Vilhelm, J.; Lokajı́ček, T. Laboratory studies of acoustic emission prior to uniaxial compressive rock failure. Int. J. Rock Mech. Min. Sci. 2000, 37, 699–704. [Google Scholar] [CrossRef]
- Mogi, K. Magnitude-frequency relation for elastic shocks accompanying fractures of various materials and some related problems in earthquakes. Bull. Earthq. Res. Inst. 1962, 40, 831–853. [Google Scholar]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, Y.; Bi, S.; Ma, J.; Yan, Y.; Cao, H. Uncertainty investigation for the classification of rock micro-fracture types using acoustic emission parameters. Int. J. Rock Mech. Min. Sci. 2023, 162, 105292. [Google Scholar] [CrossRef]
- Lajtai, E.Z. Microscopic fracture processes in a granite. Rock Mech. Rock Eng. 1998, 31, 237–250. [Google Scholar] [CrossRef]
- Lei, X.; Kusunose, K.; Rao MV, M.S.; Nishizawa, O.; Satoh, T. Quasi-static fault growth and cracking in homogeneous brittle rock under triaxial compression using acoustic emission monitoring. J. Geophys. Res. Solid Earth 2000, 105, 6127–6139. [Google Scholar] [CrossRef]
- Lei, X.L.; Kusunose, K.; Nishizawa, O.; Cho, A.; Satoh, T. On the spatio-temporal distribution of acoustic emissions in two granitic rocks under triaxial compression: The role of pre-existing cracks. Geophys. Res. Lett. 2000, 27, 1997–2000. [Google Scholar] [CrossRef]
- Lockner, D.; Byerlee, J.D.; Kuksenko, V.; Ponomarev, A.; Sidorin, A. Quasi-static fault growth and shear fracture energy in granite. Nature 1991, 350, 39–42. [Google Scholar] [CrossRef]
- Cai, M.; Morioka, H.; Kaiser, P.K.; Tasaka, Y.; Kurose, H.; Minami, M.; Maejima, T. Back-analysis of rock mass strength parameters using AE monitoring data. Int. J. Rock Mech. Min. Sci. 2007, 44, 538–549. [Google Scholar] [CrossRef]
- Gong, H.; Wang, G.; Luo, Y.; Li, X.; Liu, T.; Song, L.; Wang, X. Shear fracture behaviors and acoustic emission characteristics of granite with discontinuous joints under combinations of normal static loads and dynamic disturbances. Theor. Appl. Fract. Mech. 2023, 125, 103923. [Google Scholar] [CrossRef]
- Li, G.G. Analysis of seismic activity network characteristics based on K-kernel analysis. Acta Seismol. Sin. 2015, 37, 239–248. [Google Scholar]
- Xie, N.; Tang, H.M.; Yang, J.B.; Jiang, Q.H. Damage evolution in dry and saturated brittle sandstone revealed by acoustic characterization under uniaxial compression. Rock Mech. Rock Eng. 2022, 55, 1303–1324. [Google Scholar] [CrossRef]
- Zeng, P.; Ji, H.; Sun, L.; Zhang, Z.; Gao, Y.; Jiang, H.; Li, C. Experimental study on irreversibility of acoustic emission of rocks under different confining pressures its characteristics before main fracture. Chin. J. Mech. Eng. 2016, 35, 1333–1340. [Google Scholar]
- Zhai, M.; Xu, C.; Xue, L.; Cui, Y.; Dong, J. Loading rate dependence of staged damage behaviors of granite under uniaxial compression: Insights from acoustic emission characteristics. Theor. Appl. Fract. Mech. 2022, 122, 103633. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Wang, W.X.; Wang, B.H.; Yin, C.Y.; Xie, Y.B.; Zhou, T. Traffic dynamics based on local routing protocol on a scale-free network. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2006, 73, 026111. [Google Scholar] [CrossRef]
- Bassett, D.S.; Bullmore, E.D. Small-world brain networks. Neurosci. 2006, 12, 512–523. [Google Scholar] [CrossRef]
- Newman, M.E. Fast algorithm for detecting community structure in networks. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2004, 69, 066133. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Dynamical evolution of the community structure of complex earthquake network. Europhys. Lett. 2012, 99, 39001. [Google Scholar] [CrossRef]
- Chorozoglou, D.; Papadimitriou, E.; Kugiumtzis, D. Investigating small-world and scale-free structure of earthquake networks in Greece. Chaos Solitons Fractals 2019, 122, 143–152. [Google Scholar] [CrossRef]
- He, X.; Zhao, H.; Cai, W.; Liu, Z.; Si, S.Z. Earthquake networks based on space–time influence domain. Phys. A Stat. Mech. Its Appl. 2014, 407, 175–184. [Google Scholar] [CrossRef]
- Bao, H.; Wu, Y. Application of complex network theory to simulate microfracture propagation in rocks. Int. J. Rock Mech. Min. Sci. 2010, 47, 456–464. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Zhang, B. Analysis of fracturing network evolution behaviors in random naturally fractured rock blocks. Rock Mech. Rock Eng. 2016, 49, 4339–4347. [Google Scholar] [CrossRef]
- Zhang, A.; Xie, H.; Zhang, R.; Ren, L.; Zhou, J.; Gao, M.; Tan, Q. Dynamic failure behavior of Jinping marble under various preloading conditions corresponding to different depths. Int. J. Rock Mech. Min. Sci. 2021, 148, 104959. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Gao, F.; Wang, X. Numerical study of fracture network evolution during nitrogen fracturing processes in shale reservoirs. Energies 2018, 11, 2503. [Google Scholar] [CrossRef]
- Yan, G.; Zhang, F.; Ku, T.; Hao, Q.; Peng, J. Experimental study and mechanism analysis on the effects of biaxial in-situ stress on hard rock blasting. Rock Mech. Rock Eng. 2023, 56, 3709–3723. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Li, X. Failure characteristics of rock samples with prefabricated cracks under dynamic and static loads. Int. J. Rock Mech. Min. Sci. 2022, 146, 105188. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, G.; Gao, F.; Ye, D.; Luo, J. A complex network model for analysis of fractured rock permeability. Adv. Civ. Eng. 2020, 2020, 8824082. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Y.; Li, X. Preliminary study on dynamic mechanical properties and energy dissipation laws of 3D printed cracked rocks. Int. J. Rock Mech. Min. Sci. 2022, 151, 105205. [Google Scholar] [CrossRef]
- DL/T5368-2007; Code for Rock Tests of Hydroelectric and Water Conservancy Engineering. China Electric Power Press: Beijing, China, 2007.
- GBT50266-2013; Standard for Test Methods of Engineering Rock Mass. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2013.
- Gardner, J.K.; Knopoff, L. Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian? Bull. Seismol. Soc. Am. 1974, 64, 1363–1367. [Google Scholar] [CrossRef]
- Frohlich, C.; Davis, S.D. Single-link cluster analysis as a method to evaluate spatial and temporal properties of earthquake catalogues. Geophys. J. Int. 1990, 100, 19–32. [Google Scholar] [CrossRef]
- Biegel, R.L.; Sammis, C.G.; Dieterich, J.H. The frictional properties of a simulated gouge having a fractal particle distribution. J. Struct. Geol. 1989, 11, 827–846. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]




| (n) | x | y | z | Time |
|---|---|---|---|---|
| i | xi | yi | zi | ti |
| j | xj | yj | zj | tj |
| … | … | … | … | … |
| Network Graph (2 Nodes) | Notations | Evolved Network Graph (3 Nodes) | Notations |
|---|---|---|---|
 | <k> = 0, <c> = 0 |  | <k> = 0, <c> = 0 |
 | <k> = 0.67, <c> = 0 | ||
 | <k> = 1.33, <c> = 0 | ||
 | <k> = 1, <c> = 0 |  | <k> = 0.67, <c> = 0 |
 | <k> = 1.33, <c> = 0 | ||
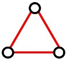 | <k> = 2, <c> = 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhao, Q.; Xiang, J.; Peng, Y. Complex Network Modeling and Analysis of Microfracture Activity in Rock Mechanics. Appl. Sci. 2025, 15, 5242. https://doi.org/10.3390/app15105242
Chen Y, Zhao Q, Xiang J, Peng Y. Complex Network Modeling and Analysis of Microfracture Activity in Rock Mechanics. Applied Sciences. 2025; 15(10):5242. https://doi.org/10.3390/app15105242
Chicago/Turabian StyleChen, Yushu, Qihua Zhao, Jindong Xiang, and Yi Peng. 2025. "Complex Network Modeling and Analysis of Microfracture Activity in Rock Mechanics" Applied Sciences 15, no. 10: 5242. https://doi.org/10.3390/app15105242
APA StyleChen, Y., Zhao, Q., Xiang, J., & Peng, Y. (2025). Complex Network Modeling and Analysis of Microfracture Activity in Rock Mechanics. Applied Sciences, 15(10), 5242. https://doi.org/10.3390/app15105242






