Proximity-Based Adaptive Indoor Positioning Method Using Received Signal Strength Indicator
Abstract
1. Introduction
- This paper calculates the optimal threshold, which is an evaluation standard for identifying proximity to a specific AP in the PAP algorithm, through quantitative measurements. By applying an optimal threshold to the PAP algorithm, indoor positioning accuracy is improved in regions with weak signals.
- To reduce RSSI-based distance estimation errors, this paper finds the relationship between RSSI and distance from data collected in various environments with and without obstacles to signal reception and optimizes the parameters of LDPLM.
- In this paper, we quantitatively evaluate signal filters to correct unstable RSSI and increase the accuracy of location estimation and design an effective filtering algorithm to improve indoor positioning accuracy.
2. Related Works
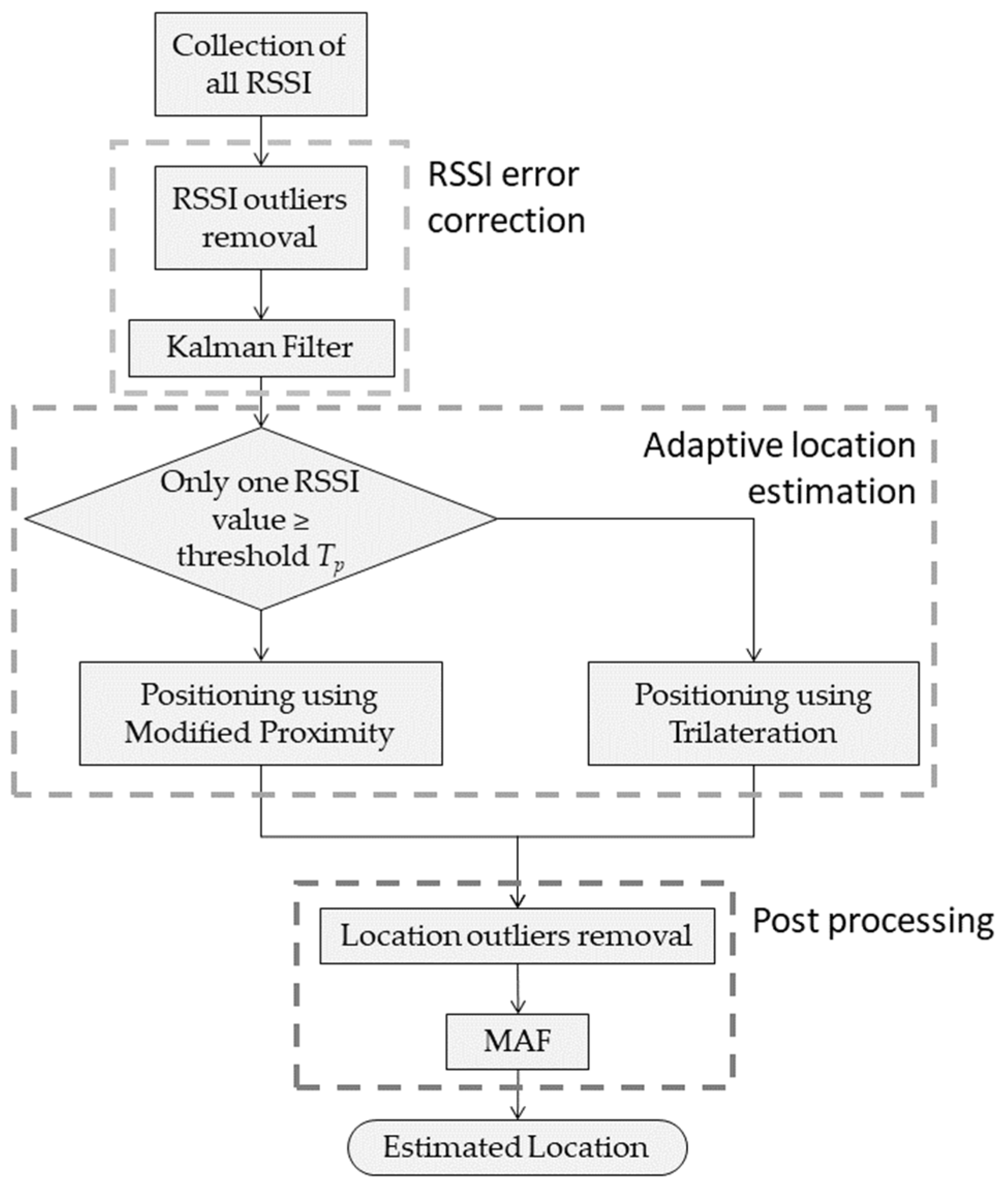
3. Proposed Indoor Positioning Method
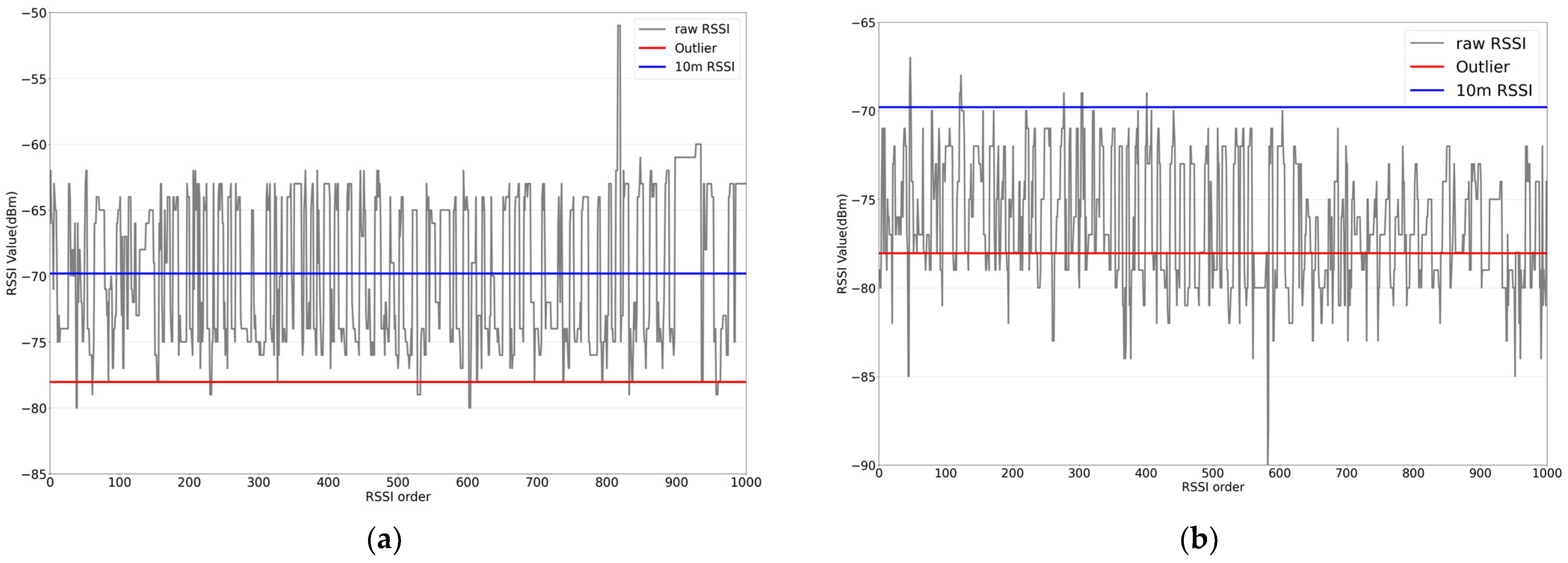
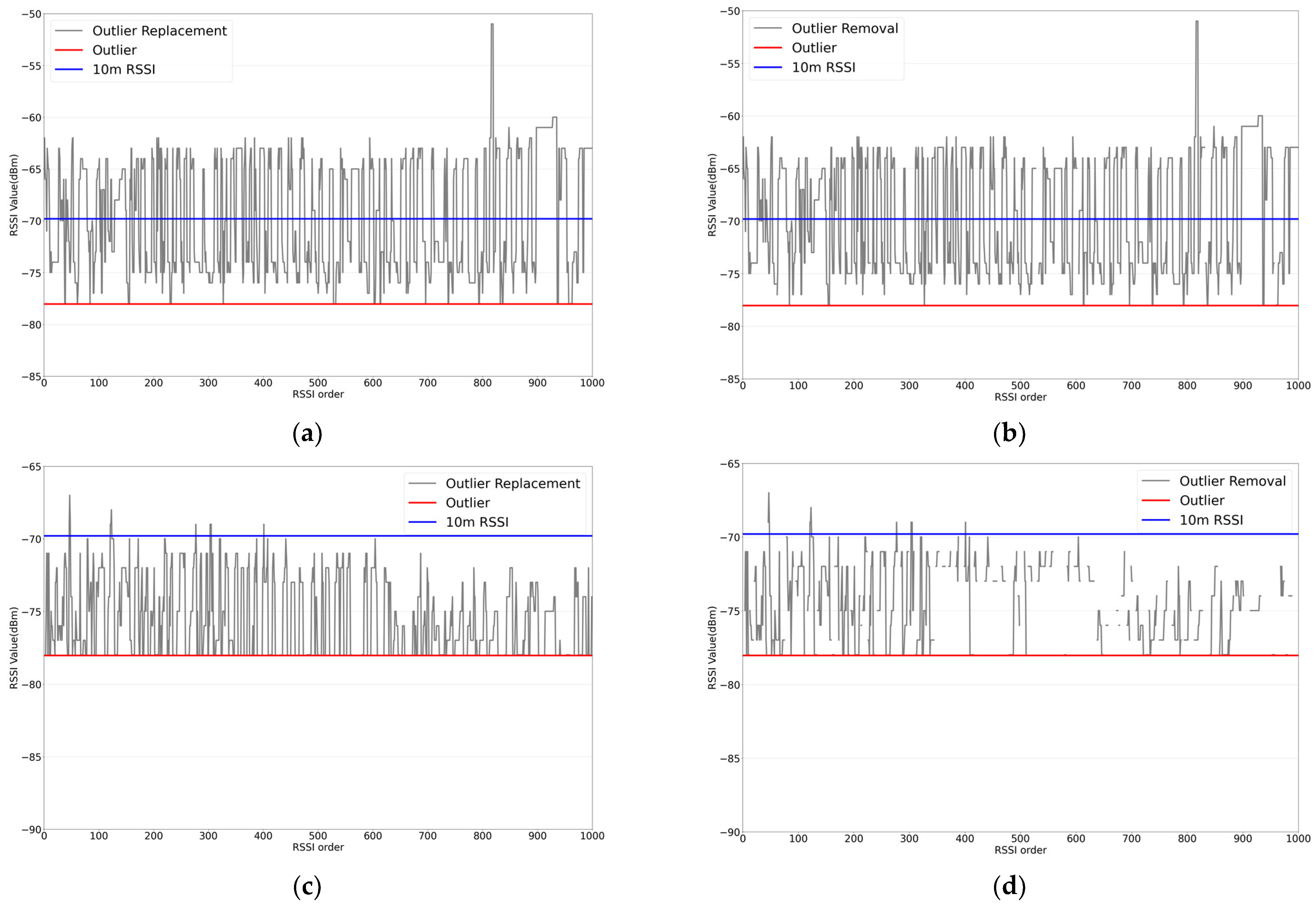
3.1. RSSI Error Correction
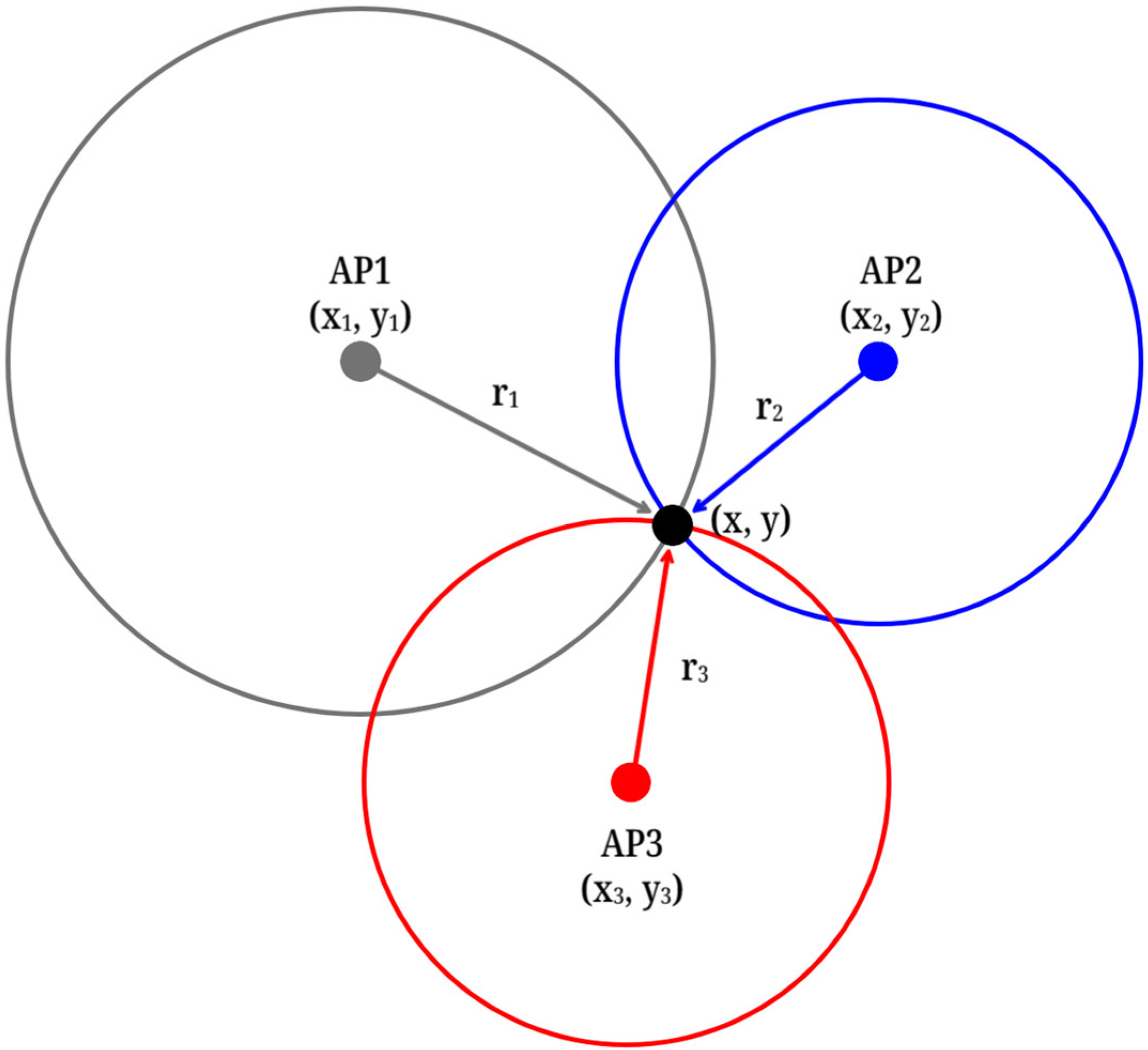
3.2. Adaptive Location Estimation
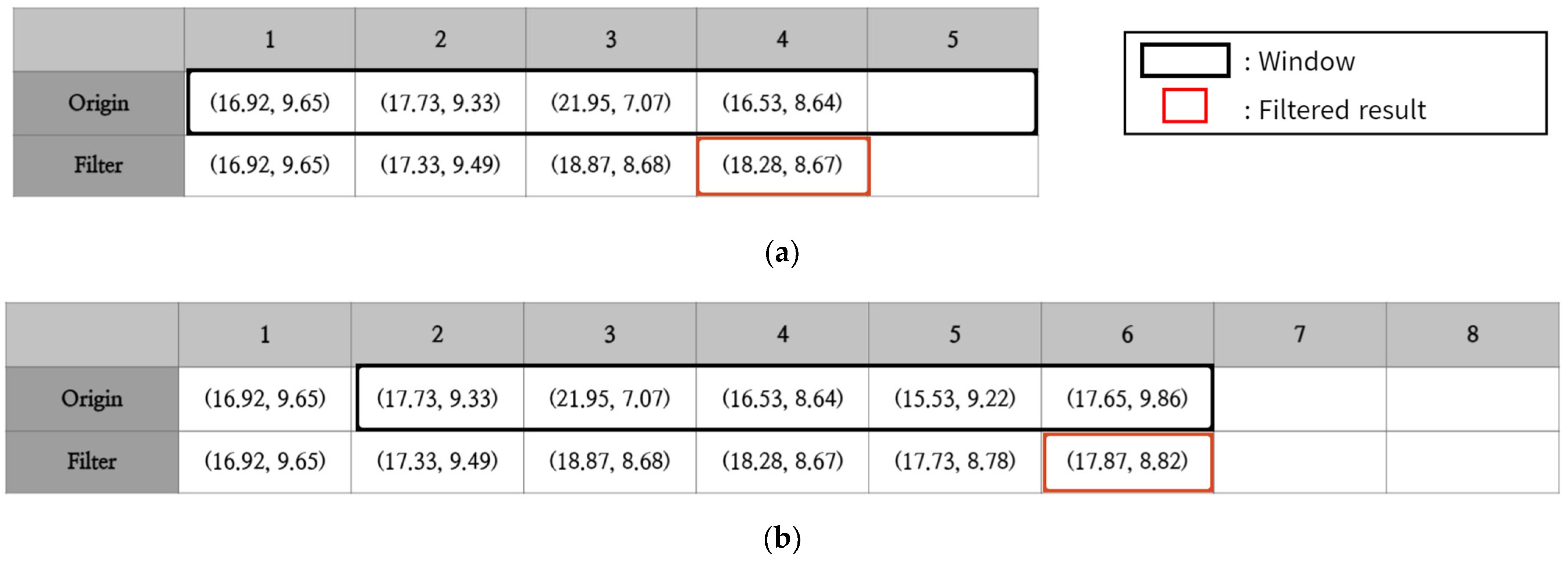
3.3. Post-Processing
4. Experimental Results
4.1. Determining the Optimal Parameters of the Log-Distance Path Loss Model
4.2. Determining the Optimal Parameters of a Kalman Filter
4.3. Experiment with Proximity-Based Adaptive Algorithm
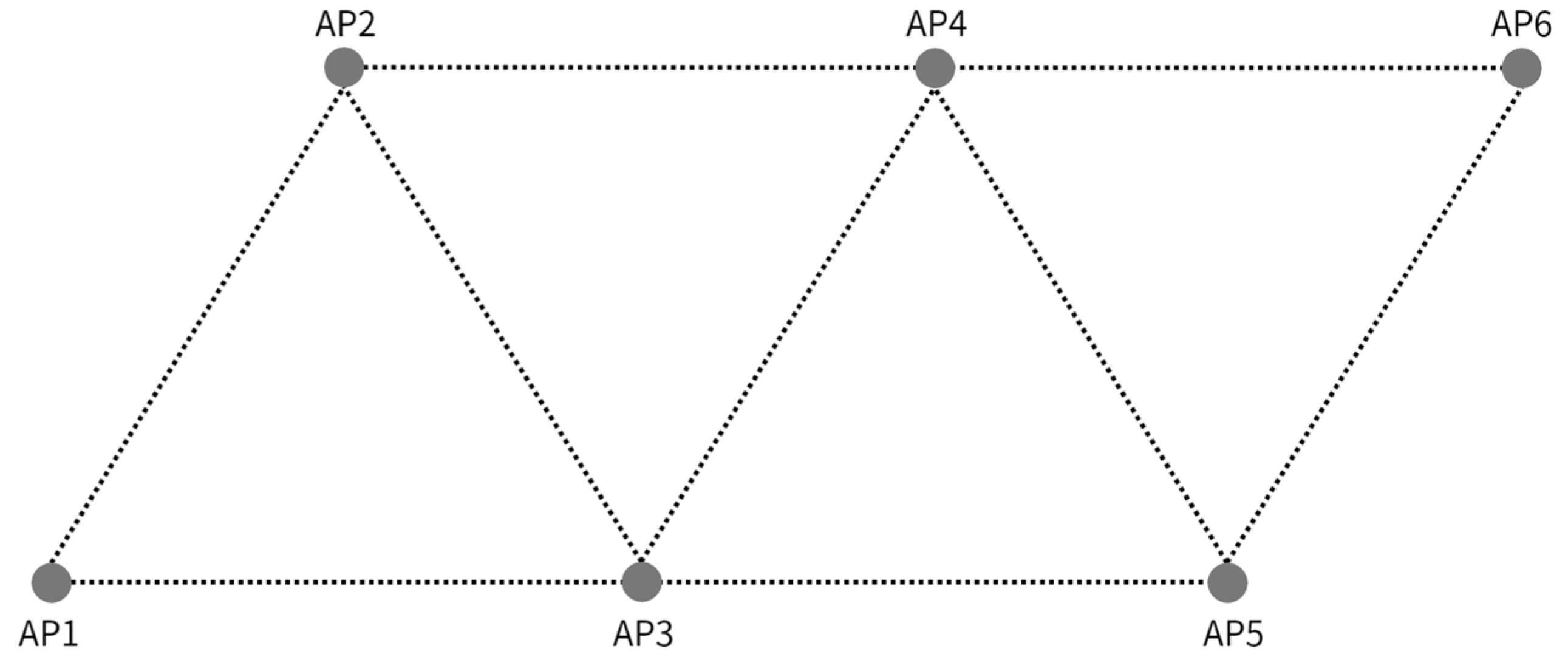
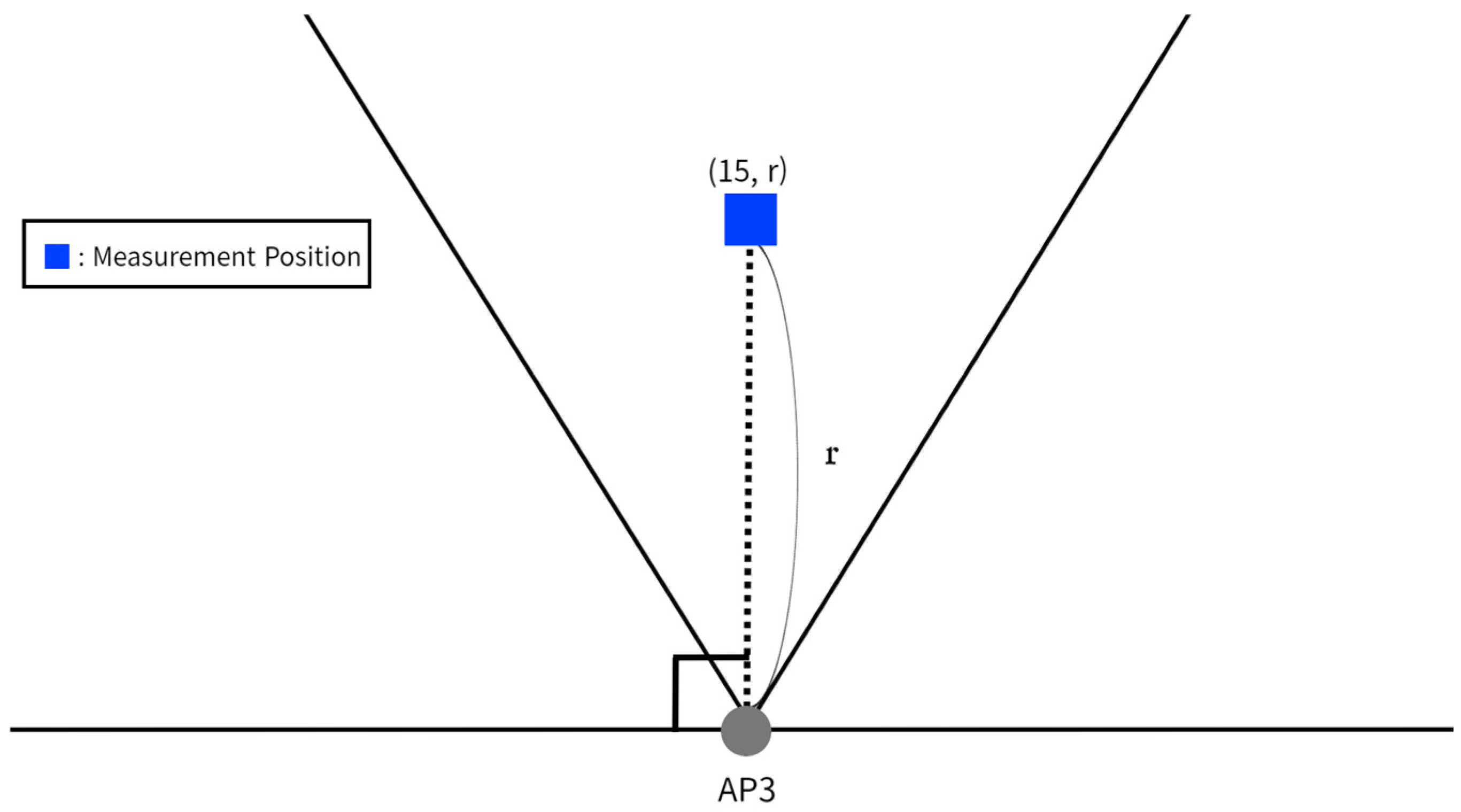
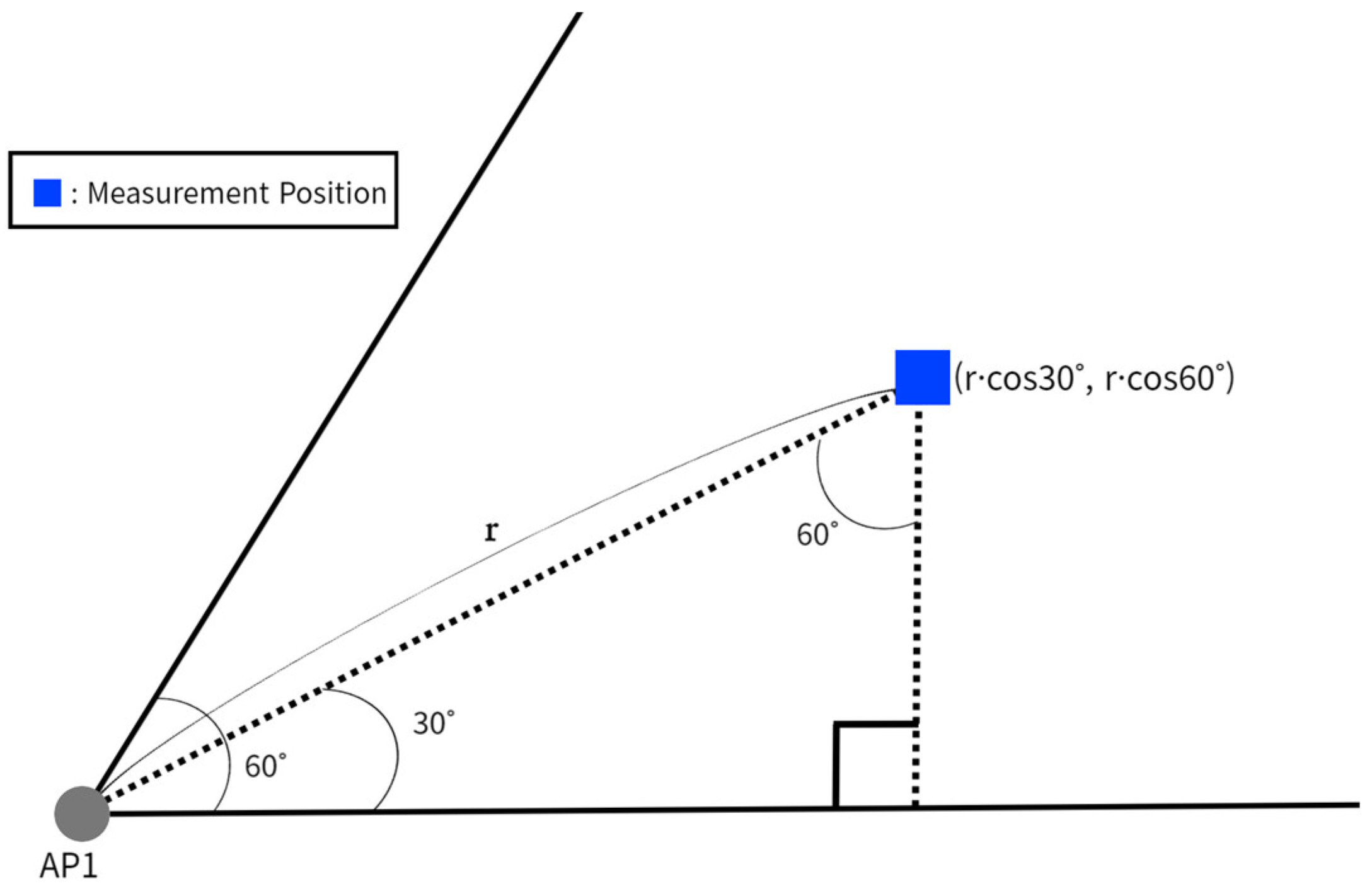
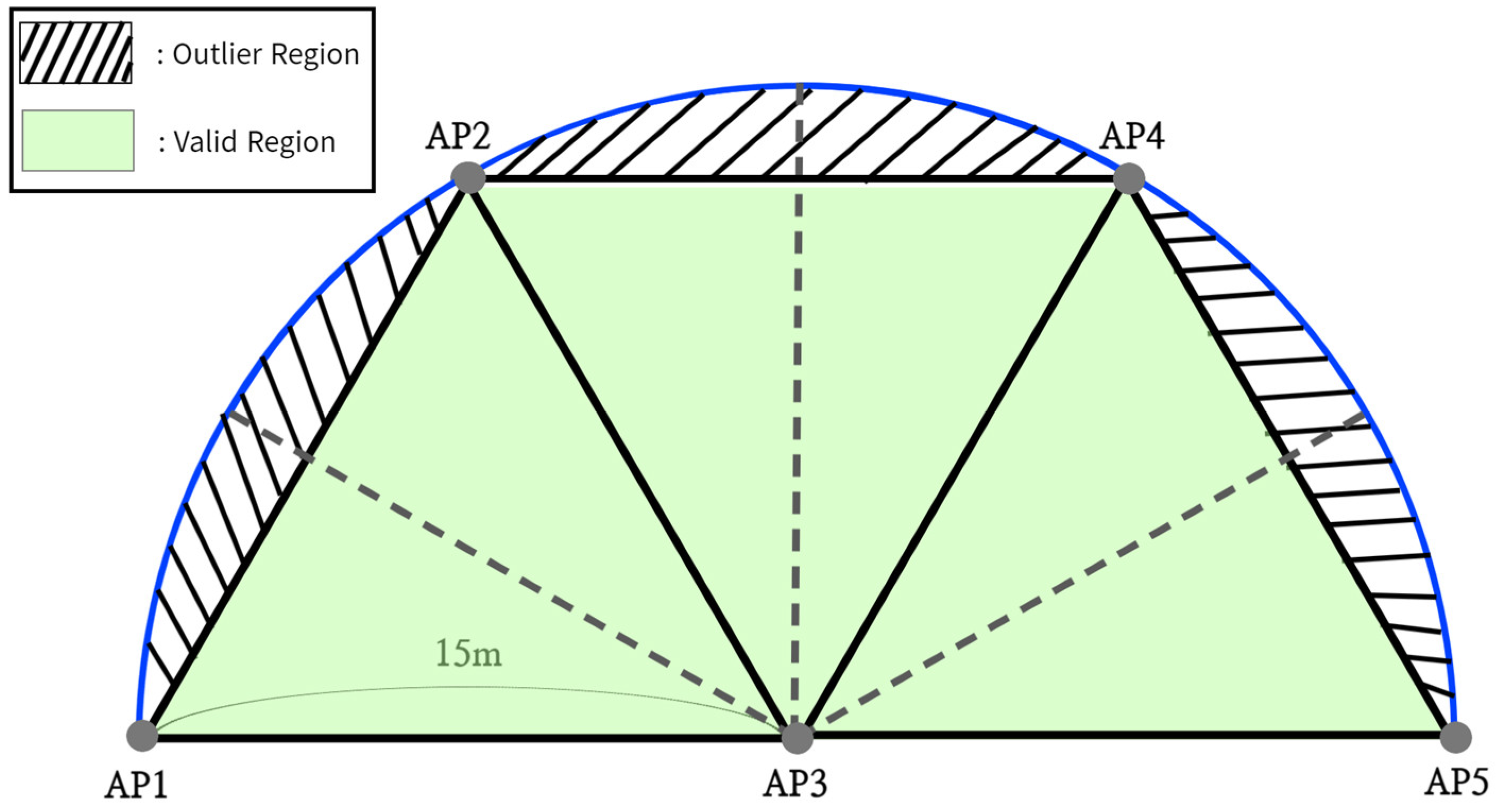
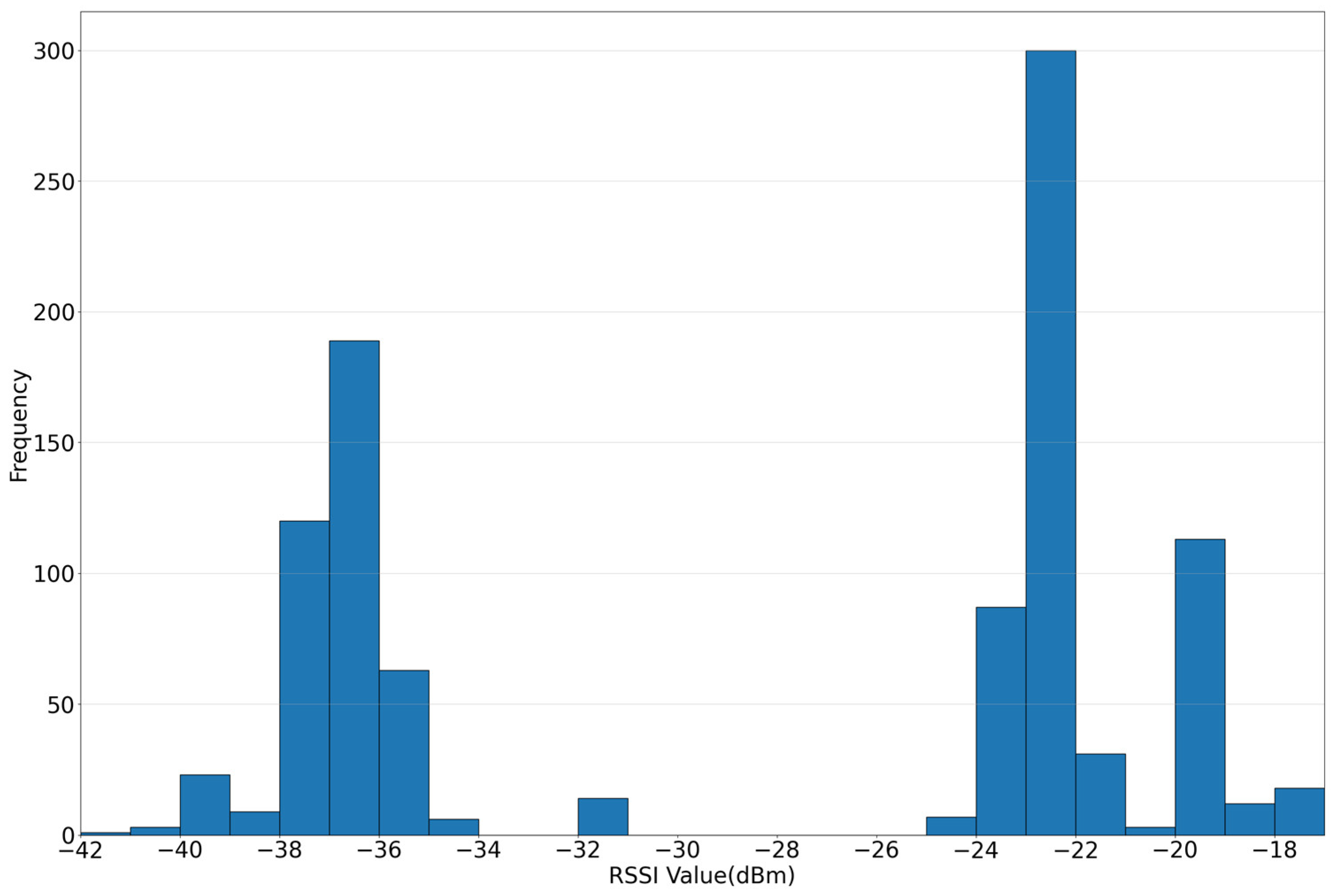
4.3.1. Proximity Threshold
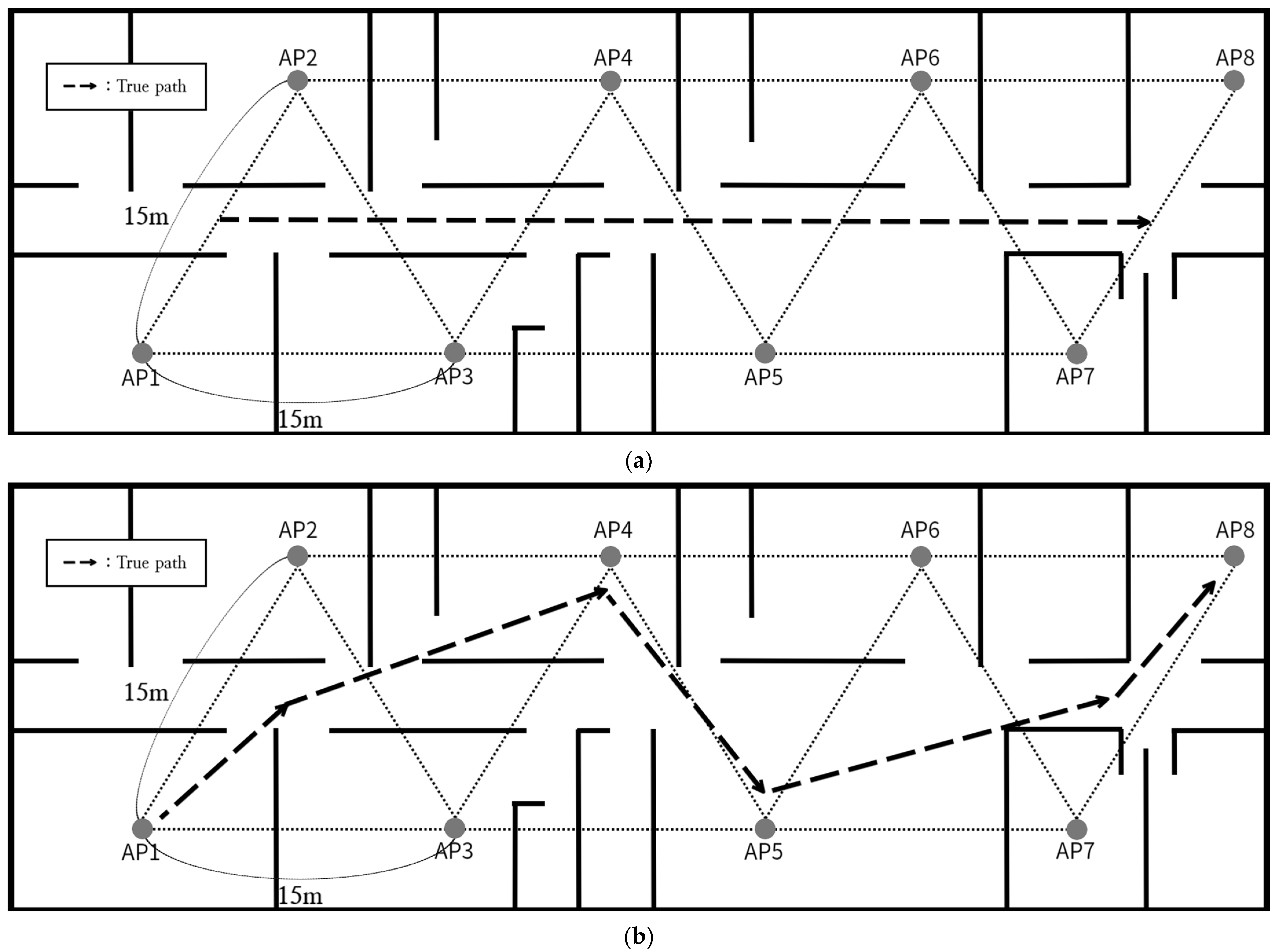
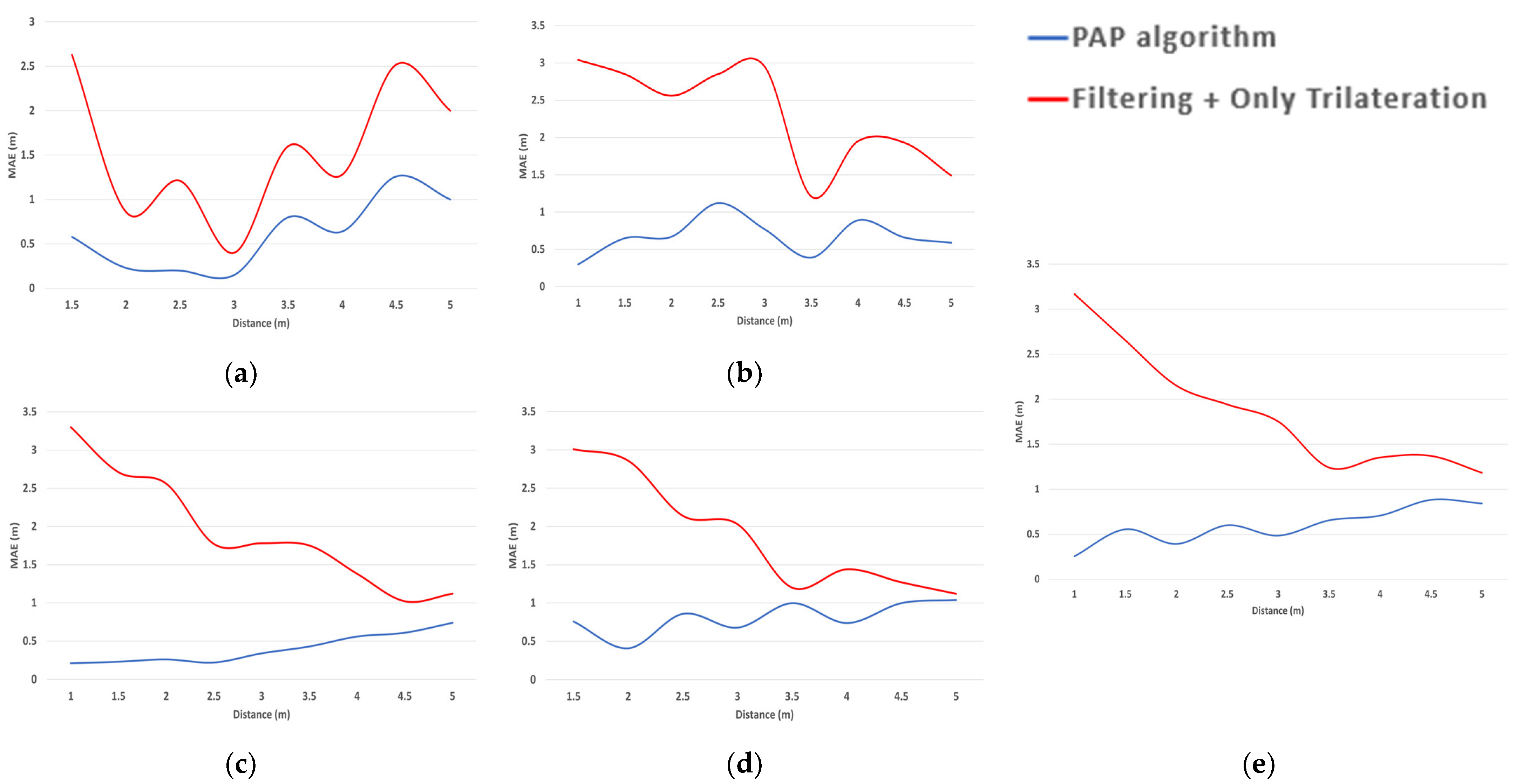
4.3.2. Experiment Evaluation in Static State
4.3.3. Experiment Evaluation in Dynamic State
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zaim, D.; Bellafkih, M. Bluetooth Low Energy (BLE) based Geomarketing System. In Proceedings of the 2016 11th International Conference on Intelligent Systems: Theories and Applications (SITA), Mohammedia, Morocco, 19–20 October 2016; pp. 1–6. [Google Scholar]
- Guerreiro, J.A.; Ahmetovic, D.; Sato, D.; Kitani, K.; Asakawa, C. Airport Accessibility and Navigation Assistance for People with Visual Impairments. In Proceedings of the CHI Conference on Human Factors in Computing Systems, Glasgow, UK, 4–9 May 2019; pp. 1–14. [Google Scholar]
- Hwangbo, H.; Kim, J.; Lee, Z.; Kim, S. Store layout optimization using indoor positioning system. Int. J. Distrib. Sens. Netw. 2017, 1, 155014771769258. [Google Scholar] [CrossRef]
- Fadzilla, M.A.; Harun, A.; Shahriman, A.B. Localization Assessment for Asset Tracking Deployment by Comparing an Indoor Localization System with a Possible Outdoor Localization System. In Proceedings of the 2018 International Conference on Computational Approach in Smart Systems Design and Applications (ICASSDA), Kuching, Malaysia, 15–17 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, Y.; Yuan, D.; Wang, G.; Xie, X.; Liu, Y.; He, T.; Zhang, D. Transloc: Transparent Indoor Localization with Uncertain Human Participation for Instant Delivery. In Proceedings of the 26th Annual International Conference on Mobile Computing and Networking (MobiCom ‘20), New York, NY, USA, 21–25 September 2020; pp. 1–14. [Google Scholar] [CrossRef]
- Gikas, V.; Dimitratos, A.; Perakis, H.; Retscher, G.; Ettlinger, A. Full-Scale Testing and Performance Evaluation of an Active RFID System for Positioning and Personal Mobility. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–6 October 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Basiri, A.; Lohan, E.S.; Moore, T.; Winstanley, A.; Peltola, P.; Hill, C.; Amirian, P.; Figueiredo e Silva, P. Indoor location based services challenges requirements and usability of current solutions. Comput. Sci. Rev. 2017, 24, 1–12. [Google Scholar] [CrossRef]
- Chen, Z.; Zou, H.; Jiang, H.; Zhu, Q.; Soh, Y.C.; Xie, L. Fusion of wifi, smartphone sensors and landmarks using the kalman filter for indoor localization. Sensors 2015, 15, 715–732. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Jing, L. Toward low-cost passive motion tracking with one pair of commodity Wi-Fi devices. IEEE J. Indoor Seamless Position. Navig. 2023, 1, 39–52. [Google Scholar] [CrossRef]
- Lee, N.; Ahn, S.; Han, D. AMID: Accurate magnetic indoor localization using deep learning. Sensors 2018, 18, 1598. [Google Scholar] [CrossRef] [PubMed]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef]
- Dong, J.; Lian, Z.; Xu, J.; Yue, Z. UWB localization based on improved robust adaptive cubature Kalman Filter. Sensors 2023, 23, 2669. [Google Scholar] [CrossRef] [PubMed]
- Daniş, F.S. Practical and parameterized fingerprinting through maximal filtering for indoor positioning. IEEE J. Indoor Seamless Position. Navig. 2023, 1, 199–210. [Google Scholar] [CrossRef]
- Noertjahyana, A.; Wijayanto, I.A.; Andjarwirawan, J. Development of Mobile Indoor Positioning System Application Using Android and Bluetooth Low Energy with Trilateration Method. In Proceedings of the 2017 International Conference on Soft Computing, Intelligent System and Information Technology (ICSIIT), Denpasar, Indonesia, 26–29 September 2017. [Google Scholar] [CrossRef]
- Bai, L.; Ciravegna, F.; Bond, R.; Mulvenna, M. A low cost indoor positioning system using bluetooth low energy. IEEE Access 2020, 8, 136858–136871. [Google Scholar] [CrossRef]
- Prasad, K.N.R.S.V.; Hossain, E.; Bhargava, V.K. Machine Learning Methods for RSS-Based User Positioning in Distributed Massive MIMO. IEEE Trans. Wirel. Commun. 2018, 17, 8402–8417. [Google Scholar] [CrossRef]
- Führling, N.; Rou, H.S.; de Abreu, G.T.F.; González, G.D.; Gonsa, O. Robust received signal strength indicator (RSSI)-based multitarget localization via gaussian process regression. IEEE J. Indoor Seamless Position. Navig. 2023, 1, 104–114. [Google Scholar] [CrossRef]
- Belmonte-Hernández, A.; Hernández-Peñaloza, G.; Martín Gutiérrez, D.; Álvarez, F. SWiBluX: Multi-sensor deep learning fingerprint for precise real-time indoor tracking. IEEE Sens. J. 2019, 19, 3473–3486. [Google Scholar] [CrossRef]
- Gufran, D.; Tiku, S.; Pasricha, S. STELLAR: Siamese multiheaded attention neural networks for overcoming temporal variations and device heterogeneity with indoor localization. IEEE J. Indoor Seamless Position. Navig. 2023, 1, 115–129. [Google Scholar] [CrossRef]
- Shang, S.; Wang, L. Overview of WiFi Fingerprinting-Based Indoor Positioning. IET Commun. 2022, 16, 725–733. [Google Scholar] [CrossRef]
- Röbesaat, J.; Zhang, P.; Abdelaal, M.; Theel, O. An improved BLE indoor localization with Kalman-based fusion: An experimental study. Sensors 2017, 17, 951. [Google Scholar] [CrossRef] [PubMed]
- Mackey, A.; Spachos, P.; Song, L.; Plataniotis, K.N. Improving BLE beacon proximity estimation accuracy through Bayesian filtering. IEEE IoT J. 2020, 7, 3160–3169. [Google Scholar] [CrossRef]
- Milano, F.; da Rocha, H.; Laracca, M.; Ferrigno, L.; Espírito Santo, A.; Salvado, J.; Paciello, V. BLE-based indoor localization: Analysis of some solutions for performance improvement. Sensors 2024, 24, 376. [Google Scholar] [CrossRef]
- Viswanathan, M.; Srinivasan, V. Wireless Communication Systems in Matlab, 2nd ed.; Independently Published: Chicago, IL, USA, 2020. [Google Scholar]
- Liu, Y.; Li, N.; Wang, D.; Guan, T.; Wang, W.; Li, J.; Li, N. Optimization Algorithm of RSSI Transmission Model for Distance Error Correction. In Proceedings of the Advances in Intelligent Information Hiding and Multimedia Signal Processing, Jilin, China, 18–20 July 2020; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Yang, J.; Deng, S.; Lin, M.; Xu, L. An adaptive calibration algorithm based on RSSI and LDPLM for indoor ranging and positioning. Sensors 2022, 22, 5689. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Chen, P.; Yang, S.; Tang, J. An indoor localization algorithm based on continuous feature scaling and outlier deleting. IEEE IoT J. 2018, 5, 1108–1115. [Google Scholar] [CrossRef]
- Ozer, A.; John, E. Improving the Accuracy of Bluetooth Low Energy Indoor Positioning System Using Kalman Filtering. In Proceedings of the 2016 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2016. [Google Scholar] [CrossRef]
- Jianyong, Z.; Haiyong, L.; Zili, C.; Zhaohui, L. RSSI Based Bluetooth Low Energy Indoor Positioning. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Republic of Korea, 27–30 October 2014. [Google Scholar] [CrossRef]
- Albraheem, L.; Alawad, S. A hybrid indoor positioning system based on visible light communication and bluetooth RSS trilateration. Sensors 2023, 23, 7199. [Google Scholar] [CrossRef]
- Shiraki, S.; Shioda, S. Contact information-based indoor pedestrian localization using bluetooth low energy beacons. IEEE Access 2022, 10, 119863–119874. [Google Scholar] [CrossRef]
- Shen, Y.; Hwang, B.; Jeong, J.P. Particle filtering-based indoor positioning system for beacon tag tracking. IEEE Access 2020, 8, 226445–226460. [Google Scholar] [CrossRef]
- Kim, Y.; Bang, H. Introduction to Kalman Filter and Its Applications; IntechOpen: Rijeka, Croatia, 2019. [Google Scholar] [CrossRef]
- Brida, P.; Matula, M.; Duha, J. Using Proximity Technolongy for Localization in Wireless Sensor Networks. Commun Sci. Lett. Univ. Zilina 2007, 9, 50–54. [Google Scholar] [CrossRef]
- Sadowski, S.; Spachos, P. Optimization of BLE Beacon Density for RSSI-Based Indoor Localiztion. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019. [Google Scholar] [CrossRef]
- Mackey, A.; Spachos, P. Performance Evaluation of Beacons for Indoor Localization in Smart Buildings. In Proceedings of the 2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Montreal, QC, Canada, 14–16 November 2017. [Google Scholar] [CrossRef]


| Outlier Removal | RSSI Correction | Position Correction | |
|---|---|---|---|
| Bai et al. [15] | None | Kalman filter | None |
| Robesaat et al. [21] | None | Kalman filter | Average filter |
| Liu et al. [25] | None | None | Firefly algorithm and particle swarm optimization |
| Yang et al. [26] | Based on Gaussian distribution | Linear regression | None |
| Fu et al. [27] | Thompson Tau test | Continuous feature scaling | None |
| Ozer and John [28] | None | Kalman filter | None |
| Jinayong et al. [29] | None | Gaussian filter | Weighted sliding window |
| Albraheem and Alawad [30] | None | None | Levenberg–Marquardt algorithm |
| Shiraki and Shioda [31] | None | Referring to previous RSSI | None |
| RSSI MAE | |||
|---|---|---|---|
| No Handling | Outlier Removal | Outlier Replacement | |
| LOS | 2.55 | 2.48 | 2.53 |
| NLOS | 4.01 | 2.69 | 3.46 |
| 3 m | 5 m | 10 m | 15 m | 10 m NLOS | 15 m NLOS | Total | |
|---|---|---|---|---|---|---|---|
| n Average | 5.52 | 4.35 | 4.35 | 3.83 | 5.05 | 4.96 | 4.68 |
| Measurement Noise | Original | R = 20 | R = 1.25 [24] | R = 2.5 [36] |
|---|---|---|---|---|
| LOS MAE | 4.47 | 2.43 | 2.48 | 2.45 |
| NLOS MAE | 3.96 | 2.77 | 2.82 | 2.78 |
| Threshold (m) | 2.0 | 3.0 | 4.0 | 5.0 |
|---|---|---|---|---|
| Side position | 1.19 | 0.96 | 0.97 | 0.97 |
| Center position | 3.26 | 3.35 | 4.22 | 4.79 |
| Other position | 5.07 | 4.83 | 4.99 | 5.21 |
| Average | 3.17 | 3.05 | 3.39 | 3.66 |
| Method | Errors (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trilateration | MP | OR | KF | LOR | MAF | Side Position | Center Position | Other Position | Average |
| O | 3.88 | 3.81 | 4.74 | 4.14 | |||||
| O | O | 3.01 | 3.30 | 4.35 | 3.55 | ||||
| O | O | O | 3.02 | 2.72 | 4.45 | 3.40 | |||
| O | O | O | O | O | 2.73 | 2.70 | 4.44 | 3.29 | |
| O | O | 0.98 | 4.11 | 4.36 | 3.15 | ||||
| O | O | O | 0.96 | 3.60 | 4.34 | 2.97 | |||
| O | O | O | O | 0.89 | 2.72 | 3.90 | 2.50 | ||
| O | O | O | O | O | O | 0.75 | 2.70 | 3.68 | 2.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.-h.; Kim, H.-j.; Kwon, S.-k. Proximity-Based Adaptive Indoor Positioning Method Using Received Signal Strength Indicator. Appl. Sci. 2024, 14, 3319. https://doi.org/10.3390/app14083319
Yoon J-h, Kim H-j, Kwon S-k. Proximity-Based Adaptive Indoor Positioning Method Using Received Signal Strength Indicator. Applied Sciences. 2024; 14(8):3319. https://doi.org/10.3390/app14083319
Chicago/Turabian StyleYoon, Jae-hyuk, Hee-jin Kim, and Soon-kak Kwon. 2024. "Proximity-Based Adaptive Indoor Positioning Method Using Received Signal Strength Indicator" Applied Sciences 14, no. 8: 3319. https://doi.org/10.3390/app14083319
APA StyleYoon, J.-h., Kim, H.-j., & Kwon, S.-k. (2024). Proximity-Based Adaptive Indoor Positioning Method Using Received Signal Strength Indicator. Applied Sciences, 14(8), 3319. https://doi.org/10.3390/app14083319









