Extending UWOC System Applications through Photon Transmission Dynamics Study in Harbor Waters
Abstract
1. Introduction
2. Materials and Methods
2.1. The Optical Parameters of the Underwater Channel
2.2. Selection of Appropriate Scattering Phase Function
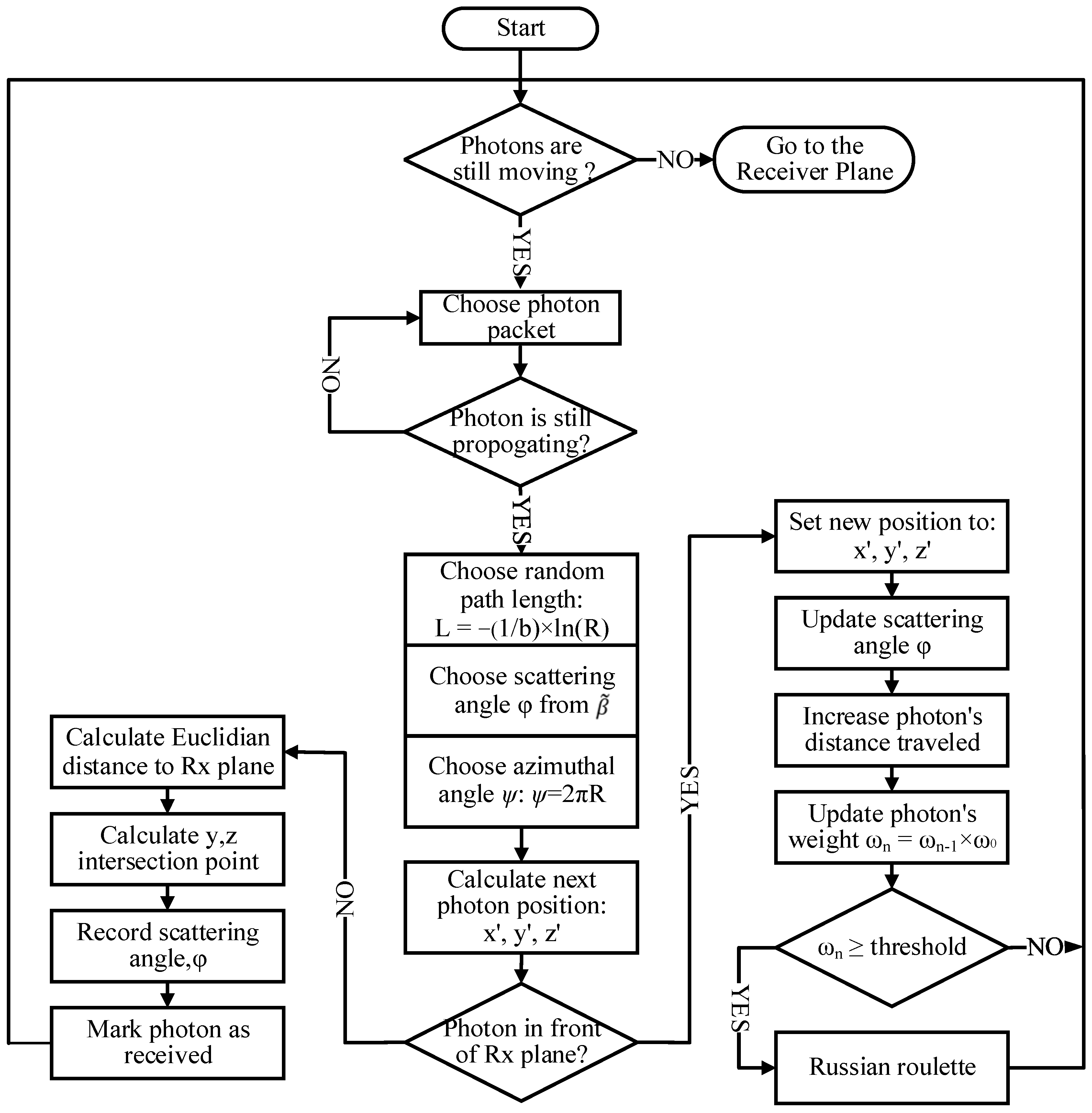
2.3. The Process of Monte Carlo Numerical Simulation
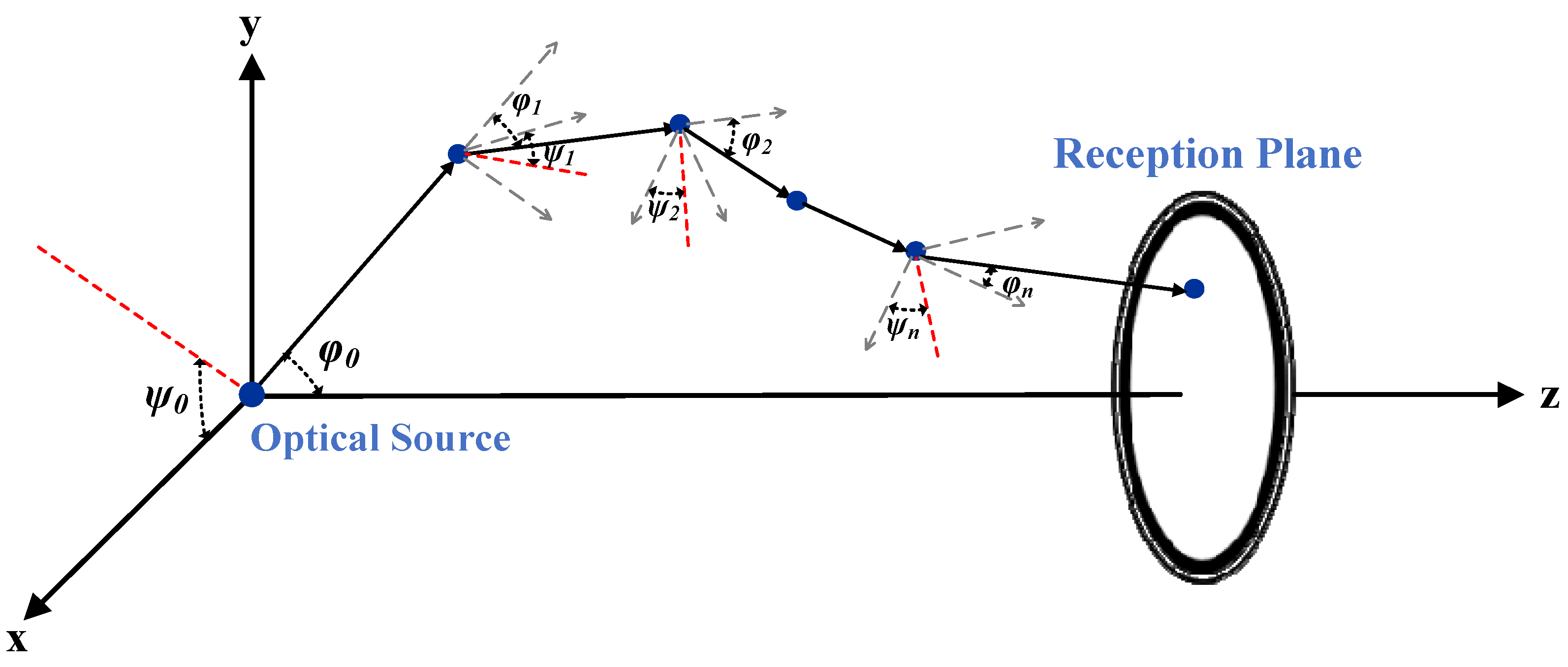
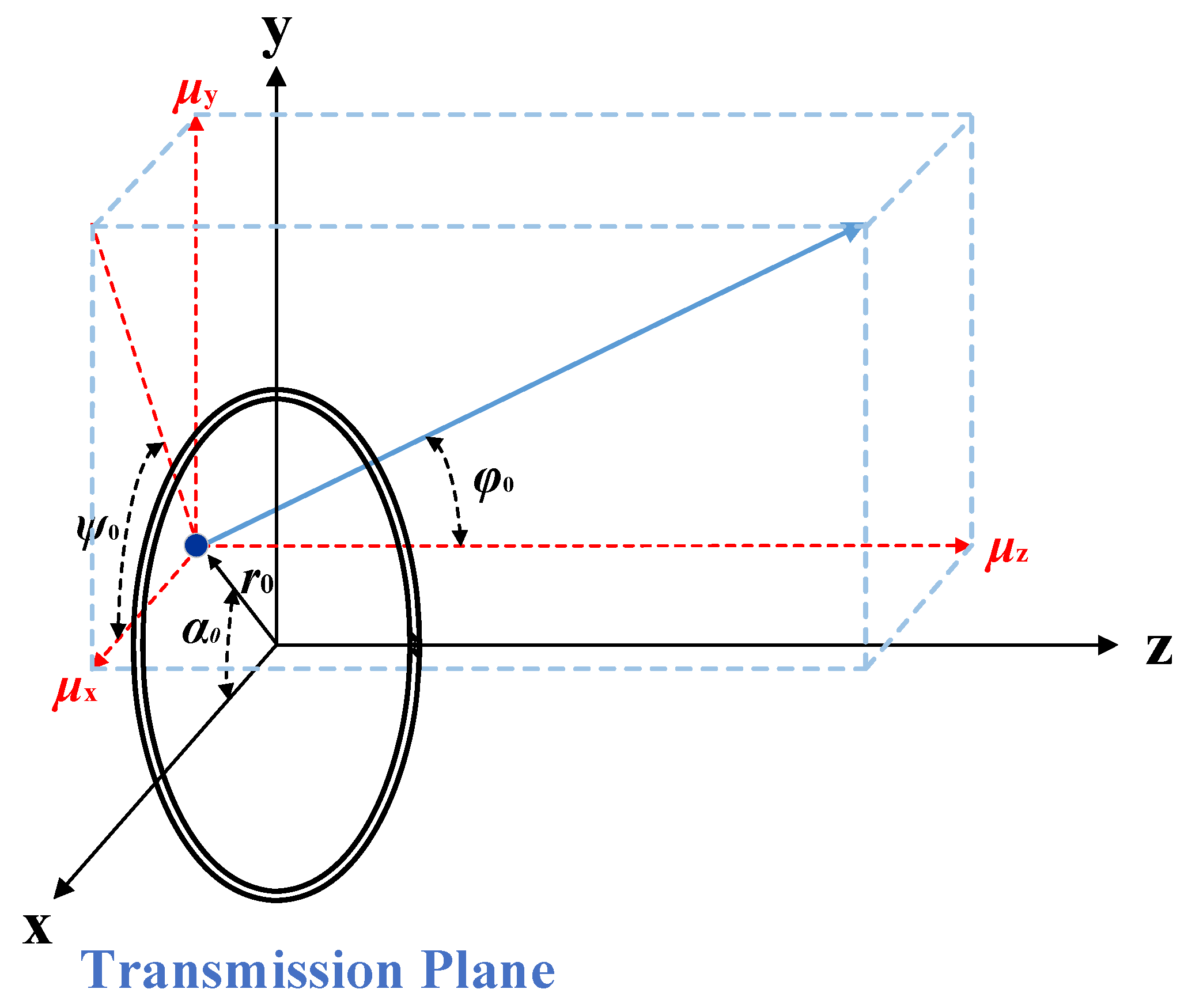
2.3.1. The Initial Parameters of Photon Packets
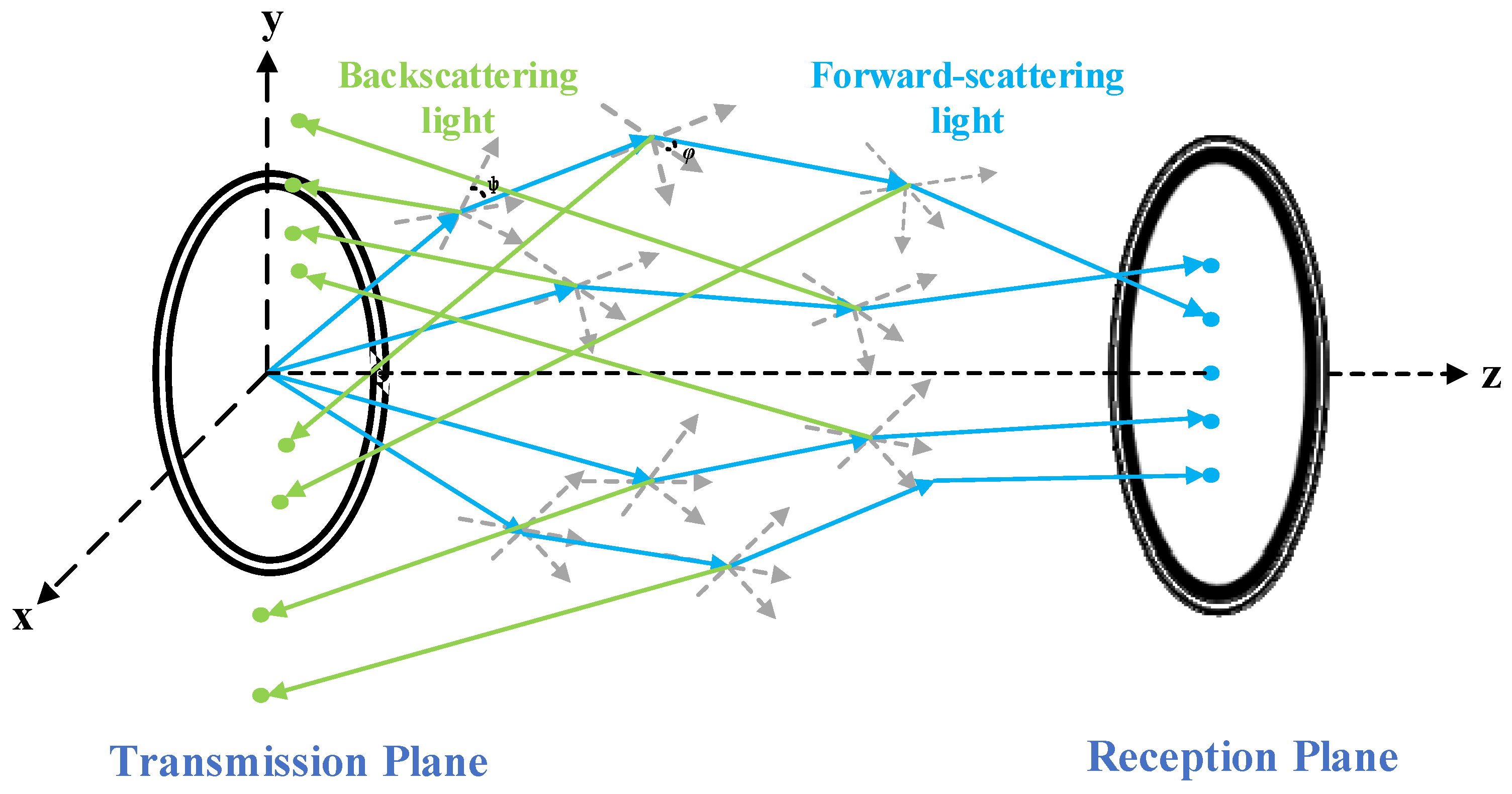
2.3.2. The Movement and Scattering of the Photon
2.3.3. Termination of Photon Motion or Reception of Photon
3. The Simulation Results and Discussion
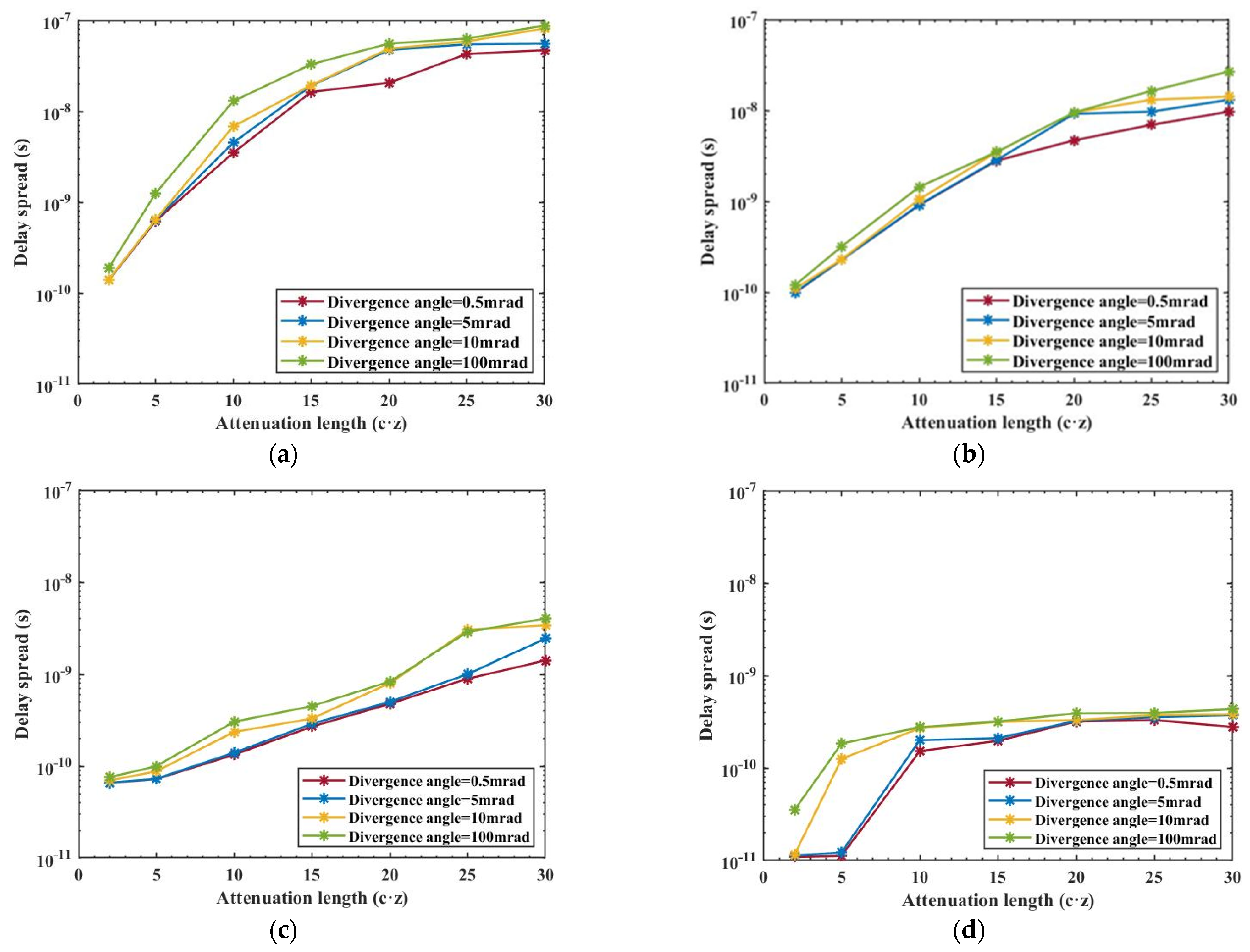
3.1. Analytical Examination of the Full Divergence Angle in Transmission
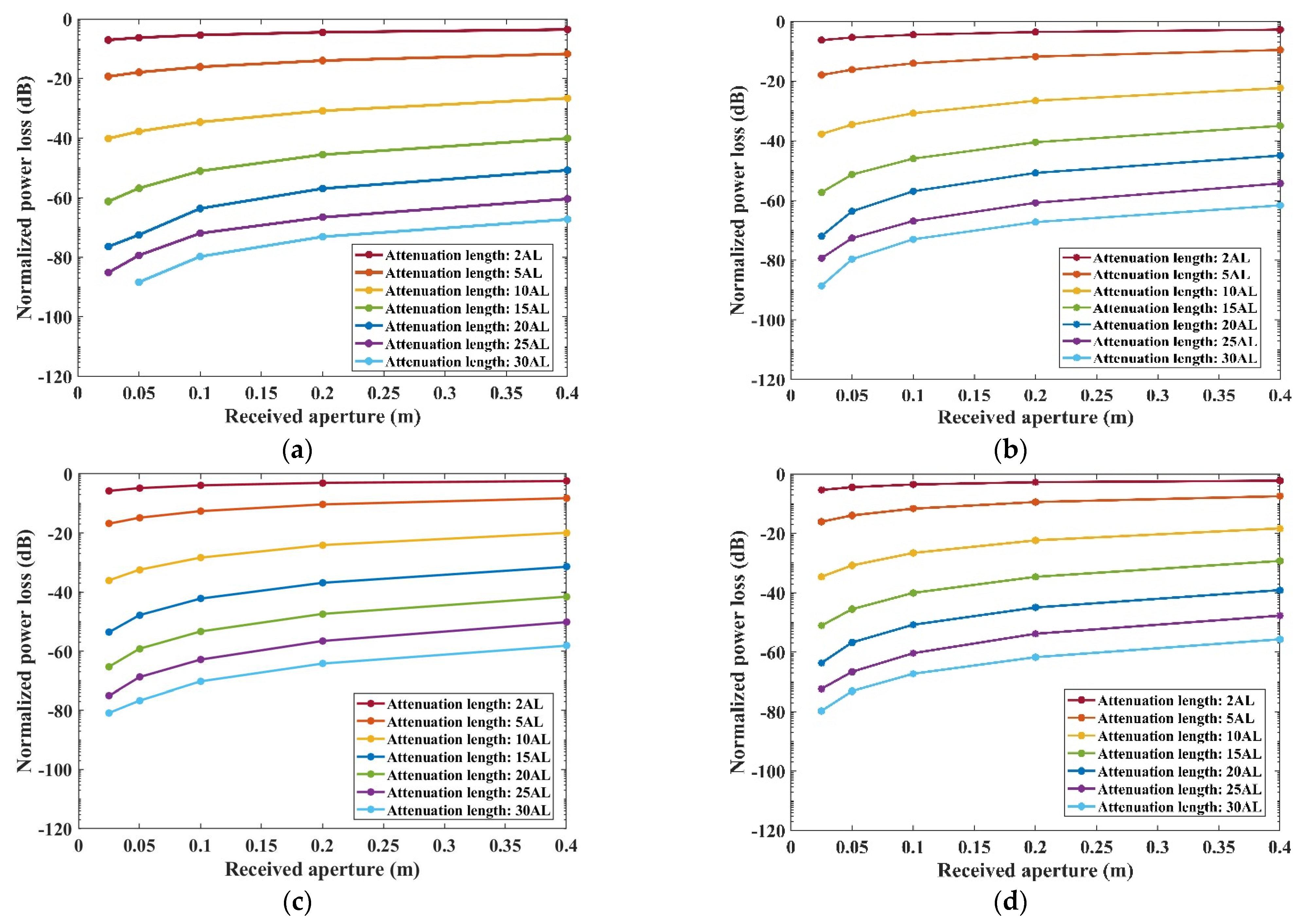
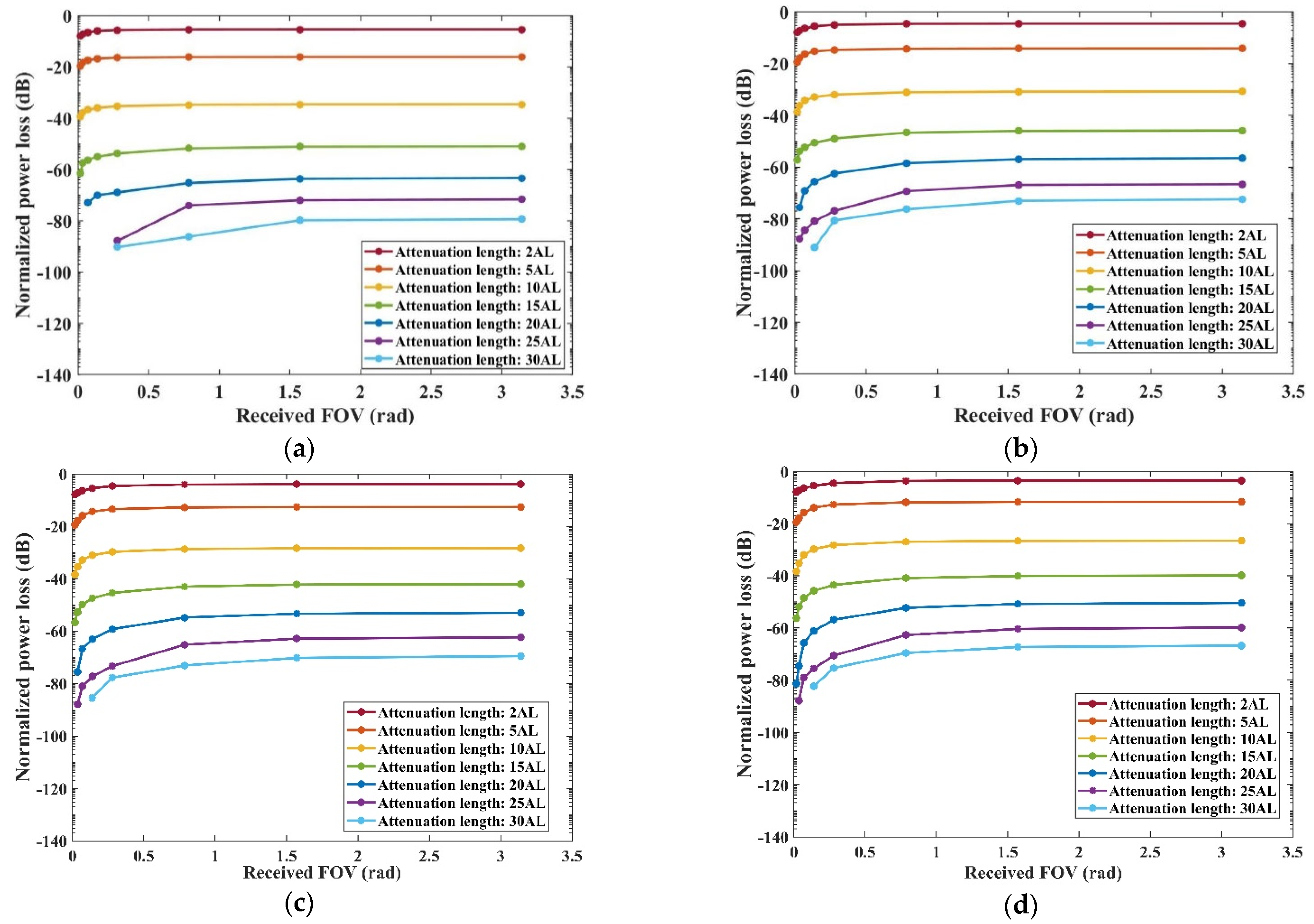
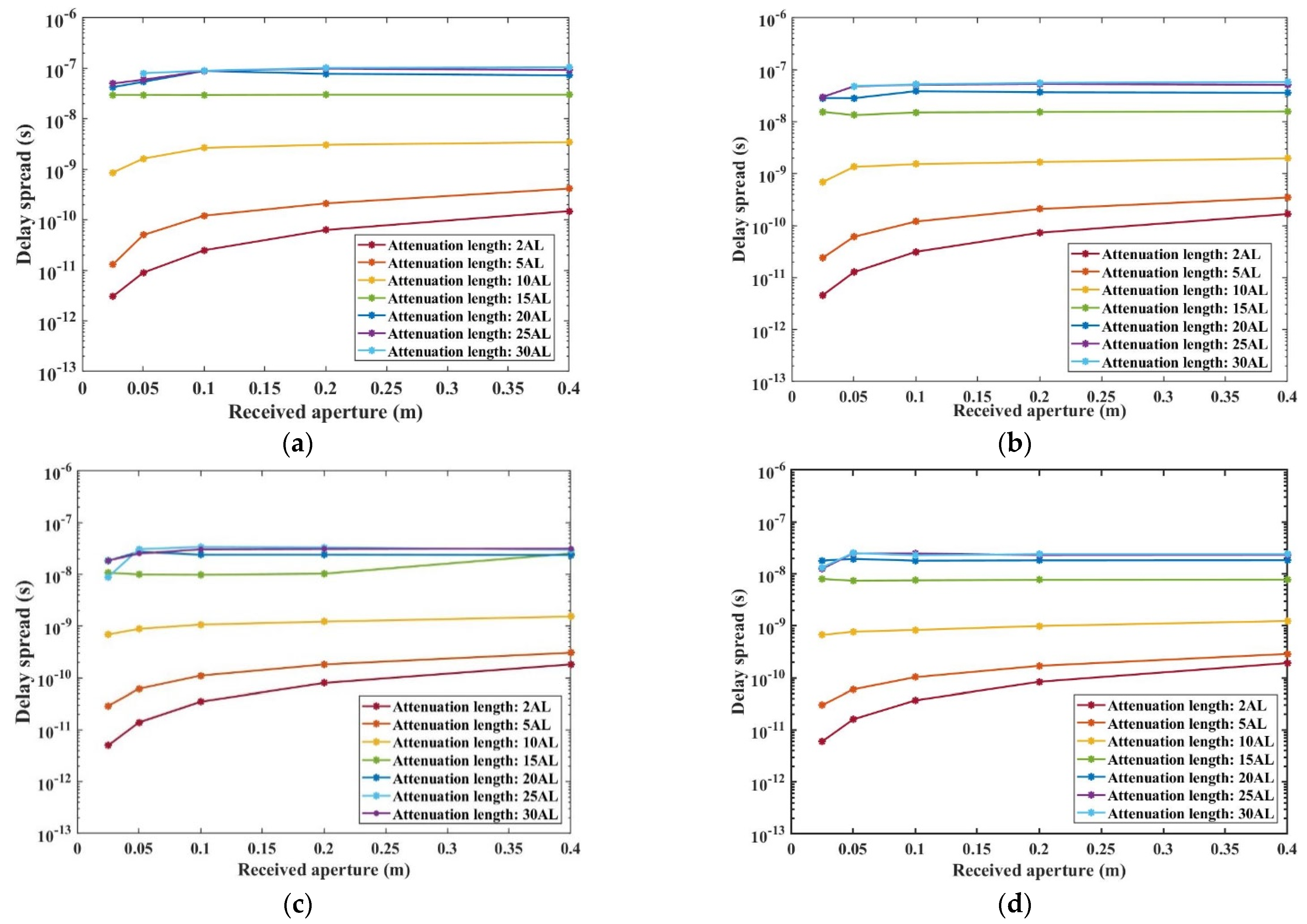
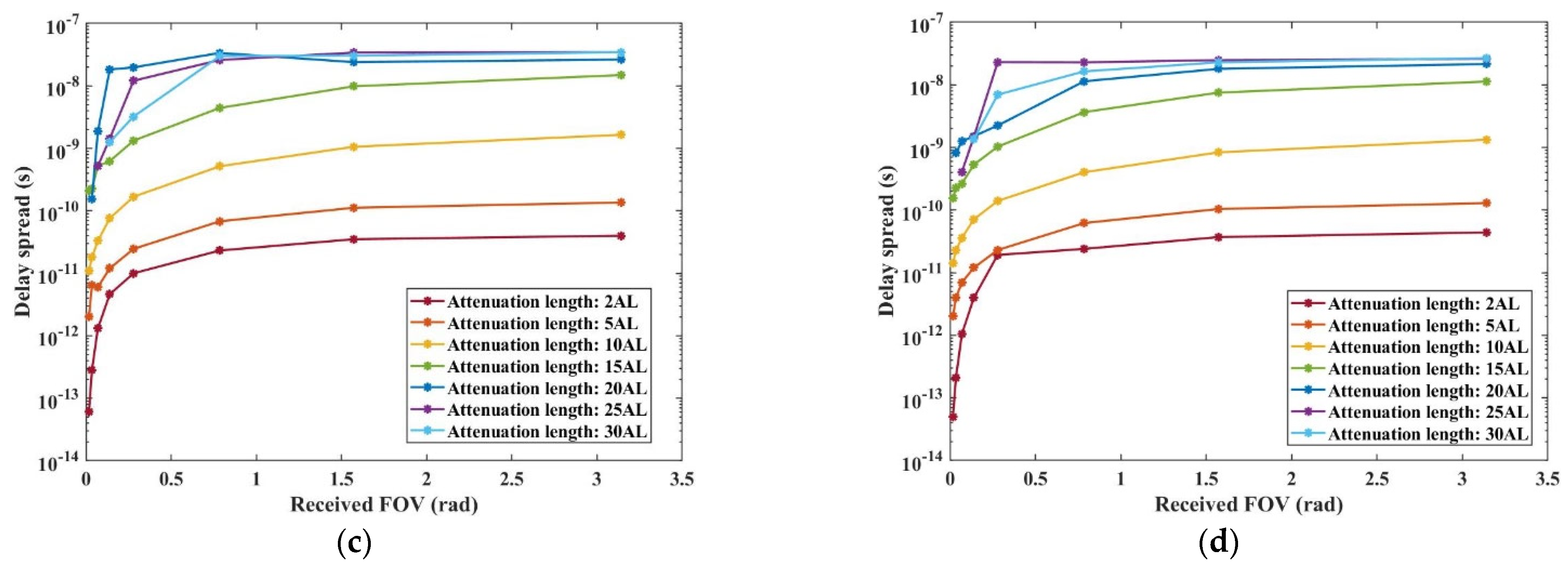
3.2. Analytical Evaluation of the Received Aperture and FOV
4. Conclusions
- Firstly, increased AL and divergence angle lead to higher received normalized power loss and time delay spread, the attenuation initially occurs at a rapid rate and then stabilizes, with these effects being more pronounced in clearer harbor water types.
- Secondly, this work reveals that the impact of communication distance on normalized power loss and time delay spread is more pronounced than that of water quality. This insight challenges that the common Beer–Lambert law no longer applies in harbor water. Communication distance, estimated by simply dividing the attenuation coefficients of different water types in many studies, is ineffective in harbor water contexts.
- Consequently, increasing the received aperture and FOV, particularly over longer communication distances, contributes minimally to reducing normalized power loss or mitigating time delay spread, thus not significantly enhancing communication quality. Based on the fixed transmitted full divergence angle, the most suitable received FOV range is about 1–3.2 rad, and the most ideal received aperture is about 0.15–0.4 m. This result holds substantial technical relevance for the engineering design of UWOC across a range of harbor water conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Yang, B.; Ye, D.; Wang, L.; Fu, K.; Piao, J.; Wang, Y. A real-time, full-duplex system for underwater wireless optical communication: Hardware structure and optical link mode. IEEE Access 2020, 8, 109372–109387. [Google Scholar] [CrossRef]
- Yang, Y.; He, F.; Guo, Q.; Wang, M.; Zhang, J.; Duan, Z. Analysis of underwater wireless optical communication system performance. Appl. Opt. 2019, 58, 9808–9814. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z. A Survey of Underwater Wireless Optical Communication. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2015. [Google Scholar]
- Urick, R.J. Principles of Underwater Sound; Peninsula: Los Altos, CA, USA, 1983. [Google Scholar]
- Xu, J. Underwater wireless optical communication: Why, what, and how? Chin. Opt. Lett. 2019, 17, 100007. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, X.; Liu, X.; Zhang, G.; Tian, P. Recent progress in and perspectives of underwater wireless optical communication. Prog. Quant. Electron. 2020, 73, 100274. [Google Scholar] [CrossRef]
- Ali, M.F.; Jayakody, D.N.K.; Chursin, Y.A.; Affes, S.; Dmitry, S. Recent advances and future directions on underwater wireless communications. Arch. Comput. Methods Eng. 2020, 27, 1379–1412. [Google Scholar] [CrossRef]
- Ma, L.; Zhou, S.; Qiao, G.; Liu, S.; Zhou, F. Superposition coding for downlink underwater acoustic OFDM. IEEE J. Ocean. Eng. 2016, 42, 175–187. [Google Scholar] [CrossRef]
- Tian, P.; Liu, X.; Yi, S.; Huang, Y.; Zhang, S.; Zhou, X.; Hu, L.; Zheng, L.; Liu, R. High-speed underwater optical wireless communication using a blue GaN-based micro-LED. Opt. Express 2017, 25, 1193–1201. [Google Scholar] [CrossRef]
- Kao, C.C.; Lin, Y.S.; Wu, G.D.; Huang, C.J. A comprehensive study on the internet of underwater things: Applications, challenges, and channel models. Sensors 2017, 17, 1477. [Google Scholar] [CrossRef]
- Sun, X.; Kang, C.H.; Kong, M.; Alkhazragi, O.; Guo, Y.; Ouhssain, M.; Weng, Y.; Jones, B.H.; Ng, T.K.; Ooi, B.S. A review on practical considerations and solutions in underwater wireless optical communication. J. Light. Technol. 2020, 38, 421–431. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.; Lv, W.; Yu, C.; Wu, J.; Zhao, M.; Qu, F.; Xu, Z.; Han, J.; Xu, J. Underwater wireless optical communication based on multi-pixel photon counter and OFDM modulation. Opt. Commun. 2019, 451, 181–185. [Google Scholar] [CrossRef]
- Wang, L.; Qi, Z.; Liu, P.; Hu, F.; Li, J.; Wang, Y. Underwater wireless video communication using blue light. J. Light. Technol. 2023, 41, 5951–5957. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, X.; Rao, J.; Wang, W. Time domain dispersion of underwater optical wireless communication. Chin. Opt. Lett. 2011, 9, 030101. [Google Scholar] [CrossRef]
- Li, J.; Luo, J.; Li, S.; Yuan, X. Centroid drift of laser beam propagation through a water surface with wave turbulence. Appl. Opt. 2020, 59, 6210–6217. [Google Scholar] [CrossRef]
- Cox, W.C., Jr. Simulation, Modeling, and Design of Underwater Optical Communication Systems. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2012. [Google Scholar]
- Shen, C.; Guo, Y.; Oubei, H.M.; Ng, T.K.; Liu, G.; Park, K.H.; Ho, K.T.; Alouini, M.S.; Ooi, B.S. 20-meter underwater wireless optical communication link with 1.5 Gbps data rate. Opt. Express 2016, 24, 25502–25509. [Google Scholar] [CrossRef]
- Sahu, S.K.; Shanmugam, P. A theoretical study on the impact of particle scattering on the channel characteristics of underwater optical communication system. Opt. Commun. 2018, 408, 3–14. [Google Scholar] [CrossRef]
- Cochenour, B.M.; Mullen, L.J.; Laux, A.E. Characterization of the beam-spread function for underwater wireless optical communications links. IEEE J. Ocean. Eng. 2008, 33, 513–521. [Google Scholar] [CrossRef]
- Ntziachristos, V. Going deeper than microscopy: The optical imaging frontier in biology. Nat. Methods 2010, 7, 603–614. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Zhao, W.; Meng, J.; Zheng, Y.; Yang, Q. Study on the backscattering disturbance in duplex underwater wireless optical communication systems. Appl. Opt. 2018, 57, 8478–8486. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Fu, M.; Sun MZhen, C.; Ji, R.; Zheng, B. Simulation of beam characteristics in long-distance underwater optical communication. In Proceedings of the Global Oceans of the Conference, Singapore–US Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; pp. 1–5. [Google Scholar]
- Boluda-Ruiz, R.; Rico-Pinazo, P.; Castillo-Vázquez, B.; García-Zambrana, A.; Qaraqe, K. Impulse response modeling of underwater optical scattering channels for wireless communication. IEEE Photonic J. 2020, 12, 7904414. [Google Scholar] [CrossRef]
- Bowen, A.D.; Jakuba, M.V.; Farr, N.E.; Ware, J.; Taylor, C.; Gomez-Ibanez, D.; Machado, C.R.; Pontbriand, C. An un-tethered ROV for routine access and intervention in the deep sea. In Proceedings of the 2013 Oceans-San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–7. [Google Scholar]
- Farr, N.E.; Ware, J.D.; Pontbriand, C.T.; Tivey, M.A. Demonstration of wireless data harvesting from a subsea node using a “ship of opportunity”. In Proceedings of the 2013 OCEANS-San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–5. [Google Scholar]
- Pontbriand, C.; Farr, N.; Hansen, J.; Kinsey, J.C.; Pelletier, L.-P.; Ware, J.; Fourie, D. Wireless data harvesting using the AUV Sentry and WHOI optical modem. In Proceedings of the OCEANS 2015-MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Hubbard, W.A.; Bellmer, R.J. Biological and chemical composition of Boston Harbor, USA. Mar. Pollut. Bull. 1989, 20, 615–621. [Google Scholar] [CrossRef]
- Ahmed, F.S.; Sensenich, B.A.; Gheni SA Znerdstrovic, D.; Dahhan, M.H. Bubble dynamics in 2D bubble column: Comparison between high-speed camera imaging analysis and 4-point optical probe. Chem. Eng. Commun. 2015, 202, 85–95. [Google Scholar] [CrossRef]
- Li, J.; Ma, Y.; Zhou, Q.; Zhou, B.; Wang, H. Channel capacity study of underwater wireless optical communications links based on Monte Carlo simulation. J. Opt. 2011, 14, 015403. [Google Scholar] [CrossRef]
- Kodama, T.; Sanusi, M.A.B.A.; Kobori, F.; Kimura, T.; Inoue, Y.; Jinno, M. Comprehensive analysis of time-domain hybrid PAM for data-rate and distance adaptive UWOC system. IEEE Access 2021, 9, 57064–57074. [Google Scholar] [CrossRef]
- Gjerstad, K.I.; Stamnes, J.J.; Hamre, B.; Lotsberg, J.K.; Yan, B.; Stamnes, K. Monte Carlo and discrete-ordinate simulations of irradiances in the coupled atmosphere-ocean system. Appl. Opt. 2003, 42, 2609–2622. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, C.; Khalighi, M.A.; Bourennane, S.; Leon, P.; Rigaud, V. Channel modeling for underwater optical communication. In Proceedings of the IEEE GLOBECOM Workshops of the Conference, Houston, TX, USA, 5–9 December 2011; pp. 833–837. [Google Scholar]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Tang, S.; Dong, Y.; Zhang, X. Impulse response modeling for underwater wireless optical communication links. IEEE Trans. Commun. 2013, 62, 226–234. [Google Scholar] [CrossRef]
- Qadar, R.; Kasi, M.K.; Ayub, S.; Kakar, F.A. Monte Carlo–based channel estimation and performance evaluation for UWOC links under geometric losses. Int. J. Commun. Syst. 2018, 31, e3527. [Google Scholar] [CrossRef]
- Zhang, J.; Kou, L.; Yang, Y.; He, F.; Duan, Z. Monte-Carlo-based optical wireless underwater channel modeling with oceanic turbulence. Opt. Commun. 2020, 475, 126214. [Google Scholar] [CrossRef]
- Freda, W.; Piskozub, J. Improved method of Fournier-Forand marine phase function parameterization. Opt. Express 2007, 15, 12763–12768. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Boss, E. Phase function effects on oceanic light fields. Appl. Opt. 2002, 41, 1035–1050. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, C.; Khalighi, M.A.; Bourennane, S.; Léon, P.; Rigaud, V. Monte-Carlo-based channel characterization for underwater optical communication systems. J. Opt. Commun. Netw. 2013, 5, 1–12. [Google Scholar] [CrossRef]
- Jiang, R.; Sun, C.; Zhang, L.; Tang, X.; Wang, H.; Zhang, A. Deep learning aided signal detection for SPAD-based underwater optical wireless communications. IEEE Access 2020, 8, 20363–20374. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, X.; Sun, C.; Chen, Z.; Li, Z.; Wang, H.; Jiang, R.; Shi, W.; Zhang, A. Over 10 attenuation length gigabits per second underwater wireless optical communication using a silicon photomultiplier (SiPM) based receiver. Opt. Express 2020, 28, 24968–24980. [Google Scholar] [CrossRef]
- Hu, S.; Mi, L.; Zhou, T.; Chen, W. 35.88 attenuation lengths and 3.32 bits/photon underwater optical wireless communication based on photon-counting receiver with 256-PPM. Opt. Express 2018, 26, 21685–21699. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D.; Gentili, B.; Gordon, H.R.; Jin, Z.; Kattawar, G.W.; Morel, A.; Reinersman, P.; Stamnes, K.; Stavn, R.H. Comparison of numerical models for computing underwater light fields. Appl. Opt. 1993, 32, 7484–7504. [Google Scholar] [CrossRef] [PubMed]
- Sahu, S.K.; Shanmugam, P. A study on the effect of scattering properties of marine particles on underwater optical wireless communication channel characteristics. In Proceedings of the OCEANS of the Conference, Aberdeen, UK, 19–22 June 2017; pp. 1–7. [Google Scholar]
- Cochenour, B.; Mullen, L.; Laux, A.; Curran, T. Effects of multiple scattering on the implementation of an underwater wireless optical communications link. In Proceedings of the OCEANS of the Conference, Boston, MA, USA, 18–21 September 2006; pp. 1–6. [Google Scholar]
- Cox, W.; Muth, J. Simulating channel losses in an underwater optical communication system. J. Opt. Soc. Am. A 2014, 31, 920–934. [Google Scholar] [CrossRef] [PubMed]
- Petzold, T.J. Volume Scattering Functions for Selected Ocean Waters; Scripps Institution of Oceanography, La Jolla Ca Visibility Lab: La Jolla, CA, USA, 1972. [Google Scholar]
- Haltrin, V.I. One-parameter two-term Henyey-Greenstein phase function for light scattering in seawater. Appl. Opt. 2002, 41, 1022–1028. [Google Scholar] [CrossRef] [PubMed]
- Fournier, G.R.; Forand, J.L. Analytic phase function for ocean water. In Proceedings of the Ocean Optics XII, Bergen, Norway, 26 October 1994; Volume 2258, pp. 194–201. [Google Scholar]
- Jaruwatanadilok, S. Underwater wireless optical communication channel modeling and performance evaluation using vector radiative transfer theory. IEEE J. Sel. Area Commun. 2008, 26, 1620–1627. [Google Scholar] [CrossRef]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Qadar, R.; Kasi, M.K.; Kakar, F.A. Monte Carlo based estimation and performance evaluation of temporal channel behavior of UWOC under multiple scattering. In Proceedings of the Oceans 2017-Anchorage, Anchorage, AK, USA, 18–21 September 2017; pp. 1–7. [Google Scholar]





| Harbor Water Types | ||||
|---|---|---|---|---|
| Harbor-I | 0.187 | 0.913 | 1.10 | 0.83 |
| Harbor-II | 0.374 | 1.826 | 2.20 | 0.83 |
| Harbor-III | 0.561 | 2.739 | 3.30 | 0.83 |
| Harbor-IV | 0.748 | 3.652 | 4.40 | 0.83 |
| Wavelength | Transmitted Photon Number | Single Photon Energy | Transmitted Light Energy |
|---|---|---|---|
| 532 nm | 1013 | 3.74 × 10−19 J | 3.74 × 10−6 J |
| Transmitted full divergence angle (2) | 0.5 mrad | 5 mrad | 10 mrad | 100 mrad | ||||
| Transmitted beam waist diameter (2) | 1.4 × 10−3 m | 1.35 × 10−4 m | 6.77 × 10−5 m | 6.77 × 10−6 m | ||||
| Received aperture | 25 mm | 50 mm | 100 mm | 200 mm | 400 mm | |||
| Received FOV | rad | rad | rad | rad | rad | rad | rad | rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.; Han, X.; Li, G.; Li, P.; Nie, W.; Liao, P.; Li, C.; Wang, W.; Xie, X. Extending UWOC System Applications through Photon Transmission Dynamics Study in Harbor Waters. Appl. Sci. 2024, 14, 2493. https://doi.org/10.3390/app14062493
Chang C, Han X, Li G, Li P, Nie W, Liao P, Li C, Wang W, Xie X. Extending UWOC System Applications through Photon Transmission Dynamics Study in Harbor Waters. Applied Sciences. 2024; 14(6):2493. https://doi.org/10.3390/app14062493
Chicago/Turabian StyleChang, Chang, Xiaotian Han, Guangying Li, Peng Li, Wenchao Nie, Peixuan Liao, Cong Li, Wei Wang, and Xiaoping Xie. 2024. "Extending UWOC System Applications through Photon Transmission Dynamics Study in Harbor Waters" Applied Sciences 14, no. 6: 2493. https://doi.org/10.3390/app14062493
APA StyleChang, C., Han, X., Li, G., Li, P., Nie, W., Liao, P., Li, C., Wang, W., & Xie, X. (2024). Extending UWOC System Applications through Photon Transmission Dynamics Study in Harbor Waters. Applied Sciences, 14(6), 2493. https://doi.org/10.3390/app14062493






