Abstract
The Internet of Vehicles (IoV) has a significant impact on improving traffic efficiency and driving safety. In this paper, we propose an intelligent transportation credit system based on blockchain, and design a crossroad passing smart contract that allows time-sensitive convoys to pass a crossroad earlier by paying traffic tokens for right-of-way trade. Second, this paper formulates the time–cost optimization problem under the premise of protecting the privacy of preceding convoys. Based on game theory with incomplete information, two right-of-way optimal bid strategies are given. Both theoretical analysis and simulation prove that the strategy proposed in this paper effectively reduces the waiting time of time-sensitive vehicles at a crossroad and increases the trade success probability, which, in turn, improves the expected total profit of convoys and achieves Pareto improvement.
1. Introduction
By vehicle-to-everything (V2X) communication such as vehicle-to-vehicle (V2V) and vehicle-to-roadside unit (V2R), Internet of Vehicles (IoV) [1,2,3,4,5] provides important technical support for intelligent transportation systems (ITS), especially in self-driving, to improve traffic efficiency and meet individual needs. For example, it can adaptively manage the passage of vehicles at crossroads according to the current traffic flow.
In blockchain [6,7,8], the same blocks are deployed locally and consistently in vehicles to provide an effective security credit system [9] and privacy protection for intelligent vehicles. However, the combination of intelligent vehicle trades and blockchain still needs extensive research. On one hand, traditional blockchain can hardly meet the requirements of IoV such as low latency and high throughput, which provides an opportunity for the development and application of blockchain with new directed acyclic graph (DAG) [10,11,12] architecture such as IoTA [13]. On the other hand, blockchain-based smart contracts [14] can automatically execute the contract terms, which improves the efficiency and reliability of execution and also reduces the errors and disputes that may occur during execution, which further ensures the security of intelligent transportation-based applications. Therefore, blockchain-enabled transportation applications based on smart contracts still need further research.
The literature [6] provides a comprehensive review of blockchain applications in IoV. It was found that blockchain is already providing security and credit systems for various application scenarios such as data protection and management, data and resource trading, traffic control and management, etc., which effectively contribute to the development of IoV. In the literature [15], a lightweight blockchain-based security protocol is proposed for secure communication and storage in IoV. The scheme provides a high level of security with low computational cost but lacks the consideration of cellular network service conditions. In the literature [16], a blockchain-based secure data collection and exchange strategy for IoV is proposed, which can effectively eliminate several potential attacks and improve security, but its efficient, flexible, and practical implementation requires further research. In the literature [17], a blockchain and deep-learning-based privacy protection and security framework for IoV (P2SF-IoV) is proposed, which effectively ensures the secure transmission of data in the network. However, due to the large number of urban vehicles, its efficiency and scalability have not been tested. The literature [18] proposes a blockchain-based decentralized trust management scheme using smart contracts. It is used to maintain and update reliable and consistent trust values across the network, as well as an incentive scheme to encourage peers to perform well.
The field of traffic control and management is an important application scenario for IoV. Blockchain and its smart contracts provide a better solution for automated traffic control and management systems with its support for decentralized management, availability, automation, and immutability [6]. The literature [19] proposes an intelligent transport system, where a credit token method based on blockchain is used for vehicles to pay for services. Concerning convoy driving, a queueing model for self-driving cars in free-flowing traffic has been proposed in the literature [20], which is much better than the single-vehicle model in terms of fuel consumption. However, the driver’s brainpower and the vehicle’s computing power consumption have yet to be introduced into the energy optimization problem as a whole.
The crossroad signal control problem is an important part of intelligent transportation. The literature [21] proposes an attribute and efficient blockchain-based model, i.e., the semicentralized traffic signal control (SCTSC) model. It also strikes a balance between privacy and information availability. However, this scheme has not yet considered the need for vehicle personalization and the transaction speed, and scalability of the blockchain in dense scenarios. In the literature [22], a traffic signal control mechanism based on federated blockchain is proposed, which can intelligently switch traffic signals, quickly assign green light duration, and ensure road safety. Smart contracts and artificial intelligence technologies are also used to control signal duration and coordinate signal management optimization and decision making. This solution can meet the safety requirements of IoV.
In summary, there has been much research on IoV credit systems based on blockchain to solve intelligent transportation problems. In addition, the application of blockchain technology in crossroad signal control has attracted more and more attention. However, there are still some unsolved problems in the current research.
- The existing research is mainly focused on a specific transportation problem, and the lack of an overall intelligent system solution that can unify each transportation spot makes the actual landing application slow.
- For the problem of passing a crossroad, the personalized needs of vehicles have not been considered. For example, time-sensitive vehicles are eager to pass the crossroads quickly, and credit-sensitive vehicles can be supplemented with time in exchange for traffic tokens.
- The need to protect the privacy of intelligent vehicles has not yet been addressed.
- The fixed-bidding strategy is not flexible with limited trade success probability.
To solve the above problems, we propose a blockchain-based solution for time-sensitive convoys to reduce waiting time and pass a crossroad earlier. The main contributions of this paper include the following:
- An intelligent traffic credit system is proposed to record all the vehicles’ behaviors such as driving too slow, traffic accidents, and negotiating the sequence of crossing an intersection, punish bad behaviors such as vehicle violations by deducting traffic tokens, and reward traffic tokens to vehicles for good behaviors, thus creating a good intelligent autonomous traffic environment that is fair, efficient, and safe.
- We propose a blockchain-based smart contract for convoys passing crossroads order negotiation, and the vehicle nodes automatically invoke the relevant smart contracts to perform V2V crossroad passing orders. It allows time-sensitive convoys to apply and negotiate with convoys ahead of them to pass earlier and pay for it according to the game’s optimal bid.
- A time–cost optimization problem is formulated under the premise of protecting the privacy of the convoy ahead. Based on the incomplete information static game, two optimal bidding solutions for right-of-way trading are given. They effectively increase the probability of making a deal and realizing Pareto improvement.
The rest of the paper is organized as follows. Section 2 proposes an intelligent transportation credit system based on traffic tokens and describes its roles and applied scenarios in the IoV. Section 3 mathematically models a crossroad passing problem and describes its smart contract process. Section 4 proposes a game-based right-of-way trade strategy and two optimal bidding solutions. Section 5 simulates the two proposed optimal bidding solutions and gives a performance comparison. The Monte Carlo simulation results agree with their theoretical derivation. Section 6 summarizes the entire paper.
2. An Intelligent Transportation Credit System Based on Blockchain
In this paper, we propose an intelligent transportation credit system based on blockchain. Compared with the traditional centralized system, the main advantages of this distributed system include:
- To guarantee driving safety, it is impossible to change the crossroad passing orders by attacking a single vehicle or a few vehicles, where each vehicle maintains a ledger.
- The same accounts distributed on the vehicles effectively ensure traceability and responsibility confirmation after traffic accidents.
- The original and resold owners are aware of a vehicle’s condition via all the historical information including the details of accidents recorded by this system.
Mining the requirements of crossroad traffic scenarios for variable throughput, low latency, scalability, etc., IoTA is selected as the blockchain architecture of this system.
2.1. Typical Application Scenarios
The system distributes traffic tokens. A vehicle enters the system with an initial traffic token of 0t and allows for a certain amount of overdraft. The total number of traffic tokens for the entire road transport credit system is fixed, and they circulate according to the regulations to maintain a safe and efficient transport environment, thus creating a healthy and autonomous ITS. Traffic tokens circulate in the following scenarios:
- Speed suggestion: It provides a reference speed suggestion. If multiple vehicles issue speed warnings and simultaneously verify that the vehicle ahead is significantly below a current reference speed, a speed warning is issued to the vehicle. If the vehicle does not accelerate in a period, a certain number of traffic tokens are deducted from the vehicle to the warning vehicles behind it for a reward.
- Convoy driving: To improve efficiency and safety, convoy driving is a good idea. A vehicle is chosen for the convoy lead, which is responsible for speed determination and negotiating with other convoys for the passing order. Other vehicles in the convoy pay a certain amount of traffic tokens to the lead vehicle.
- Road accident responsibility confirmation: The distributed ledger is used to determine the responsibility and traceability of accidents. Traffic accidents caused by violating traffic rules or V2X-negotiated overtaking agreements will result in a larger amount of traffic tokens being deducted from the offending vehicle.
- Congestion evacuation: It helps to clear the congestion caused by an accident as quickly as possible and avoid secondary accidents by sending a congestion message to surrounding vehicles. Vehicles receiving the message will either avoid entering the congested lane or leave the congested lane as quickly as possible. Vehicles that help maintain traffic safety are rewarded with a certain number of traffic tokens from neighboring receiving vehicles.
- Right-of-way trade: In dense urban scenarios, fairness and efficiency dictate that the first arriving convoy passes the crossroad first. If a convoy is more time-sensitive, it initiates a trade, negotiates and pays a certain amount of traffic tokens for right-of-way. The convoy that gives up the right-of-way receives a certain number of traffic tokens.
2.2. Traffic Token-Based System at a Crossroad
In this section, we study the convoy passing mechanism at a crossroad [23,24,25,26,27,28,29,30], which is an important scenario for this intelligent transportation credit system. Specifically, we consider how convoys can pass a crossroad in a safe and orderly manner according to the vehicle-mounted smart contract.
Figure 1 shows the proposed system architecture. A road side unit (RSU) at a crossroad, which is a full node, maintains an independent IoTA chain that records traffic information for its crossroad and neighboring roads. Vehicles are light nodes that only record traffic information related to the road they are currently traveling on. When a vehicle is about to enter a crossroad, it joins the chain, creates a crossroad passing trade record, and begins maintaining a local chain. When a vehicle leaves the current road for a while, in addition to the traffic events closely related to itself, it will automatically delete the previously outdated road information to simplify maintenance and ensure there is enough memory space.
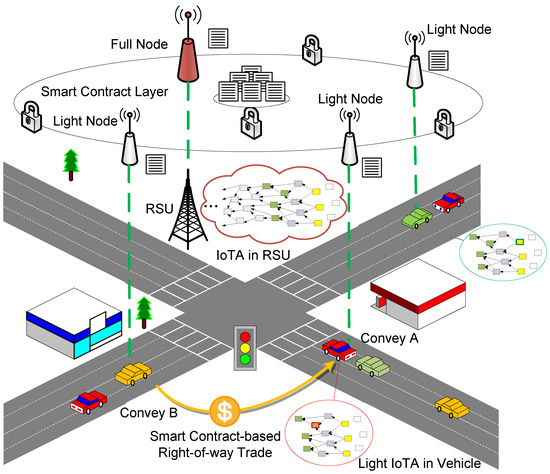
Figure 1.
A crossroad maintains an IoTA chain with smart contracts installed on an RSU, which is a full node, and vehicles, which are light nodes.
3. A Crossroad Passing Model
The research was conducted in a typical crossroad scenario, as shown in Figure 1. It can be transformed into other types of intersections with simple constraints such as the number of streets connected. There are four roads connected to the crossroad, and each road has two lanes, one for left turns and going straight, and the other for right turns. In the following research, we first make some assumptions and then model the problem.
3.1. Assumptions
We research a driverless scenario with the following assumptions about road design, vehicle behavior rules, and communication capabilities.
- A control line (CL) is designed on each road at L meters from the crossroad. As soon as a vehicle enters the adjacent road, it enters the corresponding lanes to turn left and go straight, or right turn to drive according to vehicle path planning.
- Once the vehicles enter the CL near the crossroad, each convoy stores the IoTA chain of the crossroad clearance order with the help of RSU. Under smart contract algorithms including gaming, the passing order is negotiated, agreed and strictly followed by all vehicles.
- The vehicle has built-in sensing and computing capability, which can sense the distance between vehicles, vehicle speed, and other information.
- Vehicles in the convoy maintain the same speed. And with the help of sensing, vehicles in the convoy can adjust the distance between each other according to moving speed, and automatically maintain the distance with the vehicle ahead.
- Between different convoys on the same road, the first and last vehicle in the convoy can sense the driving information of other convoys, such as the speed and distance of the convoys ahead and behind.
- Among different convoys from conflict roads around the crossroad, driving information about vehicles in front and behind the order is needed. For example, the current position of the last or first vehicle in the neighboring convoy in front of or behind the order and the time when to leave or arrive at the crossroad.
The above is necessary for efficient convoy driving and orderly crossroad passing based on V2V.
3.2. Basic Rule of First Arrive-First Pass
Because right-turn vehicles in all lanes can pass at any time without colliding with vehicles in other lanes, each green-light phase is for a certain direction’s left-turn and straight lane to pass the crossroad. The longest waiting time for the vehicle in direction k is , where .
In particular, if no vehicles are waiting at the crossroad in a certain direction but left-turning or vehicles going straight enter the CL line, they head towards the crossroad. Let be the remaining time for the first vehicle to reach the crossroad. The longest waiting time here is . If none of the vehicles in that direction enter within the CL line, then .
Suppose the longest waiting time of the first vehicle on the road in the four directions east, north, west, and south of the crossroad is , respectively. Let denote the mth maximum value of them, where . Then are order statistics corresponding to .
Assuming that , it can be obtained that . The crossroad passing order in the current moment is
where indicates that the current mth pass order belongs to vehicles in the kth direction.
This scheme allows a road direction whose first vehicle waits for the longest time to pass first, which has two advantages.
- It maintains basic fairness for vehicles passing a crossroad by preventing one lane from having to wait all the time.
- It avoids having a current green light for a lane with no vehicles in it and wasting time.
3.3. A Smart Contract to Obtain a Passing Order
A smart contract process for a newly arrived convoy to obtain a passing order is designed, as shown in Figure 2, which is a basic framework for the convoy passing smart contract in Section 4.
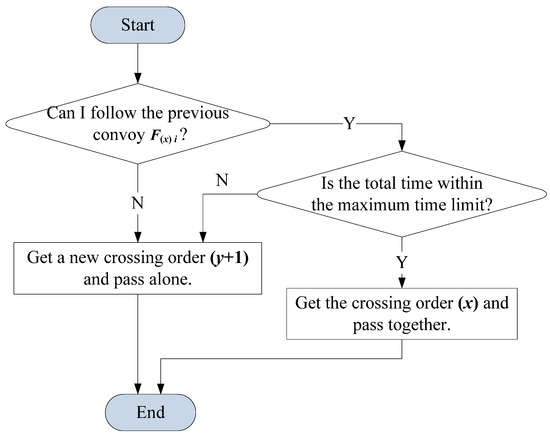
Figure 2.
Initial smart contract process for a new convoy to obtain a passing order.
In the following, we discuss the design of the two core judge modules of convoy following criterion and maximum green light duration.
3.4. Convoy Following Criterion
Suppose that the first vehicle in the convoy arrives at the crossroad at , and the entire convoy passes the crossroad stop line at . Let be the guard time interval when changing to another crossroad direction to pass.
- 1.
- Whenthe convoy will pass the crossroad together with the convoy and get the passing order of .
- 2.
- Whenthere are two conditions.
① If
after the convoy has passed the crossroad, it turns directly to the road direction whose passing order is , which is generally more efficient. So, the convoy gets the passing order of .
② If
after the convoy has passed the crossroad, the convoy with passing order is further away from the crossroad than the convoy . And it is more efficient to wait for the entire passing of the convoy , which also obtains order , to pass together. So, when convoy passes the crossroad, let the convoy continue to pass. Moreover, it is better for convoy to accelerate to the crossroad after receiving an order , which improves road efficiency and saves energy.
3.5. Green Light Duration
In this part, we discuss the green light duration for a certain direction, which represents the time for vehicles on that road to pass the crossroad continuously. To think about fairness, the maximum and minimum green light durations of a single direction are strictly limited. Suppose that the green light time of the xth passing order direction road is , whose upper and lower bounds are and , respectively. Thus,
- 1.
- Minimum Green Light DurationThe minimum green light time is limited to the single passing of the convoy that originally received this passing order, which does not allow any other convoy to follow. In other words, its minimum is only the time for convoy to pass.
- 2.
- Maximum Green Light DurationAssume that the start time for the xth passing order direction road to pass is , the actual end time is , and the longest end time for allowance is . So,Suppose that the time when the last vehicle of the next convoy on the same road leaves the crossroad stop line is .If , thenIt is guaranteed that all the convoy will pass the crossroad at this time, and that convoy cannot follow it and will get the latest passing order .If , thenThe convoy receives the passing order and passes the crossroad together with the convoy .
This section mathematically models the convoy passing crossroad problem. A convoy follows the arrival order at the crossroad and passes sequentially. In terms of overall passing efficiency, a convoy following criterion is designed. A maximum green light duration is designed for fairness. Several methods for determining a convoy’s passing order are based on the principle of minimizing the total passing time at the crossroad.
However, the value of the same elapsed time may be different for different vehicles. Some vehicles consume more fuel per minute, and some are more sensitive to time which is presented as the time cost factor , etc. For example, a fully loaded bus is more time-sensitive than a private car with only one passenger. This is a common situation in road transportation. So, if you are time-sensitive and need to get to your destination as soon as possible by navigating a crossroad surrounded by convoys, how to arrive speedily is a problem.
4. Right-of-Way Trade Strategy
In this section, a smart contract is designed for right-of-way trade. Thus, the time-sensitive convoy can negotiate with the convoy ahead and obtain the right-of-way by paying traffic tokens. The whole process is executed according to a smart contract process, and the transaction is recorded in the blockchain.
We attempt to rationally reduce the waiting time of time-sensitive traffic participants at crossroads. This is another important innovation of this work. Specifically, the newly arrived convoy negotiates with the convoy ahead in exchange for early passing.
4.1. A Whole Smart Contract Designed for Crossroad Passing
However, if each vehicle speaks its own words, a distributed V2V transaction can cause traffic confusion at the intersection. In this paper, an IoTA is used as the credit guarantee for the whole crossroad passing order negotiation process, and a smart contract is pre-installed on the crossroad RSU and vehicle terminals. The whole crossroad passing order negotiation process is carried out under the strict smart contract process, as shown in Figure 3, and the information is recorded and packaged on the blockchain for tamper-proofing and to ensure that vehicles pass the crossroad in a safe and orderly manner.
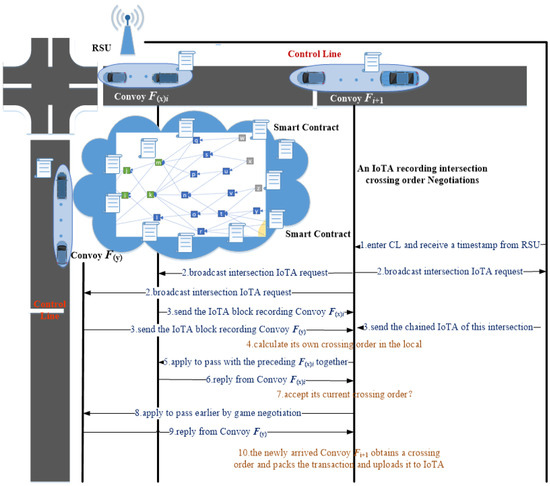
Figure 3.
An IoTA and its smart contract including right-of-way trade for a newly arrived convoy to obtain a passing order in a crossroad.
4.2. Meaningful Circumstances for Right-of-Way Trade
A and B are two neighbor-order convoys such as and , respectively, in two conflicting road directions. First, some assumptions and definitions are made for the derivation.
- and are the time cost factors for convoys A and B, respectively. The larger the parameter, the more sensitive it is to time.
- Exchanging the right-of-way helps convoy B ahead of schedule for , while leading A’s delay for .
- The time cost represented as C is assumed to be linearly related to the time t and time cost factor, i.e., . The time cost profit reduction of B associated with its early passing is , and the increased time cost profit of A is denoted as .
Secondly, we analyze and give a conclusion on meaningful circumstances suitable for A and B to make a right-of-way deal. Two conditions must be met before trading.
- Condition 1: Early passing only makes sense if A and B have a time conflict in passing the crossroad, i.e., Equation (10) is satisfied.Equation (10) is equal to .
- Condition 2: Based on satisfying Equation (10), if and only ifThere is a Pareto optimization after swapping the passing order. Such an exchange makes sense.
Transaction Price: However, the right-of-way is not free. Convoy B has to negotiate with A by gaming and finally reach a concession price . That is, B pays A for traffic tokens in exchange for the right-of-way.
This concession price is set so that both convoys A and B benefit from the concession and achieve a Pareto improvement.
4.3. Privacy-Preserving Static Game-Based Optimal Bids Problem
In this part, we discuss the optimal bids problem of two neighbor-order convoys for the right-of-way trade based on a two-party static Bayesian Game. The set of participants in the game is .
Suppose that , , and are public information that is known by both A and B. However, is private information whose exact value is known only to A itself. Assume that the value space of the time cost factor is . The time cost factor of A is denoted by , . Similarly, the time cost factor of B is denoted by , . Let and denote the set of optional bidding actions for convoys A and B, respectively, where and .
The cost to A of giving the right-of-way is
B’s profit from passing the crossroad early is
To reach an agreement in a short time, A and B bid simultaneously according to the static game model. If buyer B’s bid is higher than seller A’s bid , both sides reach an agreement and B pays the average of the two bids to A. Otherwise, no agreement can be reached. Thus, the function of reaching a deal is
The profit functions of A and B are
The two convoys each maximize their profit and create an optimization problem to solve for the optimal bids of both convoys.
Convoy A knows the true value of . Thus, the optimal bid is
Convoy B, however, knows the probability distribution of the value of instead of its exact value. We infer the conditional probability distribution of A’s time cost over the current value of to find B’s maximum expected payoff.
Compared to the static game with complete information, solving the game with incomplete information is more complex with more uncertainty.
4.4. Optimal Bids Solution 1: Convoy A Takes the Optimal Bid with Complete Information
Because the above optimization problem is complex and difficult to solve, we first discuss the optimal bids problem for A and B under complete information.
4.4.1. Optimal Bids with Complete Information
If A and B both know the value of each other’s factors including , , and , the optimal bidding problem can be simplified to the following equations.
In the case where is known, convoy A’s profit is maximized when takes the maximum value. Similarly, in the case where is known, convoy B’s profit is maximized when takes the minimum value.
Therefore, the profit of two convoys is maximized when
Thus, Equation (22) is the Pareto frontier of this function of Equations (20) and (21).
From the multi-objective optimization, the optimal reconciliation solution is calculated as follows assuming that , where and represent the maximum profit of A and B, respectively.
The optimal bidding problem is modeled as
The problem is solved as
4.4.2. Optimal Bids with Incomplete Information
The above result is for two convoys with complete information. Usually, however, convoys need privacy protection. To facilitate the solution, four assumptions are made for the incomplete information game problem.
- Assumption 1: Suppose that and are independently and identically distributed according to a uniform distribution in the range of [0, 1].
- Assumption 2: Convoy A knows the values of , , , . Whereas convoy B knows the values of , , , and that .
- Assumption 3: Because convoy A has complete information, the optimal bid of A is
- Assumption 4: Because B knows that A has complete information, A will bid .
According to Equations (15) and (19), we derive the expected profit for B, which is a function of
Because each function of the three segments and their connecting points are continuous, the function is continuous. We calculate the maximum value of each segment and make a comparison and analysis.
To summarize, in the static game where A has complete information and B has incomplete information, the optimal bids of A and B are the following, respectively.
The corresponding maximum expected profit for B is
4.5. Optimal Bids Solution 2: Convoy A Bids the Same as Convoy B
Another solution to the incomplete information game problem is based on A’s belief that its optimal bid is . Four assumptions are made to facilitate the solution. The first two assumptions are the same as Assumptions 1 and 2 in Section 4.4.2. The other two are new.
- Assumption 3: Convoy B will submit its optimal bid to obtain its maximum expected profit .
- Assumption 4: Convoy A has complete information and A can obtain the optimal bid .
- According to Equation (22) in Section 4.4.1, the optimal bid of A should be equal to , , and B knows the optimal bid strategy of A.
For convoy B, it does not know the exact value of but it knows that , according to Assumption 1. Then, analysis is given under different values of .
- 1.
- If ,from Equations (12), (15) and (19), is derived as follows
- 2.
- If , is derived as follows
And B’s optimal bid is the point where function obtains its global maximum value. We calculate the maximum value of each segment and make a comparison. To summarize, in the static game where A has complete information and B has incomplete information, the optimal bids of A and B are as follows.
The corresponding maximum profit expectation for B is
4.6. Theoretical Performance Comparison and Analysis
In this part, we provide a theoretical performance comparison between the above two optimal bid solutions for right-of-way.
4.6.1. Trade Success Probability
According to the analyzed trade success conditions in Section 4.2 and Section 4.3, a deal is made only if . The trade success probability of Solution 1 is derived under the optimal bids in Section 4.4.2.
However, the trade success probability of Solution 2 is derived under the optimal bids in Section 4.5.
According to Equations (35) and (36), the trade success probability curves are shown in Figure 4a. When is relatively small, the trade success probability increases as increases, with Solution 1 having a higher trade success probability than Solution 2 at the same . As increases, the trade success probabilities of Solution 1 and Solution 2 successively reach 1. As continues to increase, both solutions are certain to make a trade. Therefore, the trade success probability performance of Solution 1 is better than that of Solution 2.
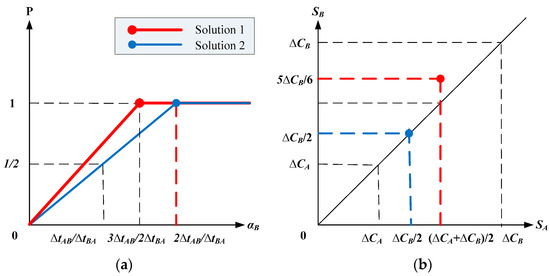
Figure 4.
Performance comparison between two solutions, where red is of Solution 1 and blue is of Solution 2. (a) The trade success probability for two solutions; (b) the optimal bid points for two solutions.
4.6.2. Trade Profits
According to Equations (29) and (33), the optimal bid points are shown in Figure 4b. It can be seen that the optimal bids’ relation of the two solutions is as follows.
It is derived that Solution 1 has a larger profit for A, and Solution 2 has a larger profit for B.
As shown in Figure 4b, the optimal bid of Solution 2 is on the line . However, the optimal bid point of Solution 1 is higher than the line . It shows that B’s profit is smaller than Solution 1 due to the loss because B’s incomplete information only burdened itself. In Solution 2, however, B chooses its maximum profit under incomplete information first, leading to B’s higher profit. Contrasting to complete information, this is a good representation of the loss from incomplete information.
5. Simulation Results and Analysis
In this section, the performance of the right-of-way trade strategy based on the V2V game is evaluated. The simulation parameters are listed in Table 1.

Table 1.
Simulation parameters.
Figure 5 shows the expected profit of B in Solution 1 with various bids and cost factors under and using the Monte Carlo simulation. It can be also seen that the theoretical optimal bid and expected profit obtained by Equations (29) and (30) are highly consistent with the simulation results, and it shows that Equation (29) is valid. In addition, the larger is, the larger expected profit of B can be achieved.
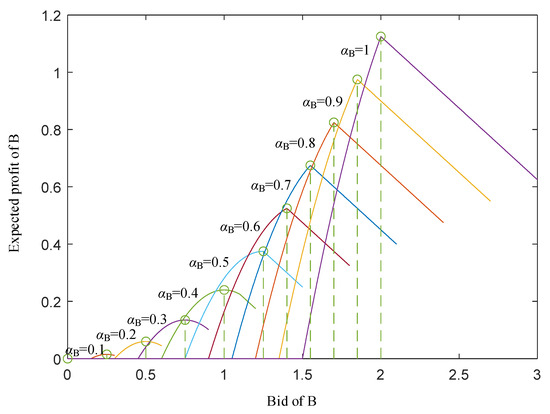
Figure 5.
The expected profit of B in Solution 1. (The dotted line is the theoretical optimal bid and expected profit).
Figure 6 shows the profits of B in Solution 1 by the optimal bid with various . It can be seen that when is below a certain threshold and is above a certain threshold, no deal can be made and the profit of B is zero. And The profit of B increases with , and decreases with .
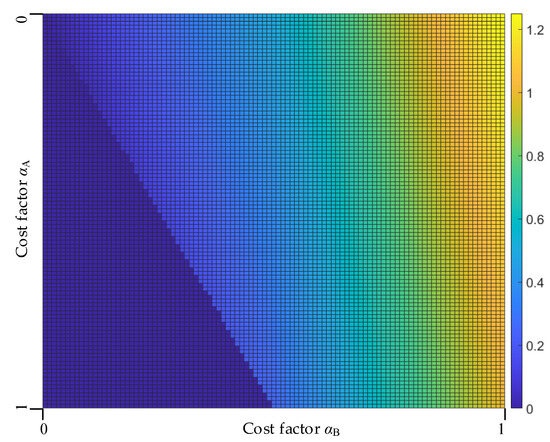
Figure 6.
The profits of B in Solution 1 by the optimal bid with various .
Figure 7 shows the expected profit of B in solution 2 with various bids and cost factors under and using the Monte Carlo simulation. It can be also seen that the theoretical optimal bid and expected profit obtained by Equations (33) and (34) are highly consistent with the simulation results.
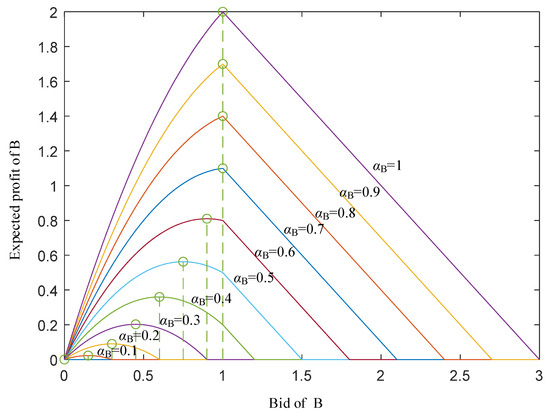
Figure 7.
The expected profit of B in solution 2. (The dotted line is the theoretical optimal bid and expected profit).
Figure 8 shows the cumulative distribution functions (CDFs) of the total profit of A and B in Solution 1 and Solution 2 and compares them with the theoretical upper bound and the random bid. As can be seen, the CDFs of the total profits of Solution 1 and Solution 2 are closer to the theoretical upper bound and much larger than the random bids, which means that Solution 1 and 2 can improve the performance to near perfection. In addition, relatively speaking, the total profit of Solution 1 is slightly greater than that of Solution 2.
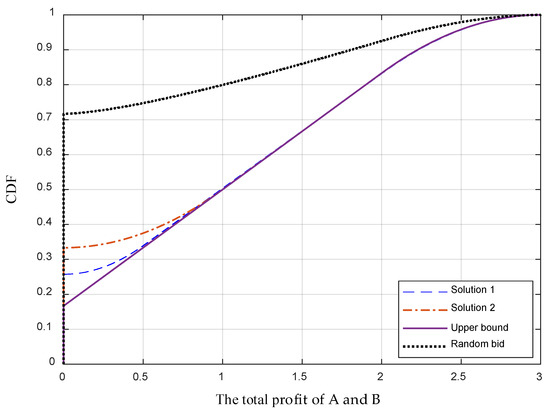
Figure 8.
Cumulative distribution function (CDF) of the total profit of A and B.
Figure 9 shows the profits of A and B in Solutions 1 and 2 and compares them with the random bid. As can be seen, the total profits of A and B in Solution 1 and 2 are equal to each other and much higher than that of random bid. However, Solution 1 is more favorable for A, and Solution 2 is more favorable for B. In some extreme cases of Solution 2, e.g., and , the profit of A is closer to 0. Both methods achieve Pareto improvement and are effective methods.
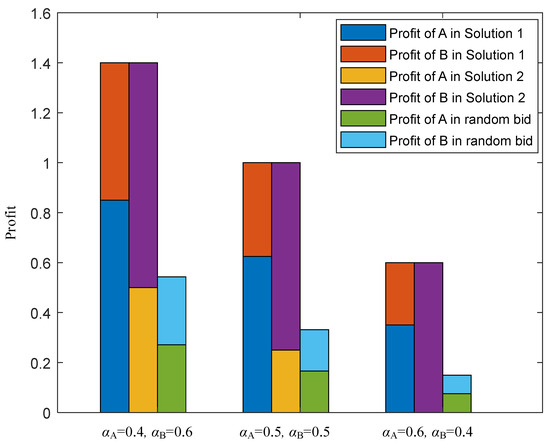
Figure 9.
Profits for A and B in Solutions 1 and 2.
6. Conclusions
In this paper, we propose a blockchain-based smart contract for right-of-way trades for urban crossroad passing problems. The solution addresses the needs of time-sensitive convoys that want to reduce the waiting time at a crossroad. Based on game theory, two optimal bidding strategies for rights-of-way trade are given to achieve Pareto improvement while protecting the privacy of the convoy ahead.
In future research, other applications of traffic token-based intelligent credit systems, such as convoy formation and traffic management and control in multi-crossroads, can be expanded on this basis to further improve traffic efficiency and ensure traffic safety.
Author Contributions
Methodology, C.L. and H.W.; Software, C.L. and L.X.; Validation, C.L. and L.X.; Formal analysis, Y.L.; Investigation, C.D. and J.L.; Writing—original draft, C.L.; Writing—review and editing, H.W., Y.L., L.X. and C.D.; Supervision, H.W.; Project administration, C.L.; Funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities 2022JBMC016, the Basic Research Program under Grant JCKY2022XXXX145, the Science and Technology Research and Development Plan of China Railway Co., Ltd. (No. K2022G018), Natural Science Foundation of China under Grant U21A20445 and 62221001, State Key Laboratory of Advanced Rail Autonomous Operation (No. RCS2022ZT013).
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, H.; Ota, K.; Dong, M. Learning IoV in 6G: Intelligent Edge Computing for Internet of Vehicles in 6G Wireless Communications. IEEE Wirel. Commun. 2023, 3, 1–6. [Google Scholar] [CrossRef]
- Xu, X.; Yao, L.; Bilal, M.; Wan, S.; Dai, F.; Choo, K.K.R. Service Migration Across Edge Devices in 6G-Enabled Internet of Vehicles Networks. IEEE Internet Things J. 2022, 9, 1930–1937. [Google Scholar] [CrossRef]
- Zhou, X.; Bilal, M.; Dou, R.; Rodrigues, J.J.P.C.; Zhao, Q.; Dai, J.; Xu, X. Edge Computation Offloading with Content Caching in 6G-Enabled IoV. IEEE Trans. Intell. Transp. Syst. 2023, 1, 1–15. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, K.; Hossain, E. Green Internet of Vehicles (IoV) in the 6G Era: Toward Sustainable Vehicular Communications and Networking. IEEE Trans. Green Commun. Netw. 2022, 6, 391–423. [Google Scholar] [CrossRef]
- Khan, W.U.; Javed, M.A.; Nguyen, T.N.; Khan, S.; Elhalawany, B.M. Energy-Efficient Resource Allocation for 6G Backscatter-Enabled NOMA IoV Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9775–9785. [Google Scholar] [CrossRef]
- Mollah, M.B.; Zhao, J.; Niyato, D.; Guan, Y.L.; Yuen, C.; Sun, S.; Lam, K.; Koh, L.H. Blockchain for the Internet of Vehicles Towards Intelligent Transportation Systems: A Survey. IEEE Internet Things J. 2021, 8, 4157–4185. [Google Scholar] [CrossRef]
- Yuan, M.; Xu, Y.; Zhang, C.; Tan, Y.; Wang, Y.; Ren, J.; Zhang, Y. TRUCON: Blockchain-Based Trusted Data Sharing with Congestion Control in Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3489–3500. [Google Scholar] [CrossRef]
- Li, C.; Wu, H.; Xiong, L.; Lu, Y. An IoV-PBFT Consensus-Based Blockchain for Collaborative Congestion Avoidance and Simulation Test. Wirel. Commun. Mob. Comput. 2022, 1–19. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Y.; Hei, X.; Zhu, L.; Ji, W. A Novel IoV Block-Streaming Service Awareness and Trusted Verification Scheme in 6G. IEEE Trans. Veh. Technol. 2021, 70, 5197–5210. [Google Scholar] [CrossRef]
- Chai, H.; Leng, S.; Wu, F.; He, J. Secure and Efficient Blockchain-Based Knowledge Sharing for Intelligent Connected Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14620–14631. [Google Scholar] [CrossRef]
- Sheikh, M.; Aghaei, J.; Chabok, H.; Roustaei, M.; Niknam, T.; Kavousi-Fard, A.; Shafie-Khah, M.; Catalao, J.P.S. Synergies Between Transportation Systems, Energy Hub and the Grid in Smart Cities. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7371–7385. [Google Scholar] [CrossRef]
- Rathore, H.; Sai, S.; Gundewar, A. Social Psychology Inspired Distributed Ledger Technique for Anomaly Detection in Connected Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7092–7107. [Google Scholar] [CrossRef]
- Liu, Y.; Li, D.; Li, R.; Zhao, Z.; Zhu, Y.; Zhang, H. Secure and Efficient Stigmergy-Empowered Blockchain Framework for Heterogeneous Collaborative Services in the Internet of Vehicles. IEEE Commun. Mag. 2023, 61, 186–192. [Google Scholar] [CrossRef]
- Li, Z.; Alazab, M.; Garg, S.; Hossain, M.S. PriParkRec: Privacy-Preserving Decentralized Parking Recommendation Service. IEEE Trans. Veh. Technol. 2021, 70, 4037–4050. [Google Scholar] [CrossRef]
- Vishwakarma, L.; Nahar, A.; Das, D. LBSV: Lightweight Blockchain Security Protocol for Secure Storage and Communication in SDN-Enabled IoV. IEEE Trans. Veh. Technol. 2022, 71, 5983–5994. [Google Scholar] [CrossRef]
- Karim, S.M.; Habbal, A.; Chaudhry, S.A.; Irshad, A. BSDCE-IoV: Blockchain-Based Secure Data Collection and Exchange Scheme for IoV in 5G Environment. IEEE Access 2023, 11, 36158–36175. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, P.; Tripathi, R.; Gupta, G.P.; Kumar, N. P2SF-IoV: A Privacy-Preservation-Based Secured Framework for Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22571–22582. [Google Scholar] [CrossRef]
- Singh, P.K.; Singh, R.; Nandi, S.K.; Ghafoor, K.Z.; Rawat, D.B.; Nandi, S. Blockchain-Based Adaptive Trust Management in Internet of Vehicles Using Smart Contract. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3616–3630. [Google Scholar] [CrossRef]
- Ren, Q.; Man, K.L.; Li, M.; Gao, B.; Ma, J. Intelligent design and implementation of blockchain and Internet of things-based traffic system. Int. J. Distrib. Sens. Netw. 2019, 15, 1–12. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, T.; Qiu, T.; Lv, N.; Pei, Q. Smart-Contract-Based Economical Platooning in Blockchain-Enabled Urban Internet of Vehicles. IEEE Trans. Ind. Inform. 2020, 16, 4122–4133. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, J.; Xu, G.; Zhang, Z.; Wang, H.; Dai, H.N.; Wu, Y.; Wang, W. SCTSC: A Semicentralized Traffic Signal Control Mode with Attribute-Based Blockchain in IoVs. IEEE Trans. Comput. Soc. Syst. 2019, 6, 1373–1385. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D. Adaptive Traffic Signal Control Mechanism for Intelligent Transportation Based on a Consortium Blockchain. IEEE Access 2019, 7, 97281–97295. [Google Scholar] [CrossRef]
- Kamal, M.A.S.; Hayakawa, T.; Imura, J. Development and Evaluation of an Adaptive Traffic Signal Control Scheme Under a Mixed-Automated Traffic Scenario. IEEE Trans. Intell. Transp. Syst. 2020, 21, 590–602. [Google Scholar] [CrossRef]
- Dai, R.; Ding, C.; Wu, X.; Yu, B.; Lu, G. Coupling Control of Traffic Signal and Entry Lane at Isolated Intersections Under the Mixed-Autonomy Traffic Environment. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10628–10642. [Google Scholar] [CrossRef]
- Rafter, C.B.; Anvari, B.; Box, S.; Cherrett, T. Augmenting Traffic Signal Control Systems for Urban Road Networks with Connected Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1728–1740. [Google Scholar] [CrossRef]
- Pham, V.H.; Ahn, H.S. Distributed Stochastic MPC Traffic Signal Control for Urban Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8079–8096. [Google Scholar] [CrossRef]
- Xu, K.; Huang, J.; Kong, L.; Yu, J.; Chen, G. PV-TSC: Learning to Control Traffic Signals for Pedestrian and Vehicle Traffic in 6G Era. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7552–7563. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, M.; Hong, W.; Wang, C.; Tao, G.; Wang, Y. Optimizing Signal Timing Control for Large Urban Traffic Networks Using an Adaptive Linear Quadratic Regulator Control Strategy. IEEE Trans. Intell. Transp. Syst. 2022, 23, 333–343. [Google Scholar] [CrossRef]
- Long, G.; Wang, A.; Jiang, T. Traffic Signal Self-Organizing Control with Road Capacity Constraints. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18502–18511. [Google Scholar] [CrossRef]
- Ma, D.; Zhou, B.; Song, X.; Dai, H. A Deep Reinforcement Learning Approach to Traffic Signal Control with Temporal Traffic Pattern Mining. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11789–11800. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).