Dependence of the Preload on the Tightening Torque for Hydraulic Plugs
Abstract
1. Introduction
2. Materials and Methods
- Calibration of the torque wrench and force sensors of the plugs.
- Lubrication of the threads.
- Tightening of the plugs till loose contact with valve housing.
- Placement of the torque wrench on the plug head.
- Zeroing of the sensors.
- Tightening and loosening of the plugs three times.
- Removing the plugs.
- Degreasing of plug and valve threads.
- Repetition of steps from 3 to 7.
Data Processing
3. Results
4. Discussion
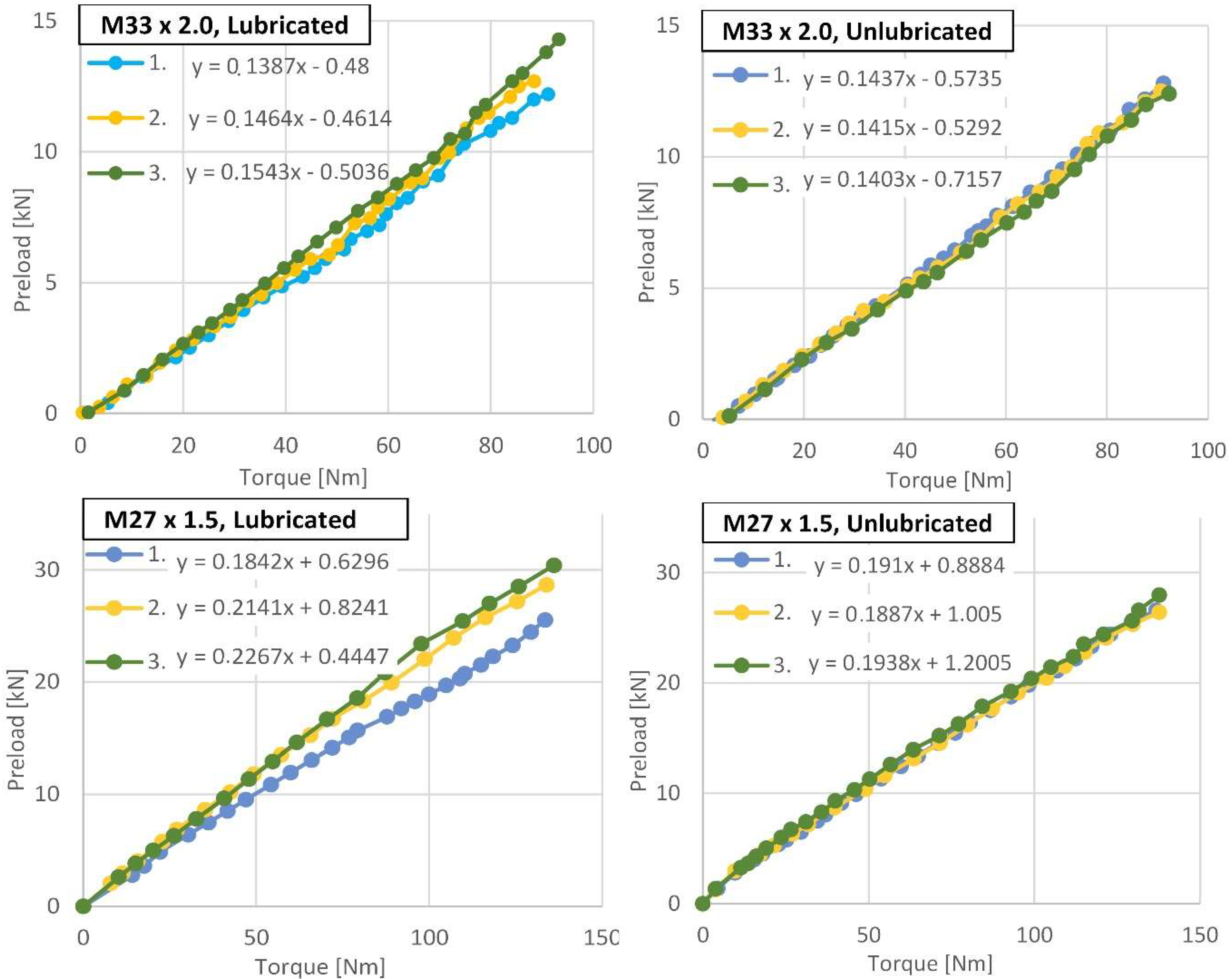
4.1. Determination of the Preload–Torque Relationship Requires Measurements
4.2. Average Tightening Results and Influence of Lubrication
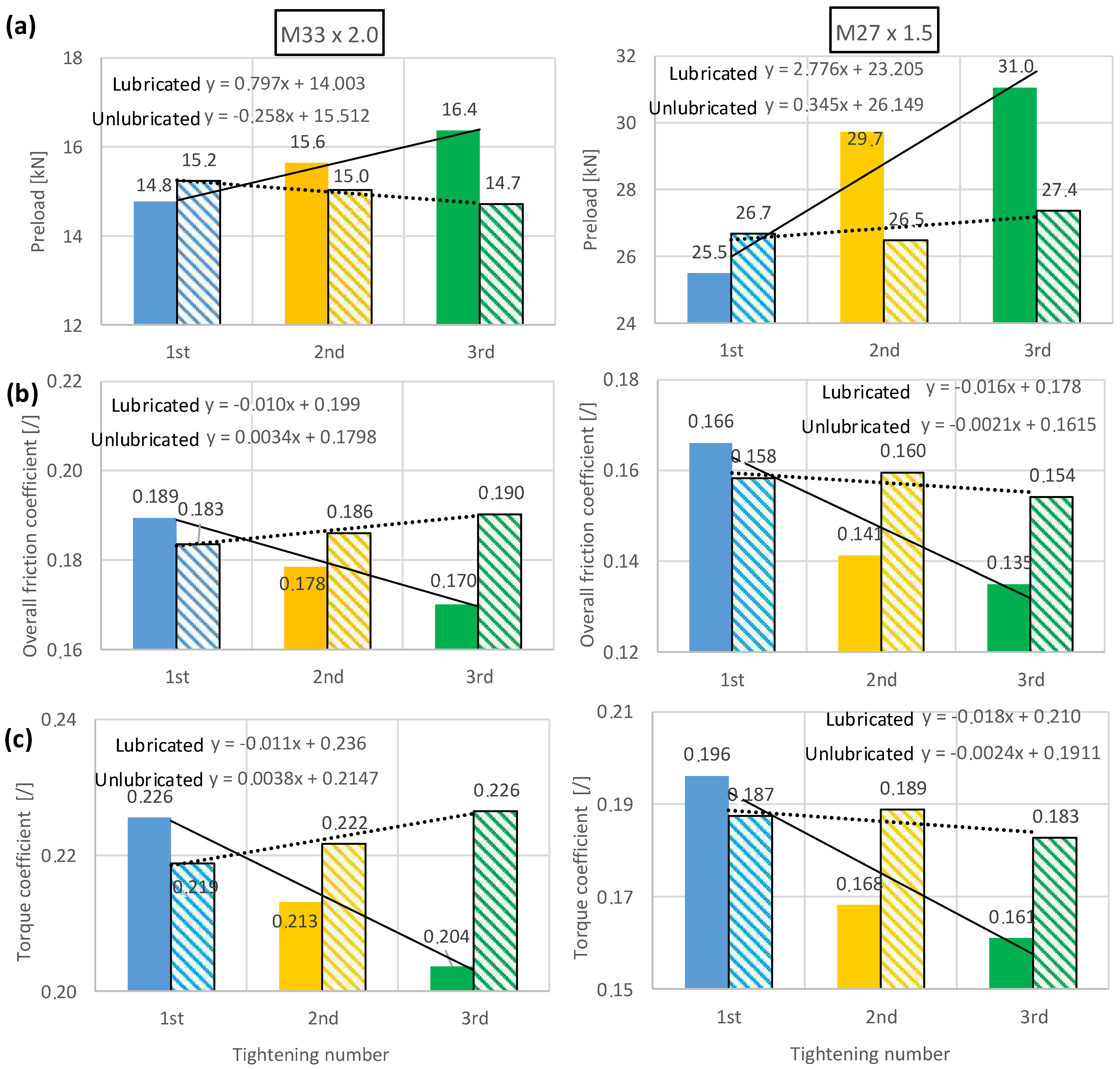
4.3. Repeated Tightening Influence
4.4. Minimization of Repeated Tightening Influence
4.5. Preload Error in Case of Usage of Friction Coefficients from the Literature
4.6. Limitations and Future Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
Appendix A.1. Calibration of the Force Sensors

Appendix A.2. Calibration of the Torque Wrench
References
- Čelik, A.; Jerman, B.; Majdič, F. Design guidelines for non-standard plugs. In Proceedings of the International Conference Fluid Power 2023, Maribor, Slovenia, 20–21 September 2023. [Google Scholar]
- Lovrec, D.; Kalb, R.; Tic, V. Ionic Hydraulic Fluids and Seal-Material Compatibility. Appl. Sci. 2024, 14, 2187. [Google Scholar] [CrossRef]
- Lovrec, D.; Tic, V. Suitability of Test Procedures for Determining the Compatibility of Seal Materials with Ionic Hydraulic Fluids. Polymers 2024, 16, 2551. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Pérez, A.M.; Pulido-Calvo, I. Analysis and viability of microturbines in hydraulic networks: A case study. J. Water Supply Res. Technol. AQUA 2019, 68, 474–482. [Google Scholar] [CrossRef]
- Okorn, I.; Nagode, M.; Klemenc, J.; Oman, S. Analysis of Additional Load and Fatigue Life of Preloaded Bolts in a Flange Joint Considering a Bolt Bending Load. Metals 2021, 11, 449. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design; McGrawHill: New York, NY, USA, 2011. [Google Scholar]
- Schmid, S.R.; Hamrock, B.J.; Jacobson, B.O. Fundamentals of Machine Elements; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Bickford, J. An Introduction to the Design and Behavior of Bolted Joints, 3rd ed.; Revised and Expanded; Taylor & Francis: New York, NY, USA, 1995. [Google Scholar]
- Drumheller, J. Fundamentals of Torque-Tension and Coefficient of Friction Testing; White Paper 21; PCB Piezotronics: Depew, NY, USA, 2021. [Google Scholar]
- Shoberg, R.S. Engineering Fundamentals of Threaded Fastener Design and Analysis. Fastening 2000, 6, 26–29. [Google Scholar]
- Alsardia, T. Bolt Preload Variations During Repeated Tightenings. Acta Polytech. Hung. 2024, 21, 133–150. [Google Scholar] [CrossRef]
- Nassar, S.A.; El-Khiamy, H.; Barber, G.C.; Zou, Q.; Sun, T.S. An experimental study of bearing and thread friction in fasteners. J. Tribol.-T Asme 2005, 127, 263–272. [Google Scholar] [CrossRef]
- Nassar, S.A.; Ganeshmurthy, S.; Ranganathan, R.M.; Barber, G.C. Effect of tightening speed on the torque-tension and wear pattern in bolted connections. J. Press Vess.-T Asme 2007, 129, 426–440. [Google Scholar] [CrossRef]
- Eliaz, N.; Gheorghiu, G.; Sheinkopf, H.; Levi, O.; Shemesh, G.; Ben-Mordechai, A.; Artzi, H. Failures of bolts in helicopter main rotor drive plate assembly due to improper application of lubricant. Eng. Fail. Anal. 2003, 10, 443–451. [Google Scholar] [CrossRef]
- Miao, R.S.; Shen, R.L.; Zhang, S.H.; Xue, S.L. A Review of Bolt Tightening Force Measurement and Loosening Detection. Sensors 2020, 20, 3165. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Vincenzi, N. Failure analysis of bolted joints Effect of friction coefficients in torque-preloading relationship. Eng. Fail. Anal. 2011, 18, 364–373. [Google Scholar] [CrossRef]
- Motosh, N. Development of Design Charts for Bolts Preloaded up to Plastic Range. J. Eng. Ind.-T Asme 1976, 98, 849–851. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Vincenzi, N. Experimental Analysis on the Tightening Torque—Preloading Force Relationship in Threaded Fasteners. Proc. Asme Int. Mech. Eng. Congr. Expo. 2012, 3 Pts A and B, 525–533. [Google Scholar]
- Cabrera, M.; Tizani, W.; Ninic, J.; Wang, F.Y. Experimental and numerical analysis of preload in Extended Hollo-Bolt blind bolts. J. Constr. Steel Res. 2021, 186, 106885. [Google Scholar] [CrossRef]
- VDI 2230; Systematic Calculation of High Duty Bolted Joints—Joints with One Cylindrical Bolt. Verein Deutscher Ingenieure (VDI): Düsseldorf, Germany, 2014.
- DIN EN ISO 16047:2005-10; Fasteners—Torque/Clamp Force Testing. Deutsches Institut für Normung: Berlin, Germany, 2005.
- Ganeshmurthy, S.; Nassar, S.A. Finite Element Simulation of Process Control for Bolt Tightening in Joints With Nonparallel Contact. J. Manuf. Sci. Eng.-T Asme 2014, 136, 021018. [Google Scholar] [CrossRef]
- Yazawa, S.; Hongo, K. Distribution of Load in the Screw Thread of a Bolt Nut Connection Subjected to Tangential Forces and Bending Moments. Jsme Int. J. I-Solid Mech. Strength Mater. 1988, 31, 174–180. [Google Scholar] [CrossRef][Green Version]
- Yu, Q.M.; Zhou, H.L.; Wang, L.B. Finite element analysis of relationship between tightening torque and initial load of bolted connections. Adv. Mech. Eng. 2015, 7, 1687814015588477. [Google Scholar] [CrossRef]
- Eccles, W.; Sherrington, I.; Arnell, R.D. Frictional changes during repeated tightening of zinc plated threaded fasteners. Tribol. Int. 2010, 43, 700–707. [Google Scholar] [CrossRef]
- Morgan, R.C.; Henshall, J.L. The torque-tension behaviour of 22 × 1.5 mm bolts for fixing spigot-located wheels on heavy commercial vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1996, 210, 209–214. [Google Scholar] [CrossRef]
- Güler, B.; Gürsel, K.T. Experimental analysis of the friction coefficient effect of the zinc-lamella coated fasteners on bolt preload and tightening momentExperimentelle Analyse der Wirkung des Reibungskoeffizienten von Zink-Lamelle beschichteten Befestigungselementen auf Schrauben-Vorspannkraft und-Anzugsmoment. Mater. Werkst 2019, 50, 696–705. [Google Scholar] [CrossRef]
- Zheng, M.P.; Liu, Z.F.; Yan, X.; Niu, N.N.; Zhang, T.; Li, Y. Initial losing behavior of pre-tightening force for threaded fastener during repeated tightening. Eng. Fail. Anal. 2022, 134, 106021. [Google Scholar] [CrossRef]
- EN 10277:2018; Bright Steel Products—Technical Delivery Conditions. European Committee for Standardization (CEN): Brussels, Belgium, 2018.
- Strain Gage Bridge Configurations. Available online: https://www.ni.com (accessed on 22 November 2024).
- Klöcker, M.; Westphal, S. Investigations of friction-relevant parameters to ensure reliable bolted joints. MATEC Web. Conf. 2017, 94, 04007. [Google Scholar] [CrossRef]


| Plug–Valve Connection | Condition | Preload [kN] | Overall Friction Coefficient [/] | Torque Coefficient [/] |
|---|---|---|---|---|
| M33 × 2.0 | Lubricated | 15.60 ± 0.65 b** | 0.18 ± 0.008 b* | 0.21 ± 0.009 b* |
| Unlubricated | 15.00 ± 0.21 b*** | 0.19 ± 0.003 b*** | 0.22 ± 0.003 b*** | |
| M27 × 1.5 | Lubricated | 28.76 ± 2.37 | 0.15 ± 0.013 | 0.18 ± 0.015 |
| Unlubricated | 26.84 ± 0.38 | 0.16 ± 0.002 | 0.19 ± 0.003 |
| Relative Dimension | M33 × 2.0 | M27 × 1.5 | Difference Relative to M33 [%] |
|---|---|---|---|
| 0.83 | 0.85 | −2.4 | |
| 0.030 | 0.028 | 6.7 | |
| 0.0164 | 0.0094 | 42.7 | |
| 0.80 | 0.92 | −15.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hladnik, J.; Majdič, F.; Čelik, A.; Jerman, B. Dependence of the Preload on the Tightening Torque for Hydraulic Plugs. Appl. Sci. 2024, 14, 11920. https://doi.org/10.3390/app142411920
Hladnik J, Majdič F, Čelik A, Jerman B. Dependence of the Preload on the Tightening Torque for Hydraulic Plugs. Applied Sciences. 2024; 14(24):11920. https://doi.org/10.3390/app142411920
Chicago/Turabian StyleHladnik, Jurij, Franc Majdič, Anže Čelik, and Boris Jerman. 2024. "Dependence of the Preload on the Tightening Torque for Hydraulic Plugs" Applied Sciences 14, no. 24: 11920. https://doi.org/10.3390/app142411920
APA StyleHladnik, J., Majdič, F., Čelik, A., & Jerman, B. (2024). Dependence of the Preload on the Tightening Torque for Hydraulic Plugs. Applied Sciences, 14(24), 11920. https://doi.org/10.3390/app142411920






