Three-Dimensional MT Conductive Anisotropic and Magnetic Modeling Using A − ϕ Potentials Employing a Mixed Nodal and Edge-Based Element Method
Abstract
1. Introduction
2. Methods
2.1. A − ϕ Formulations
2.2. Boundary Conditions
2.3. Finite Element Method Analysis
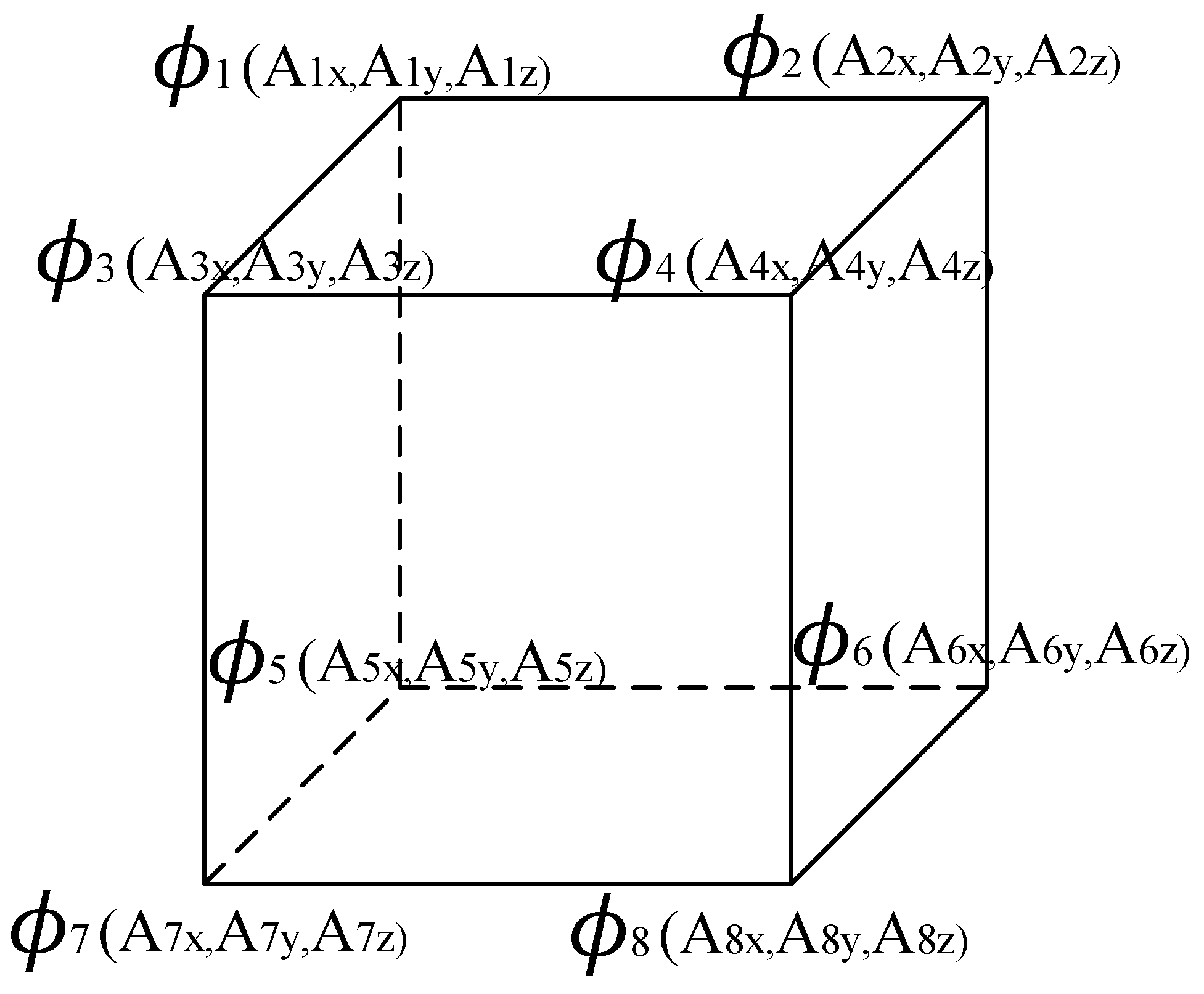
2.3.1. Mixed Nodal and Edge-Based Elements
2.3.2. Galerkin Method of Weighted Residuals
- (1)
- Multiply both sides of Equation (8) by , and then perform integration over the entire study domain, as follows:
- (2)
- Considering the divergence theorem (Equation (19)),
2.3.3. Electromagnetic Fields
2.4. Parameters Selection
3. Results
3.1. Validating the Accuracy
3.1.1. One-Dimensional Magnetic Model
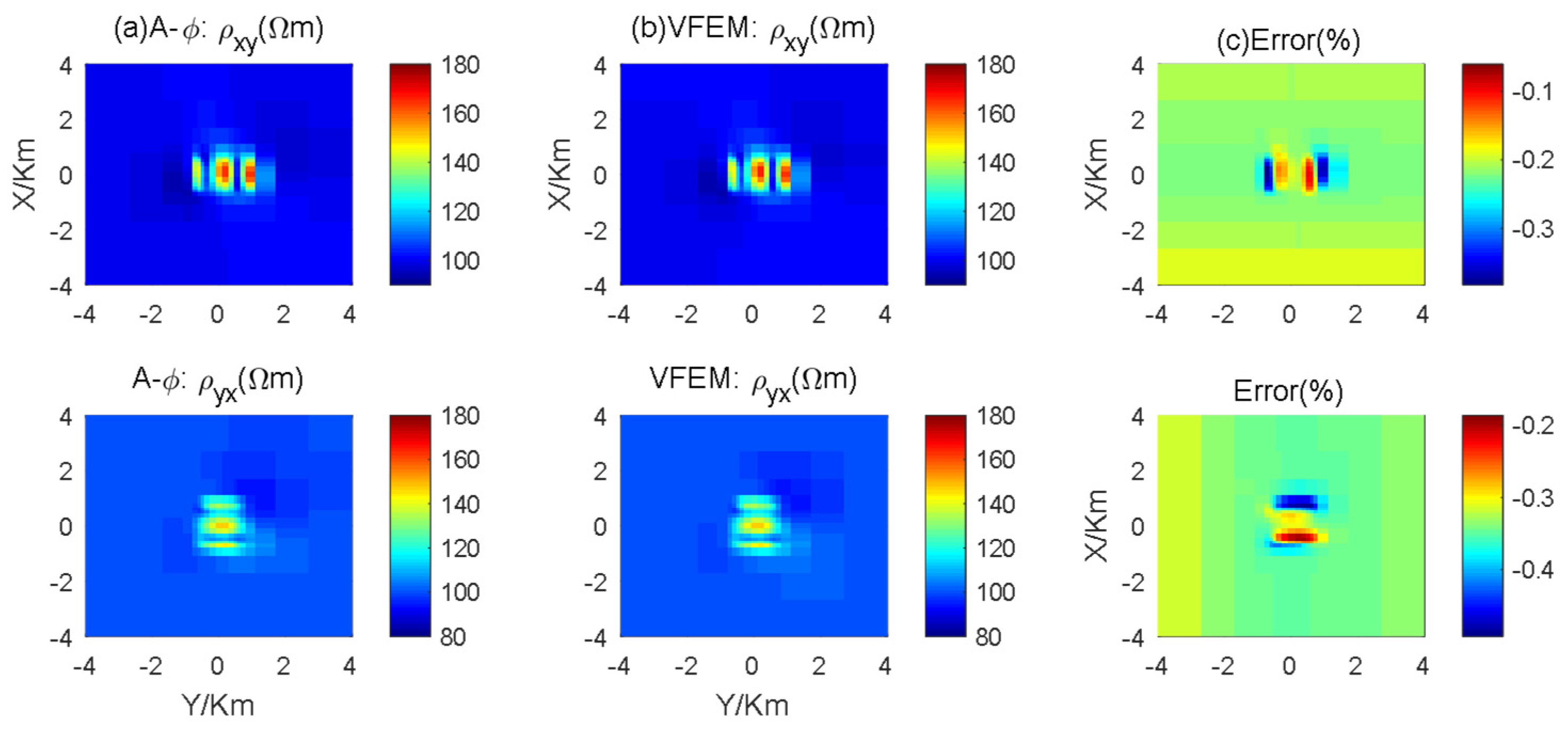
3.1.2. Three-Dimensional Anisotropic Model
3.2. Typical Models
3.2.1. Deep-Depth Model
3.2.2. Marine Model
4. Discussion
4.1. Advantages of Mixed Elements over Nodal Elements
4.2. Typical Models
4.2.1. Deep-Depth Model
4.2.2. Marine Model
5. Conclusions
- (1)
- The algorithm, whether applied at low frequencies (0.001 Hz) or in cases of high resistive contrasts, demonstrates robust performance; it works well for modeling deep Earth and ocean models with strong resistivity contrasts.
- (2)
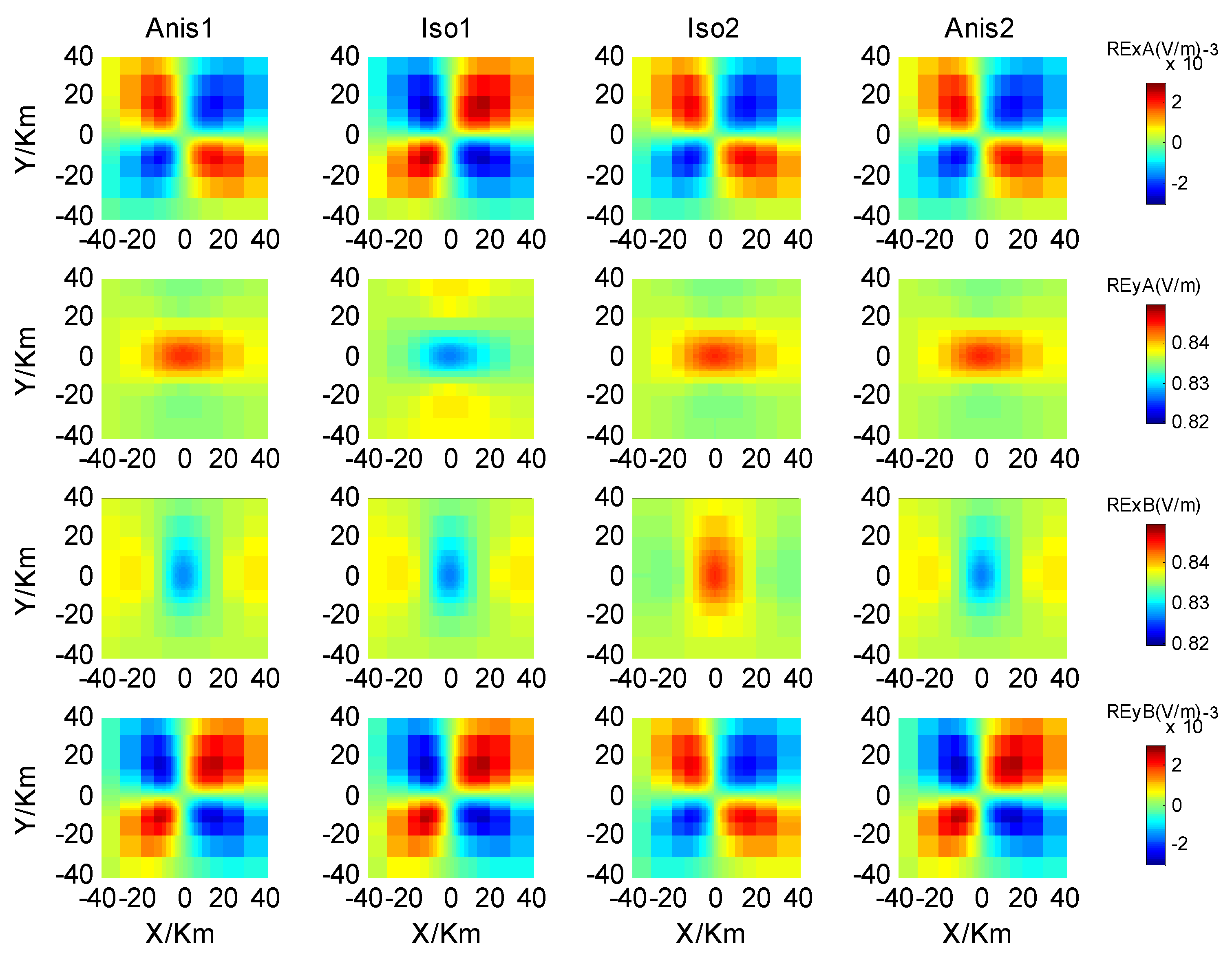
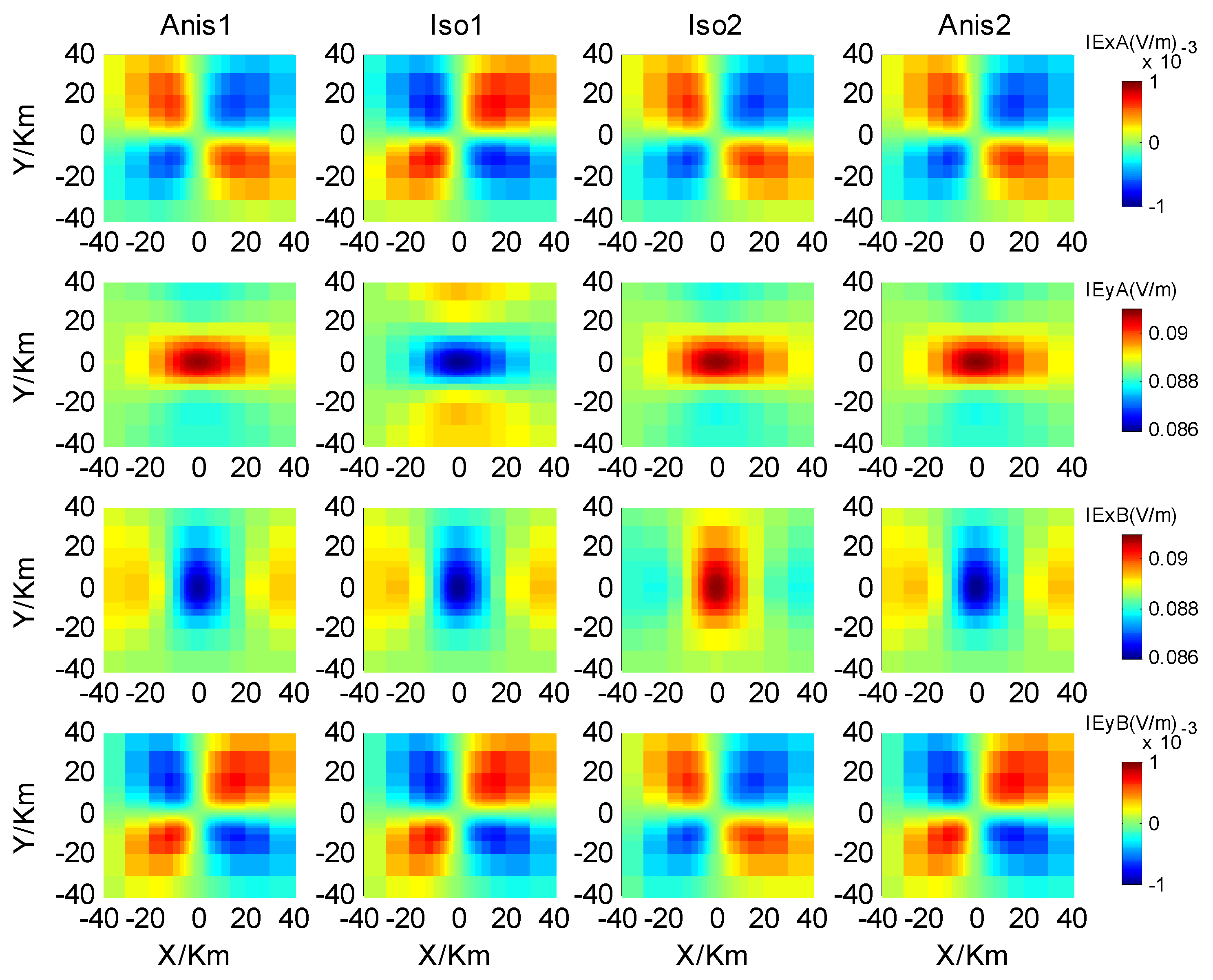
- The horizontal electric fields induced by Ex are predominantly influenced by conductivity in the x-direction, while the horizontal electric fields induced by Ey are primarily influenced by conductivity in the y-direction. Conductivity in the z-direction has a negligible impact on the horizontal electric fields. Additionally, it would be helpful to explain the effect of anisotropy on MT responses in practical surveys.
- (3)
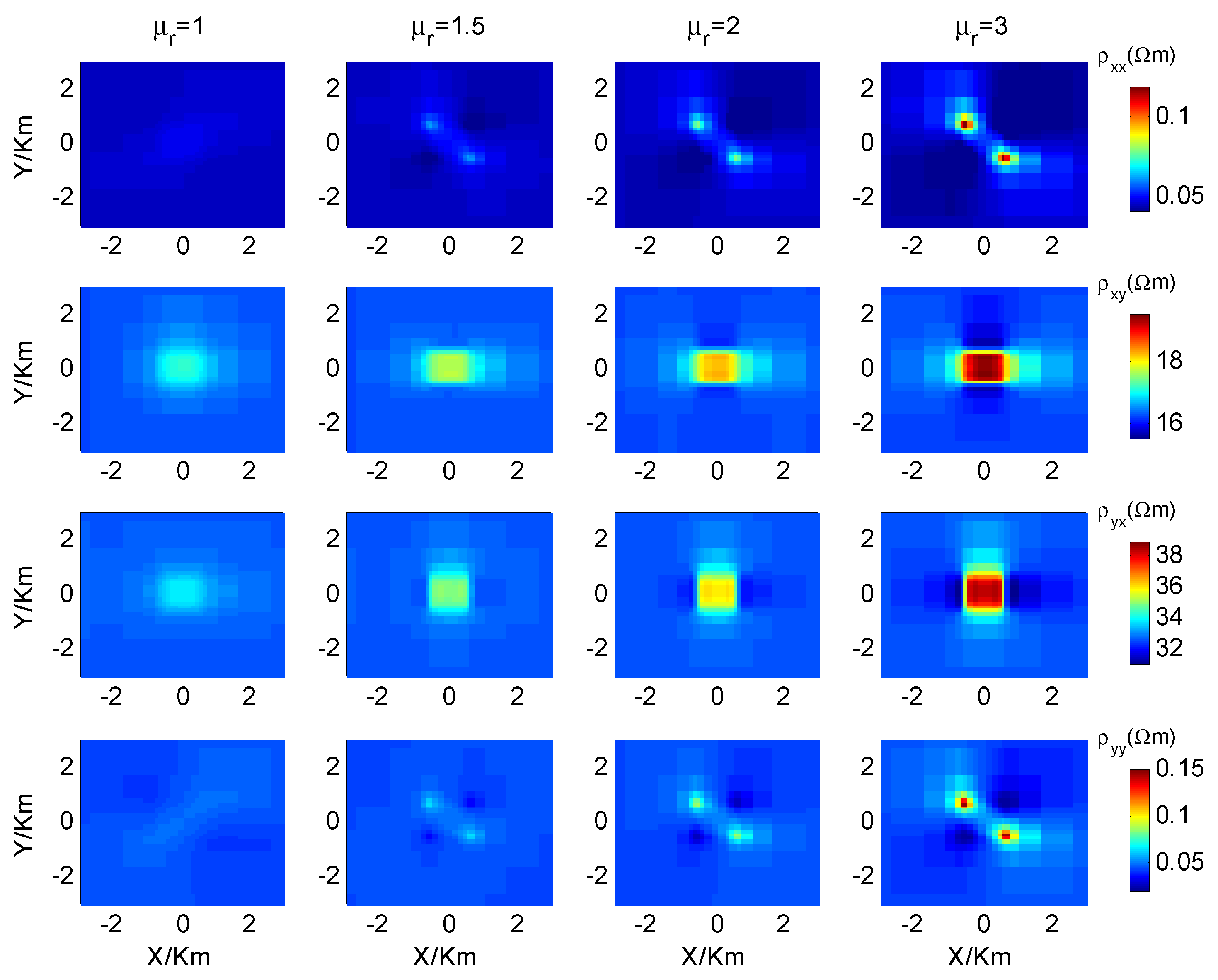
- More attention on evaluating the influences of magnetic permeability in magnetite-rich areas is needed. The practical geological environment of Earth is extremely complex; the apparent resistivities and phases could be significantly distorted, or even reversed, due to the existence of non-zero magnetic susceptibility.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chave, A.D.; Jones, A.G. (Eds.) The Magnetotelluric Method: Theory and Practice; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Varentsov, I.M.; Kulikov, V.A.; Yakovlev, A.G.; Yakovlev, D.V. Possibilities of magnetotelluric methods in geophysical exploration for ore minerals. Izv. Phys. Solid Earth 2013, 49, 309–328. [Google Scholar] [CrossRef]
- Tan, H.D.; Yu, Q.F.; Booker, J.; Wei, W. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method. Chin. J. Geophys. 2003, 46, 705–711. [Google Scholar]
- Cai, H.; Xiong, B.; Han, M.; Zhdanov, M. 3D controlled-source electromagnetic modeling in anisotropic medium using edge-based finite element method. Comput. Geosci. 2014, 73, 164–176. [Google Scholar] [CrossRef]
- Ren, Z.H.; Chen, C.; Tang, J. Accurate volume integral solutions of direct current resistivity potentials for inhomogeneous conductivities in half space. J. Appl. Geophys. 2018, 151, 40–46. [Google Scholar] [CrossRef]
- Haber, E.; Ascher, U.M.; Aruliah, D.A.; Oldenburg, D.W. Fast simulation of 3D electromagnetic problems using potentials. J. Comput. Phys. 2000, 163, 150–171. [Google Scholar] [CrossRef]
- Badea, E.A.; Everett, M.E.; Newman, G.A.; Biro, O. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials. Geophysics 2001, 66, 786–799. [Google Scholar] [CrossRef]
- Xiao, T.; Huang, X.; Wang, Y. Three-dimensional magnetotelluric modelling in anisotropic media using the A-phi method. Explor. Geophys. 2019, 50, 31–41. [Google Scholar] [CrossRef]
- Yu, N.; Chen, Z.; Wu, X.; Kong, W.; Chen, H.; Li, T.; Feng, X. Unstructured grid finite element modeling of the three-dimensional magnetotelluric responses in a model with arbitrary conductivity and magnetic susceptibility anisotropies. IEEE Trans. Geosci. Remote Sens. 2024, 62, 2002013. [Google Scholar] [CrossRef]
- Linde, N.; Pedersen, L.B. Evidence of electrical anisotropy in limestone formations using the RMT technique. Geophysics 2004, 69, 909–916. [Google Scholar] [CrossRef]
- Wannamaker, P.E. Anisotropy versus heterogeneity in continental solid earth electromagnetic studies: Fundamental response characteristics and implications for physicochemical state. Surv. Geophys. 2005, 26, 733–765. [Google Scholar] [CrossRef]
- Evans, R.L.; Hirth, G.; Baba, K.; Forsyth, D.; Chave, A.; Mackie, R. Geophysical evidence from the MELT area for compositional controls on oceanic plates. Nature 2005, 437, 249. [Google Scholar] [CrossRef] [PubMed]
- Pek, J.; Verner, T. Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media. Geophys. J. Int. 1997, 128, 505–521. [Google Scholar] [CrossRef]
- Kong, W.; Lin, C.; Tan, H.; Peng, M.; Tong, T.; Wang, M. The effects of 3D electrical anisotropy on magnetotelluric responses: Synthetic case studies. J. Environ. Eng. Geophys. 2018, 23, 61–75. [Google Scholar] [CrossRef]
- Li, Y. Finite Element Modeling of Electromagnetic Fields in Two-and Three-Dimensional Anisotropic Conductivity Structures. Ph.D. Thesis, University of Gottingen, Gottingen, Germany, 2000. [Google Scholar]
- Löwer, A.; Junge, A. Magnetotelluric Transfer Functions: Phase Tensor and Tipper Vector above a Simple Anisotropic Three-Dimensional Conductivity Anomaly and Implications for 3D Isotropic Inversion. Pure Appl. Geophys. 2017, 174, 2089–2101. [Google Scholar] [CrossRef]
- Xiao, T.; Liu, Y.; Wang, Y.; Fu, L.Y. Three-dimensional magnetotelluric modeling in anisotropic media using edge-based finite element method. J. Appl. Geophys. 2018, 149, 1–9. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Z.; Li, Y. Adaptive finite element modelling of three-dimensional magnetotelluric fields in general anisotropic media. J. Appl. Geophys. 2018, 151, 113–124. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, X.; Xiao, T.; Cai, H.; Li, J.; Peng, R.; Long, Z. Three-dimensional edge-based finite element modeling of magnetotelluric data in anisotropic media with a divergence correction. J. Appl. Geophys. 2021, 189, 104324. [Google Scholar] [CrossRef]
- Xiao, T.; Wang, Y.; Huang, X.; He, G.; Liu, J. Magnetotelluric responses of three-dimensional conductive and magnetic anisotropic anomalies. Geophys. Prospect. 2020, 68, 1016–1040. [Google Scholar] [CrossRef]
- Jin, J.M. The Finite Element Method in Electromagnetics, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Mickus, K. Magnetic Method. 2023. Available online: https://www.researchgate.net/publication/228994566_Magnetic_Method (accessed on 21 July 2024).
- Chen, L.; Xiao, T.; Liu, J.; Zheng, X.; Liu, J.; Wang, Y. One-dimensional magnetotelluric modeling in magnetic and resistive axial anisotropic media. Prog. Geophys. 2022, 37, 2373–2380. (In Chinese) [Google Scholar]
- Yadav, G.S.; Lal, T. A Fortran 77 program for computing magnetotelluric response over a stratified earth with changing magnetic permeability. Comput. Geosci. 1997, 23, 1035–1038. [Google Scholar] [CrossRef]


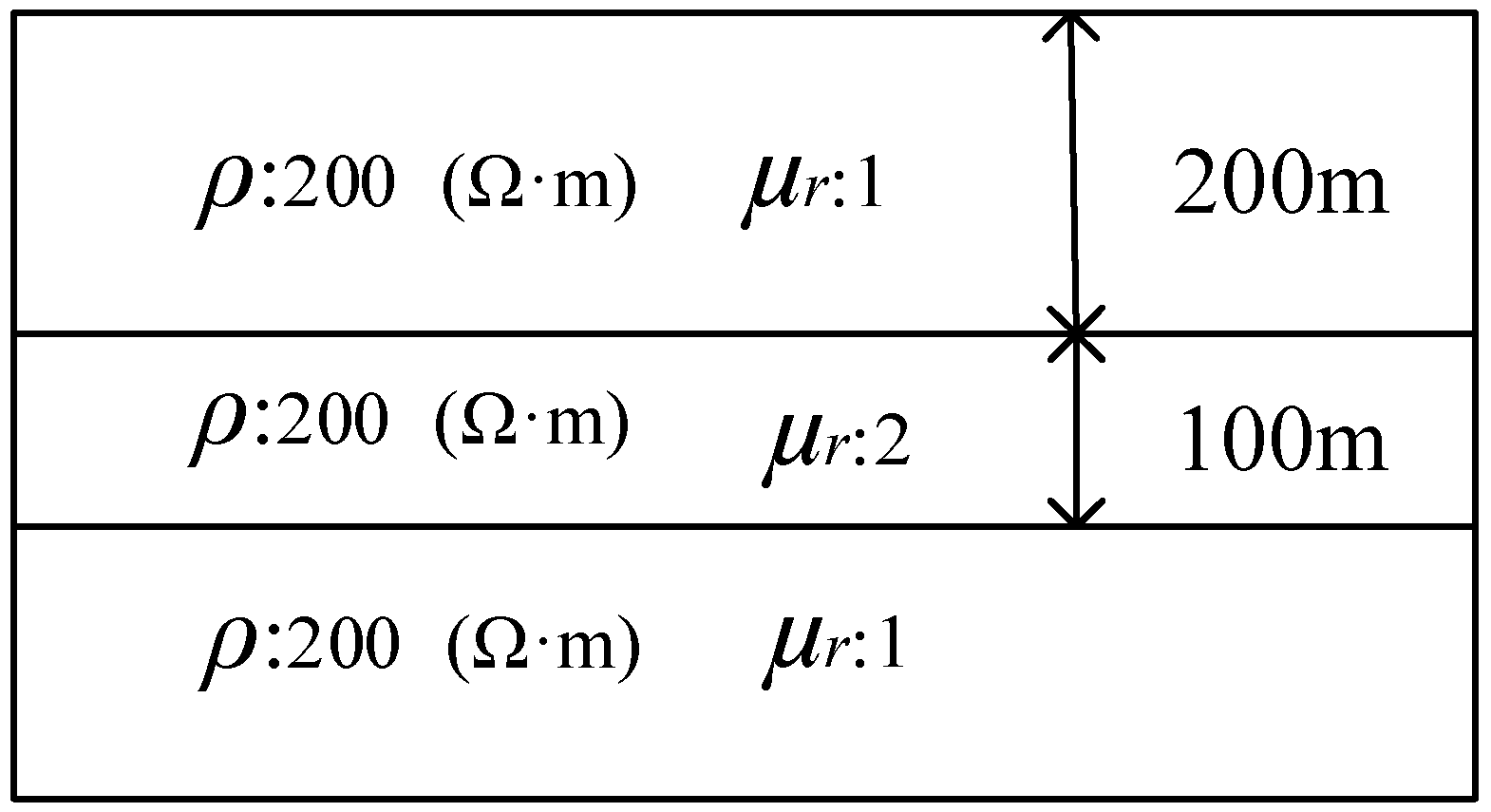
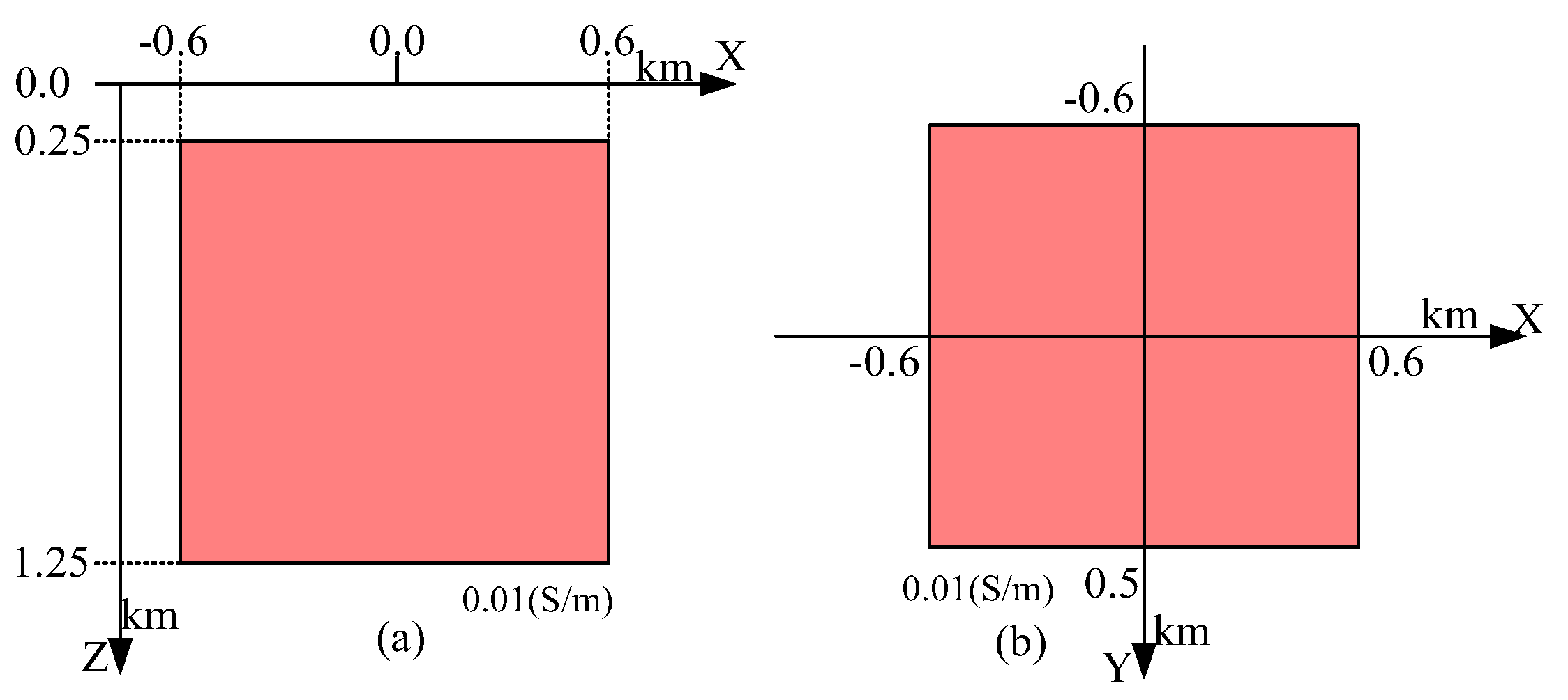


| Frequencies (Hz) | ) | Realtive Errors (%) | |
|---|---|---|---|
| 1D | 3D | ||
| 100 | 240.3 | 240.8 | 0.21 |
| 40 | 231.7 | 231.4 | 0.13 |
| 20 | 224.1 | 223.5 | 0.27 |
| Method | Grids in x-, y-, and z- Direction | Degrees of Freedom | Number of Non-Zero Elements |
|---|---|---|---|
| Nodal method | 20 × 20 × 20 | 37,044 | 1,914,046 |
| 35 × 35 × 35 | 186,624 | 9,506,418 | |
| 50 × 50 × 50 | 530,604 | 27,283,608 | |
| Mixed nodal and edge-based element method | 20 × 20 × 20 | 35,721 | 1,290,361 |
| 35 × 35 × 35 | 182,736 | 6,817,756 | |
| 50 × 50 × 50 | 522,801 | 19,763,401 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Yi, M.; Zhou, J.; Cheng, L.; Song, T.; Gong, C.; Yang, B.; Xiao, T. Three-Dimensional MT Conductive Anisotropic and Magnetic Modeling Using A − ϕ Potentials Employing a Mixed Nodal and Edge-Based Element Method. Appl. Sci. 2024, 14, 9019. https://doi.org/10.3390/app14199019
Zhou Z, Yi M, Zhou J, Cheng L, Song T, Gong C, Yang B, Xiao T. Three-Dimensional MT Conductive Anisotropic and Magnetic Modeling Using A − ϕ Potentials Employing a Mixed Nodal and Edge-Based Element Method. Applied Sciences. 2024; 14(19):9019. https://doi.org/10.3390/app14199019
Chicago/Turabian StyleZhou, Zongyi, Mingkuan Yi, Junjun Zhou, Lianzheng Cheng, Tao Song, Chunye Gong, Bo Yang, and Tiaojie Xiao. 2024. "Three-Dimensional MT Conductive Anisotropic and Magnetic Modeling Using A − ϕ Potentials Employing a Mixed Nodal and Edge-Based Element Method" Applied Sciences 14, no. 19: 9019. https://doi.org/10.3390/app14199019
APA StyleZhou, Z., Yi, M., Zhou, J., Cheng, L., Song, T., Gong, C., Yang, B., & Xiao, T. (2024). Three-Dimensional MT Conductive Anisotropic and Magnetic Modeling Using A − ϕ Potentials Employing a Mixed Nodal and Edge-Based Element Method. Applied Sciences, 14(19), 9019. https://doi.org/10.3390/app14199019





