Multi-Objective Evolutionary Neural Architecture Search with Weight-Sharing Supernet
Abstract
1. Introduction
- In this study, we design a multi-objective evolutionary NAS framework based on a weight-sharing supernet. This framework combines the population optimization strategy from evolutionary algorithms with the weight-sharing concept of one-shot models to alternately optimize the weight parameters and the architecture parameters in neural networks. It can explore promising network architectures in complex and large search spaces with high efficiency.
- We propose a bi-population MOEA/D algorithm within the above EC-NAS framework. By setting up two sub-populations to solve different optimization tasks and incorporating a communication mechanism between the sub-populations, the algorithm can thoroughly explore different regions of the search space and obtain uniformly distributed network architectures with high performance and diversity.
- Extensive experiments are conducted on several real-world image datasets of varying sizes and complexities. Compared with different types of representative NAS methods, the experimental results validate the efficiency and transferability of the proposed framework and algorithm in searching for effective neural network architectures.
2. Related Works
2.1. Reinforcement-Learning-Based Neural Architecture Search
2.2. Gradient-Based Neural Architecture Search
2.3. Evolutionary-Computation-Based Neural Architecture Search
2.3.1. Population Initialization and Encoding Strategy
2.3.2. Population Updating Strategy
2.3.3. Population Evaluation Strategy
3. Multi-Objective Evolutionary Neural Architecture Search Framework Based on Weight-Sharing Supernet
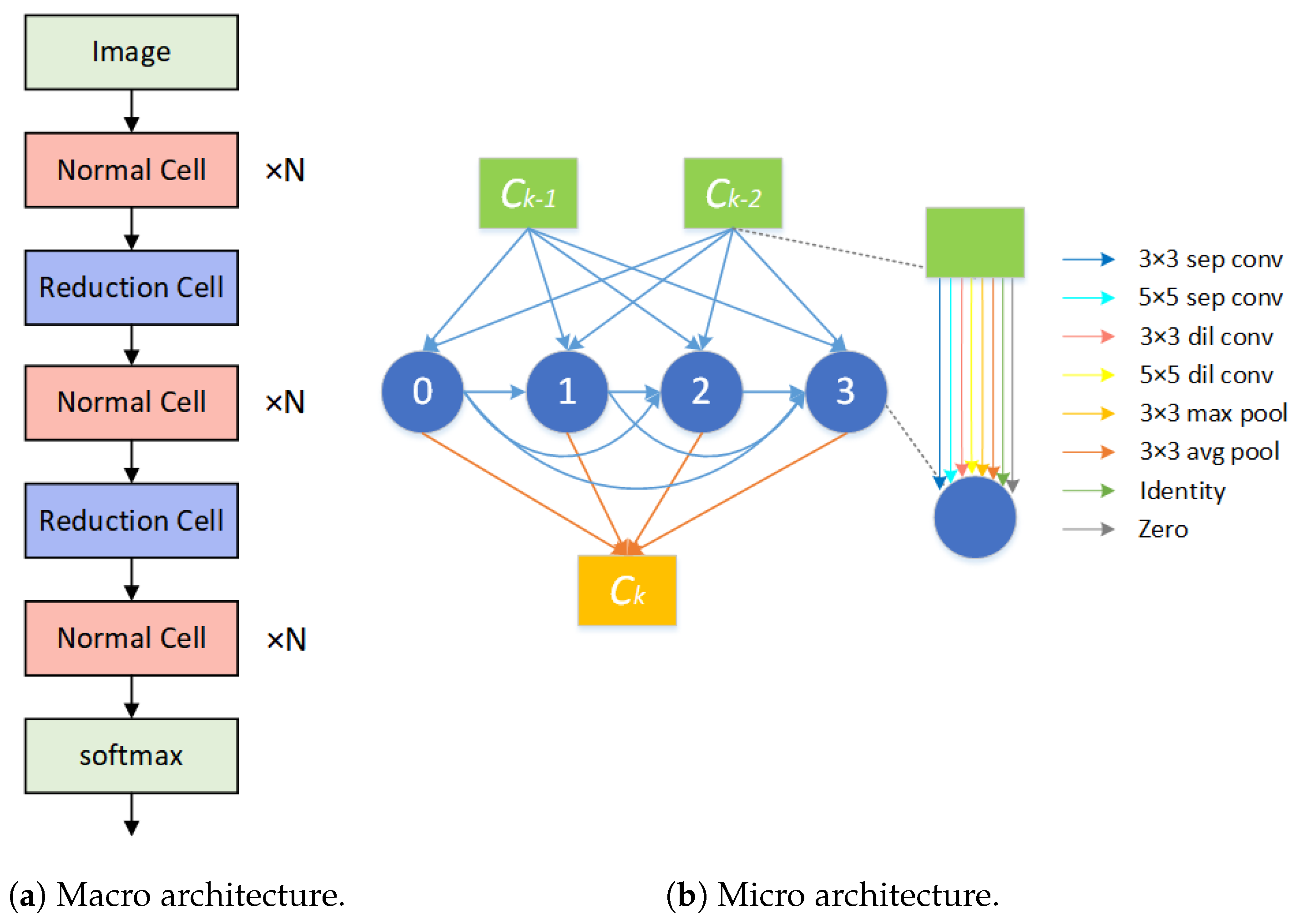
3.1. Search Space
- Convolution: and separable convolutions, and dilated separable convolutions;
- Pooling: max pooling, average pooling;
- Others: Identity, zeroize.
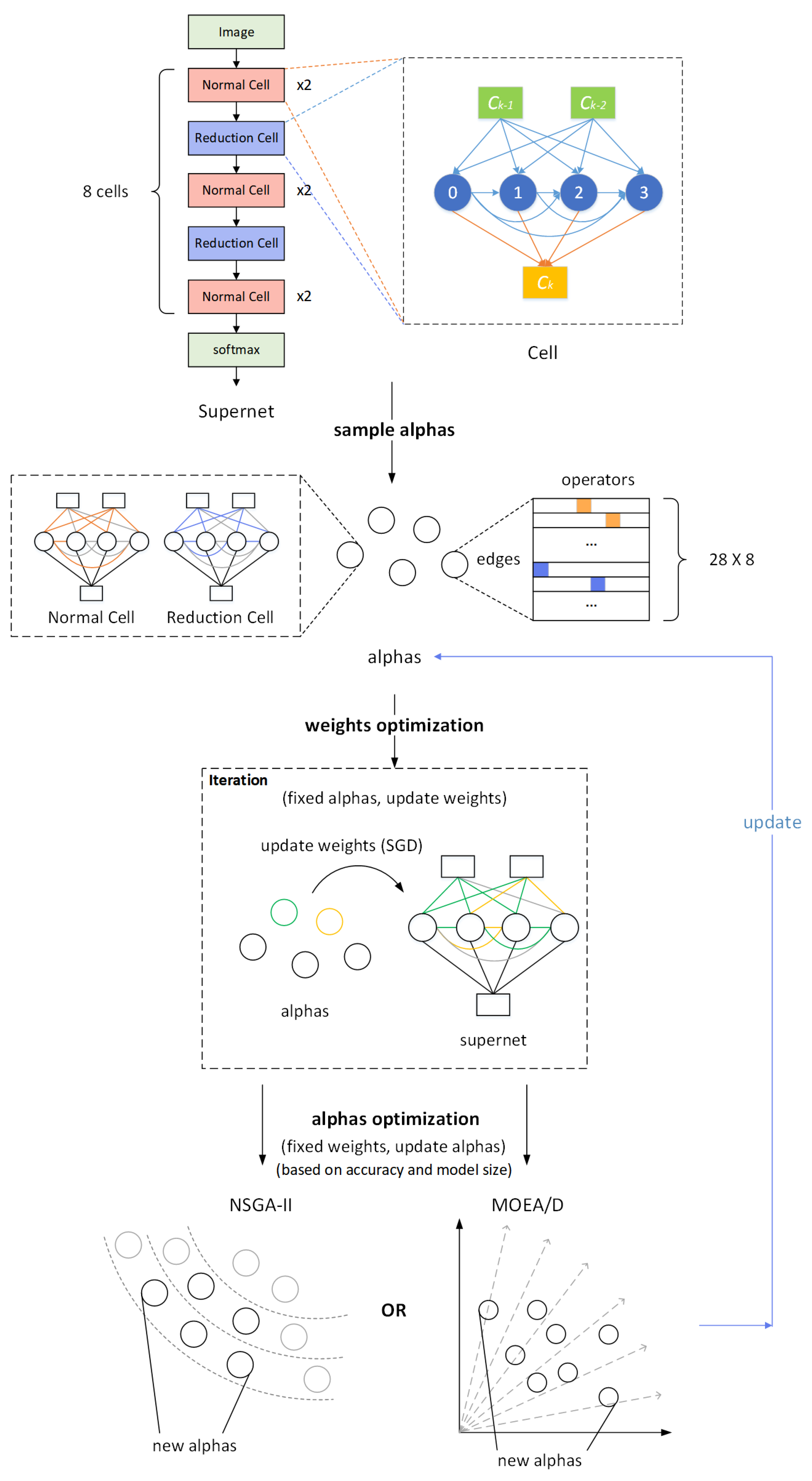
3.2. Supernet Configuration
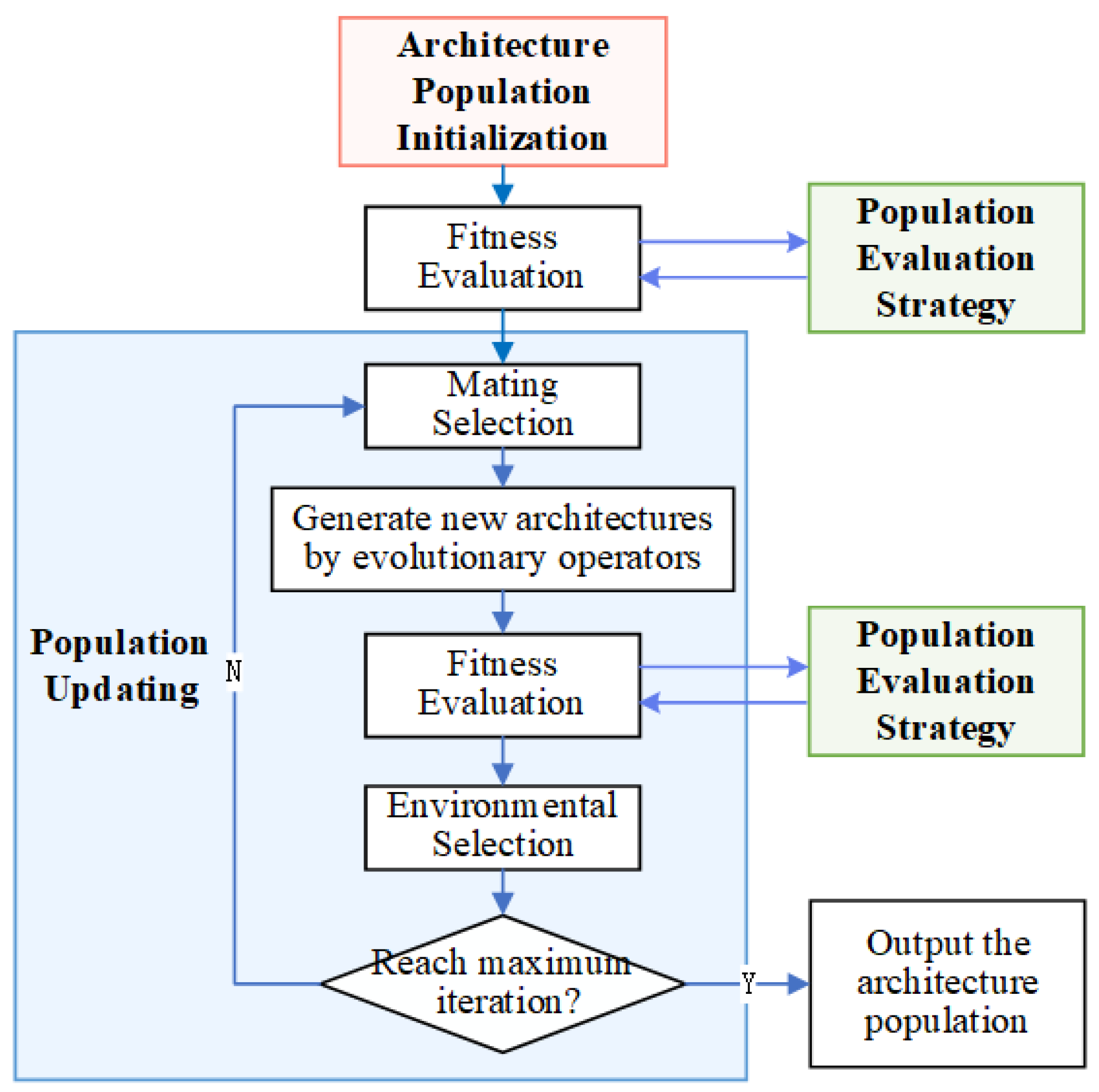
3.3. Algorithm Flow
3.3.1. Search Phase: Encoding and Population Initialization
3.3.2. Search Phase: Population Updating and Evaluation
3.3.3. Final Evaluation Phase
4. Multi-Objective Evolutionary Neural Architecture Search Algorithms
4.1. Traditional Multi-Objective Evolutionary Neural Architecture Search Algorithms
4.2. Bi-Population MOEA/D-Based Neural Architecture Search Algorithm
| Algorithm 1 Bi-population MOEA/D-based NAS algorithm |
|
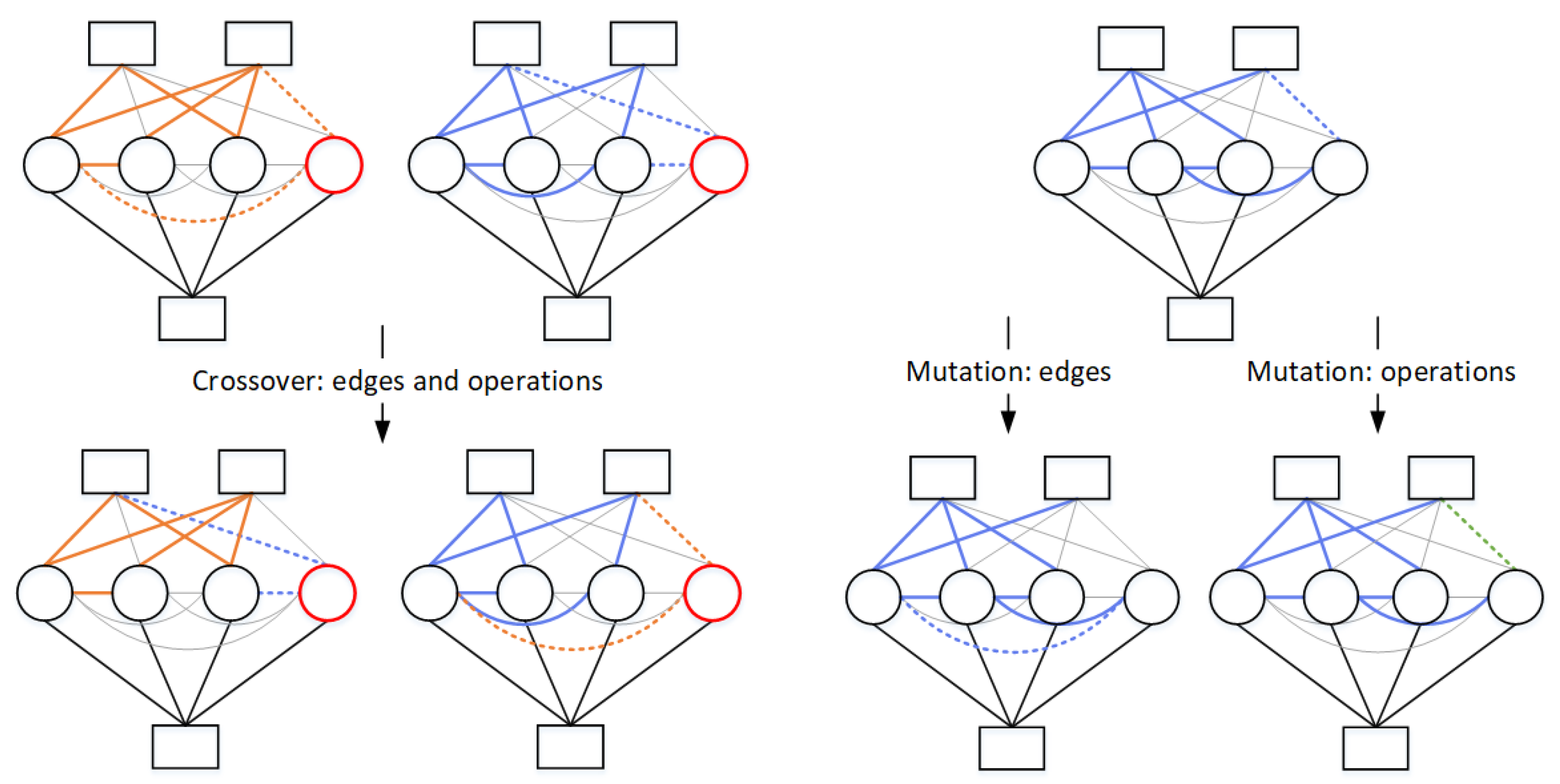
4.3. Evolutionary Operators
5. Experiments
5.1. Search Performance Comparison on CIFAR-10 Dataset
5.1.1. Experimental Settings
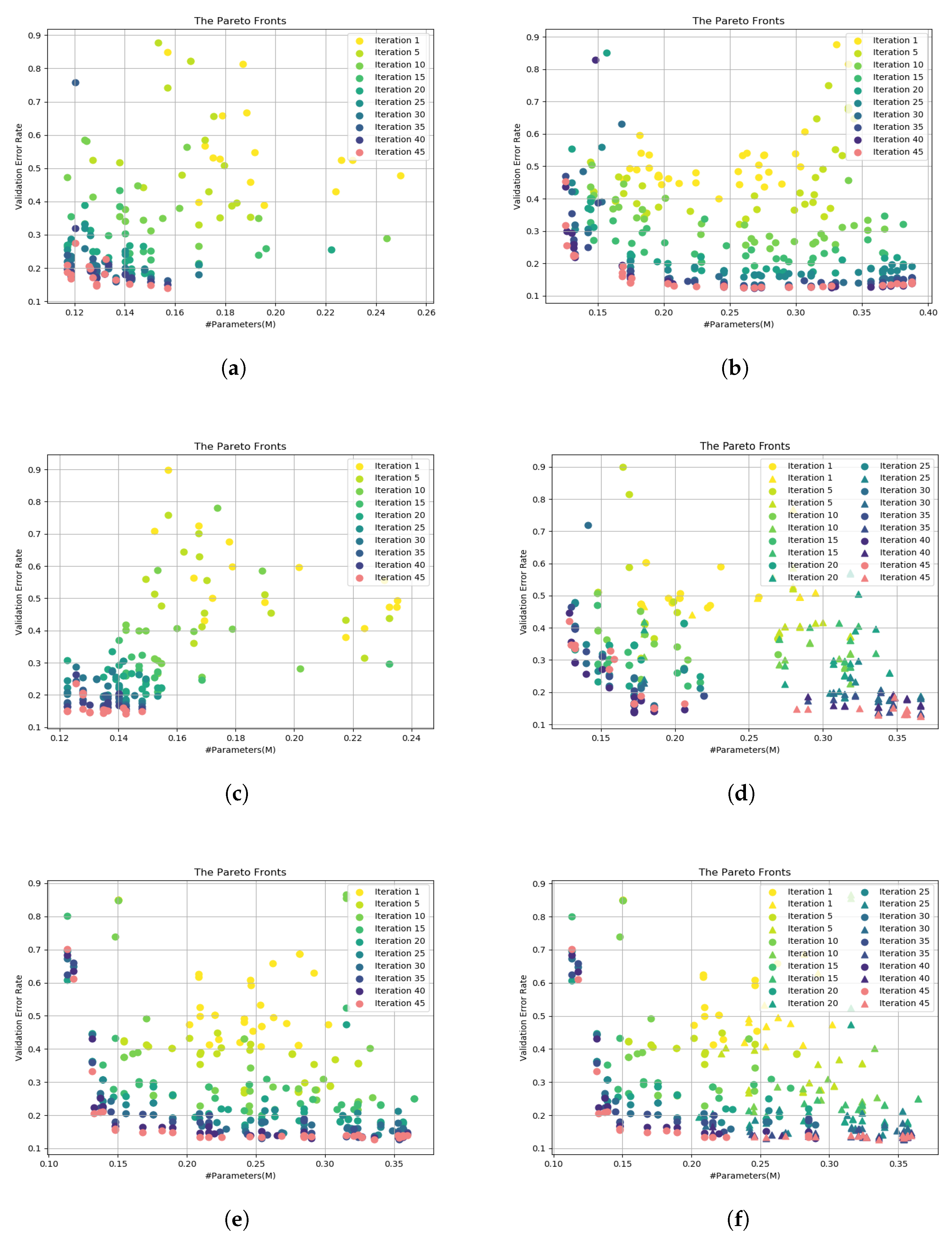
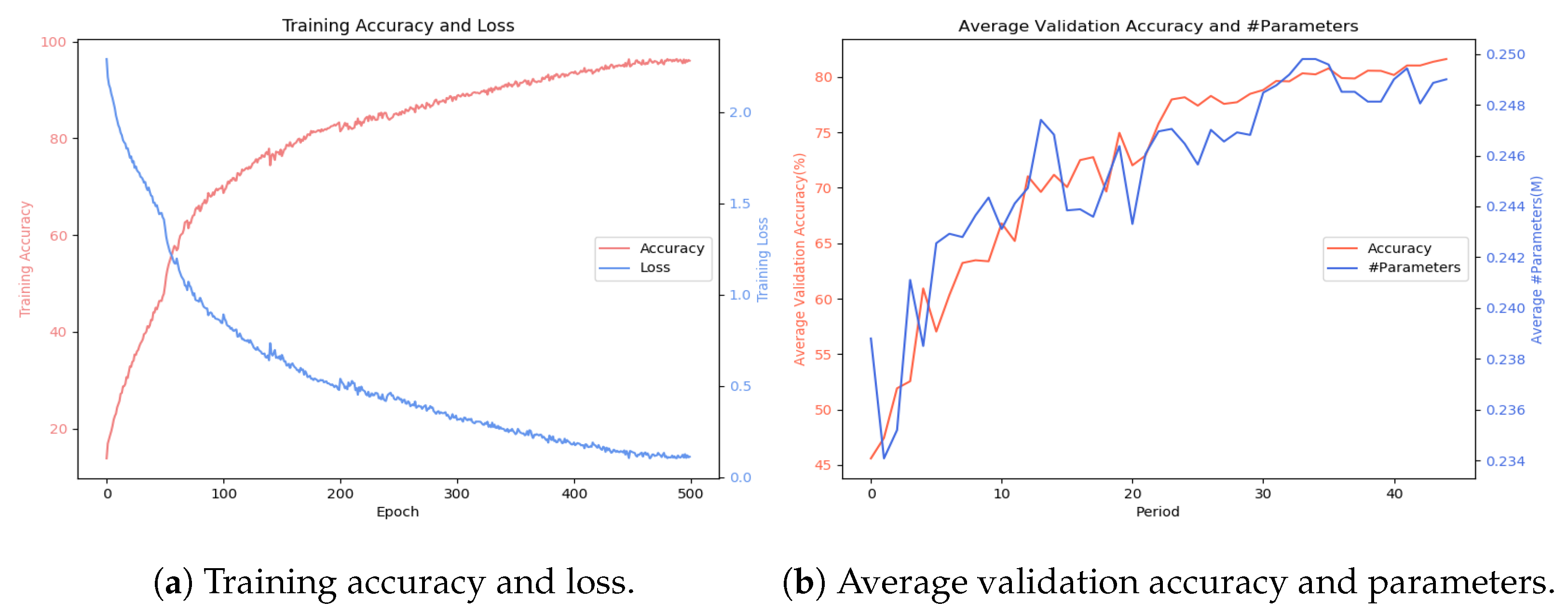
5.1.2. Experimental Results
5.2. Test Performance Comparison on CIFAR-10 Dataset
5.2.1. Comparison Algorithms
5.2.2. Experimental Results
5.3. Test Performance Comparison on Mini-ImageNet Dataset
5.3.1. Experimental Settings
5.3.2. Comparison Algorithms
5.3.3. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Zhang, Y.; Chan, W.; Jaitly, N. Very deep convolutional networks for end-to-end speech recognition. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; IEEE: New York, NY, USA, 2017; pp. 4845–4849. [Google Scholar]
- Wu, Y.; Schuster, M.; Chen, Z.; Le, Q.V.; Norouzi, M.; Macherey, W.; Krikun, M.; Cao, Y.; Gao, Q.; Macherey, K.; et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv 2016, arXiv:1609.08144. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Liu, Y.; Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G.; Tan, K.C. A survey on evolutionary neural architecture search. IEEE Trans. Neural Networks Learn. Syst. 2021, 34, 550–570. [Google Scholar] [CrossRef]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1–21. [Google Scholar]
- Lu, Z.; Whalen, I.; Boddeti, V.; Dhebar, Y.; Deb, K.; Goodman, E.; Banzhaf, W. Nsga-net: Neural architecture search using multi-objective genetic algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; pp. 419–427. [Google Scholar]
- Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-scale evolution of image classifiers. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 2902–2911. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4780–4789. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Efficient multi-objective neural architecture search via lamarckian evolution. arXiv 2018, arXiv:1804.09081. [Google Scholar]
- Yang, Z.; Wang, Y.; Chen, X.; Shi, B.; Xu, C.; Xu, C.; Tian, Q.; Xu, C. Cars: Continuous evolution for efficient neural architecture search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1829–1838. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578. [Google Scholar]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing neural network architectures using reinforcement learning. arXiv 2016, arXiv:1611.02167. [Google Scholar]
- Liu, Y.; Jia, X.; Tan, M.; Vemulapalli, R.; Zhu, Y.; Green, B.; Wang, X. Search to distill: Pearls are everywhere but not the eyes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7539–7548. [Google Scholar]
- Cai, H.; Chen, T.; Zhang, W.; Yu, Y.; Wang, J. Efficient architecture search by network transformation. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Cai, H.; Zhu, L.; Han, S. Proxylessnas: Direct neural architecture search on target task and hardware. arXiv 2018, arXiv:1812.00332. [Google Scholar]
- Ahmed, K.; Torresani, L. Maskconnect: Connectivity learning by gradient descent. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 349–365. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Dong, X.; Yang, Y. Searching for a robust neural architecture in four gpu hours. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1761–1770. [Google Scholar]
- Darwish, A.; Hassanien, A.E.; Das, S. A survey of swarm and evolutionary computing approaches for deep learning. Artif. Intell. Rev. 2020, 53, 1767–1812. [Google Scholar] [CrossRef]
- Xie, L.; Yuille, A. Genetic cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1379–1388. [Google Scholar]
- Loni, M.; Sinaei, S.; Zoljodi, A.; Daneshtalab, M.; Sjödin, M. DeepMaker: A multi-objective optimization framework for deep neural networks in embedded systems. Microprocess. Microsyst. 2020, 73, 102989. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Completely automated CNN architecture design based on blocks. IEEE Trans. Neural Networks Learn. Syst. 2019, 31, 1242–1254. [Google Scholar] [CrossRef] [PubMed]
- Javaheripi, M.; Samragh, M.; Javidi, T.; Koushanfar, F. GeneCAI: Gene tic evolution for acquiring c ompact AI. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 350–358. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Deb, K.; Agrawal, R.B. Simulated binary crossover for continuous search space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Evolving deep convolutional neural networks for image classification. IEEE Trans. Evol. Comput. 2019, 24, 394–407. [Google Scholar] [CrossRef]
- Lorenzo, P.R.; Nalepa, J. Memetic evolution of deep neural networks. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 505–512. [Google Scholar]
- Lu, Z.; Whalen, I.; Dhebar, Y.; Deb, K.; Goodman, E.D.; Banzhaf, W.; Boddeti, V.N. Multiobjective evolutionary design of deep convolutional neural networks for image classification. IEEE Trans. Evol. Comput. 2020, 25, 277–291. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Zhang, C.; Shao, H.; Li, Y. Particle swarm optimisation for evolving artificial neural network. In Proceedings of the SMC 2000 Conference Proceedings, 2000 IEEE International Conference on Systems, Man and Cybernetics, ‘Cybernetics Evolving to Systems, Humans, Organizations, and Their Complex Interactions’ (cat. no. 0. IEEE), Nashville, TN, USA, 8–11 October 2000; Volume 4, pp. 2487–2490. [Google Scholar]
- Fielding, B.; Zhang, L. Evolving image classification architectures with enhanced particle swarm optimisation. IEEE Access 2018, 6, 68560–68575. [Google Scholar] [CrossRef]
- He, C.; Ye, H.; Shen, L.; Zhang, T. Milenas: Efficient neural architecture search via mixed-level reformulation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11993–12002. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Smash: One-shot model architecture search through hypernetworks. arXiv 2017, arXiv:1708.05344. [Google Scholar]
- Sun, Y.; Wang, H.; Xue, B.; Jin, Y.; Yen, G.G.; Zhang, M. Surrogate-assisted evolutionary deep learning using an end-to-end random forest-based performance predictor. IEEE Trans. Evol. Comput. 2019, 24, 350–364. [Google Scholar] [CrossRef]
- Lu, Z.; Deb, K.; Goodman, E.; Banzhaf, W.; Boddeti, V.N. Nsganetv2: Evolutionary multi-objective surrogate-assisted neural architecture search. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part I 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 35–51. [Google Scholar]
- Rawal, A.; Miikkulainen, R. From nodes to networks: Evolving recurrent neural networks. arXiv 2018, arXiv:1803.04439. [Google Scholar]
- Črepinšek, M.; Liu, S.H.; Mernik, M.; Ravber, M. Long term memory assistance for evolutionary algorithms. Mathematics 2019, 7, 1129. [Google Scholar] [CrossRef]
- Pham, H.; Guan, M.; Zoph, B.; Le, Q.; Dean, J. Efficient neural architecture search via parameters sharing. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4095–4104. [Google Scholar]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8697–8710. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: http://www.cs.utoronto.ca/~kriz/learning-features-2009-TR.pdf (accessed on 30 January 2024).
- Zheng, H.; An, K.; Ou, Z. Efficient neural architecture search for end-to-end speech recognition via straight-through gradients. In Proceedings of the 2021 IEEE Spoken Language Technology Workshop (SLT), Online Conference, 19–22 January 2021; IEEE: New York, NY, USA, 2021; pp. 60–67. [Google Scholar]
- Guo, Z.; Zhang, X.; Mu, H.; Heng, W.; Liu, Z.; Wei, Y.; Sun, J. Single path one-shot neural architecture search with uniform sampling. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVI 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 544–560. [Google Scholar]
- Ying, C.; Klein, A.; Christiansen, E.; Real, E.; Murphy, K.; Hutter, F. Nas-bench-101: Towards reproducible neural architecture search. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 7105–7114. [Google Scholar]
- Dong, X.; Yang, Y. Nas-bench-201: Extending the scope of reproducible neural architecture search. arXiv 2020, arXiv:2001.00326. [Google Scholar]
- Liu, H.; Simonyan, K.; Vinyals, O.; Fernando, C.; Kavukcuoglu, K. Hierarchical representations for efficient architecture search. arXiv 2017, arXiv:1711.00436. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]


| Parameters | Description | Value |
|---|---|---|
| Number of warm-up epochs | 50 | |
| Number of update periods | 45 | |
| Number of weight optimization epochs per period | 10 | |
| Population size | 32 | |
| Number of weight vectors | 16 | |
| T | Number of neighbours | 4 |
| Aggregation function | ||
| Crossover rate | 0.5 | |
| Mutation rate | 0.1 | |
| Number of exchanged individuals | 3 |
| Architecture | Test Error (%) | #Params (M) | Search Cost (GPU Days) | Search Method |
|---|---|---|---|---|
| DenseNet-BC | 3.46 | 25.6 | - | Manual design |
| ENAS | 2.91 | 4.2 | 4 | Reinforcement learning |
| NASNet-A | 2.65 | 3.3 | 2000 | Reinforcement learning |
| DARTS-V1 | 3.00 | 3.3 | 1.5 | Gradient based |
| DARTS-V2 | 2.76 | 3.3 | 4 | Gradient based |
| AmoebaNet-A | 3.12 | 3.1 | 3150 | Evolution |
| Hierarchical evolution | 3.75 | 15.7 | 300 | Evolution |
| NSGA-Net-1 | 3.85 | 3.3 | 8 | Evolution (MO) |
| NSGA-Net-2 | 2.50 | 26.8 | 4 | Evolution (MO) |
| LEMONADE-1 | 3.69 | 1.1 | 80 | Evolution (MO) |
| LEMONADE-2 | 3.05 | 4.7 | 80 | Evolution (MO) |
| LEMONADE-3 | 2.58 | 13.1 | 80 | Evolution (MO) |
| CARS-B | 2.87 | 2.7 | 0.4 | Evolution (MO) |
| CARS-C | 2.84 | 2.8 | 0.4 | Evolution (MO) |
| CARS-E | 2.86 | 3.0 | 0.4 | Evolution (MO) |
| CARS-H | 2.66 | 3.3 | 0.4 | Evolution (MO) |
| Bi-MOEA/D-NAS-1 | 2.80 | 2.53 | 0.5 | Evolution (MO) |
| Bi-MOEA/D-NAS-2 | 2.86 | 2.71 | 0.5 | Evolution (MO) |
| Bi-MOEA/D-NAS-3 | 2.85 | 2.88 | 0.5 | Evolution (MO) |
| Bi-MOEA/D-NAS-4 | 2.72 | 3.26 | 0.5 | Evolution (MO) |
| Architecture | Top-1 Acc (%) | Top-5 Acc (%) | #Params (M) | Search Cost (GPU Days) | Search Method |
|---|---|---|---|---|---|
| ResNet34 | 76.88 | 91.73 | 21.34 | - | Manual Design |
| MobileNet-V2 | 76.77 | 92.46 | 2.35 | - | Manual Design |
| NASNet | 77.25 | 91.37 | 5.24 | 2000 | Reinforcement Learning |
| DARTS-V2 | 74.97 | 90.78 | 4.60 | 4 | Gradient Based |
| GDAS-LEVEL2 | 74.84 | 90.83 | 5.47 | 0.21 | Gradient Based |
| AmoebaNet-A | 76.76 | 91.10 | 4.65 | 3150 | Evolution |
| CARS-C | 75.20 | 90.74 | 4.07 | 0.4 | Evolution (MO) |
| CARS-E | 75.26 | 90.94 | 4.26 | 0.4 | Evolution (MO) |
| CARS-F | 75.92 | 90.79 | 4.42 | 0.4 | Evolution (MO) |
| CARS-G | 76.14 | 91.34 | 4.56 | 0.4 | Evolution (MO) |
| Bi-MOEA/D-NAS-1 | 76.46 | 91.36 | 3.73 | 0.5 | Evolution (MO) |
| Bi-MOEA/D-NAS-2 | 76.99 | 91.38 | 3.96 | 0.5 | Evolution (MO) |
| Bi-MOEA/D-NAS-3 | 76.89 | 91.40 | 4.17 | 0.5 | Evolution (MO) |
| Bi-MOEA/D-NAS-4 | 77.10 | 91.58 | 4.66 | 0.5 | Evolution (MO) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Zhu, K.; Li, Y.; Li, Y.; Gong, Y. Multi-Objective Evolutionary Neural Architecture Search with Weight-Sharing Supernet. Appl. Sci. 2024, 14, 6143. https://doi.org/10.3390/app14146143
Liang J, Zhu K, Li Y, Li Y, Gong Y. Multi-Objective Evolutionary Neural Architecture Search with Weight-Sharing Supernet. Applied Sciences. 2024; 14(14):6143. https://doi.org/10.3390/app14146143
Chicago/Turabian StyleLiang, Junchao, Ke Zhu, Yuan Li, Yun Li, and Yuejiao Gong. 2024. "Multi-Objective Evolutionary Neural Architecture Search with Weight-Sharing Supernet" Applied Sciences 14, no. 14: 6143. https://doi.org/10.3390/app14146143
APA StyleLiang, J., Zhu, K., Li, Y., Li, Y., & Gong, Y. (2024). Multi-Objective Evolutionary Neural Architecture Search with Weight-Sharing Supernet. Applied Sciences, 14(14), 6143. https://doi.org/10.3390/app14146143







