Evaluating the Accuracy of the Reverse Engineering Process of Worn, Non-Standard Spur Gears—Pilot Studies
Abstract
:1. Introduction
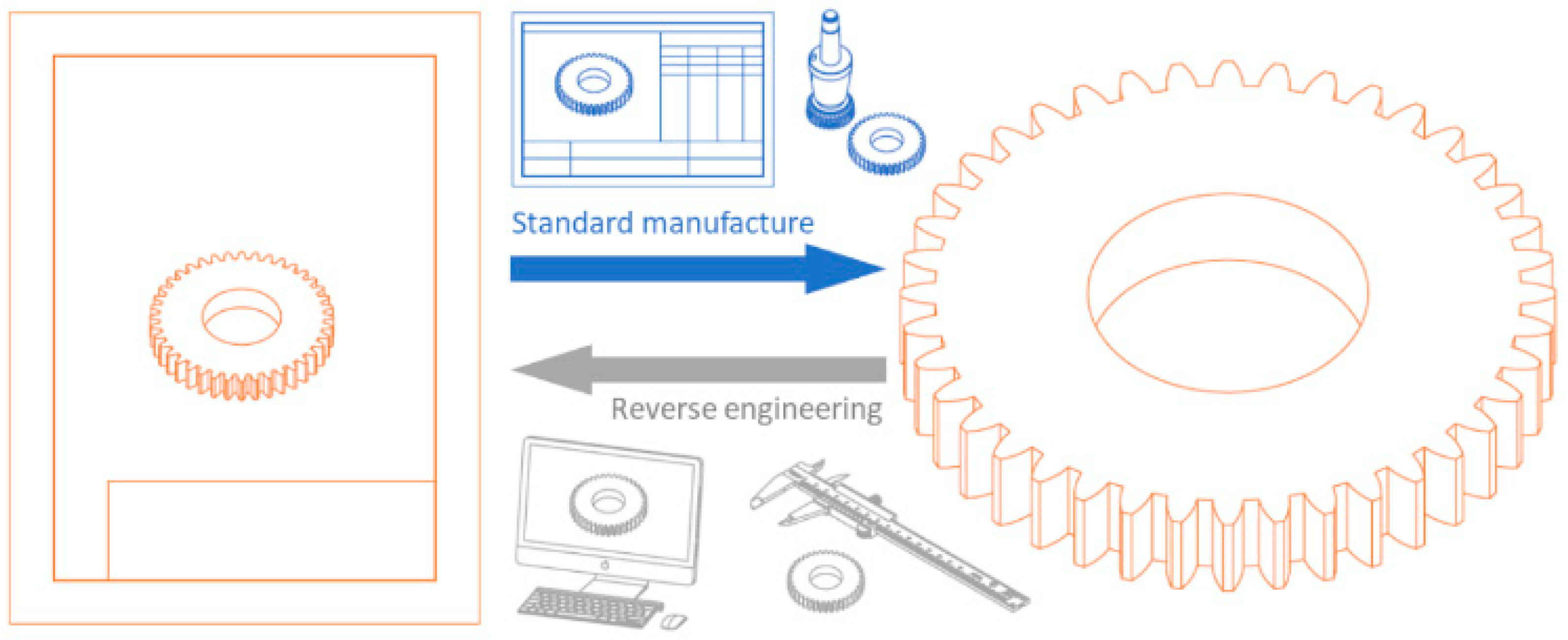
2. Materials and Methods
2.1. Tested Gear Wheels
2.2. Conventional Measuring Instruments Used
2.3. Conventional Measurement Techniques Used
- measurement of the tip diameter and measurement of the root diameter in the case of gears with an even number of teeth,
- measurement of the distance AB from the tip of the tooth to the bottom of the opposite root in the cases of gears with an odd number of teeth.
2.4. The Model Used Compares the Nominal Gear with the Recreated Gear
2.5. The Model Used for the Statistical Analysis of the Results
- micrometer screw and nut error ,
- flatness error of the anvil and spindle ,
- parallelism error of the anvil and spindle measuring surfaces ,
- perpendicularity error of the spindle measuring surfaces relative to its axis ,
- error in the lower measurement range ,
- bow deformation error for ,
- error related to the elastic deformation of the measured object ,
- error related to immobilizing the spindle with a clamp ,
- roughness error of the measurement surfaces ,
- parallax error ,
- temperature error (for steel and negligible),
- micrometer setting error .
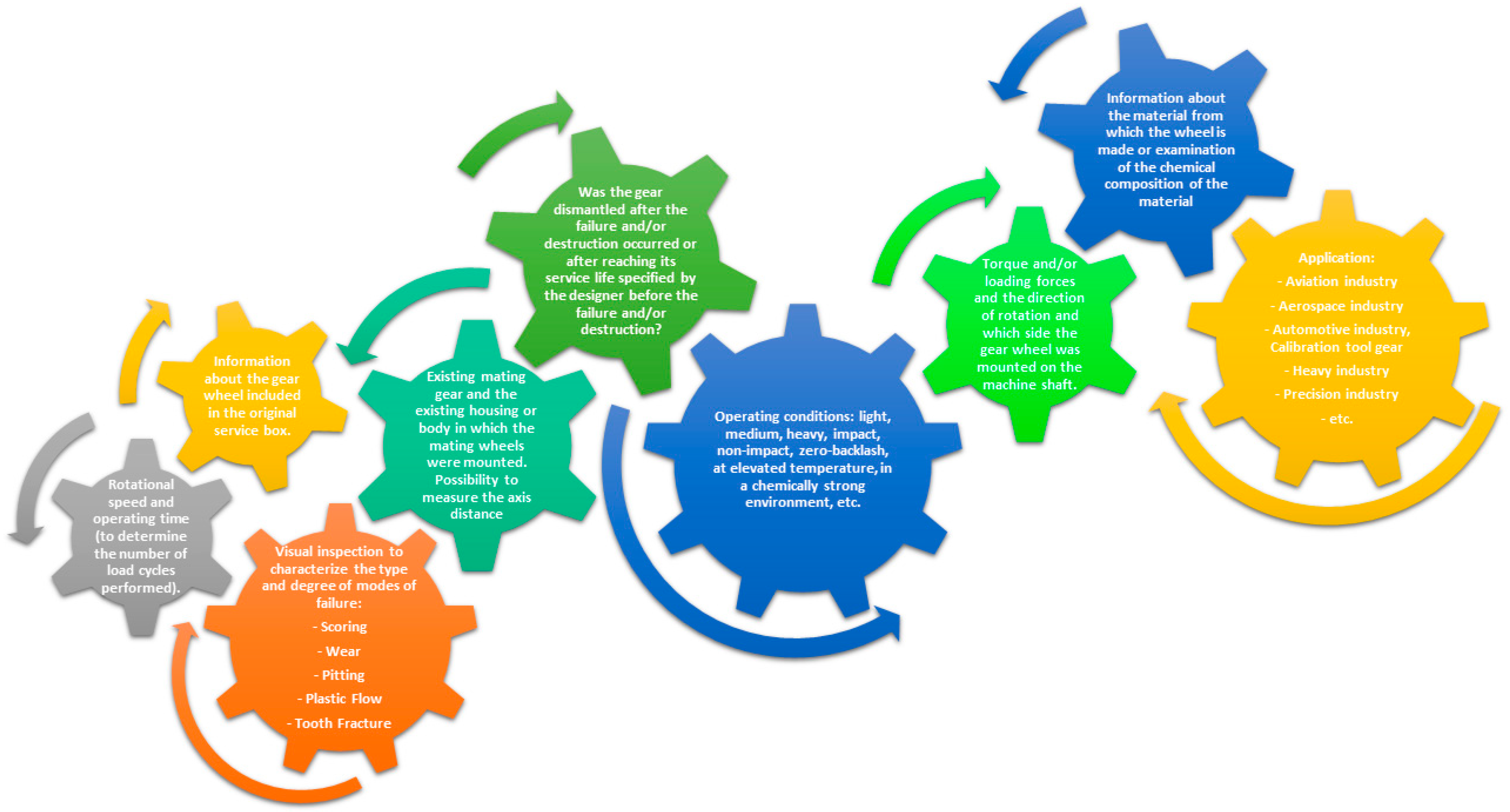
3. Additional Observation
Module as a Random Variable in the Population
4. Results and Discussion
4.1. True Deviations and the IT Grade of the Tested Gear Wheel
4.2. Measurement Results in Statistical Analysis
4.3. Synthesis of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Coordinate Measuring Machine | Single pitch deviation | ||||
| Equation of Identical Gears | Chordal base pitch deviation | ||||
| Lower Specification Limit | Total cumulative pitch deviation | ||||
| Maximum Permissible Error | |||||
| Nominal Size | |||||
| Process Capability Ratio (; ) | Radial clearance | ||||
| Reverse Engineering | Radial clearance factor | ||||
| Student–Fisher dispersion | Pitch diameter | ||||
| Upper Specification Limit | Tip diameter | ||||
| Base diameter | |||||
| Used as a subscript means: estimated | Root diameter | ||||
| Used as a subscript means: maximal value | Any given diameter | ||||
| Used as a subscript means: minimal value | Whole depth | ||||
| Used as a subscript means: original | Addendum | ||||
| Dedendum | |||||
| Profile angle | Span measurement | ||||
| Profile angle in radians | Module | ||||
| Profile angle at a given diameter | Number of measurements | ||||
| Profile angle at a given diameter in radians | Number of teeth spanned | ||||
| Tolerance increment between gear tooth qualities | Base pitch | ||||
| Standard deviation | S–F deviation | ||||
| Tooth thickness at pitch diameter | |||||
| Total profile deviation | Tooth thickness at a given diameter | ||||
| Tooth thickness deviation | Tolerance zone | ||||
| Span measurement deviation | Average | ||||
| Pitch error | Shift factor | ||||
| Runout error | Whole depth factor | ||||
| Base diameter deviation | Number of the teeth |
References
- Krogstle, L.; Walter, M.S.J.; Wartzack, S.; Martinsen, K. Towards a more Comprehensive Understanding of Tolerance Engineering Research Importance. Procedia CIRP 2015, 27, 29–34. [Google Scholar] [CrossRef]
- Konecki, K.; Kołodziej, A.; Wojtkowiak, D.; Talaśka, K. Issues related to the reconstruction of the geometry of the DP6 inch cylindrical gear in the context of reverse engineering using conventional techniques and measuring instruments. AIP Conf. Proc. 2023, 2976, 020008. [Google Scholar] [CrossRef]
- Sáenz-Nuño, M.A.; Lorente-Pedreille, R. ISO Tolerance specification in reverse engineering. Procedia Manuf. 2017, 13, 472–479. [Google Scholar] [CrossRef]
- ISO 286-1:2010; Geometrical Product Specifications (GPS)—ISO Code System for Tolerances on Linear Sizes—Part 1: Basis of Tolerances, Deviations and Fits. ISO: Geneva, Switzerland, 2010.
- Kaisarlis, G.J. A Systematic Approach for Geometrical and Dimensional Tolerancing in Reverse Engineering. In Reverse Engineering—Recent Advances and Applications; Telea, A.C., Ed.; IntechOpen: Rijeka, Croatia, 2012; pp. 133–160. ISBN 978-953-51-0158-1. [Google Scholar] [CrossRef]
- Kaisarlis, G.J.; Diplaris, S.C.; Sfantsikopoulos, M.M. Position tolerancing in reverse engineering: The fixed fastener case. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2007, 221, 457–464. [Google Scholar] [CrossRef]
- Kaisarlis, G.J.; Diplaris, S.C.; Sfantsikopoulos, M.M. Geometrical position tolerance assignment in reverse engineering, Int. J. Comput. Integr. Manuf. 2008, 21, 89–96. [Google Scholar] [CrossRef]
- ISO 2768-1; General Tolerances—Part 1: Tolerances for Linear and Angular Dimensions without Individual Tolerance Indications. ISO: Geneva, Switzerland, 1989.
- Kaisarlis, G.J.; Diplaris, S.C.; Sfantsikopoulos, M.M. A Knowledge-Based System for Tolerance Allocation in Reverse Engineering. In Proceedings of the 33rd International MATADOR Conference; Hayhurst, D.R., Ed.; Springer: London, UK, 2000. [Google Scholar] [CrossRef]
- Geng, Z.; Bidanda, B. Tolerance estimation and metrology for reverse engineering based remanufacturing systems. Int. J. Prod. Res. 2022, 60, 2802–2815. [Google Scholar] [CrossRef]
- Geng, Z.; Sabbaghi, A.; Bidanda, B. Reconstructing original design: Process planning for reverse engineering. IISE Trans. 2023, 55, 509–522. [Google Scholar] [CrossRef]
- ASME Y14.5; Dimensioning and Tolerancing. ASME: New York, NY, USA, 2009.
- ISO/TC 213; Dimensional and Geometrical Product Specifications and Verification. ISO: Geneva, Switzerland, 2019.
- Konecki, K.; Wojtkowiak, D.; Talaśka, K.; Kołodziej, A.; Domek, G. Issues related to an attempt to recreate the geometry of a non-standard spur gear. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1199, 012105. [Google Scholar] [CrossRef]
- PN-82/M-53200/A1; Narzędzia Pomiarowe—Przyrządy Mikrometryczne—Wymagania. PKN: Warszawa, Poland, 1998.
- DIN 863-1:2017-02; Geometrical Product Specifications (GPS)—Micrometers—Part 1: Micrometers for External Measurements; Maximum Permissible Errors. DIN: Berlin, Germany, 1999.
- Mahr Group. Brochure: Katalog Zbiorczy|Technika Pomiarów Produkcyjnych (Informal Translation: Collective Catalog|Production Measurement Techniques); Mahr Group: Göttingen, Germany, POL05 V1, 3758450–01.10.2005; Printed in Germany; pp. PG–17.
- Mahr Group Website. Available online: https://metrology.mahr.com/fileadmin/catalogs/OnlineCatalogs/Mahr-Metrology/index.php?catalog=Mahr-Metrology-PL&lang=pl (accessed on 19 January 2024).
- Jezierski, J. Analiza Tolerancji i Niedokładności Pomiarów w Budowie Maszyn (Informal Translation: Analysis of Tolerances and Measurement Inaccuracies in Machine Construction), 3rd ed.; Wydawnictwa Naukowo-Techniczne WNT: Warszawa, Poland, 1994; ISBN 83-204-2906-4. [Google Scholar]
- Konecki, K.; Kołodziej, A.; Pytliński, R. Equation of Identity for Two Spur Gears with Straight Teeth Having Two Different Alternative Sets of Geometric Parameters. AIP Conf. Proc. 2023, 2976, 030003. [Google Scholar] [CrossRef]
- Konecki, K.; Kołodziej, A.; Wojtkowiak, D.; Talaśka, K. Simulation of different geometric variants of spur gears in the context of their complete identity. AIP Conf. Proc. 2023, 2976, 030018. [Google Scholar] [CrossRef]
- Spitas, C.; Spitas, V. Can non-standard involute gears of different modules mesh? Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 1305–1313. [Google Scholar] [CrossRef]
- Spitas, C.; Spitas, V. Generating standard 20° involute pinions with increased fillet strength by using 25° rack cutters with non-standard module. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 1297–1304. [Google Scholar] [CrossRef]
- Wojtkowiak, D.; Konecki, K. Stress analysis of the zero-backlash gear transmission. AIP Conf. Proc. 2023, 2976, 030011. [Google Scholar] [CrossRef]
- Ochęduszko, K. Koła Zębate t. 3 Sprawdzanie (Informal Translation: Gears, Volume 3—Checking), 8th ed.; Wydawnictwa Naukowo-Techniczne WNT: Warszawa, Poland, 2012; p. 238. ISBN 9788363623067. EAN: 9788363623067. [Google Scholar]
- DIN 3961:1953-09; Tolerances for Cylindrical Gear Teeth; Bases. DIN: Berlin, Germany, 1953.
- DIN 3967 | Calculator (mechanicalcheck.com). Available online: https://www.mechanicalcheck.com/en/din3967/calc/ (accessed on 19 January 2024).
- Lynwander, P. Gear Tooth Scoring Design Considerations for Spur and Helical Gearing, Gear Technology, May/June 1985. pp. 7–13, 48. Available online: https://www.geartechnology.com/ext/resources/issues/0585x/Lynwander.pdf (accessed on 26 May 2024).
- Faure, L. Classification of Types of Gear Tooth Wear—Part I, Gear Technology, November/December 1992. pp. 32–38. Available online: https://www.geartechnology.com/ext/resources/issues/1192x/faure.pdf?1633055058 (accessed on 26 May 2024).
- Faure, L. Classification of Types of Gear Tooth Wear—Part II, Gear Technology, November/December 1992. pp. 34–40. Available online: https://www.geartechnology.com/ext/resources/issues/0193x/faure.pdf?1633055062 (accessed on 26 May 2024).
- Broszura, Instytut Inżynierii Mechanicznej Wydziału Politechnicznego “-Pracownia Inżynierii Mechanicznej-” Uniwersytet Kaliski im. Prezydenta Stanisława Wojciechowskiego (University of Kalisz, Poland). Available online: https://uniwersytetkaliski.edu.pl/wp-content/uploads/2024/02/iim-12.02.2024.pdf (accessed on 18 March 2024).


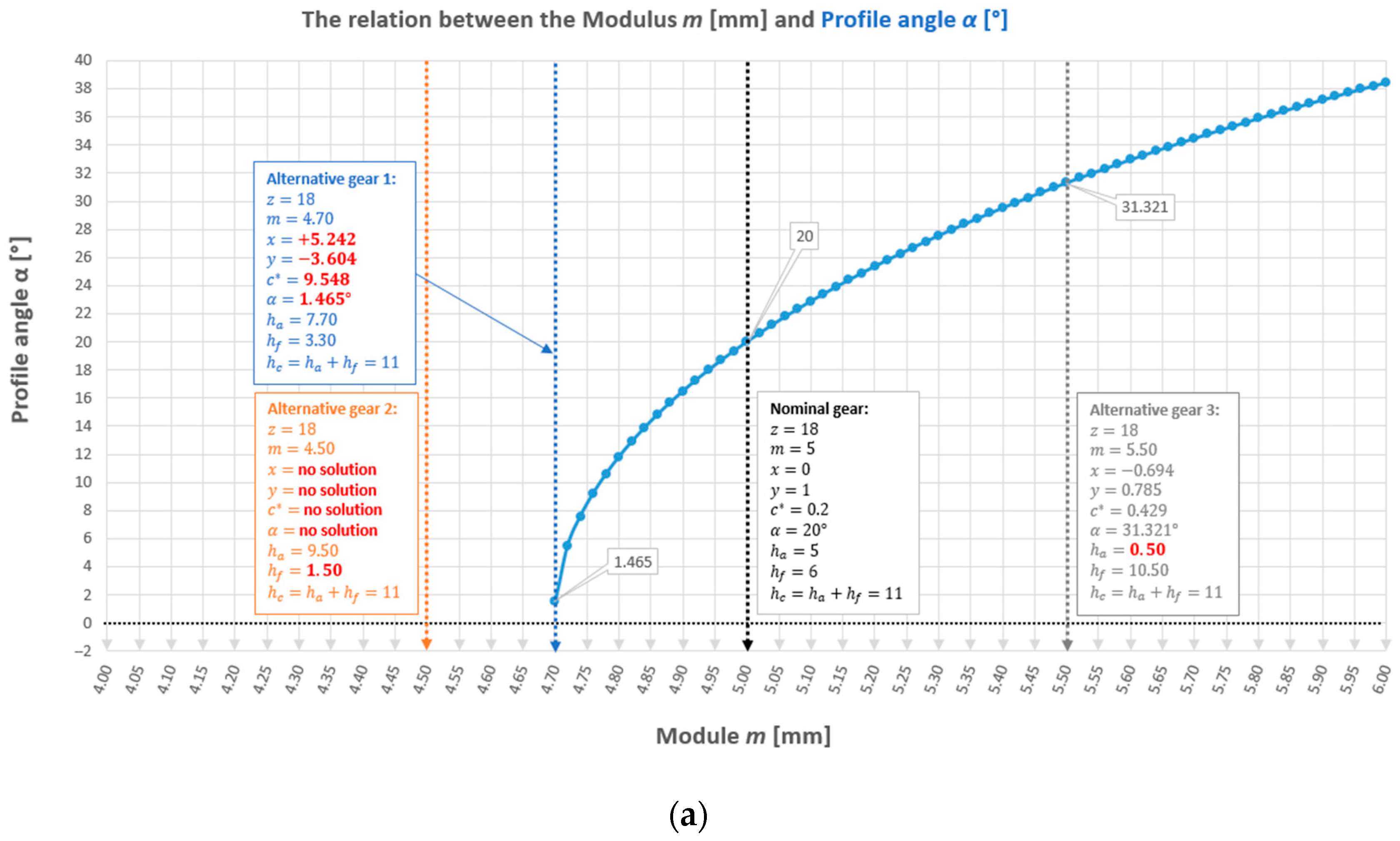












| No. | Mark | z | m | α | y | x | c* |
|---|---|---|---|---|---|---|---|
| 1 | 16 | 13 | 3.020 | 21.018° | 0.9924 | −0.0421 | 0.1675 |
| 2 | 13 | 18 | 4.980 | 26.325° | 0.7950 | +0.0695 | 0.3830 |
| 3 | 2 | 42 | 4.029 | 21.104° | 1.0189 | +0.4184 | 0.1463 |
| 4 | 2 | 42 | 4.029 | 21.104° | 1.0189 | +0.4184 | 0.1463 |
| 5 | 3 | 30 | 4.410 | 25.572° | 0.9012 | −0.5423 | 0.5196 |
| 6 | 5 | 29 | 1.020 | 22.888° | 0.9283 | −0.5263 | 0.3002 |
| 7 | 11 | 17 | 4.980 | 19.358° | 1.0065 | −0.0641 | 0.1958 |
| 8 | 6 | 18 | 4.980 | 26.325° | 0.8632 | +0.0695 | 0.2525 |
| m | α | y | x | c* | pb [mm] | dx [mm] | sx [mm] |
|---|---|---|---|---|---|---|---|
| 1.98 | 18.344° | 1.028 | −0.0876 | 0.200 | 5.904 | 113 | 1.485 |
| 1.97 | 17.445° | 1.034 | +0.0507 | 0.165 | |||
| 1.96 | 16.490° | 1.032 | +0.1981 | 0.180 | |||
| 1.95 | 15.466° | 1.020 | +0.3576 | 0.216 |
| m | α | y | x | c* | |
|---|---|---|---|---|---|
| The recreated gear | 1.97 | 17.538° | 1.0339 | +0.0509 | 0.1658 |
| The identical gear (EIG) | 1.98 | 18.432° | 1.0278 | −0.0874 | 0.1666 |
| The nominal gear | 1.98 | 18.344° | 1.0280 | −0.0876 | 0.2 |
| Type of Error | φ | Module Range m [mm] | |||
|---|---|---|---|---|---|
| do 0.6 | od 0.6 do 1.6 | od 1.6 do 4 | od 4 do 10 | ||
| Δe Δtp Δo Δt0 | 1.4/1.6 | ||||
| Δrs | 1.4/1.6 | ||||
| ∑Δt0 | 1.4/1.6 | ||||
| Δg | 1.4 | ||||
| Δr | 1.4 | ||||
| ΔM | 1.4 | ||||
| Type of Error | IT Grade | |||||
|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | |
| Δe Δtp Δo Δt0 Δrz ∑Δt0 | 1 | 1.4 | 1.96 | 2.74 | 3.84 | 6.15 |
| Δg Δr ΔM | 1 | 1.4 | 1.96 | 2.74 | 3.84 | 5.36 |
| Gear | Drawing Information | Calculated Errors in 5 to 10 IT Grades according to DIN 3961 | Qualified for IT Grade | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Mark | IT Grade Information | According to the Standard | Permissible Errors [mm] | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 16 | 7 | DIN 3967 | ΔM = 0.028 Δg = 0.030 Δtp = ? | 0.010 0.010 0.005 | 0.014 0.014 0.007 | 0.020 0.020 0.010 | 0.027 0.028 0.014 | 0.038 0.040 0.020 | 0.054 0.055 0.032 | 8 |
| 2 | 13 | – | – | ΔM = 0.022 Δg = 0.025 Δtp = ? | 0.012 0.013 0.006 | 0.017 0.018 0.009 | 0.024 0.025 0.013 | 0.033 0.036 0.018 | 0.047 0.050 0.025 | 0.065 0.070 0.039 | 7 |
| 3 | 2 | – | – | ΔM = 0.035 Δg = 0.037 Δtp = ? | 0.013 0.013 0.007 | 0.018 0.019 0.010 | 0.025 0.026 0.013 | 0.034 0.037 0.019 | 0.048 0.051 0.026 | 0.067 0.072 0.042 | 8 |
| 4 | 2 | – | – | ||||||||
| 5 | 3 | – | – | Δtp = 0.010 | 0.007 | 0.009 | 0.013 | 0.018 | 0.025 | 0.040 | 6 |
| 6 | 5 | 7 | DIN 3962 | Δg = 0.030 Δtp = ? | 0.008 0.004 | 0.012 0.006 | 0.016 0.009 | 0.023 0.012 | 0.032 0.017 | 0.045 0.027 | 9 |
| 7 | 11 | 9 | DIN | ΔM = 0.024 Δtp = ? | 0.012 0.006 | 0.017 0.009 | 0.024 0.012 | 0.033 0.017 | 0.046 0.024 | 0.065 0.039 | 7 |
| 8 | 6 | I | industry standard | ΔM = 0.054 Δg = 0.060 Δtp = ? | 0.012 0.013 0.006 | 0.017 0.018 0.009 | 0.024 0.025 0.013 | 0.033 0.036 0.018 | 0.047 0.050 0.025 | 0.089 0.070 0.039 | 9 |
| Gear Designation | IT Grade | |||||
|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | |
| No. 1 Mark 16 | x | |||||
| No. 2 Mark 13 | x | |||||
| No. 3 Mark 2 | x | |||||
| No. 4 Mark 2 | x | |||||
| No. 5 Mark 3 | x | |||||
| No. 6 Mark 5 | x | |||||
| No. 7 Mark 11 | x | |||||
| No. 8 Mark 6 | x | |||||
| Gear Designation | Direction | Degree of Shift Δ1 and Δ2 [‰] | |
|---|---|---|---|
| Relative to Average | Relative to Median | ||
| No. 1 Mark 16 | → | 1.028 | 1.254 |
| No. 2 Mark 13 | → | 0.918 | 0.704 |
| No. 3 Mark 2 | ← | 0.595 | 0.722 |
| No. 4 Mark 2 | ← | 5.676 | 4.109 |
| No. 5 Mark 3 | ← | 0.261 | 0.181 |
| No. 6 Mark 5 | → | 0.464 | 0.972 |
| No. 7 Mark 11 | → | 1.141 | 1.141 |
| No. 8 Mark 6 | → | 0.171 | 0.009 |
| IT Grade wg DIN 3961 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model ↓ | 8 | 7 | 8 | 8 | 6 | 9 | 7 | 9 | Suma pkt. | Occurrence in All Measured Gears? | Verdict |
| XI | ➂ | ➁ | ➁ | 75 | YES | Second best | |||||
| X | ➁ | ➀ | ➀ | ➂ | 110 | YES | Best | ||||
| IX | ➀ | ➂ | ➁ | 75 | – | – | |||||
| VIII | ➁ | ➂ | ➀ | 70 | – | – | |||||
| VII | ➀ | ➁ | 60 | – | – | ||||||
| VI | ➀ | ➂ | 45 | – | – | ||||||
| V | ➁ | 25 | – | – | |||||||
| IV | ➁ | ➂ | 30 | – | – | ||||||
| III | ➀ | ➁ | 50 | – | – | ||||||
| II | 0 | – | – | ||||||||
| I | ➀ | 30 | – | – | |||||||
| Gear No.→ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| Mark→ | 16 | 13 | 2 | 2 | 3 | 5 | 11 | 6 | |||
| Explanations: | Estimator Ratio > 100% | ||||||||||
| ➀→ | 30 points | ➀ | Estimator Ratio < 100%, 1st place | ||||||||
| ➁→ | 20 points | ➁ | Estimator Ratio < 100%, 2nd place | ||||||||
| ➂→ | 10 points | ➂ | Estimator Ratio < 100%, 3rd place | ||||||||
| 5 points | Estimator Ratio < 100% | ||||||||||
| Gear | True IT Grade | Estimator Ratio in Model X [%] | Δtp According to DIN 3961 [mm] | Ttrue [mm] | Tdesig [mm] | Δtp Designed [mm] | Designed IT Grade |
|---|---|---|---|---|---|---|---|
| No 1. Mark 16 | 8 | 81 | ±0.014 | 0.028 | 0.023 | ±0.012 | 7–8 |
| No 2. Mark 13 | 7 | 80 | ±0.013 | 0.026 | 0.021 | ±0.011 | 6–7 |
| No 3. Mark 2 | 8 | 65 | ±0.019 | 0.038 | 0.025 | ±0.013 | 7 |
| No 4. Mark 2 | 8 | 93 | ±0.019 | 0.038 | 0.035 | ±0.018 | 8 |
| No 5. Mark 3 | 6 | 100 | ±0.009 | 0.018 | 0.018 | ±0.009 | 6 |
| No 6. Mark 5 | 9 | 53 | ±0.017 | 0.034 | 0.018 | ±0.009 | 7 |
| No 7. Mark 11 | 7 | 83 | ±0.012 | 0.024 | 0.020 | ±0.010 | 6 |
| No 8. Mark 6 | 9 | 81 | ±0.025 | 0.050 | 0.041 | ±0.021 | 8 |
| Explanations: | An increase of two IT grades (gear would have to be made more precisely) | ||||||
| An increase of one IT grade (gear would have to be made more precisely) | |||||||
| The IT grade remains the same | |||||||
| Remains the same IT grades or increases by one IT grade (more precisely) | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konecki, K.; Wojtkowiak, D.; Talaśka, K. Evaluating the Accuracy of the Reverse Engineering Process of Worn, Non-Standard Spur Gears—Pilot Studies. Appl. Sci. 2024, 14, 6090. https://doi.org/10.3390/app14146090
Konecki K, Wojtkowiak D, Talaśka K. Evaluating the Accuracy of the Reverse Engineering Process of Worn, Non-Standard Spur Gears—Pilot Studies. Applied Sciences. 2024; 14(14):6090. https://doi.org/10.3390/app14146090
Chicago/Turabian StyleKonecki, Karol, Dominik Wojtkowiak, and Krzysztof Talaśka. 2024. "Evaluating the Accuracy of the Reverse Engineering Process of Worn, Non-Standard Spur Gears—Pilot Studies" Applied Sciences 14, no. 14: 6090. https://doi.org/10.3390/app14146090
APA StyleKonecki, K., Wojtkowiak, D., & Talaśka, K. (2024). Evaluating the Accuracy of the Reverse Engineering Process of Worn, Non-Standard Spur Gears—Pilot Studies. Applied Sciences, 14(14), 6090. https://doi.org/10.3390/app14146090







