A Study on Deformation Characteristics and Stability of Soft Surrounding Rock for a Shallow-Buried Tunnel
Abstract
1. Introduction
2. Engineering Overview
3. Tunnel Stability Based of In-Site Monitoring
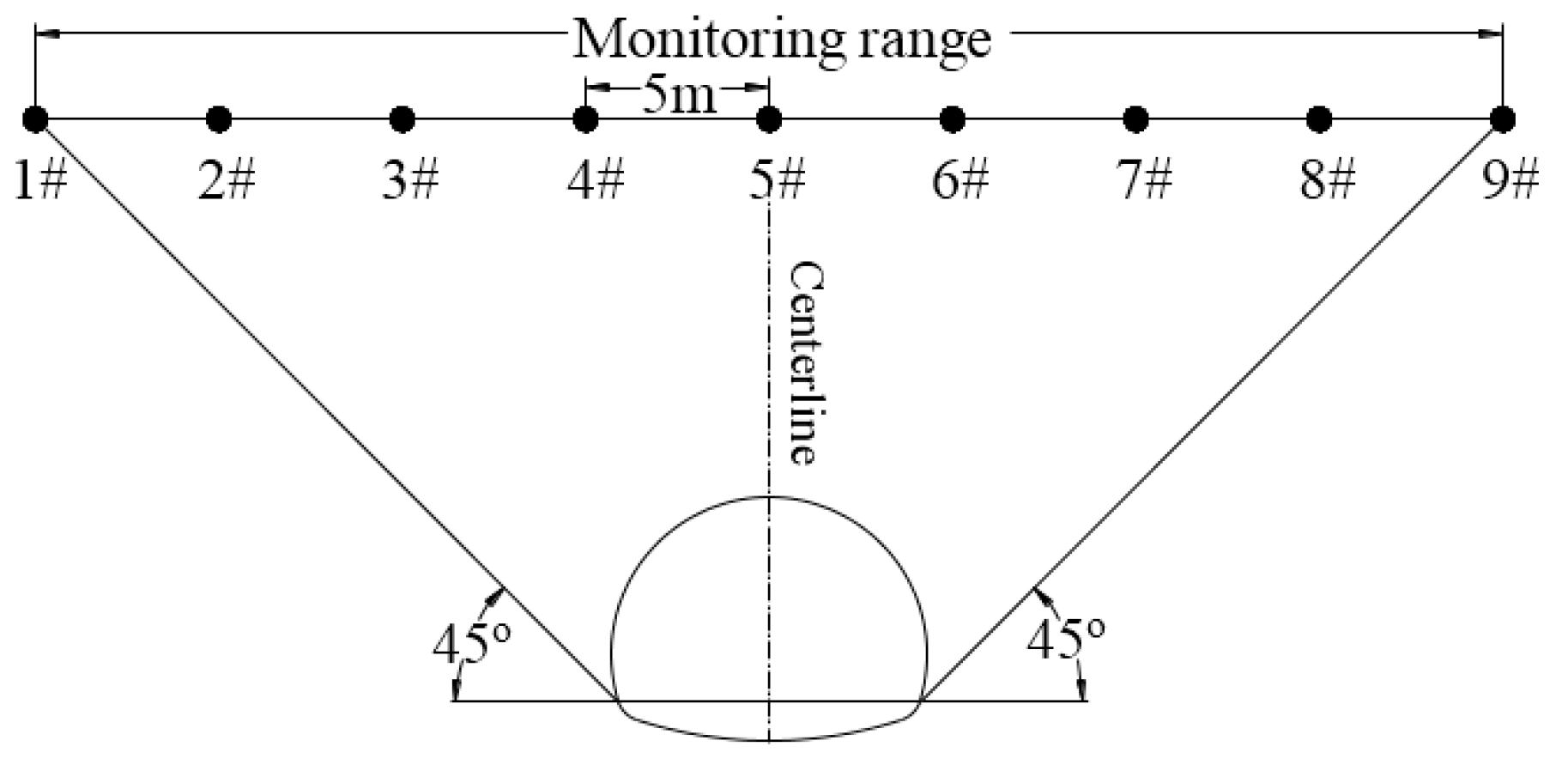
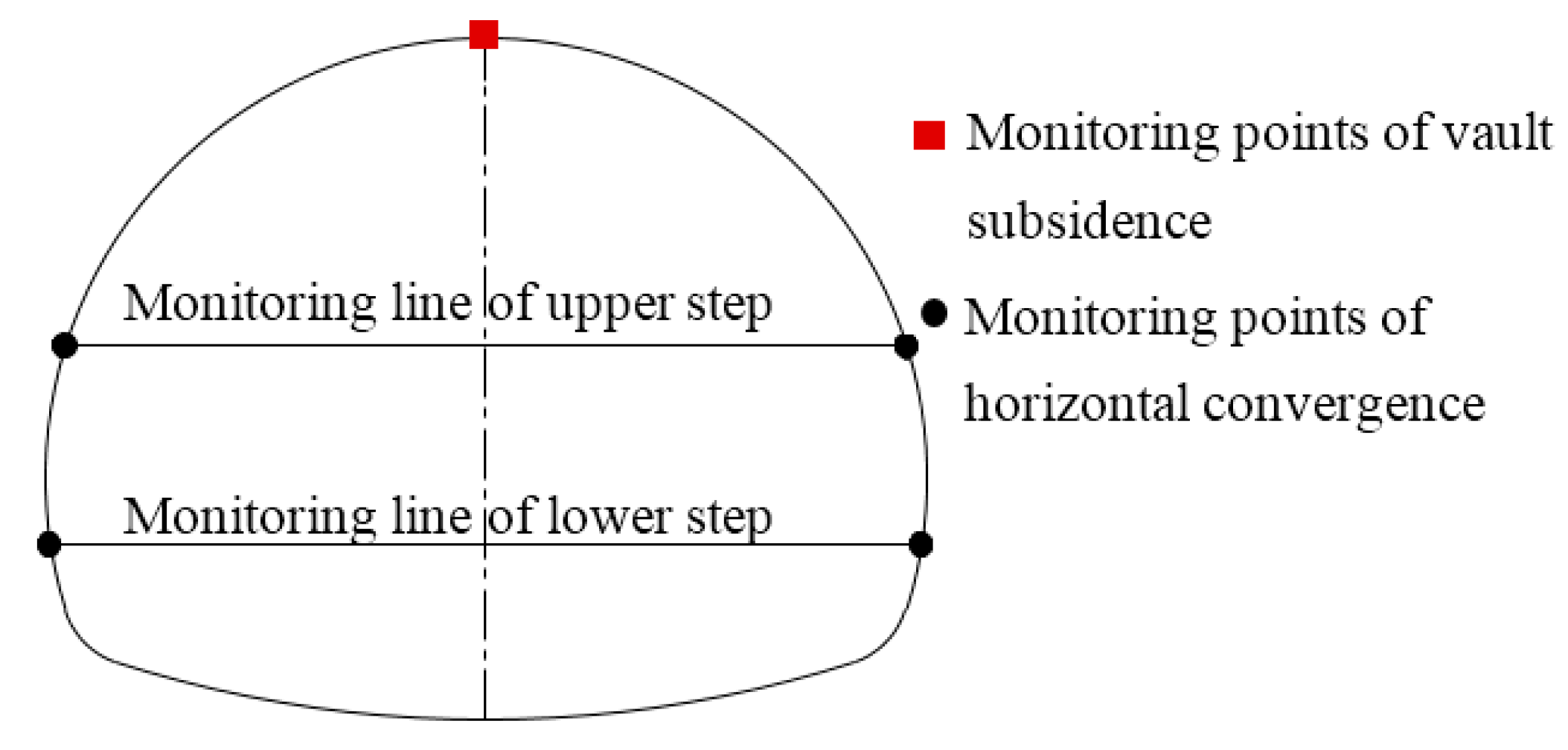
3.1. Layout Scheme of Monitoring Points
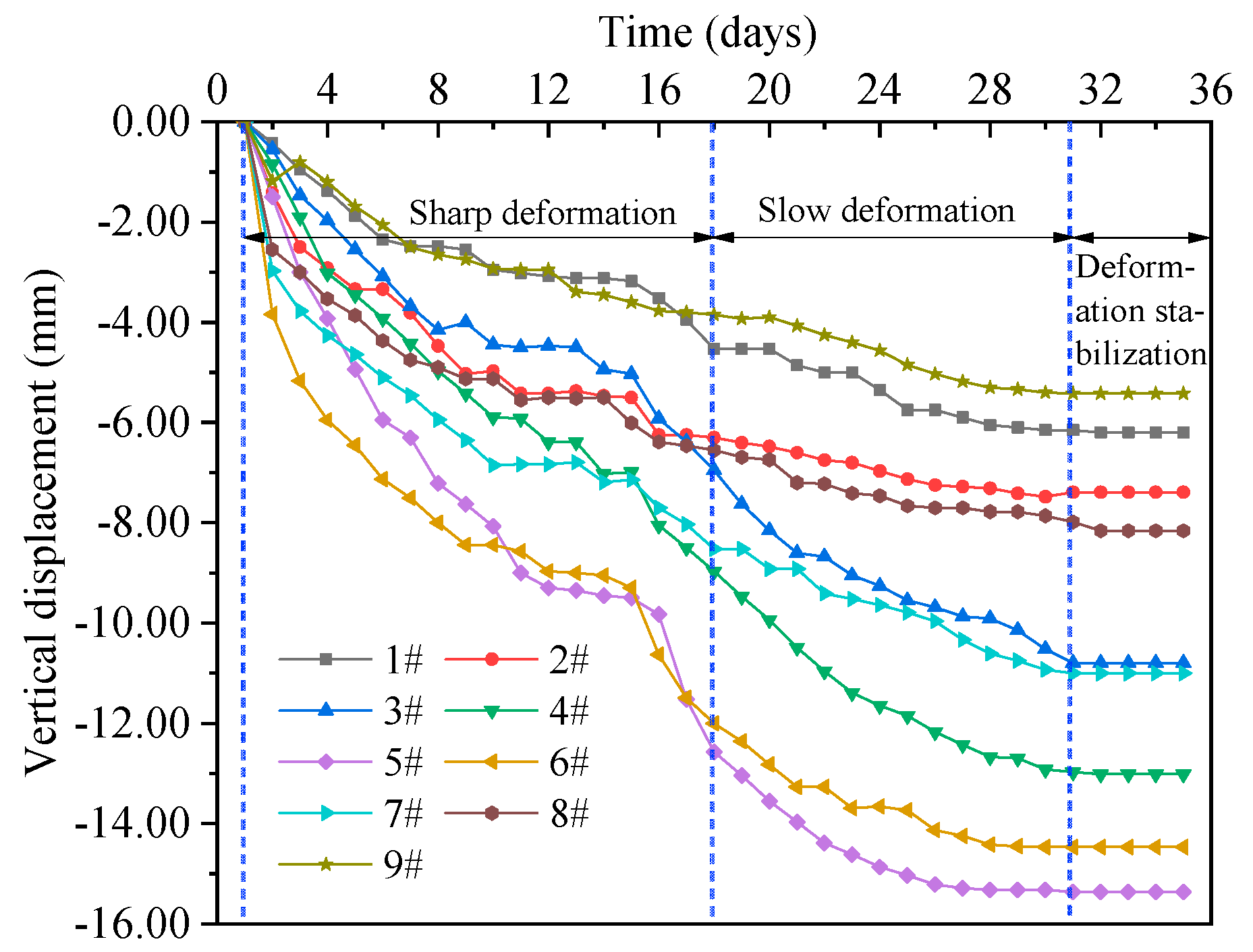
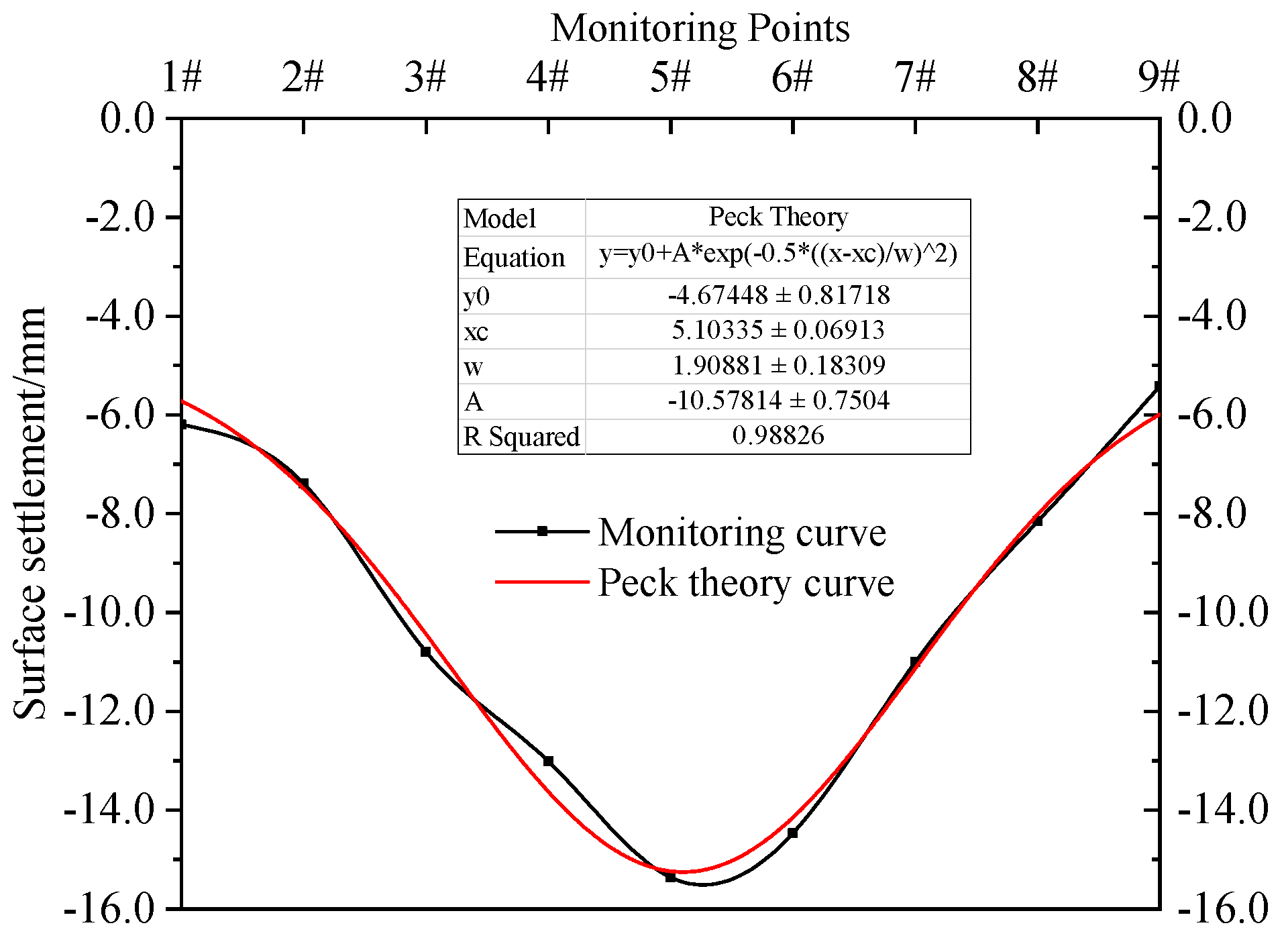
3.2. Analysis of Surface Settlement
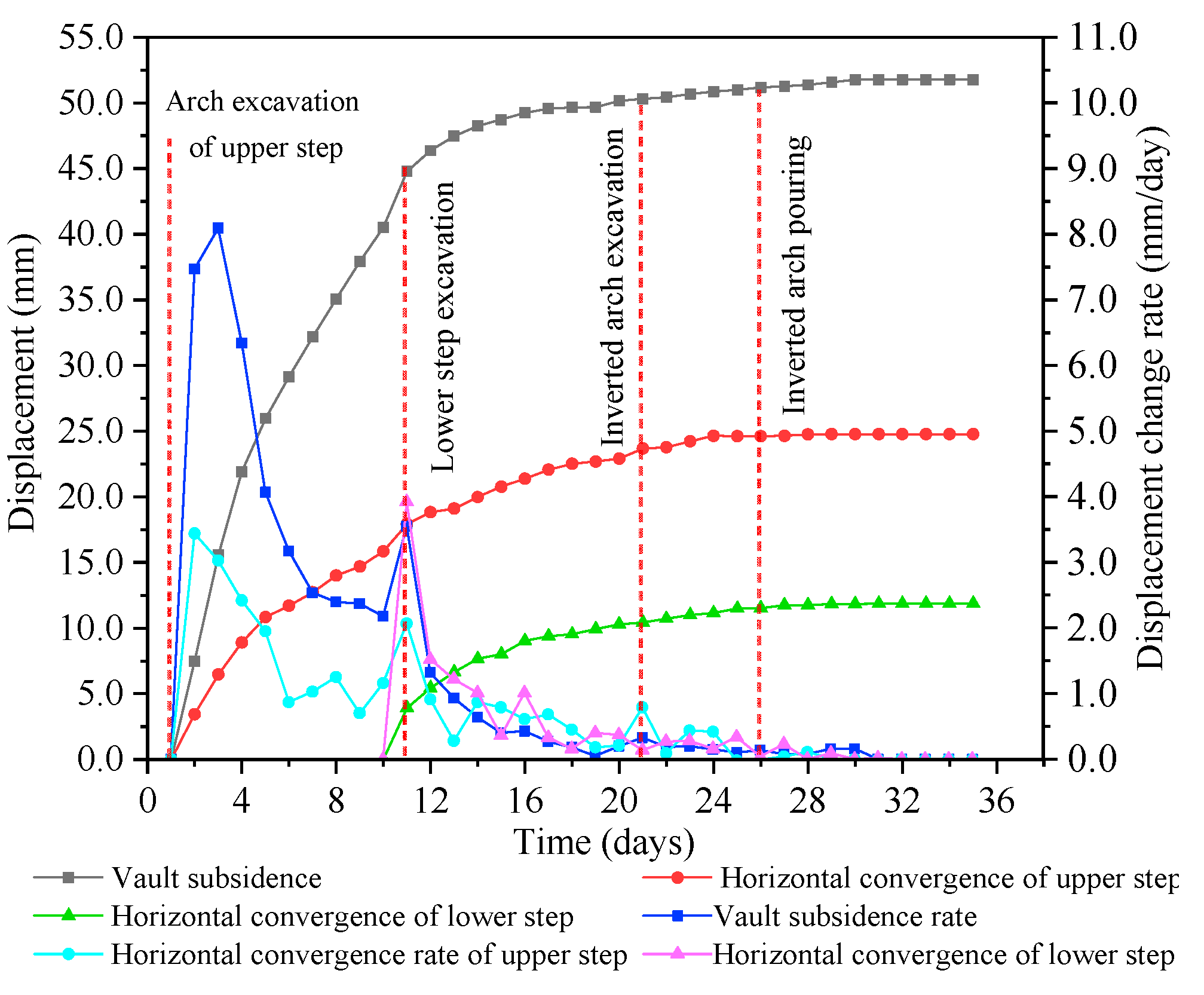
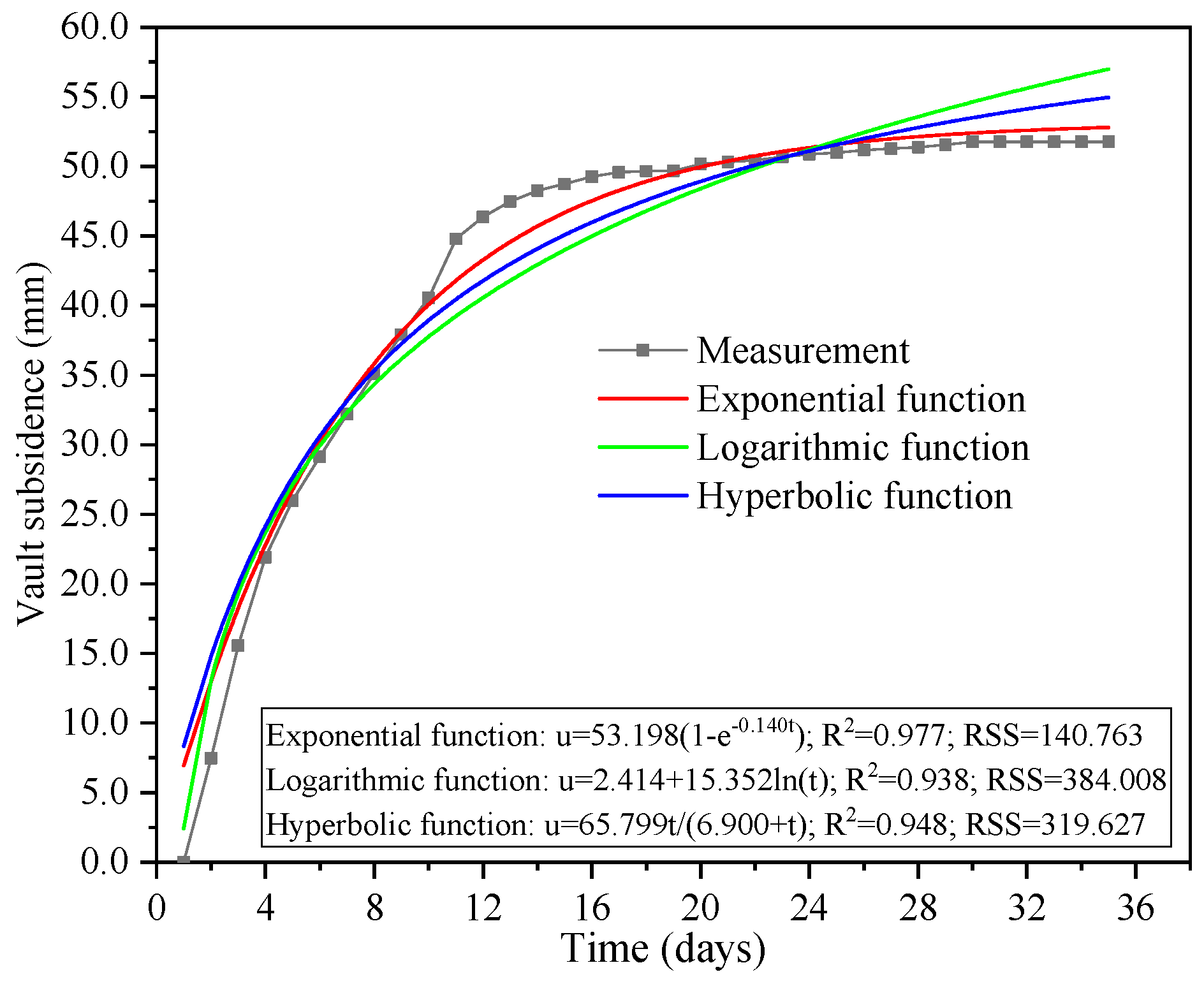
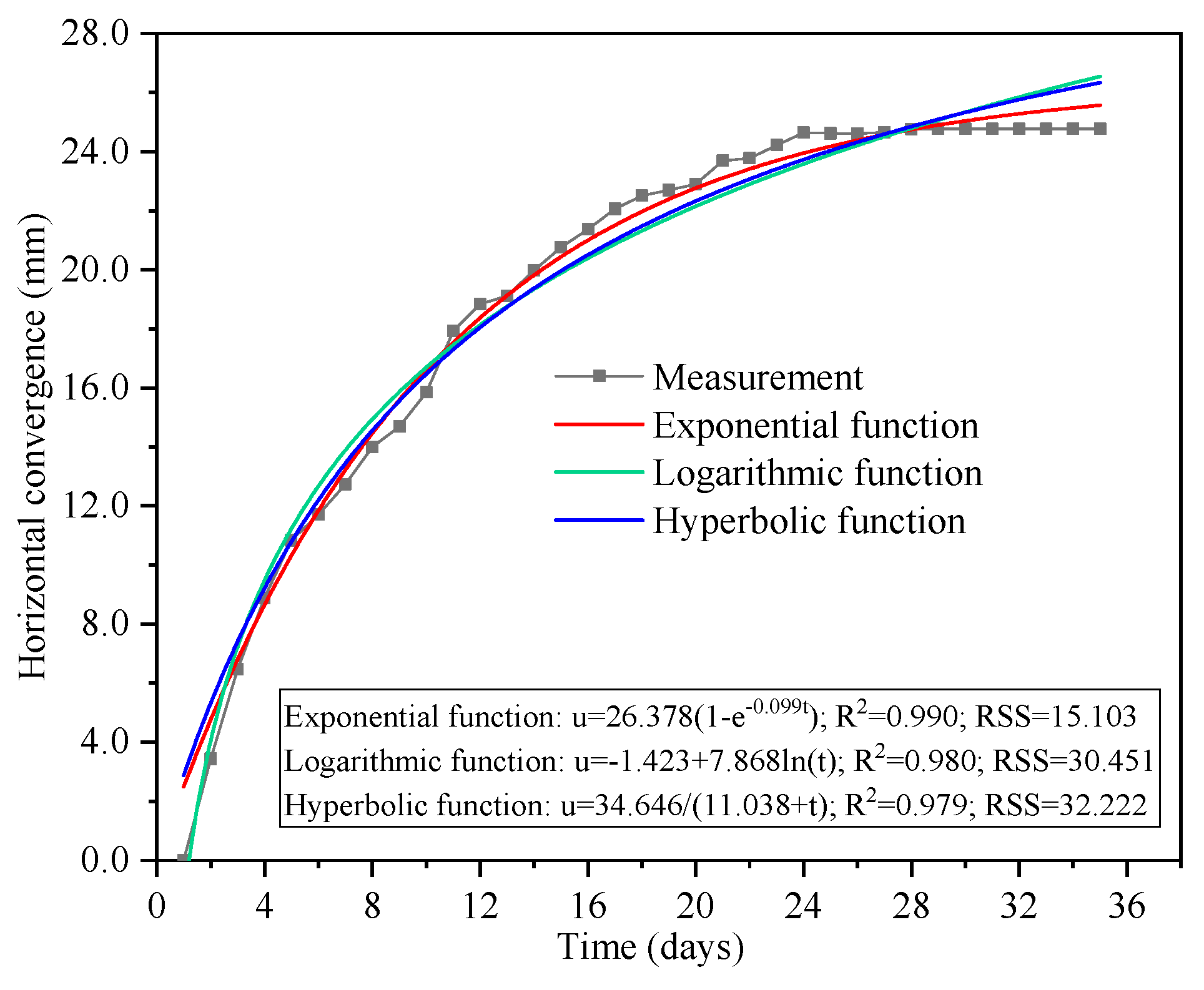
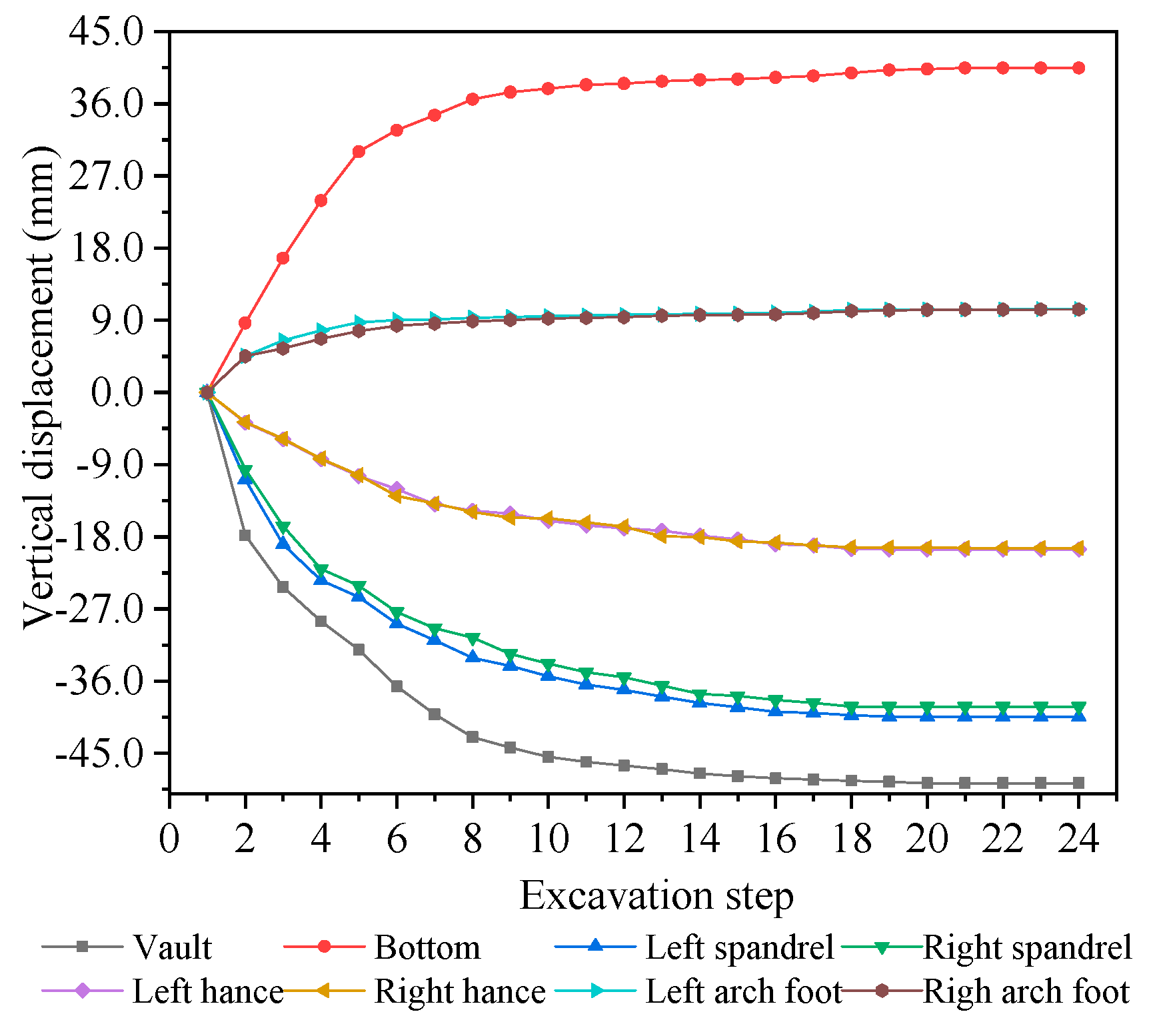
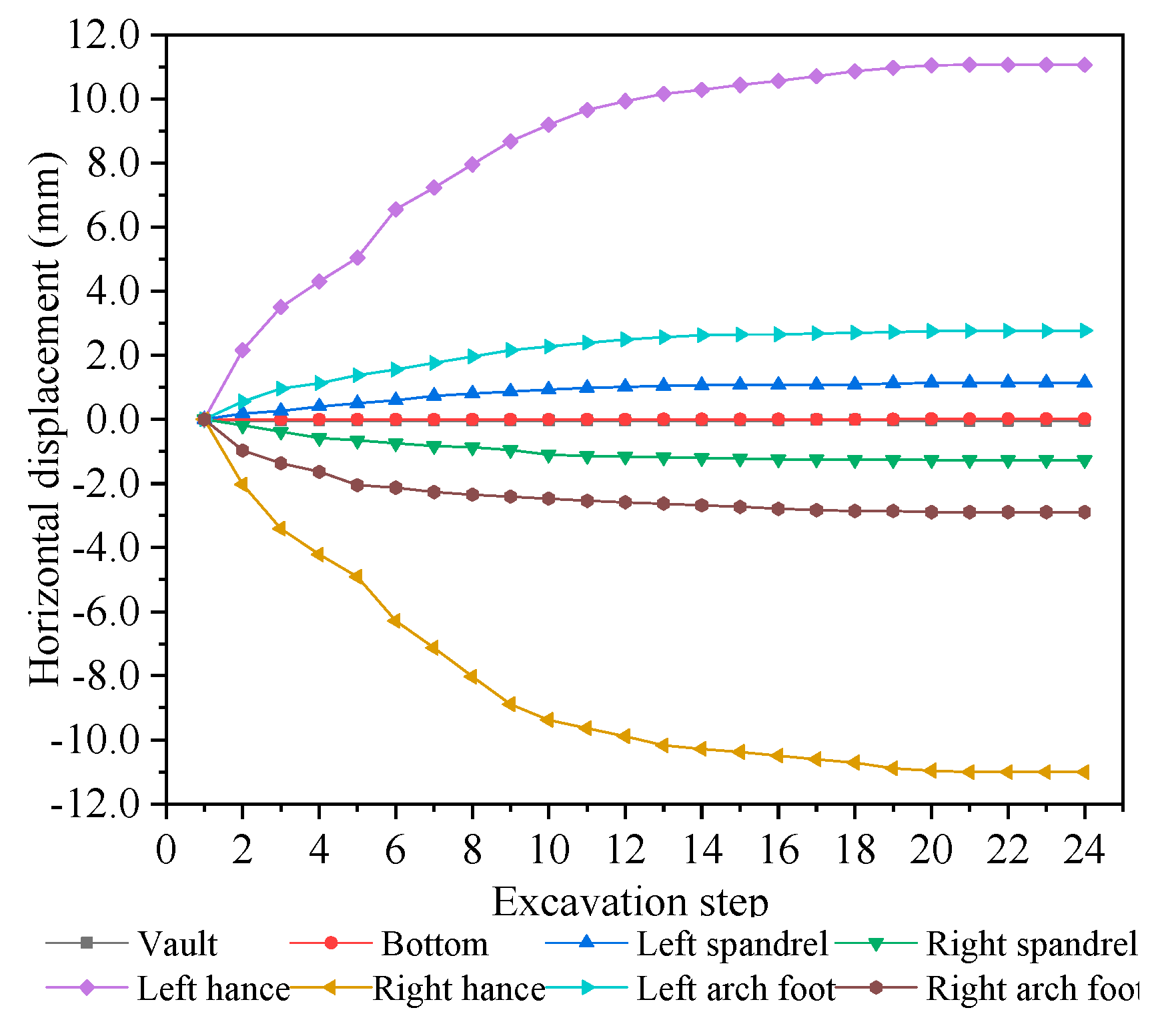
3.3. Monitoring and Analysis of Subsidence of Vaults and Horizontal Convergence
4. Numerical Simulation Analysis of Tunnel Stability
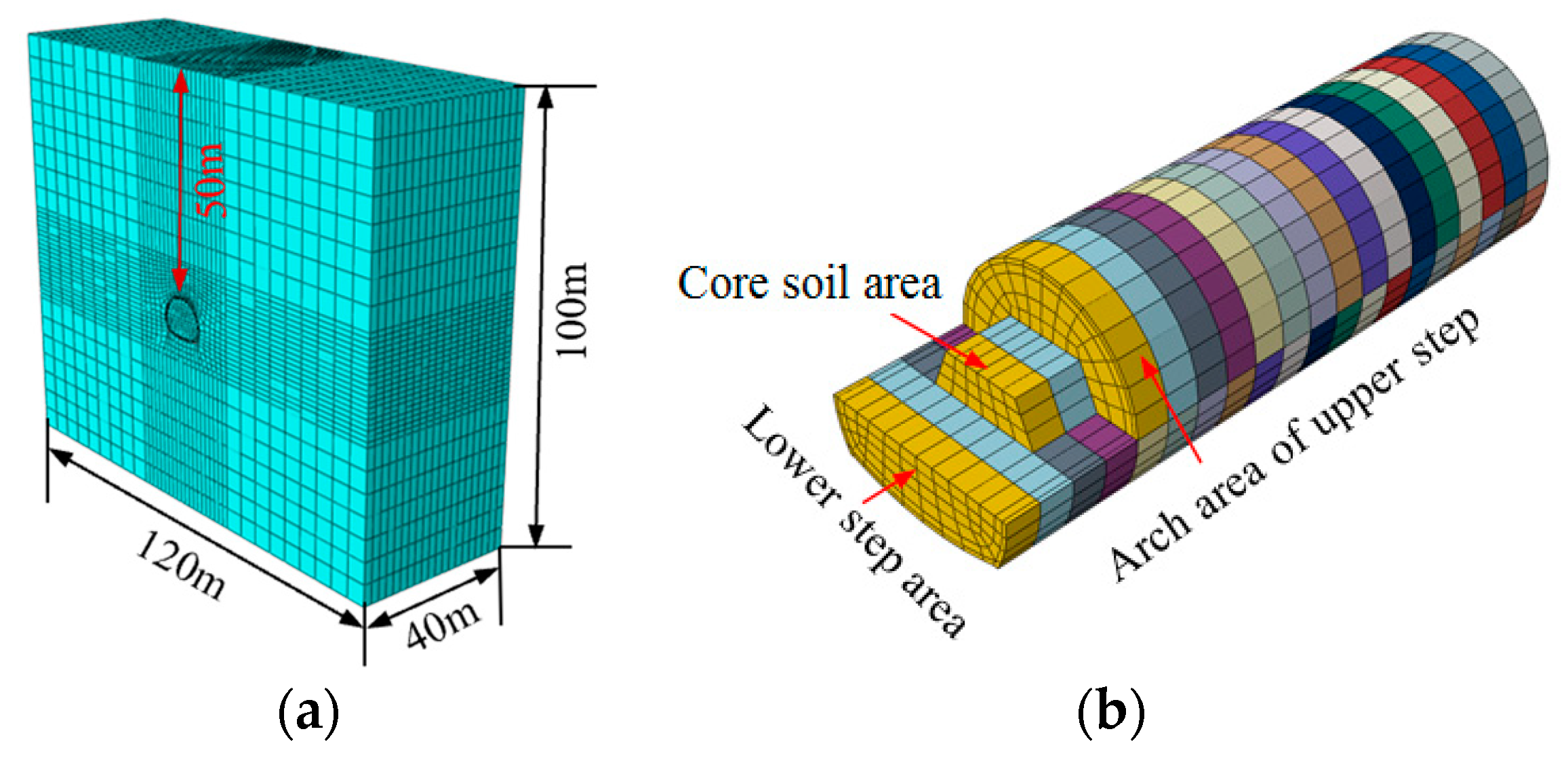
4.1. Modeling
4.2. Results of Simulation and Analysis
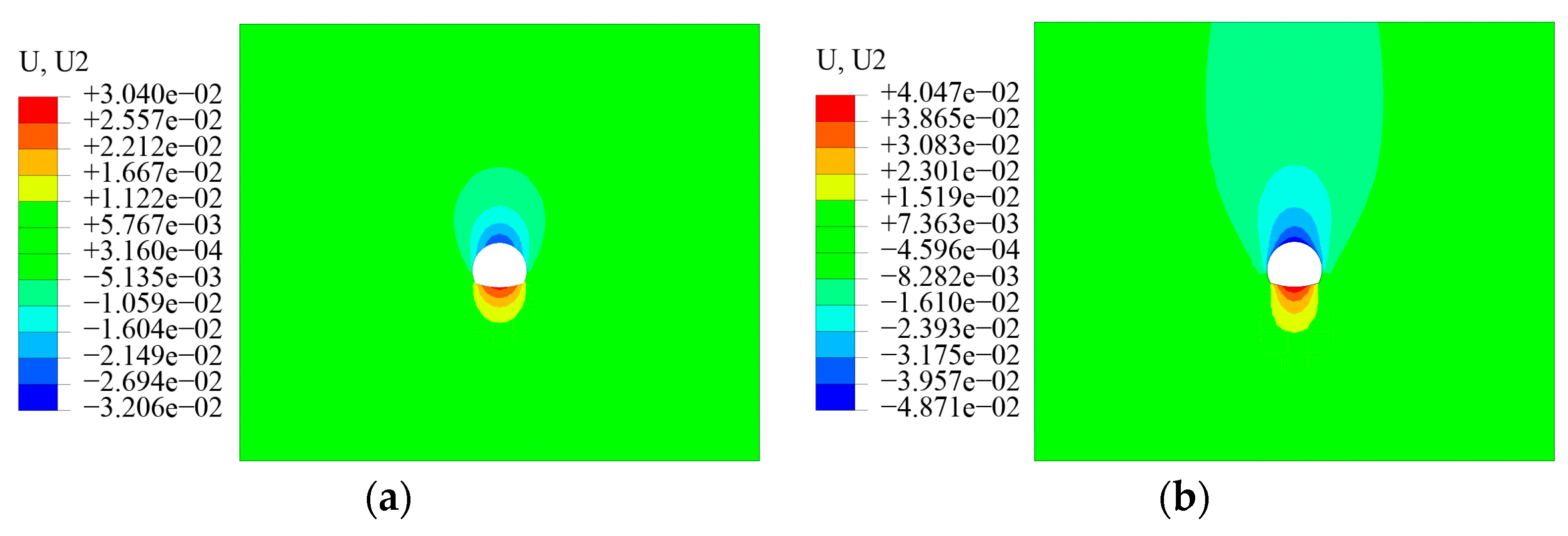
4.2.1. Displacement of Surrounding Rock
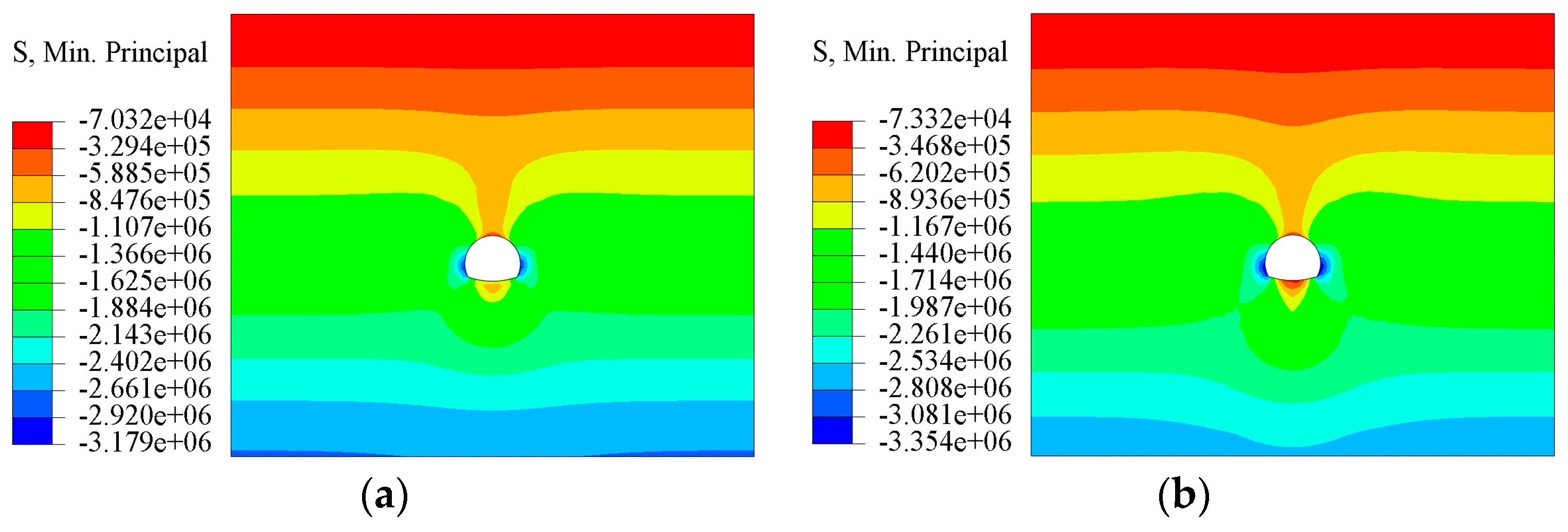
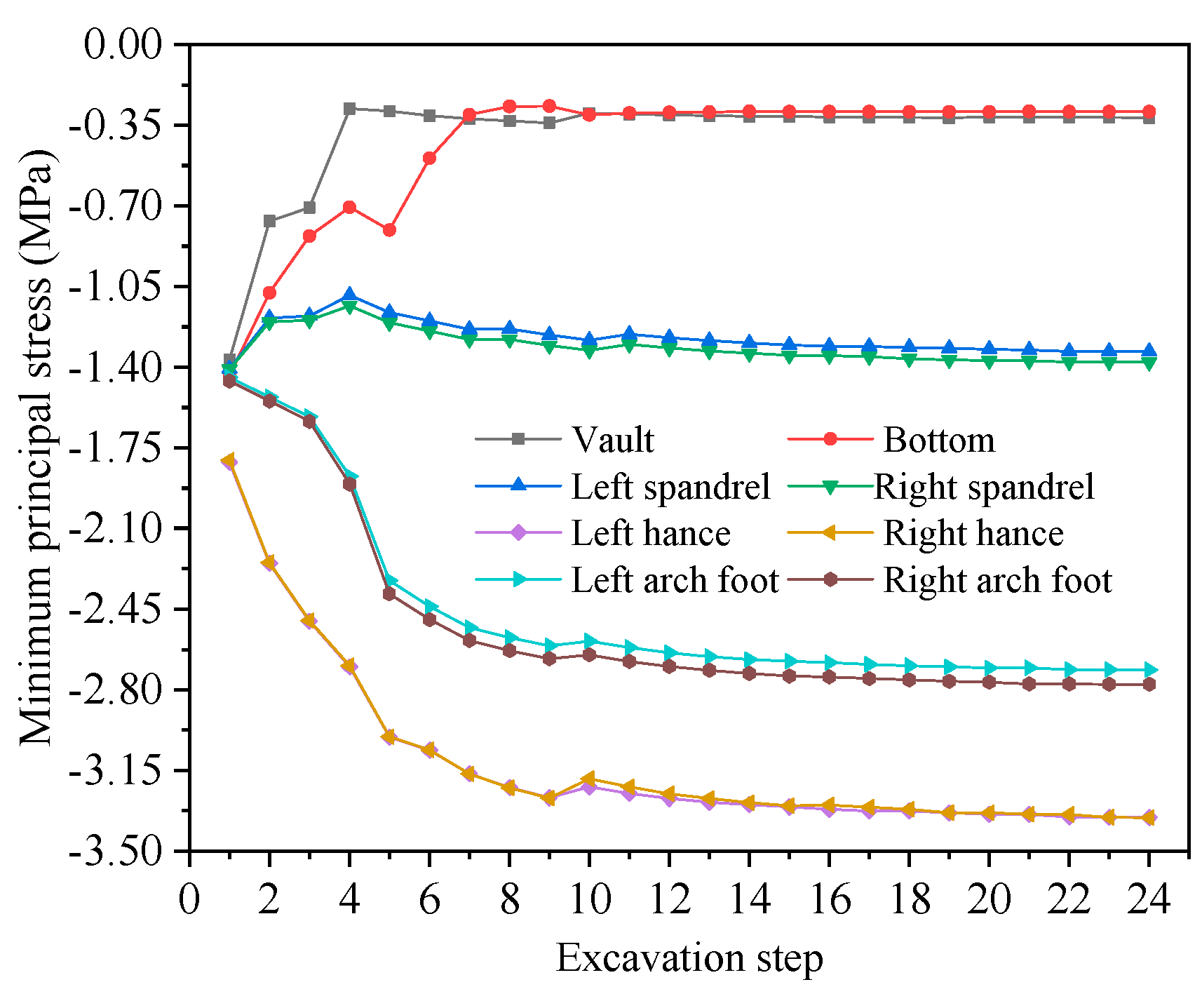
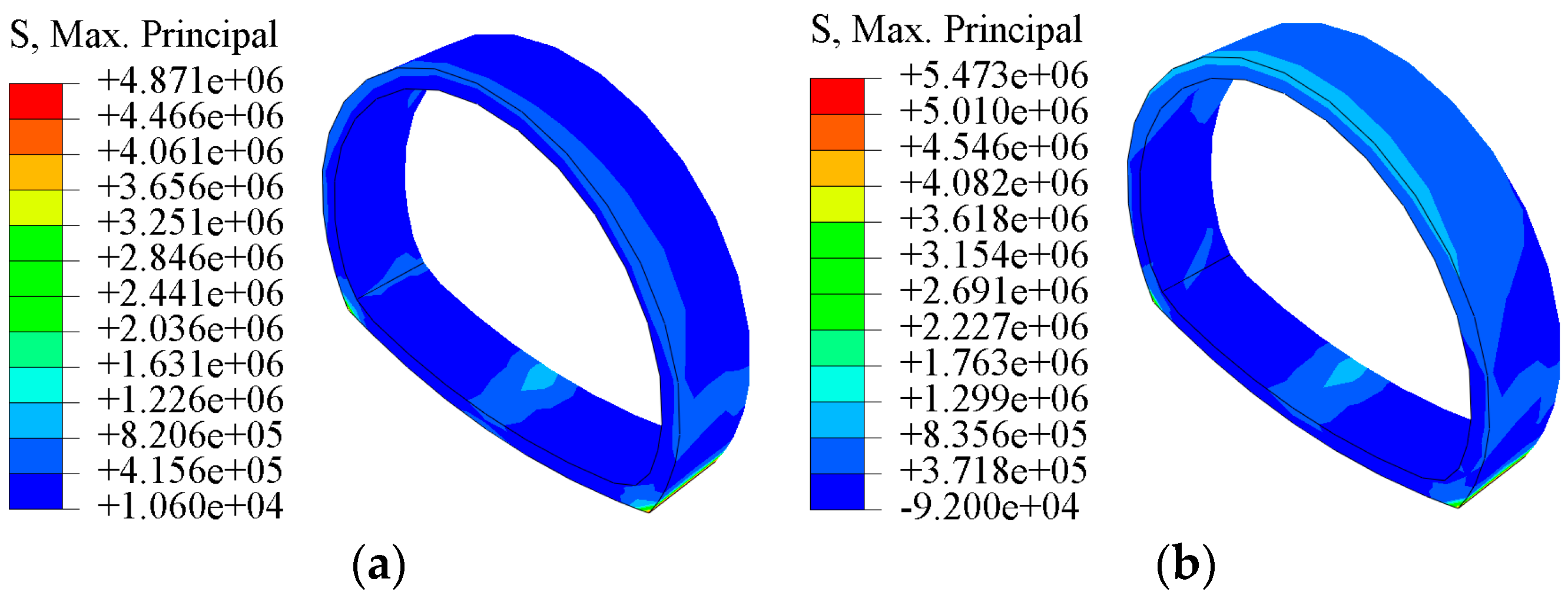
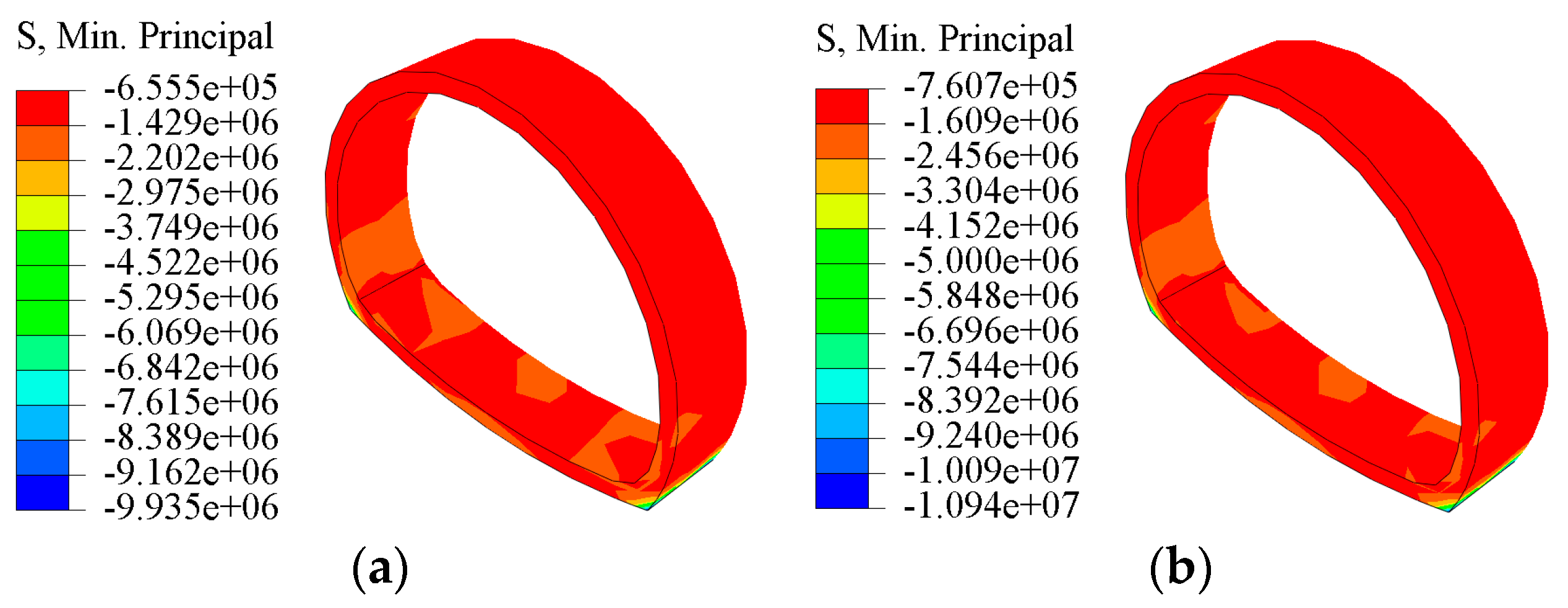
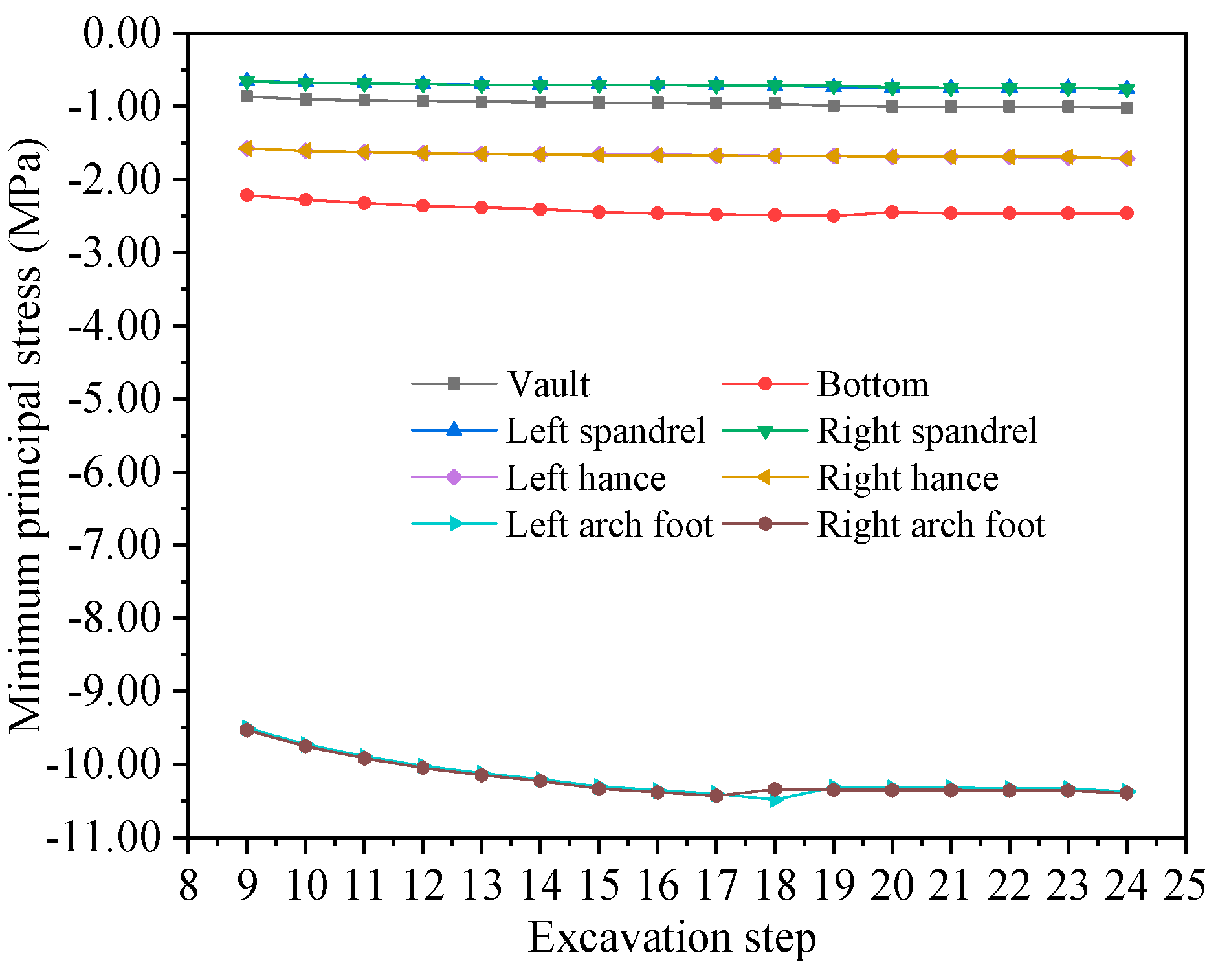
4.2.2. Stress Analysis of Surrounding Rock of the Tunnel
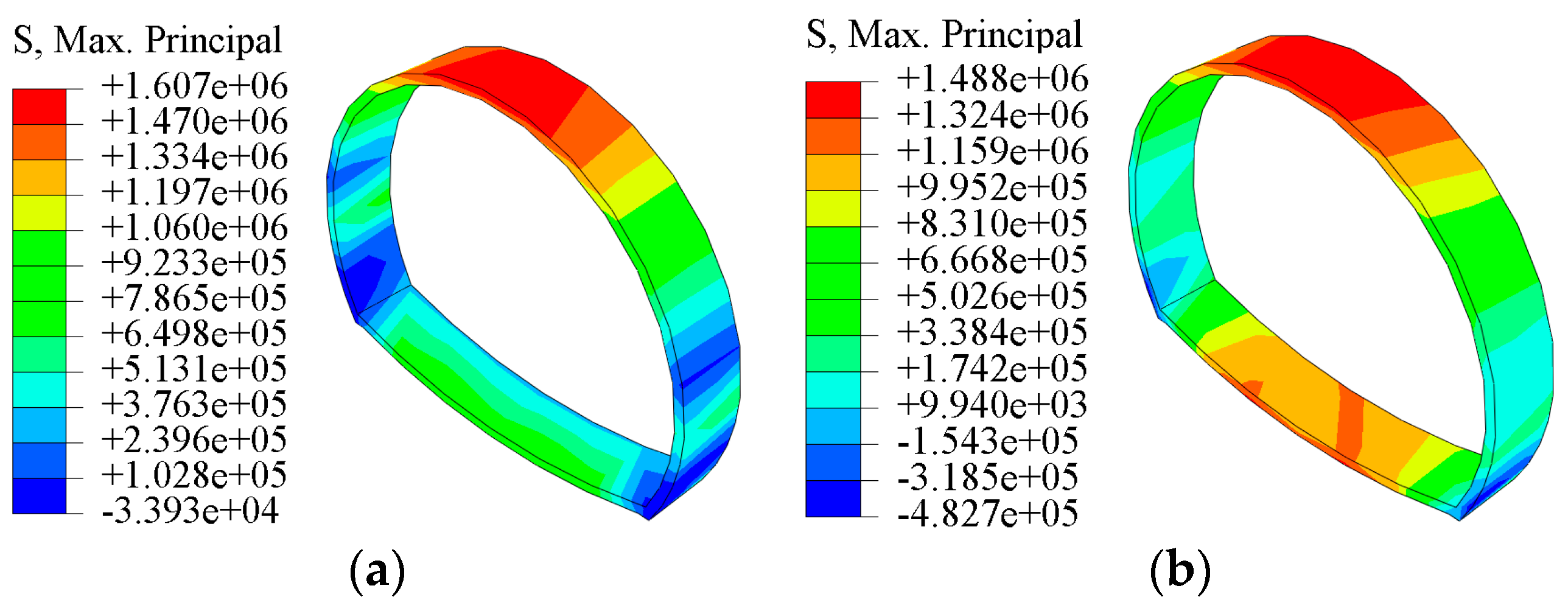
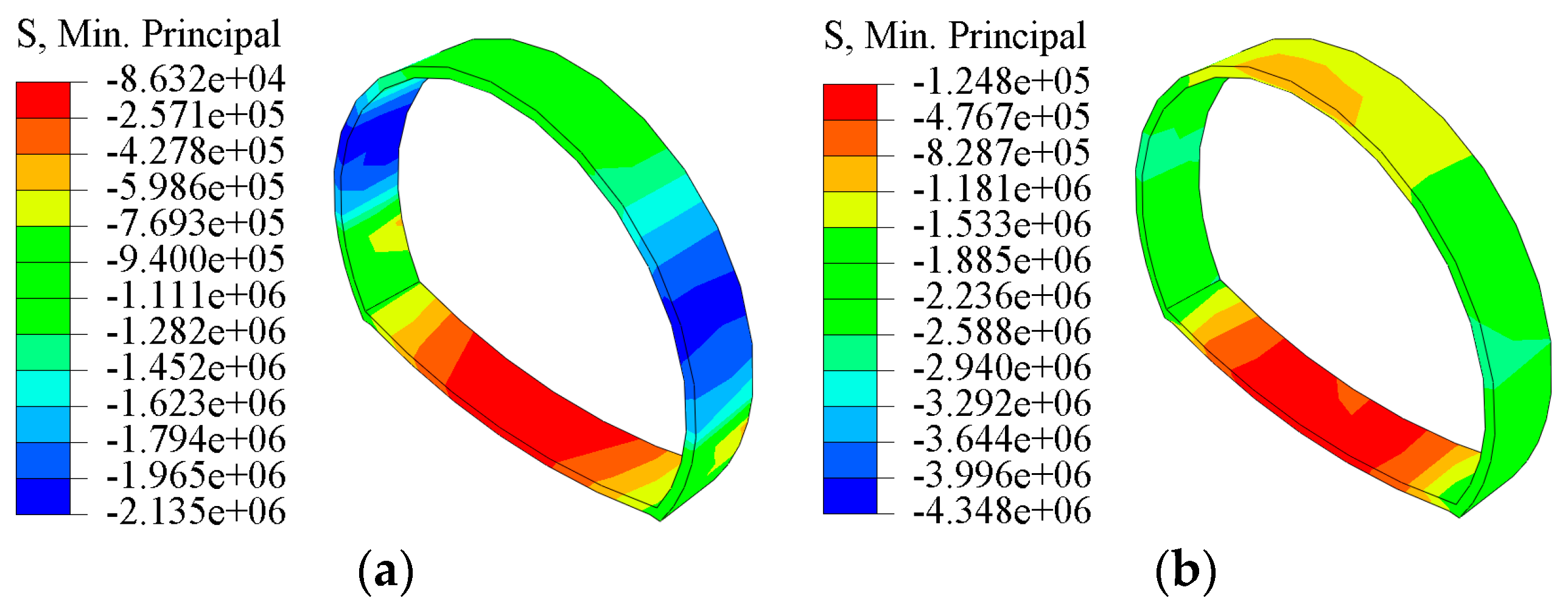
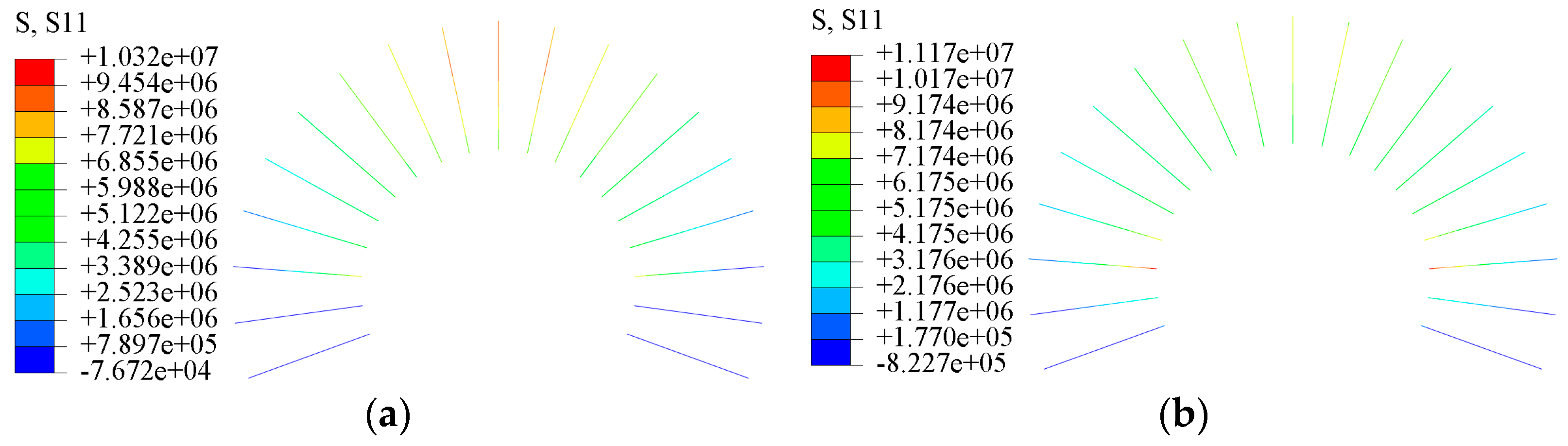
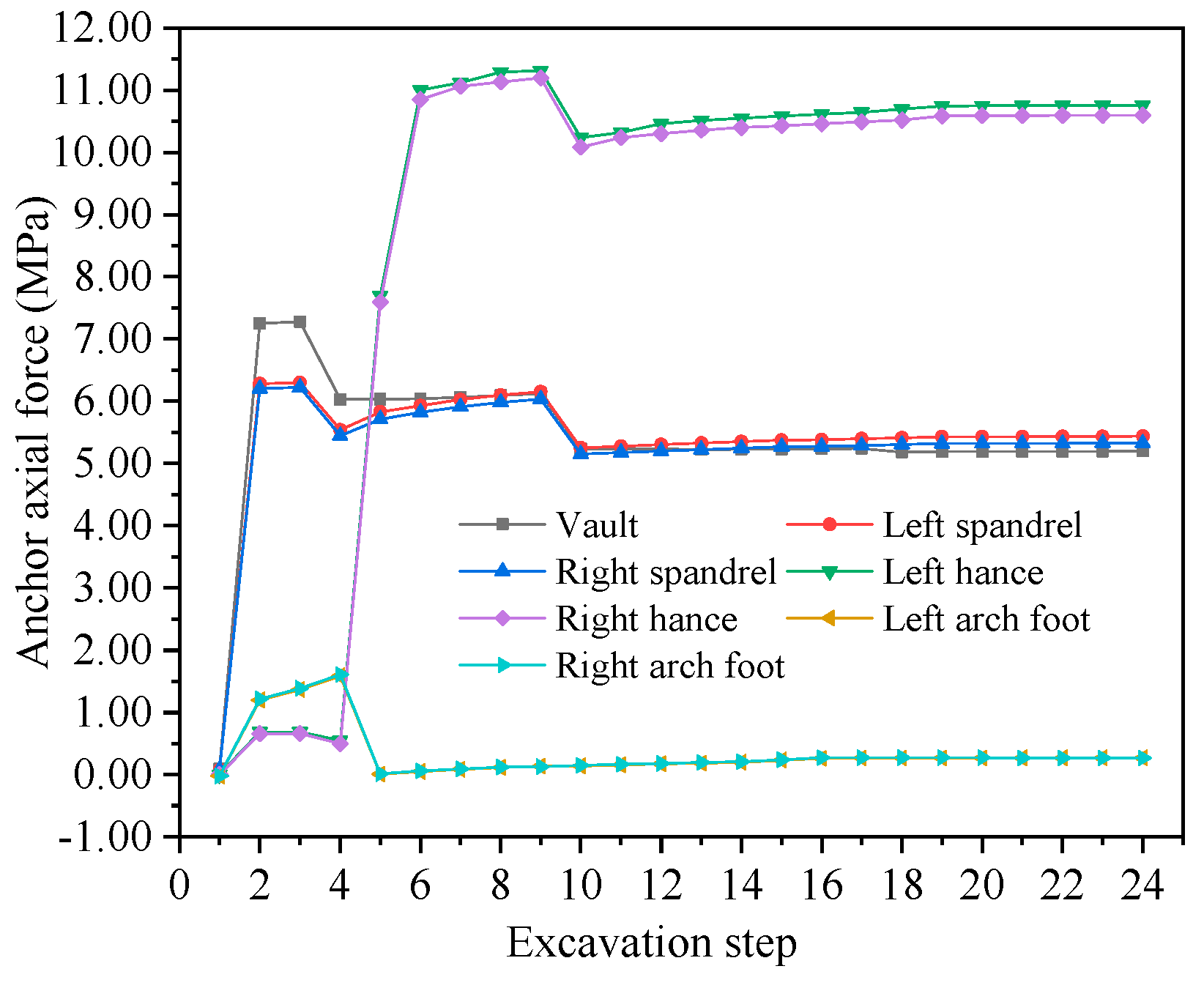
4.2.3. Stress Analysis of Supports
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.C.; Sun, W.F.; Yang, W.L.; Wang, K.; Wang, X. Study on response regularity of tunnel supporting structure characterized with soft-rock large deformation. J. Highw. Transp. Res. Dev. 2021, 38, 91–99. [Google Scholar]
- Zhao, L.H.; Li, D.J.; Yang, F.; Li, L.; Cheng, X. Dimensionless parameter diagrams for the active and passive stability of a shallow 3d tunnel face. KSCE J. Civ. Eng. 2019, 23, 866–878. [Google Scholar]
- Wu, X.-Z.; Liu, Q.-S.; Huang, P.; Zhang, D.; Dai, C.-L. Application of “three-section and four-step” safety treatment technology for tunnel collapse. J. Highw. Transp. Res. Dev. 2022, 39, 123–131. [Google Scholar]
- Yuan, R.; Xiong, W.L.; He, Y.; Cui, K. Analysis on the law of ground settlement in shallow tunnel excavation in composite layered strata. J. Southwest Jiaotong Univ. 2021, 57, 1000–1005. [Google Scholar]
- Li, T.; Cui, Y.; Cao, Y.J.; Ji, Y.; Guo, H.M. Calculation method of surface settlement caused by tunnel construction in rock-soil composite stratum. China Railw. Sci. 2020, 41, 73–80. [Google Scholar]
- Su, Y.; Su, Y.H.; Zhao, M.H. Estimation method of ultimate deformation of soft rock tunnel based on Hoek-Brwon criterion. Chin. J. Rock Mech. Eng. 2021, 40, 3033–3040. [Google Scholar]
- Sun, Z.Y.; Zhang, D.L.; Hou, Y.J.; Li, A. Determination of deformation law and stability criterion of tunnel surrounding rock in whole process based on field measured data. Chin. J. Geotech. Eng. 2021, 43, 1261–1270. [Google Scholar]
- Yang, C.Z.; Wu, Y.J.; Wang, W.; Tang, Y. Analysis on spatial effect of excavation of large section soft rock tunnel. Chin. J. Undergr. Space Eng. 2021, 17, 511–519. [Google Scholar]
- Abdellah, W.R.; Ali, M.A.; Yang, H.-S. Studying the effect of some parameters on the stability of shallow tunnels. J. Sustain. Min. 2018, 17, 20–33. [Google Scholar] [CrossRef]
- Deng, B.; Rao, H.G.; Liao, W.P.; Gao, S.M. Research on support structure optimization of soft rock Tunnel. J. Railw. Sci. Eng. 2017, 14, 2203–2213. [Google Scholar]
- Yang, F.J.; Zhang, C.Q.; Zhou, H.; Liu, N.; Zhang, Y.; Azhar, M.U.; Dai, F. The long-term safety of a deeply buried soft rock tunnel lining under inside-to-outside seepage conditions. Tunn. Undergr. Space Technol. 2017, 67, 132–146. [Google Scholar]
- Lv, J.K.; Yang, J.S.; Zheng, X.C.; Tang, Y.; Xie, Y.P.; Liang, X. Study on large deformation collapse mechanism and control measures for large section tunnel face in Badong formation mudstone. J. Cent. South Univ. 2024, 55, 1418–1432. [Google Scholar]
- Xu, H.; Zhang, Y.; Guo, G.H.; Cai, M.; Li, Y.X.; Chen, Z. Method for calculating penetration range of grouting slurry in the reinforced tunnel by high-pressure rotary jet grouting from ground. Rock Soil Mech. 2023, 44, 2064–2072. [Google Scholar]
- Zuo, Q.J.; Li, X.Y.; Zhao, X.Q.; Li, P.; Zhu, S.; Han, B.X. Mechanical characteristics and force slow-release method of support structure of expansive soft rock tunnels. Chin. J. Rock Mech. Eng. 2023, 42, 2190–2202. [Google Scholar]
- Jia, J.Q.; Wang, H.T.; Li, J.; Zhang, X.; Hu, G.Z. Stability analysis of tunnel supports under complex conditions. Rock Soil Mech. 2010, 31, 3599–3603. [Google Scholar]
- Ding, X.L.; Zhang, Y.T.; Huang, S.L.; Chi, J.J.; Zhang, C.J.; Liu, D.X. Large deformation mechanism of surrounding rock masses of tunnels, prediction method of squeezing large deformation and its application. Chin. J. Rock Mech. Eng. 2023, 42, 521–544. [Google Scholar]
- Bian, K.; Liu, J.; Liu, Z.; Liu, S.; Ai, F.; Zheng, X.; Ni, S.; Zhang, W. Mechanisms of large deformation in soft rock tunnels: A case study of Huangjiazhai tunnel. Bull. Eng. Geol. Environ. 2019, 78, 431–444. [Google Scholar] [CrossRef]
- Zhao, L.L.; Yang, W.B.; Pan, W.T.; Wu, F.Y.; Wang, Z.L.; Yang, Z.C. Study on model test and numerical simulation of layered soft rock tunnel construction with different large deformation grades. Chin. J. Rock Mech. Eng. 2024, 43, 454–467. [Google Scholar]
- Jiang, S.; Zhu, Y.; Li, Q.; Zhou, H.; Tu, H.L.; Yang, F.J. Dynamic prediction of surface settlement and analysis of influencing factors for tunnel excavation. Rock Soil Mech. 2022, 43, 195–204. [Google Scholar]
- Zhang, Z.; Shi, X.; Wang, B.; Li, H. Stability of NATM tunnel faces in soft surrounding rocks. Comput. Geotech. 2018, 96, 90–102. [Google Scholar] [CrossRef]
- Zou, J.-F.; Qian, Z.-H.; Xiang, X.-H.; Chen, G.H. Face stability of a tunnel excavated in saturated nonhomogeneous soils. Tunn. Undergr. Space Technol. 2019, 83, 1–17. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. Stability of unlined square tunnels in Hoek-Brown rock masses based on lower bound analysis. Comput. Geotech. 2019, 105, 249–264. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, Z.J.; Xu, H.Y.; Du, Y.L.; Hou, W.M. Study on deformation characteristic curve and deformation mechanism of tunnel in XiGeDa stratum. China Civ. Eng. J. 2018, 51, 107–121. [Google Scholar]
- Xia, C.; Lu, G.; Bai, D.; Zhu, Z.; Luo, S.; Zhang, G. Sensitivity Analyses of the Seepage and Stability of Layered Rock Slope Based on the Anisotropy of Hydraulic Conductivity: A Case Study in the Pulang Region of Southwestern China. Water 2020, 12, 2314. [Google Scholar] [CrossRef]
- Guo, X.L.; Tan, Z.S.; Li, L.; Zhu, Z.G. Study on the construction time of secondary liningin phyllite tunnel under high geo-stress. China J. Highw. Trans. 2020, 33, 249–261. [Google Scholar]
- JTG/T3660-2020; Technical Specification for Construction of Highway Tunnel. Ministry of Transport of the People’s Republic of China: Beijing, China, 2020.
- Xing, Y.; Kulatilake, P.H.S.W.; Sandbak, L.A. Investigation of rock mass stability around the tunnels in an underground mine in USA using three-dimensional numerical modeling. Rock Mech. Rock Eng. 2018, 51, 579–597. [Google Scholar] [CrossRef]
- Lee, C.-L.; Shou, K.-J.; Chen, S.-S.; Zhou, W.-C. Numerical analysis of tunneling in slates with anisotropic time-dependent behavior. Tunn. Undergr. Space Technol. 2019, 84, 281–294. [Google Scholar] [CrossRef]
- Wu, H.; Fan, F.; Yang, X.; Wang, Z.; Lai, J.; Xie, Y. Large deformation characteristics and treatment effect for deep bias tunnel in broken phyllite: A case study. Eng. Fail. Anal. 2022, 135, 106045. [Google Scholar] [CrossRef]
- Tan, Z.; Li, S.; Yang, Y.; Wang, J. Large deformation characteristics and controlling measures of steeply inclined and layered soft rock of tunnels in plate suture zones. Eng. Fail. Anal. 2022, 131, 105831. [Google Scholar] [CrossRef]
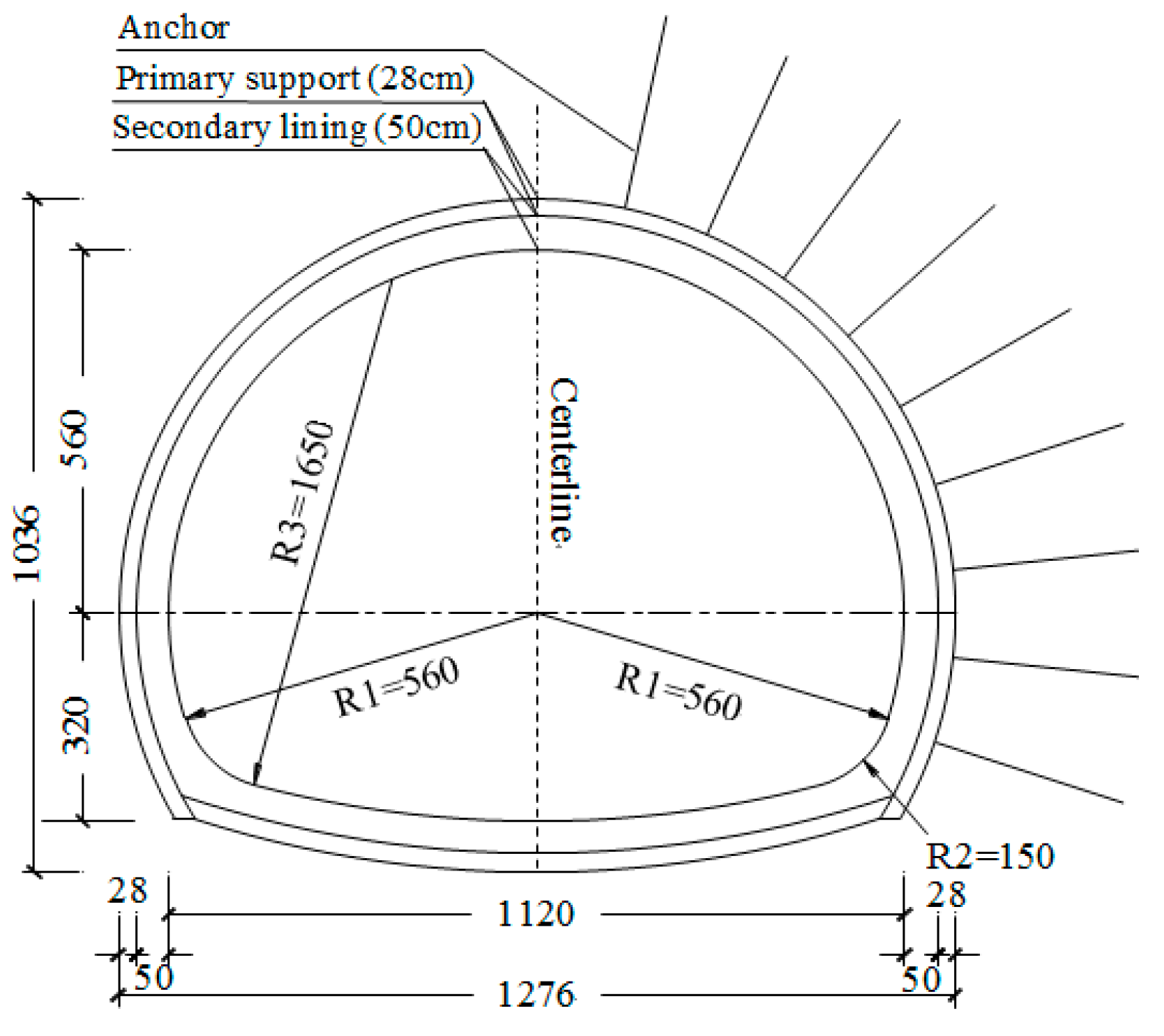






| Primary Supports | Secondary Lining | |||
|---|---|---|---|---|
| Anchor | Reinforcing Mesh | Shotcrete | Steel Arch | |
| φ22, L = 6.0 m, spacing is 75 × 150 (longitudinal × ring) | φ8(double layers), 25 × 25 cm | C25, thickness is 28 cm | I22a, spacing is 75 cm | C35 reinforced concrete, thickness = 50 cm |
| Types | Bulk Density /(kN·m−3) | Elastic Modulus /GPa | Poisson’s Ratio | Cohesion /MPa | Internal Friction Angle/Degrees |
|---|---|---|---|---|---|
| Surrounding rock | 22.5 | 0.08 | 0.30 | 0.1 | 22 |
| Primary supports | 22.0 | 26 | 0.25 | — | — |
| Secondary lining | 25.0 | 31.5 | 0.20 | — | — |
| Anchor | 78.5 | 210 | 0.20 | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Xi, B.; Wang, X.; Tenorio, V.O.; Liu, Z. A Study on Deformation Characteristics and Stability of Soft Surrounding Rock for a Shallow-Buried Tunnel. Appl. Sci. 2024, 14, 6014. https://doi.org/10.3390/app14146014
Jia J, Xi B, Wang X, Tenorio VO, Liu Z. A Study on Deformation Characteristics and Stability of Soft Surrounding Rock for a Shallow-Buried Tunnel. Applied Sciences. 2024; 14(14):6014. https://doi.org/10.3390/app14146014
Chicago/Turabian StyleJia, Jianqing, Boqi Xi, Xin Wang, Victor O. Tenorio, and Zhongshuai Liu. 2024. "A Study on Deformation Characteristics and Stability of Soft Surrounding Rock for a Shallow-Buried Tunnel" Applied Sciences 14, no. 14: 6014. https://doi.org/10.3390/app14146014
APA StyleJia, J., Xi, B., Wang, X., Tenorio, V. O., & Liu, Z. (2024). A Study on Deformation Characteristics and Stability of Soft Surrounding Rock for a Shallow-Buried Tunnel. Applied Sciences, 14(14), 6014. https://doi.org/10.3390/app14146014






