Modeling and Prediction of Surface Roughness in Hybrid Manufacturing–Milling after FDM Using Artificial Neural Networks
Abstract
1. Introduction
2. Materials, Methods and Equipment
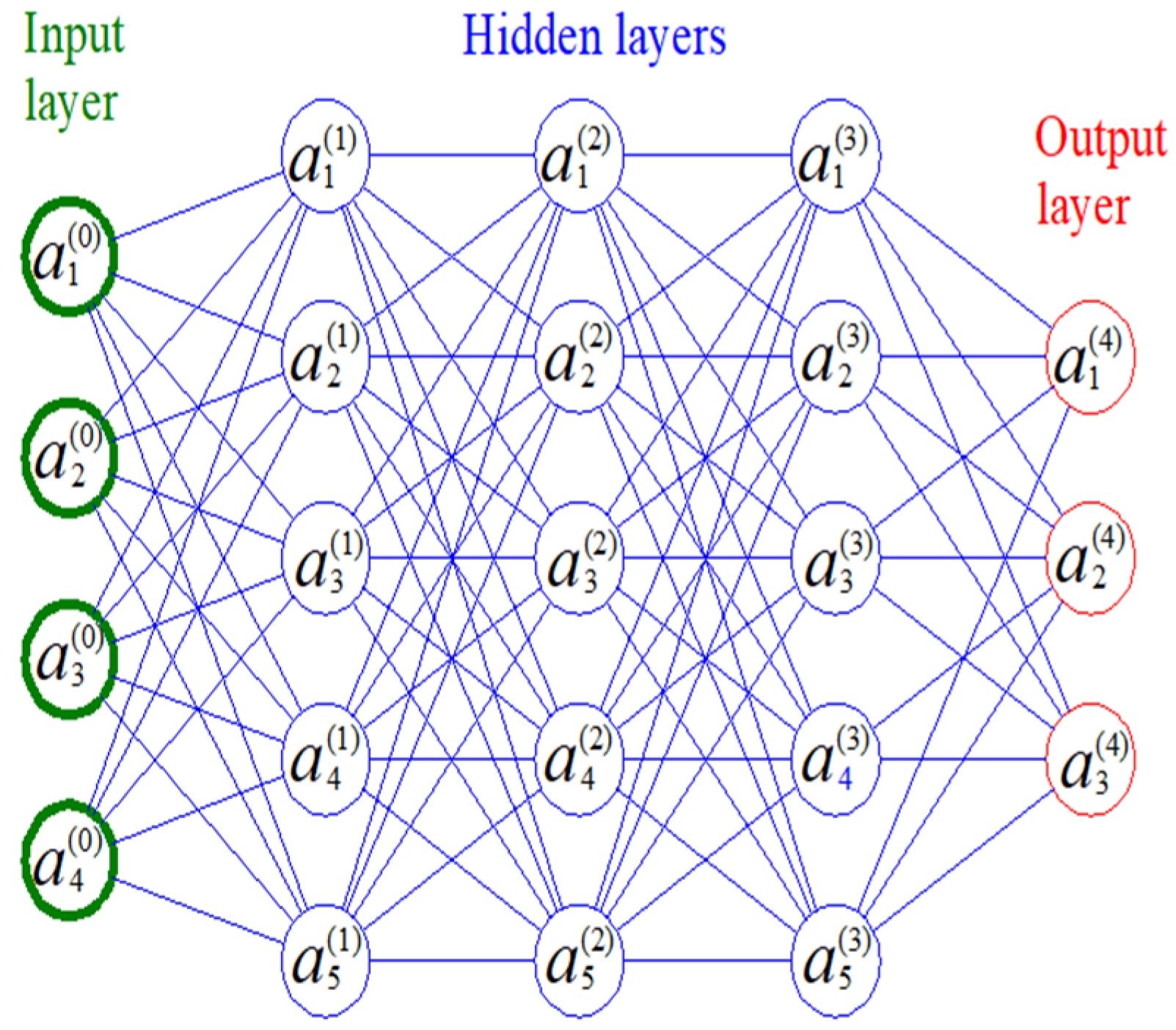
2.1. Artificial Neural Networks
2.2. Multiple Regression Analysis
- Single step or standard: All predictors enter the regression together.
- Hierarchical or sequential: Each block defines a single step, and all predictors are incorporated in the blocks.
2.3. Equipment
2.4. Experimental Setup
3. Results and Discussion
3.1. Artificial Neural Network Results
3.2. Multiple Regression Analysis Results
3.3. Obtained Evaluation
4. Conclusions
- ANN and MRA modeling can effectively predict surface roughness, with the ANN outperforming MRA. Models with more input parameters (48 in this case) produce better predictions than those with fewer parameters (27 in previous research).
- The ANN model that used the RuLU activation function gave better predictions than the model with the tanh activation function.
- ANN models with smaller numbers of neurons and hidden layers give better predictions for a small number of training parameters due to a complicated network of neurons. The ANN network itself has too many parameters in relation to the number of training examples.
- The best measured surface roughness was 1.958 μm. In the case of MRA, this was measured at 2.372 μm and calculated at 2.14 μm, while with the ANN, it was measured at 2.058 μm and calculated at 2.056 μm.
- All ANN models predict a high surface quality at a speed of 3000 or 1000 rev/min, a feed rate of 400 mm/min, and a cutting depth of 0.3 mm.
- The highest degree of correlation (determination coefficient) R2 = 0.9771 was achieved by the ANN 5-S-R model, while MRA methods gave a smaller correlation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, H.; Cheng, X.; Jiang, X.; Zheng, G.; Zhang, J.; Li, Y.; Tang, M.; Lv, F. Green Manufacturing-Oriented Polyetheretherketone Additive Manufacturing and Dry Milling Post-Processing Process Research. Processes 2022, 10, 2561. [Google Scholar] [CrossRef]
- Khorasani, A.M.; Yazdi, M.R.S.; Safizadeh, M.S. Analysis of machining parameters effects on surface roughness: A review. Int. J. Comput. Mater. Sci. Surf. Eng. 2012, 5, 68–84. [Google Scholar] [CrossRef]
- Lu, C. Study on prediction of surface quality in machining process. J. Mater. Process. Technol. 2008, 205, 439–450. [Google Scholar] [CrossRef]
- Huynh, V.M.; Fan, Y. Surface-texture measurement and characterisation with applications to machine-tool monitoring. Int. J. Adv. Manuf. Technol. 1992, 7, 2–10. [Google Scholar] [CrossRef]
- Van Luttervelt, C.A.; Childs, T.H.C.; Jawahir, I.S.; Klocke, F.; Venuvinod, P.K.; Altintas, Y.; Sato, H. Present situation and future trends in modelling of machining operations progress report of the CIRP Working Group ‘Modelling of Machining Operations’. CIRP Ann. 1998, 47, 587–626. [Google Scholar] [CrossRef]
- Dastres, R.; Soori, M. Artificial neural network systems. Int. J. Imaging Robot. 2021, 21, 13–25. [Google Scholar]
- Abdul Shukor, J.; Said, S.; Harun, R.; Husin, S.; Kadir, A. Optimising of machining parameters of plastic material using Taguchi method. Adv. Mater. Process. Technol. 2016, 2, 50–56. [Google Scholar] [CrossRef]
- Saad, M.S.; Mohd Nor, A.; Abd Rahim, I.; Syahruddin, M.A.; Mat Darus, I.Z. Optimization of FDM process parameters to minimize surface roughness with integrated artificial neural network model and symbiotic organism search. Neural Comput. Appl. 2022, 34, 17423–17439. [Google Scholar] [CrossRef]
- Boschetto, A.; Giordano, V.; Veniali, F. Surface roughness prediction in fused deposition modelling by neural networks. Int. J. Adv. Manuf. Technol. 2013, 67, 2727–2742. [Google Scholar] [CrossRef]
- García Plaza, E.; Núñez López, P.J.; Caminero Torija, M.Á.; Chacón Muñoz, J.M. Analysis of PLA Geometric Properties Processed by FFF Additive Manufacturing: Effects of Process Parameters and Plate-Extruder Precision Motion. Polymers 2019, 11, 1581. [Google Scholar] [CrossRef]
- Lyu, J.; Manoochehri, S. Dimensional prediction for FDM machines using artificial neural network and support vector regression. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019. V001T02A033. [Google Scholar]
- Nagarajan, H.P.; Mokhtarian, H.; Jafarian, H.; Dimassi, S.; Bakrani-Balani, S.; Hamedi, A.; Haapala, K.R. Knowledge-based design of artificial neural network topology for additive manufacturing process modeling: A new approach and case study for fused deposition modeling. J. Mech. Des. 2019, 141, 021705. [Google Scholar] [CrossRef]
- Kandananond, K. Surface roughness prediction of FFF-fabricated workpieces by artificial neural network and Box–Behnken method. Int. J. Metrol. Qual. Eng. 2021, 12, 17. [Google Scholar] [CrossRef]
- Benardos, P.G.; Vosniakos, G.C. Prediction of surface roughness in CNC face milling using neural networks and Taguchi’s design of experiments. Robot. Comput.-Integr. Manuf. 2002, 18, 343–354. [Google Scholar] [CrossRef]
- Beatrice, B.A.; Kirubakaran, E.; Thangaiah, P.R.J.; Wins, K.L.D. Surface roughness prediction using artificial neural network in hard turning of AISI H13 steel with minimal cutting fluid application. Procedia Eng. 2014, 97, 205–211. [Google Scholar] [CrossRef]
- Nalbant, M.; Gokkaya, H.; Toktaş, İ. Comparison of regression and artificial neural network models for surface roughness prediction with the cutting parameters in CNC turning. Model. Simul. Eng. 2007, 2007, 092717. [Google Scholar] [CrossRef]
- Hussein, H.K.; Shareef, I.R.; Zayer, I.A. Comparative Prediction and Modelling of Surface Roughness in Milling of AL-7075 Using Regression Analysis and Neural Network. Math. Model. Eng. Probl. 2022, 9, 186. [Google Scholar] [CrossRef]
- Meral, G.; Dilipak, H.; Sarikaya, M. Modeling with Regression Methods of the Thrust Forces and the Surface Roughness in the Drilling of AISI 1050 Materials. Turk. Sci. Res. Found. 2011, 4, 31–41. [Google Scholar]
- Asiltürk, I.; Çunkaş, M. Modeling and prediction of surface roughness in turning operations using artificial neural network and multiple regression method. Expert Syst. Appl. 2011, 38, 5826–5832. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Wu, K.-D.; Shih, W.-C.; Hsu, P.-K.; Hung, J.-P. Prediction of Surface Roughness Based on Cutting Parameters and Machining Vibration in End Milling Using Regression Method and Artificial Neural Network. Appl. Sci. 2020, 10, 3941. [Google Scholar] [CrossRef]
- Yilmaz, S.; Arici, A.A.; Feyzullahoglu, E. Surface roughness prediction in machining of cast polyamide using neural network. Neural Comput. Appl. 2011, 20, 1249–1254. [Google Scholar] [CrossRef]
- Tsai, Y.-H.; Chen, J.C.; Lou, S.-J. An in-process surface recognition system based on neural networks in end milling cutting operations. Int. J. Mach. Tools Manuf. 1999, 39, 583–605. [Google Scholar] [CrossRef]
- Zain, A.M.; Haron, H.; Sharif, S. Prediction of surface roughness in the end milling machining using Artificial Neural Network. Expert Syst. Appl. 2010, 37, 1755–1768. [Google Scholar] [CrossRef]
- Shie, J.R. Optimization of dry machining parameters for high-purity graphite in end-milling process by artificial neural networks: A case study. Mater. Manuf. Process. 2006, 21, 838–845. [Google Scholar] [CrossRef]
- Jafarian, F.; Taghipour, M.; Amirabadi, H. Application of artificial neural network and optimization algorithms for optimizing surface roughness, tool life and cutting forces in turning operation. J. Mech. Sci. Technol. 2013, 27, 1469–1477. [Google Scholar] [CrossRef]
- Kosarac, A.; Mladjenovic, C.; Zeljkovic, M.; Tabakovic, S.; Knezev, M. Neural-Network-Based Approaches for Optimization of Machining Parameters Using Small Dataset. Materials 2022, 15, 700. [Google Scholar] [CrossRef]
- Yanis, M.; Mohruni, A.S.; Sharif, S.; Yani, I.; Arifin, A.; Khona’Ah, B. Application of RSM and ANN in predicting surface roughness for side milling process under environmentally friendly cutting fluid. J. Phys. Conf. Ser. 2019, 1198, 042016. [Google Scholar] [CrossRef]
- Karayel, D. Prediction and control of surface roughness in CNC lathe using artificial neural network. J. Mater. Process. Technol. 2009, 209, 3125–3137. [Google Scholar] [CrossRef]
- Dhokia, V.G.; Kumar, S.; Vichare, P.; Newman, S.T.; Allen, R.D. Surface roughness prediction model for CNC machining of polypropylene. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 137–157. [Google Scholar] [CrossRef]
- Pămărac, R.G.; Petruse, R.E. Study regarding the optimal milling parameters for finishing 3D printed parts from ABS and PLA materials. Acta Univ. Cibiniensis Tech. Ser. 2018, 70, 66–72. [Google Scholar] [CrossRef]
- Amanullah, A.N.M.; Saleh, T.; Khan, R. Design and development of a hybrid machine combining rapid prototyping and CNC milling operation. Procedia Eng. 2017, 184, 163–170. [Google Scholar] [CrossRef]
- Grguraš, D.; Kramar, D. Optimization of hybrid manufacturing for surface quality, material consumption and productivity improvement. Stroj. Vestn.-J. Mech. Eng. 2017, 63, 567–576. [Google Scholar] [CrossRef]
- Li, L.; Haghighi, A.; Yang, Y. Theoretical modelling and prediction of surface roughness for hybrid additive–subtractive manufacturing processes. IISE Trans. 2019, 51, 124–135. [Google Scholar] [CrossRef]
- Abbasbhai, K.T.; Vijay, C.N.; Sourabh, J. Evaluation of Artificial Neural Networks. Int. J. Eng. 2012, 1, 1–8. [Google Scholar]
- Nigrin, A. Neural Networks for Pattern Recognition; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Nielsen, F. Neural Networks Algorithms and Applications; Niels Brock Business College: Copenhagen, Denmark, 2001; Volume 12. [Google Scholar]
- Lahiri, S.K.; Ghanta, K.C. Development of an artificial neural network correlation for prediction of hold-up of slurry transport in pipelines. Chem. Eng. Sci. 2008, 63, 1497–1509. [Google Scholar] [CrossRef]
- Djurović, S.; Stanojković, J.; Lazarević, D.; Ćirković, B.; Lazarvić, A.; Džunić, D.; Šarkoćević, Ž. Modeling and Prediction of Surface Roughness in the End Milling Process using Multiple Regression Analysis and Artificial Neural Network. Tribol. Ind. 2022, 44, 540–549. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, S.; Athaiya, A. Activation functions in neural networks. Towards Data Sci. 2017, 6, 310–316. [Google Scholar] [CrossRef]
- Multiple Regression Explanation, Assumptions, Interpretation, and Write Up. Available online: https://usq.pressbooks.pub/statisticsforresearchstudents/chapter/multiple-regression-assumptions/ (accessed on 6 March 2024).
- Reddy, B.S.; Padmanabhan, G.; Reddy, K.V.K. Surface roughness prediction tehniques for CNC turning. Asian J. Sci. Res. 2008, 1, 256–264. [Google Scholar] [CrossRef]
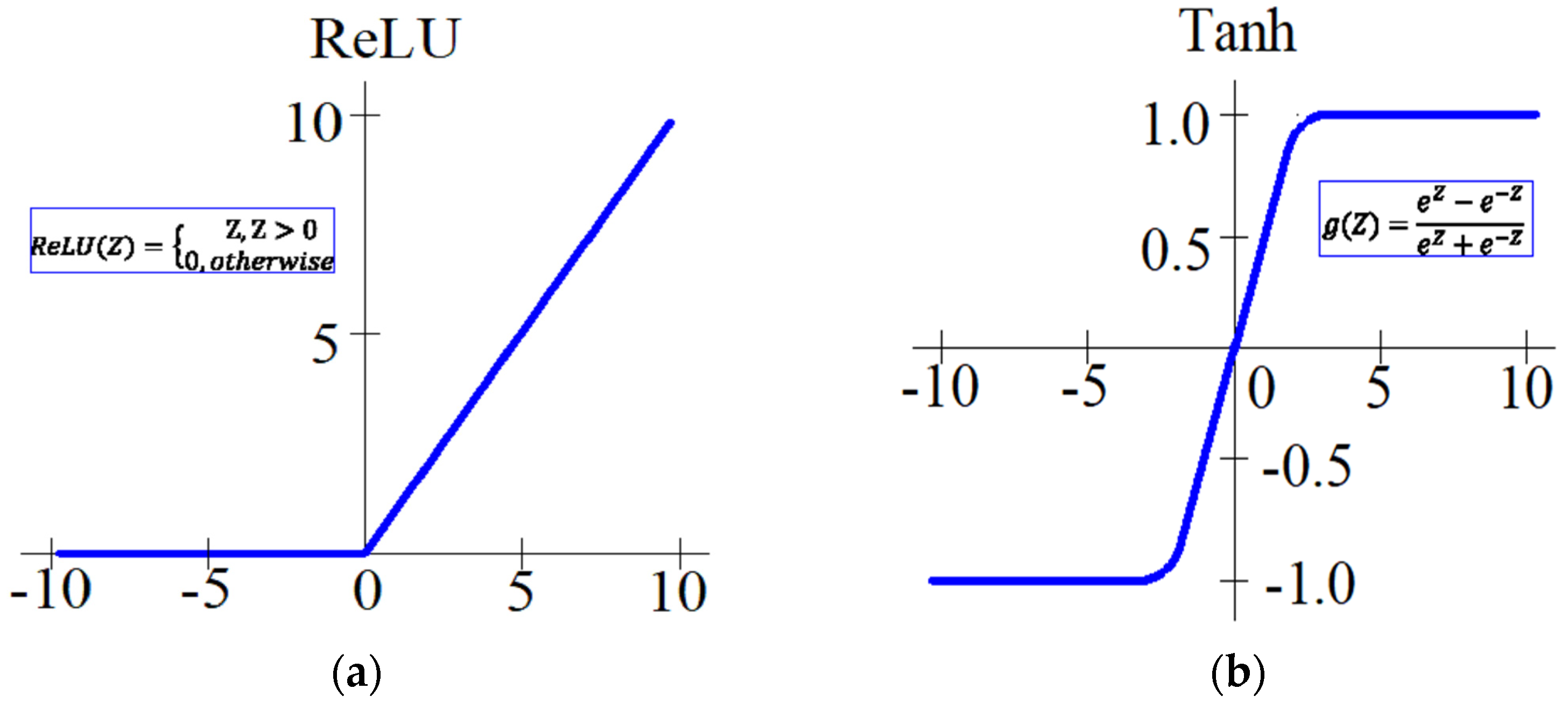



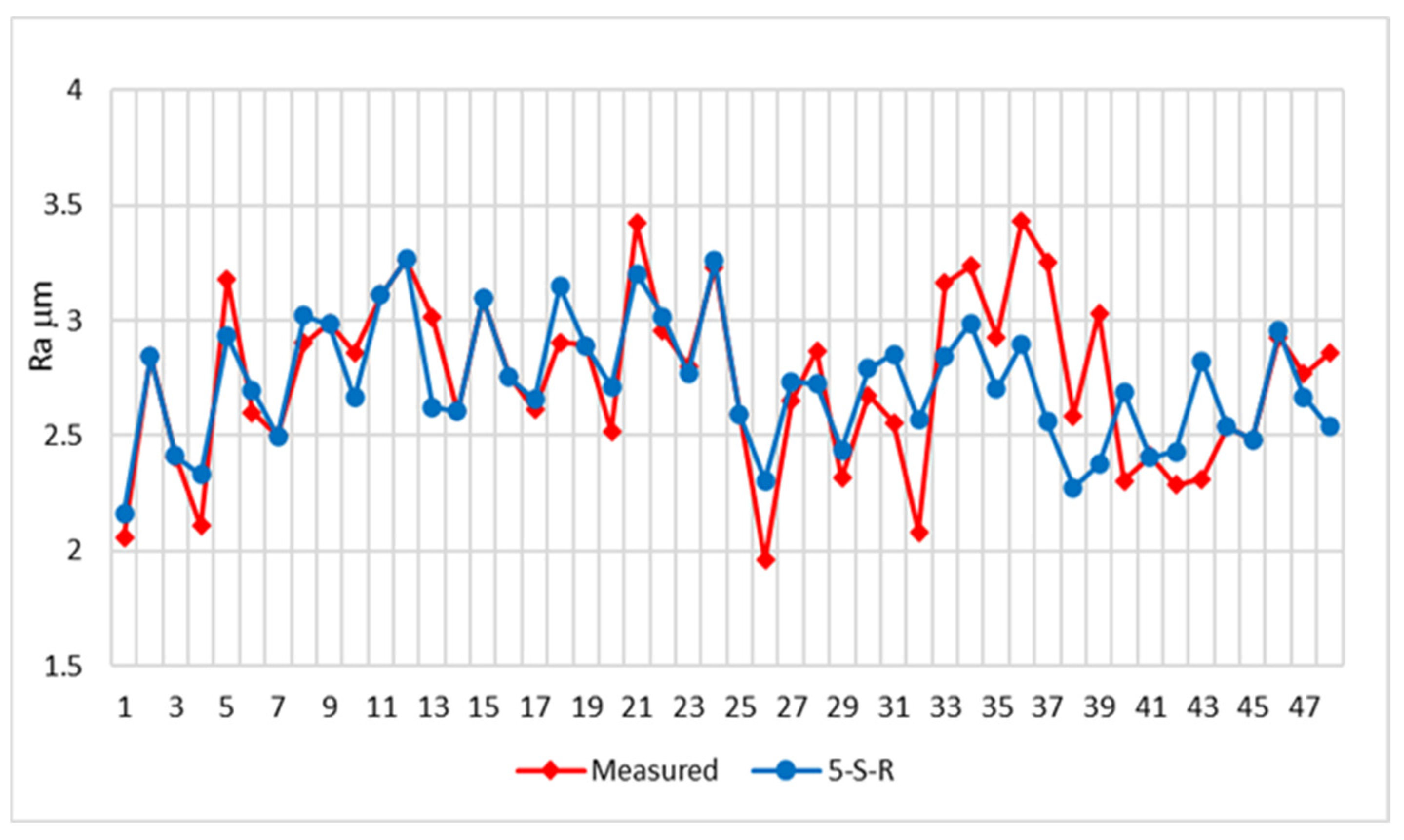
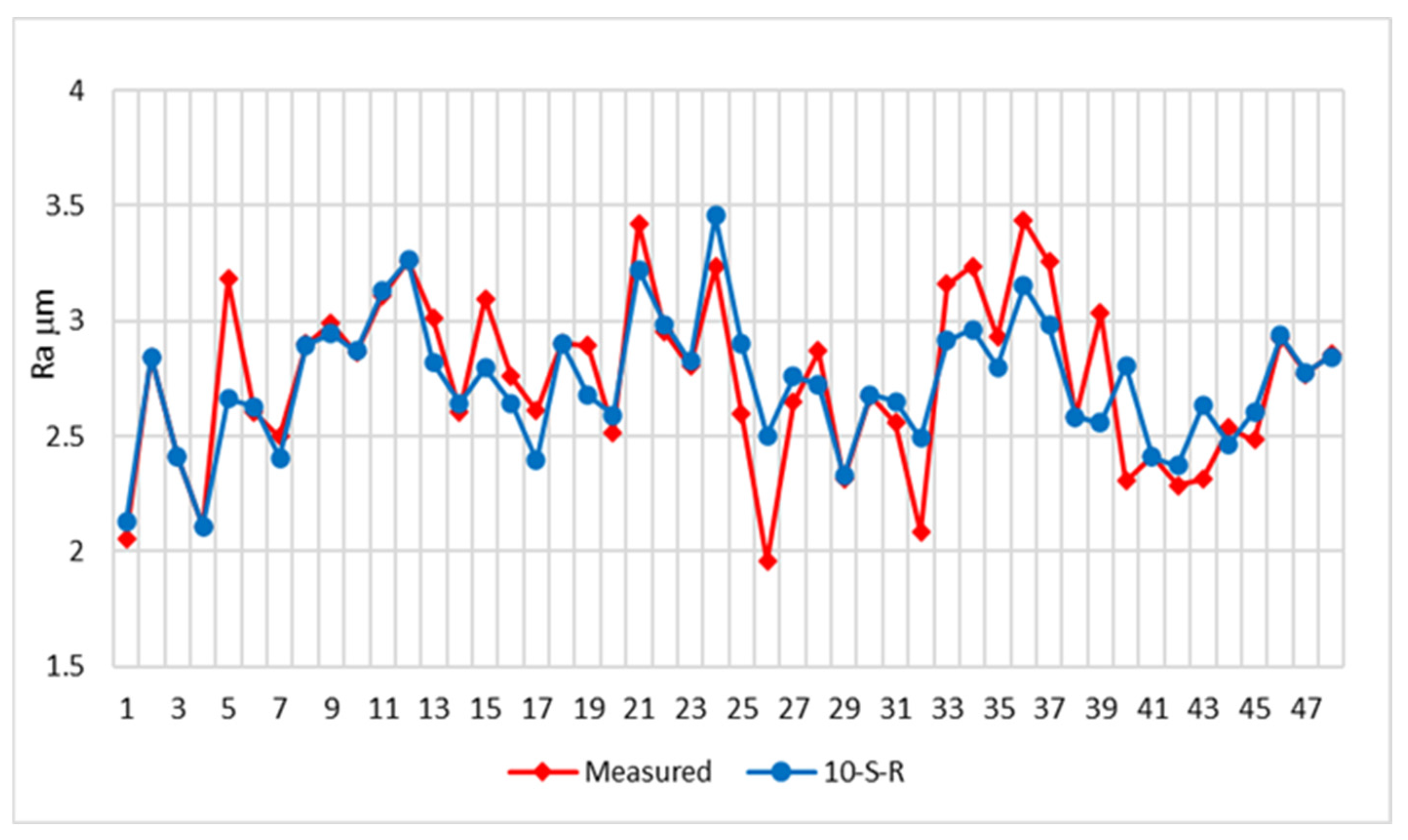

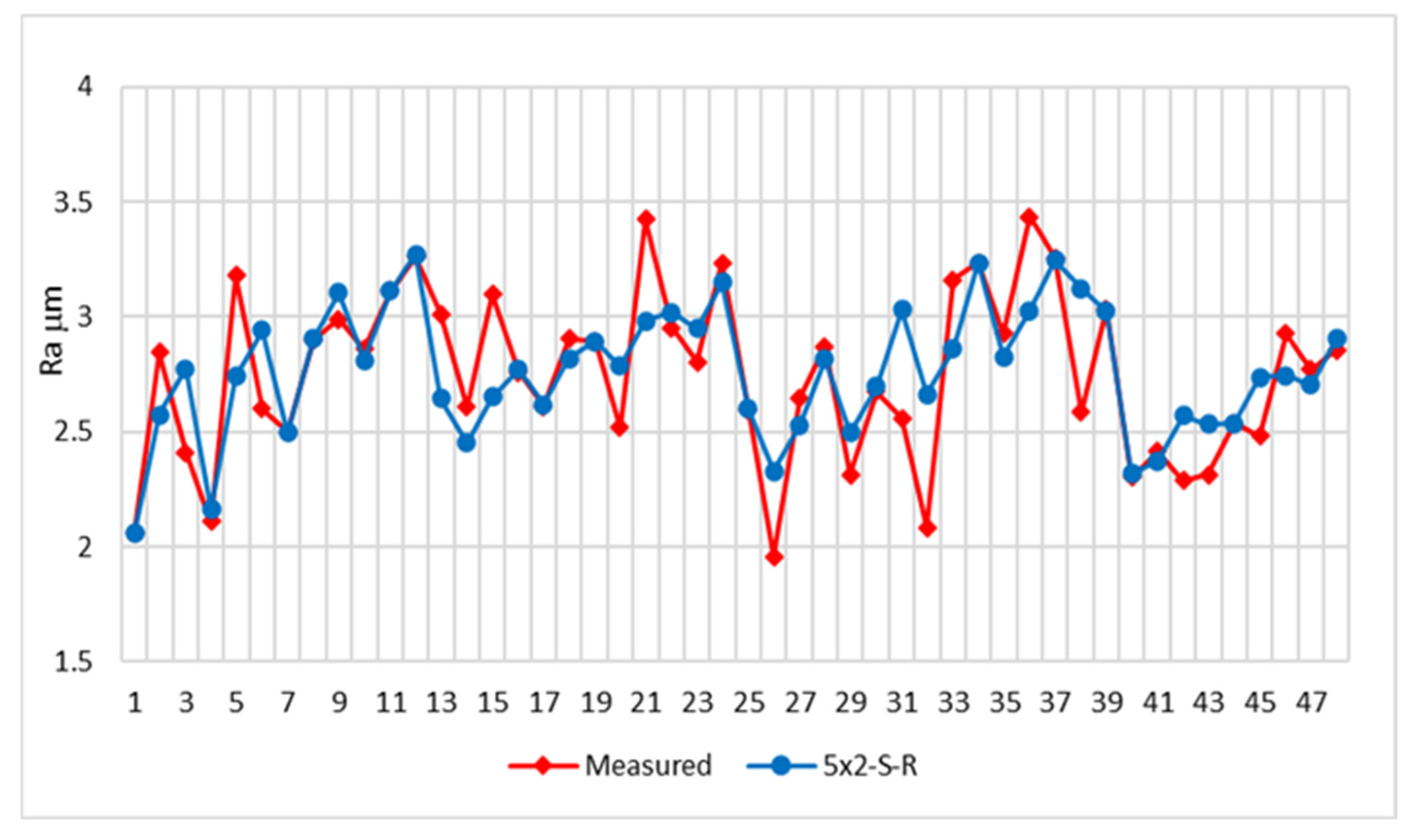
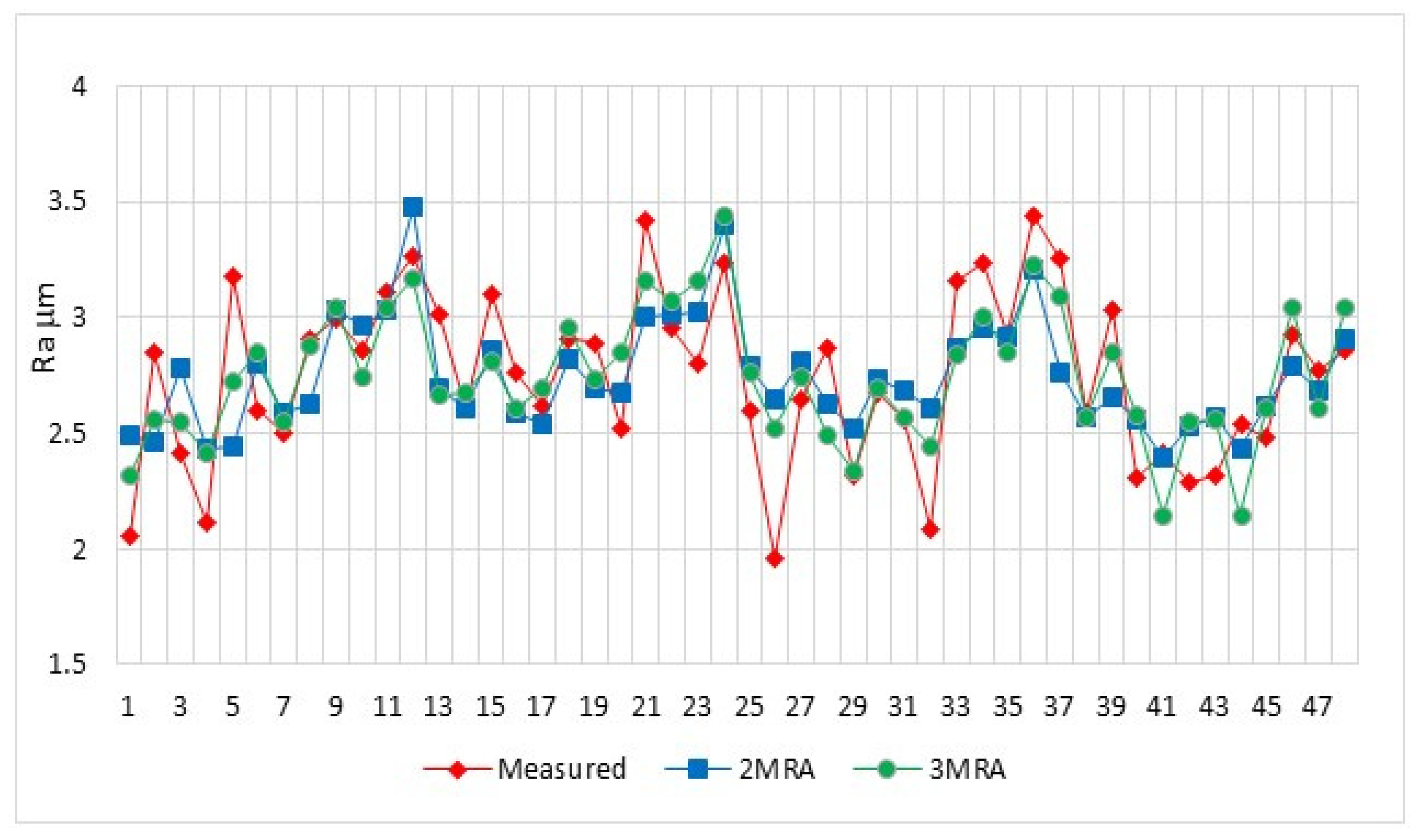

| Test No. | n, [rev/min] | Vf, [mm/min] | ap, [mm] | Ra, [μm] |
|---|---|---|---|---|
| 1 | 3000 | 400 | 0.3 | 2.058 |
| 2 | 3000 | 400 | 0.6 | 2.845 |
| 3 | 3000 | 400 | 1 | 2.41 |
| 4 | 3000 | 600 | 0.3 | 2.108 |
| 5 | 3000 | 600 | 0.6 | 3.18 |
| 6 | 3000 | 600 | 1 | 2.601 |
| 7 | 3000 | 800 | 0.3 | 2.5 |
| 8 | 3000 | 800 | 0.6 | 2.901 |
| 9 | 3000 | 800 | 1 | 2.989 |
| 10 | 3000 | 1000 | 0.3 | 2.861 |
| 11 | 3000 | 1000 | 0.6 | 3.111 |
| 12 | 3000 | 1000 | 1 | 3.261 |
| 13 | 4000 | 400 | 0.3 | 3.012 |
| 14 | 4000 | 400 | 0.6 | 2.606 |
| 15 | 4000 | 400 | 1 | 3.097 |
| 16 | 4000 | 600 | 0.3 | 2.759 |
| 17 | 4000 | 600 | 0.6 | 2.611 |
| 18 | 4000 | 600 | 1 | 2.905 |
| 19 | 4000 | 800 | 0.3 | 2.891 |
| 20 | 4000 | 800 | 0.6 | 2.519 |
| 21 | 4000 | 800 | 1 | 3.422 |
| 22 | 4000 | 1000 | 0.3 | 2.953 |
| 23 | 4000 | 1000 | 0.6 | 2.802 |
| 24 | 4000 | 1000 | 1 | 3.233 |
| 25 | 5000 | 400 | 0.3 | 2.595 |
| 26 | 5000 | 400 | 0.6 | 1.958 |
| 27 | 5000 | 400 | 1 | 2.648 |
| 28 | 5000 | 600 | 0.3 | 2.87 |
| 29 | 5000 | 600 | 0.6 | 2.314 |
| 30 | 5000 | 600 | 1 | 2.674 |
| 31 | 5000 | 800 | 0.3 | 2.557 |
| 32 | 5000 | 800 | 0.6 | 2.082 |
| 33 | 5000 | 800 | 1 | 3.161 |
| 34 | 5000 | 1000 | 0.3 | 3.236 |
| 35 | 5000 | 1000 | 0.6 | 2.928 |
| 36 | 5000 | 1000 | 1 | 3.435 |
| 37 | 6000 | 400 | 0.3 | 3.256 |
| 38 | 6000 | 400 | 0.6 | 2.585 |
| 39 | 6000 | 400 | 1 | 3.034 |
| 40 | 6000 | 600 | 0.3 | 2.304 |
| 41 | 6000 | 600 | 0.6 | 2.413 |
| 42 | 6000 | 600 | 1 | 2.286 |
| 43 | 6000 | 800 | 0.3 | 2.313 |
| 44 | 6000 | 800 | 0.6 | 2.537 |
| 45 | 6000 | 800 | 1 | 2.482 |
| 46 | 6000 | 1000 | 0.3 | 2.927 |
| 47 | 6000 | 1000 | 0.6 | 2.769 |
| 48 | 6000 | 1000 | 1 | 2.856 |
| Parameter | Specification |
|---|---|
| The layer numbers | 3 and 4 |
| The number of neurons on the layers | Input 3, Hidden 5, 7, 10, 5 × 2, Output 1 |
| The initial weights and biases | Randomly between 0 and +1 |
| Activation function | Relu and Tanh |
| Learning rate | 0.03 |
| Data normalization | From −0.5 to +0.5 |
| Data normalization | 10,000–30,000 |
| Test No. | Measured | RA-2 | RA-3 | 5-S-R | 10-S-R | 5-S-T | 5 × 2-S-R |
|---|---|---|---|---|---|---|---|
| 1 | 2.058 | 2.490 | 2.320 | 2.164 | 2.318 | 2.056 | 2.056 |
| 2 | 2.845 | 2.462 | 2.553 | 2.843 | 2.552 | 2.801 | 2.575 |
| 3 | 2.41 | 2.782 | 2.552 | 2.412 | 2.414 | 2.407 | 2.774 |
| 4 | 2.108 | 2.434 | 2.416 | 2.330 | 2.413 | 2.105 | 2.166 |
| 5 | 3.18 | 2.438 | 2.725 | 2.932 | 2.818 | 2.716 | 2.741 |
| 6 | 2.601 | 2.802 | 2.843 | 2.697 | 2.703 | 2.641 | 2.940 |
| 7 | 2.5 | 2.591 | 2.549 | 2.497 | 2.628 | 2.510 | 2.497 |
| 8 | 2.901 | 2.627 | 2.878 | 3.022 | 2.904 | 2.920 | 2.907 |
| 9 | 2.989 | 3.034 | 3.041 | 2.982 | 2.992 | 2.987 | 3.106 |
| 10 | 2.861 | 2.960 | 2.743 | 2.663 | 2.843 | 2.855 | 2.811 |
| 11 | 3.111 | 3.029 | 3.036 | 3.111 | 3.113 | 3.107 | 3.111 |
| 12 | 3.261 | 3.478 | 3.169 | 3.267 | 3.267 | 3.259 | 3.272 |
| 13 | 3.012 | 2.693 | 2.665 | 2.623 | 2.525 | 3.010 | 2.643 |
| 14 | 2.606 | 2.608 | 2.678 | 2.604 | 2.487 | 2.872 | 2.452 |
| 15 | 3.097 | 2.853 | 2.811 | 3.094 | 2.814 | 2.724 | 2.652 |
| 16 | 2.759 | 2.588 | 2.606 | 2.755 | 2.663 | 2.630 | 2.769 |
| 17 | 2.611 | 2.535 | 2.697 | 2.659 | 2.652 | 2.669 | 2.618 |
| 18 | 2.905 | 2.822 | 2.954 | 3.149 | 2.943 | 2.840 | 2.817 |
| 19 | 2.891 | 2.694 | 2.734 | 2.887 | 2.783 | 2.747 | 2.893 |
| 20 | 2.519 | 2.674 | 2.849 | 2.714 | 2.819 | 2.849 | 2.784 |
| 21 | 3.422 | 3.005 | 3.153 | 3.203 | 3.110 | 3.115 | 2.983 |
| 22 | 2.953 | 3.014 | 3.074 | 3.019 | 2.964 | 2.974 | 3.018 |
| 23 | 2.802 | 3.026 | 3.155 | 2.768 | 2.987 | 3.060 | 2.949 |
| 24 | 3.233 | 3.399 | 3.434 | 3.258 | 3.277 | 3.336 | 3.149 |
| 25 | 2.595 | 2.785 | 2.757 | 2.592 | 2.602 | 2.963 | 2.601 |
| 26 | 1.958 | 2.643 | 2.517 | 2.306 | 2.355 | 2.731 | 2.329 |
| 27 | 2.648 | 2.811 | 2.742 | 2.734 | 2.667 | 2.692 | 2.529 |
| 28 | 2.87 | 2.630 | 2.494 | 2.723 | 2.644 | 2.526 | 2.815 |
| 29 | 2.314 | 2.520 | 2.336 | 2.438 | 2.398 | 2.465 | 2.495 |
| 30 | 2.674 | 2.731 | 2.688 | 2.789 | 2.680 | 2.670 | 2.694 |
| 31 | 2.557 | 2.687 | 2.569 | 2.855 | 2.771 | 2.634 | 3.029 |
| 32 | 2.082 | 2.609 | 2.437 | 2.570 | 2.557 | 2.661 | 2.661 |
| 33 | 3.161 | 2.864 | 2.841 | 2.844 | 2.847 | 2.897 | 2.860 |
| 34 | 3.236 | 2.956 | 3.006 | 2.987 | 3.056 | 2.897 | 3.235 |
| 35 | 2.928 | 2.911 | 2.844 | 2.701 | 2.724 | 2.926 | 2.827 |
| 36 | 3.435 | 3.209 | 3.226 | 2.899 | 3.014 | 3.125 | 3.026 |
| 37 | 3.256 | 2.765 | 3.094 | 2.560 | 2.704 | 2.890 | 3.246 |
| 38 | 2.585 | 2.566 | 2.570 | 2.274 | 2.459 | 2.583 | 3.123 |
| 39 | 3.034 | 2.659 | 2.845 | 2.375 | 2.520 | 2.421 | 3.021 |
| 40 | 2.304 | 2.560 | 2.580 | 2.691 | 2.629 | 2.400 | 2.317 |
| 41 | 2.413 | 2.394 | 2.140 | 2.406 | 2.417 | 2.261 | 2.372 |
| 42 | 2.286 | 2.529 | 2.546 | 2.430 | 2.486 | 2.328 | 2.572 |
| 43 | 2.313 | 2.567 | 2.554 | 2.823 | 2.753 | 2.480 | 2.531 |
| 44 | 2.537 | 2.433 | 2.143 | 2.538 | 2.545 | 2.460 | 2.538 |
| 45 | 2.482 | 2.611 | 2.605 | 2.484 | 2.584 | 2.568 | 2.737 |
| 46 | 2.927 | 2.787 | 3.039 | 2.955 | 2.940 | 2.771 | 2.745 |
| 47 | 2.769 | 2.685 | 2.602 | 2.670 | 2.705 | 2.769 | 2.704 |
| 48 | 2.856 | 2.906 | 3.045 | 2.539 | 2.751 | 2.854 | 2.903 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djurović, S.; Lazarević, D.; Ćirković, B.; Mišić, M.; Ivković, M.; Stojčetović, B.; Petković, M.; Ašonja, A. Modeling and Prediction of Surface Roughness in Hybrid Manufacturing–Milling after FDM Using Artificial Neural Networks. Appl. Sci. 2024, 14, 5980. https://doi.org/10.3390/app14145980
Djurović S, Lazarević D, Ćirković B, Mišić M, Ivković M, Stojčetović B, Petković M, Ašonja A. Modeling and Prediction of Surface Roughness in Hybrid Manufacturing–Milling after FDM Using Artificial Neural Networks. Applied Sciences. 2024; 14(14):5980. https://doi.org/10.3390/app14145980
Chicago/Turabian StyleDjurović, Strahinja, Dragan Lazarević, Bogdan Ćirković, Milan Mišić, Milan Ivković, Bojan Stojčetović, Martina Petković, and Aleksandar Ašonja. 2024. "Modeling and Prediction of Surface Roughness in Hybrid Manufacturing–Milling after FDM Using Artificial Neural Networks" Applied Sciences 14, no. 14: 5980. https://doi.org/10.3390/app14145980
APA StyleDjurović, S., Lazarević, D., Ćirković, B., Mišić, M., Ivković, M., Stojčetović, B., Petković, M., & Ašonja, A. (2024). Modeling and Prediction of Surface Roughness in Hybrid Manufacturing–Milling after FDM Using Artificial Neural Networks. Applied Sciences, 14(14), 5980. https://doi.org/10.3390/app14145980








