Viscosity of Clayey Soils: Experimental Studies

Abstract

Due to the high rate of the development of housing, transportation and hydraulic engineering construction in the last hundred years, the study of the phenomenon of creep of clay soils has become a subject of scientific research. In the study, experimental investigations of clay soil were conducted using a simple shear device in kinematic loading mode, aimed at examining the influence of shear rate on the viscosity coefficient of the clay soil and its strength characteristics. The tests were performed at four different shear rates and three different vertical load values. Based on the results of experimental and theoretical studies, the viscosity coefficients of clay soil were obtained, and a new rheological equation was proposed, which simultaneously takes into account the influence of Coulomb friction, structural cohesion, cohesion of water–colloidal bonds and viscous resistance of the soil. It has been shown that the shear rate has a significant impact on the viscosity coefficient of clay soil, and the viscosity coefficient itself is a variable quantity, depending both on the magnitude of the applied load and the duration of its application. The obtained results can be used for further improvement of methods for calculating the settlement of structures over time, as well as for predicting the time until the bearing capacity of foundation soils is exhausted.

1. Introduction

Over the last hundred years, the study of the phenomenon of the creep of clay soils has become a subject of scientific research in connection with the active development of housing, transportation and hydraulic engineering construction. The increased attention of scientists to the creep process occurring in clay soils was caused by the fact that in a number of cases, unacceptably large deformations of various buildings, structures and roads were observed, disturbing their normal operation, and in some cases, leading to destruction.

The process of the creep of clay soils in nature manifests itself in the form of long-term settlements, displacements, rolls, horizontal displacements of structures, as well as in the form of the slow sliding of clay masses along natural slopes and slopes of structures made of soil materials.

The historical development of soil rheology began with the study of the shear creep deformations of soils. Vyalov S.S. [1] mentioned in his book that the phenomenon of shear creep is caused by two mutually opposite processes: the process of hardening (the process of damped creep causes a decrease in shear strains) and the process of soil unstrengthening (the development of the process of non-damped creep causes an increase in shear strains).

Goldshtejn M.N. believed that in the process of shear both destruction and restoration of contacts between mineral particles in the skeleton of clayey soil occur [2].

Maslov N.N. proposed to take into account the change in the viscosity of the soil skeleton in time in order to take into account the hardening of clayey soil under shear [3,4].

Based on the results of experimental studies of clay in the ring shear device, Ter-Stepanyan G.I. suggested that shear strains change discontinuously during testing under constant load [5].

To describe the process of soil creep, Meschyan S.R. [6,7,8], Goldin A.L. [9] and Ter-Martirosyan Z.G. [10] applied the Boltzmann–Volterra theory of hereditary creep. This theory as applied to soils was first used by Florin V.A. [11,12] and was subsequently developed by Maslov N.N. and Arutyunyan N.Kh. [13] to describe the creep process of hardening media (in particular, concrete), which made it possible to take into account the hardening of soils in the process of creep.

A great contribution to the development of soil rheology was made by Tertsagi K., Puzyrevsky N.P., Gersevanov N.M., Vyalov S.S., Maslov N.N., Florin V.A., Cytovich N.A., Zareckij Y.K., Goldshtejn M.N., Goldin A.L., Meschyan S.R., Ter-Stepanyan G.I., Shukle L., Rzhanitsyn A.R., Arutyunyan N.H., Ter-Martirosyan Z.G. and many other researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].

Currently, a large number of scientific works are devoted to the study of the rheological properties of clay, sandy, melted and frozen soils, in which the authors derive various equations of state describing the rheological properties of soil on the basis of theoretical, experimental and numerical studies.

Based on the performed experimental studies of clayey soil in the direct shear apparatus, Boley K. and Strokova L.A. [19] showed in their work that the time of action of compacting load before shear tests has a significant effect on the structure and properties of clays, which undoubtedly affects the strength and creep indices of clayey soil.

A hypoplastic model (a model in which there is no clear division into elastic and plastic deformation zone) for clayey soil, which includes eight parameters that can be determined in laboratory conditions on the basis of performed experiments, was proposed by Tafil and Triantafyllidis [20].

A nonlinear creep model using a fractional order derivative and a small number of parameters capable of describing the creep process of clay was proposed by Ren et al. [21]. The authors compared the proposed creep model with the Bürgers model describing the behavior of viscoelastic materials. In this work, experimental soil investigations were also conducted to study the nonlinear creep properties of clay.

A nonlinear creep model for frozen sand was proposed in [22]. The authors of this paper have validated this model based on the results of laboratory tests on frozen sand. Tests were carried out on sand samples with different particle size distribution and density in dry conditions and at different levels of shear stress and temperature.

A model reflecting the nonlinear rheological characteristics of swelling soils was proposed in [23]. The results of the performed studies showed that the proposed model well describes the viscoelastic-plastic creep deformation of the swelling soil, and the results of the analysis of this model were close to the results obtained from the performed laboratory tests of the soil in triaxial compression devices.

A viscoplastic model that is capable of describing creep and plastic deformation of rock during loading–unloading cycles was proposed by Haghighat et al. [24]. The authors of this paper performed a validation of this model based on the results obtained from triaxial tests.

A seven-component rheological model to describe the behavior of weak soil with organic matter content under different loading conditions was proposed in [25]. The model used parallel three-element components to describe the viscosity, plasticity, and elastic deformation of the soil over time.

The results of scientific studies of rheological properties of sandy soils are presented in the work of Ter-Martirosyan Z.G. et al. [26]. The authors performed experimental studies to determine the viscosity of sandy soil by performing triaxial tests in kinematic and dynamic loading modes. The paper also considers the problem of evaluating the effect of dynamic loads on the viscosity of sandy soils.

A three-dimensional elastic viscoplastic state model that is capable of describing the behavior of soils with isotachy viscosity in time was proposed in [27]. The authors of the paper gave a rather detailed description of their model and its basic equations, as well as performed the implementation of this model in a software package using the finite element method. The model was then used to simulate the results of laboratory tests, paying particular attention to the advantages and disadvantages of the model in reproducing the behavior of soft clays over time.

Studies of clay soils containing the clay mineral montmorillonite, which has pronounced creep and swelling properties, were presented by Yin and Tong [28]. Based on the data of experimental studies of clayey soil samples consisting of a mixture of bentonite and silica sand, the authors proposed a one-dimensional elastic viscoplastic model that takes into account both creep and swelling of clayey soil.

Based on the above, we can conclude that in order to describe the rheological properties of clayey soils, various methods are now widely used, which are based on the use of mechanical models, the theory of plastic flow and hereditary creep, etc. Based on these, various equations of state are derived, containing several parameters (depending on the model under consideration, the number of determined parameters will change), which can be determined during experimental studies of soil using various instruments. One such device is the simple shear device.

The deformation conditions of the soil specimen in simple shear tests are very similar to the deformation conditions occurring at the base of a number of structures (e.g., soil adjacent to the side of a pile, slope deformations of soil massifs, etc.). The study of rheological properties of soils in conditions of simple shear is currently quite relevant because it allows the consideration of the processes occurring in time in the soil mass, which is an important component in the design of various buildings and structures.

The test in a simple shear device can be characterized as follows: a process in which sliding (displacement) occurs along planes parallel to the plane of a stationary stamp (upper or lower, depending on the design of the device) at a value close to their distance from this plane. In simple shear, the cubic specimen takes the shape of an inclined parallelepiped at the end of the test.

Depending on the design and assembly method of the simple shear device, it is possible to determine not only the usual strength (specific cohesion (c), angle of internal friction $\left(\phi \right)$, angle of dilatancy $\left(\psi \right)$) and deformation (ground shear modulus (G), shear strain $\left(\gamma \right)$) characteristics of tested soil samples, but also to determine rheological parameters (ground viscosity ($\eta$)).

The concept of viscosity originates from Newton’s discovery in 1687 of the basic law of viscous liquids, according to which the internal friction in the flow of a fluid, arising «due to insufficient slip of the fluid particles», is proportional to the shear rate at which these fluid particles move relative to each other. A fluid obeying this law is called an ideal viscous (Newtonian) fluid.

In a Newtonian fluid at any shear stress different from zero, a viscous flow develops in time with a constant shear strain rate $\left(\dot{\gamma }=const\right)$, and this shear rate is directly proportional to the shear stress.

The viscosity coefficient of the soil can be determined from tests in which the relationship between the angular strain rate and the acting shear stress on the soil specimen can be determined. Thus, it can be concluded that the viscosity coefficient or, in other words, dynamic viscosity defines a measure of the resistance of the soil to its deformations. Soil viscosity is measured in Poise (1 Poise = 0.1 Pa·sec).

The viscosity of different media varies over a fairly wide range. For example, the viscosity of air is $1.8\cdot 10^{-4}$ Poise, the viscosity of water is—$1.0\cdot 10^{-2}$ Poise, the viscosity of various oils generally ranges from 0.5 to 10 Poise and the viscosity of the Earth’s crust reaches about $5.0\cdot 10^{22}$ Poise.

Based on the performed experimental studies, as well as the analysis and generalization of both his results and the results obtained by other researchers, Maslov N.N. [3] determined the following average values of the dynamic viscosity coefficient of melted clay depending on its state (consistency): soft plastic clay—$\eta$ = 10¹⁰–10¹¹ Poise; tight plastic clay—$\eta$ = 10¹²–10¹³ Poise; semi-hard clay—$\eta$ = 10¹⁴–10¹⁵ Poise; and hard clay—$\eta$ = 10¹⁵–10¹⁷ Poise.

The methodology of determining the coefficient of viscosity of soil, as well as the great variety of properties of the soils themselves have a great influence on the obtained values of viscosity coefficients for different soils, which can explain the large variation in the obtained values.

In most cases, according to Maslov N.N., there is a misinterpretation of the value itself. Indeed, taking viscosity as a constant quantity $(\eta =const)$ is valid only for a perfectly viscous (Newtonian) medium. In soils, the relationship between stress and flow rate is nonlinear, and as a consequence, the viscosity coefficient of the soil will be a variable value depending on both the magnitude of the applied load and the time of its action.

For example, at the beginning of the test, when the ground deformations are still small, the viscosity of the ground may be $10^{13}$ Poise and closer to the end of the deformation stage, the viscosity coefficient value may increase to $10^{14}$ Poise. This phenomenon was confirmed by E.S. Sobolev in his work [29] based on experimental studies on sandy soil samples in a triaxial compression device in the kinematic loading mode. Based on the results of the performed studies, the dependences of sandy soil viscosity on the angular strain rate were obtained. The presented work also described a methodology that allows the determination of the viscosity of air-dry and water-saturated sandy soil based on triaxial tests in kinematic loading mode. This methodology is based on the application of Maxwell’s elastic-viscous rheological model [29].

Based on the above, we can conclude that the deformation of soils occurs at a variable rate, unlike a Newtonian medium, but at a certain point in time, the flow velocity in soils begins to approach a constant, which allows us to apply the basic law of viscous fluid at this stage, in which the process of viscous flow occurs at a constant rate.

Based on the above, the following key conclusions can be drawn:

-

The deformability and strength of clay soils differ significantly from the deformability and strength of sandy, semi-rocky and rocky soils, especially when the time factor is taken into account;

-

The rheological properties of clay soils are always manifested in the interaction of soils with structures and the surrounding geological environment, which equally applies to the processes of creep, relaxation and changes in soil strength over time. These processes significantly influence the nature of the formation and transformation of the stress–strain state of clay soil masses in space and time, ultimately determining the operating conditions and stability of structures;

-

The historical development of soil rheology, particularly in relation to the calculations of foundation structures, initially focused on the study of creep deformations under shear conditions;

-

Rheological tests of clay soils differ from conventional, standard tests in that they pay special attention to the study of processes occurring in time. These processes manifest depending on the testing regime, testing conditions, and the moisture content of the clay soils.

The purpose of this study is to investigate the influence of shear rate on the viscosity coefficient of clay soil (and its change during the testing process) as well as its strength characteristics, including specific cohesion and its components.

2. Materials and Methods

To investigate the rheological properties of clay soil in the present work, experimental studies were carried out in a simple shear device (sample diameter d = 71.4 mm, sample height h = 23 ± 1 mm) in kinematic loading mode. Figure 1 shows a general view of the simple shear device (a) as well as the main components that make up the device (b).

One of the main advantages of this design of the simple shear device is that it allows the realization of a homogeneous stress–strain state inside the soil specimen during the test, since each individual elementary layer of the specimen moves by the same amount during shear (these conditions of deformation of the soil specimen are very similar to the deformation conditions occurring in the base of a number of structures, e.g., soil adjacent to the side surface of a pile, slope deformations of soil massifs, etc.).

It is important to note that the deformation conditions described above cannot be recreated in a direct shear device, because the contact area in this device between the upper and lower parts of the soil sample changes along the predetermined shear surface. During the test, the actual contact area between the two parts of the sample decreases, leading to an error in calculating the applied stresses (while the normal stress is assumed to be constant, its actual value increases). Additionally, during the failure of soil samples, a shear plane defined by a predetermined gap is initially prescribed. If a high-strength inclusion is encountered on the structurally prescribed shear plane, the slip surface will circumvent it. The result of such private experience is an overestimated private value of ultimate shear resistance, which complicates subsequent statistical processing: some tests have to be discarded, and the calculated values of shear resistance parameters decrease relative to the normative ones.

The procedure for preparing soil samples for testing, as well as conducting the tests themselves in a simple shear device, consists of sequentially performing the following stages:

• Making twin samples of clay soil;
• Assembly of the sample in the simple shear device;
• Setting the test parameters.

Let us examine each of these stages in more detail.

2.1. Making Twin Samples of Clay Soil

Due to the lack of the necessary number of undisturbed samples, twin samples of clayey soil with the required density and moisture parameters were specially made.

In GOST 30416-2020 “Soils. Laboratory testing. General” [30] presents a methodology for making samples of dispersed soil of disturbed composition with specified parameters of density and moisture. However, the presented method does not describe exactly how the calculated amount of water should be added to ensure even distribution of moisture within the sample and to avoid the formation of lumps of dry soil.

Based on the above, the preparation of twin clay soil samples was carried out using a special method described below [31].

Part of the dry soil sample was evenly spread from a small height (to avoid dust formation) in a thin layer in a small metal mixing tray. The amount of water calculated according to the formula [30] was poured into the atomizer-pulverizer to provide the required moisture content. Next, the water was sprayed onto the surface of the scattered soil. After moistening the top layer, the soil was mixed and leveled. The next portion of the dry soil was spread with subsequent moistening. The steps were repeated until all of the dry soil and water in the atomizer-pulverizer were used up. The moistened soil was then placed in an exicator for at least two hours to allow for a more even distribution of moisture within the sample. Next, the soil was evenly placed in a metal compaction mold to achieve the required density of the soil sample. The characteristics of the tested soil samples are presented in

Table 1. Characteristics of tested soil samples.

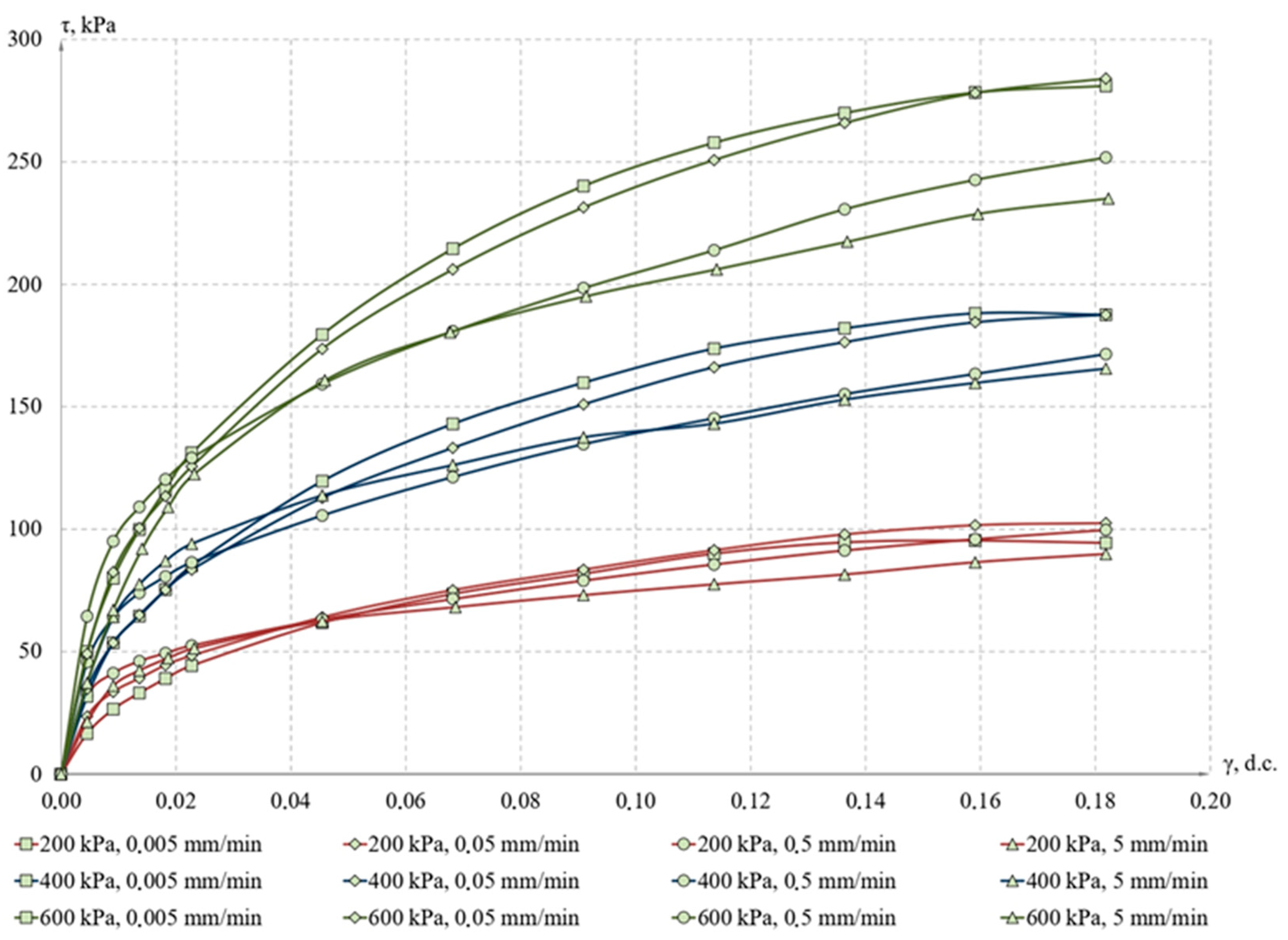
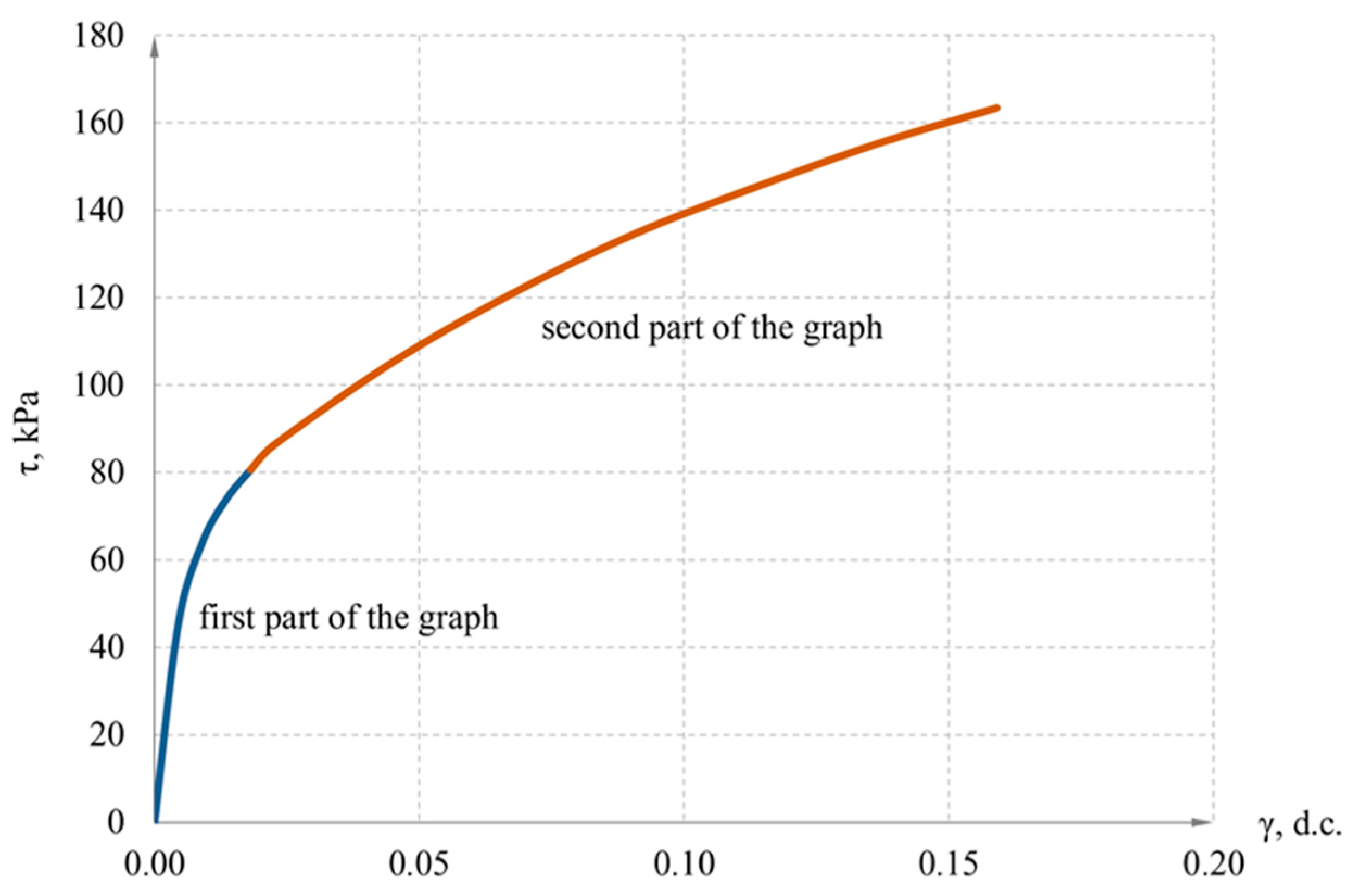
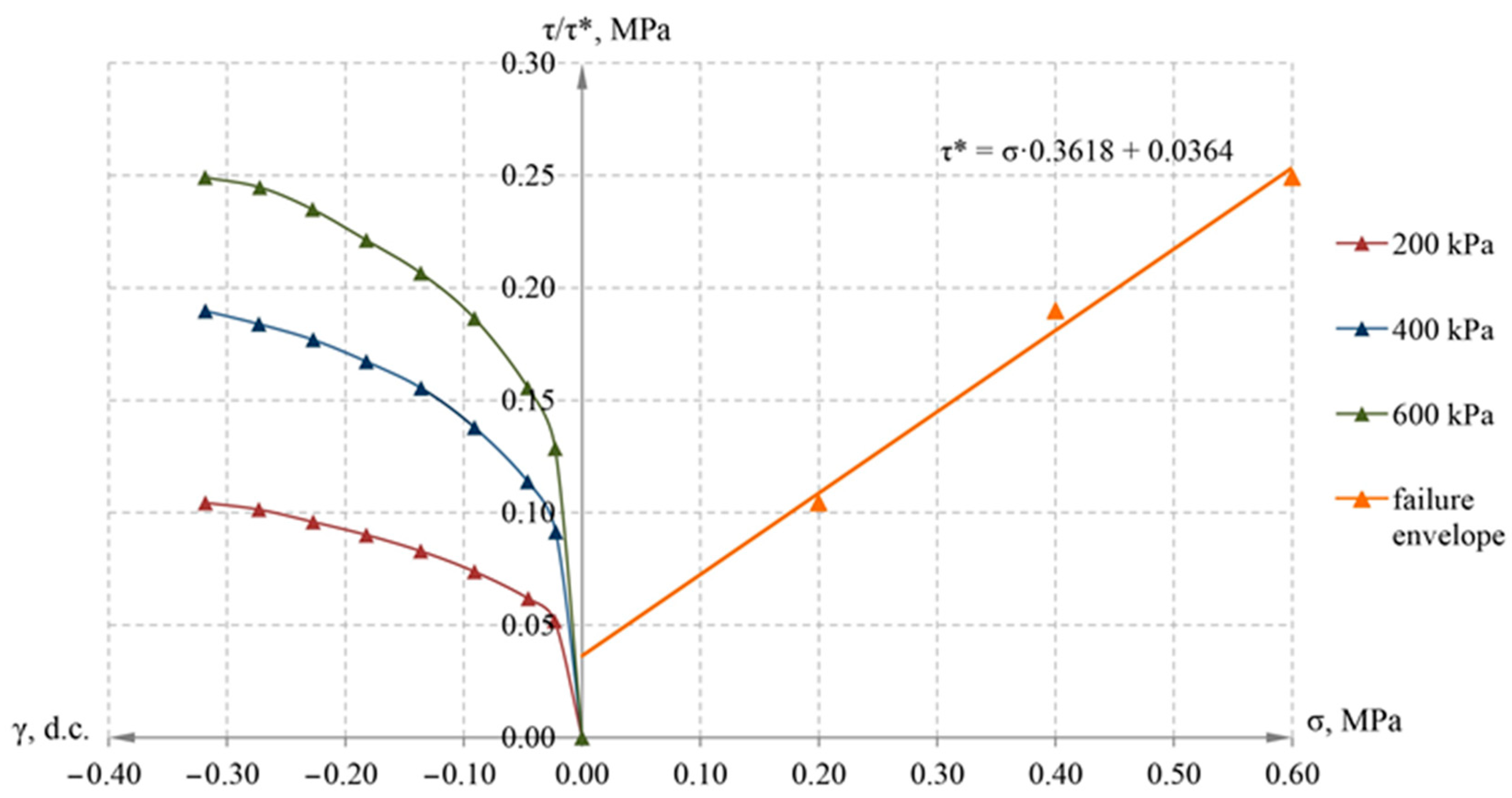
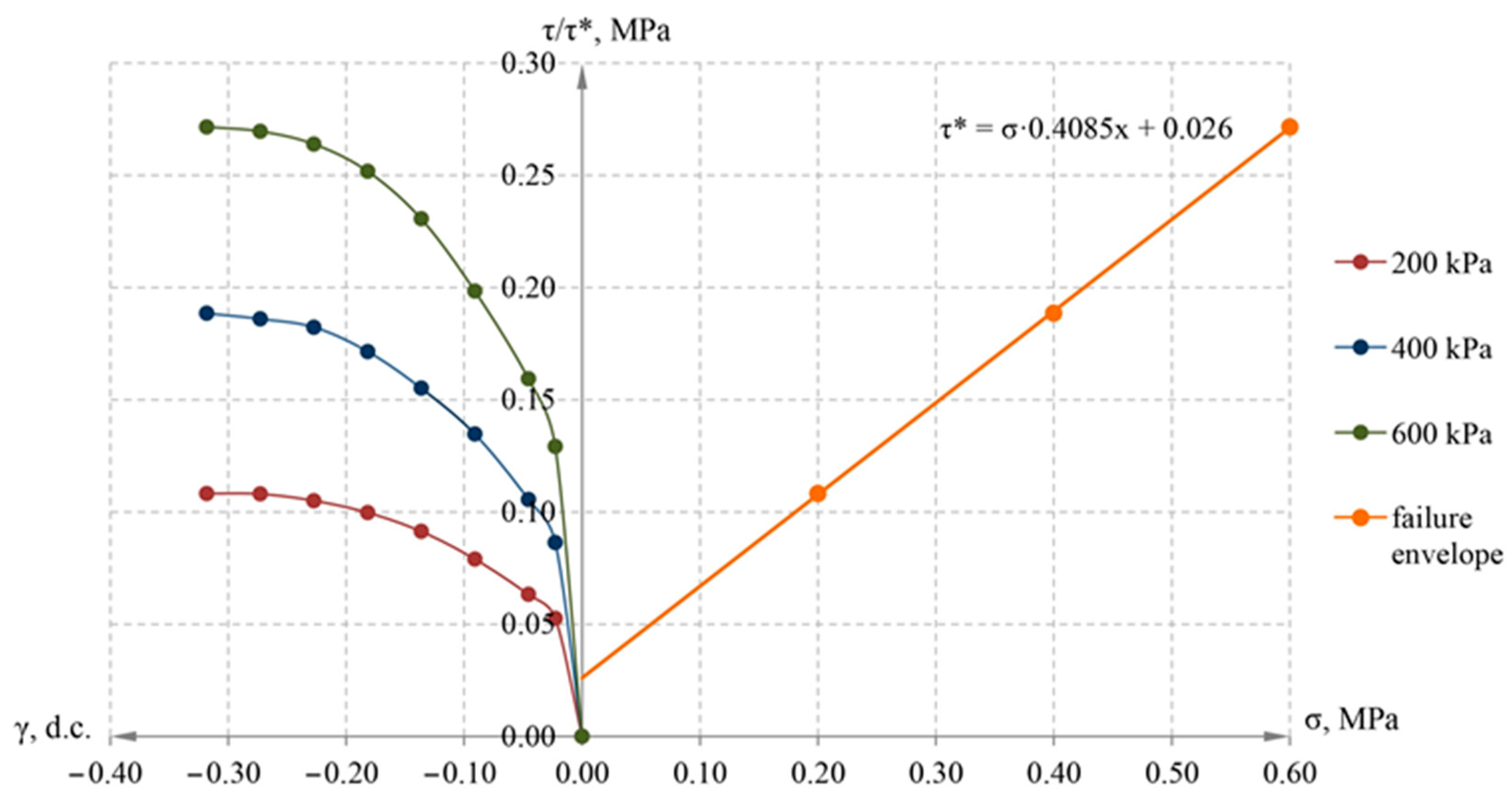
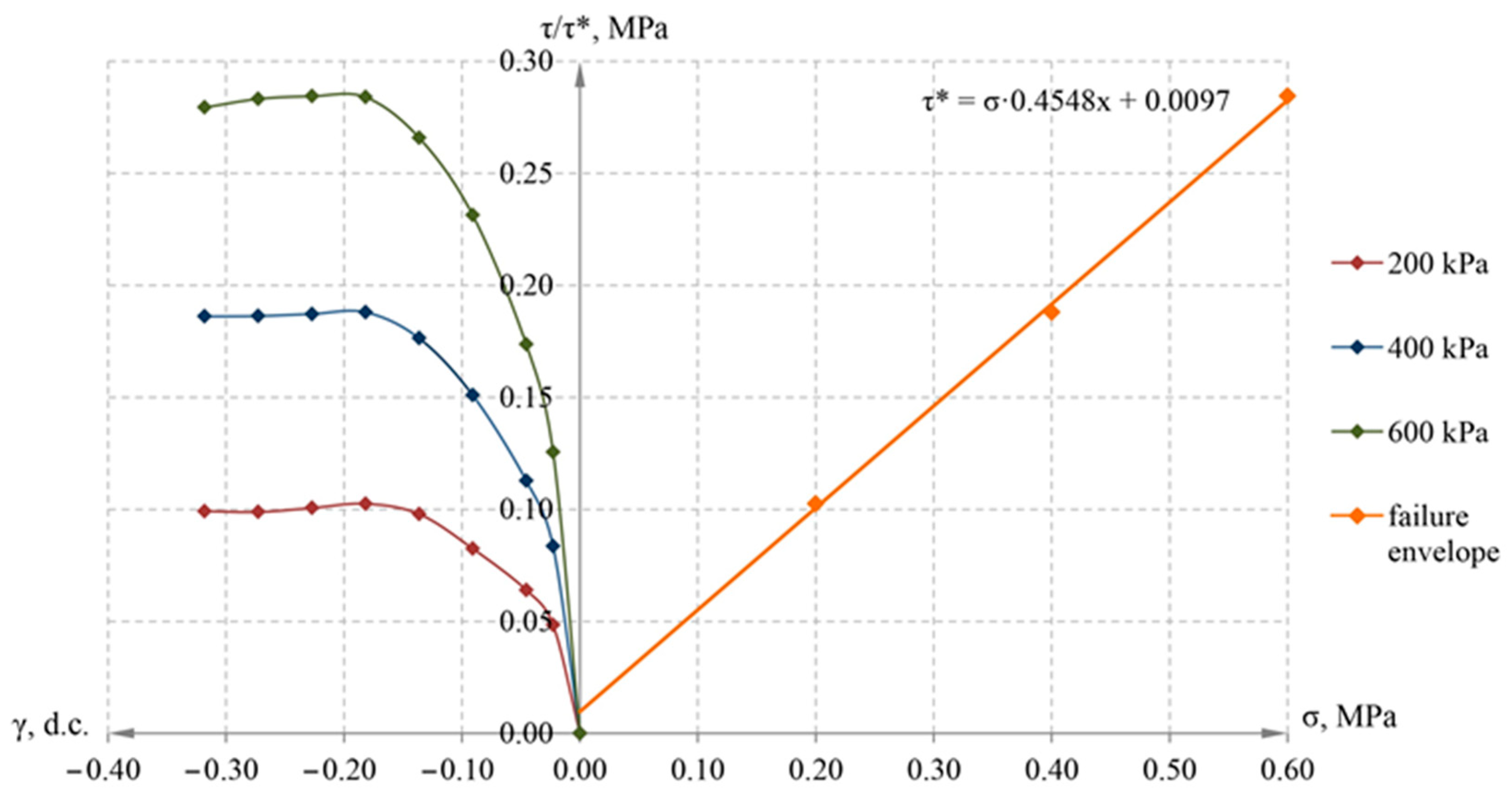
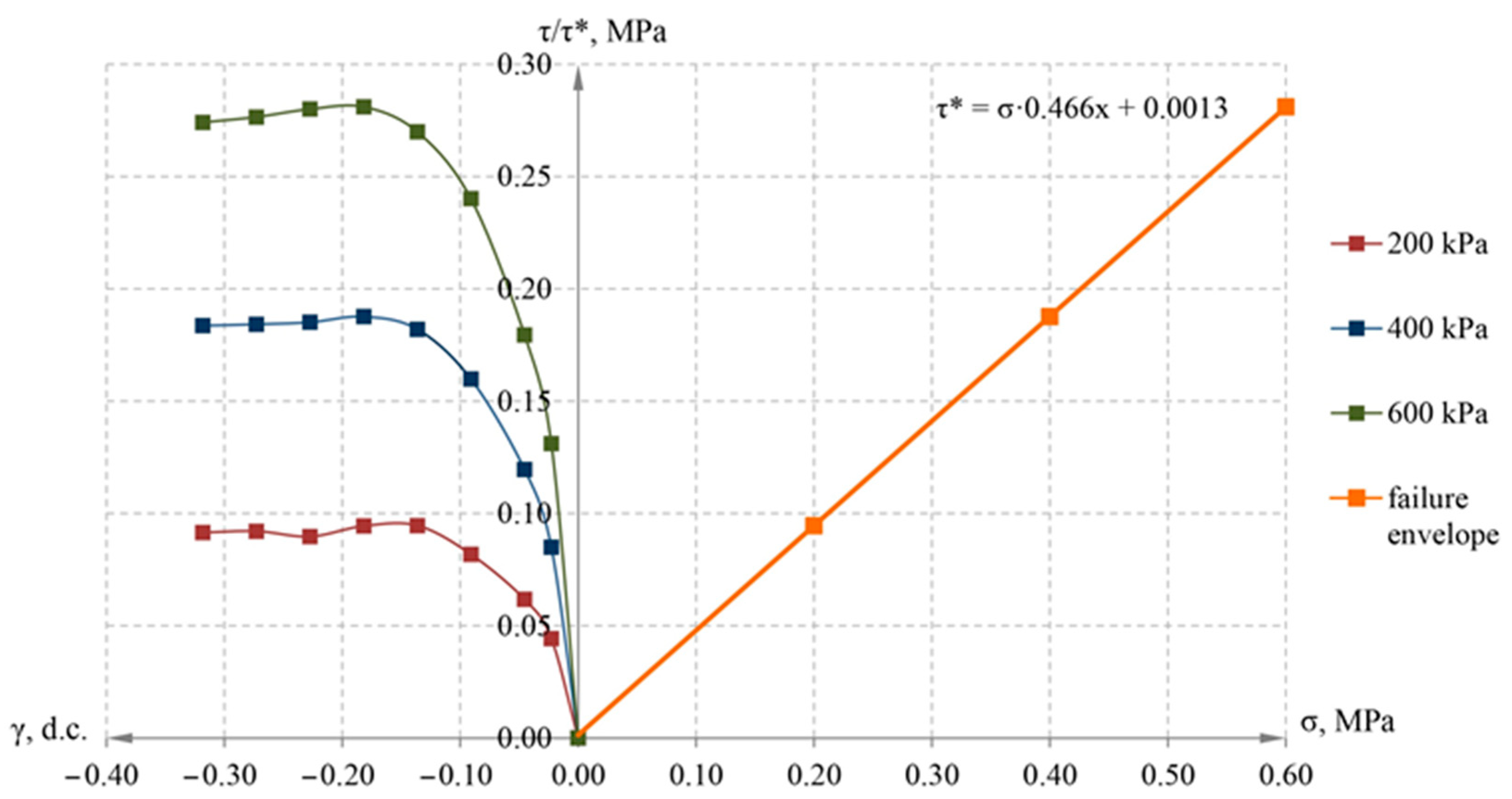
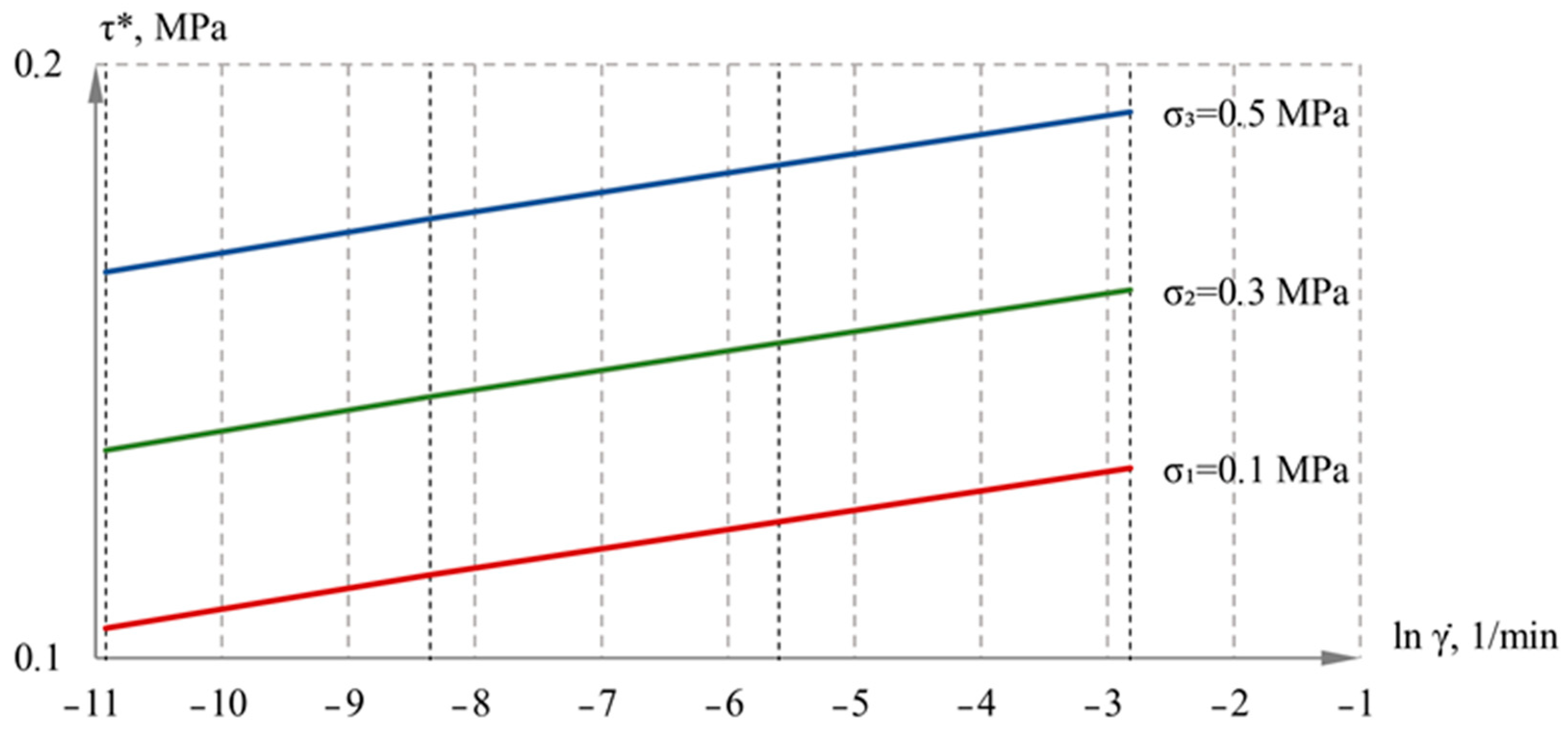
Type of Clay Soil	Plasticity Index	Index of Liquidity	Density, g/cm3	Moisture, %	Cohesion, kPa	Internal Friction Angle, Deg.
	${\mathit{I}}_{\mathit{P}}$	${\mathit{I}}_{\mathit{L}}$	$\mathit{\rho }$	$\mathit{w}$	$\mathit{c}$	$\mathit{\phi }$
Fluid-plastic loam	0.11	0.80	2.20	22	1.30–36.40 *	19.89–24.98 *

*—Values of strength parameters varies depending on the shear rate. A detailed description of the reasons for the variation in the scatter of these parameters is presented in Section 3.2. Effect of shear rate on ultimate shear resistance of clay soil.

.

2.2. Assembly of the Sample in the Simple Shear Device

A lower round stamp, corresponding to the diameter of the sample, with a metal porous disk was fixed on a square base. A soil sample encased in a rubber membrane was placed on top of the metal porous disk. In the lower part of the sample, the rubber membrane was fixed with a rubber ring, over which a metal casing was installed. Next, a stack of 25 individual rings (including 12 fluoroplastic and 13 brass rings) with special “ears” designed to ensure that all rings work together during the test was placed on top of the rubber membrane. The rings were alternated with each other to reduce friction between them. The rings were connected to each other via two vertical sliding guides that tilt during the test as shear strain accumulates. A steel ring with threaded holes was placed on top of the stack of rings, over which clamps were fastened to prevent the rings from fanning out during shear. Then, the mechanism of vertical load application was activated and the upper stamp (with a metal porous disk fixed on it) was aligned with the upper surface of the soil sample. Metal porous disks installed in the upper and lower parts of the sample are designed to realize drainage during compaction. The porous disks had a ribbed surface for better adhesion to the test soil sample. In GOST R 71042-2023 “Soils. Determination of strength characteristics by simple shear method” [32] presents a methodology describing the stage of preparation of soil samples for testing, as well as conducting the tests in a simple shear device with subsequent processing of the results.

2.3. Setting the Test Parameters

After assembling the soil sample in the simple shear device, the following parameters were set in the test program: the value of vertical load on the soil sample (kPa), shear displacement rate (mm/min) and relative shear strain (%).

3. Results

3.1. Experiment to Determine the Viscosity Coefficient of Clay Soil

In order to determine the viscosity coefficient of the fluid-plastic loam, experimental studies were carried out in a simple shear device in the kinematic loading mode ($\dot{\gamma }=const$) at four different shear displacement rates ($\dot{u}$ = 0.005 mm/min, $\dot{u}$ = 0.05 mm/min, $\dot{u }$= 0.5 mm/min, $\dot{u }$= 5 mm/min) and at three different values of vertical stress acting on the soil specimen during the test (${\sigma }_{n1}$ = 200 kPa, ${\sigma }_{n2}$ = 400 kPa, ${\sigma }_{n3}$ = 600 kPa). The tests were carried out until the ultimate relative shear strain ε = 18% was reached.

After processing the results of the laboratory tests, the graphs of the dependences of shear stresses on shear strains ($\tau -\gamma$) were obtained at various values of vertical stress ${\sigma }_n$ (Figure 2).

Taking into account that the obtained graphs of dependence of shear stresses on shear strains ($\tau -\gamma$) have a pronounced bilinear character, the coefficients of soil viscosity ($\eta$) (

Table 2. Viscosity coefficients of clayey soil.

Vertical Stress, kPa	Shear Displacement Rate, mm/min	Soil Viscosity at the First Section, kPa·min	Soil Viscosity at the Second Section, kPa·min
${\mathit{\sigma }}_{\mathit{n}}$	$\dot{\mathit{u}}$	${\mathit{\eta }}_1$	${\mathit{\eta }}_2$
200	5	226	133
	0.5	2310	1707
	0.05	21,296	21,780
	0.005	194,920	221,320
400	5	414	259
	0.5	3802	3023
	0.05	36,740	40876
	0.005	374,000	426,800
600	5	539	418
	0.5	5680	4466
	0.05	55,264	61,732
	0.005	576,840	610,720

) were determined for two characteristic parts of the graph (Figure 3).

The viscosity coefficients ($\eta$) for two characteristic sections of the graph were determined based on the simple Newton’s equation:

$$\eta =\frac{\tau }{\dot{\gamma }},$$

(1)

where $\tau$ is the shear stress [kPa] and $\dot{\gamma }$ is the shear rate [1/s].

3.2. Effect of Shear Rate on Ultimate Shear Resistance of Clay Soil

According to the well-known concept of N.N. Maslov [3,4], the ultimate shear resistance of clay soil ($\tau *$) can be represented as the sum of Coulomb friction ($\sigma tg\phi$), structural cohesion ($c_c$) and cohesion of water-colloid bonds ($c_w$), which depend on moisture content, i.e.,

$$\tau *=\sigma tg\phi +c_c+c_w,$$

(2)

Agreeing with this representation of the ultimate shear resistance of clay soil ($\tau *$), it should be noted that it does not take into account the effect of the shear rate ($\dot{\gamma }$). Indeed, under kinematic shear ($\dot{\gamma }=const$) in a soil medium possessing viscosity, viscous resistance may manifest ($c_{\dot{\gamma }}$).

Assuming that the viscous resistance is due to the viscosity of the soil as a whole, then under kinematic shear, viscous resistance will arise ($c_{\dot{\gamma }}=\dot{\gamma }\eta$). Based on the above, the total cohesion ($c$) in clay soil can be represented as the sum of structural cohesion ($c_c$), cohesion of water-colloid bonds ($c_w$) and viscous resistance ($c_{\dot{\gamma }}$), i.e.,

$$c=c_c+c_w+c_{\dot{\gamma }},$$

(3)

It is clear that in order to account for the influence of shear rate ($\dot{\gamma }$) on the shear resistance of a clay soil, it is necessary to conduct at least three tests at different shear rates (${\dot{\gamma }}_1<{\dot{\gamma }}_2<{\dot{\gamma }}_3$).

In the laboratory of the REC “Geotechnics” named after Z.G. Ter-Martirosyan (National Research Moscow State University of Civil Engineering) experimental studies were conducted on samples of fluid-plastic loam using a simple shear device in a kinematic loading mode ($\dot{\gamma }=const$) (at a constant shear displacement rate equal to $\dot{u}=\dot{\gamma }h$) at four different shear rates (${\dot{\gamma }}_1>{\dot{\gamma }}_2>{\dot{\gamma }}_3>{\dot{\gamma }}_4$) and under three different constant vertical loads (${\sigma }_1<{\sigma }_2<{\sigma }_3$) applied to the soil sample during testing.

Figure 4, Figure 5, Figure 6 and Figure 7 show the results of the tests of flow-plastic loam in the simple shear device in the kinematic loading mode ($\dot{\gamma }=const$).

Analyzing the obtained results presented in Figure 4, Figure 5, Figure 6 and Figure 7, one can conclude that there is a negligible change in the internal friction angle (when testing at different shear displacement rates), which can be explained by the limited amount of the conducted experimental studies. However, based on the obtained results, it can be concluded that the shear rate ($\dot{\gamma }$) has a significant effect on the cohesion of clay soil, which is confirmed graphically. The correlation coefficients $r_{\sigma \tau *}$ for each shear displacement rate were as follows: at $\dot{u}$ = 5 mm/min $r_{\sigma \tau *}$ = 0.9894; at $\dot{u}$ = 0.5 mm/min $r_{\sigma \tau *}$ = 0.9999; at $\dot{u}$ = 0.05 mm/min $r_{\sigma \tau *}$ = 0.9988; at $\dot{u}$ = 0.005 mm/min $r_{\sigma \tau *}$ = 1, which is sufficient for the purpose of the study.

It should be noted that numerous experimental studies conducted on samples of Quaternary clay with disturbed and undisturbed structures in the kinematic loading mode and at various values of vertical stress ${\sigma }_n$ (0.100; 0.200; 0.300 and 0.500 MPa), presented in the work of Kornoukhov M.B. [33], showed (Figure 8) that the ultimate lines at different shear rates (${\dot{\gamma }}_1>{\dot{\gamma }}_2>{\dot{\gamma }}_3>{\dot{\gamma }}_4$) have the same slope equal to $\phi =const$, and this angle does not depend on the shear rate ($\dot{\gamma }$).

The ultimate shear resistance of clay soil ($\tau *$) significantly depends on the internal friction angle ($\phi$) and the cohesive strength ($c$). The total cohesion ($c$), in turn, significantly depends on the shear rate ($\dot{\gamma }$) and as the shear rate increases, the ultimate shear resistance of clay soil increases proportionally to ($ln\dot{\gamma }$) (Figure 9).

Since, according to the experimental results, it was obtained that the structural cohesion ($c_c$) and the angle of internal friction ($\phi$) are independent of the shear rate ($\dot{\gamma }$), we present the viscous resistance ($c_{\dot{\gamma }}$) as the following relationship:

$$c_{\dot{\gamma }}=c_{{\dot{\gamma }}_0}+\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1),$$

(4)

where $\alpha$ is the experimental parameter.

Based on the analysis of the experimental research results (performed on clay soil samples) and also on the rheological model of a Maxwell viscoelastic body, we present the rheological equation for kinematic shear as applied to a soil medium in the following form:

$$\dot{\gamma }=\frac{\tau -\tau *}{\eta }+\frac{\dot{\tau }}{G},$$

(5)

where $\tau *=\sigma tg\phi +c_0$ (with $c_0=c_c+c_w$) [kPa]; η is the overall viscosity of the soil [kPa·s]; $\dot{\tau }$ is the rate of change in shear stress [kPa/s]; and G is the shear modulus of the soil [kPa].

By performing a certain grouping in Equation (5), we obtain a differential equation of the following form:

$$\dot{\tau }+\tau \cdot \frac{G}{\eta }=\frac{G}{\eta }\cdot \left(c_{\dot{\gamma }}+\tau *\right),$$

(6)

The general solution of Equation (6) is known [34] and is as follows:

$$\tau =e^{-\int \frac{G}{\eta }dt}\cdot \left\{\int \frac{G}{\eta }\cdot \left(c_{\dot{\gamma }}+\tau *\right)\cdot e^{\int \frac{G}{\eta }dt}dt+C\right\},$$

(7)

$$\tau \left(t\right)=e^{-\frac{G\cdot t}{\eta }}\cdot e^{\frac{G\cdot t}{\eta }}\cdot \left(c_{\dot{\gamma }}+\tau *\right)+C\cdot e^{-\frac{G\cdot t}{\eta }},$$

(8)

We will determine the constant of integration $C$ from the initial Condition (8) at $t=0$:

$$C=-\tau *-c_{\dot{\gamma }},$$

(9)

where ${\tau }^{\mathrm{*}}=\sigma tg\phi +c_0$ [kPa].

By substituting (9) into (8), we obtain the solution of the equation for constant shear rate ($\dot{\gamma }=const$):

$$\tau (t)=(\sigma tg\phi +c_c+c_w+c_{\dot{\gamma }})\cdot (1-e^{-\frac{G\cdot t}{\eta }}),$$

(10)

when $t\to \mathrm{\infty }$ $\tau \left(\mathrm{\infty }\right)=\sigma tg\phi +c_c+c_w+c_{\dot{\gamma }}$, with $c_{\dot{\gamma }}=\dot{\gamma }\eta$.

The obtained result corresponds to our understanding of the ultimate shear resistance (3). However, in this case, the viscous resistance ($c_{\dot{\gamma }}$) increases in direct proportion to the shear rate $\left(\dot{\gamma }\right)$, which does not correspond to the experimental results (4). This dependence can be obtained if the following relationship is taken as a rheological model:

$${\left(\dot{\gamma }/{\dot{\gamma }}_1\right)}^{\alpha /\eta }=e^{\left(\frac{\tau -\tau *}{\eta }+\frac{\dot{\tau }}{G}\right)},$$

(11)

where ${\tau }^{\mathrm{*}}=\sigma tg\phi +c_c+c_w$ [kPa].

Equation (5) can also be represented in the following form:

$$\frac{\alpha }{\eta }\mathit{ln}\left(\dot{\gamma }/{\dot{\gamma }}_1\right)=\frac{\tau -\tau *}{\eta }+\frac{\dot{\tau }}{G},$$

(12)

The solution of this equation is known [34] and is given by:

$$\tau (t)=(\sigma tg\phi +c_c+c_w+\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1))\cdot (1-e^{-\frac{G\cdot t}{\eta }}),$$

(13)

when $t\to \mathrm{\infty }$ $\tau \left(\mathrm{\infty }\right)=\sigma tg\phi +c_c+c_w+\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1)$.

It follows from Equation (13) that $c_{\dot{\gamma }}=\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1)$.

The obtained result coincides with the result of experiment (4), and using Equation (13), it is possible to construct the ($\tau *-ln\dot{\gamma }$) diagram (Figure 9), where the asymptotic lines at different shear rates are parallel and offset from each other according to the law $\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1)$.

To obtain the dependence $\left(\tau -\gamma \right)$ it is necessary to replace the time $t$ with the quantity $\gamma /\dot{\gamma }$, in Equation (13), then we obtain the following equation:

$$\tau (\gamma /\dot{\gamma })=(\sigma tg\phi +c_c+c_w+\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1))\cdot (1-e^{-\frac{G}{\eta }\cdot (\gamma /\dot{\gamma })}),$$

(14)

4. Discussion

Due to the fact that the viscosity coefficient ($\eta$) of soil depends on many factors such as time, the stress–strain state of the soil mass, temperature, humidity, rearrangement of soil particles during its compaction and creep, determining this parameter during experimental studies and subsequent interpretation of the obtained results is challenging and leads to a wide dispersion of the values obtained.

Based on the experimental studies conducted using a simple shear device in a kinematic loading mode, it has been established that the shear rate ($\dot{\gamma }$) has a significant effect on the viscosity coefficient ($\eta$) of fluid-plastic loam, namely, an inverse correlation is observed (when the shear displacement rate decreases, the viscosity coefficient increases) (Table 2).

It is shown that the viscosity coefficient is a varying value depending on both the value of the applied load and the time of its action. Therefore, when using different rheological soil models containing the viscosity parameter, it is necessary to take into account the variation of this parameter over time, rather than taking it as a constant value, as this will allow a more accurate prediction of the final settlement over time of different buildings and structures.

It was determined that at low values of shear displacement rates ($\dot{u}$ = 0.005 mm/min and $\dot{u}$ = 0.05 mm/min), the viscosity coefficient on the first section of the graph is lower than on the second section. However, with an increase in the shear displacement rate ($\dot{u}$ = 0.5 mm/min and $\dot{u}$ = 5 mm/min), opposite results were obtained (Table 2).

It should also be noted that the results of experimental studies conducted using a simple shear device in kinematic loading mode ($\dot{\gamma }=const$) showed that the shear rate ($\dot{\gamma }$) has a significant impact on the cohesion ($c$) of clay soil.

It has been found that under kinematic shear ($\dot{\gamma }=const$) of clay soil, the ultimate shear resistance ($\tau *$) depends not only on internal friction $\left(\phi \right)$, structural cohesion $\left(c_c\right)$ and cohesion of water–colloid bonds $\left(c_w\right)$, but also on the viscous resistance of the soil $\left(c_{\dot{\gamma }}\right)$.

Experiments show that with the increase in shear rate ($\dot{\gamma }$), the viscous shear resistance ($c_{\dot{\gamma }}$) increases proportionally to the logarithm of the shear rate $\left(c_{\dot{\gamma }}=c_{{\dot{\gamma }}_0}+\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1)\right)$ and this affects the rate of increase in shear stress during shear testing under kinematic loading conditions $\left(\dot{\gamma }=const\right)$.

Comparing Equations (10) and (13), it should be noted that at the same shear rate $\left(\dot{\gamma }=const\right)$ the shear stresses increase more slowly when $c_{\dot{\gamma }}=\alpha \mathit{ln}(\dot{\gamma }/{\dot{\gamma }}_1)$ (13) than when $c_{\dot{\gamma }}=\dot{\gamma }\eta$ (10). On this basis, it follows that considering the effect of shear rate on the growth rate of shear stresses is necessary.

Previously, in the works of many authors [1,2,3,4,6,11,12,14,16], it was noted that the total cohesion can be divided into two components: structural cohesion ($c_c$) and cohesion of water–colloid bonds ($c_w$). However, based on the results of experimental studies presented in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, and the analysis of the obtained results, it is clearly shown that the total cohesion ($c$) also depends on the shear rate ($\dot{\gamma }$).

Thus, it can be considered that a new rheological Equation (12) has been obtained, which can describe the dependence $\left(\tau -t\right)$ according to (10) and the dependence $\left(\tau -\gamma \right)$ according to (14) during experimental studies on clay soil samples in the kinematic loading mode $\left(\dot{\gamma }=const\right)$ and under various vertical loads $\left({\sigma }_1<{\sigma }_2<{\sigma }_3\right)$ acting on the soil sample during testing.

At present, there are quite a lot of rheological models (Newton’s model, Kelvin–Voigt viscoelastic model, Maxwell’s elastic-viscous model, Bingam–Shvedov elastic-viscoplastic model, etc.) describing the behavior of soils in time. However, none of the presented models show the effect of shear rate on the strength characteristics of clay soil. When analyzing the works of other researchers performed on similar topics, unfortunately, no work with a similar setup of experimental studies and analysis of the obtained results was found, except for the work of Kornoukhov M.B. [33]. In the comparative analysis, a high convergence with the experimental results obtained in the present work was observed.

5. Conclusions

Based on the above, it can be concluded that soil rheology is one of the most important parts of soil mechanics, as it considers the formation and change in time of the stress–strain state of soils (mainly clay soils), and also has a significant impact on the development of long-term settlement in the foundations of various buildings and structures.

This paper presents experimental studies showing the effect of shear rate on the viscosity of flow-plastic loam and proposes dependence (12) describing this phenomenon.

The performed experimental studies also show the influence of shear rate on the total cohesion of clay soil, which correlates with earlier studies presented in the work of Kornoukhov M.B. [33].

It is shown that the total cohesion can be decomposed not only into previously known components, such as structural cohesion and cohesion of water–colloid bonds, but also a third component, viscous resistance, can be identified.

The results obtained in this study can be used for further improvement of methods for calculating settlement of structures in time, as well as for predicting the time of exhaustion of the bearing capacity of foundation soils.

As part of further research, additional laboratory tests are planned to be conducted using a simple shear device in a kinematic loading mode on clay soil samples (with different plasticity index I_P and liquidity index I_L) at various shear rates and different values of vertical loads acting on the soil sample, in order to identify and determine correlation dependencies.