Parameter Design and Optimization of Grass Aerial Seeding Tower Based Computational Fluid Dynamics
Abstract
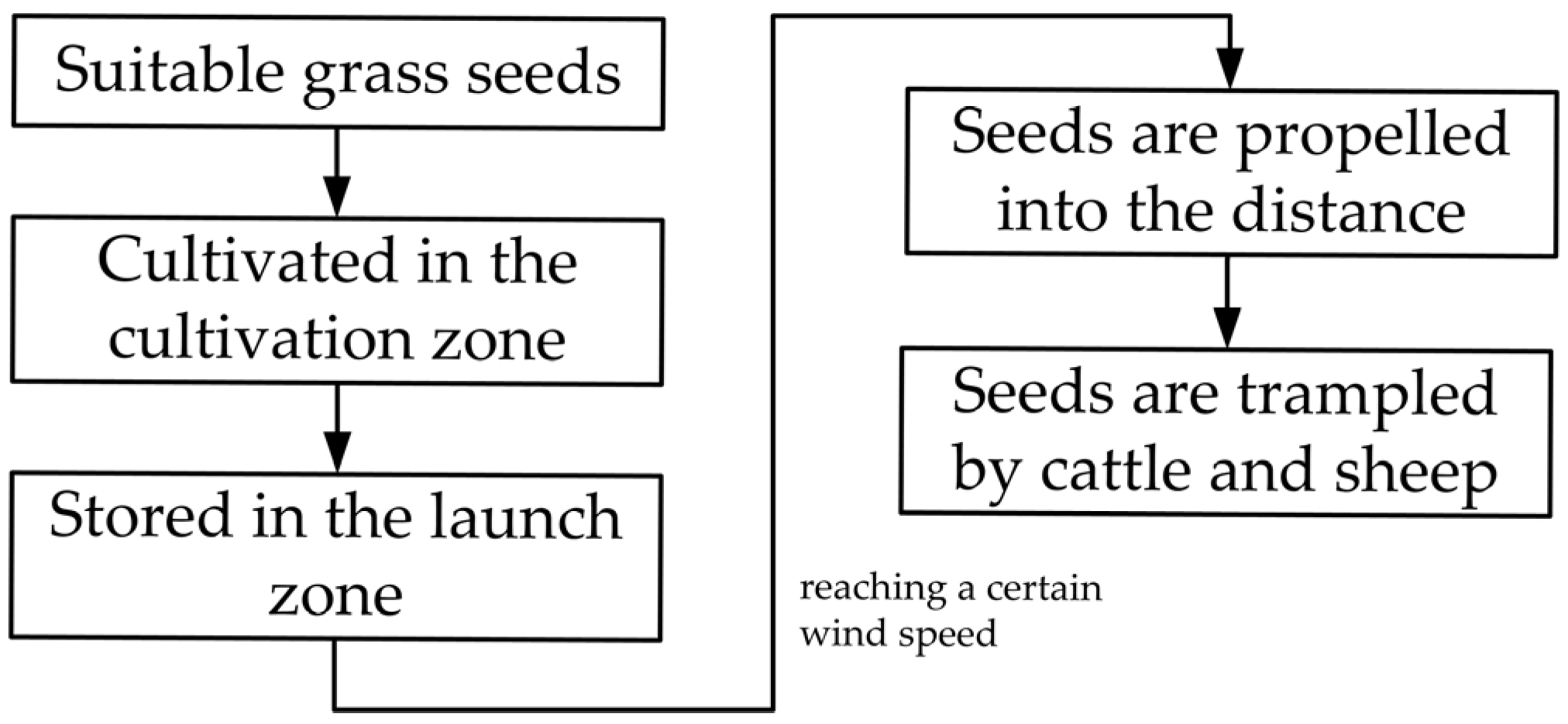
1. Introduction
2. Structure and Research Methods
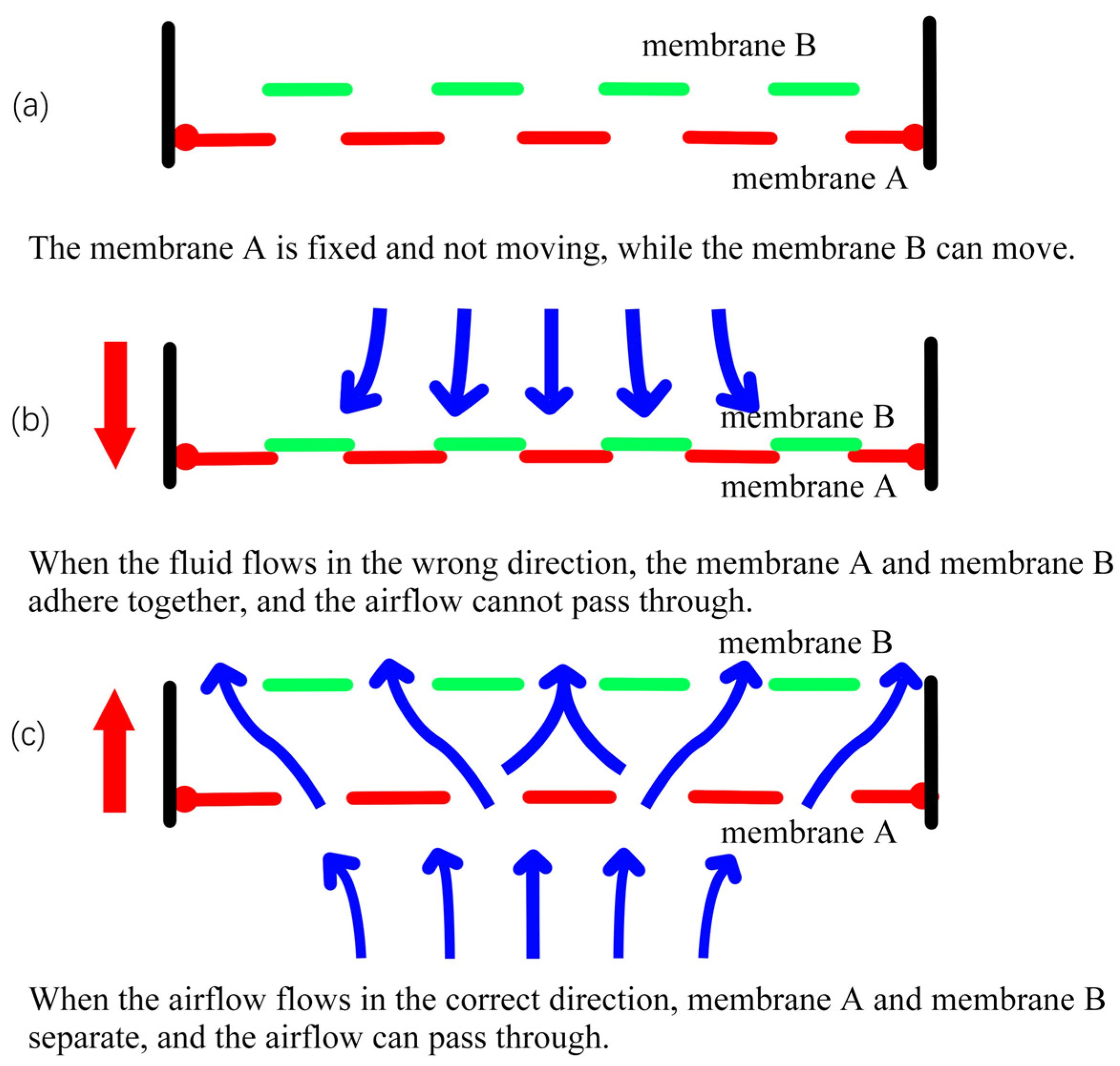
2.1. Theoretical Design Basis
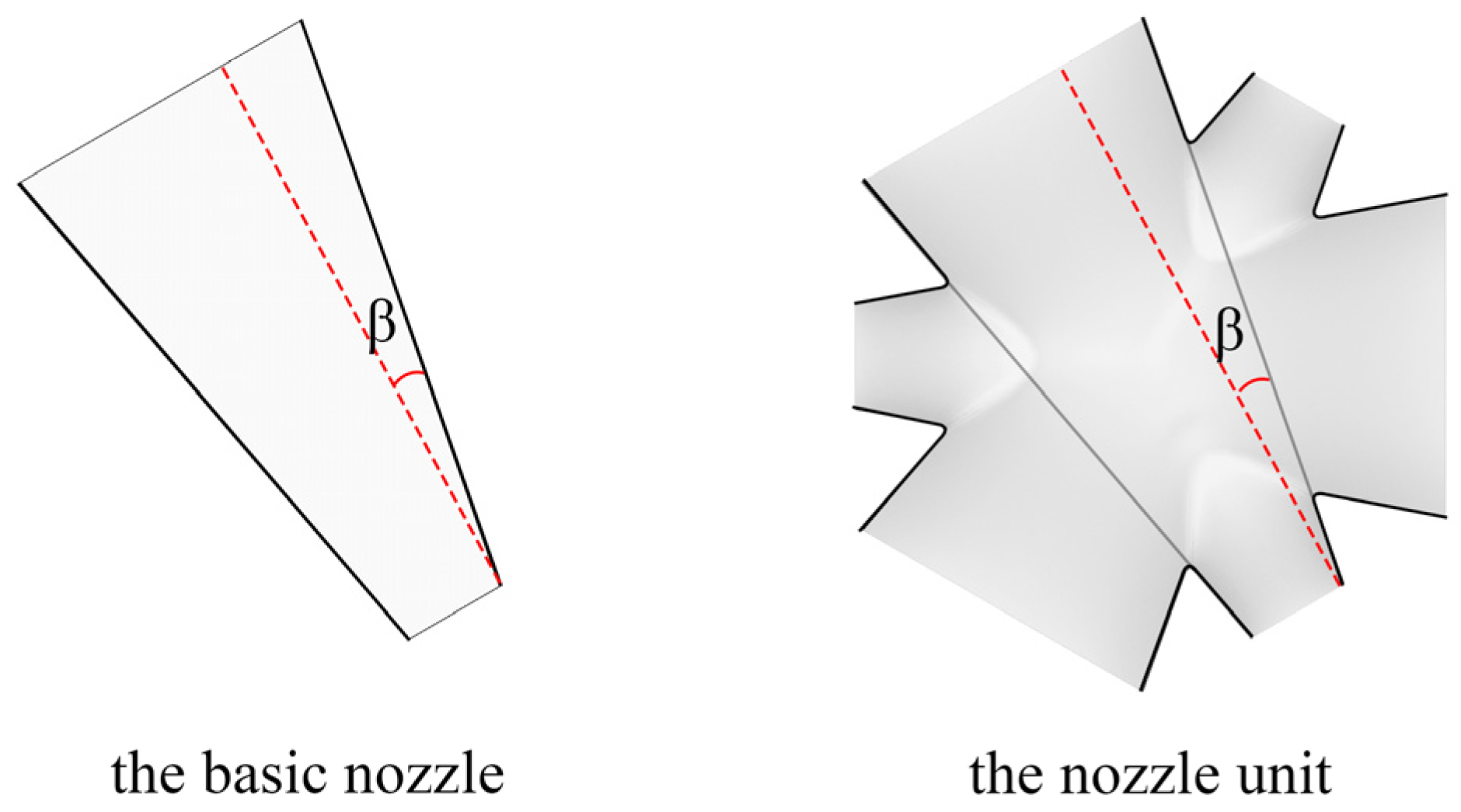
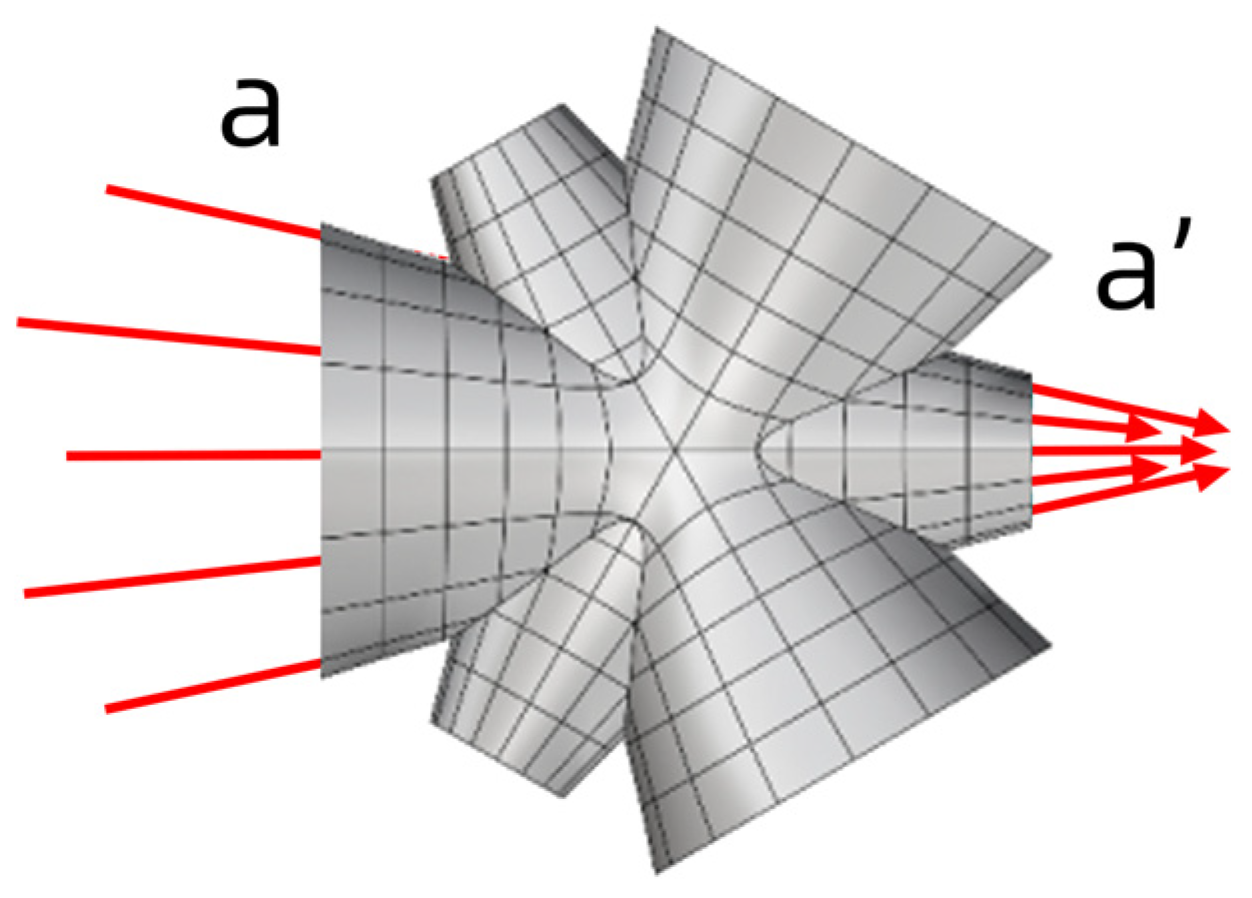
2.2. Modeling of the Basic Nozzle Unit
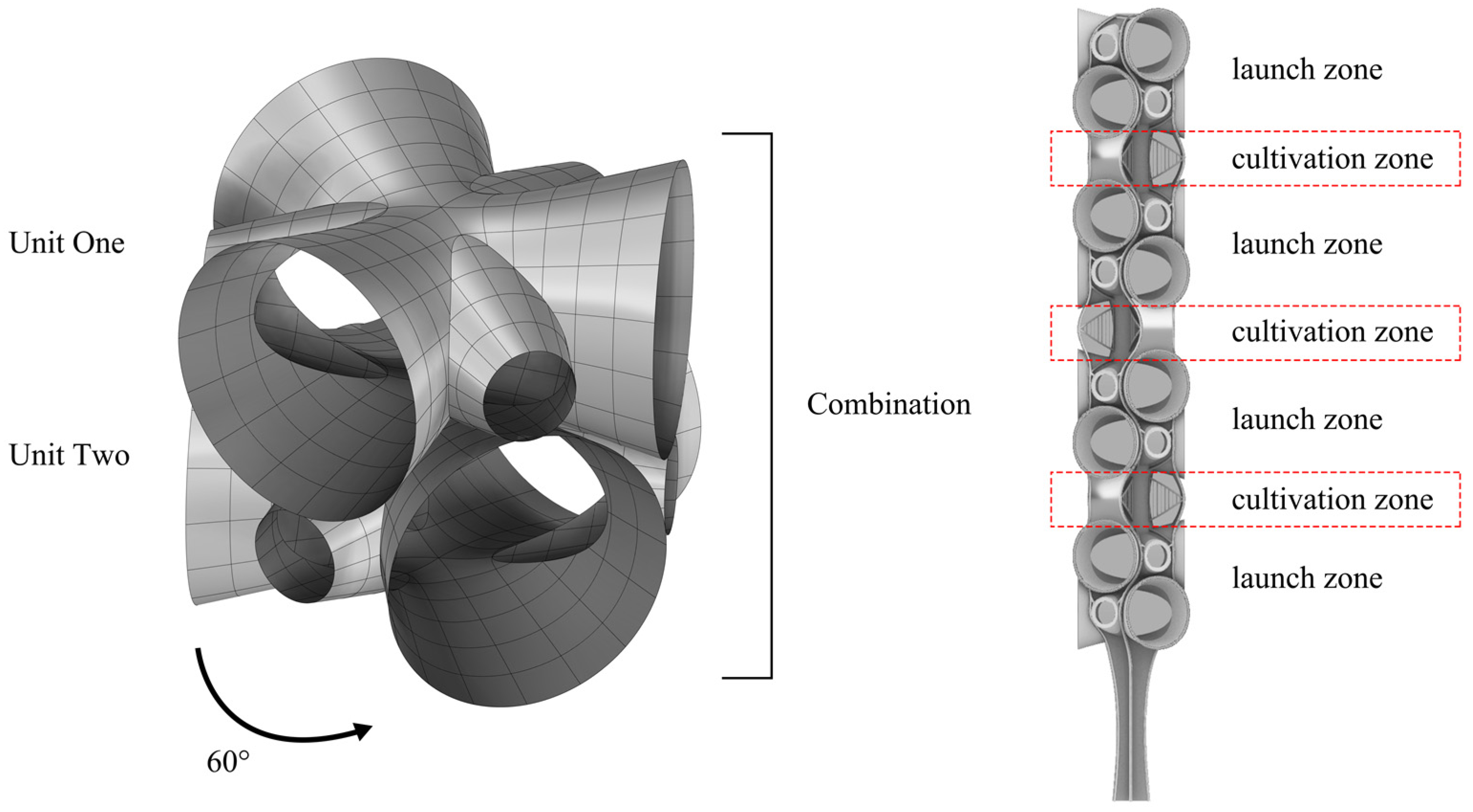
2.3. Overall Scheme Design
2.4. Launch Area Structural Design
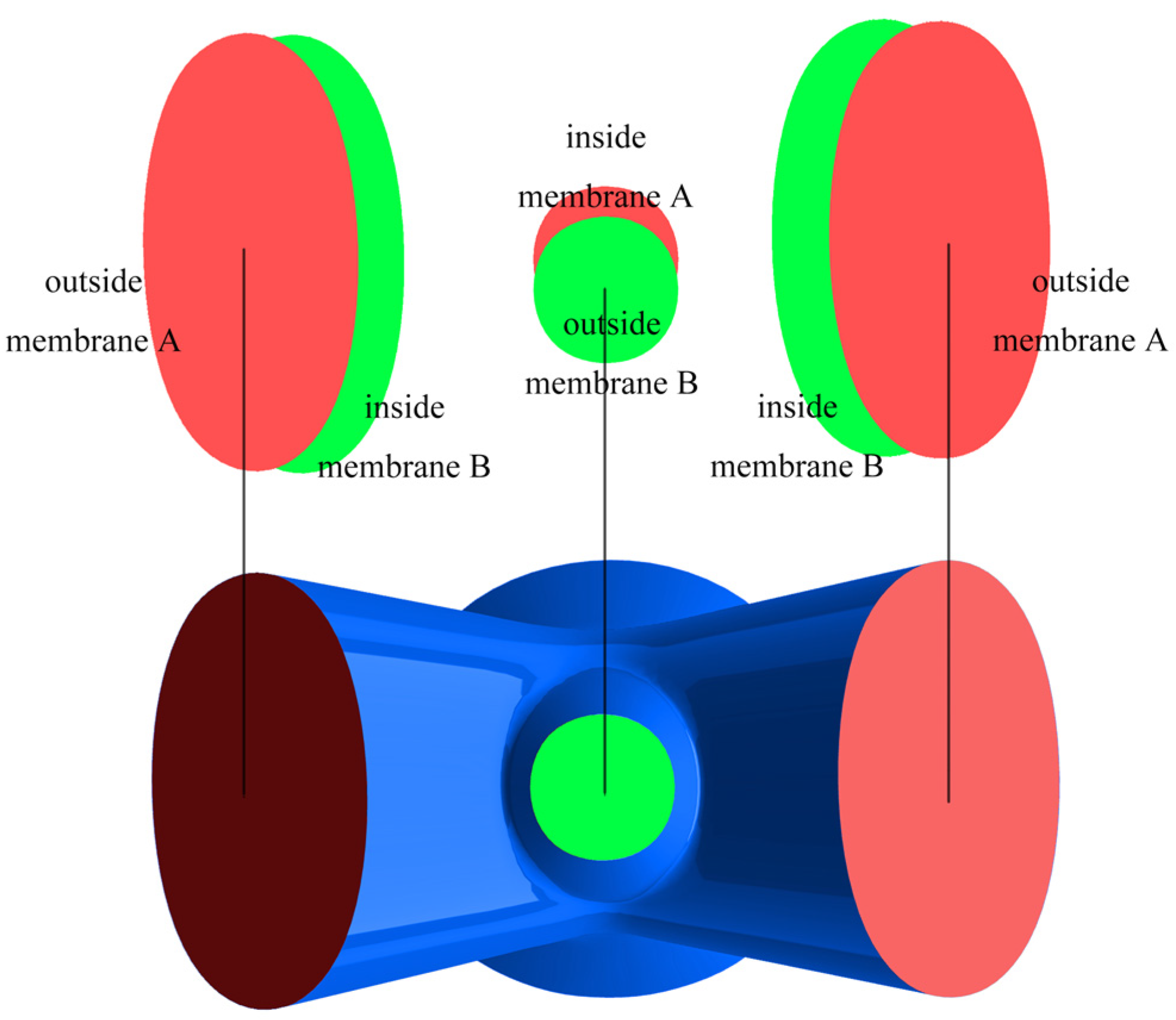
2.5. Imposing Constraints on Velocity Outlet Direction
2.6. Physical Modeling and Grid Generation
3. Parameter Design and Optimization of Basic Nozzle Unit
3.1. Evaluation of Outlet Velocity Uniformity
- (1)
- Coefficient of variation
- (2)
- Uniformity Index
3.2. Criteria for Velocity Direction Assessment
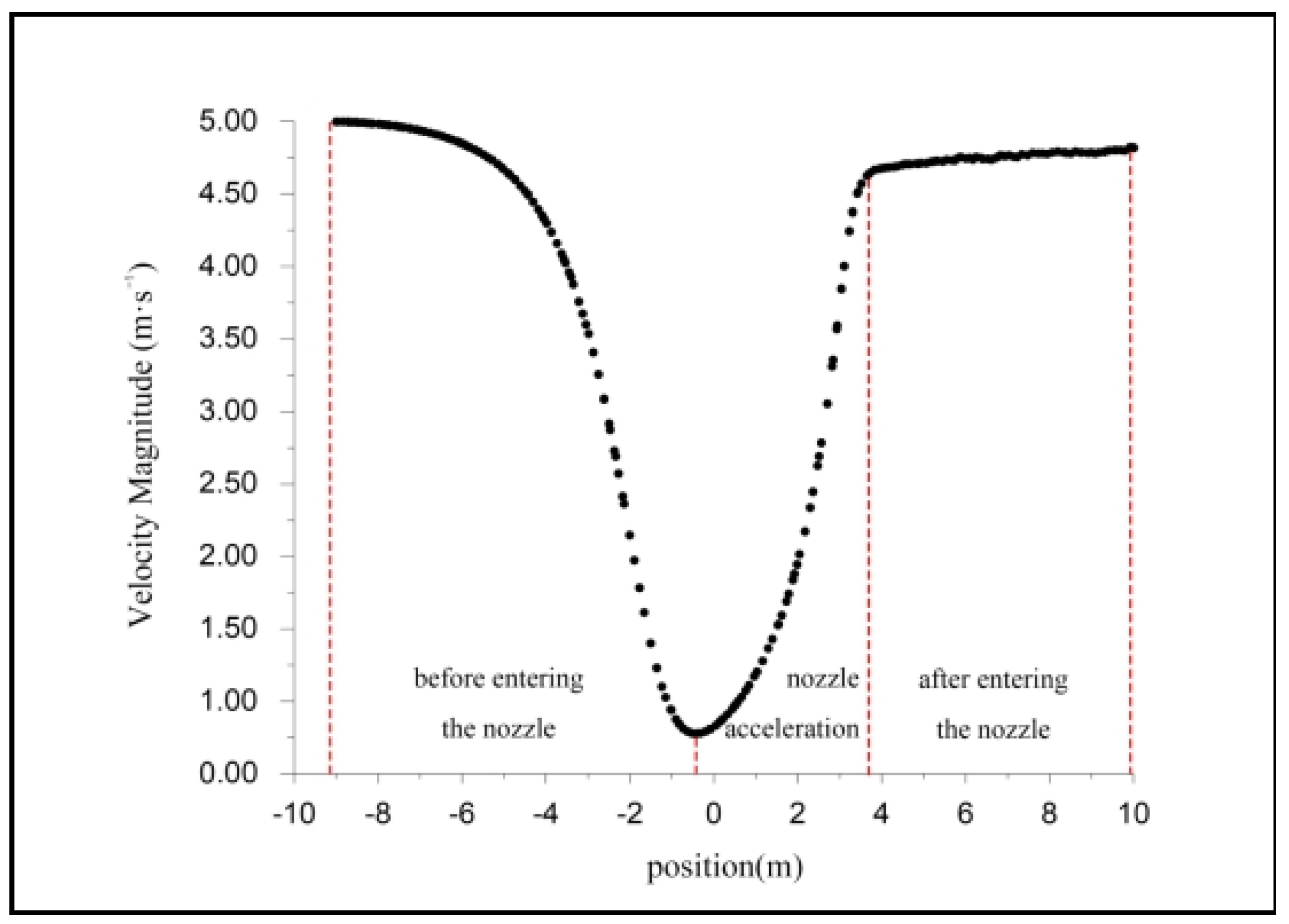
3.3. Analysis of Flow Structure
3.4. Structural Optimization Design
4. Conclusions
- (1)
- A noticeable acceleration effect is observed when the airflow passes through the nozzle unit. The airflow speed is smaller away from the outlet, and larger as well as more concentrated near the outlet.
- (2)
- As the inclination angle increases, the velocity field within the nozzle becomes more uneven, with alternating regions of high and low velocity. Turbulence intensity rises, and the overall flow uniformity decreases.
- (3)
- Through analysis and comparison, an inclination angle of 15° is suggested, maintaining good uniformity and directionality of the outlet flow while ensuring sufficient outlet flow velocity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z. Current situation and prospec of land desertification problem. Geogr. Res. 1994, 13, 104–113. (In Chinese) [Google Scholar]
- Sterk, G.; Stoorvogel, J.J. Desertification–Scientific Versus Political Realities. Land 2020, 9, 156. [Google Scholar] [CrossRef]
- AbdelRahman, M.A.E. An overview of land degradation, desertification and sustainable land management using GIS and remote sensing applications. Rend. Lincei. Sci. Fis. Nat. 2023, 34, 767–808. [Google Scholar] [CrossRef]
- Tanglin, C.; Yang, J.; Zhu, Q. Study on environmental problems and countermeasures of land desertfication in China. Heilongjiang Huanjing Tongbao 2022, 35, 97–99. (In Chinese) [Google Scholar]
- He, P.; Zhang, H.; Wang, Y.; Kang, Y.; Huang, C.; Yang, X. Analysis of influencing factors of land desertification of hexi corridor of linze county. Environ. Eng. 2016, 34, 1111–1116. (In Chinese) [Google Scholar]
- Cai, T.; Ju, C. Quantitative assessment of desertification degree in ordos grassland. J. Beljing For. Univ. 2007, 29, 227–231. (In Chinese) [Google Scholar]
- Tai, X.; Lu, L.; Jiang, Q.; Chang, D. The perception of desertification, its social impact and the adaptive strategies of ecological migrants in the desertification area, China. Chin. J. Popul. Resour. Environ. 2020, 18, 324–330. [Google Scholar] [CrossRef]
- Al-Obaidi, J.R.; Yahya Allawi, M.; Salim Al-Taie, B.; Alobaidi, K.H.; Al-Khayri, J.M.; Abdullah, S.; Ahmad-Kamil, E.I. The environmental, economic, and social development impact of desertification in Iraq: A review on desertification control measures and mitigation strategies. Environ. Monit. Assess. 2022, 194, 440. [Google Scholar] [CrossRef] [PubMed]
- Ding, G.D.; Zhao, T.N.; Fan, J.Y.; Du, H. Analysis on development of desertification assessment indicator system. J. Beljing For. Univ. 2004, 26, 92–96. (In Chinese) [Google Scholar]
- Hu, D. The evolutionary journey of the maowusu desert. Rep. West. China 2020, 16, 11–17. (In Chinese) [Google Scholar]
- Gai, Z.; Ha, S. The governance of kubuci desert promotes “emission peak & carbon neutrality”: An clarification based on the new development concept. Sci. Manag. Res. 2022, 40, 80–87. (In Chinese) [Google Scholar]
- Yang, B.; Baoyin, T. Study on restoration succession of plant community in degenerated leymus chinensis steppe after harrowing for thirty years. Chin. J. Grassl. 2014, 36, 36–42. (In Chinese) [Google Scholar]
- Qin, S. The main technical measures for aerial seeding afforestation in The Bayan-Ondor Desert. Inn. Mong. For. 2022, 8, 36–37. (In Chinese) [Google Scholar]
- Fu, B. A Small UAV with a Precise Aerial Seeding Structure. Chinese Patent CN207135486U, 27 March 2018. (In Chinese). [Google Scholar]
- Liu, Z.; Yang, X.; Peng, J. Simulation experiment of aerodynamic characteristics of laval nozzle. Res. Explor. Lab. 2021, 40, 106–110. (In Chinese) [Google Scholar]
- Chen, Z.; Liu, G.; Zhao, H.; Deng, J. Analysis of the internal flow features of a CO2 transonic nozzle and optimization of the nozzle shape profile. Appl. Therm. Eng. 2024, 238, 121945. [Google Scholar] [CrossRef]
- Pei, X.; Zhang, L.; Wang, X.; Liu, J.; Qian, Q.; Zhu, M. Design and application of intake and exhaust simulation system for altitude ground test facilities. J. Aerosp. Power 2022, 37, 2074–2089. (In Chinese) [Google Scholar]
- Chikitkin, A.; Petrov, M.; Dushkov, R.; Shifrin, E. Aerodynamic Design of a Laval Nozzle for Real Gas Using Hodograph Method. Aerospace 2018, 5, 96. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, M.; Dang, H. Experimental technique study of supersonic windy fuze dynamotor. Exp. Meas. Fluid Mech. 2004, 18, 58–61. (In Chinese) [Google Scholar]
- Gu, S.; Hao, J.; Wen, C. Air thermochemistry in the converging section of de Laval nozzles on hypersonic wind tun-nels. AIP Adv. 2022, 12, 085320. [Google Scholar] [CrossRef]
- Zhao, A.; Lin, L.; Li, P. Shape optimization of industrial supersonic nozzle based on computational fluid dynamic. China Powder Sci. Technol. 2017, 23, 6–11. (In Chinese) [Google Scholar]
- Dang, X.A.; Wang, L.L.; Yang, L.J. A Study on Novel Gas Atomization Device for Preparing Ultra Fine Metal Powder. Adv. Mater. Res. 2011, 291–294, 741–744. [Google Scholar] [CrossRef]
- Du, Y.; Chen, Y.; Zhou, Z.; Dong, C. Optimization design of nozzle flow path shape for foreign fiber sorter. J. Tianjin Polytech. Univ. 2019, 38, 76–82. (In Chinese) [Google Scholar]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Yi, Z. Theory and practice of desert “soilization” for ecological restoration. J. Chongqing Jiaotong Univ. 2016, 35, 27–32. (In Chinese) [Google Scholar]
- Li, T.; Jin, S.P.; Huang, S.Y.; Liu, W. Evaluation indices of flow velocity distribution uniformity: Comparison and application. Therm. Power Gener. 2013, 42, 60–63, 92. (In Chinese) [Google Scholar]
- Weltens, H.; Bressler, H.; Terres, F.; Neumaier, H.; Rammoser, D. Optimisation of catalytic converter gas flow distribution by CFD prediction. In SAE Technical Paper 930780; SAE International: Pittsburgh, PA, USA, 1993; pp. 1–23. [Google Scholar] [CrossRef]



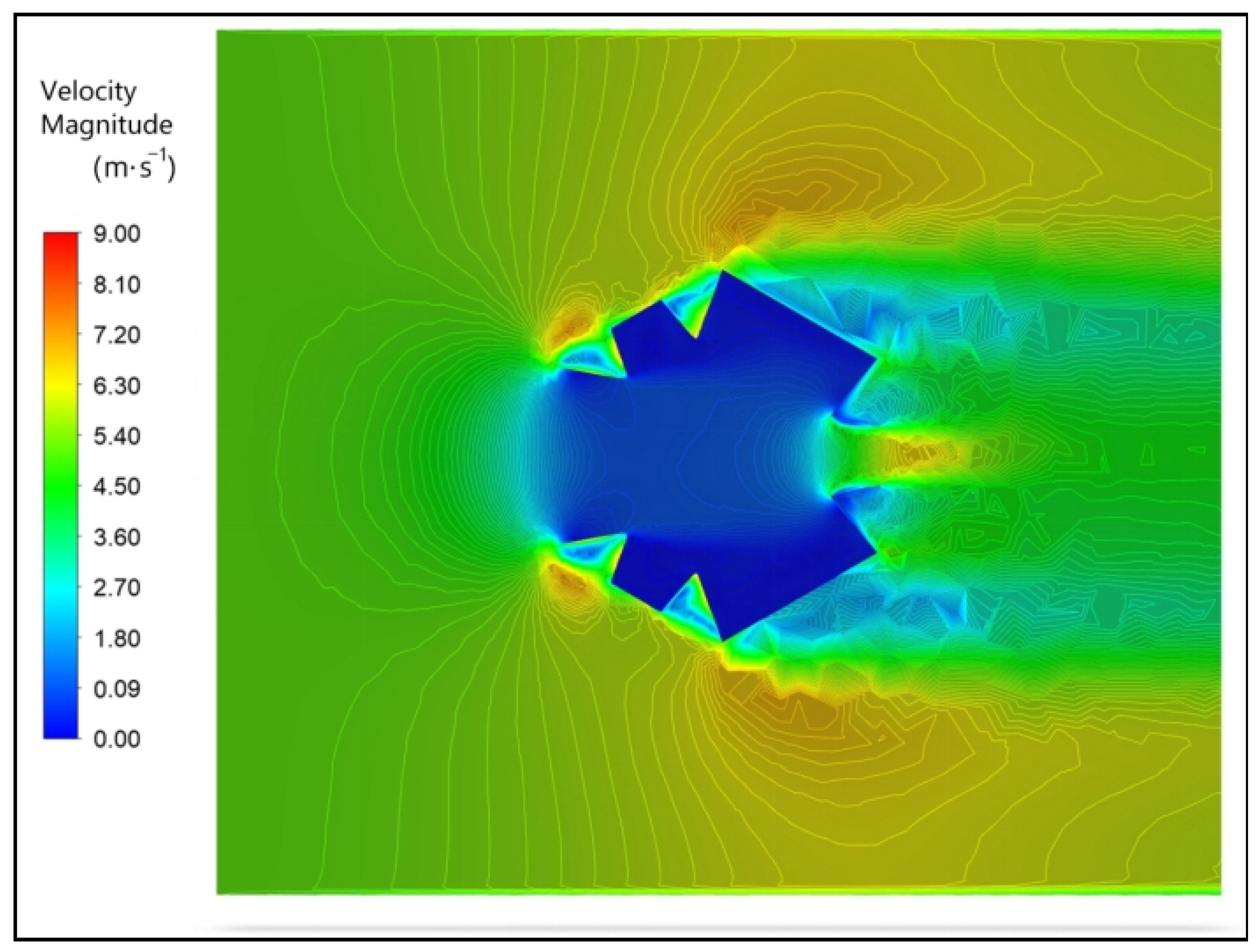
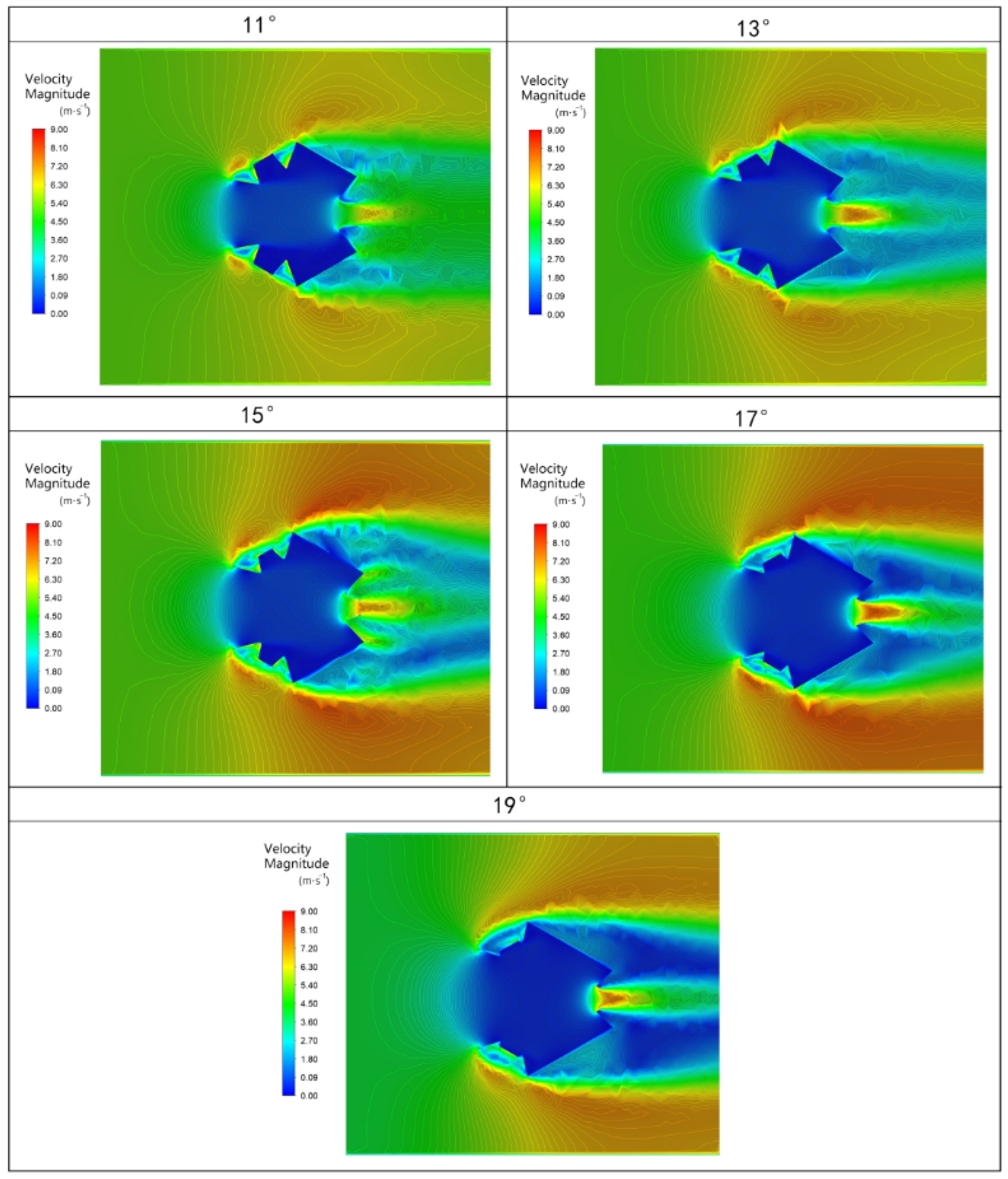
| Inclination Angle/° | Outlet Radius/mm | S | /(m·s−1) | CV | ||
|---|---|---|---|---|---|---|
| 11 | 1500 | 3.158 | 4.562 | 0.069 | 0.984 | −0.993 |
| 13 | 1650 | 5.115 | 5.616 | 0.091 | 0.983 | 0.993 |
| 15 | 1840 | 8.030 | 6.758 | 0.119 | 0.977 | 0.991 |
| 17 | 2030 | 17.117 | 8.452 | 0.203 | 0.965 | 0.982 |
| 19 | 2220 | 43.526 | 10.661 | 0.408 | 0.930 | 0.893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhang, Y. Parameter Design and Optimization of Grass Aerial Seeding Tower Based Computational Fluid Dynamics. Appl. Sci. 2024, 14, 5971. https://doi.org/10.3390/app14145971
Wang B, Zhang Y. Parameter Design and Optimization of Grass Aerial Seeding Tower Based Computational Fluid Dynamics. Applied Sciences. 2024; 14(14):5971. https://doi.org/10.3390/app14145971
Chicago/Turabian StyleWang, Bingjie, and Yingzi Zhang. 2024. "Parameter Design and Optimization of Grass Aerial Seeding Tower Based Computational Fluid Dynamics" Applied Sciences 14, no. 14: 5971. https://doi.org/10.3390/app14145971
APA StyleWang, B., & Zhang, Y. (2024). Parameter Design and Optimization of Grass Aerial Seeding Tower Based Computational Fluid Dynamics. Applied Sciences, 14(14), 5971. https://doi.org/10.3390/app14145971





