Abstract
The Susceptible–Infected–Susceptible (SIS) model in complex networks is one of the critical models employed in the modeling of virus spread. The study of the heterogeneous SIS model with a non-homogeneous nodal infection rate in finite-size networks has attracted little attention. Investigating the statistical properties of heterogeneous SIS epidemic dynamics in finite networks is thus intriguing. In this paper, we focus on the measure of variability in the number of infected nodes for the heterogeneous SIS epidemic dynamics in finite-size bipartite graphs and star graphs. Specifically, we investigate the metastable-state variance of the number of infected nodes for the SIS epidemic process in finite-size bipartite graphs and star graphs with heterogeneous nodal infection rates. We employ an extended individual-based mean-field approximation to analyze the heterogeneous SIS epidemic process in finite-size bipartite networks and star graphs. We derive the approximation solutions of the variance of the infected number. We verify the proposed theory by simulations. The proposed theory has the potential to help us better understand the fluctuations of SIS models like epidemic dynamics with a non-homogeneous infection rate.
1. Introduction
The research of modeling and analysis of infectious diffusion processes in networks, e.g., epidemics, rumors and computer viruses, have attracted ample attention over the past decades [1,2]. Compartmental models are used to describe this sort of diffusion process. The commonly used basic compartment models are the Susceptible–Infectious–Susceptible (SIS) model and the Susceptible–Infected–Recovery (SIR) model. Several theoretical frameworks such as Markov theory, message passing and mean-field approximation are employed to model the dynamics of these diffusion processes. For the sake of convenience, most conventional methods to model the epidemic dynamics implicitly hold the assumptions that, for example, the underlying network size is infinite, all individuals are fully mixed and the infection and recovery rates are homogeneous. The usage of these assumptions helps to reduce the complexity of modeling and analysis. However, real networks are usually limited in size and heterogeneous nodal infection rate. It is intriguing to investigate the impact of a given finite-size network topology over the SIS dynamics.
In this work, we focus on the heterogeneous SIS epidemic dynamics in networks with a given finite-size topology characterized by the adjacency matrix. Specifically, we investigate the SIS epidemic dynamics with each individual having a non-homogeneous infection rate or recovery rate. We derive the variance of the number of infected nodes for the heterogeneous SIS epidemic dynamics in a bipartite network and a start graph with a finite size. We experimentally verify the proposed theories.
The paper is organized as follows. Section 2 introduces several related works. In Section 3, we elaborate on the theoretical framework, followed by the approximation solutions to the variance of infection fractions for bipartite graphs and star graphs. The proposed theoretical formulas are derived. Also, we describe the simulation method employed in this paper. In Section 4, we first demonstrate the comparison between the theory and the simulation for the infection change versus time. Then, we verify the accuracy of the proposed theoretical formulas of the variance for the heterogeneous SIS process in bipartite graphs and star graphs. In Section 5, we analyze the accuracy of the proposed theoretical approximation formulas and provide several explanations. Finally, we conclude the paper in Section 6.
2. Literature Review
Much effort has been paid to the modeling and analysis of the dynamics of the homogeneous SIS process in static networks where fixed infection and recovery rates stay unchanged for each node. Pastor-Satorras et al. proposed a heterogeneous mean-field approximation (HMFA) method to characterize the impact of the heterogeneous network topology on a SIS virus spread [3]. Chakrabarti et al. proposed a time-discrete model to investigate the SIS epidemic process in networks [4]. Van Mieghem et al. [5] proposed a time-continuous theoretical framework named N-intertwined mean-field approximation (NIMFA) to model SIS epidemic dynamics in a static single finite-size network, where the infection rate as well as the recovery rate are fixed for each node in a given configuration. In [4,5], the metastable-state fraction of infected nodes and the epidemic threshold are derived, respectively, for the discrete-time and the continuous-time SIS processes in a finite-size network. Specifically, the claim that the epidemic threshold is upper-bounded by the largest eigenvalue of the adjacency matrix of the network topology is also proved.
The NIMFA is extended and adapted to modeling the SIS epidemic dynamics, where each node may have a different infection rate or recovery rate [6]. In the framework of this heterogeneous NIMFA, several general solutions to the metastable-state average number of infected nodes and the epidemic threshold are derived. Jiao et al. studied the scenario where the nodes in a network with the topology of a bipartite complete are divided into two groups and the infection rates for nodes in a specific group are identical [7]. This scenario reduces to a star graph, where outer nodes have the same infection rate that is different from the center node. Jiao et al. employed the heterogeneous NIMFA and derived the exact solution to the average steady-state number of infected nodes.
The heterogeneous dynamic process model has various applications. Wang et al. applied the heterogeneous NIMFA framework to analyze and assess interest Negative ACKnowledgments on mitigating interest flooding attacks in Named Data Networking (NDN) [8]. Cui et al. studied a susceptible–infected–water–susceptible (SIWS) model which takes in to account disease diffusion in various mediums with different infection rates [9]. Pagliara and Leonard studied the susceptible–infected–recovered–infected (SIRI) model which assumes that the a recovering individual would change their susceptibility to reinfection [10]. The incomplete immunity to reinfection leads to a different infection rate for each node.
In comparison with the statistics of epidemic dynamics such as the metastable-state number of infected nodes, the variance in the number of infected nodes does not attract enough concern. The lifetime and the survival time of an epidemic are closely related to its variance [11]. Van Mieghem and Omic investigated the variance under the framework of NIMFA with a homogeneous infection rate and curing rate [12]. With the approximation that individual viral states are independent from each other, the variance as well as its upper and lower bounds in the nodal viral state and system viral state are derived. These general solutions are exemplified with complete graphs and bipartite graphs.
3. Methodology
3.1. Theory Framework
We consider a Markov process representing the SIS process in a network with a finite size, where the topology of the network is specified by an undirected and unweighted graph G. The size N of a graph G denotes the number of nodes belonging to G. We denote by A the adjacency matrix of the topology, where an element of the matrix is equal to 1 if the connection between nodal pair i and j exists or 0 if the connection does not exist. The degree of the node i is usually defined as . Each node i could be in one of two states at a time t: the infected state, meaning that the node is capable of infecting others, or the susceptible state, meaning that the node is healthy but susceptible to infection. The infected state and the susceptible state of the node i are denoted by I or S, respectively.
The heterogeneous NIMFA is rehearsed in the following. At time t, the viral state of a node i is represented by a Bernoulli random variable . The viral state of the node i could either be the infected state with probability , or the susceptible state with probability . Assuming there is a link between an infected node i and a susceptible node j, the infection process per link connecting an infected node and a susceptible node is a Poisson process with rate , as shown in Figure 1a. The infection process for each nodal pair of infected nodes and one of its neighbors is independent. Any infected node i will achieve recovery with rate . If the node i recovers, the viral state of node i becomes from . This is called the curing process for the infected node i, which is a Poisson process with rate , as shown in Figure 1b. The curing process for each node is independent.
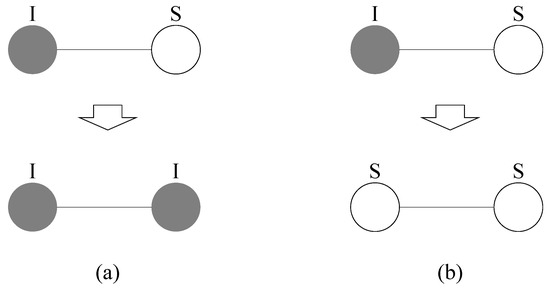
Figure 1.
Schematic diagram of two independent Poisson processes of a SIS epidemic dynamic between a nodal pair in a network. The independent processes are (a) the infection process describing an infected node infecting its susceptible neighboring node. (b) The curing process describing an infected node infecting recovered individuals.
The heterogeneous SIS epidemic process is composed of all curing processes and infection processes in a given finite-size network. It is useful to introduce the notation , named the effective infection rate, defined as . At time t, the number of infected nodes and the expected fraction of infected nodes are defined as and , respectively.
The steady state of the system composed of the SIS process in a given finite-size network actually corresponds to the metastable state [5]. The steady state, denoted by , implies
We also denote by y or , and I or , the metastable-state fraction of infected nodes and the metastable-state number of infected nodes. The only approximation employed by the NIMFA framework leads to
which means that the random variables and are assumed to be independent [5]. This assumption of independence approximation further induces
The exact Markov differential equation for the viral state of node i can be expressed as
The Markov differential Equations (4) and (5) were proposed and derived previously in [6] on p. 2. Similarly, we could obtain the differential equations for all nodal viral states, shown as
According to the properties of the Bernoulli random variable, the expectation and variance of the viral state are expressed as
According to the linearity of expectation, the expectation of could be expressed as
The variance of could be expressed as
that was derived and shown in ([13] p. 30).
3.2. Variance of Infection Fraction for Bipartite Graph
The main topologies concerned are the complete bipartite graph and the star graph. A complete bipartite graph is composed of two groups of nodes, where any nodal pair in one group does not connect and a node in one group is fully connected to all nodes in another group. As shown in Figure 2a, the nodes on the left side belong to a group of nodes, while the nodes on the right side are of another group of nodes. As shown in Figure 2b, a star graph of is a tree structure composed of one special node of degree n and the other n nodes of degree 1. The special node, referred to as the center or the root, is connected to each of the other nodes. A star graph is isomorphic to a complete bipartite graph with .
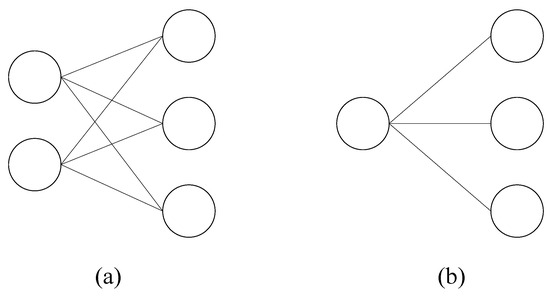
Figure 2.
Topology of networks concerned in this work. Two sorts of networks are chosen to investigate the heterogeneous SIS epidemic dynamics: (a) a complete bipartite graph with two disjoint node sets, and . (b) A star graph.
Lemma 1.
The metastable-state average number y of infected nodes for the heterogeneous SIS process in a complete bipartite network with the setting for and for , can be expressed as
where
Proof of Lemma 1.
The expression for the metastable-state fraction y of the number of infected nodes was previously proved and shown as Theorem 1 in [7]. Substituting and using leads to the expression for . □
Proposition 1.
Proof of Proposition 1.
The nodes in a complete bipartite graph are divided into two sets. Within each set, the nodes are identical for the configuration concerned, which was proven in [7]. For the node i of the complete bipartite graph with , the metastable-state fraction of infection is identical, e.g., as shown in (13). Similarly, for . Substituting in (13) and in (14) into (11) leads to
□
A complete bipartite graph is isomorphic to a star graph with the setting . A star graph of size is a tree with one rooted node as the center, having degree n and the other having degree 1 as siblings connecting to the center.
Corollary 1.
Proof of Corollary 1.
The star graph of the nodes is isomorphic to the complete bipartite graph where . Substituting into (15) and conducting some manipulations (see Appendix A for details), we can derive the corollary (16). □
3.3. Simulation Method
It is straightforward to consider the SIS process in a given finite-size network as a Markov chain where each system state is denoted by a vector . It is apparent that the state is the absorbing state, which means the system will stay unchanged if it enter into this state. Notable is that any other system states could achieve the absorbing state with a non-zero probability. The final steady state of the exact SIS process in the finite-size network is the absorbing state. The steady state of the NIMFA model corresponds to the metastable state of the exact SIS process in the finite-size network [5]. But, it is relatively hard to theoretically define and empirically detect the metastable state.
Van Mieghem et al. proposed the -SIS model and employed the steady state of the -SIS model to approximate the metastable state in the exact SIS process [14]. Through a simulation of the -SIS model, Li et al. obtained extensive empirical results with sound accuracy for various network topologies [15]. One merit of the -SIS model is that there is no absorbing state and it is unnecessary to detect the metastable state.
In this work, we implement the -SIS model and employ it as the simulation method. A self-infection Poisson process with rate is added to each node i for . Even if the system enters into the state , the probability that the system jumps out of the state is non-zero. In other words, there is no absorbing state in the -SIS model. At the beginning of a simulation instance, a portion of the nodes are selected to be infected while the others are susceptible. After a warm-up time, one can continue to run the simulation for a long time and record the change in the system state. After stopping the simulation, one can calculate any statistics of the dynamics, such as the time-average number of infected nodes, according to the records.
The simulation environment setup is described in the following section. We take the simulation time to be time units and set the self-infection rate for . For a given setup and a graph, we start one simulation and record the number of infected nodes in the graph for each time step until the end of the simulation. Finally, we can calculate the statistical properties such as the time-average value of the steady-state average number of the infected nodes. For a given setup, we only need to run one single simulation instance to calculate all related statistical properties. We can then show the relation between one of the statistical properties and the simulation time in a figure.
In this work, we also show the relation between the statistical properties as a function of infection rate. We fix the setup . Then, we change the setup of from 0 to a large enough number. For each number of , we calculate the corresponding statistical properties. Finally, we can show the relation between the metastable-state number and the infection rate in a figure.
4. Results
4.1. Time Evolution
We implement a discrete-time simulator of the -SIS model which was elaborated in Section 3.3. We first conduct experiments on the time evolution of infection and verify the existence of the metastable state of the system.
Figure 3 demonstrates a single run of the simulation, which shows the change in the fraction number of a heterogeneous SIS process as a function of time in a complete bipartite graph with the model settings and . The fraction of infected number starts at a small portion which is fixed at the very beginning of the simulation as a parameter. Then, the fraction increases rapidly into a plateau where it fluctuates between a relatively fixed range. The thick curve and the dashed thin curves denote the theoretical mean and standard deviation of the fraction of infected nodes, respectively. The theoretical mean value is calculated by (12), while the standard deviation is obtained via the square root of the variance (15), shown in Proposition 1. It appears that there exists a metastable-state mean value of the infection number which can be approximated by the steady-state average number of infected nodes calculated by the above-mentioned NIMFA model.
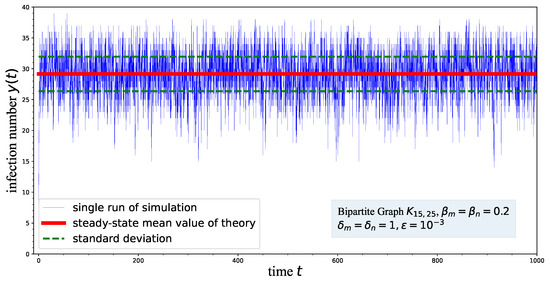
Figure 3.
Time evolution of the fraction of the infected nodes of a single run of a SIS process in a complete bipartite graph with two disjointed node sets. The thin blue curve denotes the simulation results recorded while conducting the -SIS model, while the thick red straight curve denotes the theoretical steady-state mean value (12). The dashed lines denote the standard deviation obtained via the square root of the variance (15).
4.2. Variance of Infection Fraction in Bipartite Graph
We conducted numerous simulations for the heterogeneous SIS process in the bipartite graph in order to verify the proposed theory (15) proven in Proposition 1. The number of infected nodes versus time for each run of a simulation with a specific configuration is recorded as demonstrated in Figure 3. The records with various configurations are collected and then used to calculate several statistical properties such as the steady-steady mean fraction of the infected nodes and the steady-state variance of the fraction of the infected nodes.
Take the results shown in Figure 4 as an example for the heterogeneous SIS process in a bipartite graph. The metastable-state mean and variance are compared with the corresponding steady-state theoretical results in each diagram. The markers and curves denote the metastable-state simulation results and the steady-state theoretical results, respectively. Without the loss of generality, the fraction of infected nodes are shown as a function of the infection rate while the other set of parameters is fixed. The variance of the number of the infected nodes corresponding to the mean infection fraction is also demonstrated with the same set of parameters.
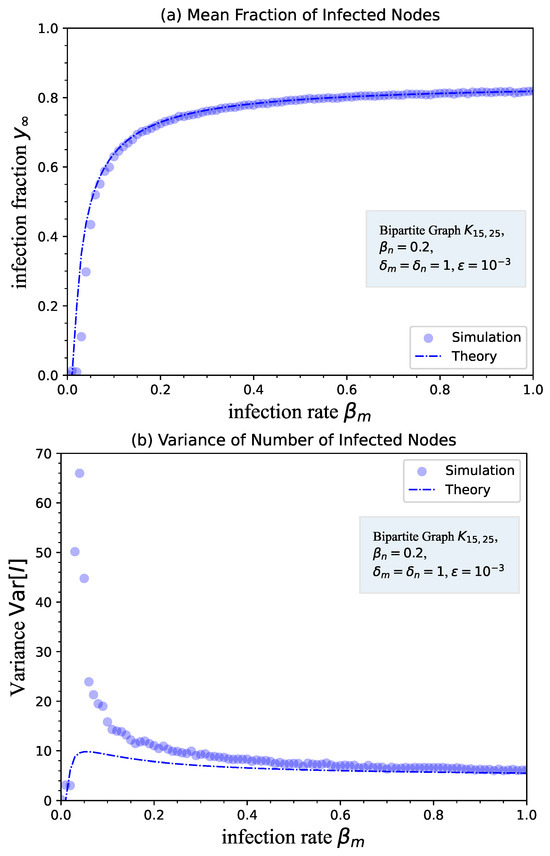
Figure 4.
Statistical properties of the heterogeneous SIS process in a bipartite graph . The scattered cycles denote the simulation results, while the dashed curves denote the theory. (a) The mean value of the steady-state fraction of infected nodes is shown, where the theory is calculated by (12). (b) The variance of the steady-state fraction of infected nodes is demonstrated, where the theory is calculated by (15).
4.3. Variance of Infection Fraction in Star Graph
We conduct numerous simulations for the heterogeneous SIS process in a star graph in order to verify the proposed theory (16) proved in Corollary 1. Take the results shown in Figure 5 as an example of a heterogeneous SIS process in a star graph. The center node is with the infection rate different to the other nodes. The comparisons of the steady-state fraction of infected nodes and the variance and the metastable-state fraction of infected nodes and the variance are demonstrated. Although the noises are relatively large in simulations for a finite-size star graph, the trend of simulation results is still apparent as shown in Figure 5.
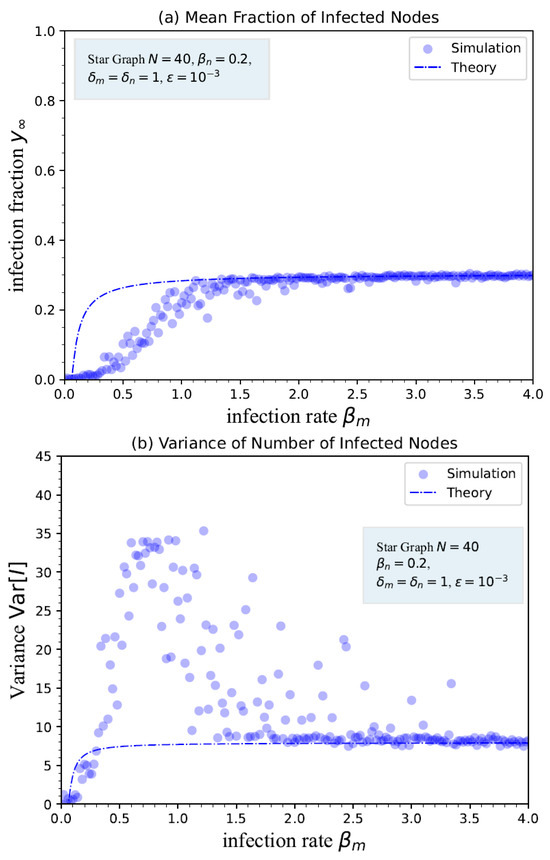
Figure 5.
Statistical properties of the heterogeneous SIS process in star graph . The scattered cycles denote the simulation results, while the dashed curves denote the theory. (a) The mean value of the steady-state fraction of infected nodes is shown, where the theory is calculated by (12). (b) The variance of the steady-state fraction of infected nodes is demonstrated, where the theory is calculated by (16).
5. Discussion
The existence of the metastable-state of the heterogeneous SIS in bipartite graphs and star graphs are verified, which is shown in Figure 3 for a non-trivial case. The statistical mean value of the fraction of infected nodes tends to stay unchanged, although the simulation result changes as time goes on. It appears that the metastable-state mean value of the fraction of infected number for the heterogeneous SIS process corresponds to the steady-state expectation value of the proposed theory. The theoretical standard deviation as the square root of the proposed variance (15) provides a relatively accurate approximation of the statistical fluctuation as shown in Figure 3. Moreover, the deviation of the fraction of the infected number according to the simulation results is restricted to a limited range, which could be predicted by the theoretical variance to some extent.
According to the comparisons shown in Figure 4, the proposed theories are capable of approximating the real heterogeneous SIS process in bipartite graphs for the range of various infection rates. Specifically, the proposed approximations of the steady-state number of infected nodes and the variance can be used to predict the metastable-state number of the infected nodes and the variance. Although the inaccuracy of the approximation is not apparent for the mean fraction of the infected number, it is relatively large for the approximation to the variance for a small range of infection rates. It is shown that the obvious discrepancy between the theory and the simulation lies in the phase transition point, e.g., the epidemic threshold. The main reason is that the NIMFA framework employed in this work has its own limitations in approximation. The homogeneous NIMFA framework could not predict a real variance larger than , where N is the network size [12]. As the infection rate grows, the accuracy of the approximations increases dramatically. For relatively large infection rates, the discrepancy between the theory and the simulation becomes tiny enough to be omitted.
It appears that the steady-state variance of the number of infected nodes calculated by (16) is capable of approximating the simulation results for a relatively large range of various infection rates, as shown in Figure 5. The discrepancy of the theory and the simulation appears near the epidemic threshold. On the other hand, compared to the scenario of the bipartite graph, the theory for the star graph performs better and more accurately predicts the variance near the epidemic threshold.
6. Conclusions
The NIMFA framework, as a sort of individual-based mean-filed approximation, is extended to modeling the heterogeneous SIS process in bipartite graphs and star graphs. Specifically, several approximations to the variance of the metastable-state fraction of infected nodes are proposed. To the best of our knowledge, this is the first attempt to analyze the statistical fluctuations of the heterogeneous SIS process in specific graphs, which has attracted little attention. The empirical works in this paper demonstrate the effectiveness of the proposed theory to some extent. Especially, the proposed variance approximations provide better accuracy for a relatively large range of infection rates, although it does not perform near the epidemic threshold.
One limitation of the approximation lies in the discrepancy between the theory and the statistical properties of real dynamics near the phase transition point. The main reason is the NIMFA framework employed and extended in this work is a first-order approximation. In future studies, the accuracy of the approximation of the variance should be improved. Selecting more accurate mean-field approximation frameworks with relatively low computational complexity [16,17,18] helps to improve the accuracy of the expectation and the variance approximation. Moreover, much attention should be paid to the bounds on the variance.
A basic assumption that most of the related works are based on is the choice of Poisson process. The Poisson process could be analyzed theoretically in the framework of the Markov theory. However, many real contact and infection activities are non-Markovian processes in networks with temporal topologies. There is a lack of some general theoretical framework to analyze the above-mentioned non-Markovian processes [19,20]. One could extend some propositions proposed in this work to these complex scenarios.
Author Contributions
Conceptualization, D.G. and L.J.; methodology, D.G.; software, D.G. and L.J.; validation, D.G., L.J., J.J. and K.M.; formal analysis, D.G.; investigation, D.G.; resources, D.G. and L.J.; data curation, D.G. and L.J.; writing—original draft preparation, D.G., L.J., J.J. and K.M.; writing—review and editing, D.G., L.J., J.J. and K.M.; visualization, D.G. and L.J.; supervision, D.G. and J.J.; project administration, D.G.; funding acquisition, D.G. and L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We would like to thank the anonymous reviewers for their insightful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SIS | Susceptible Infected Susceptible |
| NIMFA | N-Intertwined Mean-field Approximation |
| HMFA | Heterogeneous Mean-field Approximation |
Appendix A. Proof of Corollary 1
The metastable-state variance of the heterogeneous SIS process in the complete bipartite graph , shown in (15), is composed of two parts, e.g., the left-part and the right-part . We begin the proof from manipulating the left-part. Substituting (13) into the left-part leads to
For , the expression (A1) reduces to
Similarly, substituting (13) into the right-part and conducting some manipulations leads to
For , the expression (A3) reduces to
References
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925–979. [Google Scholar] [CrossRef]
- de Arruda, G.F.; Rodrigues, F.A.; Moreno, Y. Fundamentals of spreading processes in single and multilayer complex networks. Phys. Rep. 2018, 756, 1–59. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic dynamics and endemic states in complex networks. Phys. Rev. E 2001, 63, 066117. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Wang, Y.; Wang, C.; Leskovec, J.; Faloutsos, C. Epidemic thresholds in real networks. ACM Trans. Inf. Syst. Secur. 2008, 10, 1:1–1:26. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Omic, J.; Kooij, R. Virus Spread in Networks. IEEE/ACM Trans. Netw. 2009, 17, 1–14. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Omic, J. In-Homogeneous Virus Spread in Networks. arXiv 2014, arXiv:1306.2588. [Google Scholar]
- Jiao, L.; Yin, H.; Guo, D.; Lyu, Y. Heterogeneous Malware Spread Process in Star Network. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems Workshops (ICDCSW), Atlanta, GA, USA, 5–8 June 2017; pp. 265–269. [Google Scholar] [CrossRef]
- Wang, K.; Guo, D.; Quan, W. Analyzing NDN NACK on Interest Flooding Attack via SIS Epidemic Model. IEEE Syst. J. 2020, 14, 1862–1873. [Google Scholar] [CrossRef]
- Cui, S.; Liu, F.; Jardón-Kojakhmetov, H.; Cao, M. Discrete-time layered-network epidemics model with time-varying transition rates and multiple resources. Automatica 2024, 159, 111303. [Google Scholar] [CrossRef]
- Pagliara, R.; Leonard, N.E. Adaptive Susceptibility and Heterogeneity in Contagion Models on Networks. IEEE Trans. Autom. Control 2021, 66, 581–594. [Google Scholar] [CrossRef]
- Ganesh, A.; Massoulie, L.; Towsley, D. The effect of network topology on the spread of epidemics. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; Volume 2, pp. 1455–1466. [Google Scholar] [CrossRef]
- Omic, J.; Van Mieghem, P. Epidemic Spreading in Networks—Variance of the Number of Infected Nodes; Technical Report Report 20090707; Quantum and Computer Engineering Department, Delft University of Technology: Delft, The Netherlands, 2009. [Google Scholar]
- Van Mieghem, P. Performance Analysis of Communications Networks and Systems; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Cator, E. Epidemics in networks with nodal self-infection and the epidemic threshold. Phys. Rev. E 2012, 86, 016116. [Google Scholar] [CrossRef]
- Li, C.; van de Bovenkamp, R.; Van Mieghem, P. Susceptible-infected-susceptible model: A comparison of N-intertwined and heterogeneous mean-field approximations. Phys. Rev. E 2012, 86, 026116. [Google Scholar] [CrossRef]
- Cator, E.; Van Mieghem, P. Second-order mean-field susceptible-infected-susceptible epidemic threshold. Phys. Rev. E 2012, 85, 056111. [Google Scholar] [CrossRef]
- Ward, J.A.; Tapper, A.; Simon, P.L.; Mann, R.P. Micro-scale foundation with error quantification for the approximation of dynamics on networks. Commun. Phys. 2022, 5, 71. [Google Scholar] [CrossRef]
- Ortega, E.; Machado, D.; Lage-Castellanos, A. Dynamics of epidemics from cavity master equations: Susceptible-infectious-susceptible models. Phys. Rev. E 2022, 105, 024308. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Lin, Z.; Yin, Q.; Tang, M.; Guan, S.; Boguñá, M. Non-Markovian epidemic spreading on temporal networks. Chaos Solitons Fractals 2023, 173, 113664. [Google Scholar] [CrossRef]
- Kuga, K.; Tanimoto, J. Effects of void nodes on epidemic spreads in networks. Sci. Rep. 2022, 12, 3957. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).