Similarity Model Test on Stress and Deformation of Freezing Pipe in Composite Strata during Active Freezing

Abstract

In order to prevent the problem of freezing pipe fracture in the process of artificial freezing construction, taking the main shaft freezing project of Shandong Yuncheng Mine as the background and based on the similarity theory, the similarity model test of freezing pipe in the composite stratum of the active freezing section is carried out. The test results show that the distribution of freezing temperature field in sand layer and clay layer is “W”-shape, and the temperature at the interface of outer ring pipe is slightly higher than that of the inner ring pipe. The change rate of freezing temperature can be divided into three stages: rapid decreasing section, slow decreasing section, and stable section. Compared with the clay layer, the sand layer has the shorter freezing closure time and the lower freezing average temperature. The frozen pipe is always in the state of vertical compression in the clay layer, while in the state of vertical compression first and then vertical tension in the sand layer. The maximum compressive strain in the clay layer is −305 με, which is equal to the vertical compressive stress of 64.1 MPa. The maximum tensile strain in the sand layer is 406 με, which is equivalent to the tensile stress of 85.2 MPa. The bending direction of different freezing pipes is different in the different soil layers. The maximum bending strain of the frozen pipe in the clay layer is 779 με, which is 2.6 times the vertical strain at the same location, corresponding to the bending stress of 163.4 MPa and reaching 0.69 times of the yield limit of frozen pipe, while the bending strain in the sand layer is very small. The vertical strain and bending strain of freezing pipes at the interface of soil layers are very small, but the bending strain is still dominant.

1. Introduction

In the field of geotechnical engineering, the artificial freezing method is a special construction method which adopts artificial refrigeration technology to reinforce unstable stratum and isolate groundwater [1,2]. Since the freezing method was first successfully applied in a Linxi wind shaft in Kailuan, China in 1956, it has quickly become the main construction method for building shaft in deep topsoil layer [3]. So far, more than 1100 vertical shafts have been built, of which more than 600 have been built since 2000. Up to now, as many as 50 vertical shafts has been built in ultra-thick topsoil (thickness more than 400 m), of which the thickness of the main shaft and air shaft in Wanfu Coal Mine is 754.96 m (world record) [4].

One of the key factors for the success of well construction by freezing method is to ensure the safety of the freezing pipe [5]. With the increasing depth of freezing sinking, the geological conditions become more complicated, which increases the probability of freezing pipe fracture [6]. China, the former Soviet Union, Poland, and other countries have all experienced freezing pipe fracture accidents, which caused salt water leakage and frozen wall melting, resulting in shaft flooding accidents and heavy losses, such as the auxiliary shaft of Xieqiao Coal Mine, the air shaft of Dongrong No.3 Coal Mine, the main shaft of Yuncheng Coal Mine, No.2 shaft of Zapoloz No.1 Coal Mine in the former Soviet Union, and No.L-1 shaft of Liubin Copper Mine in Poland [7]. Therefore, it is very necessary to study the stress and deformation law of freezing pipe under the complex geological conditions.

According to the field investigation of frozen pipe fracture in China, 90% of the freezing pipe fracture positions are located in the clay layer or soil layer interface [8]. Since 1980, many scholars have carried out in-depth research on the fracture mechanism of freezing pipe in the deep clay layer by different research methods; see

Table 1. Research status on the fracture mechanism of frozen pipes.

Author	Published Time	Soil Texture	Research Stage	Research Method	Main Results
Yang Weihao [7]	1999	Sand–clay interbedding	Active freezing section/ Excavation construction section	Theoretical analysis/ model test	In the active freezing stage, the maximum bending stress of the freezing pipe at the soil interface can reach 80 MPa. In the excavation stage, the stress of the freezing pipe is proportional to the displacement of the freezing wall.
Yu Chuhou [9]	1991	Sand/clay/ Sand-clay interbedding	Excavation construction section	Model test	The floor heave of the working face and the advance displacement of the frozen wall are the main reasons for the possible pipe break below the excavation face. The freezing pipe at the junction of the soil layer will bear additional bending moment and shear force, and it is easy to break the pipe.
Li Jinhua [10]	2011	Sand–clay interbedding	Active freezing section	Model test	Due to the accumulation of strain energy induced by bending, it is easy to cause the freezing pipe to break during the excavation stage.
Zhou Xiaomin [11]	1996	Single soil layer	Excavation construction section	Theoretical analysis	Near the excavation section, the main force of the freezing pipe is the bending moment, accompanied by the composite action of tension and shear force, and there are multiple stress peaks. The deformation value of unit height of shaft wall and the deformation stiffness of freezing pipe are the main factors affecting the force of freezing pipe.
Jing Laiwang [12]	2000	Single soil layer	Excavation construction section	Theoretical analysis	It is pointed out that the theoretical position where the freezing pipe is most likely to break is 0.7 times the depth of the pipe.
Li Gongzhou [13]	2001	Single soil layer	Excavation construction section	Theoretical analysis	The mechanical model of the elastic foundation beam for analyzing the frozen wall near the construction section is proposed, and the calculation expression of the deformation displacement of the frozen wall based on the elastic foundation beam is derived.
Huang Shaoshi [14]	2014	Sand–clay interbedding	Excavation construction section	Numerical simulation	The distribution law of stress and displacement of freezing pipe is obtained, and the fracture position of freezing pipe is located at the junction of sandy clay and sandy soil.
Du Meng [15]	2014	Sand–clay interbedding	Excavation construction section	Numerical simulation	In the process of excavation and lining construction, the height of excavation and lining section is too high, and the exposure time of shaft wall is too long, which causes large displacement of shaft wall and floor heave of working face, which is the main reason for the fracture of freezing pipe.

for details.

Cui Guangxin [16] pointed out that the stress deformation process of freezing pipe can be roughly divided into active freezing section and excavation construction section. At the junction of sand layer and clay layer in active freezing section, there will be the large bending stress as high as 60~80 MPa. Although it cannot destroy the freezing pipe, it will also have a great impact on the safety of the freezing pipe. Most of the previous studies are about the stress and deformation law of the freezing pipe in the single clay layer during the excavation construction stage, while the research on the stress and deformation law of the freezing pipe in the composite stratum of the active freezing section is rare. Therefore, it is urgent to carry out simulation test research on stress and deformation of freezing pipe in the composite stratum of active frozen section to obtain the law of stress and deformation of freezing pipe and to predict the dangerous areas, which provides important guidance for preventing freezing pipe from breaking.

2. Similarity Model Test

Due to the limitation of laboratory equipment and environment, it is impossible to carry out the same test according to the engineering prototype. However, in order to complete the test and ensure the reliability of the test results, the test must follow the similar criteria.

2.1. Test Modeling Based on Similarity Criteria

2.1.1. Similarity Criteria

Based on the similarity theory, the local frozen pipe in the typical soil layer is selected for freezing simulation test, and the following similarity criteria are listed by combining the relevant mathematical models of temperature field, moisture field, and stress field during the freezing process.

(1)

Temperature field criterion

According to the basic equation of transient heat conduction, the heat conduction equation suitable for artificial freezing heat transfer is listed:

$$\frac{\partial t_n}{\partial \tau }=a_n\left(\frac{{\partial }^2{t}_n}{\partial r^2}+\frac{1}{r}\frac{\partial t_n}{\partial r}\right)$$

(1)

When $\tau >0$, $0<r<\infty$, the heat balance equation at the frozen front is as follows:

$${\lambda }_2\frac{\partial t_2}{\partial r}\left|r=\zeta -{\lambda }_1\frac{\partial t_1}{\partial r}\right|r=\zeta =Q\frac{d\zeta }{d\tau }$$

(2)

The initial conditions and boundary conditions are

$$t=0, t\left(r\right)=t_0$$

(3)

$$t>0, t\left(r=0\right)=t_y, t\left(\infty \right)=t_0, t\left(r=\zeta \right)=t_d$$

(4)

where $r$ is the radial distance from each point in the soil plane to the center of the freezing pipe; $t_n$ is the temperature at the position $r$, where $n=1$ represents unfrozen soil and $n=2$ represents frozen soil; $\tau$ is the freezing time; $a_n$ is the thermal conductivity coefficient; ${\lambda }_1$, ${\lambda }_2$ are the thermal conductivity of unfrozen soil and frozen soil, respectively; $\zeta$ is the boundary position coordinate of the frozen wall, which is the expansion radius of the frozen wall; $Q$ is the latent heat release during the freezing process of unit soil; $t_0$, $t_d$, $t_y$ are the initial soil temperature, freezing temperature, and cold source temperature (brine temperature), respectively.

The similarity criterion of the temperature field is obtained by analogical derivation of Equations (1) and (2):

$$\phi \left(K_0,F_0,\theta ,R\right)=0$$

(5)

where $K_0$ is Kosovich criterion; $K_0=Q/Ct$, $Q$ is the latent heat of soil mass; $C$ is the soil specific heat; $t$ is the temperature; $F_0$ is Fourier criterion; $F_0=a\tau /r^2$; $a$ is the soil thermal conductivity; $r$ is the radial distance from the freezing front to the center of the freezing pipe; $\theta$ is the temperature criterion; $R$ is the geometric criterion. Since the geotechnical material used in the test is the same as the prototype,$C_c$ and $C_a$ are both 1, and $C_{\tau }=C_l^2$ is deduced. As long as the test meets the requirements that the geometry of the frozen wall, the temperature of the cold source, the initial temperature of the soil, and the freezing time of the model are similar to those of the prototype, the similar simulation of the temperature field can be realized.

(2)

Water field criterion

Based on the water migration law and seepage equation of soil during freezing process, the suitable water field equation is listed:

$$\frac{\partial h}{\partial \tau }=b\left(\frac{{\partial }^{2}h}{\partial r^2}+\frac{1}{r}\frac{\partial h}{\partial r}\right)$$

(6)

The initial conditions and boundary conditions are

$$t=0, h=h_0$$

(7)

$$\tau >0, H\left(h=\infty \right)=h_0, h\left(h=\zeta \right)=0$$

(8)

where $h$ is the soil moisture content, and $b$ is the soil moisture conductivity coefficient.

After similarity derivation, the similarity criterion of water field is as follows:

$$\phi \left(K_0,W,R\right)=0$$

(9)

where $W$ is the humidity criterion. Because the moisture migration process and freezing process are similar in the mathematical model, both contain Fourier criterion, so under the condition of geometric similarity, as long as the temperature field is similar, the moisture field can be “self-simulated” to achieve similarity.

(3)

Stress field criterion

In the freezing process, the stress of unfrozen soil and frozen soil is quite complex, and it is very difficult to realize accurate simulation. Therefore, on the premise of ensuring the test accuracy, the actual stress field is reasonably simplified, and the relevant equations of the model stress field are obtained as follows:

$${\sigma }_r-{\sigma }_{\theta }+r\frac{d\sigma }{dr}=0$$

(10)

$${\epsilon }_r=\frac{1}{E}\left({\sigma }_r-\mu {\sigma }_{\theta }\right)=\frac{du}{dr}$$

(11)

$${\epsilon }_{\theta }=\frac{1}{E}\left({\sigma }_{\theta }-\mu {\sigma }_r\right)=\frac{u}{r}$$

(12)

$$P=\gamma HA$$

(13)

The boundary conditions are

$${\left({\sigma }_r\right)}_{r=a}=\gamma HA,{\left({\sigma }_r\right)}_{r=b}=\gamma HA,{\left({\sigma }_z\right)}_{z=H}=\gamma H$$

(14)

$${\left({\tau }_{r\theta }\right)}_{r=a}=0,{\left({\tau }_{r\theta }\right)}_{r=b}=0,{\left({\tau }_{rz}\right)}_{z=H}=0$$

(15)

where $E$ is the soil elastic modulus; ${\epsilon }_r$ and ${\epsilon }_{\theta }$ are the radial strain and tangential strain of soil, respectively; $u$ is the radial deformation displacement of soil; $\mu$ is Poisson’s ratio of soil; $\gamma$ is the bulk density of soil; $H$ is the burial depth of soil; $A$ is the lateral pressure coefficient of soil. $a$ and $b$ are the inner radius and outer radius of frozen wall.

From Equations (10)–(13), the mechanical similarity criteria $\sigma /E$, $P/\gamma H$, and the geometric similarity criteria ${\epsilon }_r$, ${\epsilon }_r$, and $u/r$ can be derived to simulate the actual stress state of deep soil. By using the same material and load as the prototype, the stress environment similar to the field condition can be provided for the model test.

2.1.2. Model Parameter

The model test is based on the main shaft freezing project of Yuncheng Mine. The freezing section of the main shaft includes 534.2 m deep alluvium from top to bottom, which is composed of fine sand layer, clay layer, and sandy clay layer. Because the frozen pipe fracture accident has occurred in the prototype project below 400 m depth, the simulation depth is 400 m. The test material is taken from the deep soil at the prototype project site, and the soil is restrained laterally with axial compression of 8 MPa applied. The test model parameters are shown in

Table 2. Freezing parameters of prototype and model.

	Outer Diameter of Freezing Pipe /mm	Outer Tube		Inner Tube		Brine Temperature /°C	Axial Compression /MPa
		Diameter /m	Hole Spacing /m	Diameter /m	Hole Spacing /m
prototype	Φ159	17.69	1.59	8.95	1.59	−20	8
Model	Φ8	0.89	0.08	0.45	0.08	−20	8

. From Table 2, the geometric scale $C_l$ of the model test is 1:19.88. According to the similarity criterion, the time scale $C_{\tau }$ is 1:395.22, and the temperature scale $C_t$ and the stress scale $C_{\sigma }$ are both 1:1.

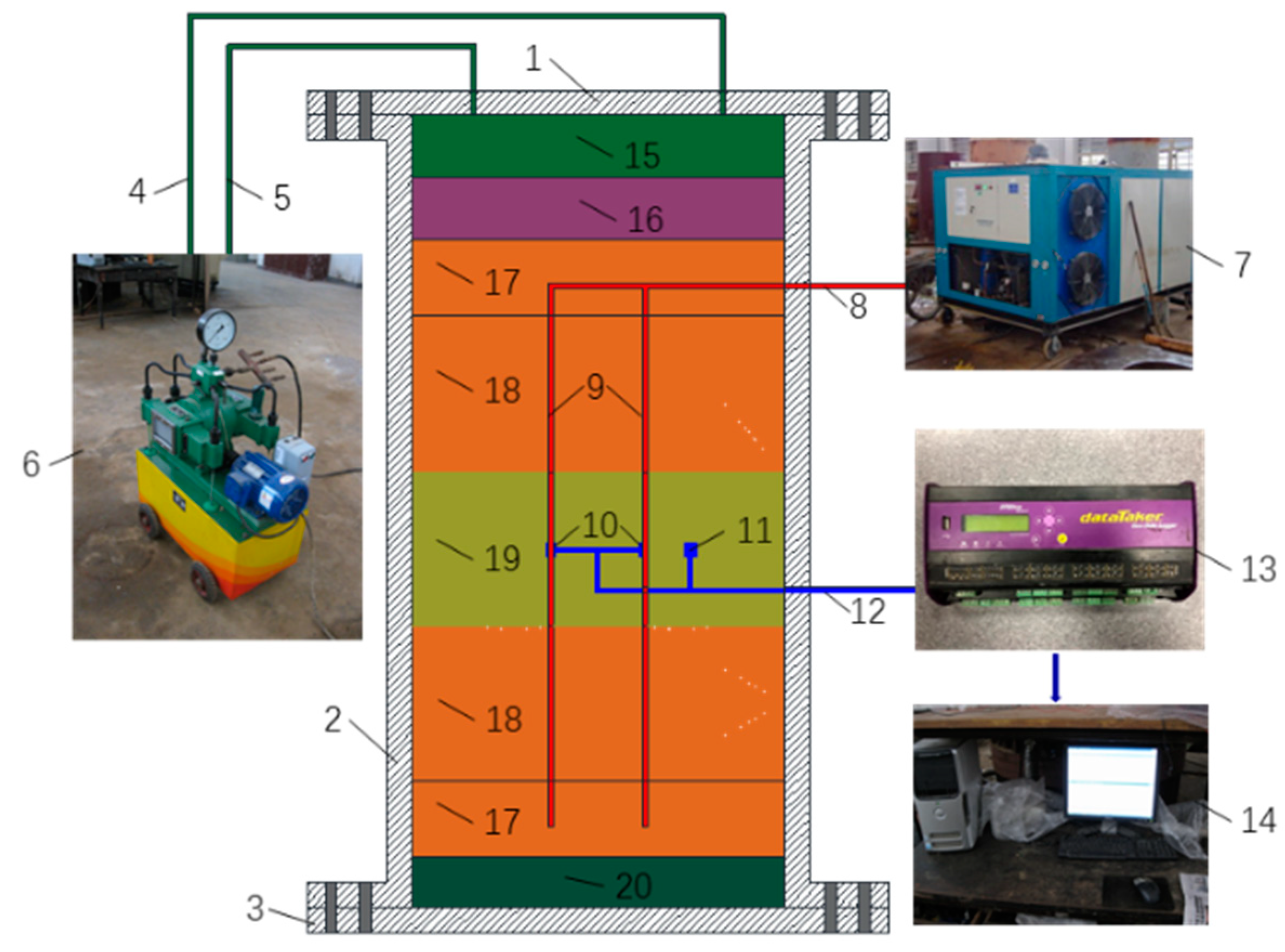
2.2. Test Device

The test device consists of the model test bench, the loading system, the freezing system, and the data testing system (Figure 1).

The model test bed is the large-scale shaft simulation test bed developed by the State Key Laboratory of Deep Geotechnical Mechanics and Underground Engineering (Figure 2). The effective test space of the test bench is Φ1.2 × 2.4 m, which can realize axial symmetry pressure, and the maximum loading pressure is 12 MPa.

The loading system is composed of the high pressure test pump, the oil pipeline, the asphalt layer, and the pressure gauge. The freezing system is composed of the refrigeration station, the freezing pipeline, and the model freezing pipe. The data testing system is composed of the sensors, the data acquisition instruments, and the computers.

2.3. Test Scheme

The test soil is sand and clay. The density of clay is 1870 kg/m³; the water content is 26.5%; the density of sand is 2080 kg/m³; and the water content is 18.2%. The temperature of frozen brine is −20 °C. The applied pressure load is 8 MPa. The order of filling soil is sand, clay, and sand from bottom to top, and the thickness of each layer is 0.5 m. T-type thermocouple and strain gauge are used to monitor soil temperature and frozen pipe strain, respectively. T-type thermocouple and strain gauge are arranged in three layers, which are arranged in the middle of sand layer, the interface of soil layers, and the middle of clay layer, respectively. In each layer, the strain gauges are arranged on the D1, D2, D3, and D4 freezing pipes, respectively, and each of them is pasted with 5 strain gauges, in which 1#, 2#, 3#, and 4# are vertical strain gauges, and 5# is transverse strain gauges, in order to measure the transverse strain of 1# caused by the Poisson effect. Ten T-type thermocouples are arranged outward along the shaft center, which are T1, T2, … T10 in turn. See Figure 3 and Figure 4 for details.

2.4. Test Process

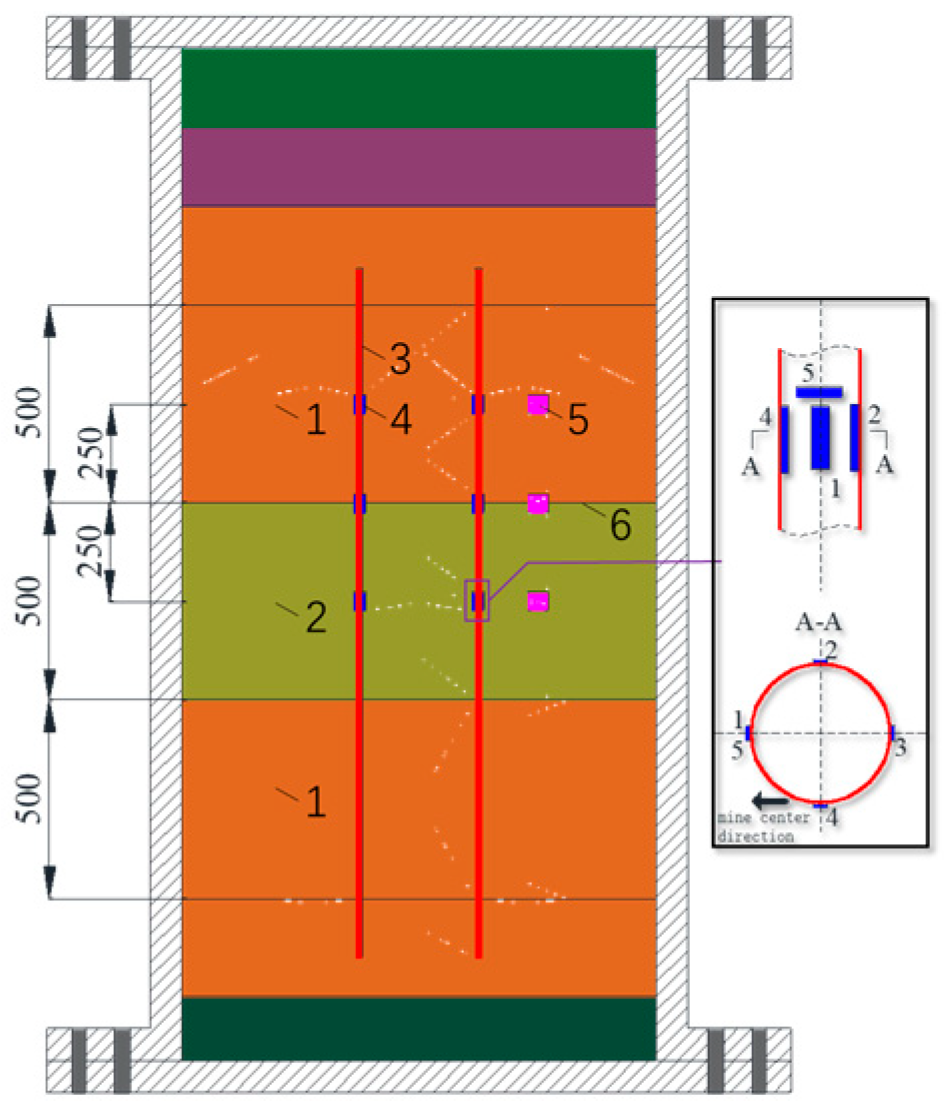
(1)

The 60° wedge was selected as the test area in the inner space of the test bench, and the non-test area was poured with concrete and equipped with insulation asbestos board to form an adiabatic rigid boundary, as shown in Figure 2b.

(2)

The soil sample was configured according to the designed moisture content and sealed for 24 h to make the moisture in the soil evenly distributed.

(3)

The pre-buried steel pipes were installed; the soils were filled in layers until the tamp to the design thickness; and the earth pressure box (showing the size of the consolidation pressure) and T-type thermocouple were installed.

(4)

The asphalt layer was cast; the top plate was installed and sealed; and the soil layer was graded pressurized consolidation.

(5)

After consolidation, the embedded steel pipes were replaced by the freezing pipe attached with strain gauge, and the asphalt layer was poured again, and the soil layer was applied the specific pressure.

(6)

Freezing was performed under the pressure holding state, and the freezing was stopped when the test target was reached.

3. Test Result and Discussion

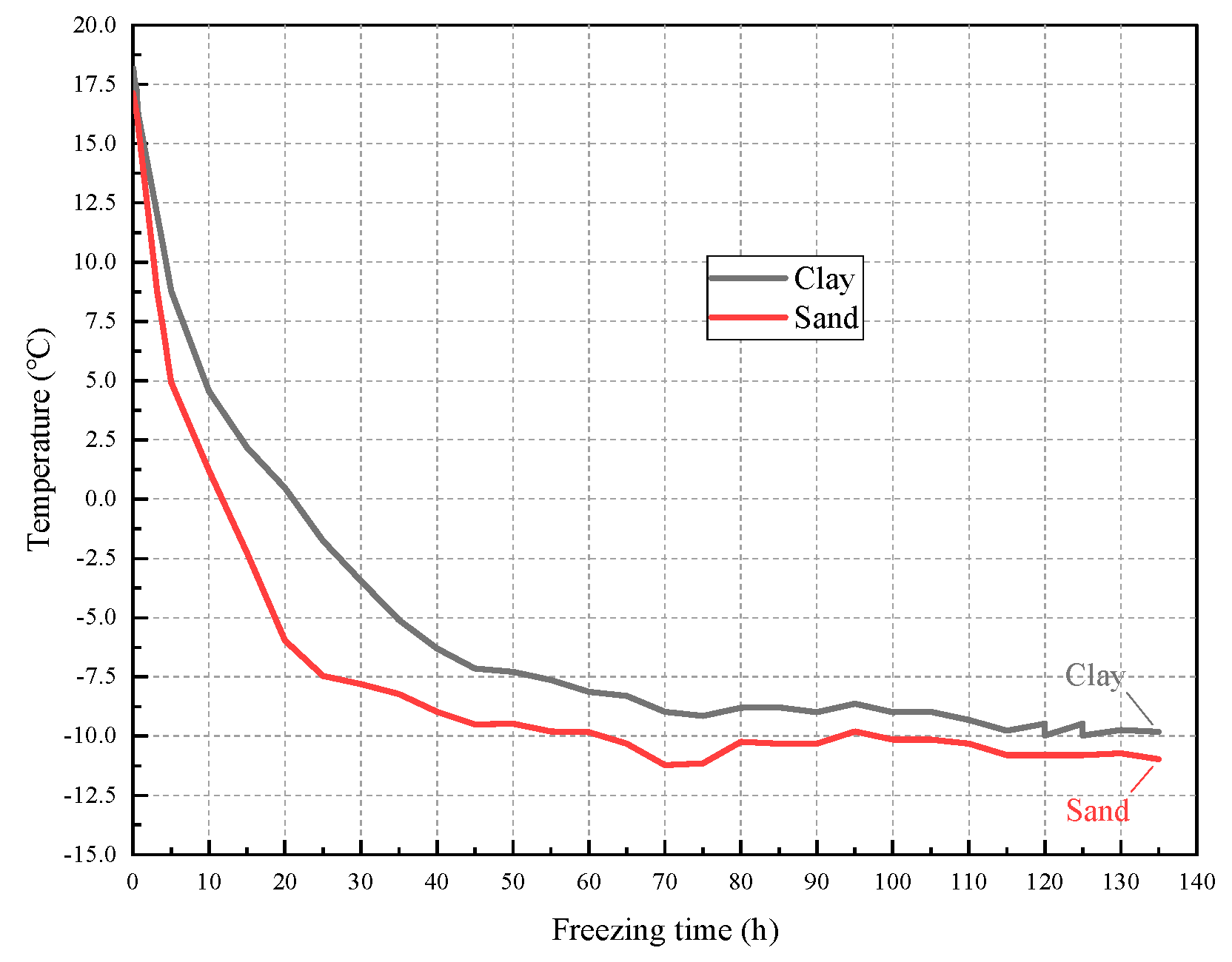
3.1. Variation Law of Freezing Temperature Field

(1) Brine temperature: According to Figure 5, the change curve of brine temperature to the circuit can be roughly divided into three stages: ① Rapid cooling section. After freezing for 9.6 h, the temperature of desalted brine decreased rapidly to −18 °C, and the average cooling rate reaches 1.88 °C/h. At the initial stage of freezing, the temperature difference of de-loop brine is small, and it rapidly increases to 7.5 °C with the increase in freezing time. ② Slow cooling section. After freezing for 18.2 h, the temperature of the desalted brine reaches the freezing design temperature of −20.2 °C. This process lasts for about 8.6 h, and the average cooling rate is 0.26 °C/d. The temperature difference of de-loop brine decreases gradually. ③ Stable section. The temperature of the desalted brine continuously fluctuates at −20 °C in this stage, with the fluctuation range of ±1.5 °C. The temperature difference of de-loop brine is gradually stable, indicating that the frozen wall is in good condition.

(2) Frozen temperature field: It can be seen from Figure 6, Figure 7 and Figure 8 that the temperature field of the sand layer and clay layer changes in a similar way. The temperature rises from the freezing pipe to both sides; the curve shape of temperature field is ‘W’; and the temperature at the interface of the outer ring pipe is slightly higher than that of the inner ring pipe.

The change rate of the freezing temperature field can also be divided into three stages: fast decreasing stage, slow decreasing stage, and stable stage. At the initial stage of freezing, the temperature drop rate of the soil around the freezing pipe is large due to the large temperature difference between the freezing brine and the soil around the freezing pipe. The farther away from the freezing pipe, the less cold the soil absorbs from the freezing pipe. With the increase in freezing time, the temperature difference between the freezing brine and the frozen soil around the freezing pipe continues to decrease, and the temperature change rate also gradually decreases until it becomes stable. However, in the whole process, the temperature decreasing rate of sand decreases faster than that of clay.

(3) It can be seen from Figure 6, Figure 7 and Figure 8 that the closure time and average temperature of the frozen wall in the sand layer are 14.8 h and −10.3 °C, while those in the clay layer are 24.5 h and −9.0 °C. It is mainly because the clay contains more bound water, while the sand contains less. In addition, the freezing of bound water requires more cooling than free water, and the specific heat of clay particle skeleton is larger than that of sand. Therefore, the cold absorbed by clay freezing is more than that of sand, which makes the freezing efficiency of clay less than that of sandy soil, resulting in the closure time and average temperature of frozen wall in sand layer being lower than those in clay layer.

3.2. Variation Law of Freezing Pipe Strain

3.2.1. Strain Gauge Data Processing Method

The stress deformation problem of freezing pipe can be simplified as the plane strain problem. On any cross section of the freezing pipe, the total strain at any point can be simplified as pure bending strain in the X direction, pure bending strain in the Y direction, and pure tension and compression strain in the Z direction, as shown in Figure 9. Furthermore, 1#, 2#, 3#, and 4# are vertical strain gages; 1# is near the shaft center, and 5# is transverse strain gauge. Their measured values are represented by ${\epsilon }_n$ (n = 1, 2, 3, 4, 5), as shown in Figure 9. The temperature strain in all directions of the freezing pipe is the same.

List the following formulas:

$${\epsilon }_1={\epsilon }_N+{\epsilon }_{mx}+{\epsilon }_T$$

(16)

$${\epsilon }_3={\epsilon }_N-{\epsilon }_{mx}+{\epsilon }_T$$

(17)

$${\epsilon }_2={\epsilon }_N+{\epsilon }_{my}+{\epsilon }_T$$

(18)

$${\epsilon }_4={\epsilon }_N-{\epsilon }_{my}+{\epsilon }_T$$

(19)

$${\epsilon }_5=-\mu \left({\epsilon }_N+{\epsilon }_{mx}\right)+{\epsilon }_T$$

(20)

where ${\epsilon }_N$ is the vertical pure tensile and compressive strain;${\epsilon }_{mx}$ and ${\epsilon }_{my}$ are the pure bending strain in the X direction and the pure bending strain in the Y direction, respectively; ${\epsilon }_T$ is the temperature strain.

According to Equations (14)–(18), it can be concluded that

$${\epsilon }_{mx}=\left({\epsilon }_1-{\epsilon }_3\right)/2$$

(21)

$${\epsilon }_{my}=\left({\epsilon }_2-{\epsilon }_4\right)/2$$

(22)

$${\epsilon }_{N=}\left({\epsilon }_1-{\epsilon }_5\right)/\left(1+\mu \right)-\left({\epsilon }_1-{\epsilon }_3\right)$$

(23)

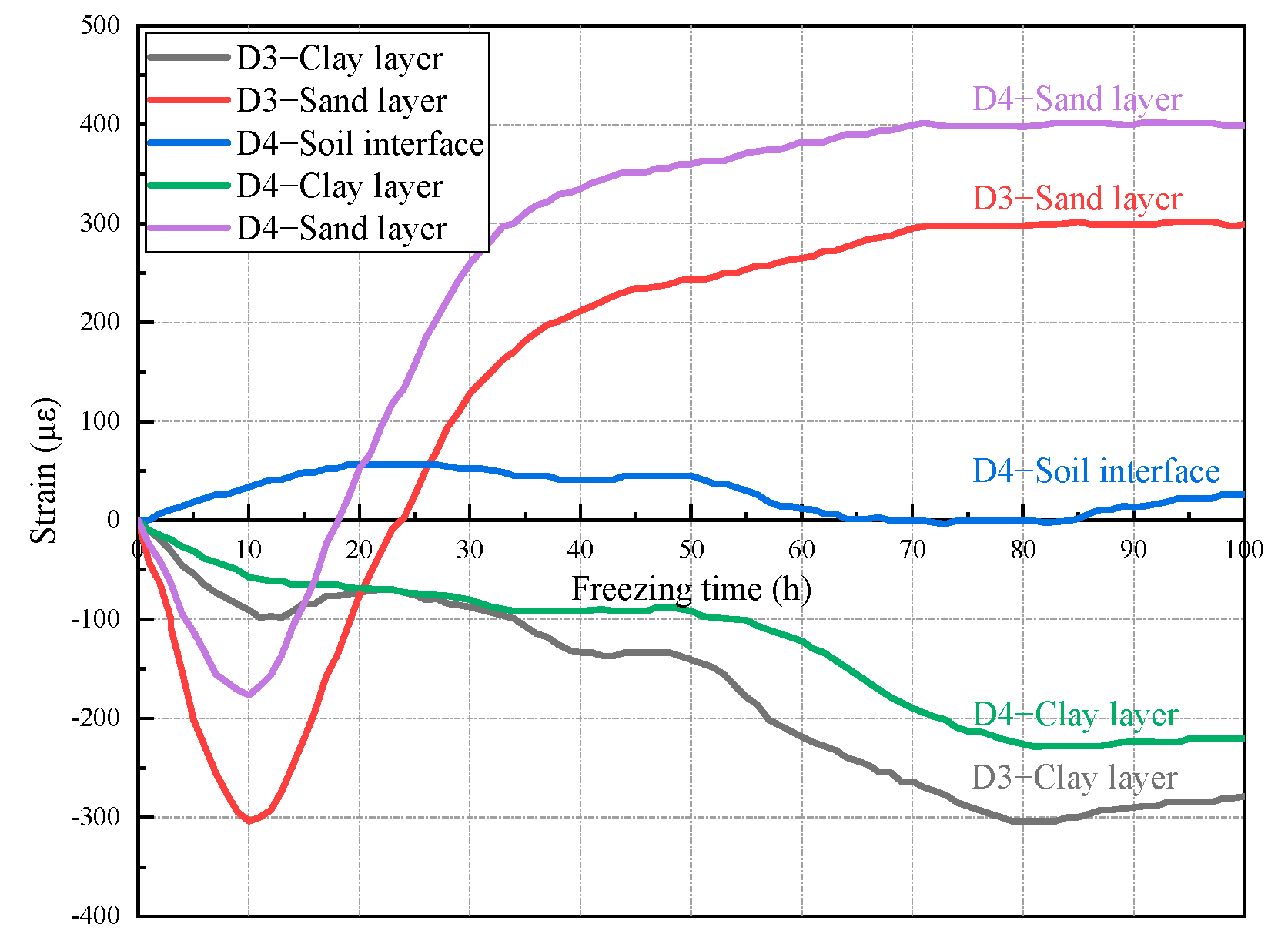
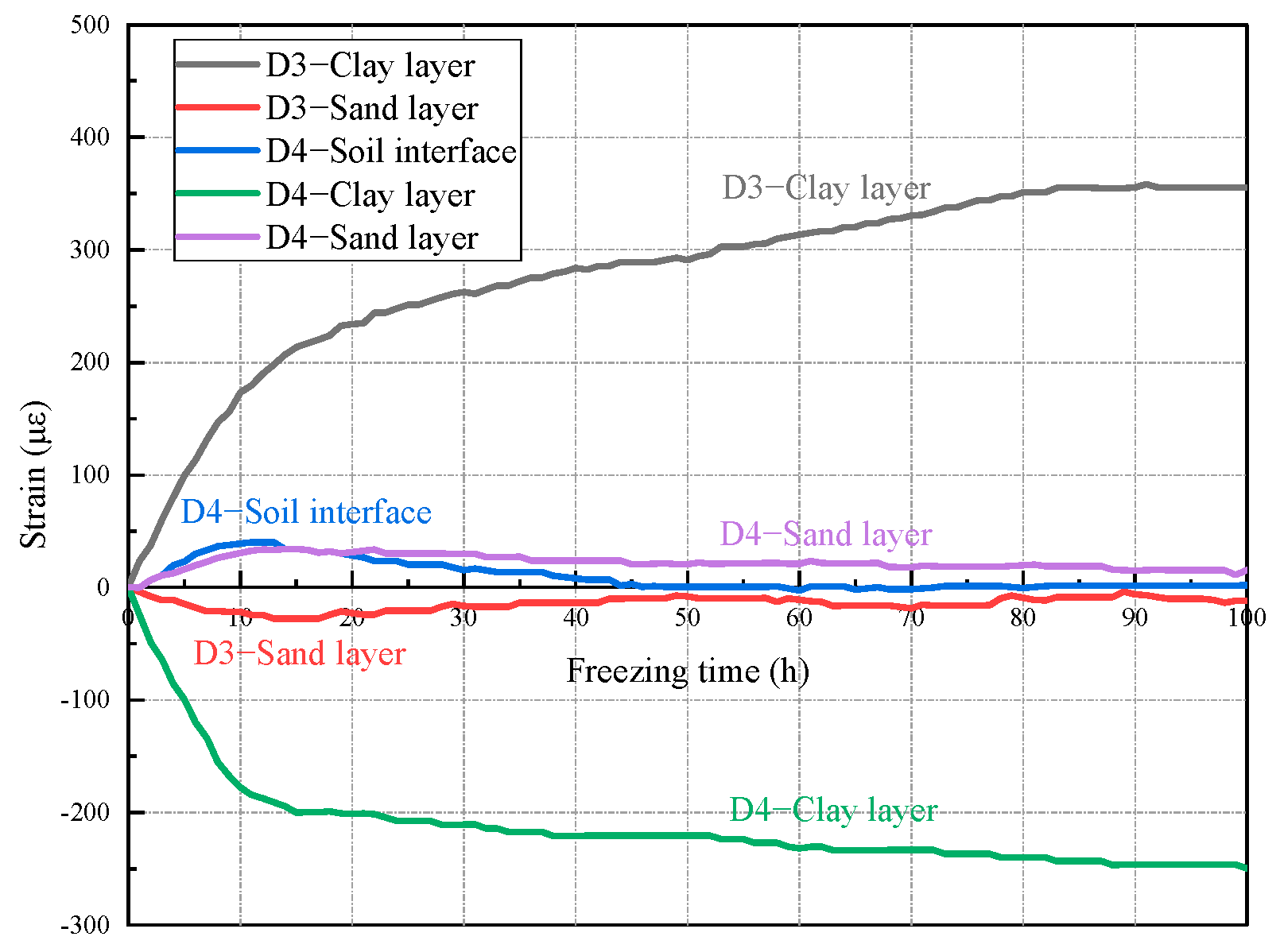
3.2.2. Analysis of Variation Law of Freezing Pipe Strain

Due to the large vertical displacement of soil in the process of compression and consolidation, most of the strain gauge leads are broken, and only part of the test data of the strain gauge are obtained. Based on Equations (19)–(21), to process the strain gauge test data, the change curves of ${\epsilon }_N$, ${\epsilon }_{mx}$, and ${\epsilon }_{my}$ of each test horizon in the different soil layers with respect to the freezing time $t$ are obtained, as shown in Figure 7, Figure 8 and Figure 9.

(1)

Pure vertical tension–compression strain ${\epsilon }_N$

It can be seen from the Figure 10 that shows the ${\epsilon }_N-t$ curve obtained from the experiment:

① The values of ${\epsilon }_N$ at the corresponding positions of the D3 and D4 freezing pipes are different, but the variation rules are similar. The different ${\epsilon }_N$ values may be due to the different consolidation degree of the soil around the two freezing pipes, resulting in different frost heave effects of the soil during the freezing process.

② The D3 and D4 freezing pipes are always under the pressure in the clay layer. During the period of 0~100 h, ${\epsilon }_N$ decreases continuously, and the ${\epsilon }_N$ of the D3 freezing pipe is the smallest, which is −305 με, corresponding to the vertical compressive stress of 64.1 MPa. There are two possible reasons for this phenomenon: first, because the development speed and stiffness of the clay layer frozen wall are smaller than those of the upper and lower sand layers frozen wall. In addition, not only is the freezing temperature of the unfrozen water in the clay layer lower than that of the sand layer, but the clay layer is also located in the middle of the two sand layers. Therefore, the frozen wall of the upper and lower sand layers is rapidly formed during the freezing process, while the frozen wall of the clay layer has not yet formed, causing the frozen wall of the upper and lower sand layers to continuously squeeze the clay layer in the vertical direction so that the vertical frost heave of the clay layer is limited, resulting in the continuous compression of the frozen pipe under the action of the clay confining force. Second, at the procedure of the compression and consolidation, due to the different consolidation characteristics of the sand and clay, the vertical compression displacement of clay layer is much larger than that of sand layer, resulting in the thickness of the clay layer after consolidation being less than that of the sand layer. As a result, the vertical frost heaving force of the clay layer is less than that of the sand layer, which results in the frozen wall of the clay layer causing the vertical compression by holding the frozen pipe.

③ The D3 and D4 freezing pipes are in the state of compression first and then tension in the sand layer. During the period of 0~10 h, ${\epsilon }_N$ decreases gradually, and the ${\epsilon }_N$ of D3 freezing pipe is the smallest, and that is −302 με, which is equivalent to the vertical compressive stress of 63.4 MPa. During the period of 10~90 h, the frozen pipe begins to change from compressive strain to tensile strain, and ${\epsilon }_N$ increases gradually. D3 and D4 freezing pipes transformed into pure tensile strain at 18 h and 24 h, respectively, and reached the maximum at 90 h. The ${\epsilon }_N$ of D4 freezing pipe is the largest, which is 406 με, corresponding to the vertical tensile stress of 85.2 MPa. During the period of 90~120 h, ${\epsilon }_N$ decreases slowly. It is mainly because in the early stage of freezing, because the temperature of the freezing pipe drops rapidly, the temperature stress generated by itself is greater than the vertical friction provided to the freezing pipe by the frost heave of the soil, causing the shrinkage strain of the freezing pipe. As the freezing brine temperature continues to decrease, the freezing wall thickness also gradually increases, which makes the bonding force between the frozen soil and the frozen pipe greater than the freezing pipe’s own temperature stress, causing the frozen soil to hold the frozen pipe and begin to expand, resulting in the frozen pipe producing tensile strain. In the later stage of freezing, because the vertical volume shrinkage of frozen soil is greater than that of frozen pipe, the frozen soil will hold the frozen pipe and shrink together, which makes the frozen pipe change from tensile strain to compressive strain, resulting in the corresponding decrease in the tensile strain of the frozen pipe.

④ The D4 freezing pipe is basically in the tensile state at the soil interface. During the whole freezing process, ${\epsilon }_N$ increases slightly at first and then decreases gradually, but it is basically very small. It may be because the D4 frozen pipe is mainly tensile strain in the sand layer and compressive strain in the clay layer, so these two kinds of soil layers will form a neutral strain surface at the interface of soil layer. As a result, the vertical tension and compression strain of the frozen pipe is not prominent at the interface of the soil layer.

(2)

Pure bending strain ${\epsilon }_m$

Figure 11 and Figure 12 are the results ${\epsilon }_{mx}-t$ and ${\epsilon }_{my}-t$ curves from the test. From Figure 9, it can be seen that the positive direction of the X-axis is the direction away from the well center, and the positive direction of the Y-axis is the direction of counterclockwise rotation around the well center. Therefore, the “+” sign in ${\epsilon }_{mx}-t$ and ${\epsilon }_{my}-t$ represents the direction away from the shaft center and counterclockwise around the shaft center, while the “−” sign is the opposite. “+” and “−” only represent the bending direction, independent of the numerical value.

It can be seen from the Figure 11 and Figure 12 that:

① In the clay layer, the ${\epsilon }_{mx}$ of D3 and D4 freezing pipes increases with the increase in freezing time and tends to be stable, but the bending direction is different. The D3 freezing pipe bends away from the shaft center, while the D4 freezing pipe bends near the shaft center. The maximum ${\epsilon }_{mx}$ of D3 freezing pipe is 351 με, which corresponds to the bending stress of 73.7 MPa. The maximum ${\epsilon }_{mx}$ of D4 freezing pipe is 249 με, which is equivalent to the bending stress of 52.3 MPa. In the sand layer, the ${\epsilon }_{mx}$ of D3 and D4 freezing pipes first increases slightly and then decreases continuously, which is generally small, and the maximum of ${\epsilon }_{mx}$ is only 47 με. The bending direction of the freezing pipe is exactly opposite to the respective bending direction in the clay layer.

② In the clay layer, the ${\epsilon }_{my}$ of the D3 and D4 freezing pipes increases with the increase in the freezing time and finally stabilizes. The bending direction is also the same, and they all bend in the direction of counterclockwise rotation around the shaft center. Among them, the ${\epsilon }_{my}$ of D3 freezing pipe is the largest, reaching 696 με, which is equivalent to the bending stress of 146.2 MPa. In the sand layer, the variation trend and the ${\epsilon }_{my}$ bending direction of D3 and D4 freezing pipes are the same, but ${\epsilon }_{my}$ is very small in both.

③ At the interface of soil layers, the ${\epsilon }_{mx}$ of the D4 freezing pipe increases firstly and then decreases, while the ${\epsilon }_{my}$ is just the opposite. The bending direction of each is always the same throughout the freezing process. The maximum value of ${\epsilon }_{mx}$ is 51 με, which is equivalent to the bending stress of 10.8 MPa, bending away from the shaft center. The ${\epsilon }_{my}$ has a maximum value of 103 με, corresponding to the bending stress of 21.7 MPa, and bends in the direction of counterclockwise rotation around the well center.

④ In the freezing process, the bending stress in the freezing pipe is mainly affected by the frost heaving development of the frozen wall in the horizontal direction. Before the freezing wall intersects, the soil around the freezing pipe quickly forms the frozen soil columns at the initial stage of freezing, resulting in frost heave, which causes mutual extrusion between frozen soil columns; after the frozen wall intersects, the frozen wall develops along the radial direction, and the pore water pressure on the inside of the frozen wall is higher than that on the outside of the frozen wall. In the process of soil frost heaving, the resistance in the shaft center direction is greater than that outside the shaft direction. In addition, the temperature of the freezing pipe towards the center of the shaft is different from that of the other side, which results in the bending and deformation of the freezing pipe. In addition, the frost heaviness of clay is stronger than that of sand. However, the vertical deformation of clay layer is limited by the frozen wall of the sand layer and can only expand the horizontal direction. Finally, due to the different development rates of the frozen columns in the upper and lower soil layers, the freezing pipe will bend at the soil interface to a certain extent.

4. Conclusions

(1)

The distribution of the freezing temperature field in different soil layers is similar, but the change rate of the freezing temperature field, the cycle time of freezing wall, and the average temperature are related to soil properties.

(2)

In the later stage of freezing, the freezing pipes in different soil layers are vertically subjected to pure tensile stress or pure compressive stress. However, in the initial stage of freezing, not only is the freezing pipe in the sandy soil layer subjected to the temporary vertical compression, but the freezing pipe in the clay layer is also always in the vertical compression state, which is different from the previous research results on the stress and deformation law of the freezing pipe in the freezing process of the single soil layer.

(3)

During the freezing process, the bending direction of different freezing pipes in different soil layers is not the same. The maximum bending strain of the frozen pipe in the clay layer can reach 779 με, which is 2.6 times the vertical strain at the same position, equivalent to 163.4 MPa, while the bending stress in the sand layer is relatively small. The accumulation of strain energy induced by bending can easily lead to the fracture of the frozen pipe in the process of digging.

(4)

The total strain of the freezing pipe is obtained by superimposing the pure vertical strain and the pure bending strain of the freezing pipe. It is concluded that the absolute value of the total strain of the freezing pipe in the clay layer is greater than that in the sand layer. By converting the strain into stress, it can be seen that the maximum tensile stress of the freezing pipe in the clay layer is 175.5 MPa, which can reach 0.75 times the yield limit of the freezing pipe, and will pose a certain degree of threat to the safety of the freezing pipe. At this time, the effective measures can be taken to improve the mechanical performance of the frozen pipe to increase the deformation capacity of the joint of the frozen pipe and reduce the strain energy stored by the frozen pipe, which will reduce the failure rate of the frozen pipe in the digging stage.

(5)

The model test results show that the freezing pipe in the composite stratum is in the spiral torsion shape. However, because the real stratum conditions are much more complex and changeable than the model tests, the real existing forms of freezing pipes in the actual stratum will be more diversified.

(6)

As the test load is only 8 MPa, the test results obtained are single and not three-dimensional enough. In the future, the model tests with different consolidation pressures and different freezing temperatures will be carried out, corresponding numerical simulation verification will be carried out for each group of model tests, and more innovative conclusions will be drawn. According to the innovative conclusions obtained, combined with the specific freezing project objects, the freezing problems and characteristics that the freezing project may face are proposed.