A New Approach to Nonlinear State Observation for Affine Control Dynamical Systems
Abstract
1. Introduction
1.1. Related Works
1.2. Paper Contribution
- A new class of nonlinear function proposed asis used instead of the function. This nonlinear function has a nonlinear characteristic and is smooth;
- Moreover, the curve shape, range, and central location of this function can be separately adjusted to adapt to the practical application of different situations and requirements;
- The saturation-like properties are used to suggest a novel asymptotically convergent extended state observer. The proposed NHOESO can enhance the observation capability and asymptotically reduce the estimation error when compared to traditional extended state observers;
- Additionally, a precise Lyapunov analysis of the NHOESO and the associated closed-loop system was performed. The NHOESO-based controller can sustain zero tracking error and is asymptotically stable.
1.3. Paper Organization
2. Problem Statement
3. Linear Extended State Observer (LESO)
4. The Proposed Nonlinear Higher-Order Extended State Observer (NHOESO)
4.1. The NHOESO Definition and Convergence Theorem
4.2. Justification for Adding an Additional Augmented State
4.3. Mismatched Disturbances
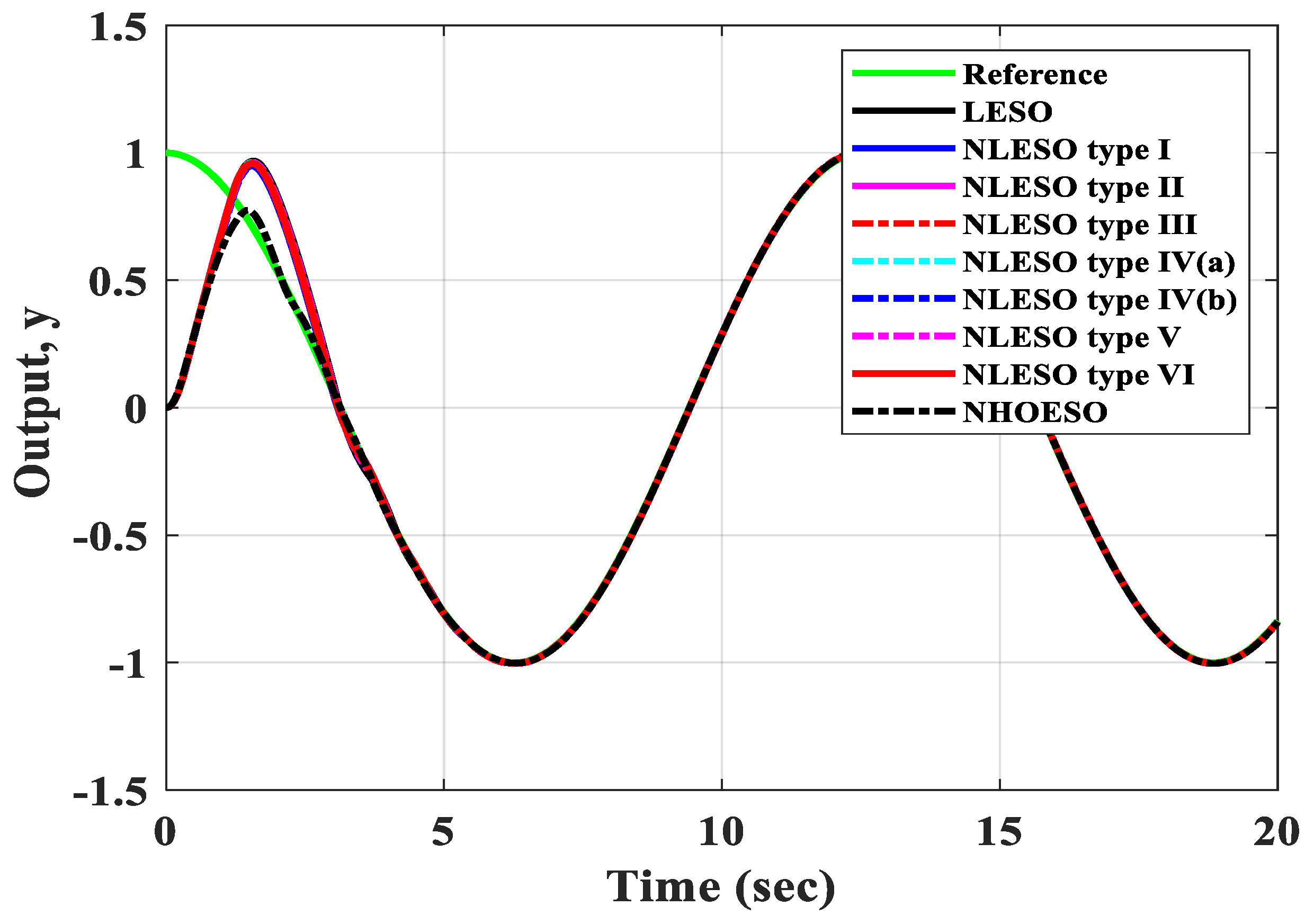
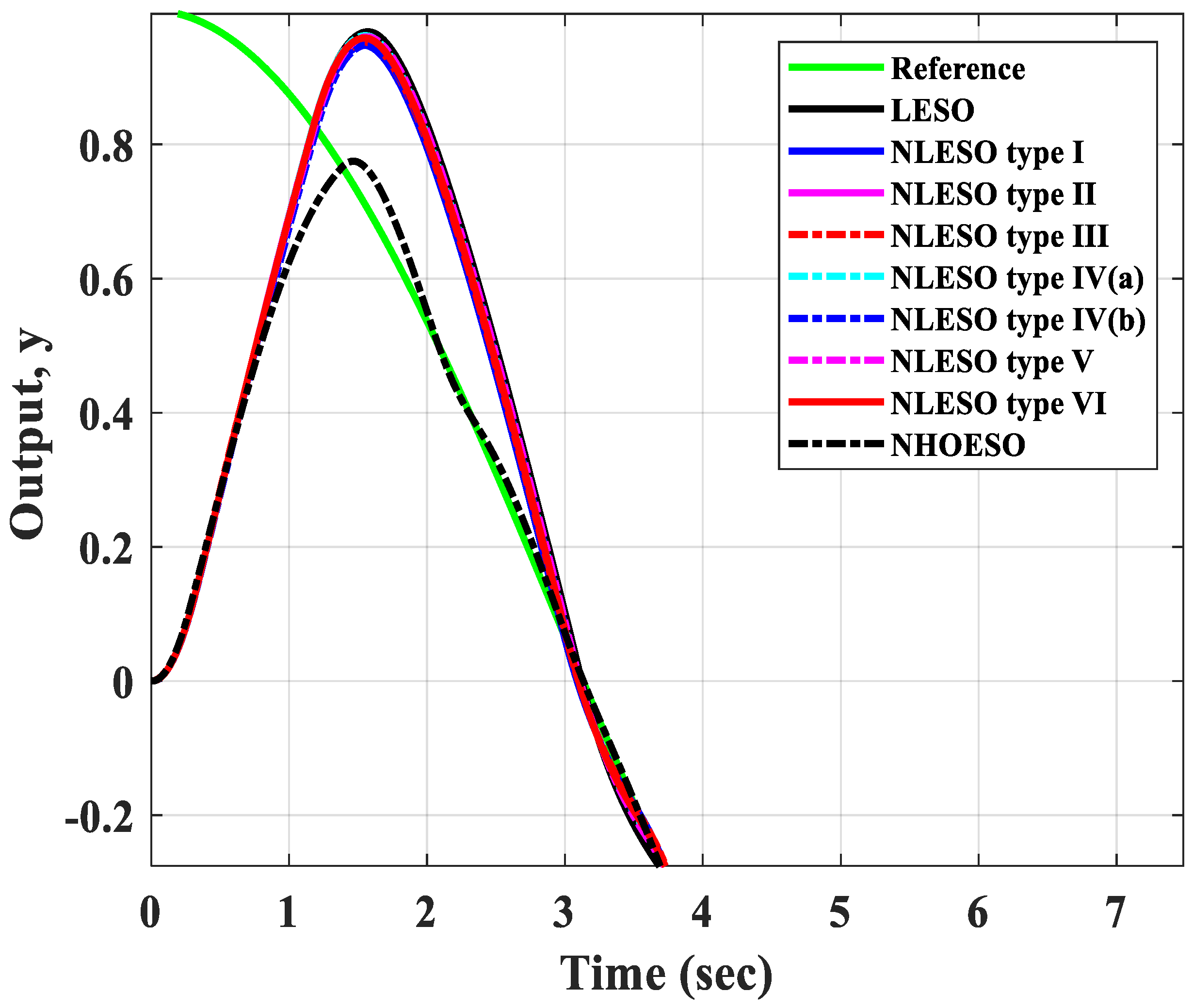
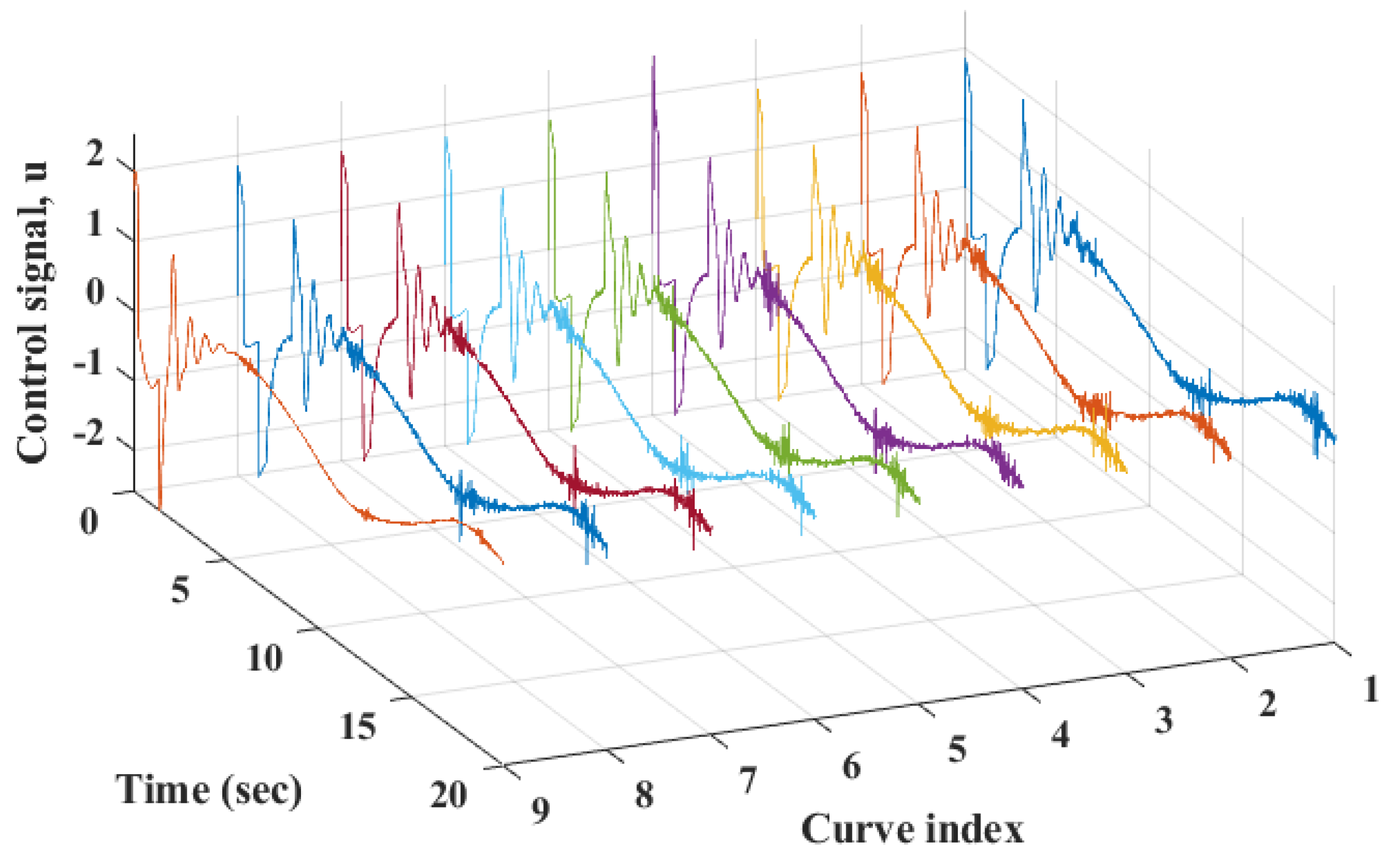
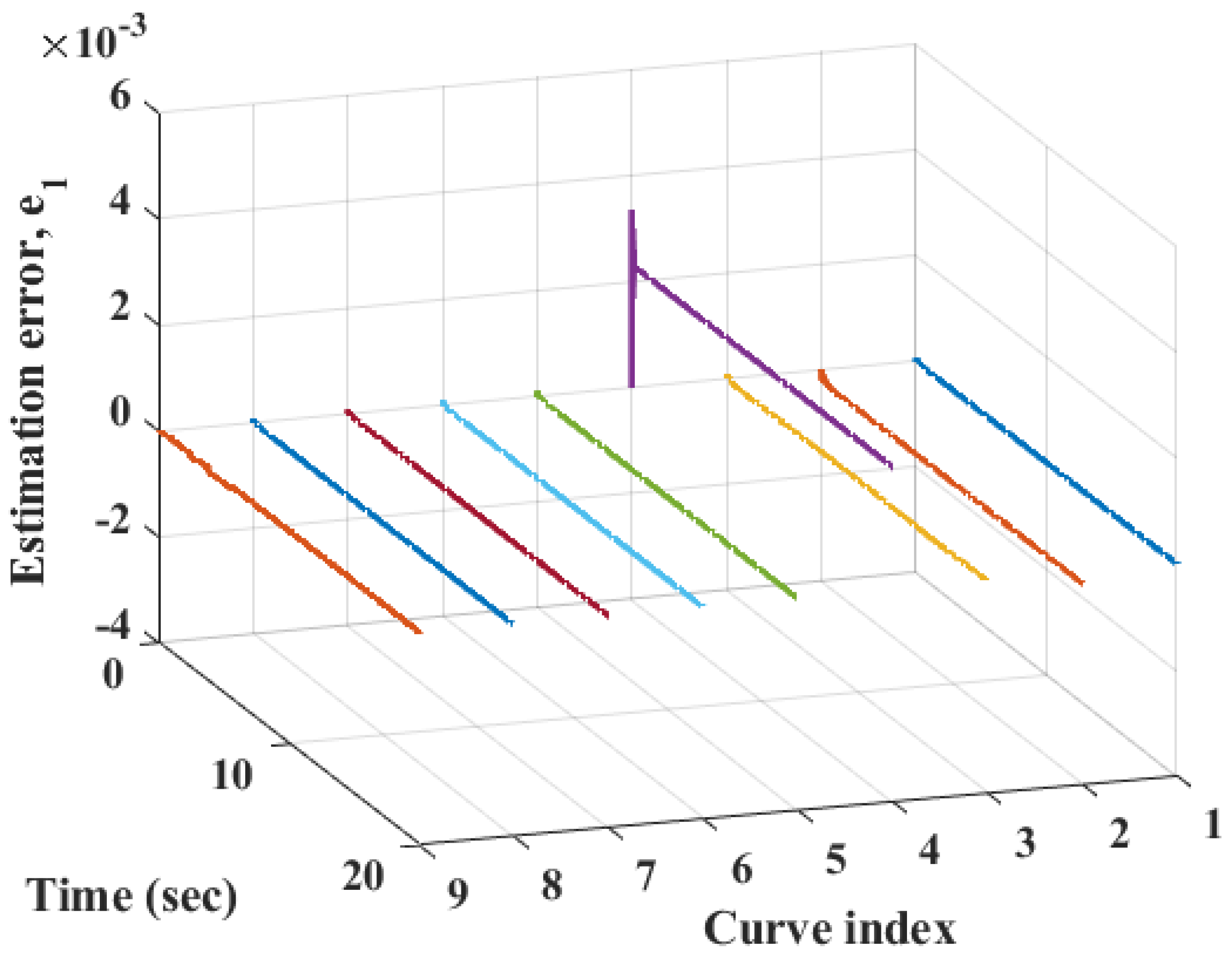
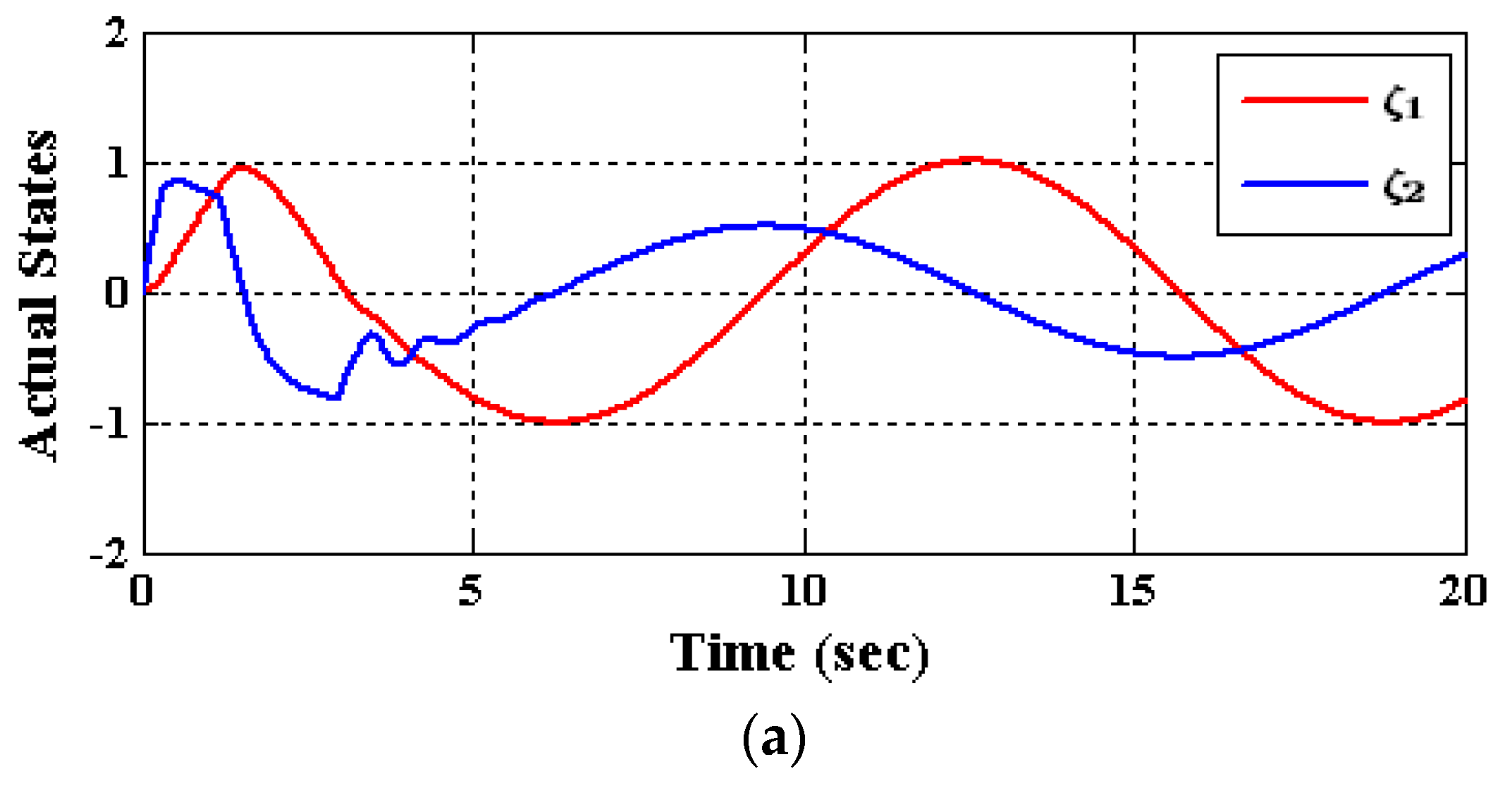
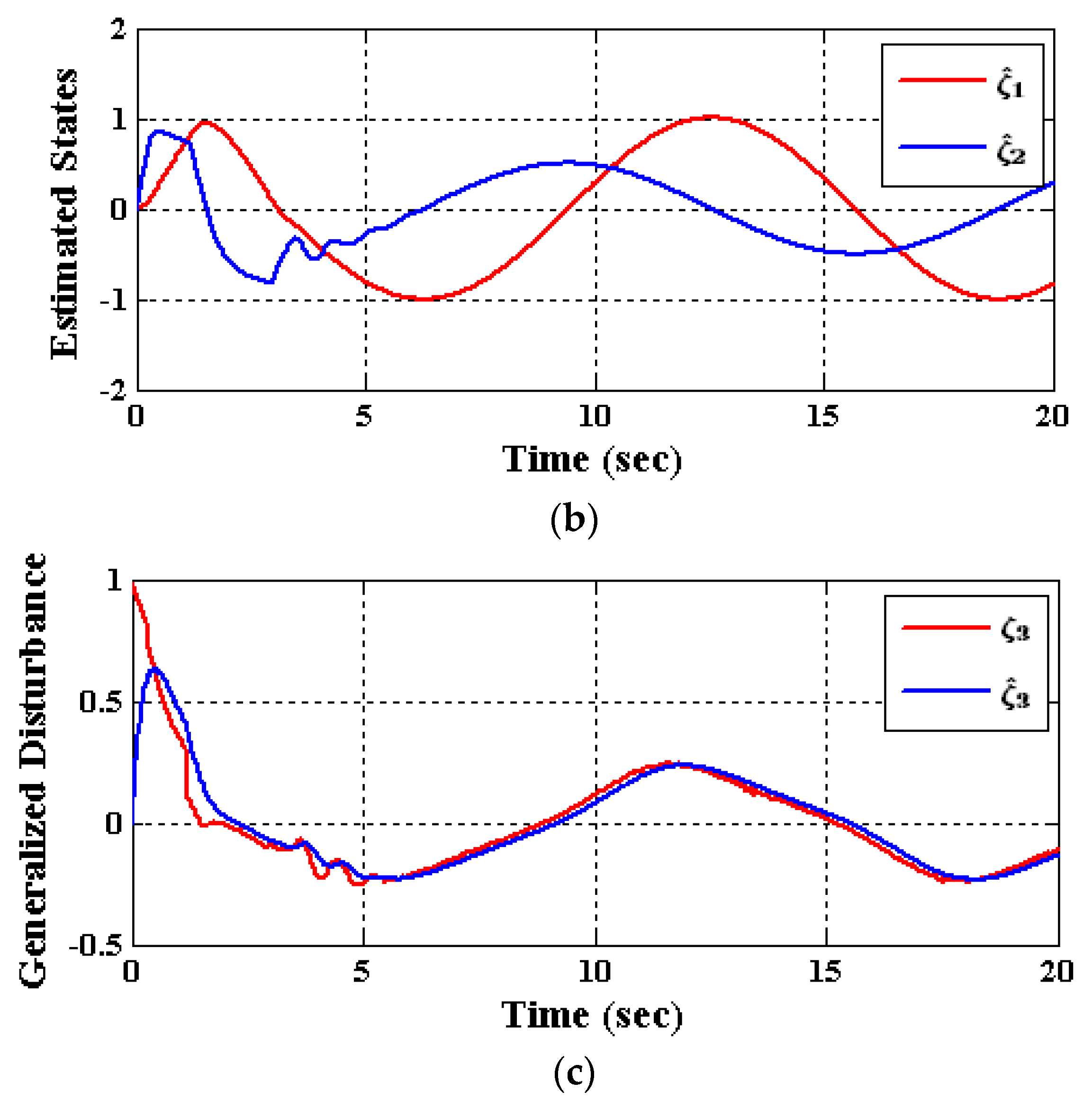
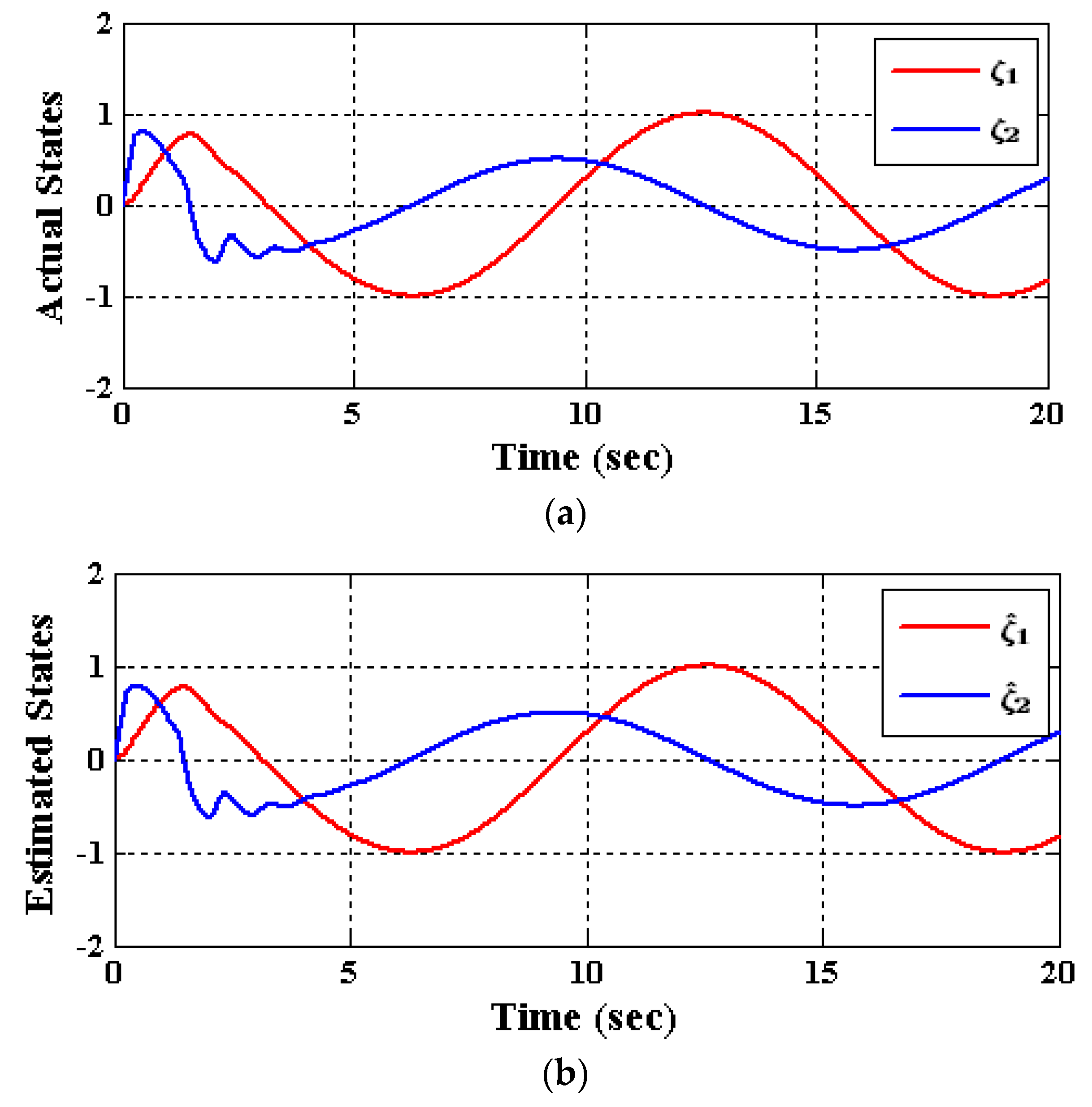
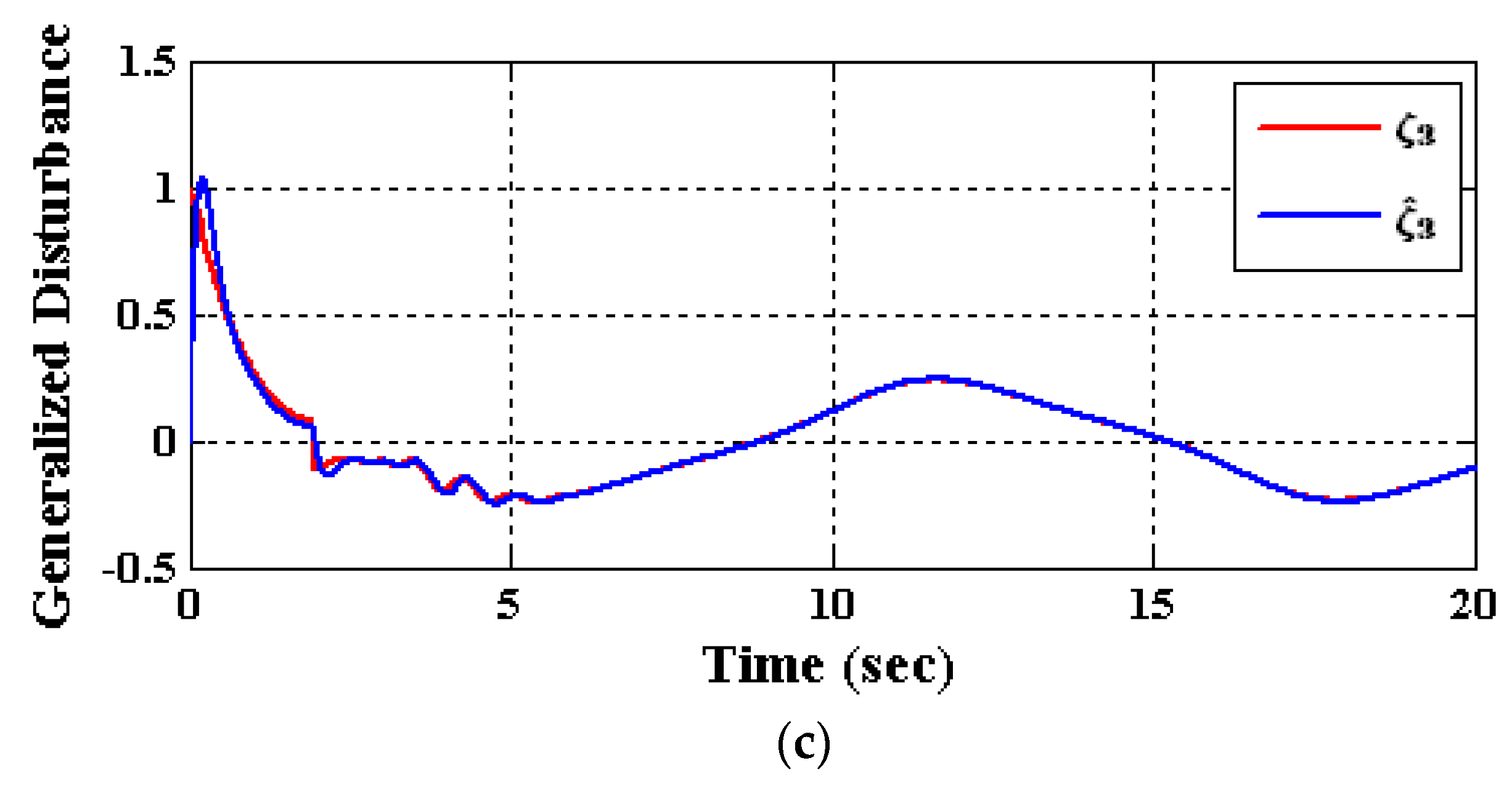
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorems 1 and 2
References
- Abdul-Adheem, W.R.; Azar, A.T.; Ibraheem, I.K.; Humaidi, A.J. Novel Active Disturbance Rejection Control Based on Nested Linear Extended State Observers. Appl. Sci. 2020, 10, 4069. [Google Scholar] [CrossRef]
- Kammogne, A.S.T.; Kountchou, M.N.; Kengne, R.; Azar, A.T.; Fotsin, H.B.; Ouagni, S.T.M. Polynomial Robust Observer Implementation based-passive Synchronization of Nonlinear Fractional-Order Systems with Structural Disturbances. Front. Inf. Technol. Electron. Eng. 2020, 21, 1369–1386. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E.; Rossell, J.M.; Vaidyanathan, S.; Zhu, Q. Adaptive self-recurrent wavelet neural network and sliding mode controller/observer for a slider crank mechanism. Int. J. Comput. Appl. Technol. 2020, 63, 273–285. [Google Scholar] [CrossRef]
- Djeddi, A.; Dib, D.; Azar, A.T.; Abdelmalek, S. Fractional Order Unknown Inputs Fuzzy Observer for Takagi–Sugeno Systems with Unmeasurable Premise Variables. Mathematics 2019, 7, 984. [Google Scholar] [CrossRef]
- Alain, K.S.T.; Azar, A.T.; Fotsin, H.B.; Romanic, K. Robust Observer-based Synchronization of Chaotic Oscillators with Structural Perturbations and Input Nonlinearity. Int. J. Autom. Control (IJAAC) 2019, 13, 387–412. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E. Adaptive Decentralised Sliding Mode Controller and Observer for Asynchronous Nonlinear Large-Scale Systems with Backlash. Int. J. Model. Identif. Control (IJMIC) 2018, 30, 61–71. [Google Scholar] [CrossRef]
- Luenberger, D.G. Observing the State of a Linear System. IEEE Trans. Mil. Electron. 1964, 8, 74–80. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Al-Kalbani, F.; Al Hosni, S.M.; Zhang, J. Active Disturbance Rejection Control of a methanol-water separation distillation column. In Proceedings of the 2015 IEEE 8th GCC Conference & Exhibition, Muscat, Oman, 1–4 February 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Abdul-adheem, W.R.; Ibraheem, I.K. Model-free active input—Output feedback linearization of a single-link flexible joint manipulator: An improved active disturbance rejection control approach. Meas. Control 2021, 54, 5–6. [Google Scholar] [CrossRef]
- Han, J. A Class of Extended State Observers for Uncertain Systems. Control Decis. 1995, 10, 85–88. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar] [CrossRef]
- Ibraheem, I.K.; Abdul-Adheem, W.R. A novel second-order nonlinear differentiator with application to active disturbance rejection Control. In Proceedings of the 1st International Scientific Conference of Engineering Sciences—3rd Scientific Conference of Engineering Science (ISCES), Diyala, Iraq, 10–11 January 2018; Volume 1, pp. 68–73. [Google Scholar] [CrossRef]
- Abdul-adheem, W.R.; Ibraheem, I.K. From PID to Nonlinear State Error Feedback Controller. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 312–322. [Google Scholar]
- Ibraheem, I.K. Anti-Disturbance Compensator Design for Unmanned Aerial Vehicle. J. Eng. 2020, 26, 86–103. [Google Scholar] [CrossRef]
- Johnson, C.D. Accommodation of External Disturbances in Linear Regulator and Servomechanism Problems. IEEE Trans. Autom. Control 1971, 16, 635–644. [Google Scholar] [CrossRef]
- Umeno, T.; Hori, Y. Robust Speed Control of DC Servomotors Using Modern Two Degrees-of-Freedom Controller Design. IEEE Trans. Ind. Electron. 1991, 38, 363–368. [Google Scholar] [CrossRef]
- Kwon, S.J.; Chung, W.K. Robust performance of the multiloop perturbation compensator. IEEE/ASME Trans. Mechatron. 2002, 7, 190–200. [Google Scholar] [CrossRef]
- Schrijver, E.; Dijk, J.V. Disturbance Observers for Rigid Mechanical Systems: Equivalence, Stability, and Design. J. Dyn. Syst. Meas. Control 2002, 124, 539–548. [Google Scholar] [CrossRef]
- Chen, W.-H. Disturbance Observer Based Control for Nonlinear Systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Mohammadi, A.; Tavakoli, M.; Marquez, H.J.; Hashemzadeh, F. Nonlinear disturbance observer design for robotic manipulators. Control Eng. Pract. 2013, 21, 253–267. [Google Scholar] [CrossRef]
- Ueki, S.; Mouri, T.; Kawasaki, H. Nonlinear Disturbance Observer for Object Grasping/Manipulation by Multi-Fingered Robot Hand. IFAC-PapersOnLine 2017, 50, 13243–13248. [Google Scholar] [CrossRef]
- Khalil, H.K. Extended High-Gain Observers as Disturbance Estimators. SICE J. Control Meas. Syst. Integr. 2017, 10, 125–134. [Google Scholar] [CrossRef]
- Li, J.; Xia, Y.; Qi, X.; Gao, Z. On the Necessity, Scheme, and Basis of the Linear-Nonlinear Switching in Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2017, 64, 1425–1435. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, Y.; Han, J. An alternative paradigm for control system design. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 4578–4585. [Google Scholar]
- Wu, S.; Dong, B.; Ding, G.; Wang, G.; Liu, G.; Li, Y. Backstepping sliding mode force/position control for constrained reconfigurable manipulator based on extended state observer. In Proceedings of the 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 477–482. [Google Scholar]
- Yang, H.; Yu, Y.; Yuan, Y.; Fan, X. Back-stepping control of two-link flexible manipulator based on an extended state observer. Adv. Space Res. 2015, 56, 2312–2322. [Google Scholar] [CrossRef]
- Zheng, M.; Chen, X.; Tomizuka, M. Extended State Observer with Phase Compensation to Estimate and Suppress High-frequency Disturbances. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 3521–3526. [Google Scholar]
- Lee, S.; Kim, Y. Design of Nonlinear Observer for Strap-down Missile Guidance law via Sliding Mode Differentiator and Extended State Observer. In Proceedings of the International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, VIC, Australia, 30 November–3 December 2016; pp. 143–147. [Google Scholar]
- Liu, B.; Jin, Y.; Chen, C.; Yang, H. Speed Control Based on ESO for the Pitching Axis of Satellite Cameras. Mathimaticl. Probl. Eng. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. Extended state observer for nonlinear systems with uncertainty. IFAC Proc. Vol. 2011, 44, 1855–1860. [Google Scholar] [CrossRef]
- Duan, H.; Tian, Y.; Wang, G. Trajectory Tracking Control of Ball and Plate System Based on Auto-Disturbance Rejection Controller. In Proceedings of the 7th Asian Control Conference, Hong Kong, China, 27–29 August 2009; pp. 471–476. [Google Scholar]
- Benxian, X.; Ping, W.; Xueping, D.; Xingpeng, Z.; Haibin, Y. Study on nonlinear friction compensation for bi-axis servo system based-on ADRC. In Proceedings of the International Conference on Information Science and Technology, (ICIST), Nanjing, China, 26–28 March 2011; pp. 788–793. [Google Scholar]
- Dejun, L.; Changjin, C.; Zhenxiong, Z. Permanent magnet synchronous motor control system based on auto disturbances rejection controller. In Proceedings of the International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 8–11. [Google Scholar]
- Jingfeng, M.A.O.; Liang, G.U.; Aihua, W.U.; Guoqing, W.U.; Xudong, Z.; Dong, C. Back-stepping Control for Vertical Axis Wind Power Generation System Maximum Power Point Tracking based on Extended State Observer. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 8649–8653. [Google Scholar]
- Xia, Y.; Yang, H.; You, X.; Li, H. Adaptive control for attitude synchronisation of spacecraft formation via extended state observer. IET Control Theory Appl. 2014, 8, 2171–2185. [Google Scholar]
- Lin, Y.; Lin, C.; Suebsaiprom, P.; Hsieh, S. Estimating evasive acceleration for ballistic targets using an extended state observer. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 337–349. [Google Scholar] [CrossRef]
- Yu, T.; Shen, S.; Li, D.; Chan, K.W. A novel coordinated auto-disturbance-rejection excitation and SVC controller. IEEE Power Eng. Soc. Gen. Meet. 2005, 1, 523–527. [Google Scholar] [CrossRef]
- Xiong, S.; Wang, W.; Liu, X.; Chen, Z.; Wang, S. A novel extended state observer. ISA Trans. 2015, 58, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.L.; Guo, B.Z. On active disturbance rejection control for nonlinear systems using time-varying gain. Eur. J. Control 2015, 23, 62–70. [Google Scholar] [CrossRef]
- Gao, K.; Song, J.; Yang, E. Stability analysis of the high-order nonlinear extended state observers for a class of nonlinear control systems. Trans. Inst. Meas. Control 2019, 41, 4370–4379. [Google Scholar] [CrossRef]
- Przybyła, M.; Kordasz, M.; Madoński, R.; Herman, P.; Sauer, P. Active Disturbance Rejection Control of a 2DOF manipulator with significant modeling uncertainty. Bull. Pol. Acad. Sci. Tech. Sci. 2012, 60, 509–520. [Google Scholar] [CrossRef]
- Pu, Z.; Yuan, R.; Yi, J.; Tan, X. A Class of Adaptive Extended State Observers for Nonlinear Disturbed Systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, D. Output Regulation and Active Disturbance Rejection Control: Unified Formulation and Comparison. Asian J. Control 2015, 18, 1–11. [Google Scholar] [CrossRef]
- Xue, W.; Huang, Y. On performance analysis of ADRC for a class of MIMO lower-triangular nonlinear uncertain systems. ISA Trans. 2014, 53, 955–962. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Ding, Z. Global output regulation for a class of lower triangular nonlinear systems: A feedback domination approach. Automatica 2017, 76, 65–69. [Google Scholar] [CrossRef]
- Guo, B.-Z.; Wu, Z.-H. Output tracking for a class of nonlinear systems with mismatched uncertainties by active disturbance rejection Control. Syst. Control Lett. 2017, 100, 21–31. [Google Scholar] [CrossRef]
- Qian, C.; Li, S.; Frye, M.T.; Du, H. Global finite-time stabilisation using bounded feedback for a class of non-linear systems. IET Control Theory Appl. 2012, 6, 2326–2336. [Google Scholar]
- Zhu, Q. Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback Control. IEEE Trans. Autom. Control 2019, 64, 3764–3771. [Google Scholar] [CrossRef]
- Ding, K.; Zhu, Q. Extended dissipative anti-disturbance control for delayed switched singular semi-Markovian jump systems with multi-disturbance via disturbance observer. Automatica 2021, 128, 109556. [Google Scholar] [CrossRef]
- Yang, X.; Wang, H.; Zhu, Q. Event-triggered predictive control of nonlinear stochastic systems with output delay. Automatica 2020, 140, 110230. [Google Scholar] [CrossRef]
- Castañeda, H.; Salas-Peña, O.S.; de León-Morales, J. Extended observer based on adaptive second order sliding mode control for a fixed wing UAV. ISA Trans. 2017, 66, 226–232. [Google Scholar] [CrossRef] [PubMed]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 12th ed.; Pearson Education: London, UK, 2011. [Google Scholar]
- Ibraheem, I.K.; Abdul-adheem, W.R. On the Improved Nonlinear Tracking Differentiator based Nonlinear PID Controller Design. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 234–241. [Google Scholar]
| Index | The Type of ESO | Dynamics |
|---|---|---|
| 1 | LESO [44] | |
| 2 | NLESO type I [33] | where |
| 3 | NLESO type II [35] | where |
| 4 | NLESO type III [34] | where ) |
| 5 | NLESO type IV(a) [53] | |
| 6 | NLESO type IV(b) [25] | |
| 7 | NLESO type V [39] | |
| 8 | NLESO type VI [29] | |
| 9 | Proposed NHOESO | where |
| Parameter | Value |
|---|---|
| 46.4494 | |
| 731.7998 | |
| 762.1222 | |
| 2879.2 | |
| 0.0150 | |
| 0.3316 | |
| 0.0047 | |
| 0.0497 | |
| 0.5331 | |
| 0.3342 | |
| 0.6166 | |
| 0.5432 |
| Index | ESO | ITAE | ISU |
|---|---|---|---|
| 1 | LESO | 1.714331 | 7.168854 |
| 2 | NLESO type I | 1.560685 | 6.682492 |
| 3 | NLESO type II | 1.613618 | 6.809034 |
| 4 | NLESO type III | 1.604350 | 6.779854 |
| 5 | NLESO type IV(a) | 1.630781 | 6.835949 |
| 6 | NLESO type IV(b) | 1.619501 | 6.696178 |
| 7 | NLESO type V | 1.657292 | 6.853151 |
| 8 | NLESO type VI | 1.610722 | 6.768733 |
| 9 | NHOESO | 0.937766 | 5.373665 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azar, A.T.; Smait, D.A.; Muhsen, S.; Jassim, M.A.; AL-Salih, A.A.M.M.; Hameed, I.A.; Jawad, A.J.M.; Abdul-Adheem, W.R.; Cocquempot, V.; Sahib, M.A.; et al. A New Approach to Nonlinear State Observation for Affine Control Dynamical Systems. Appl. Sci. 2023, 13, 3300. https://doi.org/10.3390/app13053300
Azar AT, Smait DA, Muhsen S, Jassim MA, AL-Salih AAMM, Hameed IA, Jawad AJM, Abdul-Adheem WR, Cocquempot V, Sahib MA, et al. A New Approach to Nonlinear State Observation for Affine Control Dynamical Systems. Applied Sciences. 2023; 13(5):3300. https://doi.org/10.3390/app13053300
Chicago/Turabian StyleAzar, Ahmad Taher, Drai Ahmed Smait, Sami Muhsen, Moayad Abdullah Jassim, Asaad Abdul Malik Madhloom AL-Salih, Ibrahim A. Hameed, Anwar Ja’afar Mohamad Jawad, Wameedh Riyadh Abdul-Adheem, Vincent Cocquempot, Mouayad A. Sahib, and et al. 2023. "A New Approach to Nonlinear State Observation for Affine Control Dynamical Systems" Applied Sciences 13, no. 5: 3300. https://doi.org/10.3390/app13053300
APA StyleAzar, A. T., Smait, D. A., Muhsen, S., Jassim, M. A., AL-Salih, A. A. M. M., Hameed, I. A., Jawad, A. J. M., Abdul-Adheem, W. R., Cocquempot, V., Sahib, M. A., Kamal, N. A., & Ibraheem, I. K. (2023). A New Approach to Nonlinear State Observation for Affine Control Dynamical Systems. Applied Sciences, 13(5), 3300. https://doi.org/10.3390/app13053300









