16-Channel Wavelength Division Multiplexers Based on Subwavelength Grating
Abstract
1. Introduction
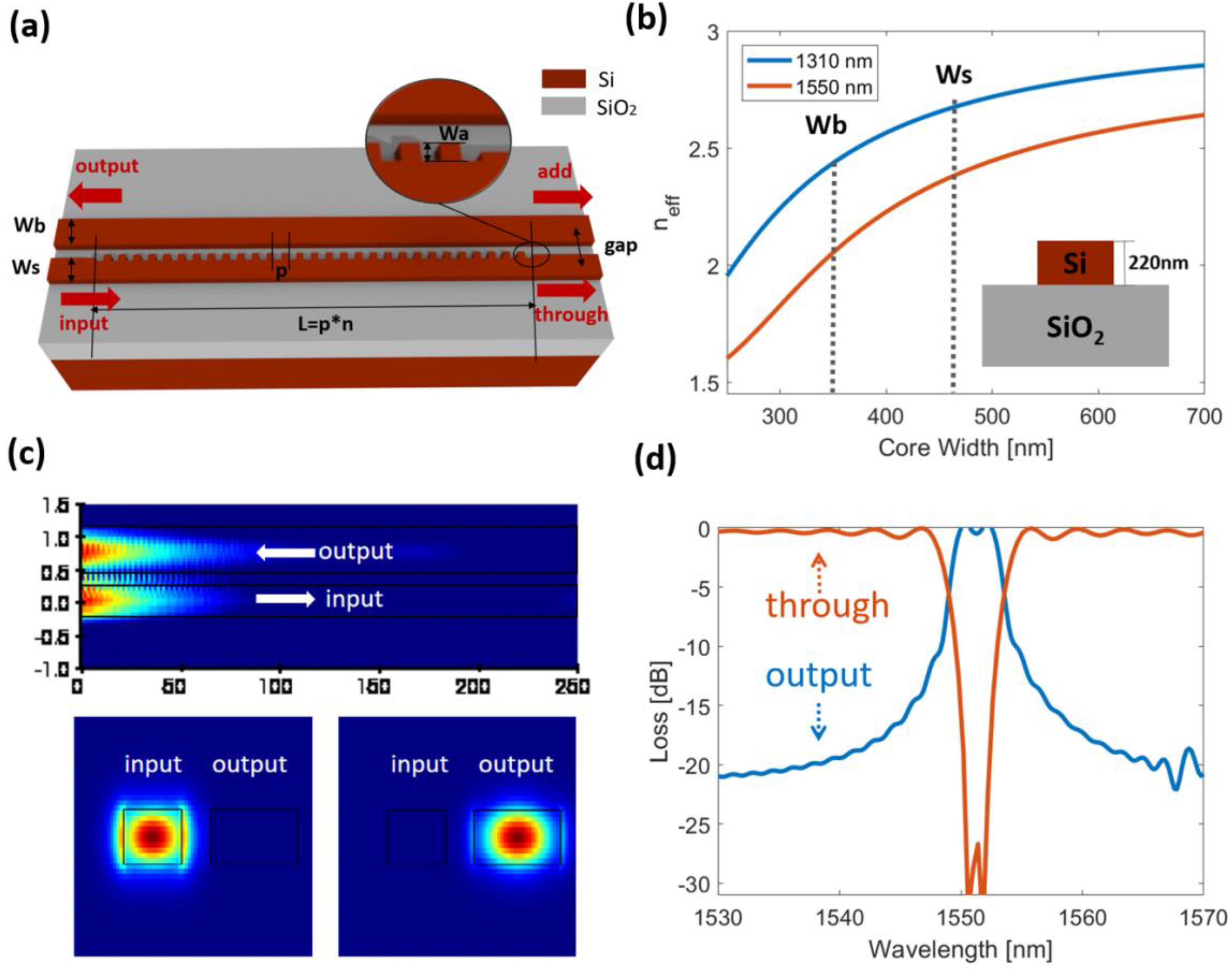
2. Structure and Method
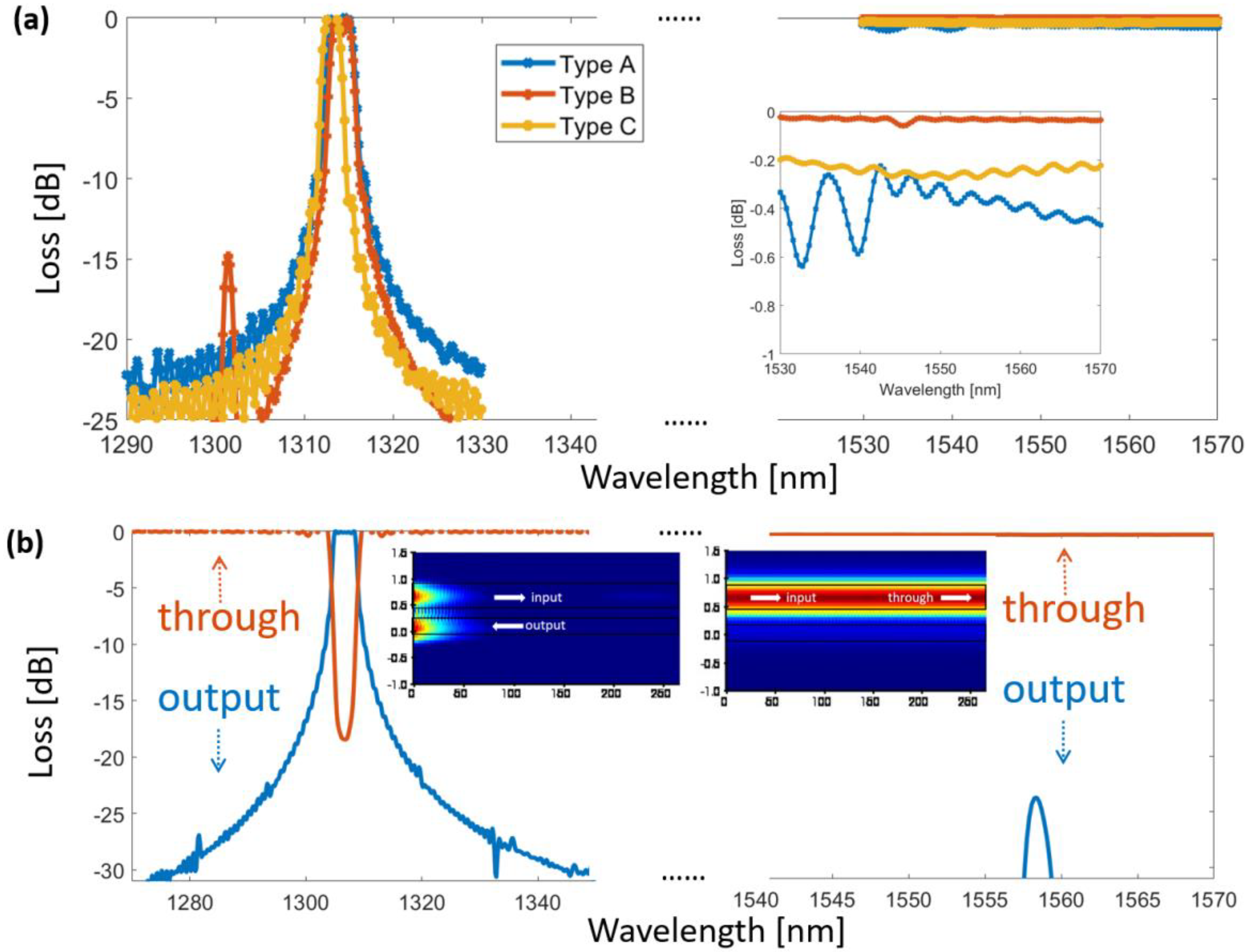
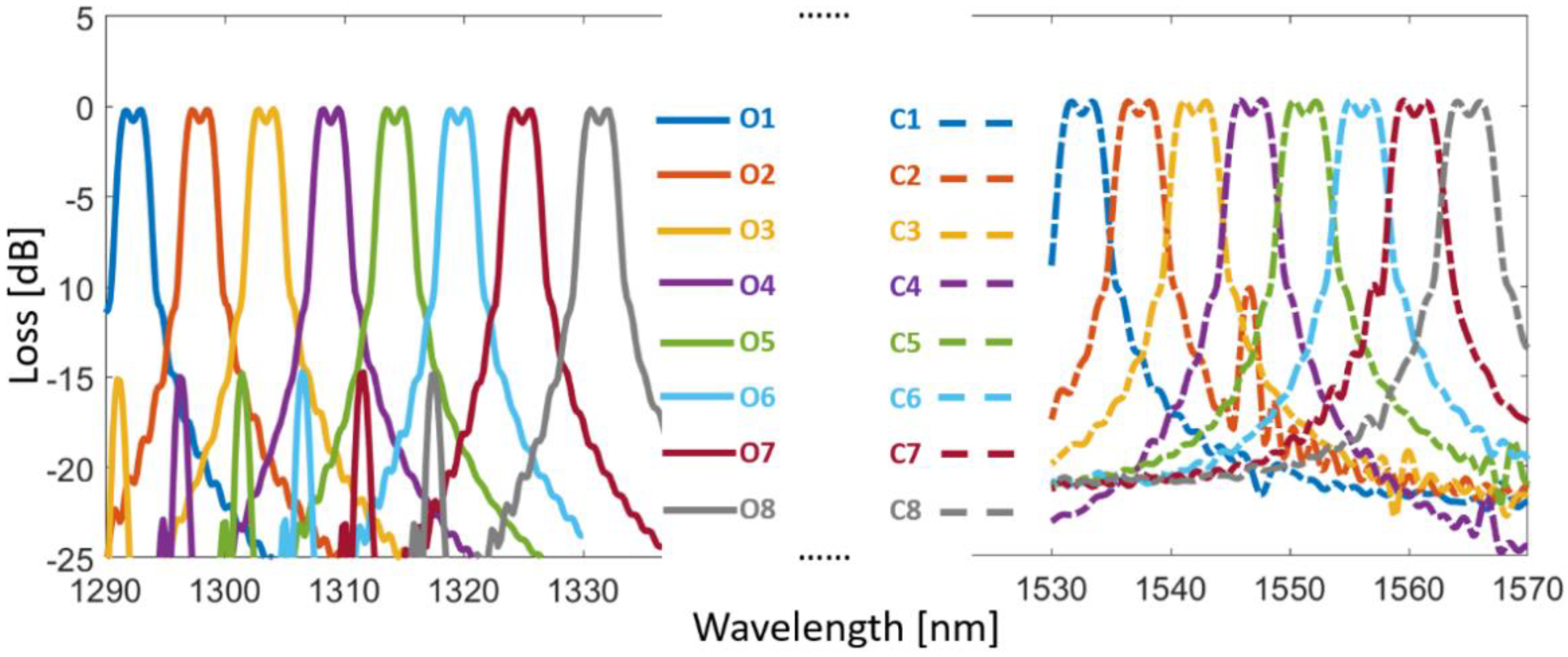
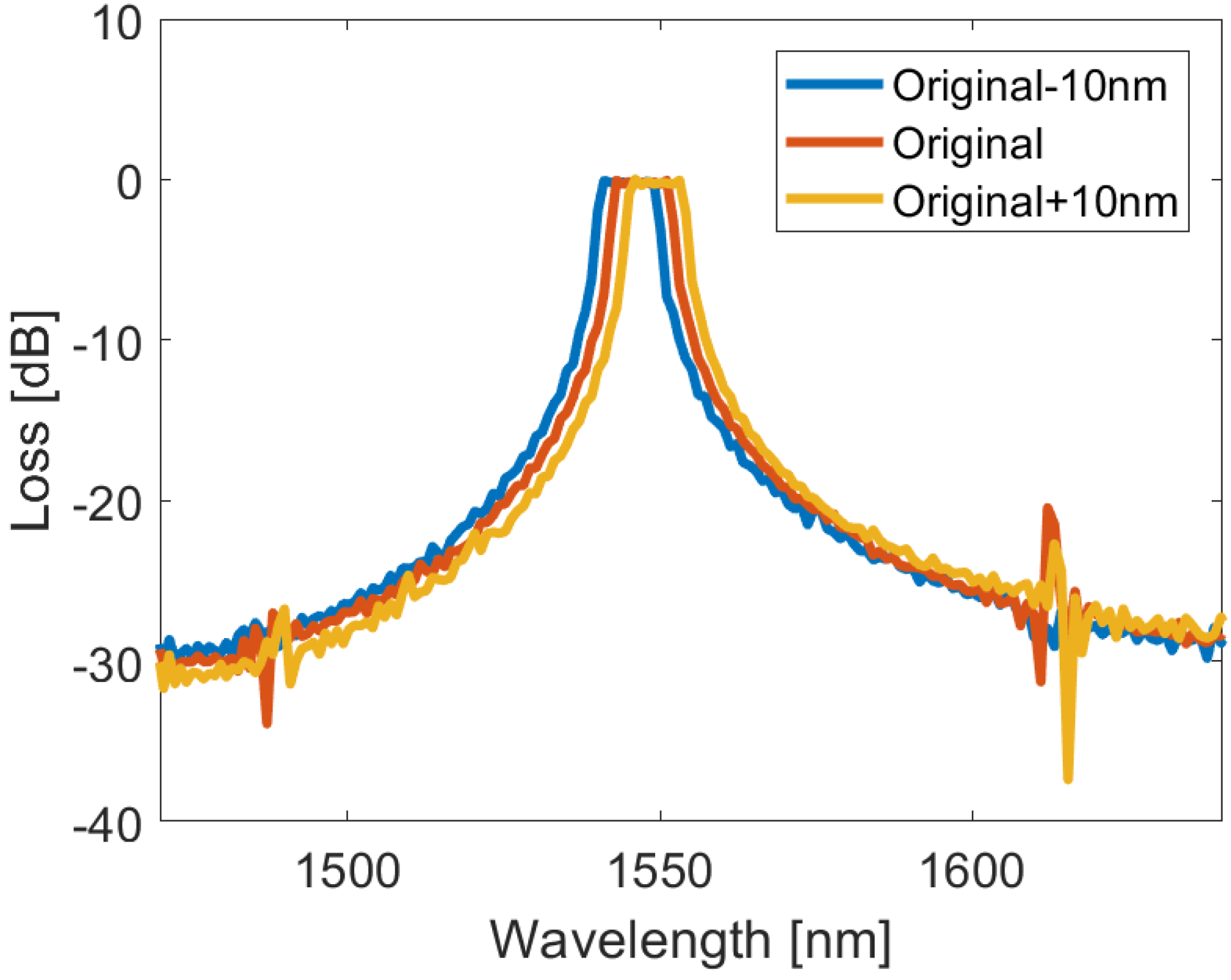
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khalighi, M.A.; Uysal, M. Survey on free space optical communication: A communication theory perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar]
- Gantz, J.; Reinsel, D.; Arend, C. The digital universe in 2020: Big data, bigger digital shadows, and biggest growth in the far east-western Europe. IDC Anal. Future 2012, 2007, 1–16. [Google Scholar]
- Thylén, L.; Wosinski, L. Integrated photonics in the 21st century. Photonics Res. 2014, 2, 75–81. [Google Scholar] [CrossRef]
- Xu, J.; Kong, M.W.; Lin, A.B.; Song, Y.H.; Yu, X.Y.; Qu, F.Z.; Han, J.; Deng, N. OFDM-based broadband underwater wireless optical communication system using a compact blue LED. Opt. Commun. 2016, 369, 100–105. [Google Scholar] [CrossRef]
- Amirabadi, M.A.; Kahaei, M.H.; Nezamalhosseni, S.A. Low complexity deep learning algorithms for compensating atmospheric turbulence in the free space optical communication system. IET Optoelectron. 2022, 16, 93–105. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W.; et al. Review of Silicon Photonics Technology and Platform Development. J. Light. Technol. 2021, 39, 4374–4389. [Google Scholar] [CrossRef]
- Dong, P.; Chen, Y.-K.; Duan, G.-H.; Neilson, D.T. Silicon photonic devices and integrated circuits. Nanophotonics 2014, 3, 215–228. [Google Scholar] [CrossRef]
- Aydin, K. Nanostructured silicon success. Nat. Photonics 2015, 9, 353–355. [Google Scholar] [CrossRef]
- Bogaerts, W.; Chrostowski, L. Silicon Photonics Circuit Design: Methods, Tools and Challenges. Laser Photonics Rev. 2018, 12, 4374–4389. [Google Scholar]
- Shi, W.; Tian, Y.; Gervais, A. Scaling capacity of fiber-optic transmission systems via silicon photonics. Nanophotonics 2020, 9, 4629–4663. [Google Scholar]
- Brackett, C.A. Dense wavelength division multiplexing networks—Principles and applications. IEEE J. Sel. Areas Commun. 1990, 8, 948–964. [Google Scholar] [CrossRef]
- Piggott, A.Y.; Lu, J.; Lagoudakis, K.G.; Petykiewicz, J.; Babinec, T.M.; Vuckovic, J. Inverse design and demonstration of a compact and broadband on-chip wavelength demultiplexer. Nat. Photonics 2015, 9, 374. [Google Scholar] [CrossRef]
- Pan, P.; An, J.; Wang, Y.; Zhang, J.; Wang, L.; Qi, Y.; Han, Q.; Hu, X. Compact 4-channel AWGs for CWDM and LAN WDM in data center monolithic applications. Opt. Laser Technol. 2015, 75, 177–181. [Google Scholar] [CrossRef]
- Shi, W.; Yun, H.; Lin, C.; Greenberg, M.; Wang, X.; Wang, Y.; Fard, S.T.; Flueckiger, J.; Jaeger, N.A.F.; Chrostowski, L. Ultra-compact, flat-top demultiplexer using anti-reflection contra-directional couplers for CWDM networks on silicon. Opt. Express 2013, 21, 6733–6738. [Google Scholar] [CrossRef] [PubMed]
- Cheben, P.; Halir, R.; Schmid, J.H.; Atwater, H.A.; Smith, D.R. Subwavelength integrated photonics. Nature 2018, 560, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Y.; Shi, Y.C. Flat-top CWDM (De) Multiplexers Based on Contra-Directional Couplers With Subwavelength Gratings. IEEE Photonics Technol. Lett. 2019, 31, 20032006. [Google Scholar] [CrossRef]
- Tao, S.; Huang, Q.; Zhu, L.; Liu, J.; Zhang, Y.; Huang, Y.; Wang, Y.; Xia, J. Athermal 4-channel (de-)multiplexer in silicon nitride fabricated at low temperature. Photonics Res. 2018, 6, 686–691. [Google Scholar] [CrossRef]
- Horst, F.; Green, W.M.; Assefa, S.; Shank, S.M.; Vlasov, Y.A.; Offrein, B.J. Cascaded Mach-Zehnder wavelength filters in silicon photonics for low loss and flat pass-band WDM (de-)multiplexing. Opt. Express 2013, 21, 11652–11658. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Yu, J. Coherent interaction between two orthogonal travelling-wave modes in a microdonut resonator for filtering and buffering applications. Opt. Express 2014, 22, 25171–25182. [Google Scholar] [CrossRef]
- Chang, L.; Xie, W.; Shu, H.; Yang, Q.F.; Shen, B.; Boes, A.; Peters, J.D.; Jin, W.; Xiang, C.; Liu, S.; et al. Ultra-efficient frequency comb generation in AlGaAs-on-insulator microresonators. Nat. Commun. 2020, 11, 1331. [Google Scholar] [CrossRef]
- Rakhshani, M.R.; Mansouri-Birjandi, M.A. Heterostructure four channel wavelength demultiplexer using square photonic crystals ring resonators. J. Electromagn. Waves Appl. 2012, 26, 17001707. [Google Scholar] [CrossRef]
- St-Yves, J.; Bahrami, H.; Jean, P.; LaRochelle, S.; Shi, W.J.O.l. Widely bandwidth-tunable silicon filter with an unlimited free-spectral range. Opt. Lett. 2015, 40, 5471–5474. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zhang, M.; Xu, H.; Tan, Y.; Shi, Y.; Dai, D. Subwavelength silicon photonics for on-chip mode-manipulation. PhotoniX 2021, 2, 11. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Y.; He, Y.; Wang, H.W.; Su, Y.K. Subwavelength structured silicon waveguides and photonic devices. Nanophotonics 2020, 9, 1321–1340. [Google Scholar] [CrossRef]
- Wang, F.; Xu, X.; Zhang, C.; Sun, C.; Zhao, J. Design and Demonstration of Compact and Broadband Wavelength Demultiplexer Based on Subwavelength Grating (SWG). IEEE Photonics J. 2022, 14, 6621606. [Google Scholar] [CrossRef]
- Mohammed, Z.; Paredes, B.; Rasras, M. A CMOS Compatible On-chip MMI based Wavelength Diplexer with 60 Gbit/s System Demonstration. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 6–10 March 2022; p. M4J. 3. [Google Scholar]

| Wb (nm) | Ws (nm) | Wa (nm) | Gap (nm) | Pitch (nm) | Duty Cycle | N | |
|---|---|---|---|---|---|---|---|
| 1310 nm | 650 | 350 | 100 | 650 | 234 | 0.5 | 855 |
| 1550 nm | 600 | 400 | 100 | 700 | 321 | 0.5 | 623 |
| Δλ (nm) | Δpitch (nm) | Loss (dB) | CT (dB) | Band (nm) | |
|---|---|---|---|---|---|
| O-band | 5 | 1.5 | 0.5 | 20 | 45 |
| C-band | 5 | 1.5 | 0.5 | 17 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Wang, L.; Zhang, L.; Wang, P.; Peng, B. 16-Channel Wavelength Division Multiplexers Based on Subwavelength Grating. Appl. Sci. 2023, 13, 1833. https://doi.org/10.3390/app13031833
Bai Y, Wang L, Zhang L, Wang P, Peng B. 16-Channel Wavelength Division Multiplexers Based on Subwavelength Grating. Applied Sciences. 2023; 13(3):1833. https://doi.org/10.3390/app13031833
Chicago/Turabian StyleBai, Yawen, Lin Wang, Lei Zhang, Pengfei Wang, and Bo Peng. 2023. "16-Channel Wavelength Division Multiplexers Based on Subwavelength Grating" Applied Sciences 13, no. 3: 1833. https://doi.org/10.3390/app13031833
APA StyleBai, Y., Wang, L., Zhang, L., Wang, P., & Peng, B. (2023). 16-Channel Wavelength Division Multiplexers Based on Subwavelength Grating. Applied Sciences, 13(3), 1833. https://doi.org/10.3390/app13031833








