Random Orthogonal Search with Triangular and Quadratic Distributions (TROS and QROS): Parameterless Algorithms for Global Optimization
Abstract
1. Introduction
- 1.
- The behavior and performance analysis of PROS, which are not available in [15], are provided here.
- 2.
- Two effective novel (1 + 1) ES based on PROS, namely TROS and QROS, are proposed and they outperform PROS on a set of benchmark problems.
- 3.
- The performance of TROS and QROS are found competitive with three well-known optimization algorithms (GA, PSO and DE) on a set of benchmark problems.
Problem Formulation
2. Analysis of the Pure Random Orthogonal Search (PROS) Algorithm
| Algorithm 1: Pure Random Orthogonal Search (PROS) |
input: nil output: the best solution vector found by the algorithm Initialize randomly from repeat  |
2.1. One-Dimensional Functions
2.2. Multi-Dimensional Functions
3. Modified PROS with Local Search Mechanism
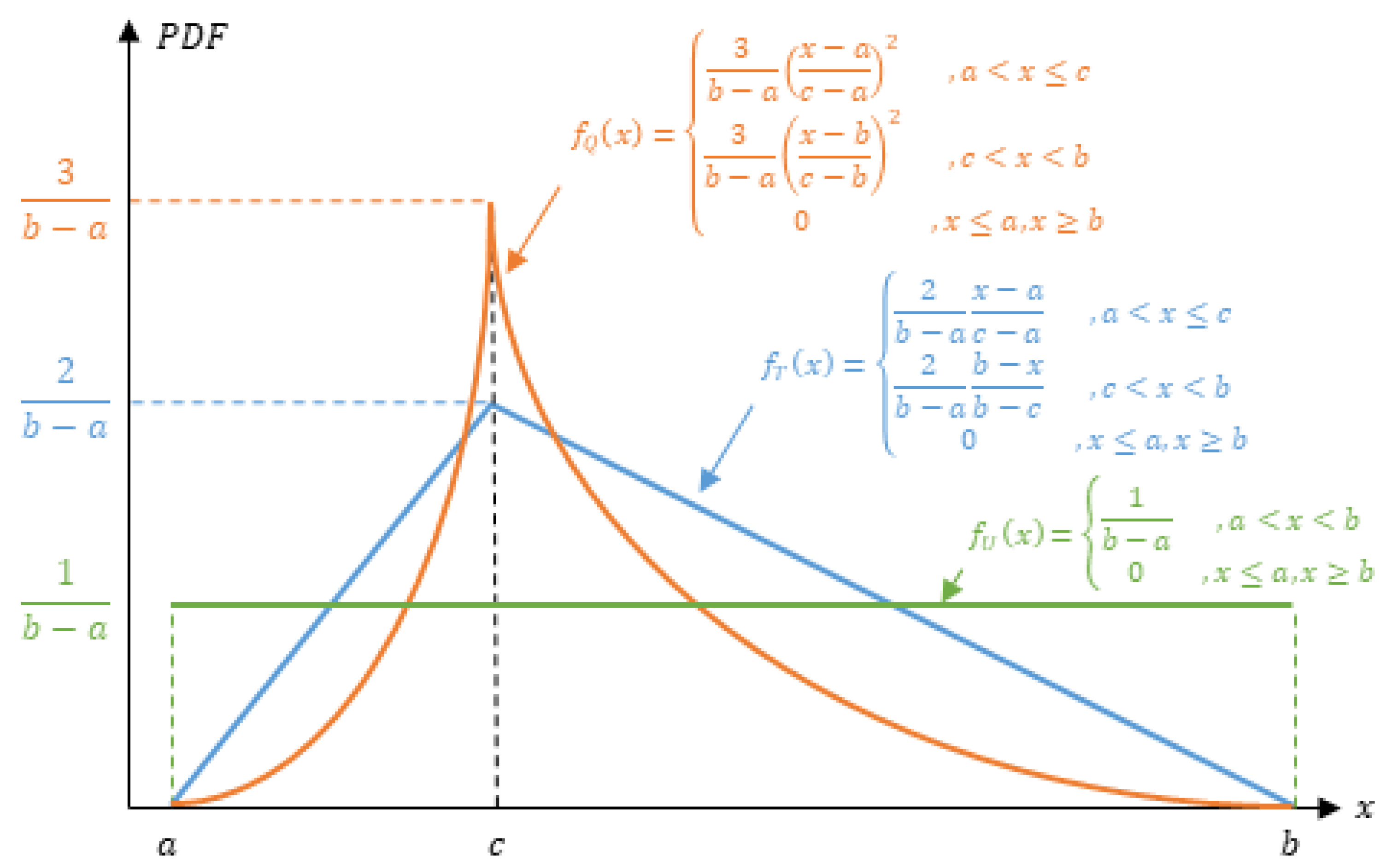
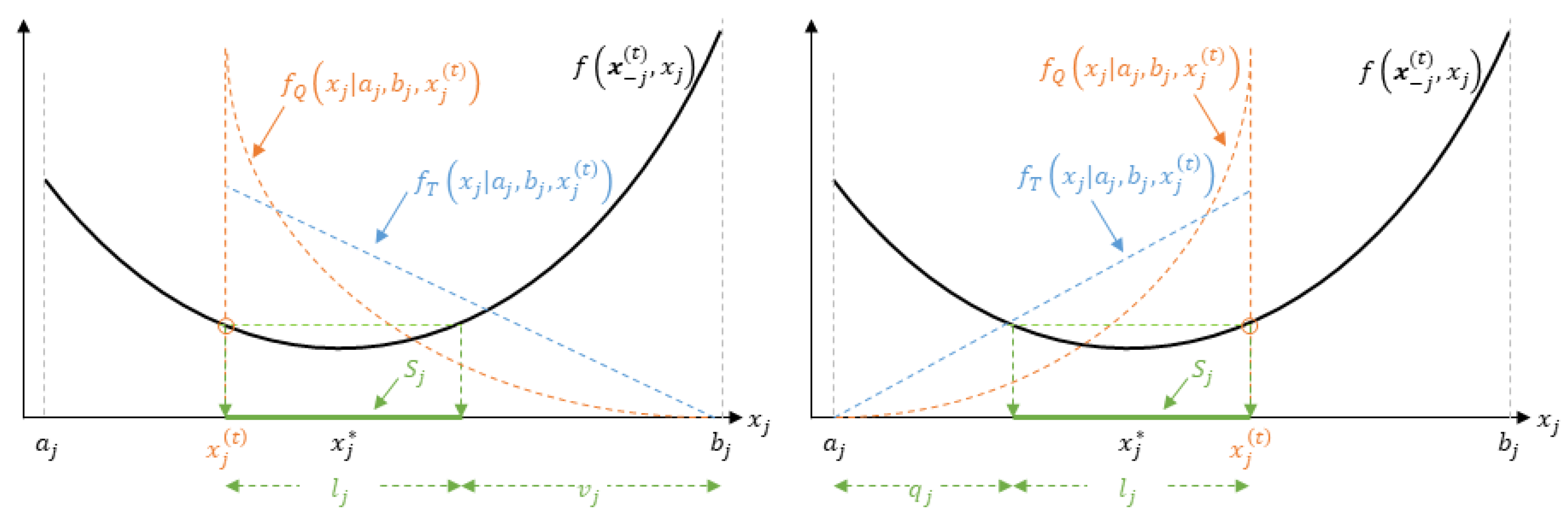
3.1. Triangular-Distributed Random Orthogonal Search (TROS)
| Algorithm 2: Triangular-Distributed Random Orthogonal Search (TROS) |
input: nil output: the best solution vector found by the algorithm Initialize randomly from repeat  |
3.2. Quadratic-Distributed Random Orthogonal Search (QROS)
| Algorithm 3: Quadratic-Distributed Random Orthogonal Search (QROS) |
input: nil output: the best solution vector found by the algorithm Initialize randomly from repeat  |
3.3. Analysis of the Modified Algorithms
4. Experiments
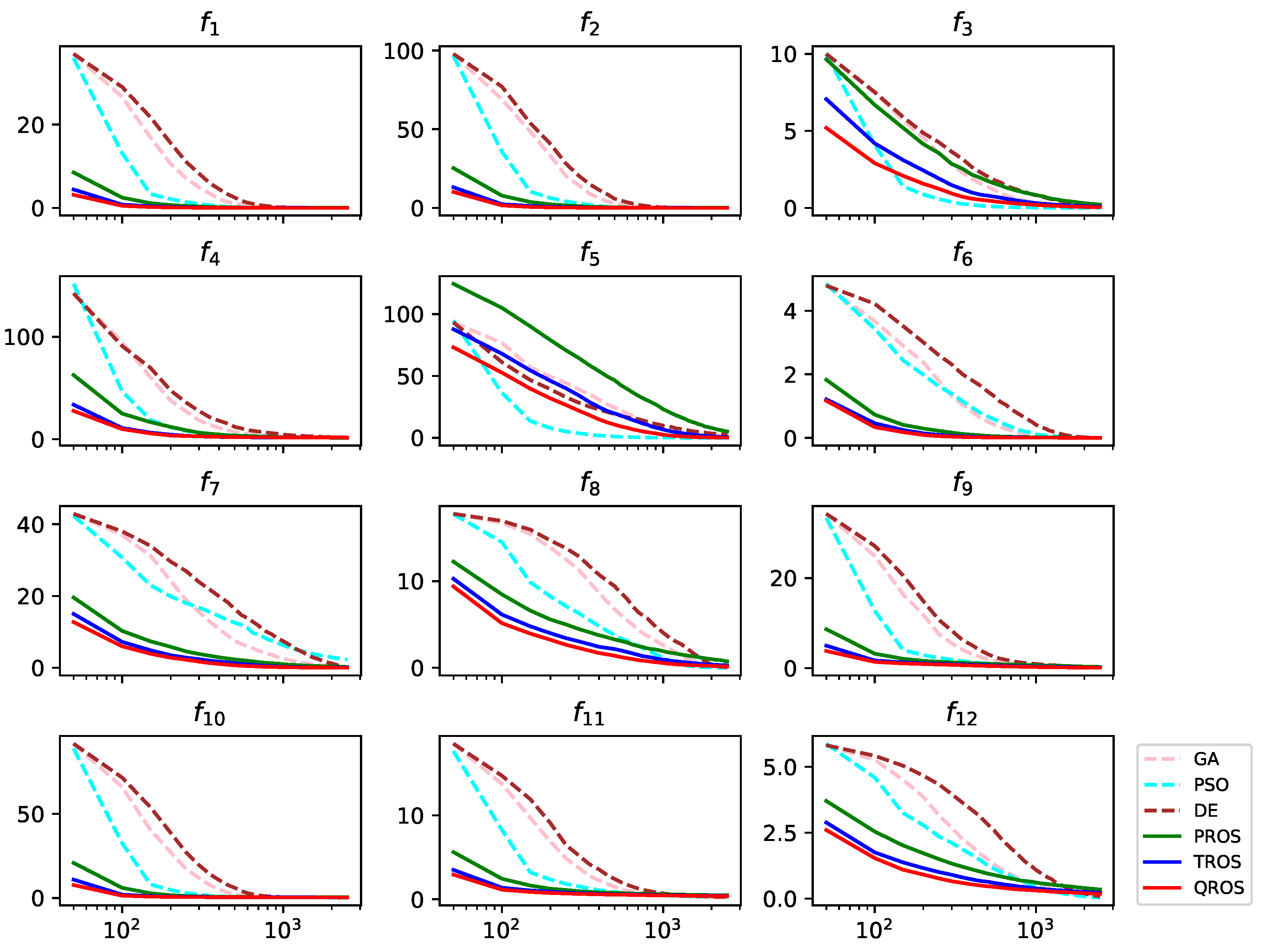
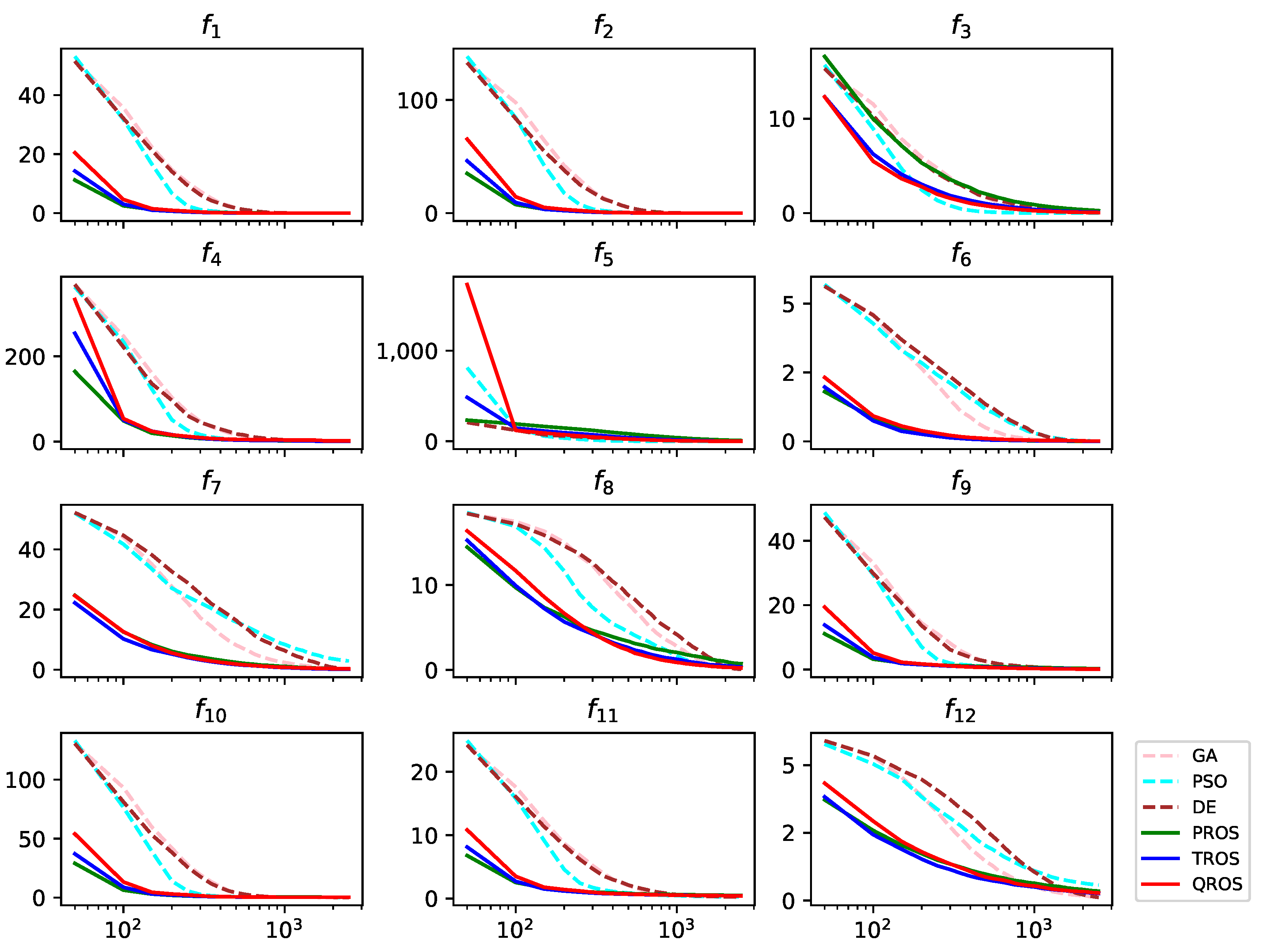
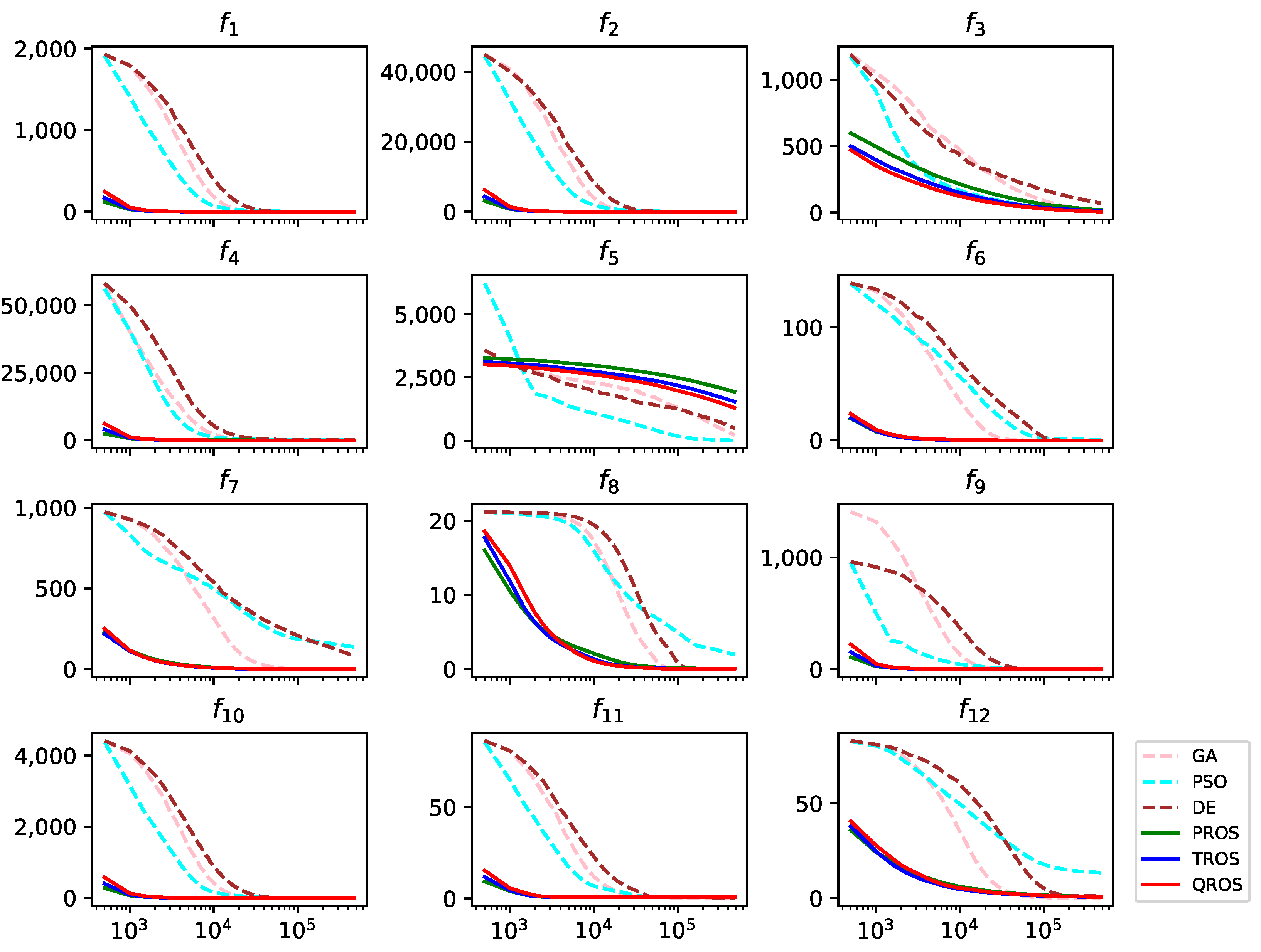
4.1. Experiment I: Basic Benchmark Problems
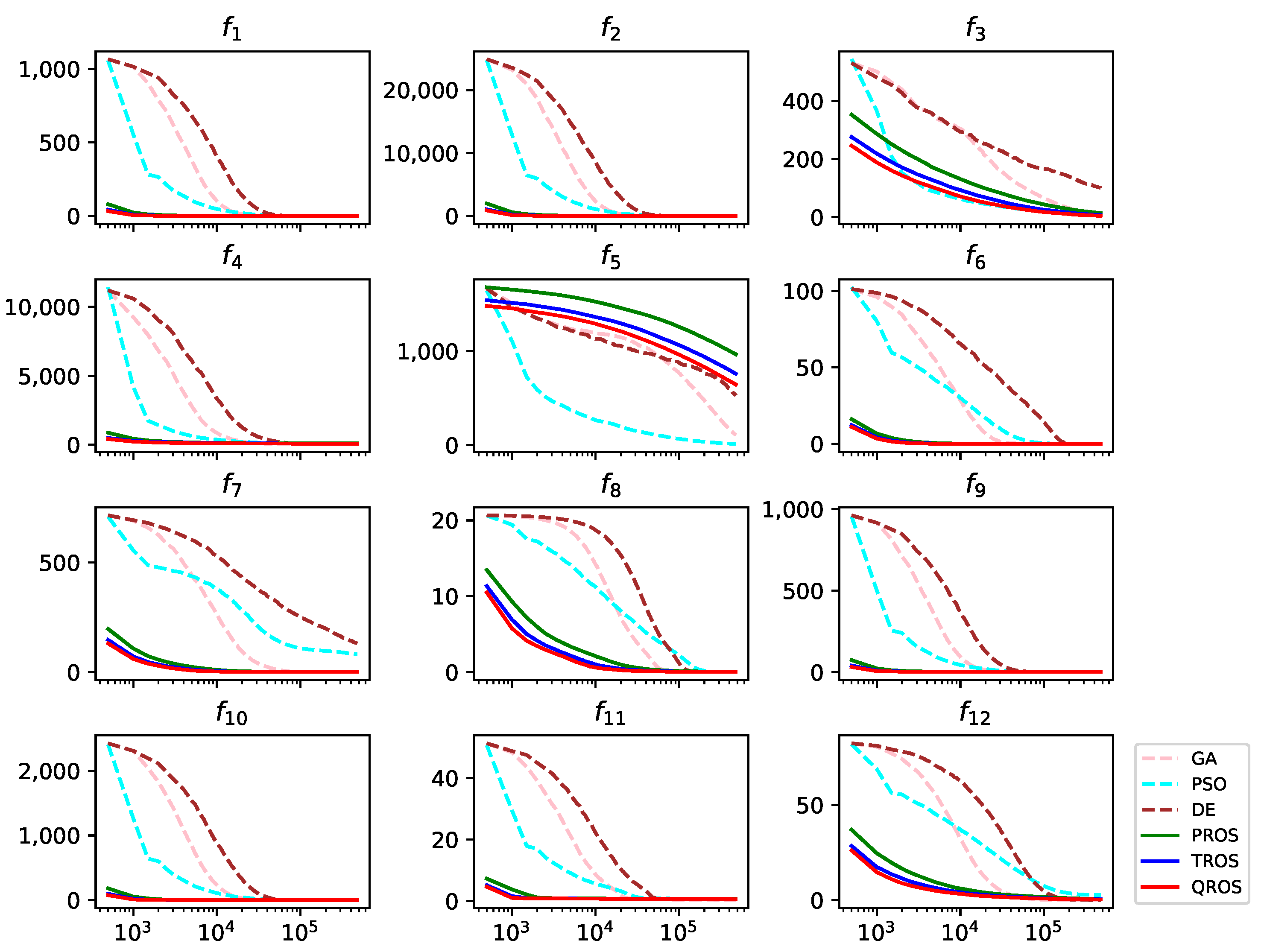
4.2. Experiment II: Random Shifted Benchmark Problems
5. Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, Y.; Zhang, H.; Li, W.; Zhou, M.; Zhang, Y.; Chaovalitwongse, W.A. Comprehensive Learning Particle Swarm Optimization Algorithm With Local Search for Multimodal Functions. IEEE Trans. Evol. Comput. 2019, 23, 718–731. [Google Scholar] [CrossRef]
- Kang, Q.; Song, X.; Zhou, M.; Li, L. A Collaborative Resource Allocation Strategy for Decomposition-Based Multiobjective Evolutionary Algorithms. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2416–2423. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Jin, Y.; Li, F. A Decision Variable Assortment-Based Evolutionary Algorithm for Dominance Robust Multiobjective Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3360–3375. [Google Scholar] [CrossRef]
- Sarker, R.A.; Kamruzzaman, J.; Newton, C.S. Evolutionary Optimization (Evopt): A Brief Review And Analysis. Int. J. Comput. Intell. Appl. 2003, 3, 311–330. [Google Scholar] [CrossRef]
- Tian, J.; Tan, Y.; Zeng, J.; Sun, C.; Jin, Y. Multiobjective Infill Criterion Driven Gaussian Process-Assisted Particle Swarm Optimization of High-Dimensional Expensive Problems. IEEE Trans. Evol. Comput. 2019, 23, 459–472. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, H.; Chugh, T.; Guo, D.; Miettinen, K. Data-Driven Evolutionary Optimization: An Overview and Case Studies. IEEE Trans. Evol. Comput. 2019, 23, 442–458. [Google Scholar] [CrossRef]
- Yang, C.; Ding, J.; Jin, Y.; Chai, T. Offline Data-Driven Multiobjective Optimization: Knowledge Transfer Between Surrogates and Generation of Final Solutions. IEEE Trans. Evol. Comput. 2020, 24, 409–423. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Jin, Y. Surrogate-Assisted Multipopulation Particle Swarm Optimizer for High-Dimensional Expensive Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4671–4684. [Google Scholar] [CrossRef]
- Zhou, Y.; He, X.; Chen, Z.; Jiang, S. A Neighborhood Regression Optimization Algorithm for Computationally Expensive Optimization Problems. IEEE Trans. Cybern. 2022, 52, 3018–3031. [Google Scholar] [CrossRef] [PubMed]
- Gutjahr, W.J. Convergence Analysis of Metaheuristics. In Matheuristics: Hybridizing Metaheuristics and Mathematical Programming; Maniezzo, V., Stützle, T., Voß, S., Eds.; Springer: Boston, MA, USA, 2010; pp. 159–187. [Google Scholar] [CrossRef]
- Zamani, S.; Hemmati, H. A Cost-Effective Approach for Hyper-Parameter Tuning in Search-based Test Case Generation. In Proceedings of the 2020 IEEE International Conference on Software Maintenance and Evolution (ICSME), Adelaide, Australia, 28 September–2 October 2020; pp. 418–429. [Google Scholar] [CrossRef]
- Gu, Q.; Wang, Q.; Xiong, N.N.; Jiang, S.; Chen, L. Surrogate-assisted Evolutionary Algorithm for Expensive Constrained Multi-objective Discrete Optimization Problems. Complex Intell. Syst. 2022, 8, 2699–2718. [Google Scholar] [CrossRef]
- Sarker, R.A.; Elsayed, S.M.; Ray, T. Differential Evolution With Dynamic Parameters Selection for Optimization Problems. IEEE Trans. Evol. Comput. 2014, 18, 689–707. [Google Scholar] [CrossRef]
- Karafotias, G.; Hoogendoorn, M.; Eiben, A.E. Parameter Control in Evolutionary Algorithms: Trends and Challenges. IEEE Trans. Evol. Comput. 2015, 19, 167–187. [Google Scholar] [CrossRef]
- Plevris, V.; Bakas, N.P.; Solorzano, G. Pure Random Orthogonal Search (PROS): A Plain and Elegant Parameterless Algorithm for Global Optimization. Appl. Sci. 2021, 11, 5053. [Google Scholar] [CrossRef]
- Vesterstrom, J.; Thomsen, R. A Comparative Study of Differential Evolution, Particle Swarm Optimization, and Evolutionary Algorithms on Numerical Benchmark Problems. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2004; Volume 2, pp. 1980–1987. [Google Scholar] [CrossRef]
- Omidvar, M.N.; Li, X.; Tang, K. Designing Benchmark Problems for Large-scale Continuous Optimization. Inf. Sci. 2015, 316, 419–436. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Hansen, N. Adaptive Encoding: How to Render Search Coordinate System Invariant. In Parallel Problem Solving from Nature—PPSN X; Rudolph, G., Jansen, T., Beume, N., Lucas, S., Poloni, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 205–214. [Google Scholar] [CrossRef]
- Loshchilov, I.; Schoenauer, M.; Sebag, M. Adaptive Coordinate Descent. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, GECCO ’11, Dublin, Ireland, 12–16 July 2011; pp. 885–892. [Google Scholar] [CrossRef]



| No. | Function | Formulation and Global Optimum | Search Space |
|---|---|---|---|
| Sphere | |||
| Ellipsoid | |||
| Schwefel 1.2 | |||
| Rosenbrock | |||
| Zakharov | |||
| Alpine 1 | |||
| Rastrigin | |||
| Ackley | |||
| Griewank | |||
| HGBat | |||
| HappyCat | |||
| Weierstrass | |||
| Settings | ||||
|---|---|---|---|---|
| Population Size | 50 | 100 | 500 | |
| Max. No. of Generations | 50 | 150 | 950 | |
| Max. No. of Objective | 2500 | 15,000 | 475,000 | |
| Function Evaluations | ||||
| No. of Runs | 100 | 100 | 30 |
| f | PROS | TROS | QROS |
|---|---|---|---|
| 4.65e-03 (4.85e-03) | 1.06e-03 (8.88e-04) | 4.13e-04 (4.54e-04) | |
| 1.38e-02 (1.68e-02) | 3.13e-03 (2.65e-03) | 1.21e-03 (1.33e-03) | |
| 2.17e-01 (1.80e-01) | 7.61e-02 (5.05e-02) | 4.32e-02 (2.99e-02) | |
| 1.34e+00 (1.17e+00) | 1.48e+00 (1.16e+00) | 1.55e+00 (1.17e+00) | |
| 5.13e+00 (6.46e+00) | 5.33e-01 (8.45e-01) | 1.28e-01 (1.81e-01) | |
| 4.81e-03 (3.68e-03) | 2.38e-03 (9.69e-04) | 1.62e-03 (7.19e-04) | |
| 2.41e-01 (2.49e-01) | 5.30e-02 (4.49e-02) | 2.91e-02 (3.01e-02) | |
| 7.48e-01 (4.80e-01) | 2.81e-01 (1.65e-01) | 1.53e-01 (8.95e-02) | |
| 2.69e-01 (1.41e-01) | 1.33e-01 (6.76e-02) | 8.98e-02 (3.69e-02) | |
| 4.01e-01 (1.40e-01) | 3.34e-01 (1.24e-01) | 2.83e-01 (1.26e-01) | |
| 4.67e-01 (1.34e-01) | 4.05e-01 (1.20e-01) | 3.72e-01 (9.48e-02) | |
| 3.49e-01 (1.04e-01) | 2.22e-01 (6.44e-02) | 1.77e-01 (4.67e-02) |
| f | PROS | TROS | QROS |
|---|---|---|---|
| 8.62e-04 (7.26e-04) | 2.38e-04 (1.85e-04) | 1.03e-04 (7.51e-05) | |
| 4.45e-03 (3.33e-03) | 1.34e-03 (1.23e-03) | 5.68e-04 (4.63e-04) | |
| 6.84e-01 (3.62e-01) | 2.52e-01 (1.35e-01) | 1.35e-01 (7.28e-02) | |
| 3.40e+00 (3.28e+00) | 3.72e+00 (2.99e+00) | 4.53e+00 (2.91e+00) | |
| 4.69e+01 (2.47e+01) | 1.40e+01 (9.29e+00) | 6.26e+00 (4.77e+00) | |
| 3.10e-03 (9.52e-04) | 1.70e-03 (5.30e-04) | 1.10e-03 (3.52e-04) | |
| 4.48e-02 (3.77e-02) | 1.24e-02 (9.46e-03) | 5.24e-03 (3.56e-03) | |
| 1.61e-01 (8.23e-02) | 7.13e-02 (3.00e-02) | 4.32e-02 (1.55e-02) | |
| 1.78e-01 (6.53e-02) | 9.15e-02 (3.68e-02) | 6.77e-02 (2.74e-02) | |
| 4.73e-01 (2.46e-01) | 4.35e-01 (1.97e-01) | 4.31e-01 (1.99e-01) | |
| 4.90e-01 (1.65e-01) | 4.30e-01 (1.49e-01) | 3.76e-01 (1.17e-01) | |
| 3.40e-01 (8.16e-02) | 2.20e-01 (4.97e-02) | 1.68e-01 (3.85e-02) |
| f | PROS | TROS | QROS |
|---|---|---|---|
| 1.12e-04 (3.30e-05) | 2.82e-05 (7.60e-06) | 1.24e-05 (4.68e-06) | |
| 2.86e-03 (9.68e-04) | 7.25e-04 (2.22e-04) | 3.29e-04 (1.32e-04) | |
| 1.34e+01 (3.13e+00) | 6.45e+00 (1.57e+00) | 3.75e+00 (8.21e-01) | |
| 8.06e+01 (3.80e+01) | 6.05e+01 (3.41e+01) | 5.48e+01 (2.46e+01) | |
| 9.66e+02 (1.63e+02) | 7.58e+02 (1.51e+02) | 6.44e+02 (1.36e+02) | |
| 2.46e-03 (3.48e-04) | 1.32e-03 (1.93e-04) | 8.85e-04 (1.26e-04) | |
| 5.81e-03 (1.72e-03) | 1.32e-03 (2.79e-04) | 6.25e-04 (1.60e-04) | |
| 2.06e-02 (3.28e-03) | 9.90e-03 (1.13e-03) | 6.49e-03 (9.52e-04) | |
| 2.63e-02 (1.51e-02) | 1.17e-02 (1.01e-02) | 1.39e-02 (1.77e-02) | |
| 5.99e-01 (2.48e-01) | 5.80e-01 (2.25e-01) | 5.66e-01 (2.27e-01) | |
| 6.51e-01 (1.28e-01) | 6.17e-01 (1.11e-01) | 6.21e-01 (1.08e-01) | |
| 5.34e-01 (4.80e-02) | 3.43e-01 (2.93e-02) | 2.61e-01 (2.84e-02) |
| f | PROS | TROS | QROS |
|---|---|---|---|
| 4.31e-03 (4.38e-03) | 1.67e-03 (3.92e-03) | 1.15e-03 (5.90e-03) | |
| 1.24e-02 (1.20e-02) | 4.41e-03 (7.05e-03) | 2.60e-03 (9.36e-03) | |
| 2.64e-01 (2.23e-01) | 9.43e-02 (8.36e-02) | 5.54e-02 (4.39e-02) | |
| 1.38e+00 (3.51e+00) | 9.47e-01 (3.44e+00) | 1.82e+00 (1.12e+01) | |
| 7.76e+00 (1.24e+01) | 8.39e-01 (1.16e+00) | 2.60e-01 (4.88e-01) | |
| 4.62e-03 (2.28e-03) | 6.57e-03 (9.53e-03) | 1.21e-02 (1.96e-02) | |
| 2.23e-01 (2.23e-01) | 1.39e-01 (3.07e-01) | 2.97e-01 (5.00e-01) | |
| 7.34e-01 (4.52e-01) | 3.27e-01 (2.86e-01) | 2.34e-01 (3.01e-01) | |
| 2.94e-01 (1.97e-01) | 1.54e-01 (7.26e-02) | 1.18e-01 (1.06e-01) | |
| 3.90e-01 (1.68e-01) | 3.18e-01 (1.22e-01) | 3.13e-01 (1.38e-01) | |
| 4.82e-01 (1.21e-01) | 4.28e-01 (1.43e-01) | 4.15e-01 (1.93e-01) | |
| 3.47e-01 (1.03e-01) | 2.64e-01 (1.33e-01) | 2.79e-01 (2.32e-01) |
| f | PROS | TROS | QROS |
|---|---|---|---|
| 8.71e-04 (5.89e-04) | 2.55e-04 (1.99e-04) | 1.64e-04 (2.97e-04) | |
| 4.64e-03 (3.58e-03) | 1.33e-03 (1.18e-03) | 9.91e-04 (2.60e-03) | |
| 7.99e-01 (4.64e-01) | 2.78e-01 (1.76e-01) | 1.62e-01 (9.67e-02) | |
| 1.35e+00 (6.26e+00) | 8.60e-01 (2.81e+00) | 8.20e-01 (2.68e+00) | |
| 6.23e+01 (4.86e+01) | 1.80e+01 (1.70e+01) | 7.34e+00 (7.04e+00) | |
| 3.12e-03 (9.80e-04) | 2.38e-03 (2.74e-03) | 6.05e-03 (9.72e-03) | |
| 4.53e-02 (3.06e-02) | 6.38e-02 (2.58e-01) | 2.65e-01 (5.19e-01) | |
| 1.64e-01 (7.02e-02) | 8.10e-02 (3.39e-02) | 6.33e-02 (1.06e-01) | |
| 1.85e-01 (6.35e-02) | 9.56e-02 (3.76e-02) | 7.97e-02 (3.49e-02) | |
| 3.84e-01 (2.06e-01) | 3.61e-01 (1.80e-01) | 3.37e-01 (1.96e-01) | |
| 4.50e-01 (1.46e-01) | 4.51e-01 (2.05e-01) | 4.45e-01 (1.92e-01) | |
| 3.31e-01 (7.39e-02) | 2.52e-01 (9.44e-02) | 3.03e-01 (2.26e-01) |
| f | PROS | TROS | QROS |
|---|---|---|---|
| 1.13e-04 (2.63e-05) | 2.88e-05 (1.00e-05) | 1.30e-05 (4.43e-06) | |
| 2.90e-03 (7.79e-04) | 7.43e-04 (3.28e-04) | 3.31e-04 (1.23e-04) | |
| 1.78e+01 (4.20e+00) | 8.55e+00 (1.75e+00) | 5.46e+00 (1.20e+00) | |
| 2.02e+01 (3.98e+01) | 2.59e+00 (8.90e+00) | 3.84e+00 (1.35e+01) | |
| 1.93e+03 (4.23e+02) | 1.55e+03 (3.24e+02) | 1.30e+03 (2.85e+02) | |
| 2.62e-03 (3.48e-04) | 1.69e-03 (5.51e-04) | 3.19e-03 (2.83e-03) | |
| 5.89e-03 (1.37e-03) | 1.58e-03 (4.07e-04) | 2.99e-01 (5.23e-01) | |
| 2.09e-02 (2.66e-03) | 9.85e-03 (1.31e-03) | 6.68e-03 (1.06e-03) | |
| 2.77e-02 (1.27e-02) | 1.92e-02 (1.70e-02) | 5.13e-02 (4.70e-02) | |
| 3.68e-01 (1.11e-01) | 3.70e-01 (1.55e-01) | 3.32e-01 (9.46e-02) | |
| 5.82e-01 (1.11e-01) | 5.74e-01 (9.44e-02) | 6.06e-01 (1.34e-01) | |
| 5.51e-01 (4.15e-02) | 3.93e-01 (1.21e-01) | 5.14e-01 (2.79e-01) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, B.K.-B.; Sung, C.W.; Wong, W.S. Random Orthogonal Search with Triangular and Quadratic Distributions (TROS and QROS): Parameterless Algorithms for Global Optimization. Appl. Sci. 2023, 13, 1391. https://doi.org/10.3390/app13031391
Tong BK-B, Sung CW, Wong WS. Random Orthogonal Search with Triangular and Quadratic Distributions (TROS and QROS): Parameterless Algorithms for Global Optimization. Applied Sciences. 2023; 13(3):1391. https://doi.org/10.3390/app13031391
Chicago/Turabian StyleTong, Bruce Kwong-Bun, Chi Wan Sung, and Wing Shing Wong. 2023. "Random Orthogonal Search with Triangular and Quadratic Distributions (TROS and QROS): Parameterless Algorithms for Global Optimization" Applied Sciences 13, no. 3: 1391. https://doi.org/10.3390/app13031391
APA StyleTong, B. K.-B., Sung, C. W., & Wong, W. S. (2023). Random Orthogonal Search with Triangular and Quadratic Distributions (TROS and QROS): Parameterless Algorithms for Global Optimization. Applied Sciences, 13(3), 1391. https://doi.org/10.3390/app13031391






