Estimation of Interaction Locations in Super Cryogenic Dark Matter Search Detectors Using Genetic Programming-Symbolic Regression Method
Abstract
:1. Introduction
1.1. Application of ML Algorithms in CDSM/SuperCDSM Experiments
1.2. Definition of Novelty and the Research Hypotheses
- Can an SE be obtained using GPSR that can accurately reconstruct the locations of the interactions in SuperCDMS detectors?
- Is it possible to obtain a set of robust SEs using GPSR with randomly tested hyperparameters and validated through k-fold cross-validation that can reconstruct the locations of the interactions in the SuperCDMS with high accuracy?
- Is it possible to achieve even higher estimation accuracy in the reconstruction of the locations’ interactions by combining multiple SEs that were obtained from different GPSR executions?
- Are all input variables required as model inputs to accurately reconstruct the interaction locations?
2. Materials and Methods
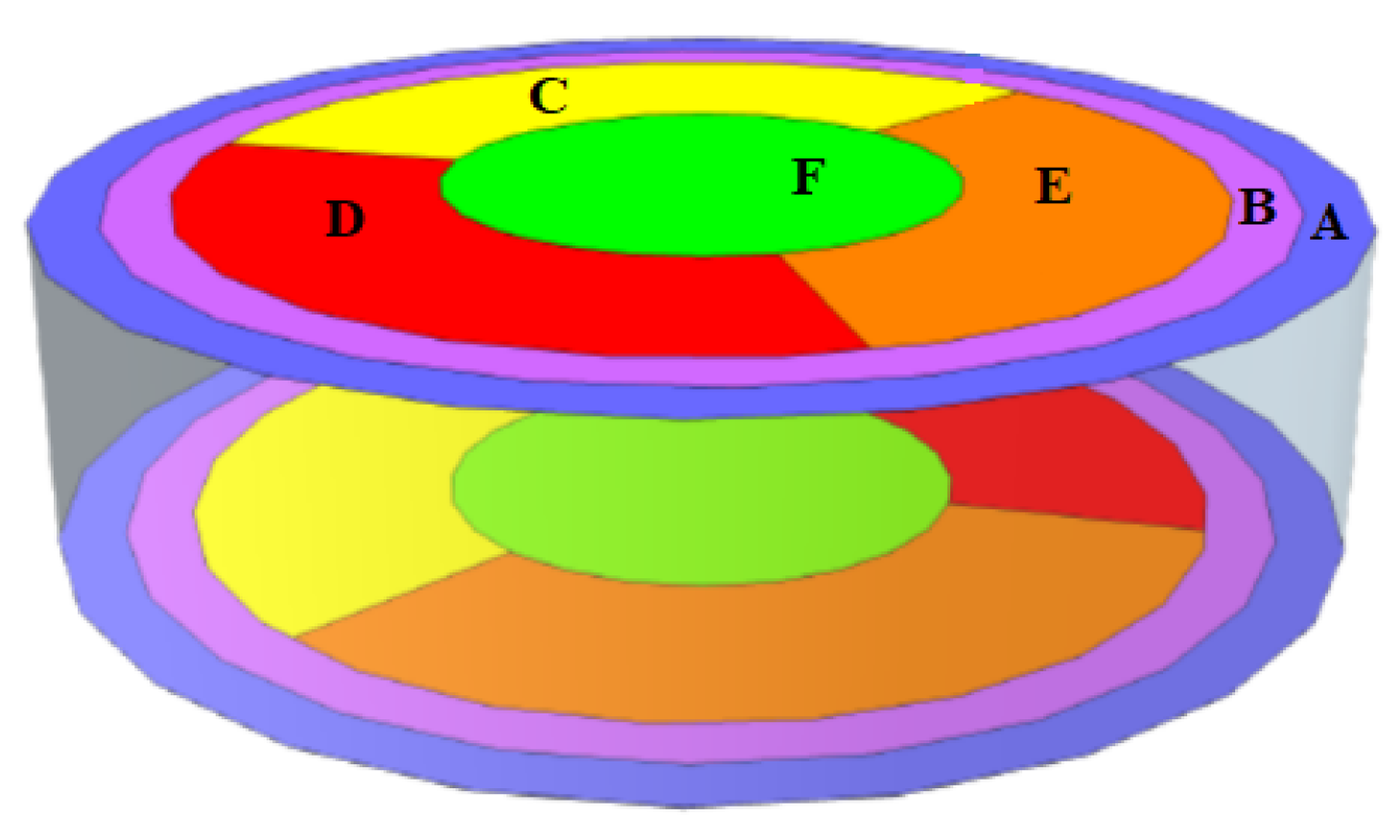
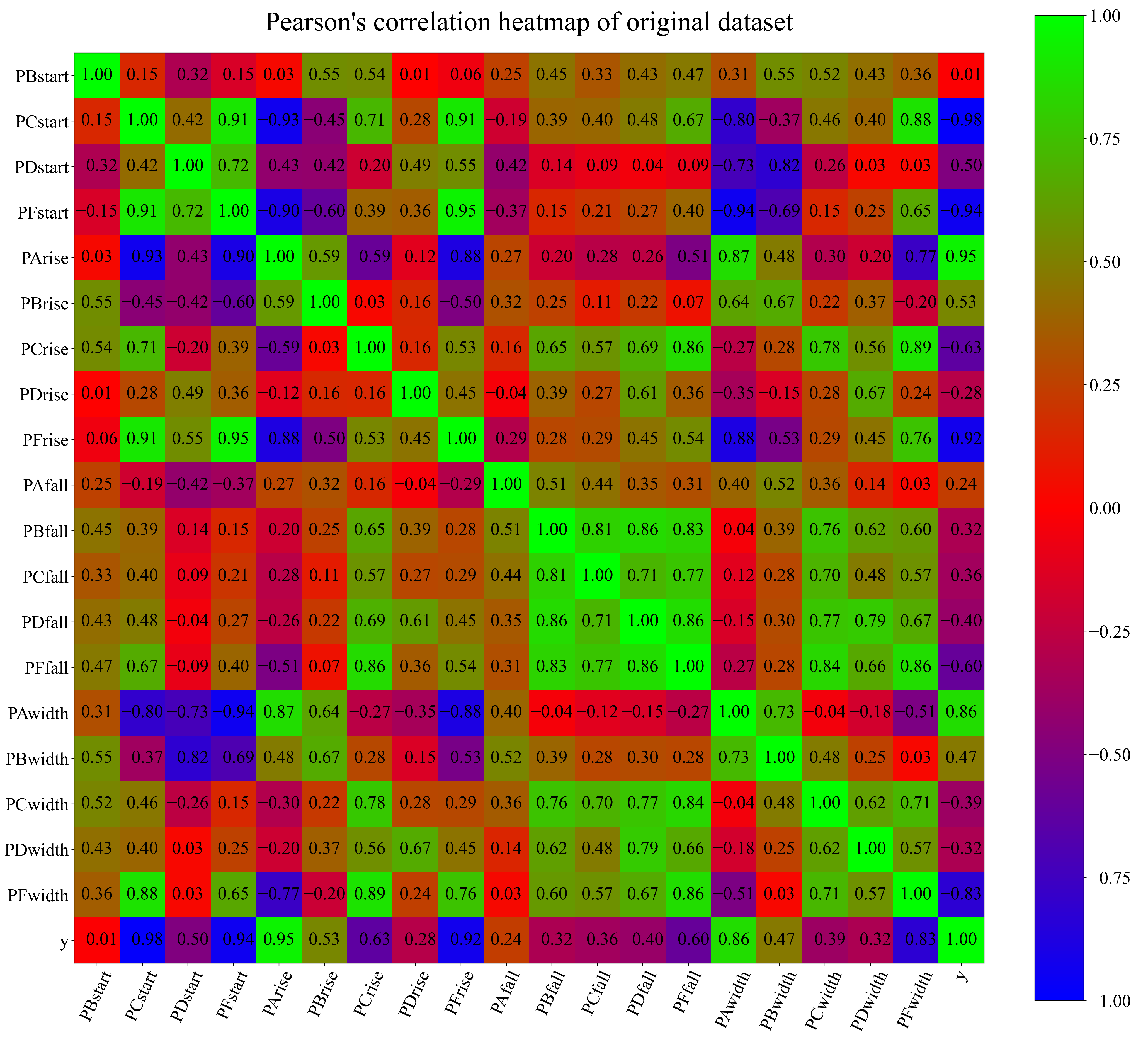
2.1. Dataset Description
- B, C, D, and F start—the time at which the signal pulse rises to 20% of the signal peak to Channel A. The variables in the original dataset are labeled as PBstart, PCstart, PDstart, and PDstart, respectively.
- A, B, C, D, and F rise—the time required for the signal to rise from 20 % to 80% of its peak. These variables in the original dataset are labeled as PArise, PBrise, PCrise, PDrise, and PFrise,
- A, B, C, D, and F width—the width of the pulse at 80% of the pulse height. The height was measured in seconds. These variables in the original dataset are labeled as PAwidth, PBwidth, PCwidth, PDwidth, and PFwidth.
- A, B, C, D, and F fall—the time required for a pulse to fall from 40% to 20 % of its peak. These variables in the original dataset are labeled as PAfall, PBfall, PCfall, PDfall, and PFfall.
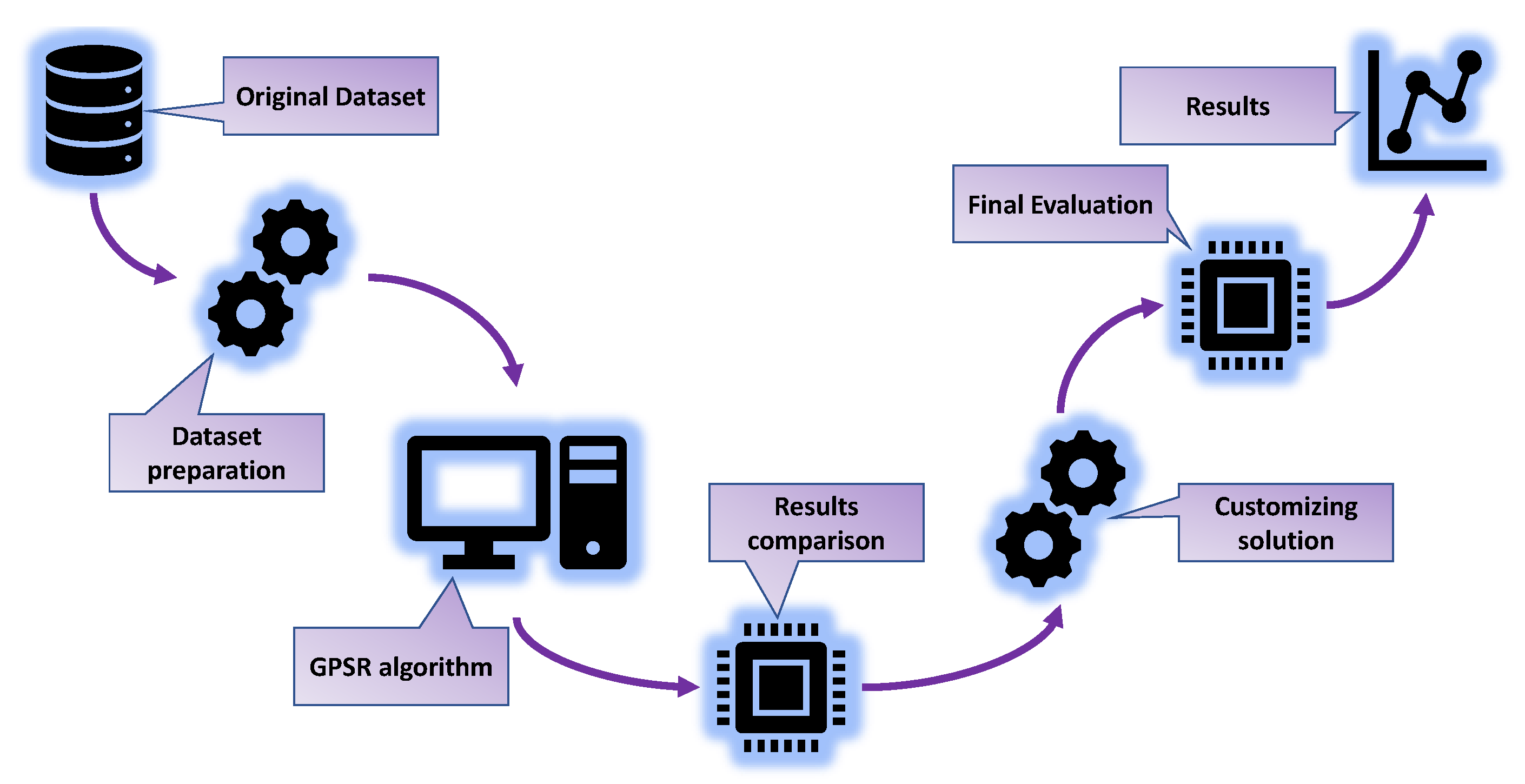
2.2. Research Methodology
- Dataset preparation—Checking the dataset for null values and deleting the first column (“Row”), which is not relevant for the analysis. Separating the dataset into input and output variables and applying of StandardScaler method on the input dataset variables. Dividing the dataset into training and testing datasets in a 70:30 ratio.
- GPSR algorithm—The GPSR algorithm is combined with a RHS to find the hyperparameters that yield the best-performing models. Perform training of GPSR on the training dataset using cross-validation, for the evaluation of the testing dataset.
- Result comparison—Perform a comparison of the best sets of SEs in terms of the estimation accuracy.
- Customizing solution—Combining the five best SEs to obtain a robust estimator for the reconstruction of the interaction locations.
- Final evaluation—Perform the final evaluation of the customized solution on the entire dataset.
2.3. Genetic Programming-Symbolic Regression
2.4. Random Hyperparameter Search
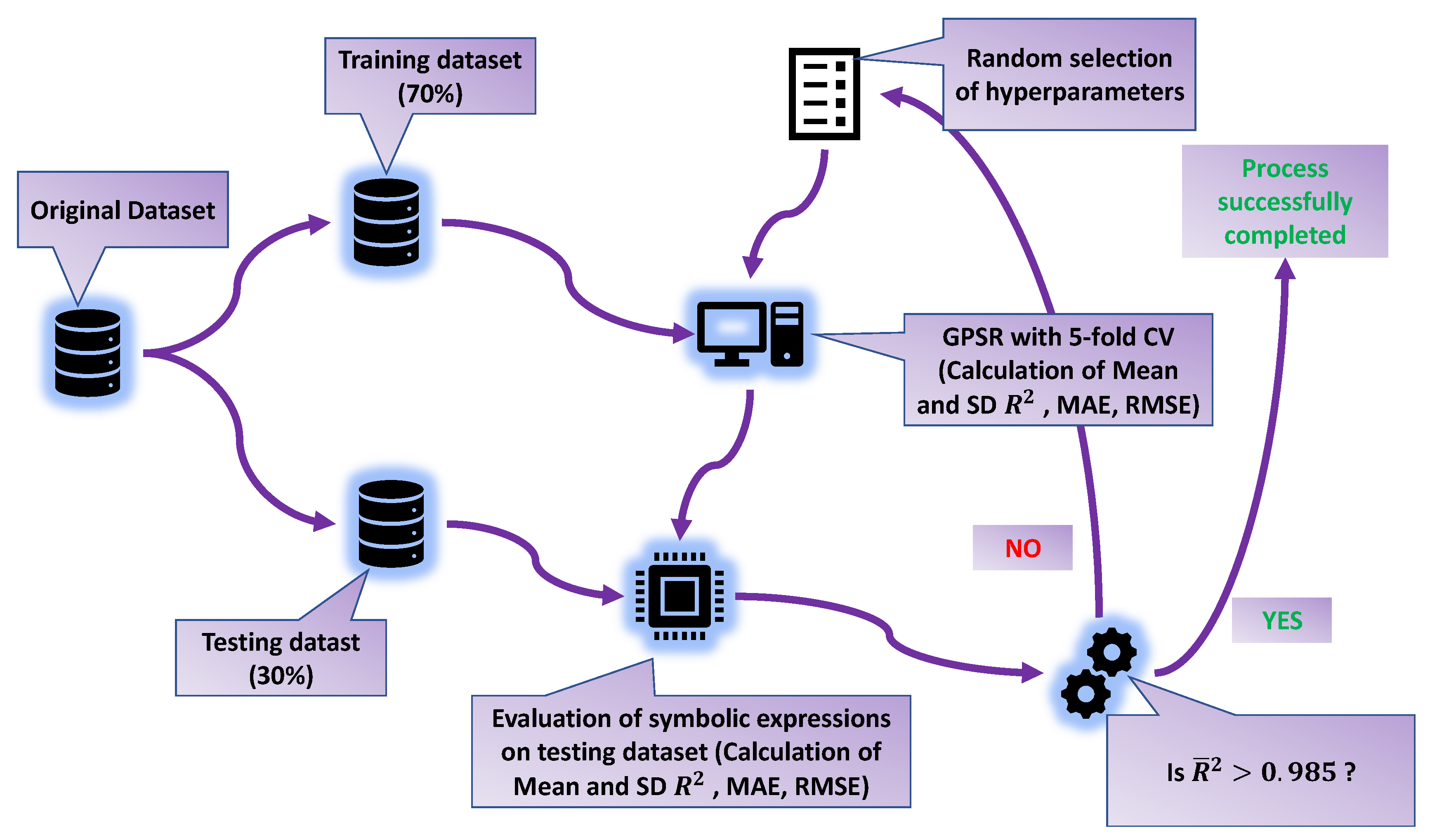
2.5. Training and Evaluation Process with the GPSR Algorithm
2.6. Performance Metrics and Methodology
- During the 5-CV, calculate the performance metric values on the training and validation sets.
- After the 5-CV process is complete, calculate the performance metrics (mean values obtained on the training dataset).
- Perform the last evaluation of the trained model (five SEs) on the testing dataset, and calculate the performance (evaluation) metric values (values achieved on the testing dataset),
- Calculate the mean and values of the performance metrics from the obtained values on the training and testing datasets.
2.7. Computational Resources
3. Results
3.1. Results Acquired Using GPSR with RHS and 5-CV
3.2. Combination of the Best SE
4. Discussion
5. Conclusions
- Using the GPSR algorithm, it was possible to obtain SEs (mathematical equations) that can estimate the interaction locations in Super Cryogenic Matter Search detectors with high accuracy.
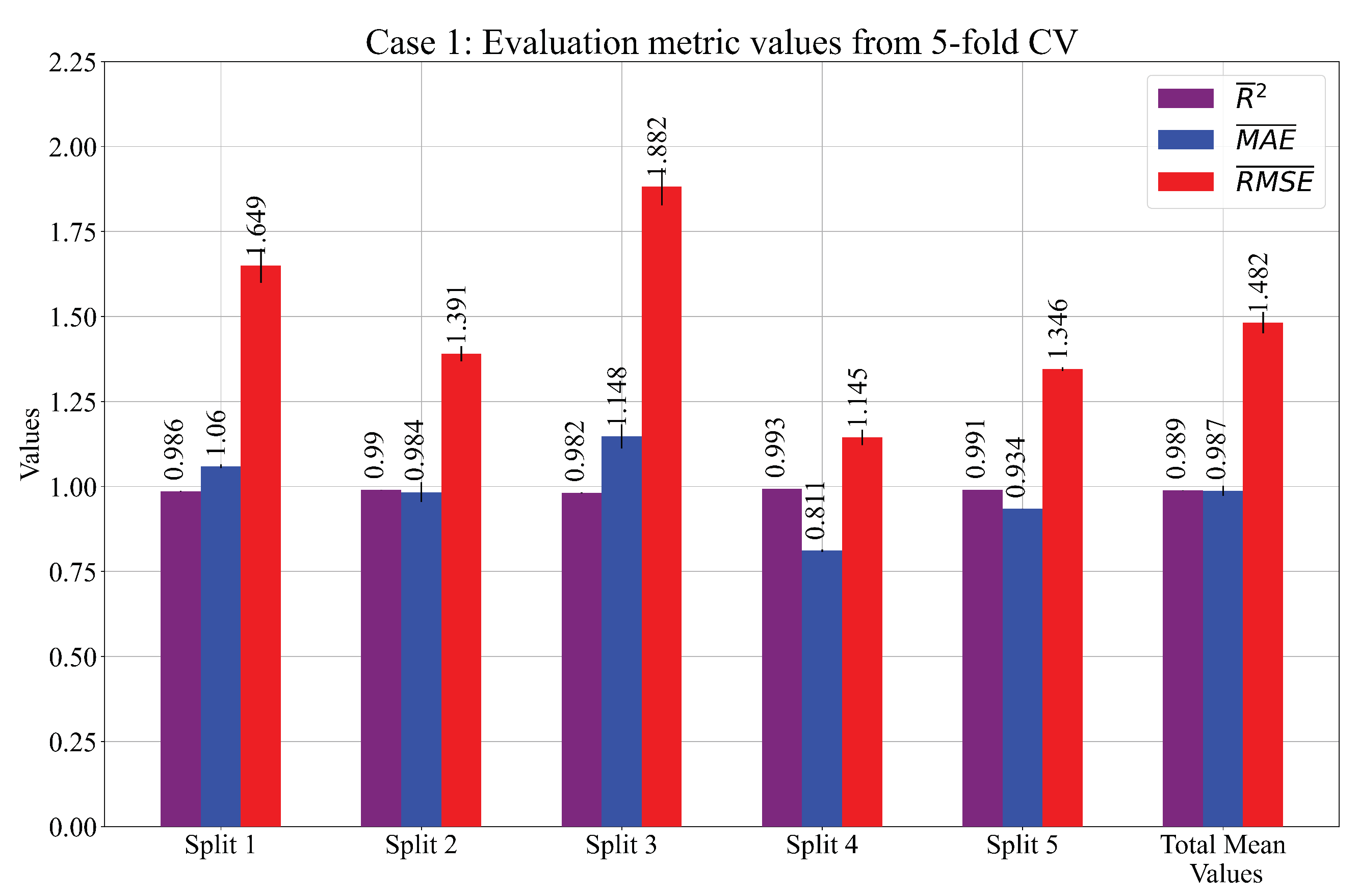
- Using a 5-CV process, the robust system of the five SEs has a more accurate estimation when compared to the estimation of only one SE. The RHS method proved to be very useful in finding the combination of the quality hyperparameters where the highest accuracy was achieved. From all the results, the best three cases of the SEs were selected and evaluated on the test set. The highest values of , , were achieved in Case 1 and are equal to , , .
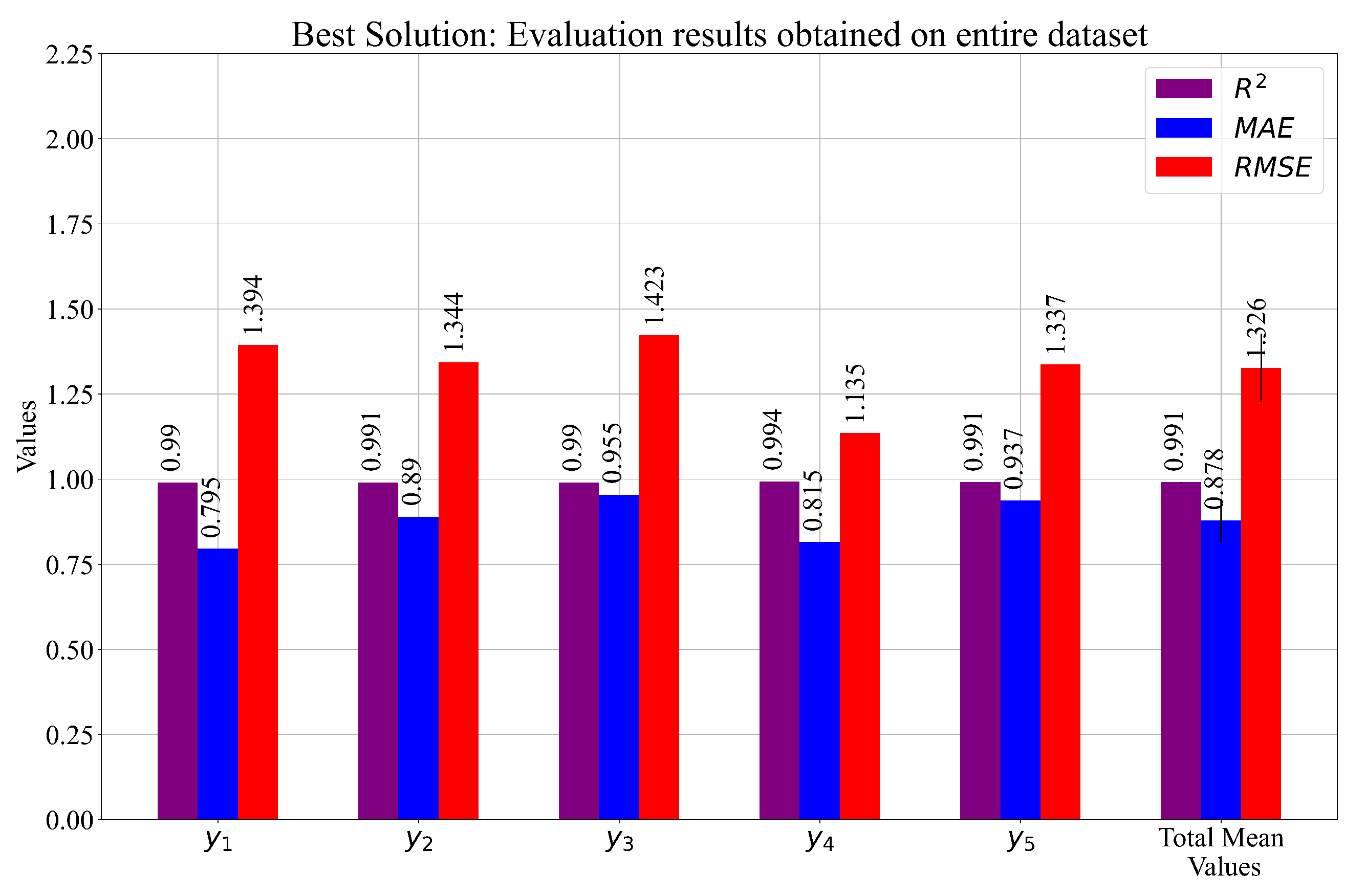
- From the obtained results, three cases were selected based on the final mean score. From these cases, the SEs that achieved the highest estimation performance were selected as the main elements of the custom set of SEs. The results of the customized solution obtained on the entire dataset were equal to , , and , respectively. The final evaluation of these equations on the entire dataset showed that this system had slightly better performance when compared to Cases 1, 2, and 3.
- Unfortunately, the custom set of SEs required all 19 input variables to compute the output. However, if only Equation (7) was used, the highest estimation accuracy could be achieved, and to compute the output, only seven input variables were required.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Description of Mathematical Functions in SEs
- Square root:
- Natural logarithm:and when natural logarithms with base 2 and 10 are used, the log in Equation (A2) is replaced with or , respectively.
- Division:
References
- Roszkowski, L.; Sessolo, E.M.; Trojanowski, S. WIMP dark matter candidates and searches—current status and future prospects. Rep. Prog. Phys. 2018, 81, 066201. [Google Scholar] [CrossRef] [PubMed]
- Akerib, D.; Alvaro-Dean, J.; Armel-Funkhouser, M.; Attisha, M.; Baudis, L.; Bauer, D.; Beaty, J.; Brink, P.; Bunker, R.; Burke, S.; et al. First results from the cryogenic dark matter search in the soudan underground laboratory. Phys. Rev. Lett. 2004, 93, 211301. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, Z.; The CDMS Collaboration. Results from the Final Exposure of the CDMS II Experiment. arXiv 2009, arXiv:0912.3592. [Google Scholar]
- Aprile, E.; Alfonsi, M.; Arisaka, K.; Arneodo, F.; Balan, C.; Baudis, L.; Bauermeister, B.; Behrens, A.; Beltrame, P.; Bokeloh, K.; et al. Dark matter results from 225 live days of XENON100 data. Phys. Rev. Lett. 2012, 109, 181301. [Google Scholar] [CrossRef] [PubMed]
- Pyle, M.; Serfass, B.; Brink, P.; Cabrera, B.; Cherry, M.; Mirabolfathi, N.; Novak, L.; Sadoulet, B.; Seitz, D.; Sundqvist, K.; et al. Surface electron rejection from ge detector with interleaved charge and phonon channels. In Proceedings of the AIP Conference Proceedings, Stanford, CA, USA, 20–24 July 2009; Volume 1185, pp. 223–226. [Google Scholar]
- Jahangir, O. Application of Machine Learning Techniques to Direct Detection Dark Matter Experiments. Ph.D. Thesis, UCL (University College London), London, UK, 2022. [Google Scholar]
- Bernardini, M.; Mayer, L.; Reed, D.; Feldmann, R. Predicting dark matter halo formation in N-body simulations with deep regression networks. Mon. Not. R. Astron. Soc. 2020, 496, 5116–5125. [Google Scholar] [CrossRef]
- Theenhausen, H.; von Krosigk, B.; Wilson, J. Neural-network-based level-1 trigger upgrade for the SuperCDMS experiment at SNOLAB. arXiv 2022, arXiv:2212.07864. [Google Scholar]
- Zhang, X.; Wang, Y.; Zhang, W.; Sun, Y.; He, S.; Contardo, G.; Villaescusa-Navarro, F.; Ho, S. From dark matter to galaxies with convolutional networks. arXiv 2019, arXiv:1902.05965. [Google Scholar]
- Lucie-Smith, L.; Peiris, H.V.; Pontzen, A. An interpretable machine-learning framework for dark matter halo formation. Mon. Not. R. Astron. Soc. 2019, 490, 331–342. [Google Scholar] [CrossRef]
- Simola, U.; Pelssers, B.; Barge, D.; Conrad, J.; Corander, J. Machine learning accelerated likelihood-free event reconstruction in dark matter direct detection. J. Instrum. 2019, 14, P03004. [Google Scholar] [CrossRef]
- FAIR-UMN. CDMS-Dataset. Available online: https://www.kaggle.com/datasets/fairumn/cdms-dataset (accessed on 12 January 2023).
- FAIR-UMN, Taihui Li. FAIR Document—Identifying Interaction Location in SuperCDMS Detectors. Available online: https://github.com/FAIR-UMN/FAIR-UMN-CDMS/blob/main/doc/FAIR%20Document%20-%20Identifying%20Interaction%20Location%20in%20SuperCDMS%20Detectors.pdf (accessed on 12 January 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Mendenhall, W.M.; Sincich, T.L.; Boudreau, N.S. Statistics for Engineering and the Sciences Student Solutions Manual; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lakatos, R.; Bogacsovics, G.; Hajdu, A. Predicting the direction of the oil price trend using sentiment analysis. In Proceedings of the 2022 IEEE 2nd Conference on Information Technology and Data Science (CITDS), Debrecen, Hungary, 16–18 May 2022; pp. 177–182. [Google Scholar]
- Poli, R.; Langdon, W.; Mcphee, N. A Field Guide to Genetic Programming; 2008. Available online: http://www.gp-field-guide.org.uk/ (accessed on 2 January 2023).
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Langdon, W.B. Size fair and homologous tree genetic programming crossovers. Genet. Program. Evolvable Mach. 2000, 1, 95–119. [Google Scholar] [CrossRef]
- Crawford-Marks, R.; Spector, L. Size Control Via Size Fair Genetic Operators In The PushGP Genetic Programming System. In Proceedings of the GECCO, New York, NY, USA, 9–13 July 2002; pp. 733–739. [Google Scholar]
- Poli, R. A simple but theoretically-motivated method to control bloat in genetic programming. In Proceedings of the European Conference on Genetic Programming, Essex, UK, 14–16 April 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 204–217. [Google Scholar]
- Zhang, B.T.; Mühlenbein, H. Balancing accuracy and parsimony in genetic programming. Evol. Comput. 1995, 3, 17–38. [Google Scholar] [CrossRef]
- Anđelić, N.; Baressi Šegota, S.; Glučina, M.; Lorencin, I. Classification of Wall Following Robot Movements Using Genetic Programming Symbolic Classifier. Machines 2023, 11, 105. [Google Scholar] [CrossRef]
- Anđelić, N.; Lorencin, I.; Baressi Šegota, S.; Car, Z. The Development of Symbolic Expressions for the Detection of Hepatitis C Patients and the Disease Progression from Blood Parameters Using Genetic Programming-Symbolic Classification Algorithm. Appl. Sci. 2022, 13, 574. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Y. Analysis of the mean absolute error (MAE) and the root mean square error (RMSE) in assessing rounding model. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kuala Lumpur, Malaysia, 13–14 August 2018; Volume 324, p. 012049. [Google Scholar]
- Di Bucchianico, A. Coefficient of determination (R 2). Encycl. Stat. Qual. Reliab. 2008, 1, eqr173. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 445, pp. 51–56.
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Stephens, T. GPLearn (2015). 2019. Available online: https://gplearn.readthedocs.io/en/stable/index.html (accessed on 2 January 2023).



| Location | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coordinate x | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Coordinate y | 0 | −3.96 | −9.98 | −12.502 | −17.992 | −19.7 | −21.034 | −24.077 | −29.5 | −36.116 | −39.4 | −41.01 | −41.9 |
| Dataset Variable | Data Points | Mean Value | Minimum Value | Maximum Value | GPSR Variable Symbol | |
|---|---|---|---|---|---|---|
| PBstart | 7151 | |||||
| PCstart | ||||||
| PDstart | ||||||
| PFstart | ||||||
| PArise | ||||||
| PBrise | ||||||
| PCrise | ||||||
| PDrise | ||||||
| PFrise | ||||||
| PAfall | ||||||
| PBfall | ||||||
| PCfall | ||||||
| PDfall | ||||||
| PFfall | ||||||
| PAwidth | ||||||
| PBwidth | ||||||
| PCwidth | ||||||
| PDwidth | ||||||
| PFwidth | ||||||
| y | −21.758 | 14.091 | −41.9 | 0 | y |
| Hyperparameter Name | Range |
|---|---|
| population_size | 1000–2000 |
| number of generations | 100–200 |
| tournament_selection | 10–500 |
| init_depth | 3–15 |
| crossover | 0.001–1.0 |
| subtree_mutation | 0.001–1.0 |
| hoist_mutation | 0.001–1.0 |
| point_mutation | 0.001–1.0 |
| stopping_criteria | 0– |
| maximum_samples | 0.99–1 |
| constant_range | −10,000–10,000 |
| parsimony_coefficient | 0– |
| Case No. | GPSR Hyperparameters (Population Size, Number of Generations, Tournament Selection, Init_Depth, Crossover, Subtree_Mutation, Hoist_Mutation, Point_Mutation, Stopping_Criteria, Max_Samples, Constant_Range, Parsimony_Coefficient) |
|---|---|
| 1 | 1978, 233, 254, (6, 15), 0.043, 0.22, 0.22, 0.43, , 0.99, (−9793.08, 1402.72), |
| 2 | 1075, 196, 461, (3, 15), 0.41, 0.4, 0.05, 0.097, , 0.99, (−8821.29, 3713.89), |
| 3 | 1500, 171, 108,(7, 11), 0.45, 0.469, 0.043, 0.0071, , 0.99, (−4076.61, 4272.87), |
| Performance metric | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Total | |
| 0.9864 | 0.9903 | 0.9821 | 0.9935 | 0.9909 | 0.9886 | ||
| 0.0009 | 0.0003 | 0.0013 | 0.0002 | 0.0001 | 0.0006 | ||
| Case 1 | 1.0599 | 0.9837 | 1.1479 | 0.8113 | 0.9342 | 0.9874 | |
| 0.0057 | 0.0291 | 0.0354 | 0.0035 | 0.0003 | 0.0148 | ||
| 1.6494 | 1.3905 | 1.8818 | 1.1445 | 1.3456 | 1.4824 | ||
| 0.0501 | 0.0222 | 0.0542 | 0.0230 | 0.0057 | 0.0311 | ||
| Performance metric | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Total | |
| 0.9889 | 0.9905 | 0.9896 | 0.9835 | 0.9860 | 0.9877 | ||
| 0.0001 | 0.0006 | 0.0001 | 0.0001 | 0.0009 | 0.0004 | ||
| Case 2 | 1.0304 | 0.8973 | 0.9593 | 1.1713 | 1.0530 | 1.0223 | |
| 0.0233 | 0.0115 | 0.0108 | 0.0006 | 0.0238 | 0.0140 | ||
| 1.5057 | 1.3883 | 1.4369 | 1.7984 | 1.6564 | 1.5571 | ||
| 0.0331 | 0.0562 | 0.0062 | 0.0218 | 0.0772 | 0.0389 | ||
| Performance metric | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Total | |
| 0.9899 | 0.9856 | 0.9896 | 0.9846 | 0.9868 | 0.9873 | ||
| 0.0004 | 0.0019 | 0.0001 | 0.0001 | 0.0013 | 0.0008 | ||
| Case 3 | 0.8020 | 1.0330 | 1.0266 | 1.2512 | 1.0365 | 1.0299 | |
| 0.0041 | 0.0302 | 0.0170 | 0.0128 | 0.0328 | 0.0194 | ||
| 1.4336 | 1.7058 | 1.4429 | 1.7375 | 1.6111 | 1.5862 | ||
| 0.0489 | 0.1311 | 0.0051 | 0.0170 | 0.1016 | 0.0608 |
| Case No. | Symbolic Expression No. | Length | Depth | Average Length | Average Depth |
|---|---|---|---|---|---|
| 1 | 220 | 33 | |||
| 2 | 257 | 41 | |||
| 1 | 3 | 106 | 13 | 206.6 | 28.4 |
| 4 | 351 | 36 | |||
| 5 | 99 | 19 | |||
| 1 | 75 | 17 | |||
| 2 | 87 | 16 | |||
| 2 | 3 | 109 | 18 | 81.4 | 16.2 |
| 4 | 58 | 15 | |||
| 5 | 78 | 15 | |||
| 1 | 145 | 31 | |||
| 2 | 156 | 19 | |||
| 3 | 3 | 127 | 27 | 161.6 | 24.8 |
| 4 | 230 | 17 | |||
| 5 | 150 | 30 |
| Case Number | Evaluation Metric | Symbolic Expressions | Mean | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||||
| 0.9827 | 0.9892 | 0.9811 | 0.9934 | 0.9905 | 0.9876 | 0.0048 | ||
| 1 | 1.1180 | 0.9919 | 1.1645 | 0.8225 | 0.9619 | 1.0096 | 0.1215 | |
| 1.8649 | 1.4646 | 1.9488 | 1.1537 | 1.3810 | 1.5506 | 0.3050 | ||
| 0.9878 | 0.9896 | 0.9887 | 0.9836 | 0.9837 | 0.9867 | 0.0025 | ||
| 2 | 1.0615 | 0.9393 | 0.9894 | 1.1815 | 1.1450 | 1.0634 | 0.0911 | |
| 1.5664 | 1.4490 | 1.5057 | 1.8173 | 1.8116 | 1.6300 | 0.1551 | ||
| 0.9909 | 0.9865 | 0.9889 | 0.9828 | 0.9873 | 0.9873 | 0.0027 | ||
| 3 | 0.8032 | 1.0518 | 1.0513 | 1.3162 | 1.0666 | 1.0578 | 0.1623 | |
| 1.3529 | 1.6464 | 1.4958 | 1.8588 | 1.5978 | 1.5903 | 0.1677 | ||
| Evaluation Metric | Mean | ||||||
|---|---|---|---|---|---|---|---|
| 0.99022 | 0.990905 | 0.989798 | 0.993511 | 0.991003 | 0.991087 | 0.001291 | |
| 0.795499 | 0.889602 | 0.954781 | 0.815055 | 0.936876 | 0.878362 | 0.063662 | |
| 1.393535 | 1.343819 | 1.423247 | 1.135059 | 1.336586 | 1.326449 | 0.100901 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anđelić, N.; Baressi Šegota, S.; Glučina, M.; Car, Z. Estimation of Interaction Locations in Super Cryogenic Dark Matter Search Detectors Using Genetic Programming-Symbolic Regression Method. Appl. Sci. 2023, 13, 2059. https://doi.org/10.3390/app13042059
Anđelić N, Baressi Šegota S, Glučina M, Car Z. Estimation of Interaction Locations in Super Cryogenic Dark Matter Search Detectors Using Genetic Programming-Symbolic Regression Method. Applied Sciences. 2023; 13(4):2059. https://doi.org/10.3390/app13042059
Chicago/Turabian StyleAnđelić, Nikola, Sandi Baressi Šegota, Matko Glučina, and Zlatan Car. 2023. "Estimation of Interaction Locations in Super Cryogenic Dark Matter Search Detectors Using Genetic Programming-Symbolic Regression Method" Applied Sciences 13, no. 4: 2059. https://doi.org/10.3390/app13042059
APA StyleAnđelić, N., Baressi Šegota, S., Glučina, M., & Car, Z. (2023). Estimation of Interaction Locations in Super Cryogenic Dark Matter Search Detectors Using Genetic Programming-Symbolic Regression Method. Applied Sciences, 13(4), 2059. https://doi.org/10.3390/app13042059









