The Inversion Method Applied to the Stress Field around a Deeply Buried Tunnel Based on Surface Strain
Abstract
1. Introduction
2. Stress Field Inversion Method and Verification of Its Accuracy
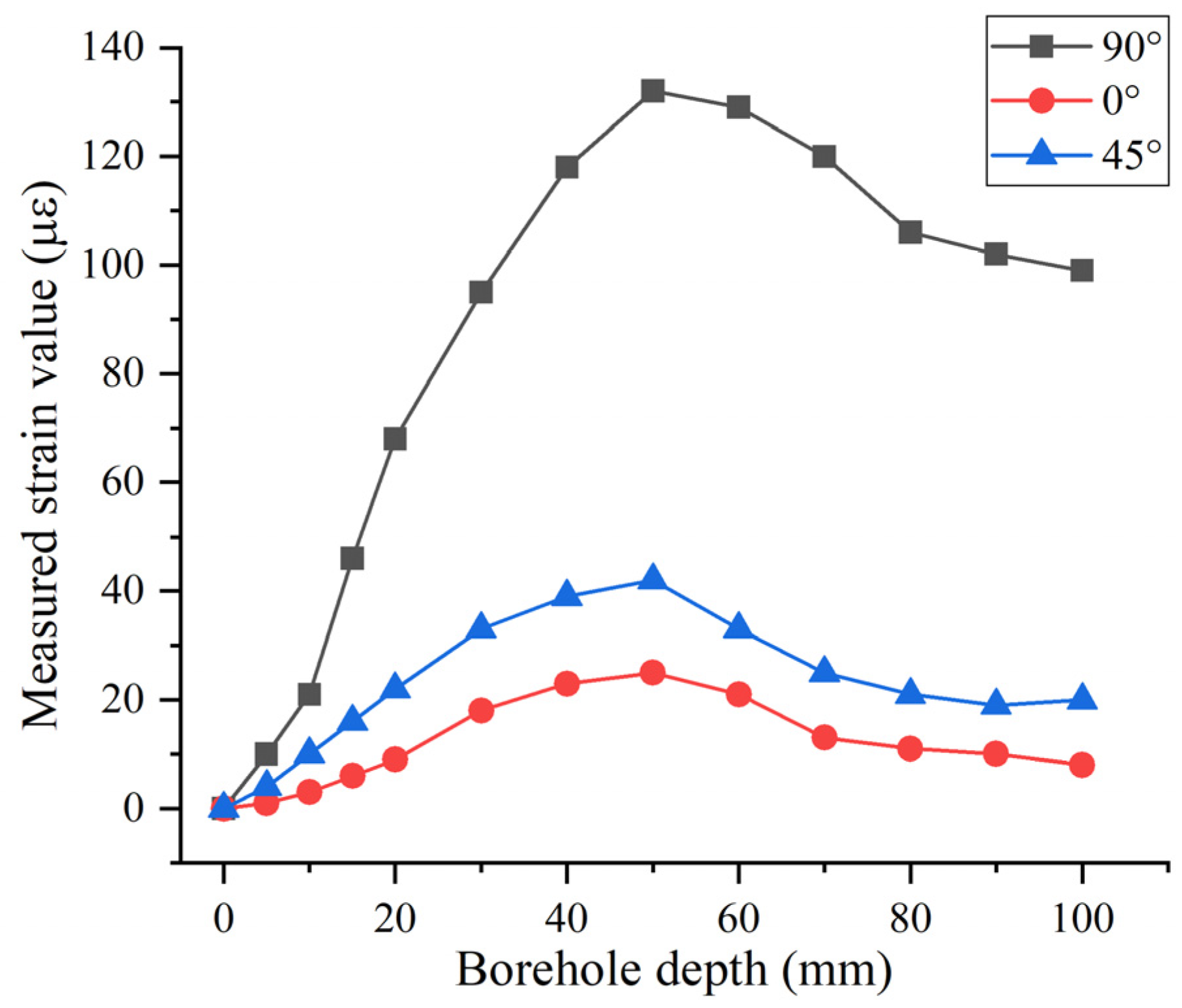
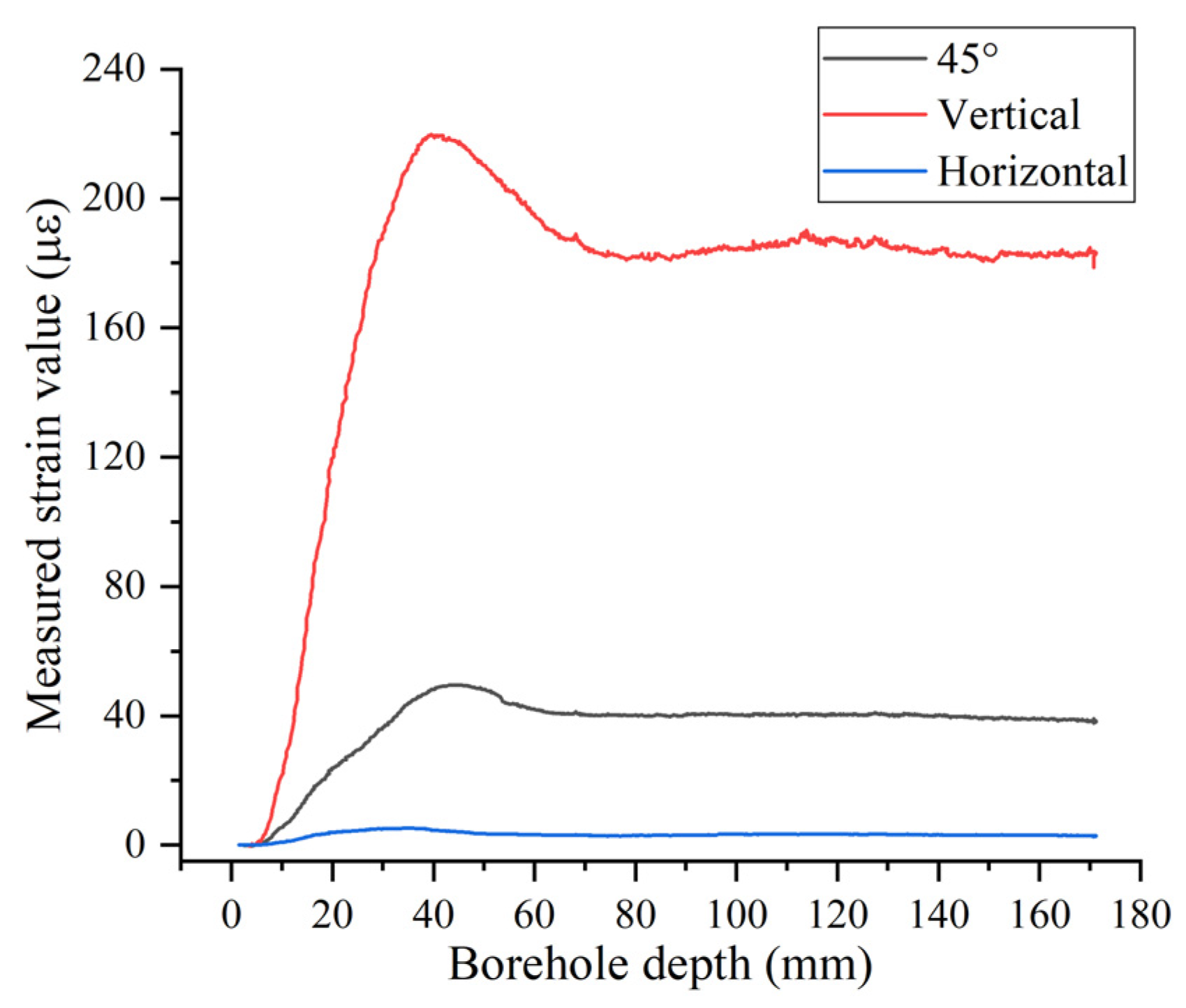
2.1. Measurement of Surface Strain on Drift Walls
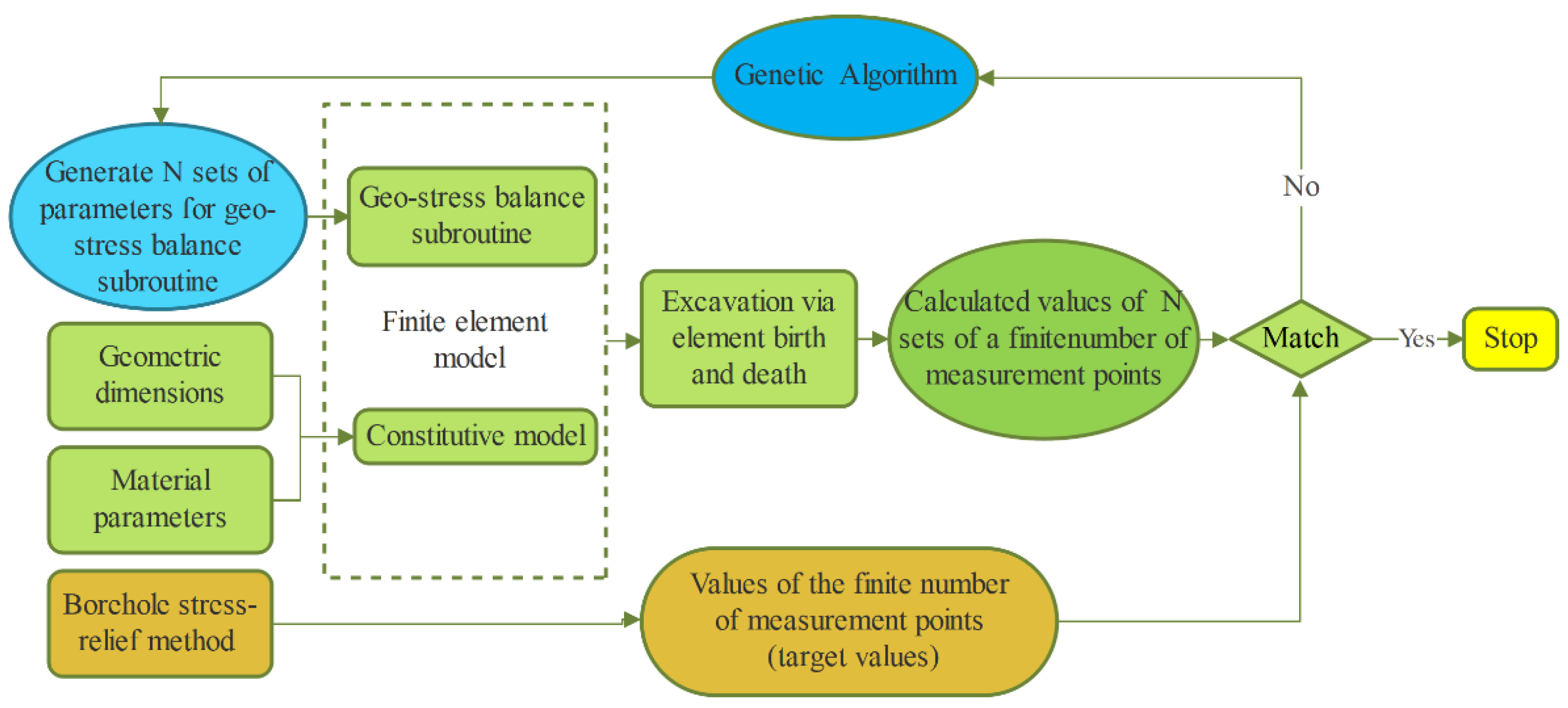
2.2. Inversion Process
- The geometric dimensions of the tunnel and rock mechanical parameters can be determined through geological surveys and rock mechanics experiments. Based on this information, a finite element model containing the tunnel is established in ABAQUS. The user subroutine SIGINI is adopted to apply the initial stress field X;
- Reasonable ranges S of parameter values for the substitute equilibrium stress subroutine in the algorithm’s main program, implemented in MATLAB™, can be defined. Within these ranges, multiple discrete arrays are generated. These arrays Xj can serve as random inputs for the parameters of the stress field subroutine;
- The stress field is calculated for each array using ABAQUS. During the calculation process, the overall equilibrium of the stress field is first established, followed by the excavation of the tunnel. Finally, the calculated strains fcm(Xj) corresponding to each array at the measurement points are obtained;
- The strains at the limited measurement points are extracted for each array, and error analysis is conducted using an error analysis subroutine and the on-site measured strain value fam(Xj). The objective function Ji for error analysis is as follows;
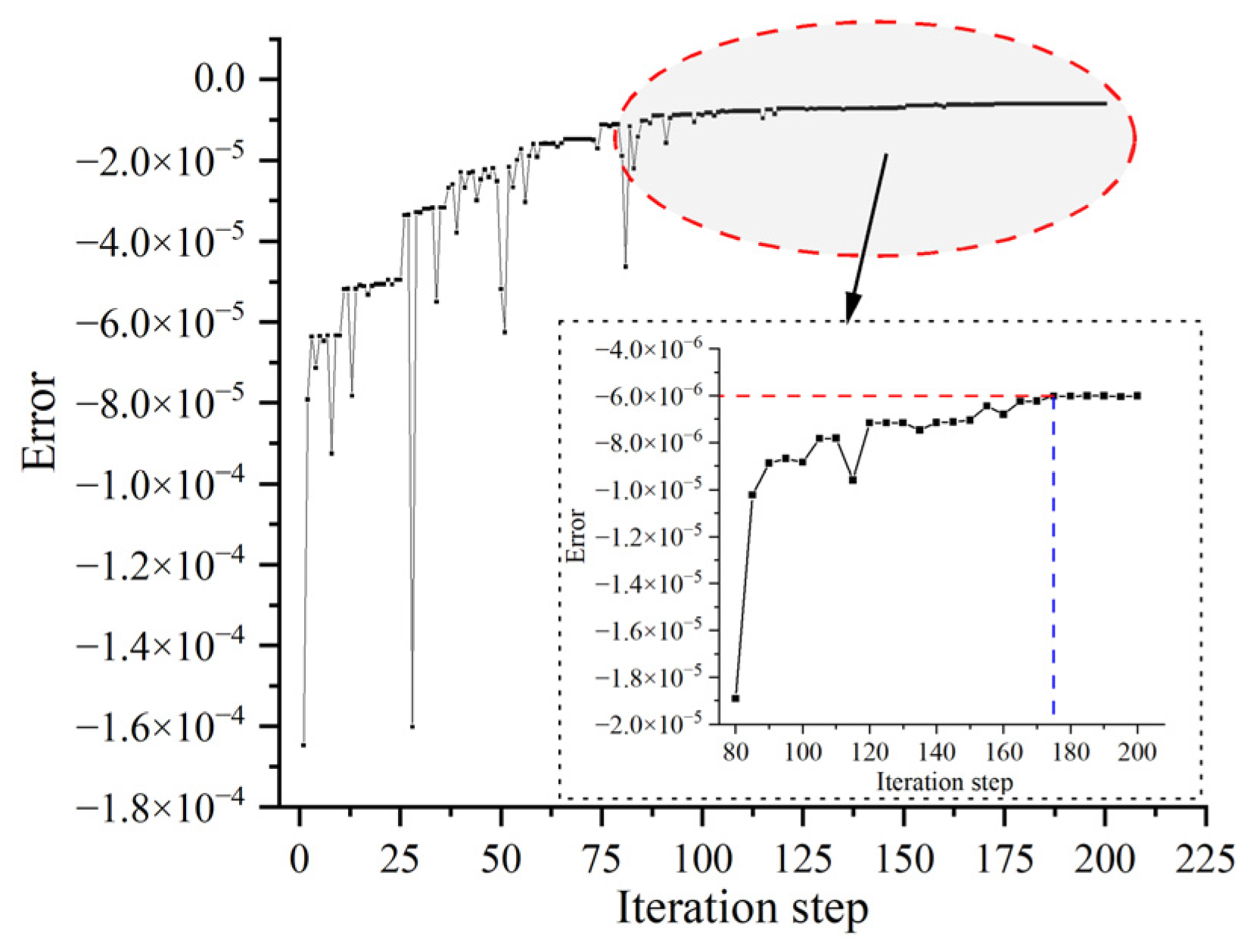
- Based on the results of the error analysis, whether or not the minimum required engineering accuracy is met can be determined. If the error meets the requirements, the program terminates. Otherwise, the parameters are mutated, new random arrays Xj are generated, and Steps 3 and 4 are repeated until the minimum error tolerance is satisfied. Finally, the optimal solution Xopt is derived:
2.3. Verification of the Accuracy of the Method
3. Engineering Applications
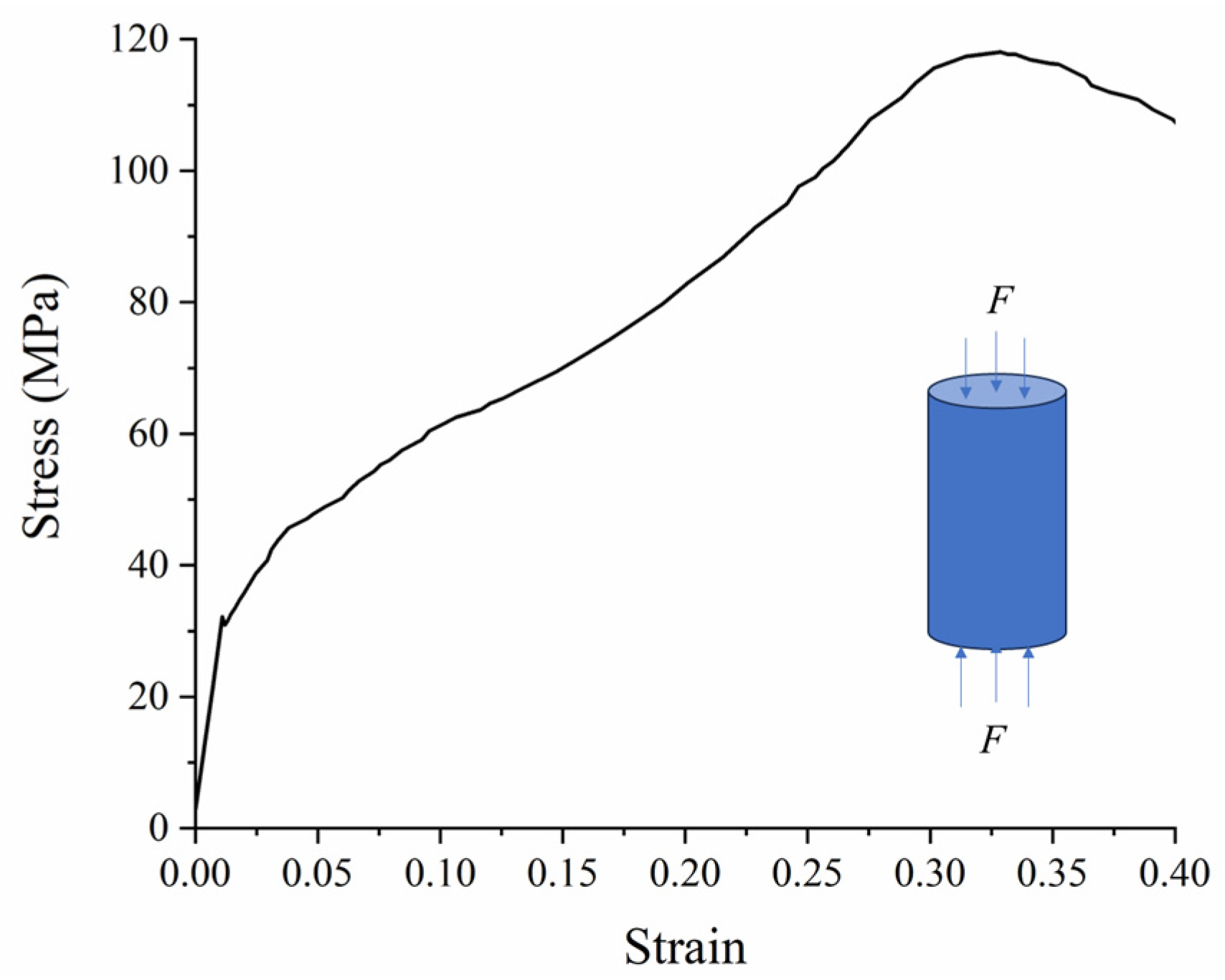
3.1. Rock Mechanics Parameters
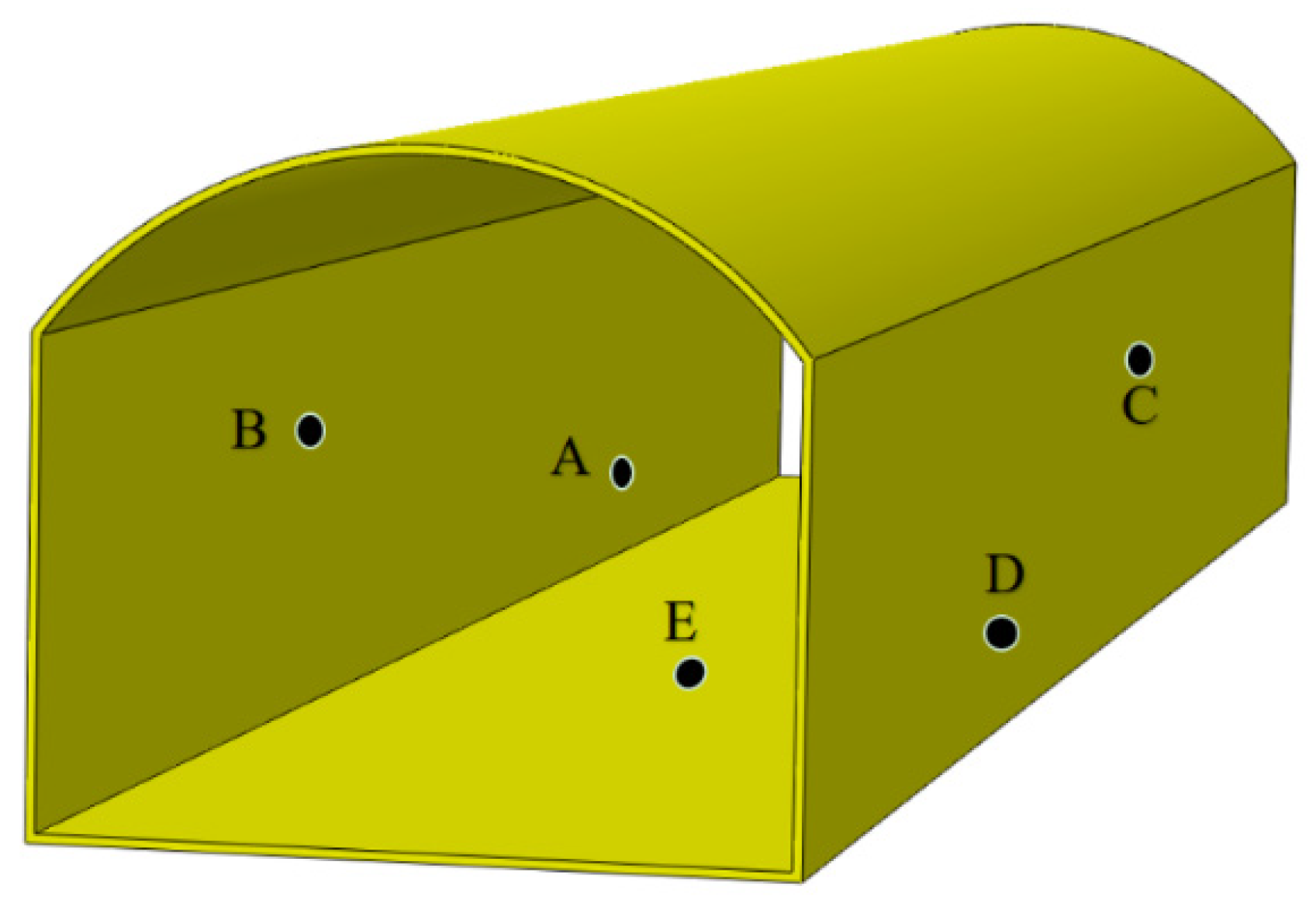
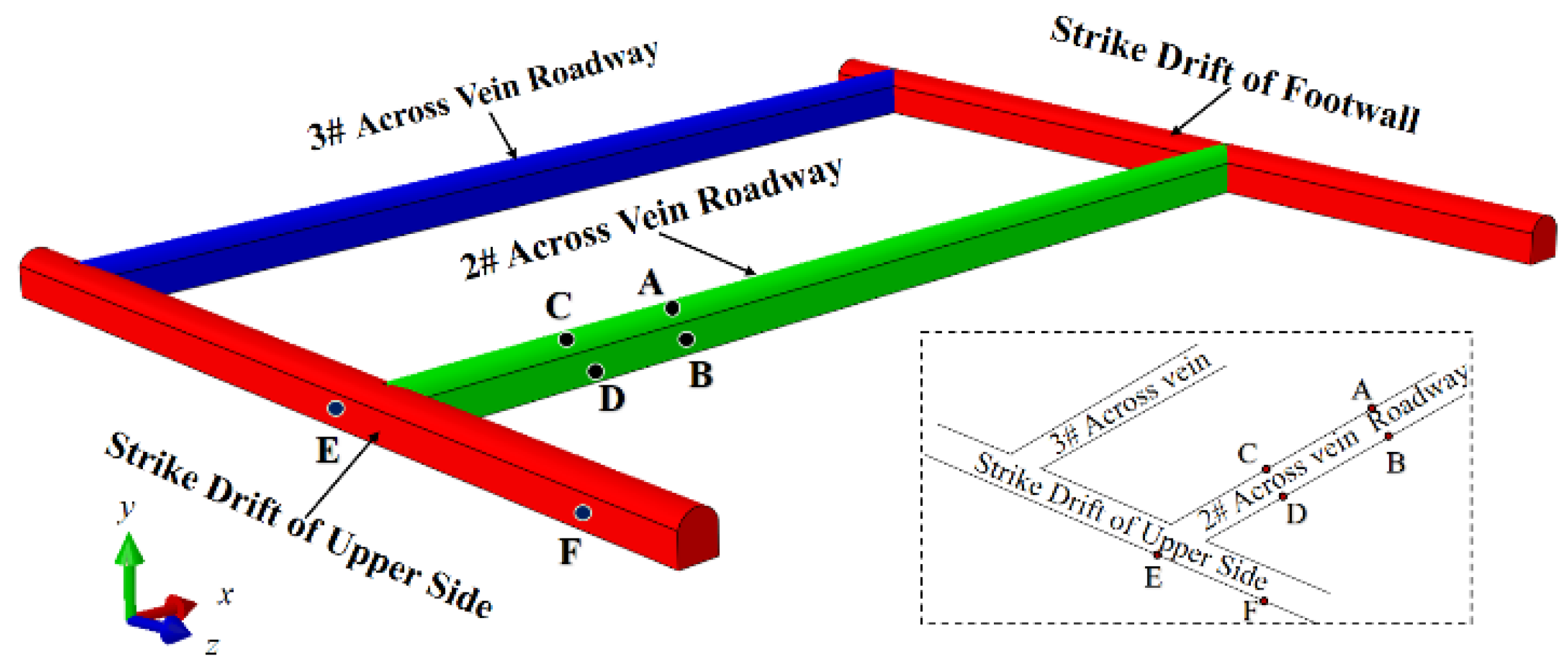
3.2. Measurement and Processing of Surface Strain
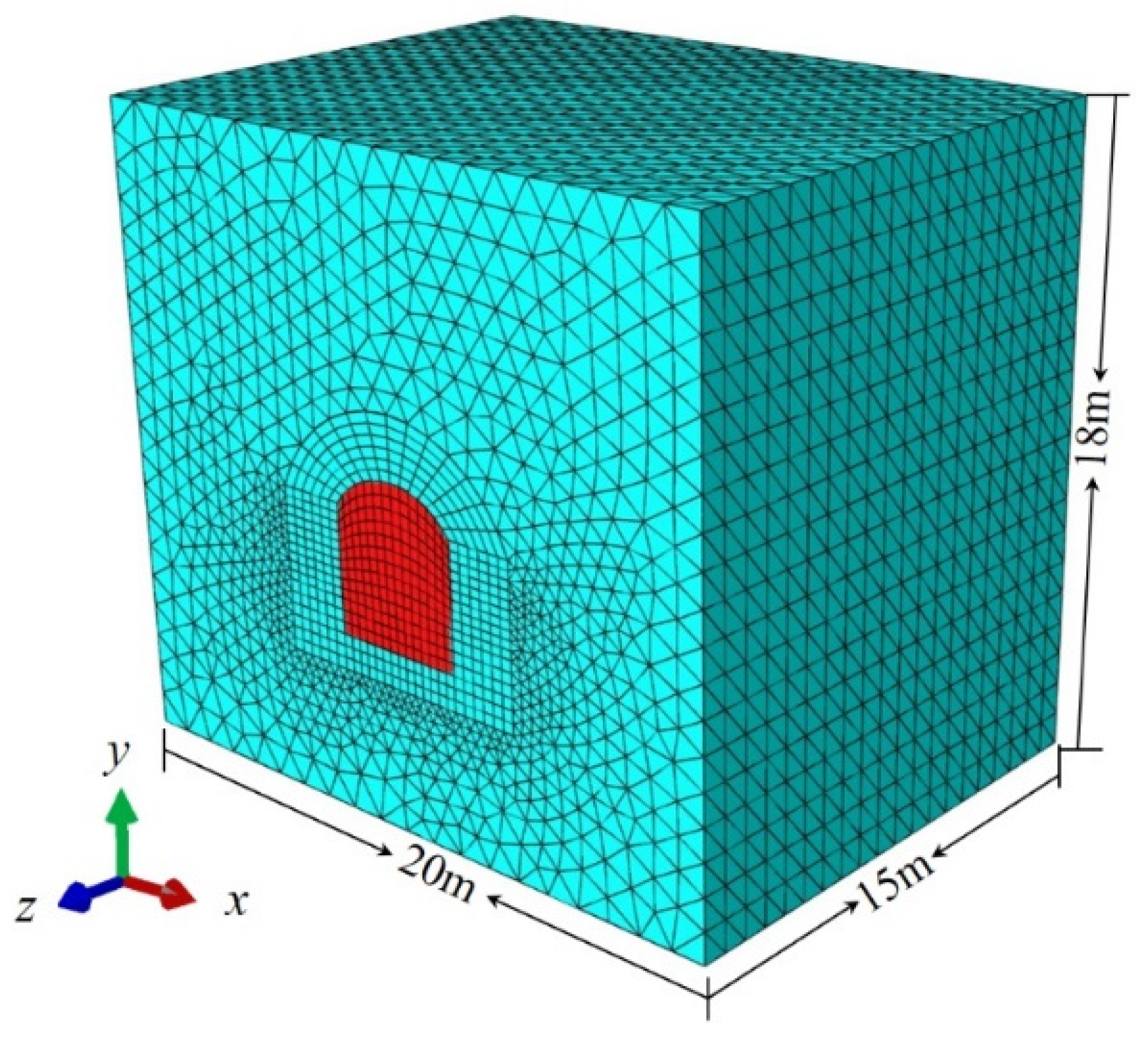
3.3. Inversion Model
3.4. Inversion of Stress Field
4. Distribution of the Stresses around the Tunnel
5. Conclusions
- The utilization of the equilibrium stress subroutine can avoid errors caused by artificial stress or displacement boundary conditions. Secondly, by directly inverting the stress field based on strain measurements, it circumvents the secondary errors introduced by calculating stresses based on elastic principles. Additionally, by considering the excavation-induced plastic damage to the surrounding rock, severe distortion of the results arising from use of the governing constitutive model can be prevented.
- Based on accuracy verification through examples and field applications in the Ma Cheng iron mine, the proposed stress inversion method can achieve an accuracy of over 90% in practical applications. Particularly for deeply buried rock masses, this method proves to be a simple and cost-effective approach.
- According to the in situ stress measurement method proposed in this study, the maximum principal stress, intermediate principal stress, and minimum principal stress in the rock at the Ma Cheng iron mine were calculated as 38.78 MPa, 25.68 MPa, and 11.63 MPa, respectively. The ratio between the maximum and minimum principal stresses is 3.33:1, and the maximum principal stress is 1.43 times greater than the intermediate principal stress. The concentration of stress is evident in the left-hand side of the tunnel arch. These findings are consistent with the observed collapse phenomena.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Xu, J.; Pan, J.; Ma, C. Plastic zone distribution laws and its types of surrounding rock in large-span roadway. Int. J. Min. Sci. Technol. 2012, 22, 23–28. [Google Scholar] [CrossRef]
- Zhang, Z.; Gong, R.; Zhang, H.; Lan, Q.; Tang, X. Initial ground stress field regression analysis and application in an extra-long tunnel in the western mountainous area of China. Bull. Eng. Geol. Environ. 2021, 80, 4603–4619. [Google Scholar] [CrossRef]
- Cai, M.; Qiao, L.; Li, C.; Yu, J.; Yu, B.; Chen, G. Application of an Improved Hollow Inclusion Technique for in-Situ Stress Measurement in Xincheng Gold Mine, China. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 735–739. [Google Scholar] [CrossRef]
- Sjöberg, J.; Klasson, H. Stress measurements in deep boreholes using the Borre (SSPB) probe. Int. J. Rock Mech. Min. Sci. 2003, 40, 1205–1223. [Google Scholar] [CrossRef]
- Funato, A.; Ito, T. A new method of diametrical core deformation analysis for in-situ stress measurements. Int. J. Rock Mech. Min. Sci. 2017, 91, 112–118. [Google Scholar] [CrossRef]
- Hayashi, K.; Sato, A.; Ito, T. In situ stress measurements by hydraulic fracturing for a rock mass with many planes of weakness. Int. J. Rock Mech. Min. Sci. 1997, 34, 45–58. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Luo, C.; Wang, X. In situ stress measurements by hydraulic fracturing in the Western Route of South to North Water Transfer Project in China. Eng. Geol. 2014, 168, 114–119. [Google Scholar] [CrossRef]
- Mohamadi, A.; Behnia, M.; Alneasan, M. Comparison of the classical and fracture mechanics approaches to determine in situ stress/hydrofracturing method. Bull. Eng. Geol. Environ. 2021, 80, 3833–3851. [Google Scholar] [CrossRef]
- Qiao, L.; Xu, Z.-H.; Zhao, K.; Li, Y.; Li, Y.; Wang, K.-J.; Cai, H. Study on Acoustic Emission In-situ Stress Measurement Techniques Based on Plane Stress Condition. Procedia Eng. 2011, 26, 1473–1481. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Chen, J.; Ma, C.; Huang, L.; Li, C.; Zhang, J.; Zhao, Y. A novel in-situ stress measurement method incorporating non-oriented core ground re-orientation and acoustic emission: A case study of a deep borehole. Int. J. Rock Mech. Min. Sci. 2022, 152, 105079. [Google Scholar] [CrossRef]
- Song, Z.; Yang, Z.; Huo, R.; Zhang, Y. Inversion Analysis Method for Tunnel and Underground Space Engineering: A Short Review. Appl. Sci. 2023, 13, 5454. [Google Scholar] [CrossRef]
- Wang, T.X.; Zheng, W.H.; Liang, S.J. Numerical Simulation of Regional Stress Field under Complex Geological Condition. Appl. Mech. Mater. 2011, 90–93, 531–536. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, S. Determination of in situ stresses and elastic parameters from hydraulic fracturing tests by geomechanics modeling and soft computing. J. Pet. Sci. Eng. 2014, 124, 484–492. [Google Scholar] [CrossRef]
- Li, F.; Wang, J.-A.; Brigham, J.C. Inverse calculation of in situ stress in rock mass using the Surrogate-Model Accelerated Random Search algorithm. Comput. Geotech. 2014, 61, 24–32. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Y.; Zhu, W.; Li, S.; Zhou, H. A modified initial in-situ Stress Inversion Method based onFLAC3D with an engineering application. Open Geosci. 2015, 7, 20150065. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Hu, A.-K.; Wang, C. Three-dimensional inversion analysis of an in situ stress field based on a two-stage optimization algorithm. J. Zhejiang Univ. Sci. A 2016, 17, 782–802. [Google Scholar] [CrossRef]
- Li, G.; Hu, Y.; Li, Q.-B.; Yin, T.; Miao, J.-X.; Yao, M. Inversion Method of In-situ Stress and Rock Damage Characteristics in Dam Site Using Neural Network and Numerical Simulation—A Case Study. IEEE Access 2020, 8, 46701–46712. [Google Scholar] [CrossRef]
- Huang, Y.; Zolfaghari, N.; Ohanian, O.J.; Bunger, A.P. Technical Note: An inversion algorithm to estimate maximum and minimum horizontal stress based on field test data for sleeve fracturing. Comput. Geotech. 2021, 137, 104274. [Google Scholar] [CrossRef]
- Qian, L.; Yao, T.; Mo, Z.; Zhang, J.; Li, Y.; Zhang, R.; Xu, N.; Li, Z. GAN inversion method of an initial in situ stress field based on the lateral stress coefficient. Sci. Rep. 2021, 11, 21825. [Google Scholar] [CrossRef]
- Jin, C.; Lu, Y.; Han, T.; Chen, T.; Cui, J.; Cheng, D. Study on Refined Back-Analysis Method for Stress Field Based on In Situ and Disturbed Stresses. Int. J. Geomech. 2021, 21, 04021141. [Google Scholar] [CrossRef]
- Zhang, F.P.; Qiu, Z.G.; Feng, X.T. Non-complete relief method for measuring surface stresses in surrounding rocks. J. Cent. South Univ. 2014, 21, 3665–3673. [Google Scholar] [CrossRef]
- Zoback, M.L. First- and second-order patterns of stress in the lithosphere: The World Stress Map Project. J. Geophys. Res. Solid Earth 2012, 97, 11703–11728. [Google Scholar] [CrossRef]
- Amadei, B.; Stephansson, O. Rock Stress and Its Measurement; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining, 3rd ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 85–141. [Google Scholar]
- Zhang, Z.; Qin, Y.; You, Z.; Yang, Z. Distribution Characteristics of In Situ Stress Field and Vertical Development Unit Division of CBM in Western Guizhou, China. Nat. Resour. Res. 2021, 30, 3659–3671. [Google Scholar] [CrossRef]






| Measurement Points | ||||||
|---|---|---|---|---|---|---|
| A | 97.37 | −263.86 | −20.31 | 61.28 | −204.97 | 68.75 |
| B | 93.85 | −249.94 | −67.14 | −76.26 | −223.13 | 58.03 |
| C | 78.86 | −204.86 | −68.03 | 9.83 | −228.99 | 78.62 |
| D | 94.72 | −327.85 | −15.71 | −135.78 | −264.40 | 84.46 |
| E | −182.64 | 68.44 | −49.09 | −11.36 | −14.86 | −11.01 |
| Target value | 19.80 | 18.00 | 12.60 | 5.40 | 3.60 | 7.20 |
| Inversion value | 19.30 | 17.69 | 12.28 | 5.45 | 3.76 | 7.34 |
| Error | 2.53% | 1.72% | 2.54% | 0.93% | 4.44% | 1.94% |
| Measurement Point | ||||||
|---|---|---|---|---|---|---|
| A | Inversion value (με) | - | −260.08 | −18.76 | - | −208.22 |
| Error (%) | - | 1.43 | 7.63 | - | 1.59 | |
| B | Inversion value (με) | - | −247.17 | −66.52 | - | −228.03 |
| Error (%) | - | 1.11 | 0.92 | - | 2.20 | |
| C | Inversion value (με) | - | −201.75 | −67.22 | - | −233.08 |
| Error (%) | - | 1.52 | 1.19 | - | 1.79 | |
| D | Inversion value (με) | - | −323.61 | −15.37 | - | −270.68 |
| Error (%) | - | 1.29 | 2.18 | - | 2.38 | |
| E | Inversion value (με) | −176.88 | - | −47.45 | −11.54 | - |
| Error (%) | 3.15 | - | 3.34 | 1.58 | - |
| Target value (MPa) | 19.80 | 18.00 | 12.60 | 5.40 | 3.60 | 7.20 |
| Inversion value (MPa) | 18.44 | 16.84 | 11.39 | 4.73 | 4.12 | 7.11 |
| Error | 6.87% | 6.44% | 9.60% | 12.41% | 14.44% | 1.25% |
| Density (kg/m3) | Compressive Strength (MPa) | Tensile Strength (MPa) | Poisson’s Ratio | Young’s Modulus (GPa) | Friction Angle (°) | Cohesion (MPa) | |
|---|---|---|---|---|---|---|---|
| Average value | 2530 | 101.15 | 8.39 | 0.26 | 72.47 | 45 | 20 |
| Standard deviation | 0.01 | 16.73 | 0.73 | 0.03 | 8.57 | 6.58 | 3.62 |
| Measurement Point | |||||
|---|---|---|---|---|---|
| A | - | −80 | −16 | - | −83 |
| B | - | −60 | 18 | - | −75 |
| C | −5.2 | −219 | - | −125 | - |
| D | 13 | −370 | - | −42 | - |
| E | 11 | −168 | - | −25 | - |
| F | 14 | −124 | - | −108 | - |
| Measurement Point | ||||||
|---|---|---|---|---|---|---|
| A | Inversion value (με) | - | 78.95 | −16.74 | - | −80.62 |
| Error (%) | - | 1.31 | 4.59 | - | 2.87 | |
| B | Inversion value (με) | - | −58.41 | 18.60 | - | −75.56 |
| Error (%) | - | 2.66 | 3.34 | - | 0.74 | |
| C | Inversion value (με) | 0.76 | 216.69 | - | −125.87 | - |
| Error (%) | - | 1.05 | - | 0.7 | - | |
| D | Inversion value (με) | 7.91 | −372.88 | - | −38.75 | - |
| Error (%) | - | 0.78 | - | 7.74 | - | |
| E | Inversion value (με) | 11.63 | −166.29 | - | −24.81 | - |
| Error (%) | - | 1.02 | - | 0.76 | - | |
| F | Inversion value (με) | 14 | −129.91 | - | −107.93 | - |
| Error (%) | - | 1.05 | - | 0.06 | - |
| Inverted Values (MPa) | 34.720 | 25.380 | 15.982 | −3.400 | −6.954 | 6.065 |
| Stress Value (Mpa) | Cosine Value with Respect to the x-Axis | Cosine Value with Respect to the y-Axis | Cosine Value with Respect to the z-Axis | |
|---|---|---|---|---|
| Maximum principal stress | 38.78 | 0.85 | −0.39 | 0.35 |
| Second principal stress | 25.68 | 0.47 | 0.84 | −0.28 |
| Minimum principal stress | 11.63 | −0.17 | 0.41 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Hao, Q.; Yang, R.; Peng, J.; Zhang, F.; Tan, S. The Inversion Method Applied to the Stress Field around a Deeply Buried Tunnel Based on Surface Strain. Appl. Sci. 2023, 13, 12507. https://doi.org/10.3390/app132212507
Yan X, Hao Q, Yang R, Peng J, Zhang F, Tan S. The Inversion Method Applied to the Stress Field around a Deeply Buried Tunnel Based on Surface Strain. Applied Sciences. 2023; 13(22):12507. https://doi.org/10.3390/app132212507
Chicago/Turabian StyleYan, Xiaobing, Qiqi Hao, Rui Yang, Jianyu Peng, Fengpeng Zhang, and Sanyuan Tan. 2023. "The Inversion Method Applied to the Stress Field around a Deeply Buried Tunnel Based on Surface Strain" Applied Sciences 13, no. 22: 12507. https://doi.org/10.3390/app132212507
APA StyleYan, X., Hao, Q., Yang, R., Peng, J., Zhang, F., & Tan, S. (2023). The Inversion Method Applied to the Stress Field around a Deeply Buried Tunnel Based on Surface Strain. Applied Sciences, 13(22), 12507. https://doi.org/10.3390/app132212507






