Time-Frequency Analysis and Neural Networks for Detecting Short-Circuited Turns in Transformers in Both Transient and Steady-State Regimes Using Vibration Signals
Abstract
:1. Introduction
2. Theoretical Background
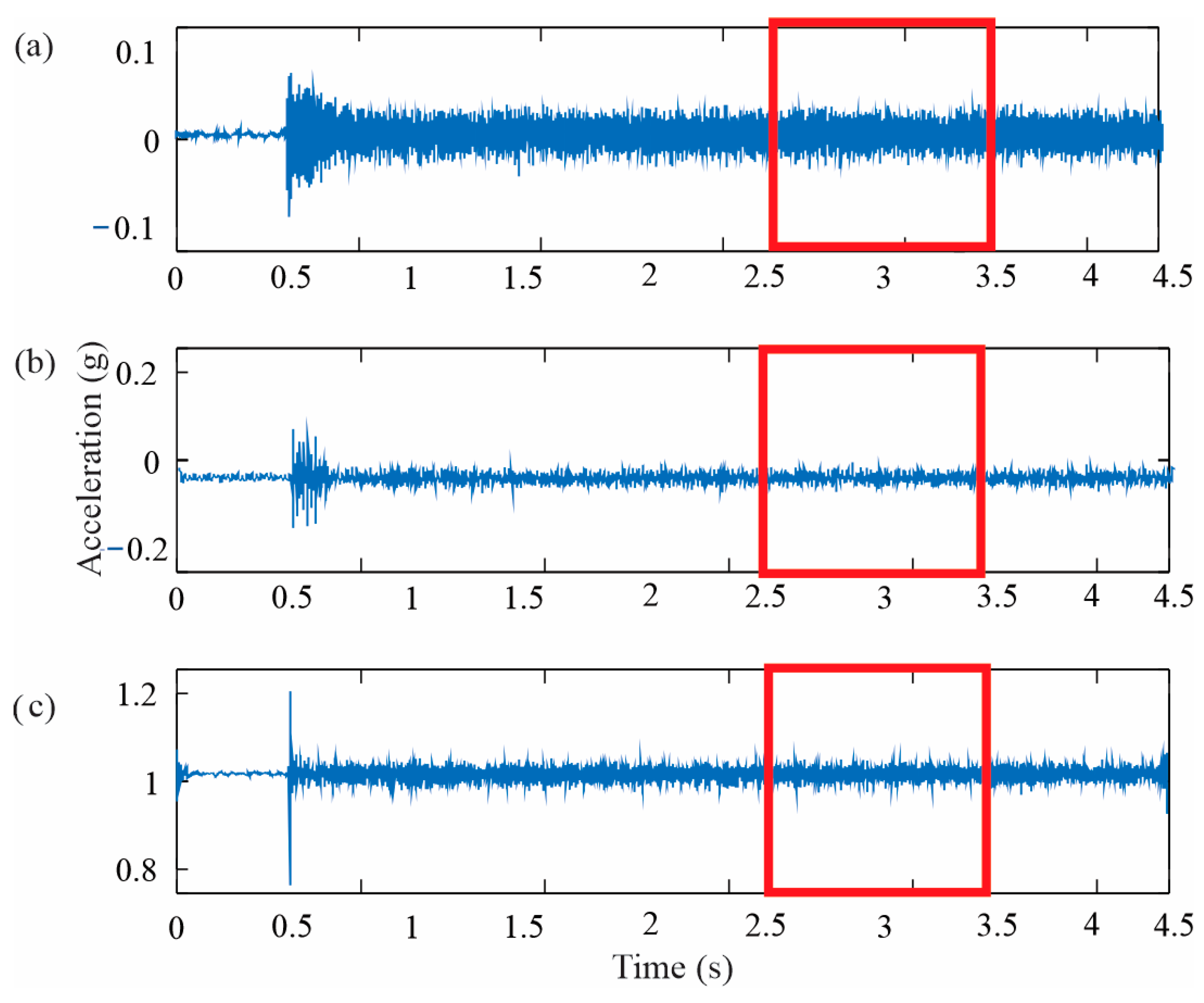
2.1. Vibrations in Transformers
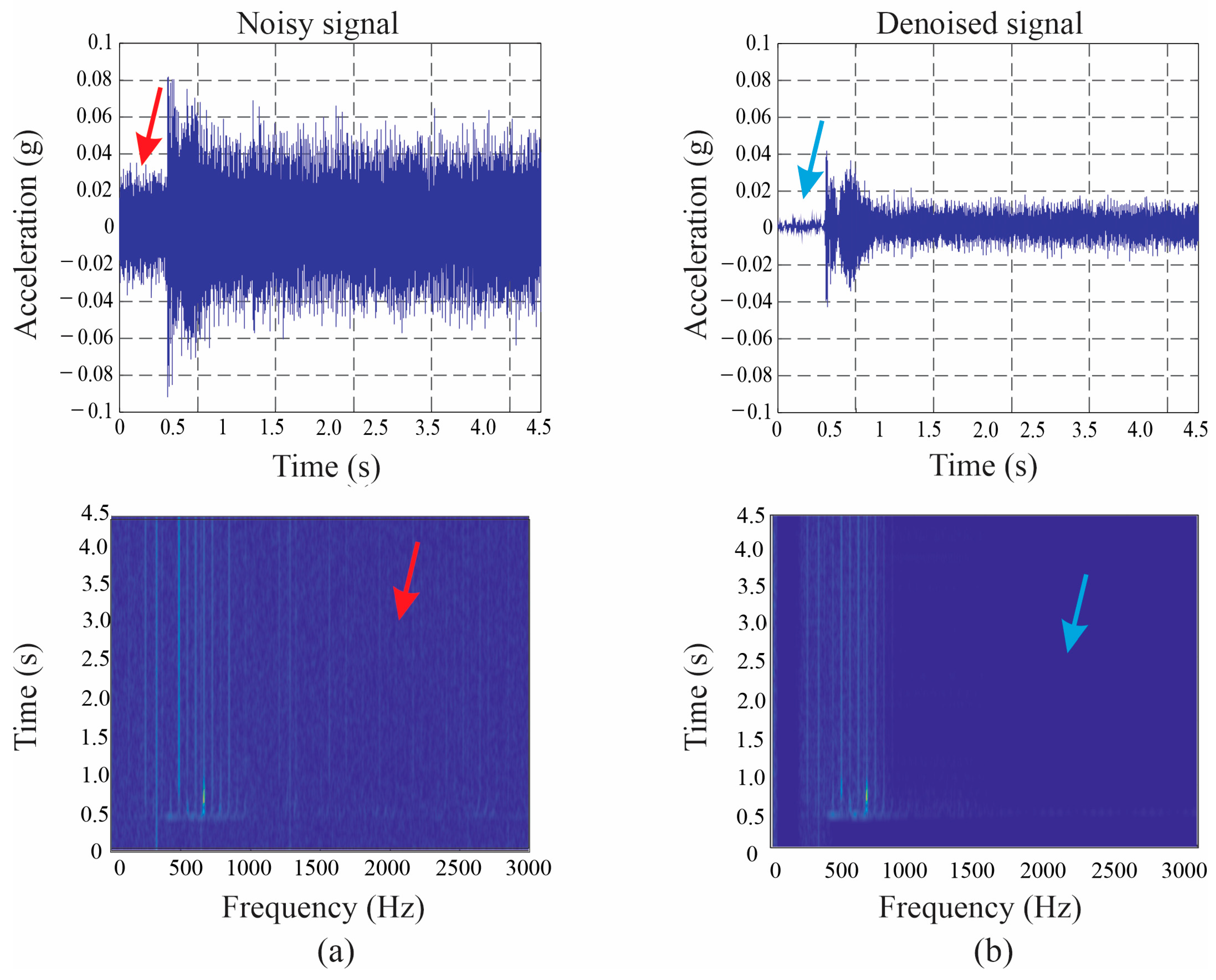
2.2. Wavelet Denoising
- Introduce a noisy signal into the process. A noisy signal is described as follows [27]:where is the original signal, is a Gaussian white noise, and is the noise level.
- In the next step, the noisy signal is decomposed using the discrete WT (DWT). This method allows for the decomposition of the signal into sets of coefficients at different frequency levels according to the following [30]:where x[m] is the original discretized signal, ψ is the discretized mother wavelet, a is a scaling parameter, n is the shift parameter that determines the location of the wavelet, and the parameter j is the decomposition level.
2.3. Short-Time Fourier Transform
2.4. Measurement Functions
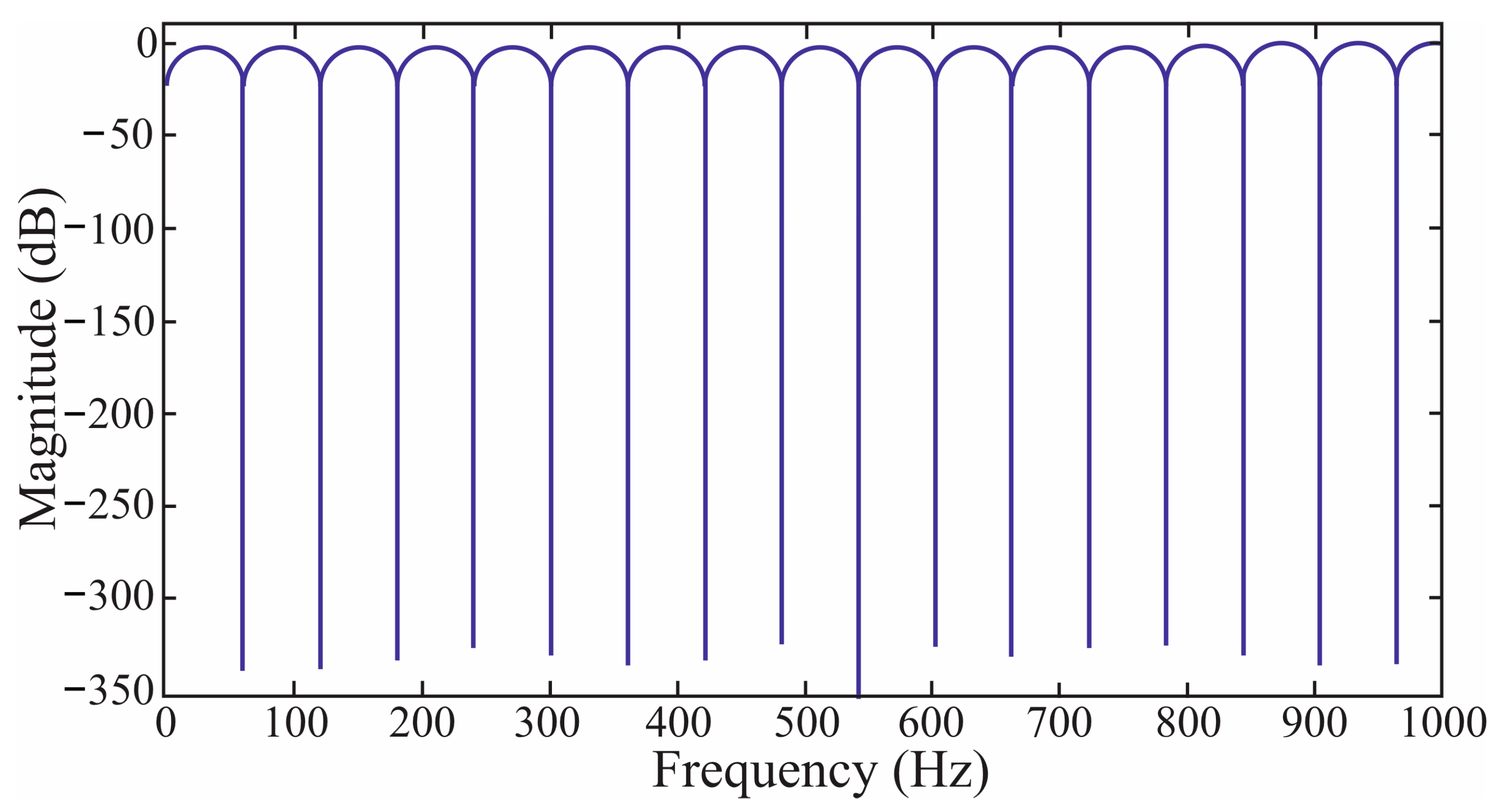
2.5. Comb Filter
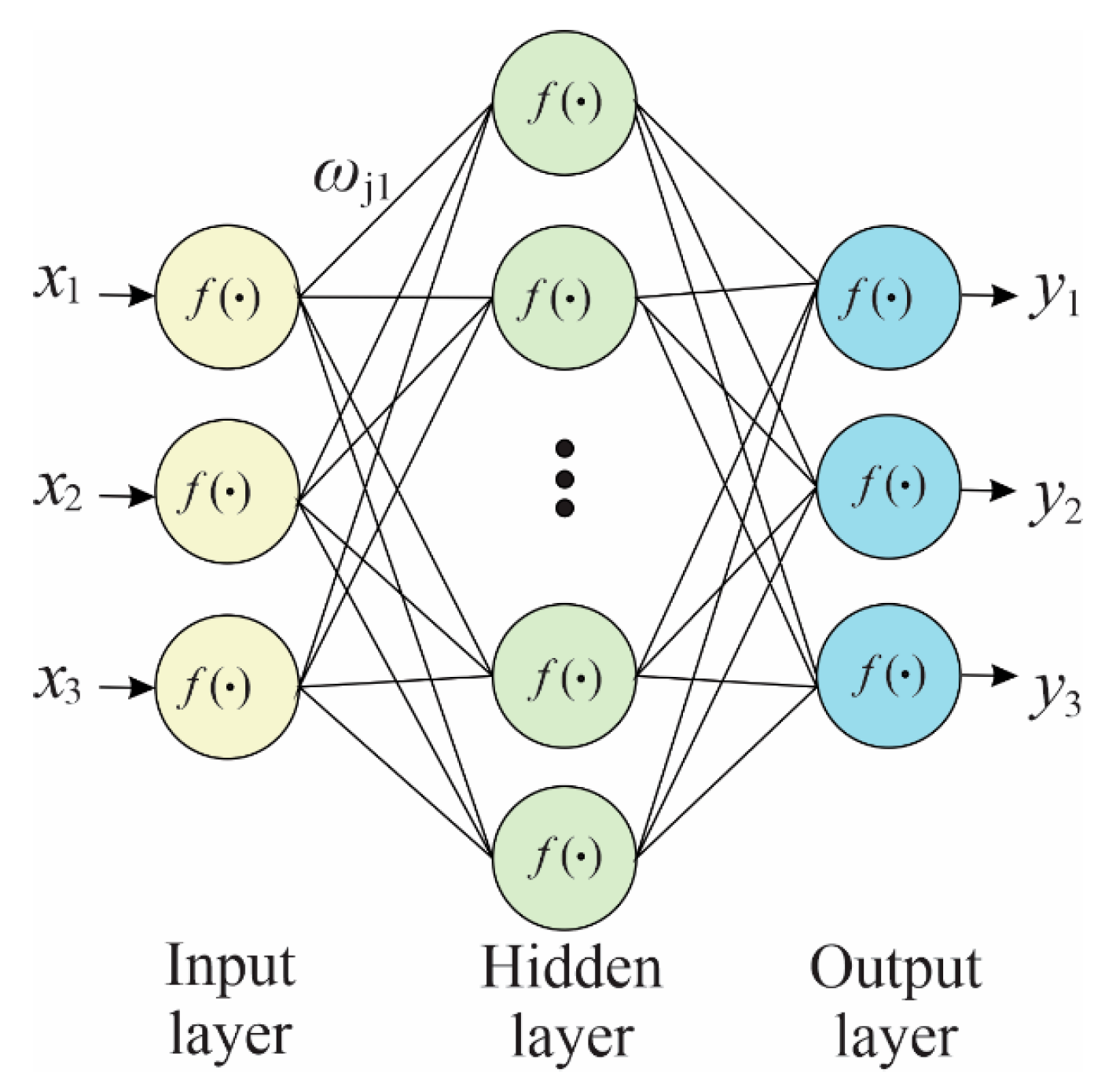
2.6. Artificial Neural Networks
3. Methodology and Experimental Setup
3.1. Proposed Methodology
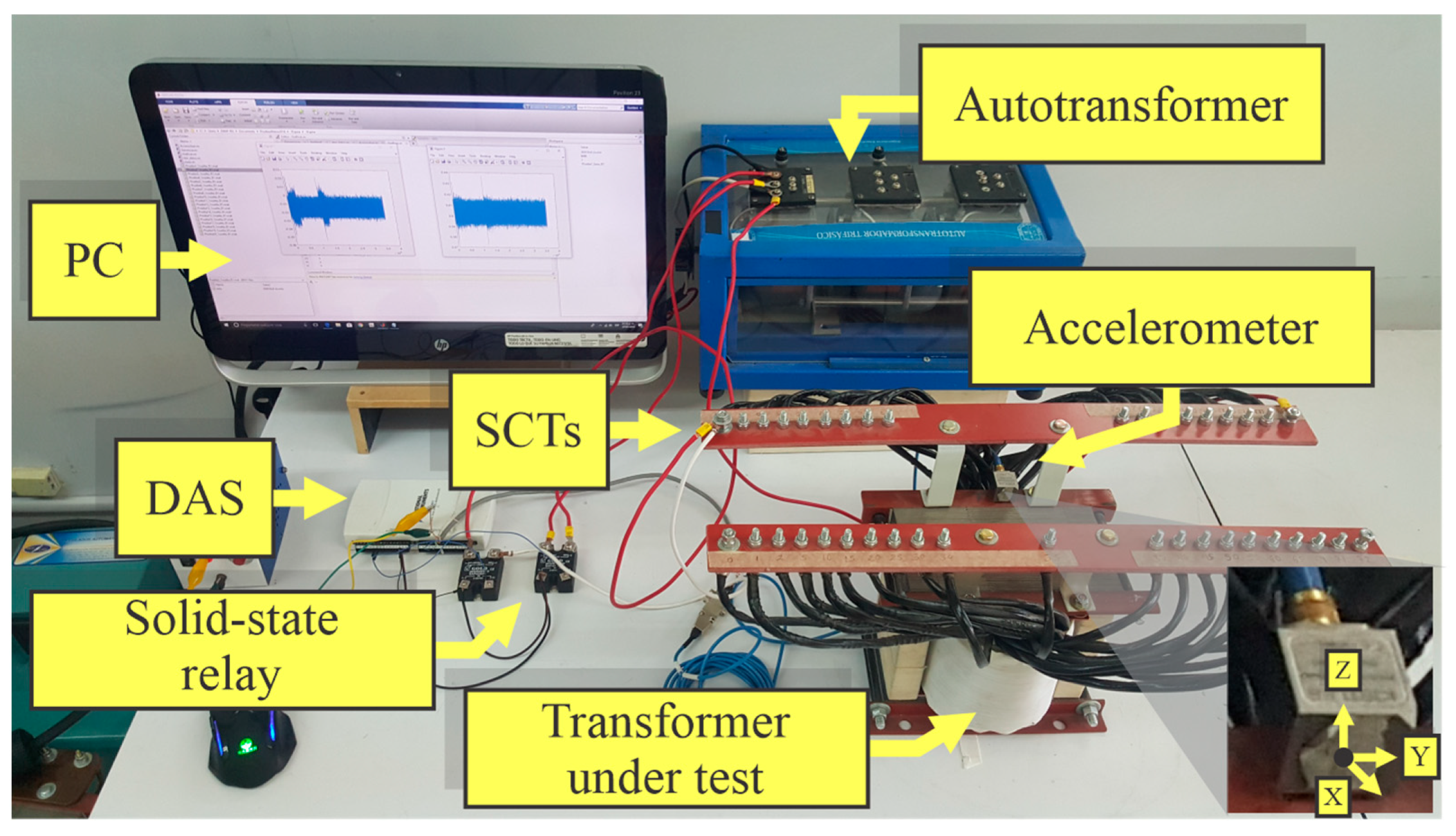
3.2. Experimentation
4. Experimentation and Results
4.1. Wavelet Denoising
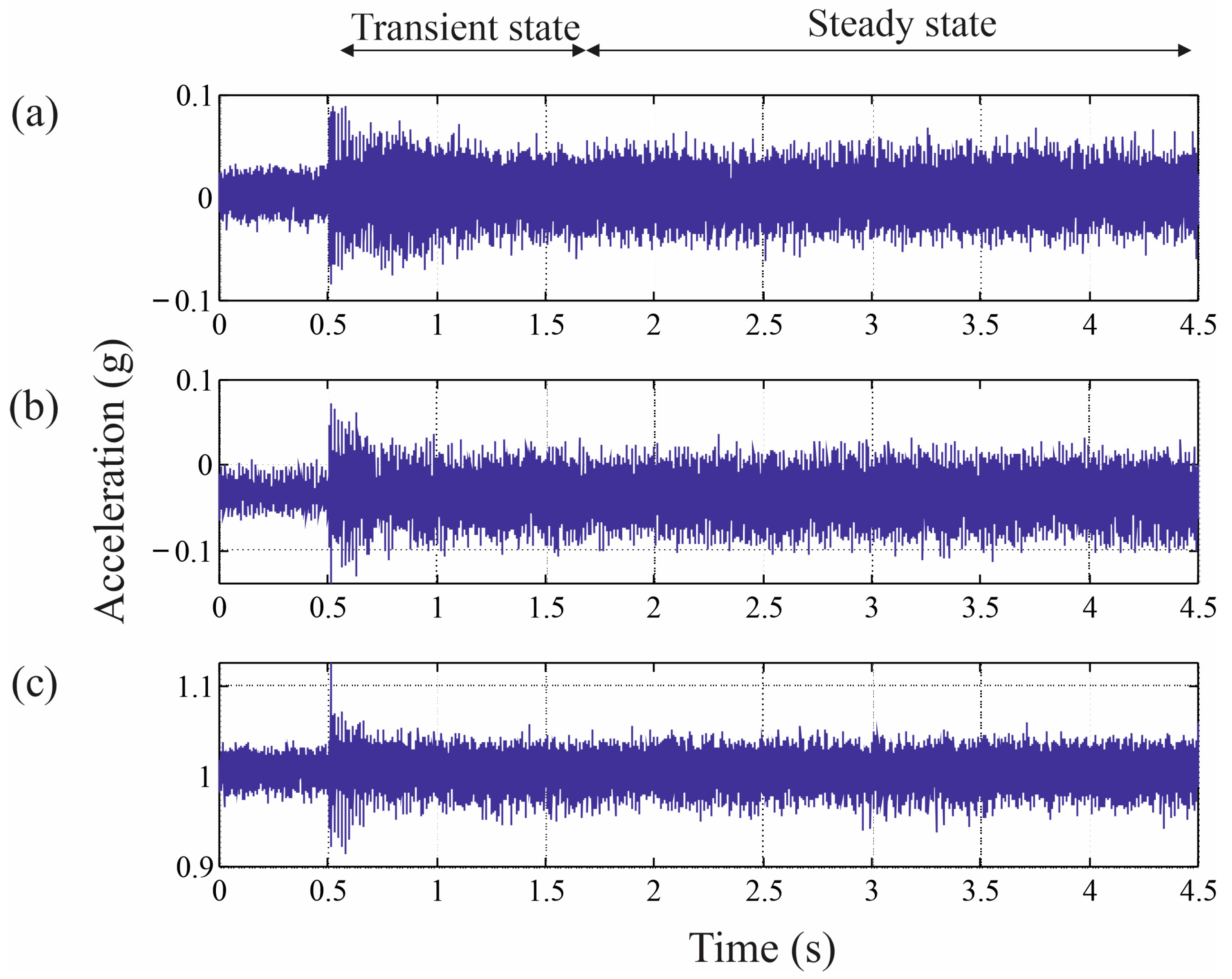
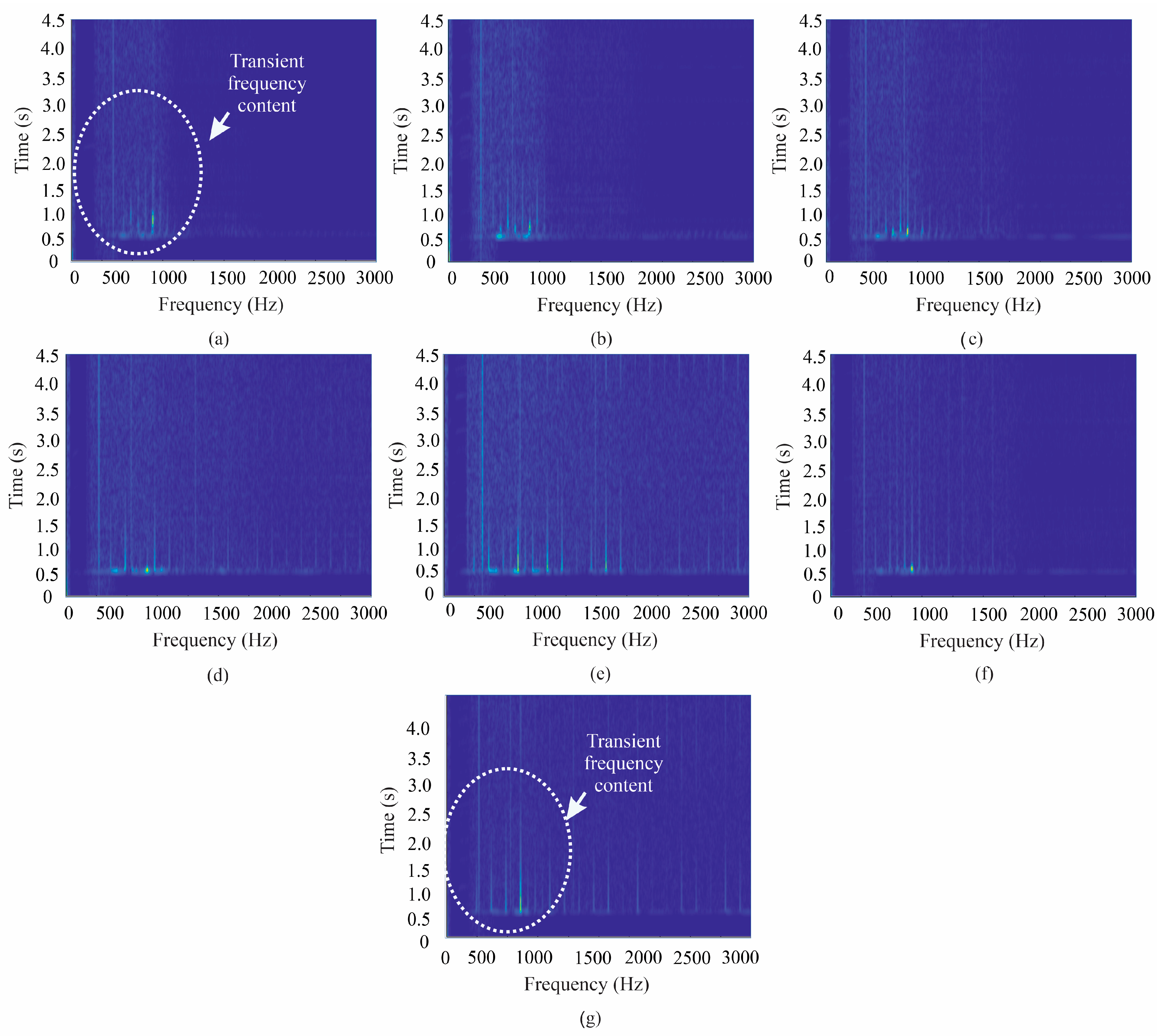
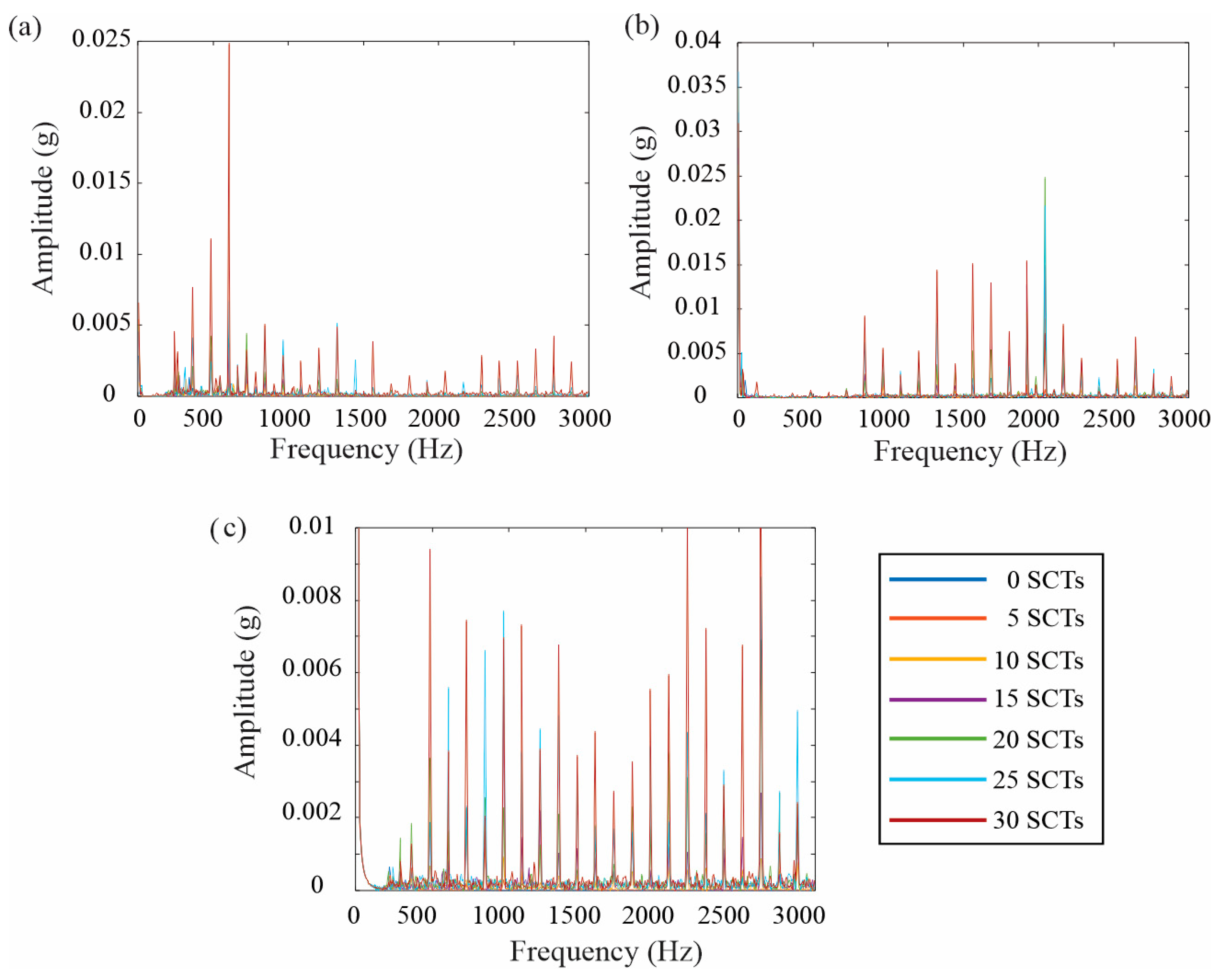
4.2. Results for the Transient State
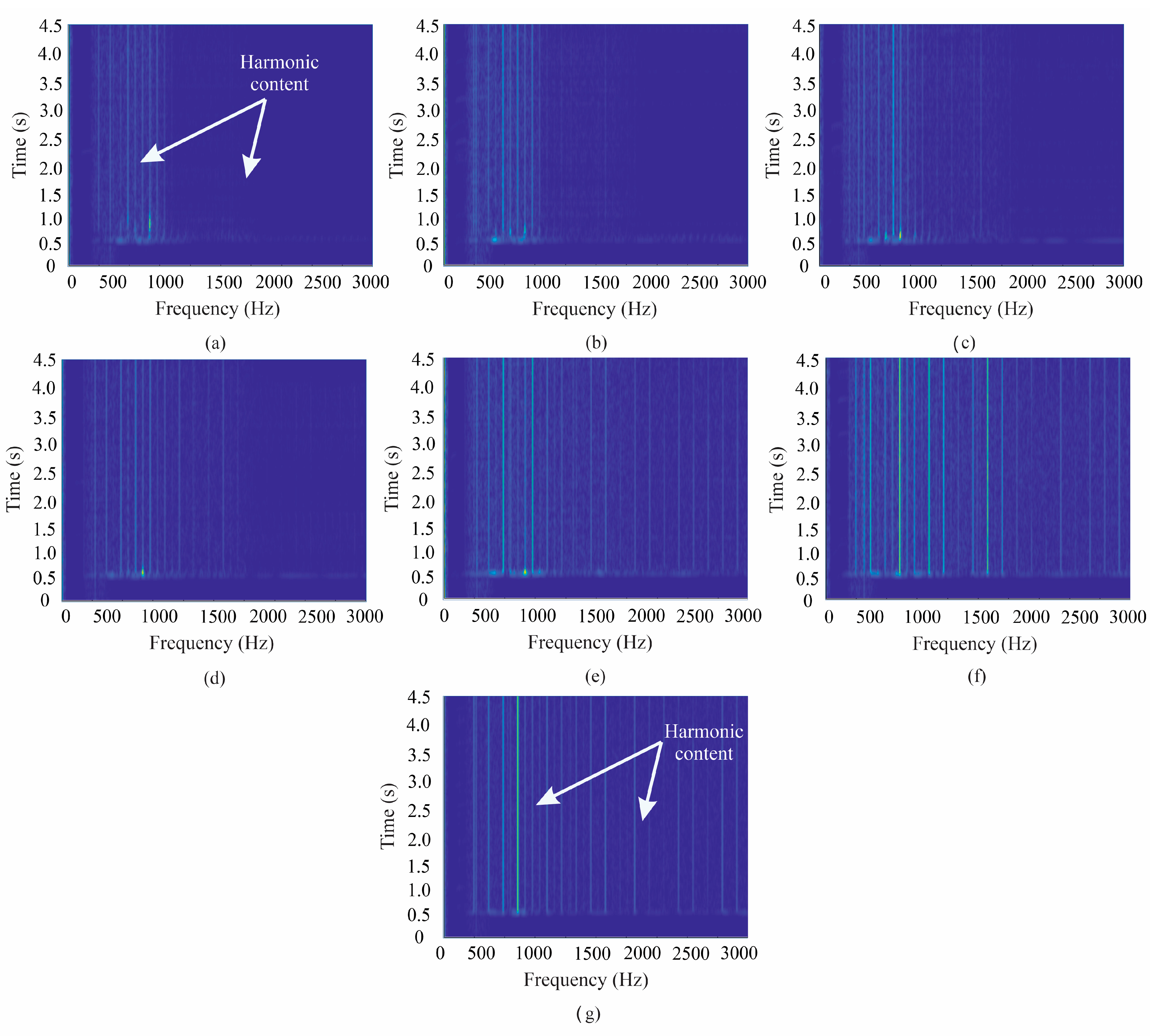
4.3. Results for the Steady State
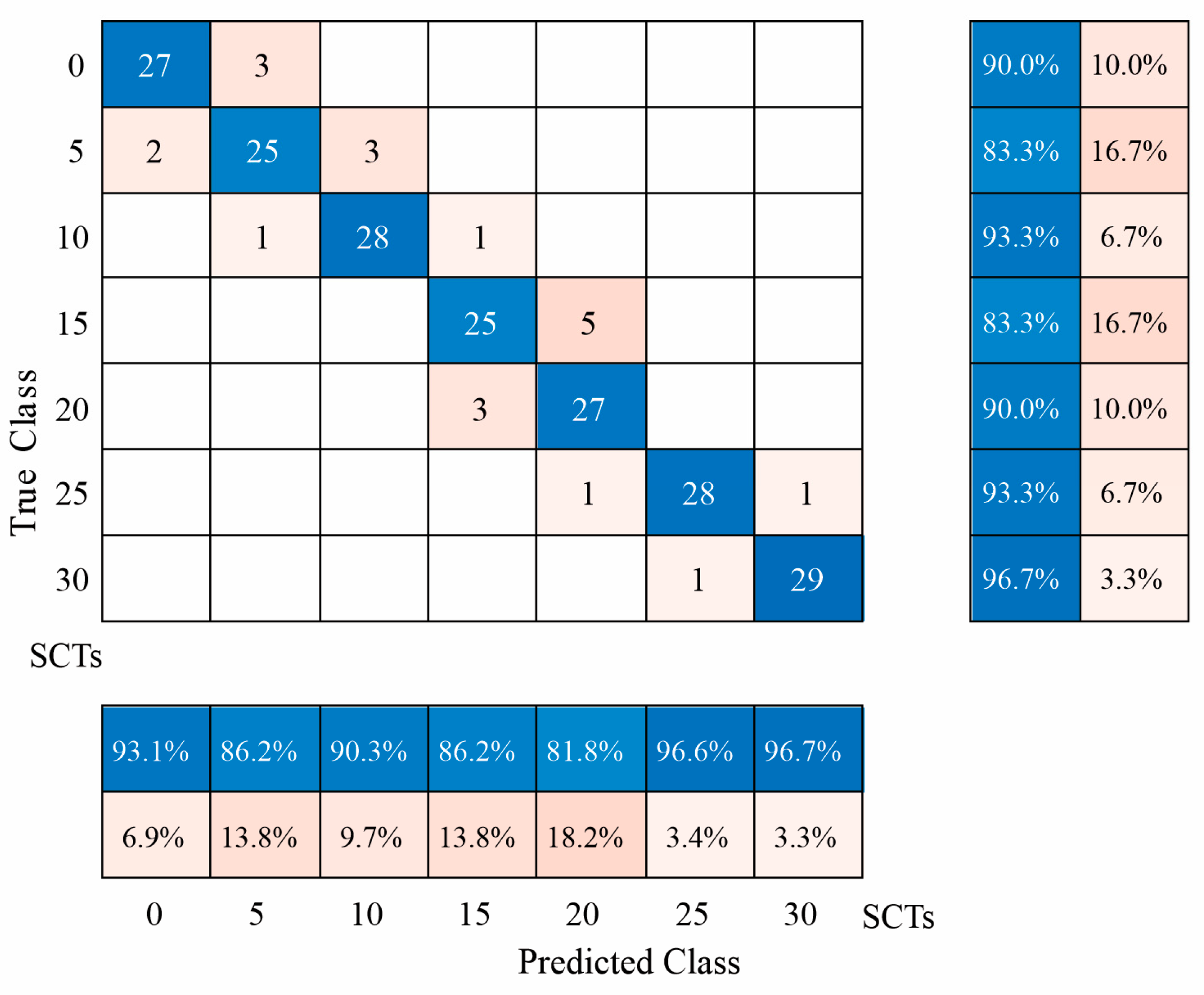
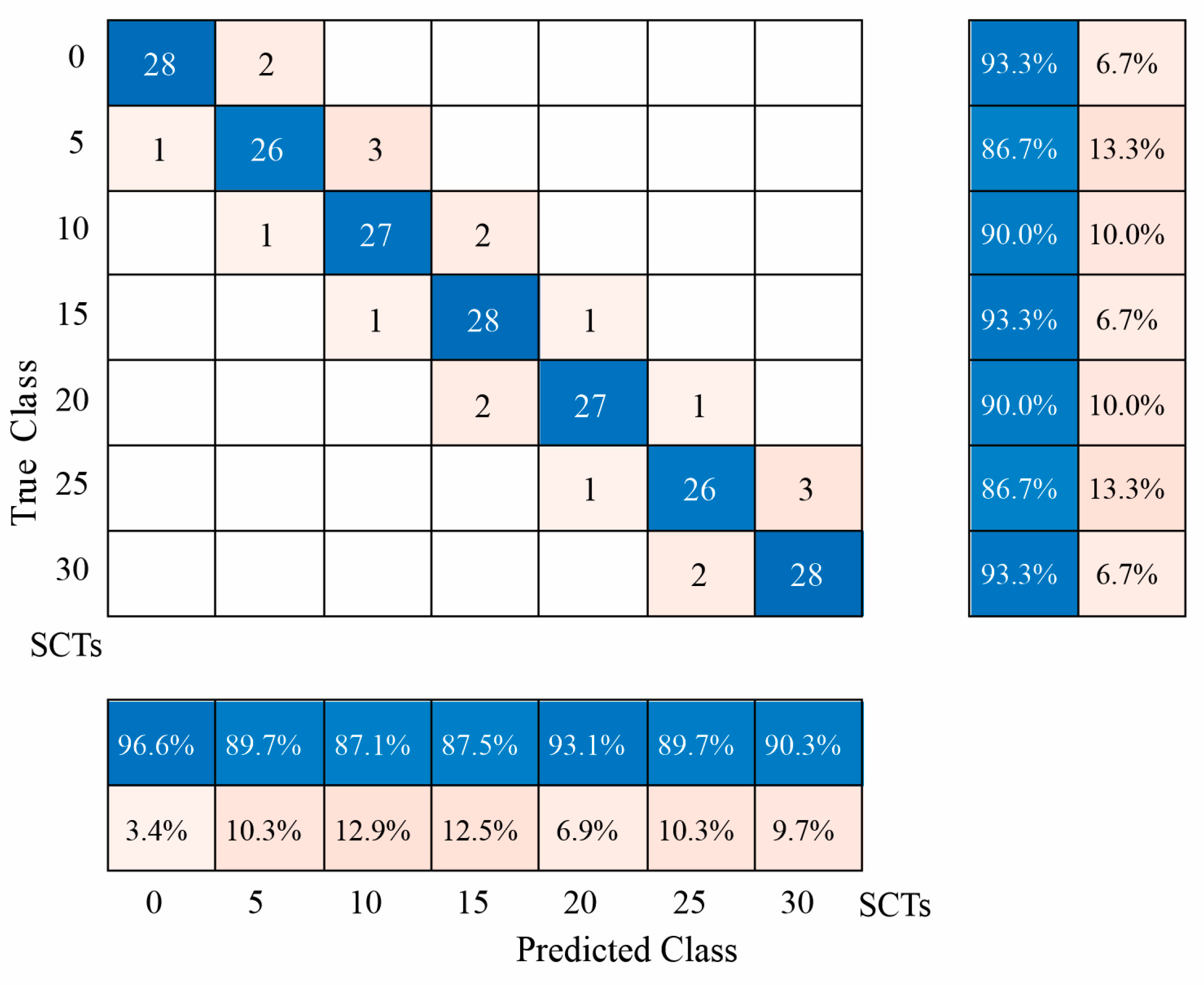
4.4. ANN Results
4.5. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khalili Senobari, R.; Sadeh, J.; Borsi, H. Frequency response analysis (FRA) of transformers as a tool for fault detection and location: A review. Electr. Power Syst. Res. 2018, 155, 172–183. [Google Scholar] [CrossRef]
- Barkas, D.; Chronis, I.; Psomopoulos, C. Failure mapping and critical measurements for the operating condition assessment of power transformers. Energy Rep. 2022, 8, 527–547. [Google Scholar] [CrossRef]
- Zhou, H.; Hong, K.; Huang, H.; Zhou, J. Transformer winding fault detection by vibration analysis methods. Appl. Acoust. 2016, 114, 136–146. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, H.; Pan, J. Detection of Winding Faults Based on a Characterization of the Nonlinear Dynamics of Transformers. IEEE Trans. Instrum. Meas. 2018, 68, 206–214. [Google Scholar] [CrossRef]
- Bagheri, M.; Zollanvari, A.; Nezhivenko, S. Transformer Fault Condition Prognosis Using Vibration Signals Over Cloud Environment. IEEE Access 2018, 6, 9862–9874. [Google Scholar] [CrossRef]
- Hong, K.; Huang, H.; Fu, Y.; Zhou, J. A vibration measurement system for health monitoring of power transformers. Measurement 2016, 93, 135–147. [Google Scholar] [CrossRef]
- Secic, A.; Krpan, M.; Kuzle, I. Vibro-Acoustic Methods in the Condition Assessment of Power Transformers: A Survey. IEEE Access 2019, 7, 83915–83931. [Google Scholar] [CrossRef]
- Borucki, S. Diagnosis of Technical Condition of Power Transformers Based on the Analysis of Vibroacoustic Signals Measured in Transient Operating Conditions. IEEE Trans. Power Deliv. 2012, 27, 670–676. [Google Scholar] [CrossRef]
- Hong, K.; Huang, H.; Zhou, J.; Shen, Y.; Li, Y. A method of realtime fault diagnosis for power transformers based on vibration analysis. Meas. Sci. Technol. 2015, 26, 115011. [Google Scholar] [CrossRef]
- Afrasiabi, S.; Afrasiabi, M.; Parang, B.; Mohammadi, M.; Samet, H.; Dragicevic, T. Fast GRNN-Based Method for Distinguishing Inrush Currents in Power Transformers. IEEE Trans. Ind. Electron. 2021, 69, 8501–8512. [Google Scholar] [CrossRef]
- De Santiago-Perez, J.J.; Rivera-Guillen, J.R.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Romero-Troncoso, R.J.; Dominguez-Gonzalez, A. Fourier transform and image processing for automatic detection of broken rotor bars in induction motors. Meas. Sci. Technol. 2018, 29, 095008. [Google Scholar] [CrossRef]
- Babaei, B.; Moradi, M. Novel Method for Discrimination of Transformers Faults from Magnetizing Inrush Currents Using Wavelet Transform. Iran. J. Sci. Technol. 2021, 45, 803–813. [Google Scholar] [CrossRef]
- Zhao, M.; Xu, G. Feature extraction of power transformer vibration signals based on empirical wavelet transform and multiscale entropy. IET Sci. Meas. Technol. 2018, 12, 63–71. [Google Scholar] [CrossRef]
- Lu, S.; Gao, W.; Hong, C.; Sun, Y. A newly-designed fault diagnostic method for transformers via improved empirical wavelet transform and kernel extreme learning machine. Adv. Eng. Inform. 2021, 49, 101320. [Google Scholar] [CrossRef]
- Wu, X.; Li, L.; Zhou, N.; Lu, L.; Hu, S.; Cao, H.; He, Z. Diagnosis of DC Bias in Power Transformers Using Vibration Feature Extraction and a Pattern Recognition Method. Energies 2018, 11, 1775. [Google Scholar] [CrossRef]
- Seo, J.; Ma, H.; Saha, T. Probabilistic wavelet transform for partial discharge measurement of transformer. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1105–1117. [Google Scholar] [CrossRef]
- Hussain, M.; Refaat, S.; Abu-Rub, H. Overview and partial discharge analysis of power transformers: A literature review. IEEE Access 2021, 9, 64605–64857. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Valtierra-Rodriguez, M.; Granados-Lieberman, D.; Olivares-Galvan, J.C.; Escarela-Perez, R. The application of EMD-based methods for diagnosis of winding faults in a transformer using transient and steady state currents. Measurement 2018, 117, 371–379. [Google Scholar] [CrossRef]
- Shang, H.; Xu, J.; Li, Y.; Lin, W.; Wang, J. A Novel Feature Extraction Method for Power Transformer Vibration Signal Based on CEEMDAN and Multi-Scale Dispersion Entropy. Entropy 2021, 23, 1319. [Google Scholar] [CrossRef]
- Hong, K.; Wang, L.; Xu, S. A Variational Mode Decomposition Approach for Degradation Assessment of Power Trans-former Windings. IEEE Trans. Instrum. Meas. 2019, 68, 1221–1229. [Google Scholar] [CrossRef]
- Huerta-Rosales, J.R.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P.; Camarena-Martinez, D.; Valtierra-Rodriguez, M. Vi-bration signal processing-based detection of short-circuited turns in transformers: A nonlinear mode decomposition ap-proach. Mathematics 2020, 8, 575. [Google Scholar] [CrossRef]
- Shah, A.M.; Bhalja, B.R. Discrimination between internal faults and other disturbances in transformer using the sup-port vector machine-based protection scheme. IEEE Trans. Power Del. 2013, 28, 1508–1515. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Romero-Troncoso, R.J. Multirate signal processing to improve FFT-based analysis for detecting faults in induction motors. IEEE Trans. Ind. Inform. 2017, 13, 1291–1300. [Google Scholar] [CrossRef]
- He, Q.; Nie, J.; Zhang, S.; Xiao, W.; Ji, S.; Chen, X. Study of Transformer Core Vibration and Noise Generation Mechanism Induced by Magnetostriction of Grain-Oriented Silicon Steel Sheet. Shock. Vib. 2021, 2021, 8850780. [Google Scholar]
- Yadav, S.; Mehta, R.K. Modelling of magnetostrictive vibration and acoustics in converter transformer. IET Electr. Power Appl. 2021, 15, 332–347. [Google Scholar] [CrossRef]
- Matti, M.S.; Al-Sulaifanie, A.K. Wavelet Denoising Based on Genetic Algorithm. In Proceedings of the 2018 International Conference on Advanced Science and Engineering (ICOASE), Duhok, Iraq, 9–11 October 2018; Volume 1, pp. 75–80. [Google Scholar]
- Li, Q.; Zhu, Z.; Xu, C.; Tang, Y. A novel denoising method for acoustic signal. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar]
- Aggarwal, R.; Singh, J.K.; Gupta, V.K.; Rathore, S.; Tiwari, M.; Khare, A. Noise Reduction of Speech Signal using Wavelet Transform with Modified Universal Threshold. Int. J. Comput. Appl. 2011, 20, 14–19. [Google Scholar] [CrossRef]
- Dautov, C.P.; Ozerdem, M.S. Wavelet transform and signal denoising using Wavelet method. In Proceedings of the 2018 26th Signal Pro-cessing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar]
- Rivera-Guillen, J.R.; De Santiago-Perez, J.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Romero-Troncoso, R.J. Enhanced FFT-based method for incipient broken rotor bar detection in induction motors during the startup transient. Measurement 2018, 124, 277–285. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; Rivera-Guillen, J.R.; Basurto-Hurtado, J.A.; De-Santiago-Perez, J.J.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P. Convolutional Neural Network and Motor Current Signature Analysis during the Transient State for Detection of Broken Rotor Bars in Induction Motors. Sensors 2020, 20, 3721. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Signal Processing: Principles, Algorithms, and Applications, 4/E; Pearson Education India: Noida, India, 2007. [Google Scholar]
- Rivera-Guillen, J.R.; de Santiago-Perez, J.J.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Perez-Soto, G.I.; Trejo-Hernandez, M. Time-Domain Diagnosing Algorithm for Automatic Broken Rotor Bar Detection in Induction Motors. In Proceedings of the 2018 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 14–16 November 2018; pp. 1–5. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Umar, A.M.; Linus, O.U.; Arshad, H.; Kazaure, A.A.; Gana, U.; Kiru, M.U. Comprehensive Review of Artificial Neural Network Applications to Pattern Recognition. IEEE Access 2019, 7, 158820–158846. [Google Scholar] [CrossRef]
- Suthar, V.; Vakharia, V.; Patel, V.K.; Shah, M. Detection of compound faults in ball bearings using multiscale-SinGAN, heat transfer search optimization, and extreme learning machine. Machines 2022, 11, 29. [Google Scholar] [CrossRef]
- Wieczorek, J.; Guerin, C.; McMahon, T. K-fold cross-validation for complex sample surveys. Stat 2022, 11, e454. [Google Scholar]



| SCTs | |||||||
|---|---|---|---|---|---|---|---|
| Signal | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| Vx | 1 | 1.0787 | 1.1394 | 1.3116 | 1.3564 | 1.8395 | 2.7043 |
| Vy | 1 | 0.9002 | 1.2071 | 1.2624 | 1.2409 | 1.8031 | 1.8108 |
| Vz | 1 | 1.0071 | 1.0095 | 1.0291 | 1.0341 | 1.0795 | 1.0709 |
| SCTs | |||||||
|---|---|---|---|---|---|---|---|
| Signal | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| Vx | 1 | 1.1750 | 1.2670 | 1.5372 | 1.8855 | 2.5642 | 2.7475 |
| Vy | 1 | 1.0455 | 1.8513 | 2.4707 | 2.5634 | 2.6960 | 3.3665 |
| Vz | 1 | 1.0228 | 1.7007 | 3.1712 | 3.9219 | 5.1645 | 6.0375 |
| SCT Class | Accuracy | Recall | Specificity | Precision | F1-Score |
|---|---|---|---|---|---|
| 0 | 0.9000 | 0.9000 | 0.9889 | 0.9310 | 0.9153 |
| 5 | 0.8333 | 0.8333 | 0.9778 | 0.8621 | 0.8475 |
| 10 | 0.9333 | 0.9333 | 0.9833 | 0.9032 | 0.9180 |
| 15 | 0.8333 | 0.8333 | 0.9778 | 0.8621 | 0.8475 |
| 20 | 0.9000 | 0.9000 | 0.9667 | 0.8182 | 0.8571 |
| 25 | 0.9333 | 0.9333 | 0.9944 | 0.9655 | 0.9492 |
| 30 | 0.9667 | 0.9667 | 0.9944 | 0.9667 | 0.9667 |
| SCT Class | Accuracy | Recall | Specificity | Precision | F1-Score |
|---|---|---|---|---|---|
| 0 | 0.9333 | 0.9333 | 0.9944 | 0.9655 | 0.9492 |
| 5 | 0.8667 | 0.8667 | 0.9833 | 0.8966 | 0.8814 |
| 10 | 0.9000 | 0.9000 | 0.9778 | 0.8710 | 0.8852 |
| 15 | 0.9333 | 0.9333 | 0.9778 | 0.8750 | 0.9032 |
| 20 | 0.9000 | 0.9000 | 0.9889 | 0.9310 | 0.9153 |
| 25 | 0.8667 | 0.8667 | 0.9833 | 0.8966 | 0.8814 |
| 30 | 0.9333 | 0.9333 | 0.9833 | 0.9032 | 0.9180 |
| Reference | Signal Processing Methods | Analyzed State | Number of Sensors Employed | Detected Faults | Severity Levels | Automatic Diagnosis |
|---|---|---|---|---|---|---|
| Proposal | Wavelet denoising and FT-based methods | Transient and steady | 1 | SCTs | 6 | ANNs |
| [3] | Electromagnetic force analysis | Steady | 5 | Winding loosening | 3 | -- |
| [13] | Empirical wavelet transform and HT | Transient and steady | 2 | Winding deformation | 3 | -- |
| [19] | CEEMDAN and multiscale dispersion entropy | Steady | 1 | Winding and core loosening | 1 | Density peaks clustering |
| [20] | VMD and WT | Steady | 1 | Winding deformation | 3 | CNN |
| [21] | NMD and HT-based RMS | Transient and steady | 1 | SCTs | 6 | FLS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Granados-Lieberman, D.; Huerta-Rosales, J.R.; Gonzalez-Cordoba, J.L.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Camarena-Martinez, D. Time-Frequency Analysis and Neural Networks for Detecting Short-Circuited Turns in Transformers in Both Transient and Steady-State Regimes Using Vibration Signals. Appl. Sci. 2023, 13, 12218. https://doi.org/10.3390/app132212218
Granados-Lieberman D, Huerta-Rosales JR, Gonzalez-Cordoba JL, Amezquita-Sanchez JP, Valtierra-Rodriguez M, Camarena-Martinez D. Time-Frequency Analysis and Neural Networks for Detecting Short-Circuited Turns in Transformers in Both Transient and Steady-State Regimes Using Vibration Signals. Applied Sciences. 2023; 13(22):12218. https://doi.org/10.3390/app132212218
Chicago/Turabian StyleGranados-Lieberman, David, Jose R. Huerta-Rosales, Jose L. Gonzalez-Cordoba, Juan P. Amezquita-Sanchez, Martin Valtierra-Rodriguez, and David Camarena-Martinez. 2023. "Time-Frequency Analysis and Neural Networks for Detecting Short-Circuited Turns in Transformers in Both Transient and Steady-State Regimes Using Vibration Signals" Applied Sciences 13, no. 22: 12218. https://doi.org/10.3390/app132212218
APA StyleGranados-Lieberman, D., Huerta-Rosales, J. R., Gonzalez-Cordoba, J. L., Amezquita-Sanchez, J. P., Valtierra-Rodriguez, M., & Camarena-Martinez, D. (2023). Time-Frequency Analysis and Neural Networks for Detecting Short-Circuited Turns in Transformers in Both Transient and Steady-State Regimes Using Vibration Signals. Applied Sciences, 13(22), 12218. https://doi.org/10.3390/app132212218








