Abstract
This paper presents the results of complex scientific research aimed at developing a prototype fiber-optic system for controlling the technical condition of buildings, structures, and extended objects. The aim is to develop a quasi-distributed type of fiber-optic control system without electrical signals, with the minimum possible cost of one measurement point. The fiber-optic sensors are based on a new method of controlling the parameters of the light spot by means of a hardware-software complex. The proposed monitoring system is quasi-distributed, is able to determine the damaged and most stressed and deformed areas of load-bearing reinforced concrete structures of buildings at the stage of their occurrence, and will allow for the taking of preventive measures for their protection. The research was carried out on a laboratory bench working together with the hardware-software complex; pixel analysis of changes in the area of the spot and its intensity was used as a fiber-optic sensor. A single-mode optical fiber of the G.652.D 9/125 μm standard was used, with a wavelength of 650 nm. The monitoring system can perform the function of pressure measurement on the building structure, establish the damage zone, and signal in case of an abrupt change in parameters in case of structure destruction. Laboratory tests have shown that the number of channels can be increased to 16 or 32. With the help of this system, it is possible to monitor the technical condition of the underground and above-ground parts of buildings or structures and control their integrity in real-time.
1. Introduction
Nowadays, new buildings are being constructed intensively. In some cases, there may be a violation of construction technology, possibly soil scour, when, after the building or structure is put into operation, there is a situation with the appearance of cracks in the foundation and load-bearing structures [1,2,3]. It is necessary to monitor the process of changing the stress-strain state of the monolithic reinforced concrete foundation to identify the dangerous emergency zone of stress concentration and cracking at an early stage. It is also necessary to monitor the growth of already-formed cracks and the load on the reinforcement. A significant advantage of using digital fiber optic technologies is the low cost of optical fiber, immunity to electromagnetic interference and stray leakage currents, fire safety, low power consumption, and durability. Optical fiber can be in a building structure for more than 50 years and can transmit information using a light wave over a considerable distance. Since the largest part of the reinforced concrete foundation is hidden in the ground, it is not always possible to find the places of its damage by visual inspection or non-destructive testing. This is a rather serious challenge for scientists and developers who develop new diagnostic and monitoring tools in construction.
Cracks in monolithic reinforced concrete structures of buildings [4,5,6] pose a danger because, in the absence of control over their growth and opening, the actual technical condition of the structure is unknown, and the consequences of operating such structures can be quite severe (Figure 1). There are known methods of non-destructive testing to detect defects in reinforced concrete and stone structures. Ultrasonic structural probing of reinforced concrete structures is a flaw detection method. Its principle is based on analyzing useful echo signals (reflections from defects in the structure and its parts) [7,8]. Non-destructive methods of assessing concrete and stone structure stability include using ground penetrating radar (GPR) [9,10]. Another tool for determining the strength of concrete is the Schmidt rebound hammer, which is a surface hardness meter [11,12,13]. Knowing the relationship between the compressive strength of concrete and the rebound of the hammer, it is possible to estimate the strength parameter of concrete. The authors in the work [14] point out that Schmidt’s jackhammer cannot accurately and directly fail to estimate the strength of concrete. The study [15] suggests using the SHM-X crackmeter and the classical geodetic method. The paper [16] demonstrates the use of LiDAR and the optimal dataset method to improve the crack-finding result. The important point is that with the help of non-destructive testing tools, only periodic monitoring can be carried out, while the cost of services is quite high since only specially trained people can work with them [17,18,19].

Figure 1.
Cracks in the foundation.
So, the issue of continuously monitoring and controlling buildings’ technical conditions for the growth of cracks in monolithic concrete and reinforced concrete structures remains unresolved. Developing effective tools for early diagnosis of distributed and significant objects is very important. To monitor the technical condition of buildings and structures, there are successfully used tensometric, acoustic piezoelectric transducers, molecular-electronic, and fiber-optic strain gauges [20]. Among them, the most widespread are electrical sensors: strain gauges in thin rectangular foil strips with labyrinth wiring diagrams. The disadvantages of strain gauges are their limited length (up to 800 m), many cables, and the high cost of one control point.
A scientific analysis of works that propose the use of optical fiber as a sensor and various options for monitoring the technical condition of reinforced concrete structures has been carried out. A popular solution is using FOS based on Bragg gratings [21,22,23]. The paper [24] presents a method for measuring the stress-strain state and total deformation of tensile stress concentration zones during concrete shrinkage using optical fibers and Bragg gratings. Some studies deal with developing systems for probing the slippage of reinforcing bars and joints in concrete structures based on Bragg gratings [25]. In study [26], fiber strain gauges with Bragg grating were proposed to detect damaged areas in bridge structures. There are systems for predicting normal deformations in pre-stressed concrete structures. The method uses Bragg gratings, a simplified analytical model of a concrete structure, and neural networks [27]. The use of Bragg gratings, in addition to their positive aspects, carries a sufficient complexity of the FOS design and a high cost. There are FOS based on the principle of operation of the Mach–Zehnder interferometer [28,29,30], which are designed to search for ultrasonic stress waves. The sensitivity of such sensors is highly dependent on the length of the optical fiber, and there is also a high noise level.
Fabry–Perot interferometers are also used to assess the condition of concrete structures [31,32]. In terms of the FOS application based on the operation of the Fabry–Perot interferometer, there is a crosstalk for eliminating which several basic methods are combined at once. In study [33], a hybrid system of a quasi-distributed FOS is described, which operates on the principle of a Fabry–Perot interferometer and Bragg gratings. Another method uses the Rayleigh scattering principle in a distributed FOS system [34,35]. This method allows for obtaining data with a rather high spatial resolution, but it has limitations in the form of a measurement distance of up to 100 m. There are also systems using the Brillouin scattering principle [36,37,38].
There are studies showing comparisons between traditional methods and methods using FOS. In [39], an experiment was carried out comparing the operation of a strain gauge, an FOS, and the digital image correlation (DIC) method in monitoring the propagation of fatigue in concrete beams. In this experiment, an ODiSI 6108 system was used for the optical measurement of mechanical stresses and temperature distribution, a 3D DIC system, and five strain gauges from Hottinger–Baldwin–Messtechnik. According to the experiment results, the FOS and the DIC gave more detailed data on the stress distribution in the structure compared with strain gauges. At the same time, FOS provides a very efficient assessment of important parameters using a relatively small amount of data. A similar but more extensive study was carried out at the UCLouvain in Belgium [40], comparing the data obtained from distributed FOS installed inside a concrete structure to measure displacements and deformations of reinforcing bars with surface deformation data obtained using micrometers, linear differential transducers (LVDTs), and DIC systems. The ODiSI 6104 system was used as a distributed FOS. Empirical assumptions were used in which some parameters were overestimated or underestimated, while distributed FOS made it possible to measure the deformation penetration into blocks of concrete walls. The data were obtained with a higher resolution. At the same time, the software of the distributed FOS system imposes restrictions on the measurement of only 10–15% of deformations. The authors’ works on using original design solutions in developing hardware and software complex mechanisms were considered [41].
The fundamental difference between the idea and analogs existing in the world is the development of a hardware-software complex capable of working with a single-mode OF [42] and analyzing the data obtained from changes in the pixels of a light spot incident on the surface of a television matrix. Using a single-mode optical fiber makes it possible to significantly increase the distance from the installation site of the FOS to the data processing unit. Preliminary studies have been carried out on using OF to control the integrity of concrete beams [43]. A single-mode optical fiber has a stepped profile, which is described by the Gaussian distribution, and the light spot contains a significant amount of noise, especially when the temperature changes, which complicates the measurement process [44]. Only intelligent processing of the received data with the help of a specialized hardware and software complex allows for solving the above problems. Previously, similar work was carried out on developing an FOS to control a monolithic array of mine workings and concrete support. In papers [45,46], there is a description of the FOS and the hardware-software complex. These principles will be used later. The analysis shows that there is a problem of diagnosing the destruction of building structures, including monolithic ones, and the development of methods and means of effective control of this process, especially at an early stage, is required, especially when it is still impossible to detect cracks during visual inspection. The cost of fiber optics is relatively low, about 10 US dollars per 1 km of length. Compared to a copper pair, this is a meager cost. In contrast to string sensors based on OF, it is possible to build a FOSM not only of a point type but of a distributed and a quasi-distributed type.
Given the need to develop highly efficient means of remote monitoring load-bearing reinforced concrete structures, including columns, floor slabs and coatings, walls, flights of stairs, and foundations, experimental studies were conducted to solve the problems mentioned above. The basis of the monitoring system for monolithic reinforced concrete structures, including floors with pre-stressed beams, is a fiber-optic technology based on monitoring changes in the parameters of a light wave passing through an optical fiber under mechanical action on it. Optical fibers are very widely used in various fields of technology. The industry has mastered the production of fiber-optic sensors for monitoring different physical quantities. These sensors have some advantages over electrical ones.
Existing monitoring systems have a rather high cost per measurement point and a limitation in the distance from the data processing unit to the sensor. The use of OF will allow for an increase in this distance up to 30 km, while the power consumption for data transmission is only a few milliwatts. The fundamental difference between the idea and the existing analogs in the world is in the development of a hardware-software complex able to work with single-mode fiber optic fiber and analyze the data obtained by changing the pixels of the light spot falling on the surface of the TV matrix. It should be noted that the fiber-optic system for monitoring the technical condition of buildings, structures, and any extended objects has high noise immunity and low power loss in the measuring channels. At the same time, the length of measurement channels can be tens of kilometers.
Thus, the purpose of this research work is to conduct experimental studies of intelligent fiber-optic systems for monitoring damage to reinforced concrete foundation structures with the development of conceptual foundations for the physical and mathematical models of processes in optical fibers.
2. Materials and Methods
2.1. Experimental Research Methods and Materials Used
In the experiments, samples of cement beams that imitated a monolithic reinforced concrete structure were used. This structure can be a foundation. The size of the samples was X = 50 mm, Y = 50 mm, and Z = 400 mm. Five samples of cement beams were made of PC-400D cement, steel reinforcing bars, and sand with the addition of water. Inside the beams, four steel reinforcing bars with a diameter of 4 mm were inserted, on which an optical fiber was fixed with plastic ties. The number of fiber optic sensors was selected arbitrarily and ranged from 1 to 2 for each steel reinforcing bar. Conditions of mortar hardening were chosen naturally during 28 days in water, according to the GOST 310.4-81 [47] cement methods for determining bending and compressive strength.
The beams were tested and brought to failure using a hydraulic measuring press (PGI-500) (Saratov, Russia). PGI-500 is periodically checked and has a certificate of verification (VL-2-03-18000654). This press is used in the building materials laboratory for strength and for testing concrete beams in compression by creating a variable force value from 0 to 500 kN (50,986 kgf).
A liquid crystal display is available to monitor the compression force and other parameters. The tests were carried out according to state GOST 310.4-81 [47] conditions for cement methods for determining bending and compressive strength. The temperature in the laboratory room varied within 24–25 °C. Movement of the beam along the axes OX = 0 m; OY = 0 m; and OZ = 0 m at pressure application. Before starting the experiments, the integrity of fiber-optic sensors was checked, and parameters of additional losses were set using the optical power meter Smart Pocket OLP-38 (San Jose, CA, USA) and the optical radiation source Smart Pocket OLS-34/35/36 (San Jose, CA, USA) was used. All fiber-optic sensors remained undamaged after filling the beams and drying.
As a result, each beam necessarily had 4 FOSs. The rest were reserved and were not used in the experiment, as they were needed to replace the main ones in case of damage. Next, a 9/125 µm Corning (Corning, NY, USA) single-mode quartz fiber (G.652.D standard [48]) with a 248 µm vinyl coating was used as a fiber optic sensor. The top layer of the protective plastic coating was between 1 and 2.5 mm. A wooden mold was specially made to fill the beams, into which the sand-cement mortar was poured. The manufactured cement beams gained strength within 28 days. Figure 2 shows the manufacturing process of concrete beams and placing fiber optic sensors in them.

Figure 2.
The process of pouring concrete beams.
The optical fiber used in the studies has a shell made of glass with a density of n1 = 1.4570, which is lower than the core density of n2 = 1.4625. The refractive indices correspond to the condition n1 < n2. Then, the beam deviates from the OF axis by an angle of not more than (90°-α), and the ratio of n1 and n2 can be expressed as sin α = n1/n2. At the same time, there is an equality of the angles of incidence and refraction αin = αout, which provides a total internal reflection of the pulse light wave (mode) [46].
Using a DVP 740 welding machine (Hunan, China), SC-type optical connectors were mounted on each fiber optic sensor. The SC connectors used a 2.5 mm UPC (ultra-physical contact) polished ferrule. Figure 3 shows the process of mounting optical connectors using a DVP 740 welding machine and the tools used to remove the sheath (Hunan, China).

Figure 3.
The process of mounting optical connectors with the use of the DVP 740 welding machine.
The experiments were carried out using a hydraulic press for testing building materials (P-125) (Lida, Russia). The press is a set that consists of a loading device and a control panel. The measuring unit contains a torsion force meter and a diagram apparatus. The measuring range is from 125 to 625 kN, and the indication range is from 0 to 625 kN; the division value is 1.25 kN; the admissible load measurement error in forward stroke starts at 20% of the largest value of the measurement range but is not lower than 10% of the maximum limit load; and the percentage of the measured load is ±2. The concrete beam was placed on two supports, and the third support was used to develop pressure on the center of the beam. To control the displacement of the plates, a vernier caliper with a digital indication in the 0–150 mm range and with a resolution of 0.01 mm and accuracy of ±0.01 mm (Sichuan, China) was used. Figure 4 shows the process of putting pressure on a concrete beam and its destruction.

Figure 4.
Carrying out the experiment.
As mentioned earlier, the optical fiber was pre-embedded in the body of the reinforced concrete beam. With pressure on the beam in the central part, its expansion occurs due to stress concentration and the formation of cracks. When the beam is destroyed, it is deformed, so the steel reinforcement to which the fiber-optic sensors are attached is also deformed. The put-forward hypothesis was tested during the experiment that the optical fiber could work as a sensitive sensor for identifying damage to a monolithic reinforced concrete structure. The method is based on the control of changes in the properties of light passing through the optical fiber under mechanical action, which makes it possible to establish the numerical value of mechanical stresses or deformations in the beam body as well as to determine the limiting value at which a crack can occur. The proposed method makes it possible to establish the locations of local hidden defects (cracks) in reinforced concrete structures’ foundations and use them in the future on other long-building structures. The experiment allows simulation of complicated operating conditions, for example, during flooding and destroying a monolithic reinforced concrete foundation. When the foundation concrete is destroyed, dislocation and cracking can be established.
Figure 5 shows the scheme of the experiment: Several fiber-optic sensors (2) are located in the body of beam 1, which are fixed on steel reinforcing bars, and rod (3) presses on beam (1) from above. The other two rods are located on the bottom of plate (4). The location of rod 3 makes it possible to destroy the beam during bending. The top of plate 5 is lowered onto the beam providing load (6), and is transmitted through rod (3). This is how the standard tests of reinforced concrete beam samples are carried out to determine their bending strength. In the center of the beam, the mechanical stress concentrator and the zone of irreversible deformation are formed, where cracks (7) are generated. Fiber-optic sensors are connected to data processing unit (9) using optical patch cords with SC connectors (8). Each optical patch cord is equipped on both sides with connectors of the SC type. Selecting these connectors is arbitrary, and they can be replaced by others without any problems, for example, by the FC type. The data processing unit has four main parts: (10)—module containing laser and optical splitter; (11)—module of photodetector, the number of which corresponds to the number of channels; (12)—microprocessor module of video image pre-processing and coordination with the computer; and (13)—DC source for power supply of photomatrixes and laser. The coherent source of laser radiation has a wavelength in the visible light range of 650 nm, and permissible deviations are not more than 5 nm. In the experiments, InGaAs (laser launcher level CLASS IIIB) semiconductor lasers with a power of 10 mW or more were used. The laser power was 20 mW. It is possible to use a laser with a power of up to 30 mW and a 650–850 nm wavelength. An optical splitter is used to split the beam into several channels, which distributes the light wave’s energy in equal proportions between all the channels.
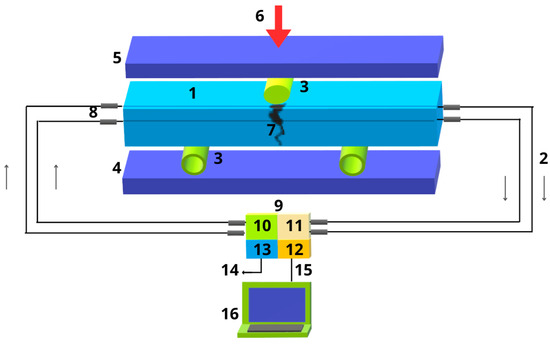
Figure 5.
Schemes for measuring the values of mechanical stresses and determining the location of the defect. 1—body of beam; 2—fiber-optic sensors; 3—rod; 4—bottom of plate; 5—top of plate; 6—load; 7—cracks; 8—connectors; 9—data processing unit; 10—module containing laser and optical splitter; 11—module of photodetector; 12—microprocessor-based data processing and matching unit; 13—direct current source; 14—power cord; 15—USB cable; 16—personal computer.
In the experiment, an optical splitter of the PLCM-1U4U-SC (Shenzhen, China) type was used by dividing it into four channels with a ratio of ¼, so the light wave energy was divided into each channel in the ratio of 25%. For more channels, one can use splitters with a ratio of 1/8, 1/16, or 1/32. Increasing the number of channels will require increasing the laser power, and the power of the laser used depends on the length of the fiber-optic communication line of the sensor with the data processing unit. The laser beam passing through the FOS 2 falls on the photodetector 11, which captures all the changes in intensity formed on the surface of the photo matrix. A stepped profile is formed at the exit from the OF, which the Gaussian distribution law can describe. A high-resolution photo matrix on the surface of which a light spot falls is installed at the exit from the optical fiber.
The manufactured optical module (Figure 6) has a sealed housing, and its parts are glued with a sealant that does not allow penetration of external light rays, which can lead to malfunction, into the interior. At the end of the optical conductor is a fiber optic connector of SC type with a 2.5 mm diameter tip and a physical contact connector (UPC Ultra).

Figure 6.
Optical modules.
For each channel, it is necessary to use a separate photo matrix, which converts the light signal into an electrical one and sends it to the microprocessor-based data processing and matching unit (12). It is connected via a USB cable (15) to the personal computer (16). To operate unit 9, a direct current source (13) with a power cord (14) is required. To operate the hardware-software complex, specially developed software is installed on the personal computer (16). The method of optical-electronic analysis of the light spot is used. The highest intensity of radiation is in zone 1. It is the brightest zone and unsuitable for study as it makes a lot of noise (Figure 7). There is a study changing the number of pixels in zone 2.
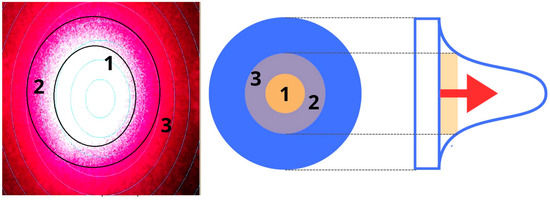
Figure 7.
The light spot: 1—core; 2—transition boundary; 3—shell.
Figure 8 shows a positive image of the light spot formed at the end of the optical fiber and further incident on the photo matrix under various impacts on the optical fiber. As the mechanical force on the sensor increases, the loss increases, and the emission intensity of the light spot decreases. Also, as the length of the optical fiber increases, its losses increase, and the size of the light spot decreases. It is found that this process is characteristic of the single-mode optical fiber of the G-652 standard [48] at a wavelength of 650 nm (red). Considering the degradation of the light spot, it is necessary to increase the laser power when increasing the length of the optical fiber used as a sensor.

Figure 8.
Images of the light spot at different loadings show spot degradation.
2.2. Development of Theoretical Bases for Physical and Mathematical Models of Electron-Optical Phenomena in Fiber-Optic Functional Elements
2.2.1. Conceptual Foundations of the Physical and Mathematical Model
The theoretical part presented in this paper, in terms of content, is a presentation of the conceptual and theoretical foundations of the physical and mathematical model of electron-optical processes (in general, nonlinear) associated with the interaction of a monochromatic electromagnetic wave with the substance of an optical fiber element under the external conditions established in the model. Obviously, a rigorous physical model of such processes should be based on the solution of the kinetic equation, which allows us to calculate the concentrations of optically active centers (atoms, molecules, atomic groups, etc.), which are the scattering centers of the external optical signal (optical relaxers), as well as excessive (over equilibrium) concentrations of electrically charged particles (electrophysical relaxers) moving under the action of the electric and magnetic fields of the wave in the potential field of the crystal lattice. The solution of the kinetic equation should be constructed together with the Maxwell equations for the electromagnetic wave field in the substance of the fiber optic material. In general, a comprehensive solution to the problem will require, in the long run, the development of schemes and methods that are quite complex in theoretical terms, firstly, related to the choice of correct physical methodology in the construction of the kinetic equation of electron-optical processes in optical fiber (OF), including kinetic coefficients describing at the microscopic level the processes of interaction of the external electromagnetic field (optical signal) with optical centers and with electrophysical relaxants. Secondly, it will be necessary to choose a convenient, from the point of view of comparing the results of theory and experiment, methodology for experimental evaluations of the investigated microscopic processes (light scattering, electric polarization, and light refraction), which will require determining both the list of experimentally determined electrical and optical parameters and the scheme of precision measurements of these parameters. At this research stage, including in this paper, do not set the above tasks. Here we limit ourselves only to the description of conceptual bases and schemes of realization of the nonlinear kinetic theory of electron-optical effects in optical fibers planned for the future.
Thus, the purpose of Section 2 is to develop conceptual (corresponding to the schemes and experimental conditions) bases for the physical and mathematical model of the optoelectrical processes occurring in an optical fiber element during its interaction with a monochromatic electromagnetic wave (optical signal coming from a coherent radiation source) in a wide range of electromagnetic wave and temperature parameters. At the same time, the final analytical relations between the calculated macroscopic parameters of the system will be established by generalized phenomenological (without detailing the structure and properties of the kinetic equation and its boundary and initial conditions) and approximate (in terms of the physical specificity of the dependences observed in the experiment) methods. Our main task, in Section 2, will be reduced to the formulation of the final mathematical expression establishing the relationship between the optical characteristics of the process (intensity of the light flux, refractive index of the substance) and the electro-optical characteristic of the system under study measured in the experiment. It is possible that in the process of refinement of the structure and general form of the electro-optical kinetic equation and its joint solution with Maxwell’s equations, both intermediate and final equations of the model will appear, significantly influencing the final calculation formulas. Methodologies and schemes for measuring the electro-optical characteristics of the system will not be developed in this work. The solution to all these issues will be the subject of research in subsequent works based on this preliminary theoretical study.
A comparison of the results of numerical calculations performed according to the theoretical formulas and measured in the experiment will not be carried out in this paper. The theoretical section is given after the experimental section because it is subsidiary and, so far, is not directly compared with the experiment. The analytical part of this work is dealing with the development of the theoretical foundations of a mathematical model of nonlinear electronic optical processes in an elastically deformable element (working body) of fiber-optic controlling and measuring devices (electromagnetic radiation sensors, strain analyzers, radiation recorders, optical signal converters, etc.). The analytical solutions will be performed based on the equations of the phenomenological model [49], taking into account the elastic deformations of the fiber material effect on the characteristics of the output optical signal (interacting with the recording photographic plate) and on the refractive index n of the fiber material in the range of wavelengths and intensities of the incoming optical signal specified in the experiment (light flux incident on the cross section of the fiber optic element). As an experimental sample, a horizontal (as well as a vertical) beam (with a fiber-optic wire laid along its axis) loaded by external forces and experiencing longitudinal and transverse deformations is taken [50].
The research methodology will be constructed based on the laws of geometric and wave optics within the framework of the phenomenological theory of optical-electric processes associated with the interaction of a light wave (optical signal) with the substance of the fiber optic element (FO). The study of quantum effects when describing optical-mechanical phenomena in the fiber optic sample under study will not be carried out. All theoretical considerations in this work are limited by the provisions of the electrodynamics of a continuous medium and the classical wave theory of light.
2.2.2. Basic Provisions of the Physical and Mathematical Model
Let us consider a model of a single-mode cylindrical (with diameter d and length of generatrix l for the “core” or working part) of the fiber optic element, onto the cross section of which falls a monochromatic light fluxed from a source of coherent radiation (laser emitting at wavelengths in the visible optical range). The direction perpendicular to the cross section of the sample (cylinder axis) is taken as the coordinate axis OZ.
Suppose a light ray with a wavelength and wave vector falls from the air onto the surface (input cross section) of a fiber optic sample at the geometric center of this cross section O at an angle to the normal to the surface. Here, is a vector drawn along the direction of the vector of light velocity in the air to the point of reconnection of the incident light ray with the point O and, further, to the intersection of the input light ray (in the direction of its further motion in the sample, without taking into account refraction) with the side surface of the cylindrical sample at some point M. In this case, the vector direction is chosen along the direction of the wave vector, from which the initial phase (in this model, the spatial component of the phase of the incident light beam in the direction of the vector ) is equal to . In this case, the phase velocity vector (the velocity of moving lines of constant phase) of the incident light wave is defined along the direction of the wave vector and is equal to the vector . The circular frequency of the light wave, in this case, is . The solution of the classical Dalembert wave equation for this case is known and has the form of a plane monochromatic wave , where .
A light ray or electromagnetic wave refracted in the sample, moving in the substance with velocity , wavelength , and wave vector , at point M, will be described by the spatial component of phase . The direction of the phase velocity vector (velocity of moving lines of constant phase) of the refracted light wave is determined by the direction of the wave vector . The solution of the Dalembert equation for this case, calculated at point M, has the form , where . The question of the methodology of calculating the theoretical refractive index of light in matter , as noted in Section 2.2.1, remains, within the framework of this article, open due to the lack of a rigorous or at least approximately defined scheme for constructing and analyzing the kinetic equation describing the physical mechanism of electromagnetic wave propagation in the substance of the fiber optic element, taking into account all related effects, including both optical and electrophysical phenomena. In any case, the generalized expression for the theoretical refractive index of light in matter will be modeled, considering nonlinear optical-electrical effects as a function of the parameters of the electromagnetic wave (frequency and amplitude), the temperature of the element, and the molecular characteristics of matter.
The concept of the angle of deviation of the light ray refracted in the optical fiber (as well as in any other sample) with wave vector from the direction of the light ray entering the sample with wave vector is used in this model. The expression for the phase difference between the refracted and incident light rays (electromagnetic waves) at the above-mentioned M point may be necessary for further development of this model. It is not excluded that the study of the description of optical-electrical processes in the optical fiber, from the point of view of wave and geometrical optics, may require the calculation of phase differences of the refracted and incident rays at other points of the system. In this case, this phase difference is taken as the sought value. Further, , where is a unit vector chosen in the direction of the vector . Then, according to . It is easy to see that in the absence of refraction of the light ray, when n = 1, equalities hold , , which allows us to interpret this result as a criterion for the reliability of the formula . Further, this expression will be used when constructing the more rigorous mathematical model of optical-electric processes in the fiber-optic element in the single-mode fiber-optic communication line, in particular when calculating the refractive index of an electromagnetic wave in the working element of the system.
Further studies of semi-empirical and theoretical methods of parameter determination make it possible to choose two main directions. In the first direction, the value is determined from the model’s experimental parameters using the system’s geometrical characteristics, including θ, d (diameter of the cylindrical specimen), and b (distance from the center of the cross-section O to the point M). A study of this case is given in Appendix A. The second direction is modeled as a multifactor function depending on , , and molecular parameters of the model and on temperature. It can be represented as a function of the form . Here, is the angle between the direction of the light beam coming out of the sample and the normal to the surface of the registration element (photographic plate). The parameter represents a variety of different characteristic molecular parameters (activation energies of relaxers (conductivity ions) on ionic-molecular chemical bonds; frequencies of natural vibrations of ions near the equilibrium position (localized at the sites of the crystal lattice); width of the potential barrier for ions, etc.); and structure parameters (depending on the physicochemical properties and the type and geometry of the crystal structure of the fiber optic sample [46,47].
During the study of the processes of the interaction of an electromagnetic wave with the substance of a fiber optic sample, classified as a dielectric or semiconductor, according to the transformed equation , when passing to a dimensionless variable , from the expression , assuming that the main optical effects occur in a spatial region in size comparable to the lattice constant a, in a wide range of wavelengths, including the optical range, due to and, accordingly, , we take the electric and magnetic components of the wave in the forms , .
Then, taking the displacement current due to the electric field in the form , where, is the inductive (high-frequency) component of the complex dielectric permittivity (CDP) of the optical fiber material, and neglecting the relaxation (low-frequency) polarization of the sample [47,48], we calculate the volumetric power density of the electric field of an electromagnetic wave in an optical fiber in the following form [46]:
The volumetric power density of the magnetic field of an electromagnetic wave in a non-magnetic optical fiber is calculated based on approximate equalities , and is reduce to the following form:
The volumetric power density of the electromagnetic field of the wave is calculated, taking into account the identity , from the expression .
Taking into account the fact that, in this approximation, when estimating the dielectric permittivity of the sample, only the processes of induction polarization realized in the high-frequency range are taken into account, we assume the refractive index of a light wave in a non-magnetic optical fiber in the form .
The calculation of the intensity of the electromagnetic wave in the form gives the distribution of the volumetric power density of the electromagnetic field of the wave at angles (between the direction of the wave vector of the wave and the normal to the surface of the sensitive light-receiving plate).
The calculated value of the refractive index of an optical fiber is performed in a generalized analytical form , and its experimental value (necessary for comparing the results of theory and experiment) is calculated from expression (3).
The study of the refractive index of the fiber optic material in the most general case should be carried out using the methods of kinetic theory and electrodynamics of a continuous medium [46,51], which describe the patterns of relaxation processes associated with the interaction of the electric and magnetic fields of an electromagnetic wave (optical signal) with structural elements (ionic and molecular subsystems, electrons of the outer shells of the atoms of the structure, various types of vacancies) of the crystal lattice. Here, the mathematical set of elements is accepted. The influence of crystal structure parameters on the relaxation times of optical-electric processes is determined by the numerical values of the above-mentioned characteristic molecular parameters or groups of parameters related to various substructures (sublattices) that are in a state of stationary interactions with each other, described by the unperturbed Hamiltonian of the crystal lattice, taking into account theoretical model assumptions adopted based on experimental data. The temperature of the substance significantly affects the kinetics of relaxation polarization. The refractive index is influenced by the geometric characteristics of the crystal structure (primarily the type of lattice symmetry, lattice constant, and linear dimensions of the sample d) and optical-geometric parameters (angle of incidence of the beam on the surface of the material and angle between the wave vector of the optical signal (ray) refracted in the sample and the normal vector to the surface of the photodetector (detection screen) [49,50,51]. In the region of anomalously high polarization nonlinearities, the parameters of external field influences (frequency and amplitude of the wave) and the input (before entering the crystal) intensity of the electromagnetic wave begin to influence the polarization coefficients, complex dielectric and magnetic permeability, and refractive index of the substance.
The quantity measured in the experiment is the averaged over angles the function (3).
Thus, within the framework of this paper, we have described a scheme for calculating the physical characteristics of electron-optical processes in fiber-optic elements without using kinetic theory methods (as a simplified model). The connection between the schemes of experiments and the final formulas of the theoretical model (expression (4)) is of a generalized nature, where the angularly averaged distribution of the intensity of the optical signal I () registered on the photo plate measured in the experiment is compared with the value of the bulk energy density of the electromagnetic field in the optical fiber element, the methods of measurement of which will be investigated in the future.
Zero approximation of perturbation theory in dimensionless small deformation parameters , in expression (4) gives the calculated (theoretical) value of the experimentally measured volumetric power density of the electromagnetic field of the wave detected by a sensitive membrane (photographic plate) after refraction of the outgoing (primary optical signal) in an undeformed fiber optic sample.
2.2.3. Effect of Fiber Optic Element Deformations on the Physical and Mathematical Model
A presentation of mathematical methods for taking into account the influence of the deformation parameters of a fiber-optic element on its refractive index and, in general, on the experimentally measured value of the volumetric power density of an electromagnetic wave (optical signal recorded on a photographic plate) will be given below.
The proposed methods for analyzing the influence of elastically deformed states of a fiber-optic element (both from the point of view of longitudinal and transverse deformations) on its optical characteristics are not fundamentally new, but are limited to known methods of the theory of elasticity and are based on calculations of dependencies of the form , where are the parameters in the model , , where , , are, respectively, the values of the length and radius of the cross section of a horizontal cylindrical beam (loaded with external force influences) inside which, in the direction of the e axis, a fiber optic cable is stretched, experiencing the corresponding deformation effects.
A more detailed mathematical description of the relations between the longitudinal and transverse deformation parameters of the modeled OM element is given in Appendix B.
Comparison of the refractive index in the non-deformed state and, considering deformations, by expanding the analytical function:
into an infinite power series in dimensionless small parameters ,
This will allow, after substituting (6) into the kinetic equations and the d’Alembert equation, us to study the previously indicated effects of the fiber material deformed state in various approximations of perturbation theory in small parameters , starting from the “zero” approximation (in the absence of deformation) and, further, up to higher orders of smallness, to reveal the effects of the orders in function (6) on nonlinearities caused by the deformed state of the sample (effects of photoelasticity and thermoelasticity). The effect of the temperature range and the parameters of the electromagnetic field of the wave is manifested in nonlinear optoelectrical effects, depending, at the mathematical level, on the ratio of the energies of the thermal motion of the relaxers and the energies of the relaxers in the field of the electromagnetic wave. The parameters of the electromagnetic field of the wave may impact the effects of the deformed state, and vice versa.
The purpose of the theoretical part of this work is not reduced to the detailed study of the physical mechanisms of the photoelasticity and thermoelasticity effects and related solutions to the equations of the phenomenological model, but is limited, at this stage, to a central descriptive approach, based on which, in subsequent developments, an extended scheme of analytical description of nonlinear electronic optical effects in deformable samples of fiber-optic elements in a wide range of temperatures and parameters of the electromagnetic field of the wave will be disclosed.
Rigorous analytical studies of the laws of change in the intensity of the optical signal in the optical fiber , as in the case of the function , should be built using the methods of nonlinear kinetic theory, in combination with the methods of regression analysis, by minimizing inconsistencies in the results of theoretical and experimental numerical estimates. Then, in the general case, the deformation-averaged increment over the angles of the volumetric power density of an electromagnetic wave in an optical fiber [48]:
The numerical study of expression (7) will be carried out using specialized high-speed software and hardware, the development and implementation of which is also a separate complex task that is beyond the scope of this work and will be performed in the future.
3. Hardware and Software Complex
The proposed WAMS does not use the methods of optical interferometry and reflectometry, as well as fiber Bragg gratings and long-period fiber gratings. The refusal of the known method of optical interferometry is due to the dependence of the propagation phase of a light wave on temperature, so a change in temperature by 1 °C can cause a false alarm in the absence of a mechanical effect on the sensor. The use of a distributed WAMS based on optical reflectometry methods or Bragg gratings is due to the higher cost of one measurement point and the peculiarity of the distributed system operation associated with using one OF. Considering that it can be damaged during the operation of technological equipment and its movement, the work will be left without a pressure control system. It is also necessary to consider the specifics of the sensor placement in the hole drilled in the roof of the work, and this is a quasi-distributed measurement system. The proposed quasi-distributed WAMS contains a new principle of data construction and processing. A quasi-distributed WAMS can have an unlimited number of channels.
Figure 9 shows a photo of the moment of setting up the program for controlling the mechanical impact of fiber-optic sensors. The hardware-software complex was configured during the experiments to work with four sensors.

Figure 9.
Setting up a mechanical impact control program.
The program operates in two modes: measurement and alarm, triggered by a sudden parameter change. The hardware-software complex allows for controlling the stress-strain state of a monolithic reinforced concrete structure. When the program starts, a reference image is taken to compare all the following ones to measure changes.
In the camera settings block, the values of the parameters for the number of frames from the camera for averaging and reducing camera noise, the number of images (measuring values) for one detection period, and the threshold value of the pixel color in grayscale at which triggering will occur directly affect the sensitivity of detection. In the camera settings, one can also set the number of triggers (motion detection) in a row before the ALARM signal and the value of the motion detection threshold (the number of white pixels); when exceeded, the motion will be detected.
The graph in the monitoring block (Figure 10) shows changing the number of pixels above the set brightness threshold between two consecutive measurements; the scale is limited by the set field “motion detection sensitivity threshold value”. The scale is marked at 20% of the maximum, indicating numerical values.

Figure 10.
The mode of displaying incoming and processed.
The essence of the method (Figure 11) is as follows: from the radiation source (1) (semiconductor laser 650 nm) with a power of 10–30 mW, the light wave passes through the optical patch cord (3), which has optical connectors (2) (SC type) for switching the sensor with the data processing unit and the laser. The optical fiber is inside the concrete beam (4) and is the sensor through which the light wave passes. At the output of the VOD-installed optical module (5) is a transparent screen on which a light spot (6) is projected, and then the rays of the spot fall on the surface of the photo matrix (7), which converts the optical signal into an electrical signal and performs its pre-processing using the built-in graphics microprocessor. When a mechanical load is applied to the lateral surface of the optical fiber, a microbead is formed in it, and refractive parameters change, which leads to a change in the properties of the passing light wave. All changes are recorded by the photo matrix and the program.
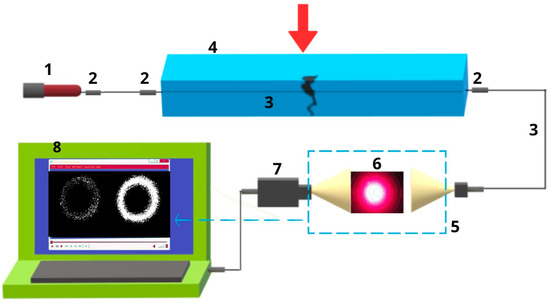
Figure 11.
Explanatory diagram explaining the method. 1—radiation source; 2—optical connectors; 3—optical patch cord; 4—concrete beam; 5—VOD-installed optical module; 6—light spot; 7—photo matrix; 8—computer screen.
Figure 12 shows the pictures from the computer screen showing how the light wave’s intensity changes with increasing force on the fiber optic sensor after converting a positive image to a negative image. The external load on the beam was created using a laboratory press (Figure 4). Analyzing the pictures from the computer screen, one can conclude that increasing the impact force causes changes in the pixels of the light spot, which can be used for the numerical estimation of the impact on the OF. Figure 9 shows how the shape of the spot changes from left to right if conditions are formed under which different forces are applied to the fiber optic sensor. At the initial stage, only individual white dots, which are noise, are visible on the screen. Then, two impacts on the sensor with different strengths are recorded. The screen reflects that with a weak impact on the sensor, the spot has more black pixels, and with increasing the impact on the fiber optic sensor, the number of white pixels on the screen increases.

Figure 12.
Image of a negative light spot from a computer screen.
4. Results and Discussion
As a result of automated data approximation, one-factor mathematical models were obtained. Each measurement was performed 20 times. The confidence probability is P = 0.95, and the Student’s distribution quantile is t = 2.0098 for a given confidence probability with the number of degrees of freedom. The relative measurement error is δ = 3.5%.
The beam after testing is shown in Figure 13.

Figure 13.
A laboratory sample of the beam after testing.
The data on the dependence of optical power loss on press pressure were obtained (Figure 14).
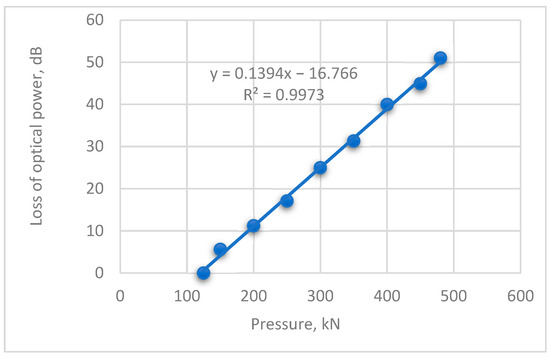
Figure 14.
Dependence of optical power loss of 650 nm fiber with increasing press pressure force.
The optical power loss of a fiber with a wavelength of 650 nm depends on a step-by-step increase in the pressure force of the press. In the course of the experiment, it was found that the increase in pressure on the beam led to an increase in additional losses formed in the optical fiber. Since the fiber was subjected to mechanical bending, part of the radiation that went beyond the shell, respectively, was lost. It was found that there is a direct correlation between the structural force (beam deformation) and the intensity of the light optical spot formed on the surface of the photo matrix. Accordingly, there is a direct correlation between the structural force and the level of additional losses in the optical fiber. The intensity of the optical radiation spot formed on the surface of the photomatrix decreases in direct proportion to the value of the applied pressure at the center of the tested reinforced concrete beam, and additional losses of optical radiation power increase. The observed process is related to the photoelastic effect, as the optical fiber undergoes microbending during the deformation of the reinforced concrete beam. Accordingly, the optical wave transmission parameters change due to changes in the refractive index between the sheath and the fiber core.
It is known that amplitude sensors are simpler in contrast to phase-sensitive sensors. This will make it possible to create a relatively simple in-design system with a low manufacturing cost since it does not use expensive electron-optical components, for example, an optical circulator, as in [39,40]. Unlike the known optical interferometry methods [28,29,30], the proposed system is insensitive to external temperature fluctuations, which is very important for noise immunity since the working conditions are the observed temperature fluctuations of a real construction object. The proposed system uses optoelectronic analysis, which analyzes video images, which provides simplicity in the sensor design and reduces the cost of the system as a whole in contrast to Bragg gratings embedded in the optical conductor [24,25,26], which require analysis of the reflected spectrum using an expensive spectrum analyzer. The low price will allow for implementation during construction. Laboratory tests of the system have shown that the number of channels can be increased to 16 or 32. The number of channels depends on the computing power of the microprocessor device and can be increased if more channels are needed. Currently, a four-channel monitoring system is being developed, which will allow control of the building structure in four zones. The length of each zone will be 50 m. The main difference between the proposed method and other methods is the optoelectronic analysis of the optical wave passing through the sheath of the optical fiber, unlike analogs, which monitor changes in the intensity of the light wave passing through the core of the optical fiber. Unlike the multi-pixel photodetector, the use of a multi-pixel one allows estimating the intensity over the entire area of the light spot coming out of the optical fiber and falling on the surface of the photodetector. The experiments showed that the stronger the impact on the fiber-optic sensor, the more white pixels were formed on the system’s screen. It should be noted that a spot of a round shape is formed at strong impact. Another difference is the transformation of the light spot from positive to negative, which allows it to darken the core of the optical fiber and control only the intensity conducted through its sheath. Further, the negative is converted into a black pixel pattern, and without impact on the fiber optic sensor, the pixel pattern does not change. In the research process, the absence of interference was recorded, which was reflected on the screen in the form of separate white pixels. The reason for this phenomenon is the non-coherence of the laser radiation source. Accordingly, it is necessary to eliminate this to equip the source with more effective current and voltage stabilization devices to increase the coherence parameters.
5. Conclusions
The conducted research allowed the development of a new damage control method for reinforced concrete building structures. This method is based on the intellectual optical-electronic analysis of additional losses formed at microbends of the optical fiber when a part of the radiation from the core into the sheath spreads along it to the photodetector, which converts optical parameters into electrical ones. Then, the hardware-software complex performs intelligent analysis of the optical wave, first of all its intensity. A conceptual physical and mathematical model of opto-electrical processes occurring in an optical fiber has also been developed. The obtained results of experimental studies have shown that the AIC is able to control the change of load on the reinforced concrete beam, with the obtained values allowing to plot the dependence of additional losses on the applied pressure with fairly good linearity. AIC is able to monitor not only the change of load on the reinforced concrete beam but also to record the fact of its destruction, which is very useful from a practical point of view. Since AIC is used to control the integrity of reinforced concrete structures and foundations, timely notification of the danger of destruction of the structure will allow you to take measures to strengthen it. It is also possible to determine the place of damage where cracks have formed. Unlike existing analogs, the proposed AIC has a more straightforward design and is low-cost. Using single-mode optical fiber and optoelectronic analysis to assess the change in the intensity of the optical spot allows for the formation of a numerical picture of pixels. These changes are directly related to changes in the load on the reinforced concrete beam. The higher the load level on the reinforced concrete beam, the greater the number of white pixels reflected in the program window. Unlike the known methods of optical interferometry, the proposed method has no problems with interference caused by changes in the temperature of the optical fiber inside the reinforced concrete structure. Based on the proposed AIC, a quasi-distributed system for monitoring the state of the reinforced concrete structure can be created. In this case, each sensor will control a strictly defined zone 10 to 50 m long. The length of the zone will depend on the specific needs of the personnel involved in the operation of the building or reinforced concrete structure.
Author Contributions
Methodology, V.Y. and A.M.; Investigation, A.M., Y.N., A.A. and Y.S.; Writing—original draft, A.M., V.K., Y.N. and L.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP14869145; Development of an intelligent fiber-optic system for monitoring the geotechnical condition of mining pits and sections).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
For the model of a single-mode cylindrical fiber optic element described in Section 2.2.2, the monochromatic light flux from the source is incident on the cross section of the sample in the direction of its axis, taken as the coordinate axis OZ. Then, the difference in the path of the reflected and refracted rays, in the adopted geometric model , calculated from expressions , , taking into account the equalities and, can be represented in the form . Further, an approximate expression for the phase difference of these rays , gives the expression , which is similar, both in the structure of the formula and in its content to the expression previously constructed, in Section 2.2.2, . Since vector oriented, as defined in Section 2.2.2, along the direction of the incident light ray (in the direction in which the unit vector is selected, ), obviously characteristic of the model under study is the equality . This result can be interpreted as another criterion for the reliability of the formula .
As a special case, consider the model of a single-mode cylindrical fiber optic element, the refractive index of which at wavelengths in the visible optical range satisfies the condition . In this case, according to the geometric model described in Section 2.2.2, .
According to the geometric model we accept, we determine the difference in the path of the refracted and incident rays , where b—parameter added to (Section 2.2.2). Then, the phase difference between the incident and refracted wave takes the following form:
based exp. (A1) and exp. , and introducing the notation , we construct the characteristic equation , which allows us to calculate the refractive index of the optical fiber
Appendix B
With minor deviations from Hooke’s law, the potential energy of a stressed body with the accuracy of a term of the fourth degree in the expansion with displacements in the longitudinal direction coinciding with the axis of the beam) is calculated:
In (A3), the known from the elasticity theory coefficients , , and are used. The coefficient of relative solid extension is [51], where is relative longitudinal elongation and is Poisson coefficient that is calculated taking into account the parameter. Accepting , where is the relative transverse expansion (elongation or compression), [51]. Using , , there is , from where, assuming the cross section to be round and the longitudinal deformations to be elongations (compressions), the following is obtained:
From the condition of the equilibrium the following is obtained:
In (A5), , are the radius of the beam cross section in the non-deformed and arbitrarily deformed state, is the beam mass, is the external force (mechanical) load concentrated in the geometrical center of the beam symmetry axis, and is the Young modulus of the beam material [51].
Expression (A5) for the Poisson coefficient can be interpreted for the case of transverse expansion , when , as well as for compression , when . The theoretical study of the effect of the sample geometric parameters , , its deformation parameters , , and temperature on its optical properties (in general, the effect of photoelasticity), in particular, on the value of the refractive index of the optical fiber material in the optical (high-frequency) range (without taking into account relaxation-polarization phenomena and conductivity) should be performed from the solutions of the system of kinetic equations [47,48] describing, in combination with the d’Alembert equation, nonlinear electronic optical processes in a deformable material. Here, () are the parameters of the electromagnetic field of the wave. The parameter is a set of different characteristic structural parameters of relaxers (molecular centers of light scattering in a substance), including the activation energy, on ionic-molecular chemical bonds, the frequencies of natural vibrations of relaxers near the equilibrium position (localized at the nodes of the crystal lattice), the potential barrier width, etc., and the structure parameters (depending on the physical and chemical properties, type, and geometry of the crystal structure of the fiber optic sample [51].
References
- Barre, F.; Bisch, P.; Chauvel, D.; Cortade, J.; Coste, J.; Dubois, J.; Erlicher, S.; Gallitre, E.; Labbé, P.; Mazars, J.; et al. Control of Cracking in Reinforced Concrete Structures; Wiley: Hoboken, NJ, USA, 2016; pp. 1–226. ISBN 9781119347088. [Google Scholar]
- Chrysanidis, T.A.; Panoskaltsis, V.P. Experimental investigation on cracking behavior of reinforced concrete tension ties. Case Stud. Constr. Mater. 2022, 16, e00810. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, Y. Corrosion-induced cracking propagation of RC beams subjected to different corrosion methods and load levels. Constr. Build. Mater. 2021, 286, 122913. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, Q. Numerical Study of Multi-species Transport in Cracked Concrete Under External Load. Cailiao Daobao/Mater. Rep. 2023, 37, 21120077. [Google Scholar] [CrossRef]
- Cheng, P.; Zhang, L.; Lin, G.; Qian, K.; Qian, X.; Ruan, S. Analysis of Initial Cracking of an Interface between a Bundled Lipped Channel–Concrete Composite Wall and an Infill Wall. Appl. Sci. 2022, 12, 7110. [Google Scholar] [CrossRef]
- Furtado, A. Assessment and Retrofitting of Building Structures: Experimental Testing and Modelling—Editorial. Appl. Sci. 2023, 13, 486. [Google Scholar] [CrossRef]
- Concu, G.; Trulli, N. Concrete Defects Sizing by Means of Ultrasonic Velocity Maps. Buildings 2018, 8, 176. [Google Scholar] [CrossRef]
- Kartashev, V.G.; Kachanov, V.K.; Sokolov, I.V.; Shalimova, E.V.; Kontsov, R.V.; Voronkova, L.V. Ultrasonic structural probing of products based on materials with a complex structure by analyzing the statistical characteristics of the structural noise. Russ. J. Nondestruct. Test. 2015, 51, 360–373. [Google Scholar] [CrossRef]
- Capozzoli, L.; Rizzo, E. Combined NDT techniques in civil engineering applications: Laboratory and real test. Constr. Build. Mater. 2017, 154, 1139–1150. [Google Scholar] [CrossRef]
- Spears, M.; Hedjazi, S.; Taheri, H. Ground penetrating radar applications and implementations in civil construction. J. Struct. Integr. Maint. 2023, 8, 36–49. [Google Scholar] [CrossRef]
- Chybiński, M.; Kurzawa, Z.; Polus, Ł. Problems with Buildings Lacking Basic Design Documentation. Procedia Eng. 2017, 195, 24–31. [Google Scholar] [CrossRef]
- Jain, A.; Kathuria, A.; Kumar, A.; Verma, Y.; Murari, K. Combined Use of Non-Destructive Tests for Assessment of Strength of Concrete in Structure. Procedia Eng. 2013, 54, 241–251. [Google Scholar] [CrossRef]
- Rubene, S.; Vilnitis, M. Use of the Schmidt rebound hammer for non-destructive concrete structure testing in field. Civ. Eng. 2014, 1-B, 13–19. [Google Scholar] [CrossRef]
- Brencich, A.; Cassini, G.; Pera, D.; Riotto, G. Calibration and Reliability of the Rebound (Schmidt) Hammer Test. Civ. Eng. Arch. 2013, 1, 66–78. [Google Scholar] [CrossRef]
- Sztubecki, J.; Topoliński, S.; Mrówczyńska, M.; Bağrıaçık, B.; Beycioğlu, A. Experimental Research of the Structure Condition Using Geodetic Methods and Crackmeter. Appl. Sci. 2022, 12, 6754. [Google Scholar] [CrossRef]
- Błaszczak-Bąk, W.; Suchocki, C.; Janicka, J.; Dumalski, A.; Duchnowski, R.; Sobieraj-Żłobińska, A. Automatic Threat Detection for Historic Buildings in Dark Places Based on the Modified OptD Method. ISPRS Int. J. Geo-Inf. 2020, 9, 123. [Google Scholar] [CrossRef]
- Ali-Benyahia, K.; Kenai, S.; Ghrici, M.; Sbartaï, Z.-M.; Elachachi, S.-M. Analysis of the accuracy of in-situ concrete characteristic compressive strength assessment in real structures using destructive and non-destructive testing methods. Constr. Build. Mater. 2023, 366, 130161. [Google Scholar] [CrossRef]
- Ptacek, L.; Strauss, A.; Bos, C.; Peyerl, M. Quality control of concrete curing. In Proceedings of the 18th Fib Symposium, Lisbon, Portugal, 14–16 June 2021; pp. 720–728. [Google Scholar]
- Cristofaro, M.T.; Nudo, R.; Tanganelli, M.; D’Ambrisi, A.; De Stefano, M.; Pucinotti, R. Issues concerning the assessment of concrete compressive strength in existing buildings: Application to a case study. Struct. Concr. 2017, 19, 795–805. [Google Scholar] [CrossRef]
- Zaprudnov, V.; Branch, B.; Seregin, N. Moscow State Building University (NIU MGSU) Methods and means of monitoring building structures technical condition. For. Bull. 2019, 23, 108–115. [Google Scholar] [CrossRef]
- Shadab, A.; Raghuwanshi, S.K.; Kumar, S. Advances in Micro-Fabricated Fiber Bragg Grating for Detection of Physical, Chemical, and Biological Parameters—A Review. IEEE Sens. J. 2022, 22, 15650–15660. [Google Scholar] [CrossRef]
- Kim, S.-T.; Park, Y.-S.; Yoo, C.-H.; Shin, S.; Park, Y.-H. Analysis of Long-Term Prestress Loss in Prestressed Concrete (PC) Structures Using Fiber Bragg Grating (FBG) Sensor-Embedded PC Strands. Appl. Sci. 2021, 11, 12153. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, J.; Wang, Y.; Zhang, Q.; Duan, J.; Zhang, Z.; Huang, X.; You, Z. Principles and Application of Polyimide Fiber Bragg Gratings for Surface Strain Measurement. Appl. Sci. 2017, 7, 995. [Google Scholar] [CrossRef]
- Yang, L.; Li, C.; Luo, C. Thermal Strain Detection for Concrete Structure Cold Shrinkage under Stress Constraint with FBG. Sensors 2022, 22, 9660. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.; Mesquita, E.; Alberto, N.; Melo, J.; Marques, C.; Antunes, P.; André, P.S.; Varum, H. Fiber Bragg Grating Sensors for Reinforcing Bar Slippage Detection and Bond-Slip Gradient Characterization. Sensors 2022, 22, 8866. [Google Scholar] [CrossRef] [PubMed]
- Banda, P.; Della Tamin, M.; Meyer, J. Applied Quasi-Distributed Fibre Bragg Grating Strain Sensors in Structural Damage Sensing of a Bridge Structure. SAIEE Afr. Res. J. 2022, 113, 75–87. [Google Scholar] [CrossRef]
- Pereira, M.; Glisic, B. Physics-Informed Data-Driven Prediction of 2D Normal Strain Field in Concrete Structures. Sensors 2022, 22, 7190. [Google Scholar] [CrossRef]
- Lan, C.; Zhou, W.; Xie, Y. Detection of Ultrasonic Stress Waves in Structures Using 3D Shaped Optic Fiber Based on a Mach–Zehnder Interferometer. Sensors 2018, 18, 1218. [Google Scholar] [CrossRef]
- Png, W.; Lin, H.; Pua, C.; Lim, J.; Lim, S.; Lee, Y.; Rahman, F. Feasibility use of in-line Mach–Zehnder interferometer optical fibre sensor in lightweight foamed concrete structural beam on curvature sensing and crack monitoring. Struct. Heal. Monit. 2018, 17, 1277–1288. [Google Scholar] [CrossRef]
- Bremer, K.; Weigand, F.; Zheng, Y.; Alwis, L.S.; Helbig, R.; Roth, B. Structural Health Monitoring Using Textile Reinforcement Structures with Integrated Optical Fiber Sensors. Sensors 2017, 17, 345. [Google Scholar] [CrossRef]
- Ahmed, E.; Benmokrane, B.; Deblois, R. Field testing of GFRP-reinforced concrete bridges in Quebec. In Proceedings of the SHMII 2015—7th International Conference on Structural Health Monitoring of Intelligent Infrastructure, Torino, Italy, 1–3 July 2015. [Google Scholar]
- Tang, F.; Zhou, G.; Li, H.-N.; Verstrynge, E. A review on fiber optic sensors for rebar corrosion monitoring in RC structures. Constr. Build. Mater. 2021, 313, 125578. [Google Scholar] [CrossRef]
- Bonilla, J.T.G.; Bonilla, H.G.; Betancourtt, V.M.R.; Zamora, A.C.; Morales, M.E.S.; Ortiz, L.G.; Bonilla, A.G. Signal Analysis, Signal Demodulation and Numerical Simulation of a Quasi-Distributed Optical Fiber Sensor Based on FDM/WDM Techniques and Fabry-Pérot Interferometers. Sensors 2019, 19, 1759. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. Application study of embedded Rayleigh based Distributed Optical Fiber Sensors in concrete beams. Procedia Eng. 2017, 199, 2014–2019. [Google Scholar] [CrossRef]
- Berrocal, C.G.; Fernandez, I.; Bado, M.F.; Casas, J.R.; Rempling, R. Assessment and visualization of performance indicators of reinforced concrete beams by distributed optical fibre sensing. Struct. Health Monit. 2021, 20, 3309–3326. [Google Scholar] [CrossRef]
- Bertulessi, M.; Bignami, D.F.; Boschini, I.; Brunero, M.; Ferrario, M.; Menduni, G.; Morosi, J.; Paganone, E.J.; Zambrini, F. Monitoring Strategic Hydraulic Infrastructures by Brillouin Distributed Fiber Optic Sensors. Water 2022, 14, 188. [Google Scholar] [CrossRef]
- Morgese, M.; Domaneschi, M.; Ansari, F.; Cimellaro, G.P.; Inaudi, D. Improving Distributed Fiber-Optic Sensor Measures by Digital Image Correlation: Two-Stage Structural Health Monitoring. ACI Struct. J. 2021, 118, 91–102. [Google Scholar] [CrossRef]
- Xu, J.; Yuan, G.; Zhang, J.; Tu, Y. A long term cost effective slop safety monitoring using emergency activated Brillouin optic fiber sensors. In Proceedings of the 7th International Conference on Hydraulic and Civil Engineering and Smart Water Conservancy and Intelligent Disaster Reduction Forum, ICHCE and SWIDR, Nanjing, China, 6–8 November 2021; pp. 972–975. [Google Scholar] [CrossRef]
- Becks, H.; Baktheer, A.; Marx, S.; Classen, M.; Hegger, J.; Chudoba, R. Monitoring concept for the propagation of compressive fatigue in externally prestressed concrete beams using digital image correlation and fiber optic sensors. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 514–526. [Google Scholar] [CrossRef]
- Hoult, R.; Bertholet, A.; de Almeida, J.P. Core versus Surface Sensors for Reinforced Concrete Structures: A Comparison of Fiber-Optic Strain Sensing to Conventional Instrumentation. Sensors 2023, 23, 1745. [Google Scholar] [CrossRef]
- Nikonova, T.; Zharkevich, O.; Dandybaev, E.; Baimuldin, M.; Daich, L.; Sichkarenko, A.; Kotov, E. Developing a Measuring System for Monitoring the Thickness of the 6 m Wide HDPE/LDPE Polymer Geomembrane with Its Continuous Flow Using Automation Equipment. Appl. Sci. 2021, 11, 10045. [Google Scholar] [CrossRef]
- Mekhtiyev, A.D.; Yurchenko, A.V.; Neshina, Y.G.; Alkina, A.D.; Kozhas, A.K.; Zholmagambetov, S.R. Nondestructive Testing for Defects and Damage to Structures in Reinforced Concrete Foundations Using Standard G.652 Optical Fibers. Russ. J. Nondestruct. Test. 2020, 56, 179–190. [Google Scholar] [CrossRef]
- Mekhtiyev, A.; Bulatbayev, F.; Neshina, Y.; Siemens, E.; Alkina, A.; Shaigarayeva, T. The external mechanical effects on the value of additional losses in the telecommunications fiber optic cables under operating conditions. In Proceedings of the 6th International Conference on Applied Innovation in IT, Koethen, Germany, 13 March 2018; Volume 1, pp. 123–127. [Google Scholar] [CrossRef]
- Yurchenko, A.V.; Mekhtiyev, A.D.; Bulatbayev, F.N.; Neshina, Y.G.; Alkina, A.D. The Model of a Fiber-Optic Sensor for Monitoring Mechanical Stresses in Mine Workings. Russ. J. Nondestruct. Test. 2018, 54, 528–533. [Google Scholar] [CrossRef]
- Yurchenko, A.; Mekhtiyev, A.; Alkina, A.; Yugai, V. Passive Perimeter Security Systems Based on Optical Fibers Of G 652 Standard. In Proceedings of the International Conference on Applied Innovation in IT, Denpasar, Bali, Indonesia, 21–22 September 2019; Volume 7, pp. 31–36. Available online: https://icaiit.org/proceedings/7th_ICAIIT_1/1_6_Yurchenko.pdf (accessed on 5 March 2023).
- Yurchenko, A.V.; Mekhtiyev, A.D.; Bulatbaev, F.N.; Neshina, Y.G.; Alkina, A.D.; Madi, P.S. Investigation of additional losses in optical fibers under mechanical action. IOP Conf. Ser. Mater. Sci. Eng. 2019, 516, 012004. [Google Scholar] [CrossRef]
- GOST 310.4-81; Cements. Methods of Bending and Compression Strength Determination. Standards Publishing House Moscow: Moscow, Russia, 1983.
- ITU-T G.652; Characteristics of a Single-Mode Optical Fibre and Cable. ITU-T Study Group XV; International Telecommunication Union: Geneva, Switzerland, 1984.
- Sitharam, T.G.; Govindaraju, L. Theory of Elasticity; Springer Science and Business Media: Dordrecht, The Netherlands, 2021; pp. 1–283. [Google Scholar] [CrossRef]
- Kalytka, V.A.; Neshina, Y.G.; Madi, P.S.; Naboko, Y.P. Methods of theoretical researches the non-linear electrophysical prop-erties of solid dielectrics with compound crystalline structure. IOP Conf. Ser. Mater. Sci. Eng. 2019, 698, 022002. [Google Scholar] [CrossRef]
- Nguyen, W.; Duncan, J.F.; Jen, G.; Ostertag, C.P. Influence of matrix cracking and hybrid fiber reinforcement on the corrosion initiation and propagation behaviors of reinforced concrete. Corros. Sci. 2018, 140, 168–181. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).