Engagement Recognition Using a Multi-Domain Feature Extraction Method Based on Correlation-Based Common Spatial Patterns
Abstract
:1. Introduction
- Firstly, an engagement recognition method based on a correlation-based CSP is proposed, in which the temporal correlation is utilized as a prior to improve the effectiveness. Specifically, the original CCSP is extended into three versions by replacing various correlation coefficients (Pearson’s linear correlation coefficient, Kendall’s correlation coefficient [37], and Spearman’s correlation coefficient).
- Secondly, this study integrates information from spatial, frequency, and phase domains to fully exploit the potential of EEG data. A filter bank is combined with the original CCSP to extract features in the frequency domain and the spatial domain. Besides, the Hilbert transform is applied to obtain the amplitude and phase angle of EEG signals. Multi-domain features are integrated and fed into an SVM to realize engagement recognition.
- Thirdly, the proposed method is validated and compared with existing methods on an open dataset composed of 29 subjects. Experimental results show that it offers an efficient way to recognize the level of engagement, which is validated by its outperformance.
2. Materials and Methods
2.1. CSP-Based Methods
2.1.1. Common Spatial Patterns
2.1.2. Correlation-Based Common Spatial Patterns
2.2. Amplitude and Phase Feature Extraction
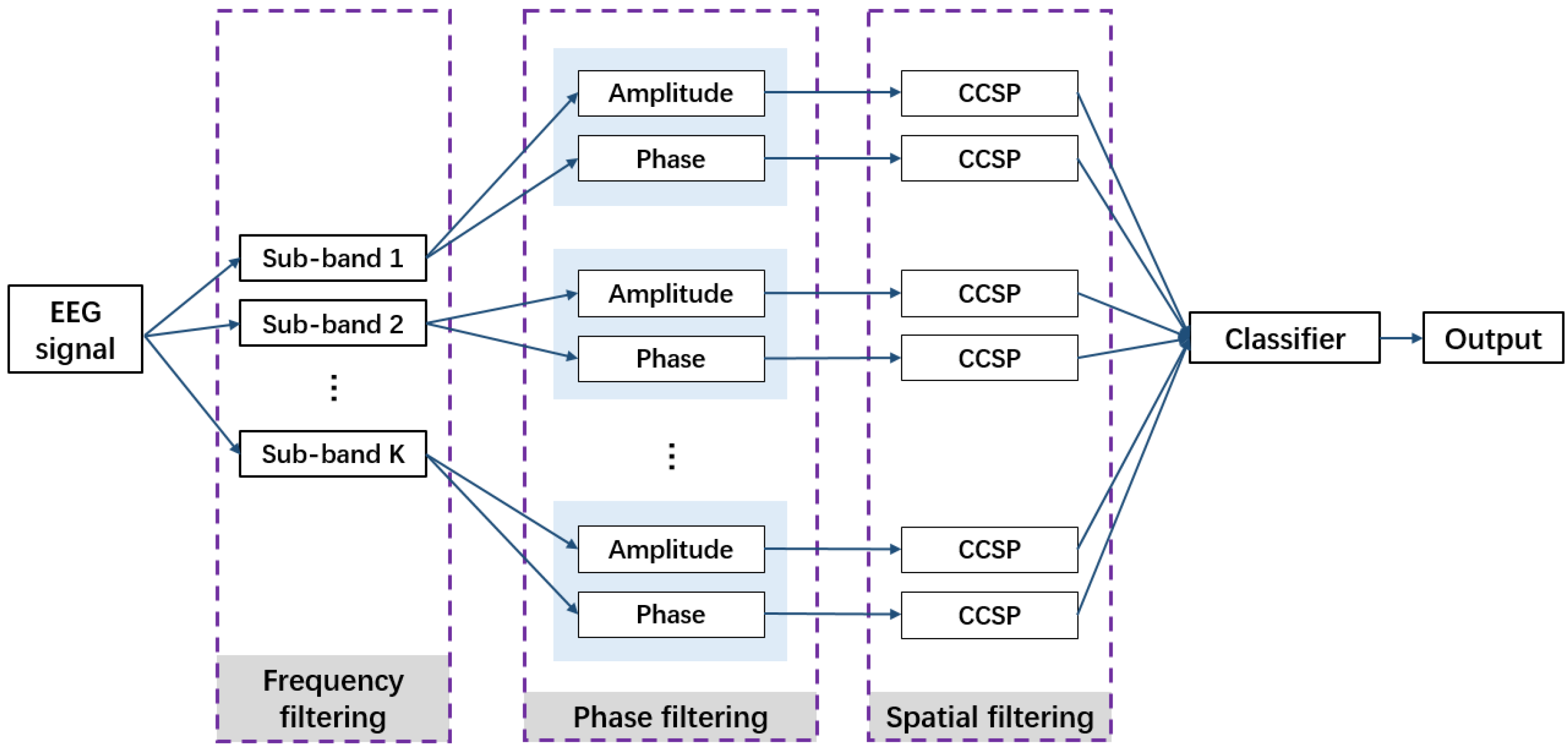
2.3. Multi-Domain Feature Extraction Method Based on Correlation-Based Common Spatial Patterns
2.4. Support Vector Machine
3. Results
3.1. Dataset
3.2. Data Pre-Processing
3.3. Effect of Filter Banks
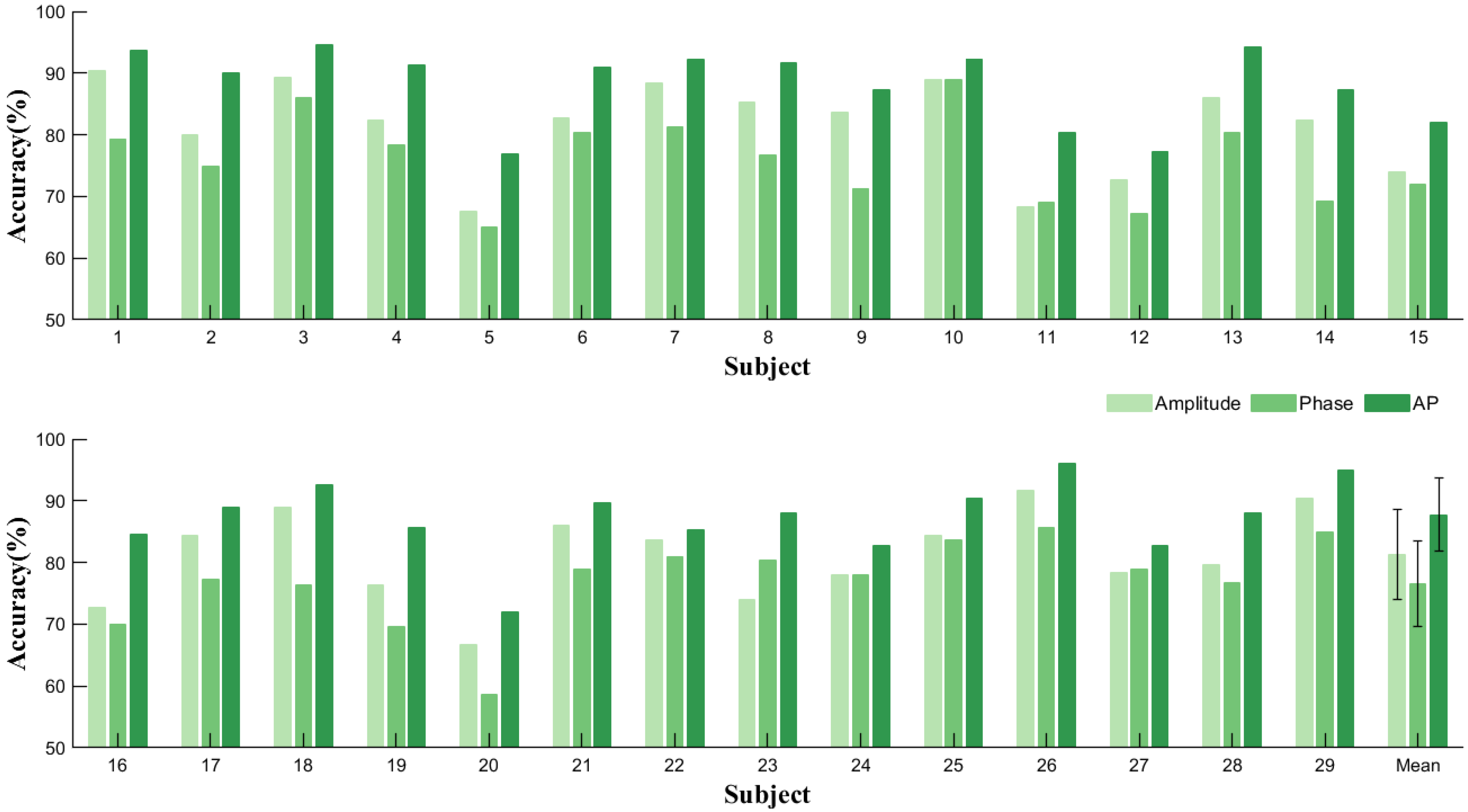
3.4. Effects of Phase Information
3.5. Effects of Correlation Coefficients
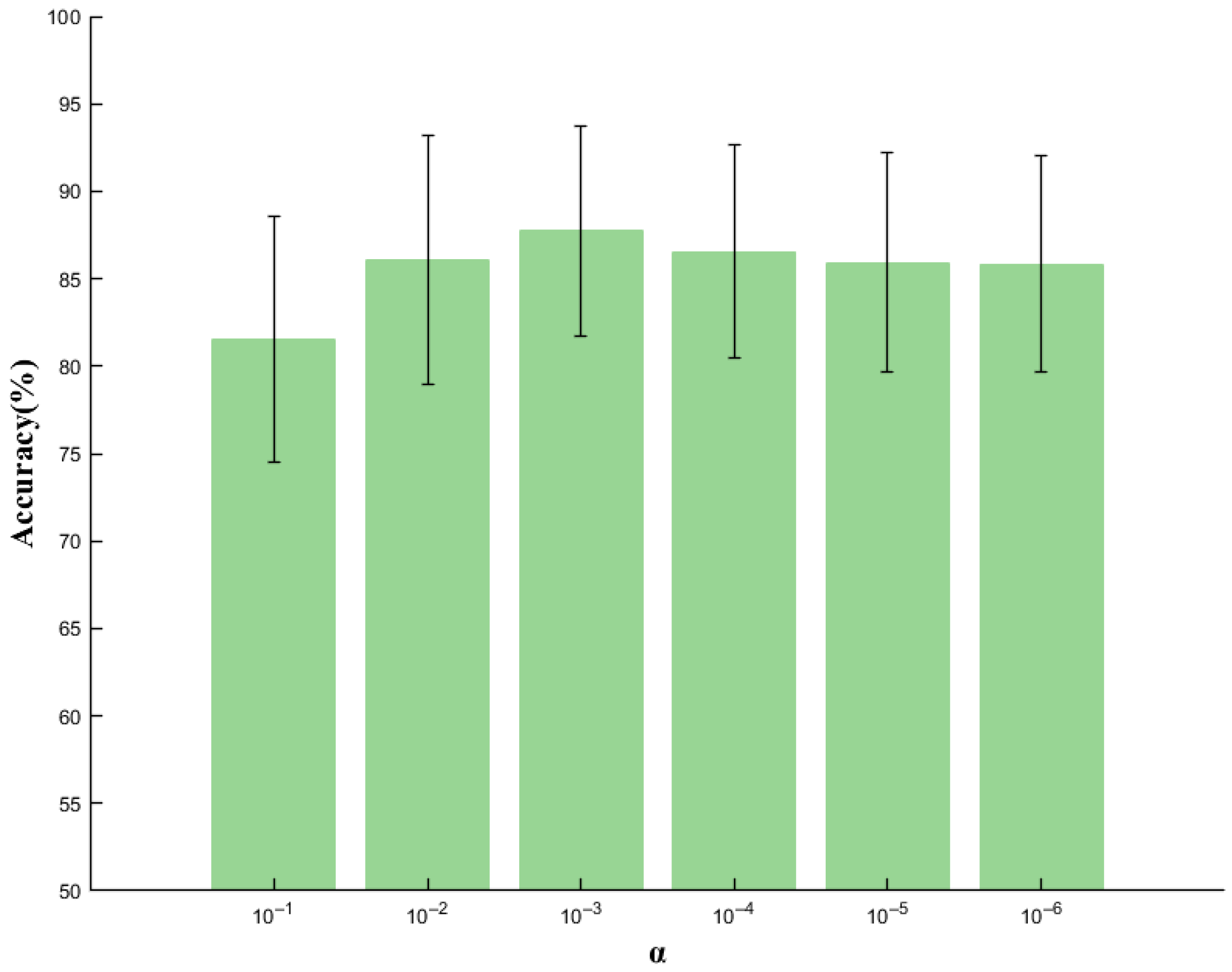
3.6. Effects of Regularization Parameter
3.7. Experimental Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Händel, M.; Bedenlier, S.; Kopp, B.; Gläser-Zikuda, M.; Kammerl, R.; Ziegler, A. The webcam and student engagement in synchronous online learning: Visually or verbally? Educ. Inf. Technol. 2022, 27, 10405–10428. [Google Scholar] [CrossRef] [PubMed]
- Glaman, R.; Chen, Q. Measurement invariance of a classroom engagement measure among academically at-risk students. Front. Psychol. 2018, 8, 2345. [Google Scholar] [CrossRef] [PubMed]
- Doo, M.Y.; Bonk, C.J. The effects of self-efficacy, self-regulation and social presence on learning engagement in a large university class using flipped Learning. J. Comput. Assist. Learn. 2020, 36, 997–1010. [Google Scholar] [CrossRef]
- Meng, F.; Xu, Y.; Liu, Y.; Zhang, G.; Tong, Y.; Lin, R. Linkages between transformational leadership, work meaningfulness and work engagement: A multilevel cross sectional study. Psychol. Res. Behav. Manag. 2022, 15, 367–380. [Google Scholar] [CrossRef] [PubMed]
- Mahalingham, T.; Howell, J.; Clarke, P.J. Attention control moderates the relationship between social media use and psychological distress. J. Affect. Disord. 2022, 297, 536–541. [Google Scholar] [CrossRef]
- Mahon, C.E.; Hendershot, B.D.; Gaskins, C.; Hatfield, B.D.; Shaw, E.P.; Gentili, R.J. A mental workload and biomechanical assessment during split-belt locomotor adaptation with and without optic flow. Exp. Brain Res. 2023, 241, 1945–1958. [Google Scholar] [CrossRef]
- Bacigalupo, F.; Luck, S.J. Alpha-band EEG suppression as a neural marker of sustained attentional engagement to conditioned threat stimuli. Soc. Cogn. Affect. Neurosci. 2022, 17, 1101–1117. [Google Scholar] [CrossRef]
- Toy, S.; Ozsoy, S.; Shafiei, S.; Antonenko, P.; Schwengel, D. Using electroencephalography to explore neurocognitive correlates of procedural proficiency: A pilot study to compare experts and novices during simulated endotracheal intubation. Brain Cogn. 2023, 165, 105938. [Google Scholar] [CrossRef]
- Cai, Y.; Li, Q.; Cao, T.; Wan, Q. Nurses’ work engagement: The influences of ambidextrous leadership, clinical nurse leadership and workload. J. Adv. Nurs. 2023, 79, 1152–1161. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Lan, J.; Ji, M.; Li, Y.; Yang, S.; You, X. The influence of self-efficacy on human error in airline pilots: The mediating effect of work engagement and the moderating effect of flight experience. Curr. Psychol. 2021, 40, 81–92. [Google Scholar] [CrossRef]
- Eiris, R.; Jain, A.; Gheisari, M.; Wehle, A. Safety immersive storytelling using narrated 360-degree panoramas: A fall hazard training within the electrical trade context. Saf. Sci. 2020, 127, 104703. [Google Scholar] [CrossRef]
- Bernhardt, K.A.; Poltavski, D.; Petros, T.; Ferraro, F.R.; Jorgenson, T.; Carlson, C.; Drechsel, P.; Iseminger, C. The effects of dynamic workload and experience on commercially available EEG cognitive state metrics in a high-fidelity air traffic control environment. Appl. Ergon. 2019, 77, 83–91. [Google Scholar] [CrossRef] [PubMed]
- Bustos-López, M.; Cruz-Ramírez, N.; Guerra-Hernández, A.; Sánchez-Morales, L.N.; Cruz-Ramos, N.A.; Alor-Hernández, G. Wearables for Engagement Detection in Learning Environments: A Review. Biosensors 2022, 12, 509. [Google Scholar] [CrossRef] [PubMed]
- Loo, S.K.; Makeig, S. Clinical utility of EEG in attention-deficit/hyperactivity disorder: A research update. Neurotherapeutics 2012, 9, 569–587. [Google Scholar] [CrossRef] [PubMed]
- Brown, K.W.; Ryan, R.M. The benefits of being present: Mindfulness and its role in psychological well-being. J. Personal. Soc. Psychol. 2003, 84, 822. [Google Scholar] [CrossRef]
- Park, W.; Kwon, G.H.; Kim, D.H.; Kim, Y.H.; Kim, S.P.; Kim, L. Assessment of cognitive engagement in stroke patients from single-trial EEG during motor rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 23, 351–362. [Google Scholar] [CrossRef]
- Li, G.; Zhou, S.; Kong, Z.; Guo, M. Closed-loop attention restoration theory for virtual reality-based attentional engagement enhancement. Sensors 2020, 20, 2208. [Google Scholar] [CrossRef]
- Ni, Y.X.; Wen, Y.; Xu, Y.; He, L.; You, G.Y. The relationship between work practice environment and work engagement among nurses: The multiple mediation of basic psychological needs and organizational commitment a cross sectional survey. Front. Public Health 2023, 11, 1123580. [Google Scholar] [CrossRef]
- Son, S.H.C.; Baroody, A.E.; Opatz, M.O. Measuring preschool children’s engagement behaviors during classroom shared reading: Construct and concurrent validity of the shared reading engagement rating scale. Early Child. Res. Q. 2023, 64, 47–60. [Google Scholar] [CrossRef]
- Dowell, K.A.; Nielsen, S.J. Caregiver engagement in youth partial hospitalization treatment. Clin. Child Psychol. Psychiatry 2021, 26, 355–366. [Google Scholar] [CrossRef]
- Goštautaitė, B.; Bučiūnienė, I. Work engagement during life span: The role of interaction outside the organization and task significance. J. Vocat. Behav. 2015, 89, 109–119. [Google Scholar] [CrossRef]
- Zennifa, F.; Ageno, S.; Hatano, S.; Iramina, K. Hybrid system for engagement recognition during cognitive tasks using a CFS+ KNN algorithm. Sensors 2018, 18, 3691. [Google Scholar] [CrossRef]
- Li, F.; Zhang, G.; Wang, W.; Xu, R.; Schnell, T.; Wen, J.; McKenzie, F.; Li, J. Deep models for engagement assessment with scarce label information. IEEE Trans. Hum.-Mach. Syst. 2016, 47, 598–605. [Google Scholar] [CrossRef]
- Hussain, M.S.; Calvo, R.A.; Chen, F. Automatic cognitive load detection from face, physiology, task performance and fusion during affective interference. Interact. Comput. 2014, 26, 256–268. [Google Scholar] [CrossRef]
- Belle, A.; Hargraves, R.H.; Najarian, K. An automated optimal engagement and attention detection system using electrocardiogram. Comput. Math. Methods Med. 2012, 2012, 528781. [Google Scholar] [CrossRef] [PubMed]
- Apicella, A.; Arpaia, P.; Frosolone, M.; Improta, G.; Moccaldi, N.; Pollastro, A. EEG-based measurement system for monitoring student engagement in learning 4.0. Sci. Rep. 2022, 12, 5857. [Google Scholar] [CrossRef] [PubMed]
- Welke, D.; Vessel, E.A. Naturalistic viewing conditions can increase task engagement and aesthetic preference but have only minimal impact on EEG quality. NeuroImage 2022, 256, 119218. [Google Scholar] [CrossRef]
- Jao, P.K.; Chavarriaga, R.; Dell’Agnola, F.; Arza, A.; Atienza, D.; Millán, J.d.R. EEG correlates of difficulty levels in dynamical transitions of simulated flying and mapping tasks. IEEE Trans. Hum.-Mach. Syst. 2020, 51, 99–108. [Google Scholar] [CrossRef]
- Booth, B.M.; Seamans, T.J.; Narayanan, S.S. An evaluation of EEG-based metrics for engagement assessment of distance learners. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; pp. 307–310. [Google Scholar]
- Rabbi, A.F.; Zony, A.; de Leon, P.; Fazel-Rezai, R. Mental workload and task engagement evaluation based on changes in electroencephalogram. Biomed. Eng. Lett. 2012, 2, 139–146. [Google Scholar] [CrossRef]
- Ruthig, J.C.; Poltavski, D.P.; Petros, T. Examining positivity effect and working memory in young-old and very old adults using EEG-derived cognitive state metrics. Res. Aging 2019, 41, 1014–1035. [Google Scholar] [CrossRef]
- Blankertz, B.; Tomioka, R.; Lemm, S.; Kawanabe, M.; Muller, K.R. Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process. Mag. 2007, 25, 41–56. [Google Scholar] [CrossRef]
- Li, P.; Xu, P.; Zhang, R.; Guo, L.; Yao, D. L1 norm based common spatial patterns decomposition for scalp EEG BCI. Biomed. Eng. Online 2013, 12, 77. [Google Scholar] [CrossRef] [PubMed]
- Lotte, F.; Guan, C. Regularizing common spatial patterns to improve BCI designs: Unified theory and new algorithms. IEEE Trans. Biomed. Eng. 2010, 58, 355–362. [Google Scholar] [CrossRef] [PubMed]
- Ghanbar, K.D.; Rezaii, T.Y.; Farzamnia, A.; Saad, I. Correlation-based common spatial pattern (CCSP): A novel extension of CSP for classification of motor imagery signal. PLoS ONE 2021, 16, e0248511. [Google Scholar]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter bank common spatial pattern (FBCSP) in brain-computer interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 2390–2397. [Google Scholar]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Chakraborty, B.; Ghosh, L.; Konar, A. Designing phase sensitive common spatial pattern filter to improve brain-computer interfacing. IEEE Trans. Biomed. Eng. 2019, 67, 2064–2072. [Google Scholar] [CrossRef]
- Li, Y.; Wang, D.; Liu, F. The auto-correlation function aided sparse support matrix machine for eeg-based fatigue detection. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 836–840. [Google Scholar] [CrossRef]
- Shin, J.; von Lühmann, A.; Blankertz, B.; Kim, D.W.; Jeong, J.; Hwang, H.J.; Müller, K.R. Open access dataset for EEG+ NIRS single-trial classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 1735–1745. [Google Scholar] [CrossRef]
- Barachant, A.; Bonnet, S.; Congedo, M.; Jutten, C. Multiclass brain–computer interface classification by Riemannian geometry. IEEE Trans. Biomed. Eng. 2011, 59, 920–928. [Google Scholar] [CrossRef]
- She, Q.; Hu, B.; Luo, Z.; Nguyen, T.; Zhang, Y. A hierarchical semi supervised extreme learning machine method for EEG recognition. Med. Biol. Eng. Comput. 2019, 57, 147–157. [Google Scholar] [CrossRef]


| Subject | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age | 28 | 25 | 26 | 23 | 27 | 34 | 28 | 29 | 27 | 32 | 31 | 29 | 33 | 27 | 25 |
| Gender | F | F | M | F | M | M | M | F | F | M | F | M | M | F | F |
| Subject | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | |
| Age | 32 | 39 | 26 | 32 | 28 | 24 | 23 | 27 | 27 | 26 | 27 | 27 | 36 | 26 | |
| Gender | M | F | F | F | F | M | F | M | M | F | F | M | F | M |
| Filter Bank | ||||||||
|---|---|---|---|---|---|---|---|---|
| Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Frequency Range (4–32 Hz) | 4–6 | 4–8 | 4–8 | 4–12 | 4–16 | 4–20 | 4–24 | 4–8 (theta) |
| 6–8 | 6–10 | 8–12 | 8–16 | 8–20 | 8–24 | 8–28 | 8–13 (alpha) | |
| 8–10 | 8–12 | 12–16 | 12–20 | 12–24 | 12–28 | 12–32 | 13–32 (beta) | |
| 10–12 | 10–14 | 16–20 | 16–24 | 16–28 | 16–32 | |||
| 12–14 | 12–16 | 20–24 | 20–28 | 20–32 | ||||
| 14–16 | 14–18 | 24–28 | 24–32 | |||||
| ⋯ | ⋯ | 28–32 | ||||||
| 30–32 | 28–32 | |||||||
| Number of filters | 14 | 13 | 7 | 6 | 5 | 4 | 3 | 3 |
| Filter Bank | ||||||||
|---|---|---|---|---|---|---|---|---|
| Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Accuracy (%) | 90.33 | 93.67 | 93.33 | 92.00 | 92.00 | 93.67 | 92.00 | 93.67 |
| 87.67 | 90.00 | 89.67 | 88.00 | 85.00 | 83.00 | 81.67 | 83.33 | |
| 94.00 | 94.67 | 95.67 | 95.00 | 94.33 | 92.00 | 91.67 | 96.00 | |
| 90.00 | 91.33 | 89.33 | 91.67 | 91.33 | 89.33 | 86.00 | 91.33 | |
| 75.00 | 77.00 | 76.67 | 77.33 | 75.00 | 75.00 | 73.67 | 76.00 | |
| 86.00 | 91.00 | 88.33 | 89.00 | 83.67 | 82.33 | 83.00 | 84.33 | |
| 94.00 | 92.33 | 93.00 | 92.67 | 91.67 | 91.67 | 92.67 | 93.33 | |
| 89.67 | 91.67 | 91.00 | 90.67 | 88.67 | 88.00 | 88.67 | 88.67 | |
| 86.33 | 87.33 | 86.33 | 85.67 | 85.00 | 85.33 | 86.00 | 87.67 | |
| 92.00 | 92.33 | 94.00 | 94.33 | 90.33 | 90.00 | 90.33 | 94.67 | |
| 76.67 | 80.33 | 79.00 | 76.67 | 75.33 | 72.67 | 74.33 | 76.00 | |
| 80.00 | 77.33 | 78.33 | 79.33 | 77.00 | 80.00 | 77.00 | 75.67 | |
| 93.00 | 94.33 | 92.67 | 93.33 | 92.00 | 90.33 | 90.67 | 90.33 | |
| 88.00 | 87.33 | 87.67 | 86.00 | 85.67 | 86.00 | 85.00 | 83.00 | |
| 80.67 | 82.00 | 82.00 | 80.00 | 75.67 | 74.00 | 70.67 | 70.67 | |
| 83.00 | 84.67 | 81.67 | 84.33 | 81.00 | 79.33 | 79.33 | 80.67 | |
| 87.33 | 89.00 | 86.67 | 85.33 | 84.00 | 83.33 | 78.00 | 82.00 | |
| 91.33 | 92.67 | 92.67 | 92.00 | 92.00 | 89.67 | 90.00 | 89.00 | |
| 79.67 | 85.67 | 86.00 | 82.33 | 78.67 | 78.33 | 79.33 | 79.67 | |
| 65.67 | 72.00 | 70.33 | 69.33 | 70.00 | 66.67 | 69.00 | 66.00 | |
| 87.00 | 89.67 | 90.33 | 89.67 | 89.00 | 85.67 | 88.67 | 87.67 | |
| 86.33 | 85.33 | 86.00 | 85.33 | 87.00 | 84.00 | 85.00 | 86.67 | |
| 82.00 | 88.00 | 87.33 | 87.33 | 83.33 | 82.33 | 82.00 | 82.67 | |
| 83.67 | 82.67 | 83.67 | 80.00 | 80.00 | 77.67 | 79.67 | 82.00 | |
| 89.00 | 90.33 | 89.33 | 92.33 | 94.00 | 91.00 | 90.33 | 90.33 | |
| 96.67 | 96.00 | 96.00 | 95.33 | 95.33 | 95.67 | 96.00 | 94.67 | |
| 79.33 | 82.67 | 82.33 | 81.67 | 80.67 | 83.33 | 77.67 | 81.33 | |
| 83.33 | 88.00 | 85.00 | 86.33 | 82.00 | 79.00 | 76.00 | 80.00 | |
| 93.33 | 95.00 | 94.67 | 92.33 | 93.67 | 92.00 | 90.67 | 92.00 | |
| Mean ± std | 85.90 ± 6.77 | 87.74 ± 5.98 | 87.21 ± 6.17 | 86.74 ± 6.40 | 85.29 ± 6.88 | 84.18 ± 7.02 | 83.62 ± 7.22 | 84.80 ± 7.50 |
| p-value | <0.01 | / | <0.05 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
| Amplitude | Phase | AP | |
|---|---|---|---|
| Mean ± std | 81.28 ± 7.25% | 76.57 ± 6.94% | 87.74 ± 5.98% |
| p-value | <0.001 | <0.001 | / |
| P-CC | K-CC | S-CC | |
|---|---|---|---|
| Mean ± std | 87.74 ± 5.98% | 87.68 ± 6.40% | 87.61 ± 6.52% |
| p-value | / | >0.1 | >0.1 |
| Comparison Results | |||||||
|---|---|---|---|---|---|---|---|
| Literature | Blankertz [32] | Ang [36] | Shin [40] | Ghanbar [35] | She [42] | Barachant [41] | Ours |
| Methods | CSP | FBCSP | CSP + ShrinkageLDA | CCSP | HSS-ELM | MDMR | MDCCSP |
| Accuracy (%) | 88.33 | 89.33 | 84.33 | 87.67 | 88.67 | 78.33 | 93.67 |
| 70.33 | 84.00 | 67.33 | 69.33 | 80.67 | 74.00 | 90.00 | |
| 82.33 | 88.67 | 82.67 | 84.33 | 86.67 | 94.00 | 94.67 | |
| 82.00 | 91.00 | 78.33 | 84.33 | 82.00 | 80.00 | 91.33 | |
| 71.67 | 73.67 | 67.33 | 74.33 | 76.00 | 75.33 | 77.00 | |
| 77.00 | 80.33 | 72.00 | 77.33 | 84.67 | 81.67 | 91.00 | |
| 88.67 | 93.33 | 86.33 | 90.00 | 89.00 | 93.00 | 92.33 | |
| 81.67 | 88.67 | 80.67 | 84.67 | 78.67 | 80.00 | 91.67 | |
| 79.33 | 82.33 | 76.33 | 79.00 | 78.00 | 73.67 | 87.33 | |
| 87.33 | 88.00 | 87.00 | 88.00 | 85.33 | 87.33 | 92.33 | |
| 64.67 | 80.67 | 68.67 | 68.67 | 75.00 | 72.33 | 80.33 | |
| 75.00 | 73.33 | 73.33 | 76.67 | 79.67 | 62.00 | 77.33 | |
| 81.00 | 87.33 | 74.33 | 83.00 | 86.67 | 84.33 | 94.33 | |
| 80.67 | 84.00 | 78.67 | 80.00 | 77.00 | 74.33 | 87.33 | |
| 71.67 | 75.33 | 68.00 | 71.67 | 65.00 | 65.33 | 82.00 | |
| 74.33 | 82.67 | 68.00 | 74.67 | 75.00 | 63.67 | 84.67 | |
| 74.00 | 81.33 | 60.33 | 77.00 | 83.67 | 83.33 | 89.00 | |
| 85.33 | 90.33 | 85.67 | 88.33 | 90.67 | 83.33 | 92.67 | |
| 74.67 | 82.00 | 71.67 | 76.33 | 81.67 | 78.00 | 85.67 | |
| 66.67 | 70.33 | 65.00 | 64.33 | 72.67 | 62.67 | 72.00 | |
| 84.67 | 86.00 | 76.00 | 81.67 | 79.67 | 84.67 | 89.67 | |
| 79.67 | 83.33 | 79.00 | 83.67 | 84.00 | 85.67 | 85.33 | |
| 75.67 | 84.33 | 74.00 | 77.33 | 84.67 | 76.00 | 88.00 | |
| 79.00 | 78.00 | 80.67 | 77.33 | 85.00 | 78.67 | 82.67 | |
| 83.00 | 86.33 | 85.00 | 90.00 | 88.33 | 77.33 | 90.33 | |
| 94.33 | 94.67 | 92.00 | 93.67 | 92.33 | 94.67 | 96.00 | |
| 68.67 | 73.67 | 71.00 | 68.67 | 72.00 | 71.00 | 82.67 | |
| 68.33 | 83.33 | 64.33 | 72.33 | 76.67 | 70.00 | 88.00 | |
| 78.00 | 91.33 | 71.33 | 78.67 | 88.33 | 91.00 | 95.00 | |
| Mean ± std | 78.21 ± 7.07 | 83.71 ± 6.20 | 75.49 ± 7.93 | 79.41 ± 7.36 | 81.64 ± 6.38 | 78.47 ± 9.05 | 87.74 ± 5.98 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Wang, Z.; Xu, T.; Zhou, T.; Hu, H. Engagement Recognition Using a Multi-Domain Feature Extraction Method Based on Correlation-Based Common Spatial Patterns. Appl. Sci. 2023, 13, 11924. https://doi.org/10.3390/app132111924
Xu G, Wang Z, Xu T, Zhou T, Hu H. Engagement Recognition Using a Multi-Domain Feature Extraction Method Based on Correlation-Based Common Spatial Patterns. Applied Sciences. 2023; 13(21):11924. https://doi.org/10.3390/app132111924
Chicago/Turabian StyleXu, Guiying, Zhenyu Wang, Tianheng Xu, Ting Zhou, and Honglin Hu. 2023. "Engagement Recognition Using a Multi-Domain Feature Extraction Method Based on Correlation-Based Common Spatial Patterns" Applied Sciences 13, no. 21: 11924. https://doi.org/10.3390/app132111924
APA StyleXu, G., Wang, Z., Xu, T., Zhou, T., & Hu, H. (2023). Engagement Recognition Using a Multi-Domain Feature Extraction Method Based on Correlation-Based Common Spatial Patterns. Applied Sciences, 13(21), 11924. https://doi.org/10.3390/app132111924







