1. Introduction
In the agricultural field, aerial vehicle swarm (UAVs) have become an important technology and are widely used for pesticide spraying, information monitoring and agricultural insurance surveys [
1]. However, the monitoring mission of a single UAV in one flight is limited by its own monitoring range and battery life, so it can only complete part of the monitoring work [
2,
3]. In order to overcome this limitation, the intelligent unmanned agricultural UAV swarm collaboration network (AUSCN) came into being [
4]. Through the collaboration of multiple UAVs, the monitoring range is expanded and more complex tasks can be completed without human intervention [
5]. The AUSCN is a distributed, non-central, wireless sensor network composed of multiple UAVs [
6]. In AUSCNs, multiple UAVs communicate with each other through the sensors mounted on the UAVs. Compared with a single UAV, AUSCNs can significantly improve work efficiency while significantly reducing the consumption of manpower and material resources [
7,
8].
With the continuous development of wireless sensor technology, intelligent unmanned AUSCNs bring many significant benefits in the agricultural field [
9,
10]. However, a key issue facing AUSCNs is how to effectively reduce their energy consumption [
11,
12]. To solve this problem, network clustering has become a feasible method. However, with the advancement of hardware technology, the number of sensors in AUSCNs has increased rapidly, resulting in the complexity of the network topology [
13,
14,
15]. It is difficult for traditional clustering algorithms to find appropriate head nodes to reduce energy consumption [
16]. Furthermore, this problem is proven to be NP-hard. Therefore, it is of great significance to propose a new AUSCN clustering evolutionary algorithm. This algorithm is expected to effectively cope with the challenges of increasing the number of sensors and reducing energy consumption, promoting the wider application of AUSCNs in the agricultural field [
1,
17].
In recent years, with the combination of UAVs with agriculture and many other scenarios, more and more people are optimizing the deployment and monitoring of UAVs and the communication between UAVs. In [
18], Issad et al. proposed a multi-objective particle swarm optimization (MOPSO) for agricultural UAV monitoring deployment. In [
19], Kiani et al. proposed incremental gray wolf optimization (I-GWO) and extended gray wolf optimization (Ex-GWO) for the path planning of agricultural robots to complete various tasks in farmland. In [
20], in order to solve problems such as UAV flight time periods, Namdev et al. proposed a WOA-OLSR algorithm to optimize the flight self-organizing network to provide energy-saving and safe routing solutions. In [
21], Shanshan et al. proposed a hybrid genetic algorithm for the optimization of UAV networks to solve the deployment problem of UAVs and thereby improve UAV group coverage. However, the above methods converge slowly and can easily fall into local optimal solutions. When faced with complex network parameters, they cannot find the optimal AUSCN clustering scheme.
Therefore, the main purpose of this paper is to propose a new niche adaptive elite evolutionary algorithm (NAEEA) to reduce the network energy consumption of AUSCNs [
22,
23]. In NAEEA, the new niche strategy can evolve the population in groups, which greatly expands the search space of the population and the diversity of the population solution, effectively improving the convergence speed of the NAEEA. The new adaptive strategy and elite strategy can effectively prevent NAEEAs from falling into premature convergence and causing evolutionary stagnation by adaptively changing the parameters of the algorithm and retaining the local optimal solution [
24]. Compared with the above heuristic algorithms, the most attractive features of this algorithm can be summarized as its fast convergence speed, high group diversity and strong global search ability. NAEEAs not only select appropriate head nodes, but also aim to solve combinatorial clustering problems [
25]. In addition, NAEEAs can solve clustering problems more effectively than original mathematical methods. Simulation results show that the newly designed NAEEA can greatly reduce the energy consumption of AUSCNs.
The main contributions of this article are as follows:
- (1)
A novel designed niche adaptive elite evolutionary algorithm (NAEEA) is proposed, which integrates the merits of elite selection and adaptive adjusting to obtain high performance. The NAEEA can choose suitable head nodes at a fast rate to reduce energy consumption in AUSCNs. Furthermore, this algorithm has an excellent convergence speed which can better deal with clustering optimization in AUSCNs.
- (2)
New elite and niche operators are designed to effectively speed up the convergence rate and avoid falling into the local optima. Moreover, a novel adaptive operator is designed, which provides a dynamic self-adapting adjustment mechanism to effectively select head nodes.
- (3)
Lots of simulations were performed for clustering in AUSCNs. The results show that the NAEEA significantly reduces the network energy consumption compared with the evolutionary algorithm (EA), simulated annealing algorithm (SA) and leapfrog algorithm (SFLA), under three different conditions (1. Different ratio of head nodes; 2. Different number of sensor nodes; 3. Different size of area.).
The paper structure is as follows: In
Section 2, the related works are discussed, and in
Section 3, an energy consumption model is introduced. Then,
Section 4 shows the process of the NAEEA. Next, in
Section 5, simulations are carried out for clustering in AUSCNs by using the NAEEA, EA, SA and SFLA. Furthermore, the discussion of the results is shown in
Section 5. In the end, the conclusion part is given in
Section 6.
2. Related Work
At present, with the rapid development of UAV technology, the application scenarios of UAVs are becoming more and more extensive. Nowadays, research on UAVs includes UAV coverage, the communication between UAVs and multi-UAV collaboration. However, the energy consumption problem of UAVs limits their applications. This issue has attracted more and more attention, and clustering technology plays a crucial role in reducing the energy consumption of AUSCNs. At the same time, with the continuous development and optimization of heuristic algorithms, more and more people are applying heuristic algorithms to the optimization research of multi-UAV collaboration [
26]. Therefore, this chapter mainly discusses two aspects: UAV application research and sensor network clustering optimization.
First, in terms of the application of UAVs, in [
27], Kiani et al. proposed an integrated model based on intelligence and mechanism applications, which were optimized by using the sand cat swarm optimization algorithm and the reverse ant colony algorithm to achieve the best planting routes. In order to select appropriate cluster heads in the UAV swarm of the cooperative communication network, in [
28], Haiyan et al. proposed a UAV clustering method based on improved cluster head selection weights to improve UAV clustering and data collection efficiency. However, that method cannot find suitable cluster heads when facing large-scale drones. In [
29], Zhang, Xiao et al. proposed a drone swarm deployment algorithm based on MOEA/D (DSDA-MOEA/D) to balance the energy consumption of all drones and maximize the lifetime of the full coverage network. However, this method cannot find the optimal coverage solution. As people pay more and more attention to network security, in [
30], Shah et al. proposed three different meta-heuristic algorithms: the cuckoo search algorithm (CUCO), the differential evolution algorithm (DEA) and the bee algorithm. The HBA is used to optimize FANET to improve throughput as well as reduce PDR and delay in order to improve communication quality and reliability. However, due to fixed algorithm parameters, this method can easily fall into local optima and fail to obtain the optimal solution. In [
31], Farrag et al. proposed a strawberry optimization algorithm (SBA) to solve the problem of unmanned placement and reduce the number of unmanned vehicles under full coverage. However, this method can easily fall into evolutionary stagnation. It is impossible to obtain a coverage solution that meets specific scenarios.
Then, in terms of the network clustering optimization of wireless sensors, in [
32], a multi-sink deployment strategy, based on an improved particle swarm clustering optimization algorithm, was proposed for clustering optimization between nodes, which can effectively increase the network life and reduces energy consumption, but that method cannot find the optimal clustering scheme while maintaining low energy consumption. In [
33], a new hierarchical adaptive energy-efficient clustering routing (HAECR) method is proposed for underwater data collection, which divides hierarchical regions according to the depth of sensor nodes, which can effectively reduce energy consumption and extend the network life, but the algorithm converges too slowly and does not take into account complex underwater biological factors. In [
34], the authors proposed a new algorithm based on social group optimization (SGO) to reduce communication distances to reduce network energy consumption. In addition, the use of new optimization techniques to dynamically select the head node can significantly reduce the energy consumption of the network. However, due to the complexity of the calculation, the convergence speed of the algorithm cannot reach an acceptable level. In [
35], the authors proposed a novel hybrid chimpanzee optimization and hunger games search (ChOA-HGS) algorithm for clustering and multi-hop routing optimization, which determines the best path of the network through the HGS routing process, to extend network life. However, the method of selecting the best head node is too complex and this method cannot be used in real systems.
Table 1 gives a detailed comparison of most UAV optimization methods in this section. In general, these methods are heuristic algorithms or improvements of heuristic algorithms, and it is easy to fall into local optima and fail to obtain the optimal solution. Due to the large number of environmental parameters in AUSCNs, these methods are difficult to obtain the optimal AUSCN network clustering scheme. Therefore, this paper proposes a new NAEEA to reduce the network energy consumption of AUSCNs. By combining heuristic algorithms, the NAEEA has excellent performance and greatly reduces network energy consumption, which is of great significance to the practical application of drones.
3. System Model
In AUSCNs, there is one sensor node on each drone, and communication between multiple UAVs is carried out through sensors on the UAV. AUSCNs have the characteristics of a large network scale, many nodes, a long monitoring cycle and a relatively large amount of data, so time-driven data acquisition is adopted. For the sake of preventing the effects of other factors, a model of the network energy consumption is adopted in this paper. The following assumptions are made for the model:
UAVs are randomly distributed in an AreaL × AreaL monitoring area. Each UAV is completely isomorphic and represents a sensor node. Each node has the same initial energy and has a unique identifier.;
After the deployment of sensor nodes, the monitoring area will be stationary;
The base station is unique and its location does not change. Its resources are very sufficient, which can completely ignore the problem of energy consumption, and has a supercomputing and processing capacity;
All sensor nodes can acquire their own position information, and wireless communication can be carried out directly between different nodes and base stations;
After data fusion, the frequency of the cluster head node sending data to the network nodes is low, and the amount of data is small. Thus, the process of data transmission between the cluster head nodes and the gateway node is not considered in the model.
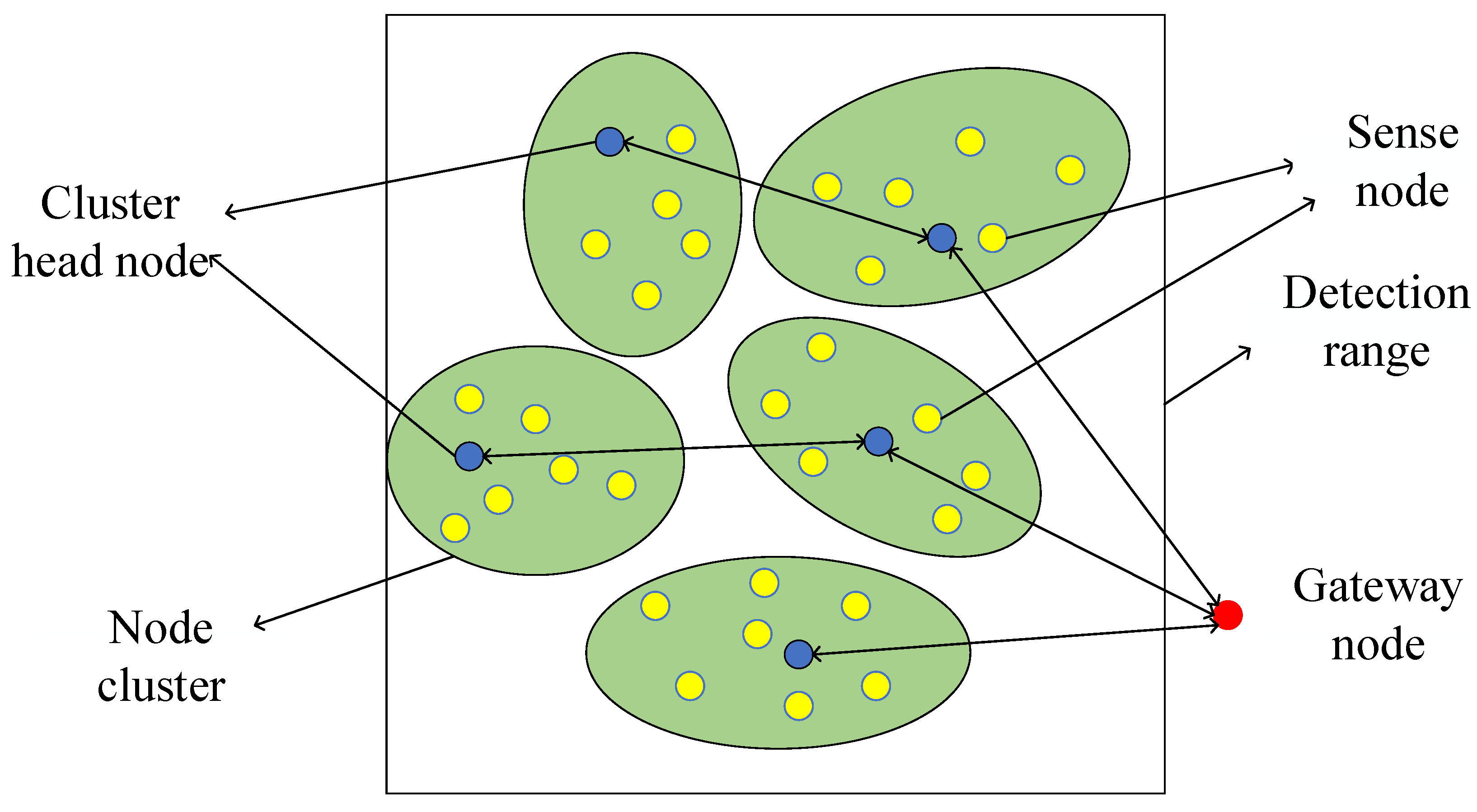
The network clustering structure of AUSCNs is shown in
Figure 1.
Figure 1 depicts the network clustering arrangement within AUSCNs, revealing a total of five cluster groups. Within each cluster group, the cluster head node is represented by the color blue, while the member node is denoted through the color yellow.
The uplink transmission steps are as follows: Firstly, the sensing nodes representing each UAV are grouped into different clusters, with a head node in each cluster. Then, sensing nodes randomly scattered in the simulation range and centralize the sensing results to the head nodes. Next, the head nodes collect the data from the sensing nodes, and transfer the data to the gateway node through multi-hop or direct methods. Finally, the gateway node summarizes the data transmitted from each cluster head node; then, the gateway node delivers data to the user for deeper processing. As for the downlink transmission phase, users distribute tasks through the gateway node, and evenly assign monitoring tasks and dispense resources in the network. In other words, the gateway node first assigns tasks to each cluster head node, and the cluster head node continues to assign tasks to the sensing nodes to complete the monitoring task.
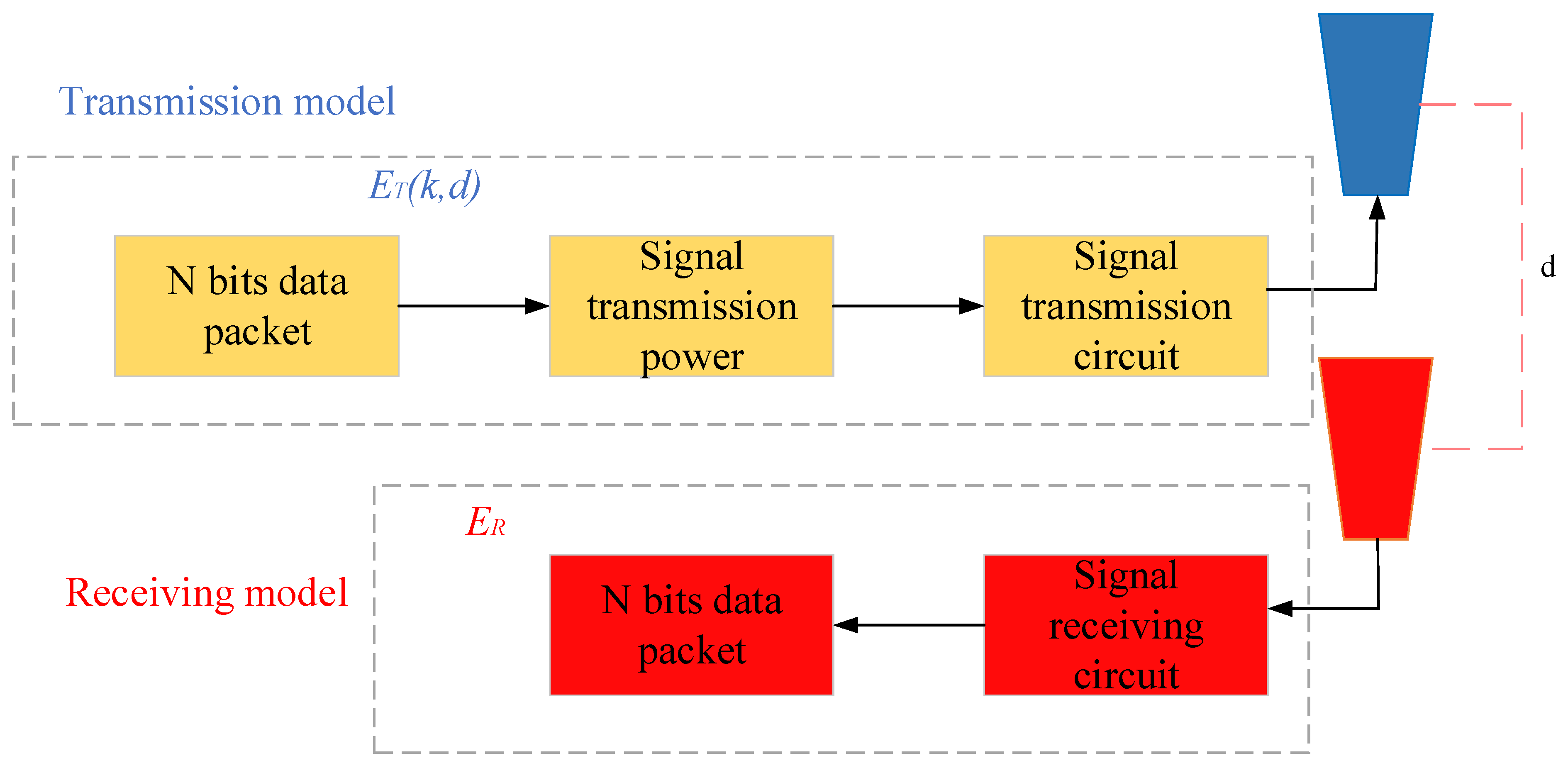
The communication energy expenditure of AUSCNs’ sensors mainly includes the energy expenditure of transmitting circuit energy, the signal amplification circuit and the receiving circuit. Of course, the transmitting part consumes the most energy, and the larger the amount of data transmitted, the greater the energy expenditure required for transmission. As far as the transmission part is concerned, the signal amplification circuit belongs to power amplification, which consumes the most energy. According to the instructions of the controller, the power is amplified to the required power level and ensures an effective transmission distance. It concerns whether the basic unit bit reception energy expenditure of the receiving circuit remains unchanged. Thus, the more data that are received, the more energy that is consumed. A model of the nodes’ communication energy consumption is shown in
Figure 2.
Figure 2 includes a transmission model and a reception model, where d is the transmission distance.
Table 2 shows the system model parameter description.
The energy consumption model consists of a transmitting module and a receiving module.
indicates the energy consumed of the transmitter when the sensor node sends k-bit data and the transmission distance is d, where
t is the communication environment parameter. Usually, it ranges from two to four, according to the environment. The energy consumption formula is able to be expressed as follows:
The energy consumption formula of the n-bit data received by the ordinary nodes is
The formula of the total energy expenditure of the nodes in the network is
where
E_(elec) represents the electronic energy parameter of the transmission circuit and the receiving circuit, which is related to coding, modulation, filtering, etc.
is the energy amplification parameter in the process of information transmission. According to different communication environments, the value of
t is generally between two and four. The worse the communication environment is, the higher the value of t is.
4. NAEEA for Clustering Optimization of AUSCNs
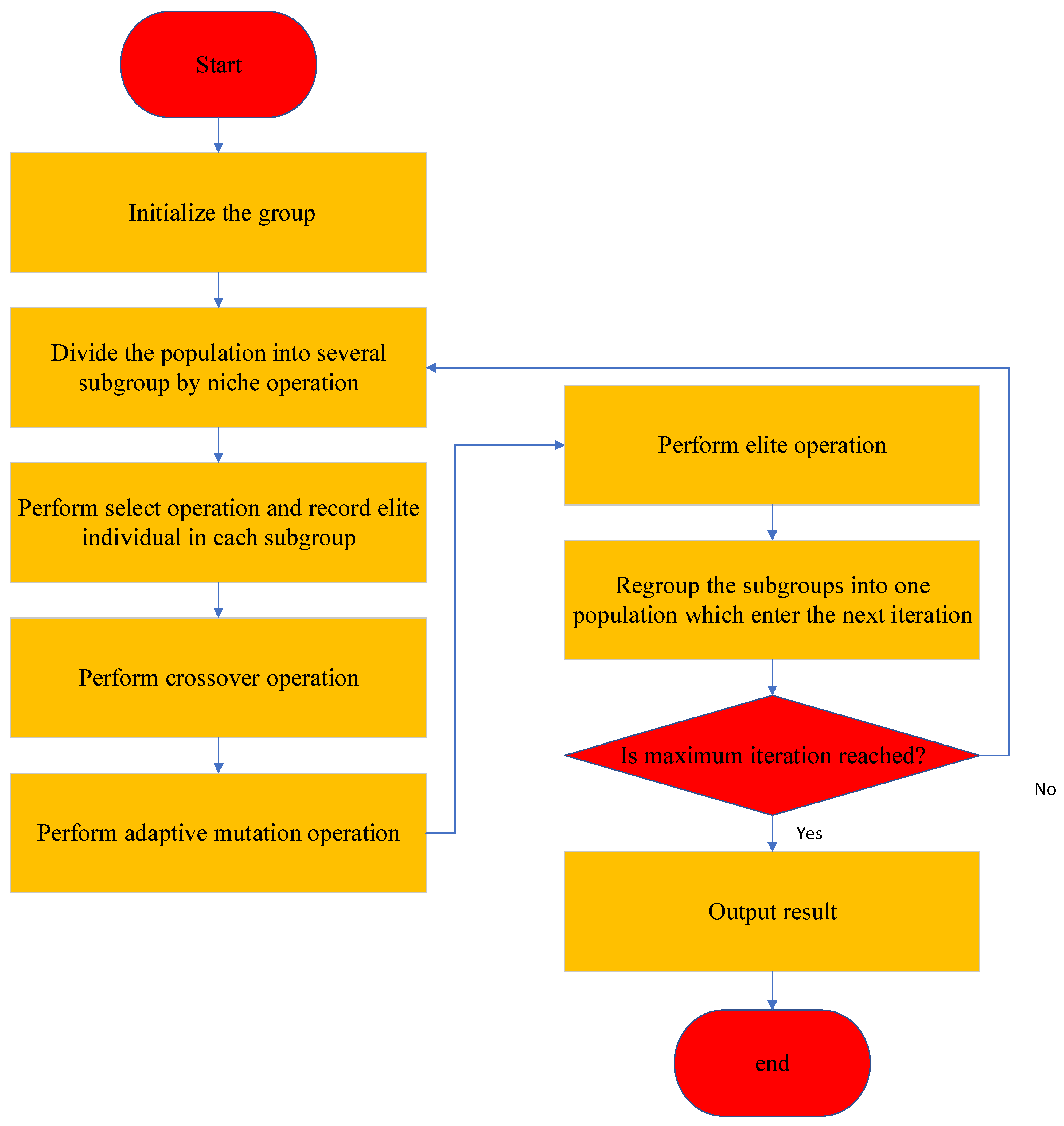
In this paper, the NAEEA is proposed to find the optimal network clustering to reduce the energy consumption of sensor nodes on UAVs in intelligent unmanned AUSCNs. The NAEEA improves the ability to solve problems by using new niche, adaptive and elite operators. On the one hand, the implementation of niche procedures can be beneficial to increase the diversity of the population, which can effectively avoid falling into local optimum. On the other hand, an adaptive strategy is useful to find a feasible solution which is close to the optimum solution. Thus, the procedure of the NAEEA can develop a practicable solution for clustering in a computationally acceptable time. The process of the NAEEA are as follows:
Step 1. Initialize the population of the NAEEA by randomly confirming the position of the cluster head.
Step 2. Divide the population into several subgroups through a niche operation.
Step 3. Calculate the fitness of the individuals in each small population, then carry out a roulette according to the fitness value to realize the selection operation of the population and save the best individual as an elite in each small population.
Step 4. Perform crossover operations for each population.
Step 5. Dynamically change the mutation probability based on individual fitness and perform an adaptive mutation operation.
Step 6. Calculate the fitness of individuals in each small population again, then find the worst individual to compare with the elite, which is found in Step 3; if the elite is better, use the elite individual to replace the worst individual; otherwise, take no operation.
Step 7. Regroup the subgroup into one population.
Step 8. In this step, judge whether the end condition is reached; go back to Step 2 if the number of generations does not reach a particular value or the termination criterion is not satisfied.
A flow chart of the NAEEA can be seen in
Figure 3.
Table 3 shows the NAEEA parameter description.
The following paragraphs give a general discussion of the NAEEA.
4.1. Population Initialization and Coding
In the problem of clustering optimization for AUSCNs by using the NAEEA, population initialization is the first and most important step. The size of the population and the method of initialization are the main factors that effect the algorithm. On the one hand, the larger the size of the population created through initialization, the wider the distribution of the population in the researching space and the better the diversity, which can avoid the evolution falling into local optimization to a certain extent. However, when the objective function is very complex, the cost of calculating all the solutions of the population to obtain the fitness function will be very high, and it will take more time to carry out an iterative evolution, which will greatly increase the time cost of the algorithm and reduce the convergence speed. On the other hand, a too-small population size will lead to the limited search space of the algorithm, and it is very easy to become stuck at locally optimal values. After balancing the advantages and disadvantages of the size of the population and the method of initialization, this algorithm uses a population size of 40. On the premise of being familiar with the search space, the initialization population can be generated according to specific rules, which can accelerate the convergence speed. Thus, the initial population is initialized using a random method.
In order to simplify the coding, the NAEEA uses binary individual coding. Firstly, the sensor nodes in the region are numbered with natural numbers. Then, a vector is used to represent the individual. The number 0 means that the node at the relevant position is the sensing node, and the number 1 indicates that the node at the relevant position is the cluster head node. As shown in
Figure 4, if an individual has ten nodes, its code is ‘0100100100′. It means that No. 2, No. 5 and No. 8 are cluster head nodes, and the others are sensing nodes.
It is assumed that there are
L sensors, and
M of them are cluster head nodes in AUSCNs when the number of individuals in the population is n. The matrix of population code is as follows:
where the letter
i indicates whether the sensor of the
n-th individual in the population is a cluster head node. When the corresponding position element in the matrix is 0, this indicates that the sensor in the
n-th individual is a sensing node. If the element is 1, it indicates that it is a cluster head node. The constraint is as follows:
This formula indicates that the number of cluster head nodes in AUSCNs is fixed as M.
4.2. Fitness Evaluation
The purpose of clustering optimization in AUSCNs is to lower the network energy expenditure. In the network energy consumption, communication energy consumption accounts for the majority. From Equation (3), it can be concluded that the total energy expenditure of the node is
. Therefore, the fitness function of this evolutionary process is as follows:
In this equation, represents the n-th individual of the population, indicates the fitness of and the energy expenditure of the cluster head selection scheme of . In the process of evolution, the lower the energy consumption, the lower the fitness, which also means the better the individual. On the contrary, the higher the energy consumption, the greater the fitness, and the individual is easier to be eliminated in the process of evolution.
4.3. Selection
In optimizing clustering in AUSCNs for reducing energy consumption, the probability of an individual being selected is in a reverse ratio to the individual fitness value. Moreover, NAEEA selection is an operation to increase the possibility of keeping excellent individuals during population iteration. Thus, the lower the fitness, the greater the probability of the individual being selected. The probability of selecting the
m-th scheme is as follows:
4.4. Crossover
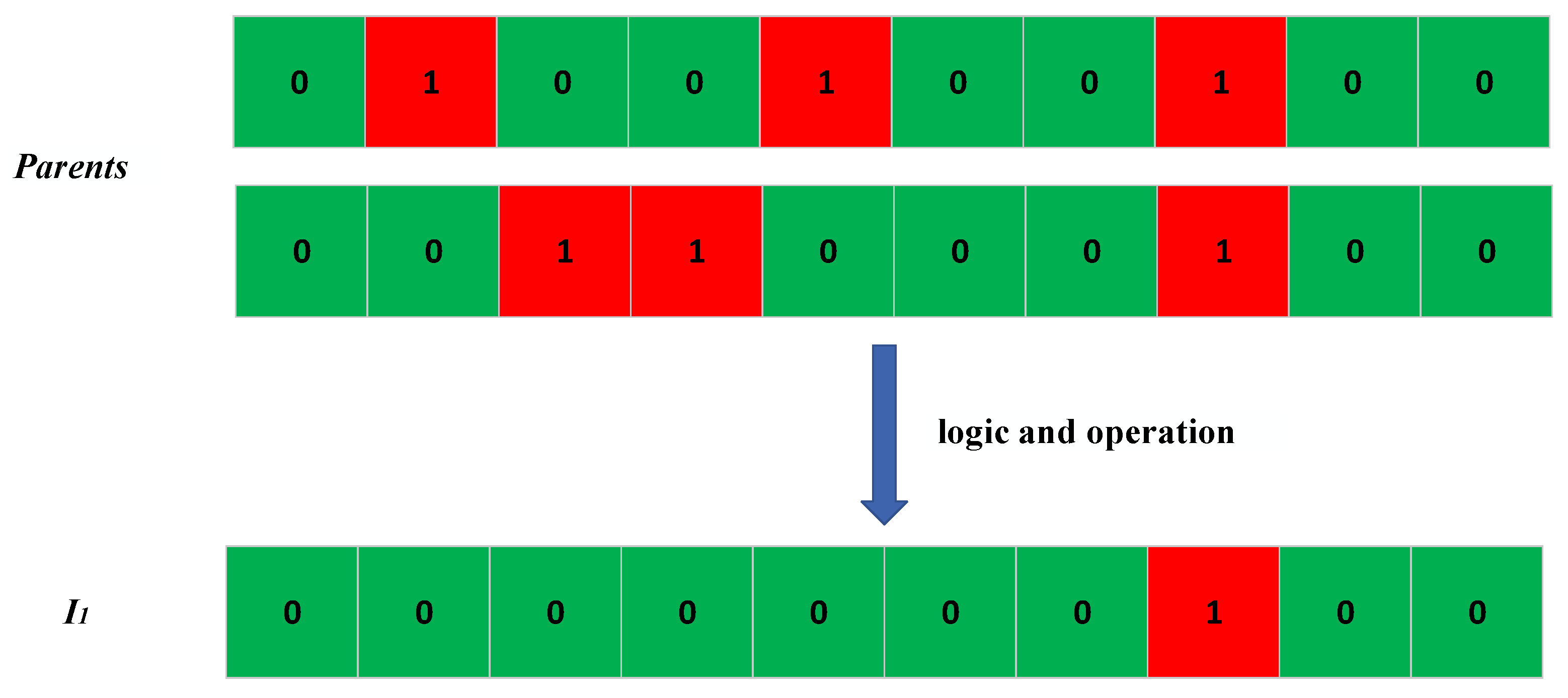
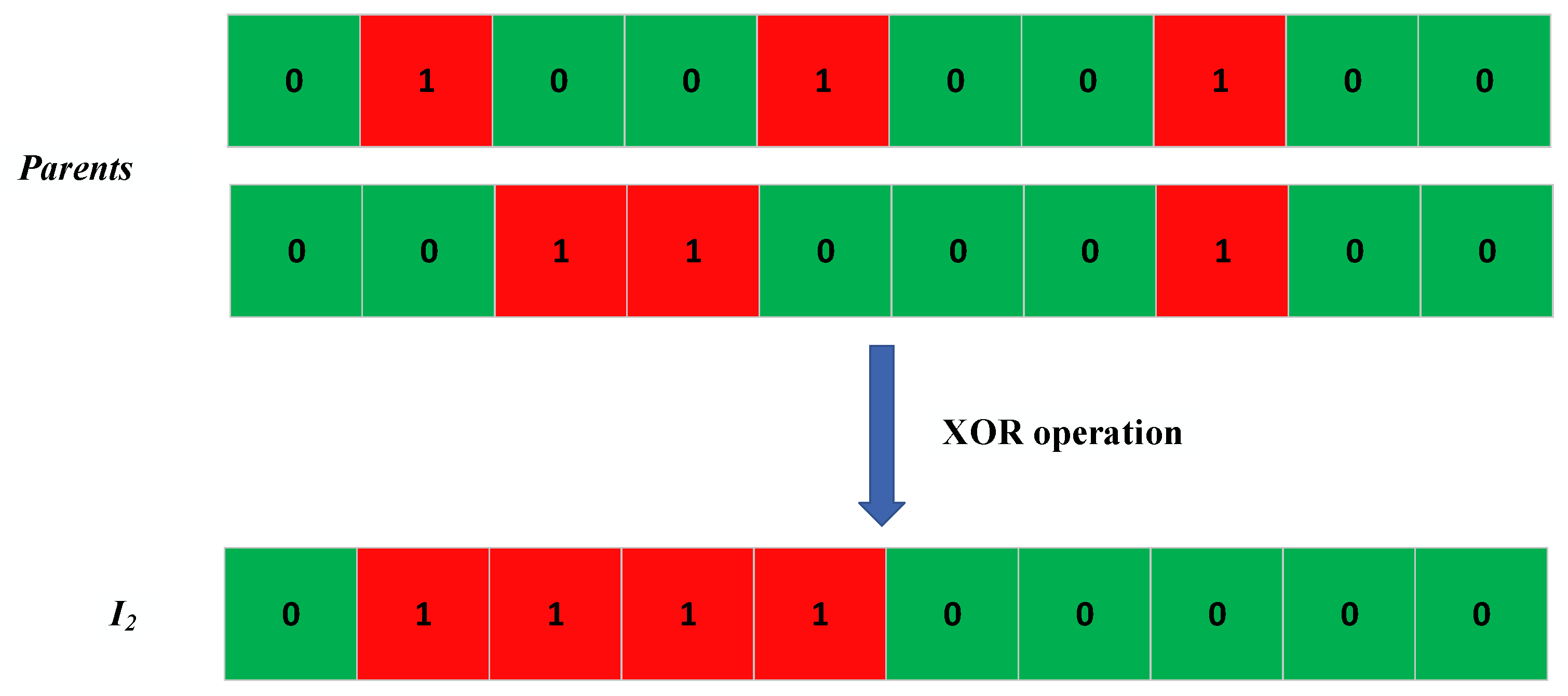
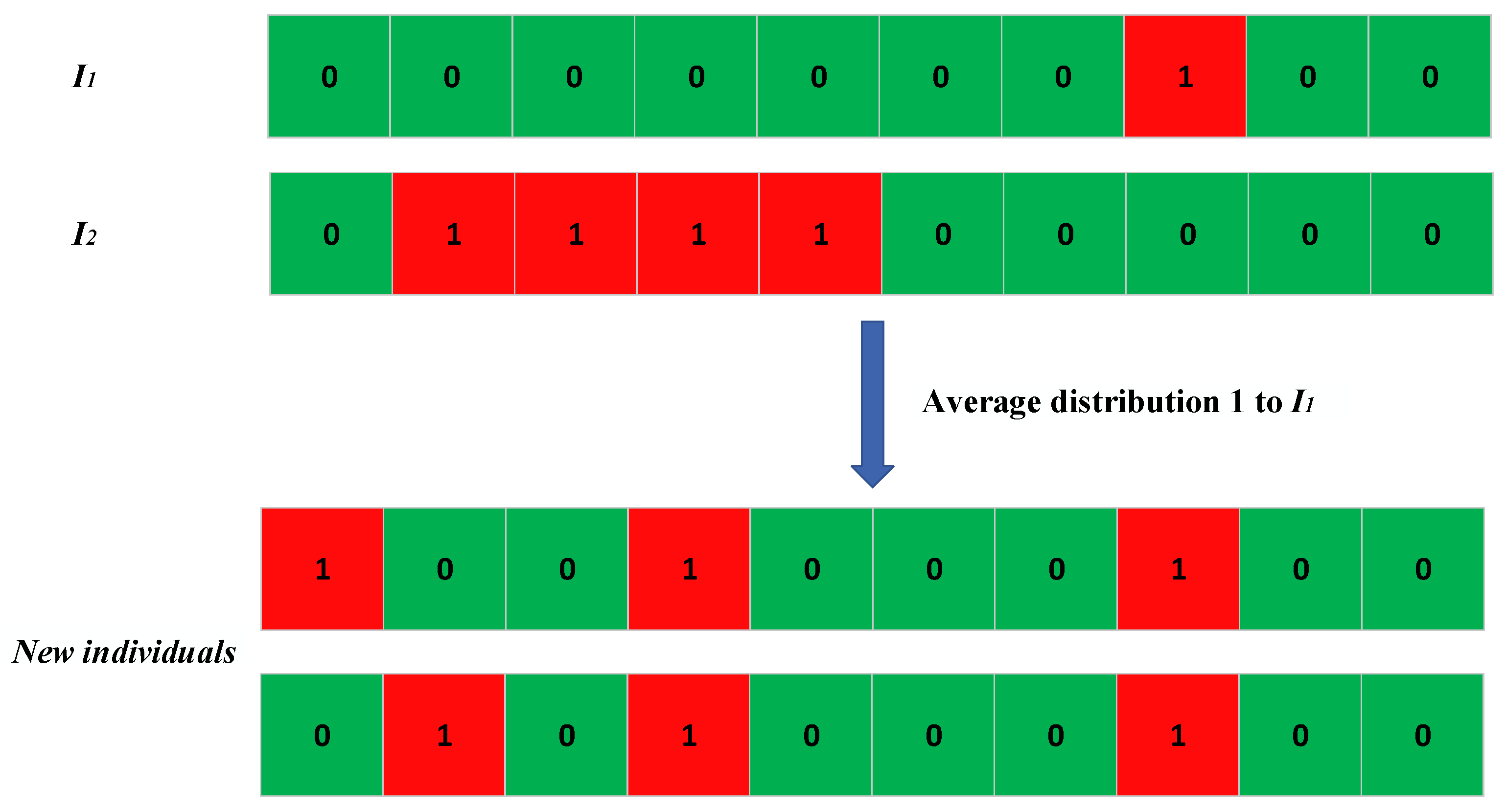
A crossover operation is used to improve the diversity of a population in solving the problem of the clustering optimization of AUSCNs to reduce energy consumption. Traditional crossover methods such as single point crossover and multi-point crossover cannot keep the number of cluster head nodes unchanged. Thus, a crossover method based on Boolean algebra is used in this chapter. The specific formula expression is as follows:
In the above formula, L is the population dimension, Parent1 and Parent2 are two different individuals in the population, and I1 and I2 are intervention vectors after logical operations. Since the number of cluster heads for each individual is limited, I1 and I2 need to be evenly distributed, as shown in
Figure 5,
Figure 6 and
Figure 7.
Figure 5 shows the intervention vector I1, obtained by performing logical operations on two individuals.
Figure 6 shows the insertion vector I2, obtained by performing logical XOR operations on two individuals. Due to the constraint on the number of cluster heads,
Figure 7 shows the new individuals generated after the average distribution operations of I1 and I2.
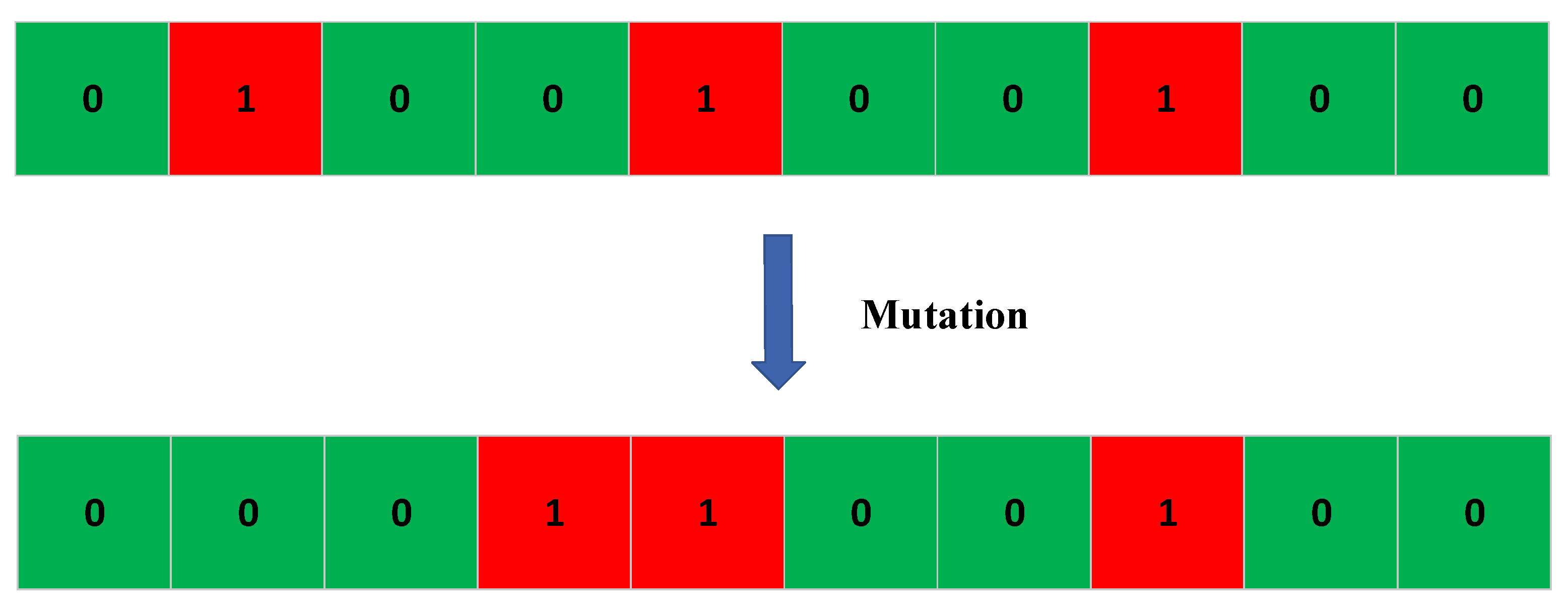
4.5. Mutation
In order to further reduce the energy consumption of AUSCNs, the NAEEA introduces some random mutation strategies. The purpose of these mutation operations is to increase the diversity of the population. In order to keep the number of cluster head nodes unchanged, when the 0 in the individual is converted to 1, the random 1 in the individual will also become 0 accordingly. The mutation operation will use a certain mutation probability, Q, to replace random bits in the individual with other non-duplicate nodes. These newly selected sensor nodes will be regarded as cluster head nodes. In the processing of each individual, a random number, Qr, is generated by using chaotic mapping, and then a mutation operation is performed. As shown in
Figure 8, the code of an individual is ‘0100100100’; when changing the 1 of the second position to 0, it needs to change a random position 0 to 1, so the new code is ‘0001100100’ (Take 0 at the fourth position and change it to 1). The specific formula expression is as follows:
In Equation (12), inew represents the newly generated cluster head node and inew does not overlap with the existing cluster head nodes in the individual.
4.6. Adaptive Operation
For better reducing the energy consumption by using the NAEEA to optimize the cluster of AUSCNs, the NAEEA employs a novel adaptive operator to adjust the mutation rate in a dynamic way. In the original evolutionary algorithm, the probability of mutation is fixed. Although the constant mutation probability simplifies the algorithm process, it also reduces the diversity in the process of population evolution. In the NAEEA, adaptive operations adjust the mutation probability according to the individuals’ fitness. It is defined as follows:
The lower the energy consumption, the lower the fitness and the probability of mutation. On the contrary, the higher the energy consumption, the greater the fitness and the probability of mutation. By dynamically adjusting the mutation probability, the probability of individuals with low energy consumption entering the next generation is improved.
4.7. Elite Operation
For better solving the problem of the clustering optimization of AUSCNs to reduce energy consumption, a brand-new elite operator is proposed to select the best individual in each generation of a population, which can speed up the search for the clustering optimization. The best individual in each small group, divided using a niche operation, is selected as an elite. Elites are used to replace the worst individuals during iteration to maintain good performance and accelerate the convergence speed.
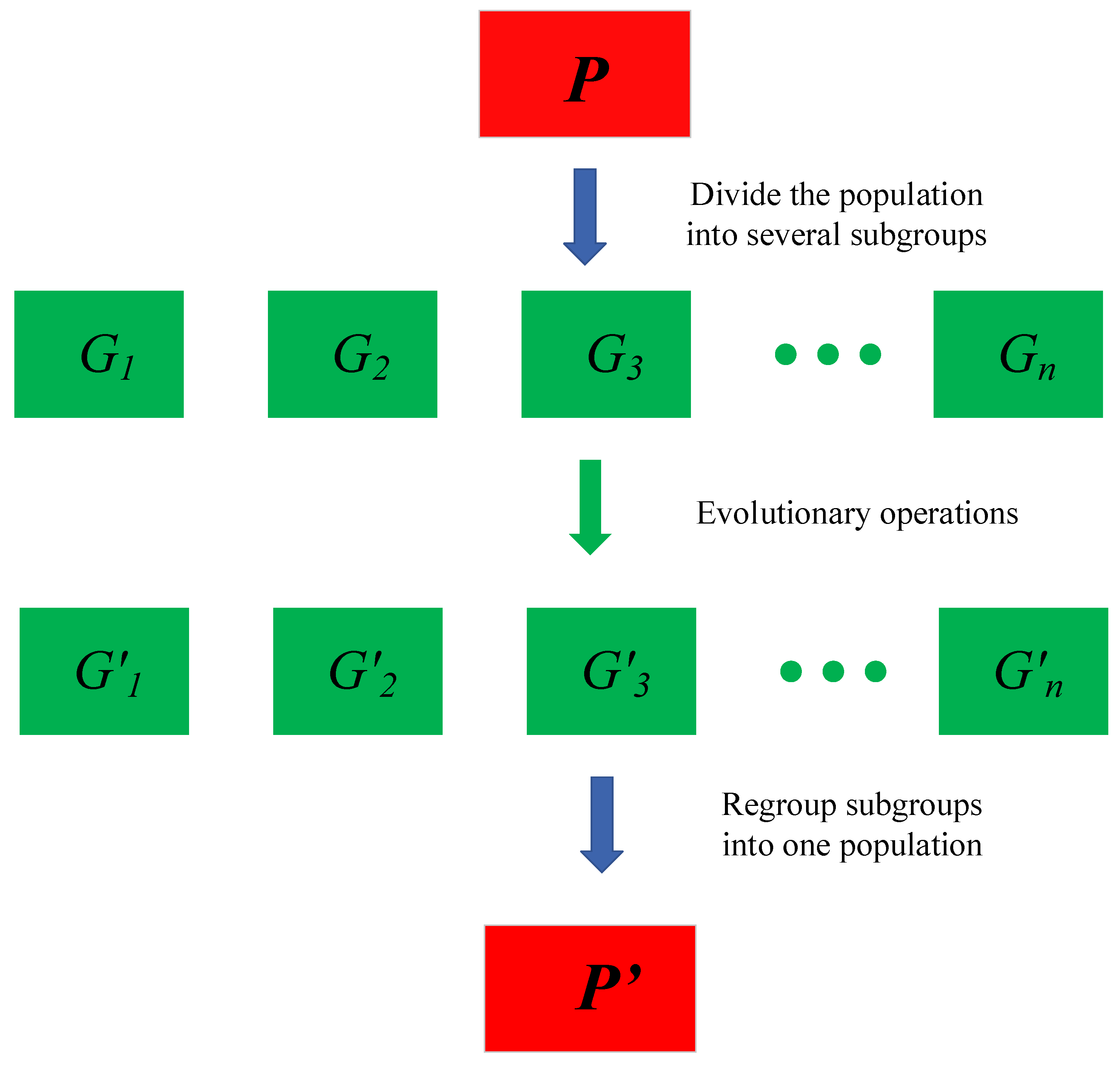
4.8. Niche Operation
In order to reduce the energy consumption of AUSCNs to a higher degree, the NAEEA adopts a new niche mechanism to enhance the diversity of the population and speed up the convergence during clustering optimization in AUSCNs. Firstly, the population is divided into n subgroups randomly. Then, for each subgroup, select, crossover, mutation and elite operation are carried out. Finally, the subgroups form a new group which enters the next iteration.
Figure 9 shows the specific process of niche strategy.
5. Simulation and Discussion
In this section, in order to verify the performance of the algorithm, data analysis is conducted on the DJI Tello UAV, and the performance of the NAEEA algorithm in solving AUSCN clustering optimization is tested through simulation experiments. The DJI Tello drone is a programmable drone with a body diameter of 17 cm and a body weight of 87 g. It can shoot 5-million-pixel photos and 720p high-definition videos, and the maximum video transmission speed is 30FPS. Specifically, the parameter information is shown in
Table 4. In the same experimental environment, the simulation results of the NAEEA are compared with the SFLA, SA and EA. Unless otherwise specified, the simulation results are the average of 10 running results. The experiments were conducted using MATLAB 2021a software on a computer equipped with Intel
® Core(TM) i5-8300H CPU, 8 GB RAM and the Windows 11 operating system.
In this experiment, in order to show that the NAEEA has a stable optimization effect in different scenarios, the simulation experiment will be carried out by setting a number of UAVs of different sizes and different cluster head ratios, as well as different monitoring area sizes, to test the proposed algorithm. The performance is tested; we conduct simulation experiments according to the IEEE 802.15.4 communication standard [
36].
Table 5 shows the detailed data of the AUSCN clustering model in the experimental environment. In the simulation experiment, the electron energy parameter is 50 nJ/bit, the power amplification parameter is 100 pJ/bit/m
2, the data volume is 1 K/bits, the communication environment parameter is 3 and the cluster head ratio is 0.05.
In addition, the population size of the NAEEA is 40, the mutation probability is 0.05, the crossover probability is 0.8, the niche grouping is two and the number of iterations is 100. In the EA, the mutation probability is 0.05 and the crossover probability is 0.8. In the SA, the initial temperature is 1000 °C, the temperature coefficient is 0.9, the Markov chain length is 100 and the number of iterations at the same temperature is 40. In the SFLA, the number of frogs is 40, the number of groups is 4, the number of iterations is 100 and the number of iterations within a group is 10. All algorithms stop running after 100 iterations, and the specific parameters are shown in
Table 6.
Table 7 shows the experimental parameters of
Figure 10, increasing the number of UAVs while fixing the cluster head ratio and monitoring range. According to the experimental parameters in
Table 7,
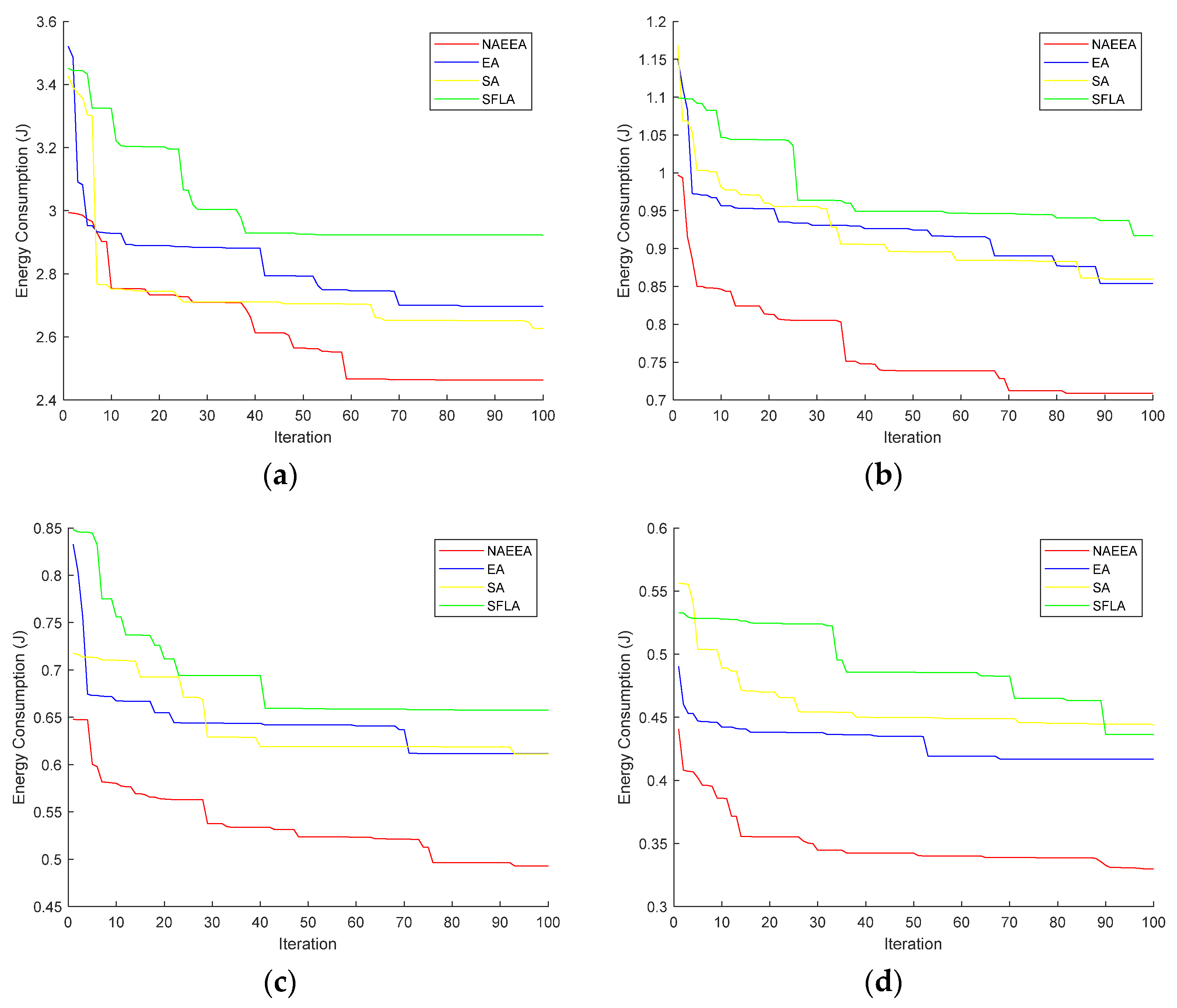
Figure 10 shows the relationship between the network energy consumption and the number of iterations for the NAEEA, EA, SA and SFLA, respectively.
Table 8 shows the network energy consumption of the four algorithms in
Figure 10 for drones of different sizes. It can be seen that the network energy consumption of the NAEEA in four different scenarios is lower than that of the EA, SA and SFLA. Moreover, as the scale of the drones increases, the network energy consumption of the four algorithms decreases.
Table 9 shows the percentage of the network energy consumption that is reduced through the NAEEA compared with the EA, SA and SFLA in the four scenarios in
Figure 10. It can be seen that the optimization effect of the NAEEA is very stable, and compared with the EA, SA and SFLA, the maximum optimization percentages are 11.43%, 12.85% and 23.86%, respectively.
Figure 10a–d are graphs of the network energy consumption of the four clustering methods of the NAEEA, EA, SA and SFLA, respectively, in UAVs of different sizes. It can be clearly seen that after 100 iterations, the network energy consumption of the NAEEA is lower than that of the EA, SA and SFLA. In
Figure 10a, the SA and EA have a certain decline in the early stages of the algorithm iterations, but they fall into evolutionary stagnation after the number of iterations reaches 25 generations, and the network energy consumption of the finally obtained clustering scheme is relatively large. The SFLA performed poorly during operation. Due to the inability to dynamically adjust the algorithm parameters, the algorithm evolved slowly. The evolution stagnated after 71 generations, and the final convergence result was higher than the other three algorithms. After the NAEEA is initialized, the population is grouped and evolved through the niche strategy, which can well expand the population search space, and the elite strategy adopted can well inherit the best individuals in the population into the next iteration, speeding up the algorithm convergence speed, so better results are obtained in the early stage of the algorithm. At the same time, because the NAEEA adopts an adaptive strategy, the algorithm can dynamically adjust the mutation probability during operation to avoid evolutionary stagnation and premature convergence that are caused by the fixed parameters of the algorithm. As can be seen from
Table 8, the final convergence network energy consumption of the four clustering methods of the NAEEA, EA, SA and SFLA are 2.17 J, 2.40 J, 2.49 J and 2.85 J, respectively. As can be seen from
Table 8, after the convergence of the four algorithms is terminated, compared with the GA, ACO and PSO, the EACACA reduces network energy consumption by 9.58%, 12.85% and 23.86%, respectively.
In
Figure 10b, it can be seen that the NAEEA obtained better values than the EA, SA and SFLA in the early iteration, and obtained a more stable clustering scheme in the 12th generation. This is because the NAEEA adopts a niche strategy, adaptive strategy and elite strategy, which can expand the diversity of the solutions of the population in the early stage of population evolution, further evolve the genes of local optimal values, speed up the convergence speed of the algorithm and avoid falling into local optimal solutions. On the contrary, due to the limitations of evolutionary strategies and fixed parameters, the EA, SA and SFLA converge slowly and easily fall into local optimal solutions. Finally, when the 100-generation iteration stopped, the final convergence network energy consumption of the four clustering methods of the NAEEA, EA, SA and SFLA were 1.98 J, 2.20 J, 2.22 J, and 2.47 J, respectively. Compared with the GA, ACO and PSO, the EACACA reduces network energy consumption by 10.00%, 10.81% and 19.84%, respectively. Similarly, the running conditions of
Figure 10c and d are the same as
Figure 10b. After the iteration stops, the network energy consumption of the NAEEA is lower than that of the EA, SA and SFLA, and better clustering can be obtained. The specific clustering scheme is shown in
Figure 11.
Figure 11 shows the AUSCN clustering diagram based on the NAEEA under different-scale UAVs within a 300 × 300 m
2 monitoring range, with a cluster head ratio of 0.05. From
Figure 11a, it can be seen that it is divided into five cluster groups, in which the white circles are the member nodes in the cluster and the middle is the cluster head node. And in
Figure 11, as the scale of the UAVs increases, the number of cluster heads also increases, and the distribution of the UAVs becomes denser.
Table 10 shows the experimental parameters of
Figure 12, increasing the monitoring range while fixing the number of UAVs and the cluster head ratio. According to the experimental parameters in
Table 10,
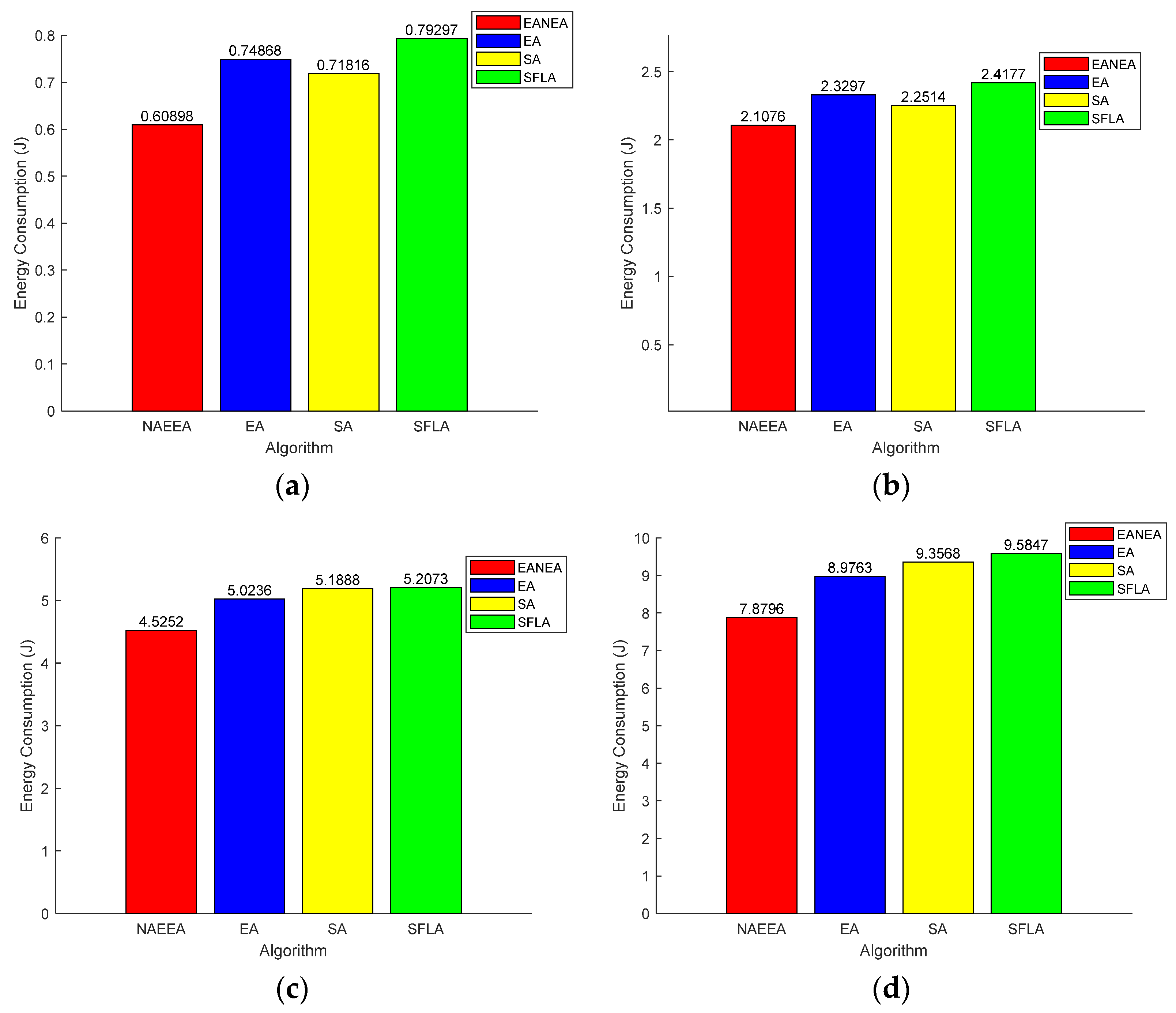
Figure 12 uses a bar chart to show the network energy consumption of the NAEEA, EA, SA and SFLA, respectively.
In
Figure 12, the network energy consumption of the four algorithms in the monitoring range of 200 × 200 m
2, 300 × 300 m
2, 400 × 400 m
2 and 500 × 500 m
2 is more intuitively displayed in the form of a bar chart. It can be seen that the NAEEA is used in the four scenarios. The network energy consumption under the NAEEA is lower than that of the EA, SA and SFLA, and as the monitoring range increases, the network energy consumption of the four algorithms increases. In
Figure 10a, the network energy consumption of the NAEEA, EA, SA and SFLA is 0.61 J, 0.75 J, 0.72 J and 0.79 J, respectively. Compared with the EA, SA and SFLA, the NAEEA reduces the network energy consumption by 18.67%, 15.28% and 22.78%, respectively. Therefore, compared with the EA, SA and SFLA, the NAEEA can generate a better clustering scheme for AUSCNs.
Table 11 shows the experimental parameters of
Figure 13; the number of UAVs and monitoring range remain unchanged, while increasing the cluster head ratio of the network. According to the experimental parameters in
Table 11,
Figure 13 shows the relationship between the network energy consumption and the number of iterations for the NAEEA, EA, SA and SFLA, respectively.
Table 12 shows the network energy consumption of the four algorithms in
Figure 13 when the cluster head ratios are 0.05, 0.1, 0.15 and 0.2. It can be seen that the network energy consumption of the NAEEA in the four different scenarios is lower than that of the EA, SA and SFLA. Moreover, as the cluster head ratio increases, the network energy consumption of the four algorithms decreases.
Table 13 visually shows that the NAEEA reduces the percentage of network energy consumption compared with the EA, SA and SFLA in the four scenarios in
Figure 13. It can be seen that the optimization effect of the NAEEA is very stable and is comparable to that of the EA, SA and SFLA; the maximum optimization percentages are 21.43%, 25.00% and 25.00%, respectively.
Figure 13a–d are graphs of the network energy consumption of the four clustering methods of the NAEEA, EA, SA and SFLA, respectively, at different cluster head ratios. It can be clearly seen that after 100 iterations, the network energy consumption of the NAEEA is lower than that of the EA, SA and SFLA. It can be seen from the simulation results that the SA keeps decreasing in the early stages of the algorithm iterations, but reaches evolutionary stagnation after the number of iterations reaches a certain number, and the final network energy consumption is high. The performance of the EA is relatively stable during the operation of the algorithm, but it is easy to fall into premature convergence during the evolution process, causing the algorithm to evolve slowly in the later stage and being unable to obtain the optimal clustering scheme. Due to the limitation of the fixed parameters during the evolution process, the SFLA results in a smaller population solution space, and the final network energy consumption is the highest. Due to the niche strategy adopted, which performs group evolution first and then fusion after population initialization, the NAEEA avoids the evolutionary stagnation that is caused by falling into local optimality. By conducting parallel searches in the solution space through adaptive strategies and elite strategies, and by dynamically adjusting the algorithm parameters during operation, the diversity of the population solutions is expanded and the convergence speed is accelerated. It can be seen from
Table 12 and
Table 13 that the network energy consumption of the NAEEA is lower than that of the EA, SA and SFLA, and under the same number of UAVs and monitoring ranges and different cluster head ratios, the network energy consumption of the NAEEA is compared with the other algorithms. The AUSCN clustering scheme generated by the NAEEA has the highest energy utilization compared to the other algorithms, with an extension of 8.89% to 21.43%, an extension of 6.46% to 25.00%, and an extension of 15.75% to 25.00%.