Meta-Learning-Based Incremental Nonlinear Dynamic Inversion Control for Quadrotors with Disturbances

Abstract

This paper proposes an online meta-learning-based incremental nonlinear dynamic inversion (INDI) control method for quadrotors with disturbances. The quadrotor dynamic model is first transformed into linear form via an INDI control law. Since INDI largely depends on the accuracy of the control matrix, a method composed of meta-learning and adaptive control is proposed to estimate it online. The effectiveness of the proposed control framework is validated through simulation on a quadrotor with 3D wind disturbances.

1. Introduction

Over the past several decades, quadrotors have seen exciting developments. Their unique advantages have led to broad applications in diverse fields, including post-disaster search and rescue, parcel delivery and environmental monitoring [1]. However, external disturbances can significantly impede the performance of quadrotors [2]. Traditional control methods, such as PID control [3], fail to maintain the ideal performance when the system faces disturbances or model uncertainties. Advanced control methods have been proposed to enhance controller robustness. Adaptive control approaches primarily manage uncertainties and dynamic changes in system models through online parameter adjustments [4,5]. However, traditional adaptive control methods often require considerable computational resources and must encompass all critical adjustable parameters, which can be a limitation especially for complex quadrotor systems with limited onboard processing power. Incremental nonlinear dynamic inversion (INDI) has demonstrated remarkable robustness against unknown perturbations [6,7]. The INDI method essentially measures the external disturbances exerted on the system. It then computes the necessary control inputs through inversion of the dynamic model to counter these disturbances. This requires the ability to accurately estimate the dynamic model of the quadrotor, which can pose a significant challenge. Specifically, given that the INDI control law contains the control matrix explicitly, the control performance largely depends on the precision of it. However, existing research does not focus on the inaccuracy of the control matrix, which could lead to performance degradation and even system instability.

When dealing with consistently changing disturbances, it is crucial to enable quadrotors to leverage information from previous flights. Learning-based methods can pre-train the control system. However, typical learning-based methods such as reinforcement learning, due to their dependence on extensive data sets and prolonged data processing [8], struggle to meet the real-time requirements of flight control. Additionally, existing learning-based methods often focus on a single environmental condition [9]. Transferring knowledge from previously learned tasks to new tasks under continuously changing environments remains an active area of research [10].

To address these challenges, meta-learning, also known as “learning to learn”, offers significant advantages [11]. It excels at quickly adapting to fresh challenges by leveraging knowledge from various other tasks. Furthermore, it maximizes the utilization of the limited data, which is particularly beneficial in data-scarce scenarios or situations requiring rapid task adaptation. In this paper, a meta-learning-based INDI control method is proposed to address the adaptation issues of quadrotors in continuously changing environments. The main contributions are as follows: (1)Aiming at decreasing the inaccuracy of the control matrix in INDI, we propose a new method composed of meta-learning and adaptive control. This approach transcends traditional techniques by leveraging the benefits of meta-learning, which equips the system to draw upon prior experiences and adapt more rapidly to unfamiliar and uncertain environments. It not only mitigates the limitations of the traditional adaptive control methods but also enhances the system’s ability to deal with dynamic and unpredictable circumstances. (2) We validate a non-asymptotic convergence result, which provides sublinear cumulative control error bounds. Through simulation experiments we show that the proposed control framework possesses a more rapid rate of convergence and a reduced magnitude of error in comparison to the Online Meta-Adaptive Control (OMAC) method [12].

The remainder of the paper is organized as follows. Section 2 introduces the dynamic model with wind disturbances for the quadrotor. Section 3 describes the INDI based trajectory tracking controller. Section 4 describes the proposed meta-learning-based INDI control framework, which is combined with adaptive control to handle uncertainties and achieve effective results. Section 5 analyzes the results of simulation experiments. Section 6 discusses the research findings in detail. Finally, Section 7 draws the conclusions.

Notation. $\Vert ·\Vert$ denotes the 2-norm for a vector. The superscript i (e.g., $x^{\left(i\right)}$) refers to the index of the environment. The subscript t (e.g., $x_t$) refers to the index of time. $B(1:)$ and $L(1:)$ refer to the first row of the matrix B and L, respectively. $A_{[1:3]}$ refers to the vector formed by the first three elements of A.

2. Quadrotor Dynamic Model

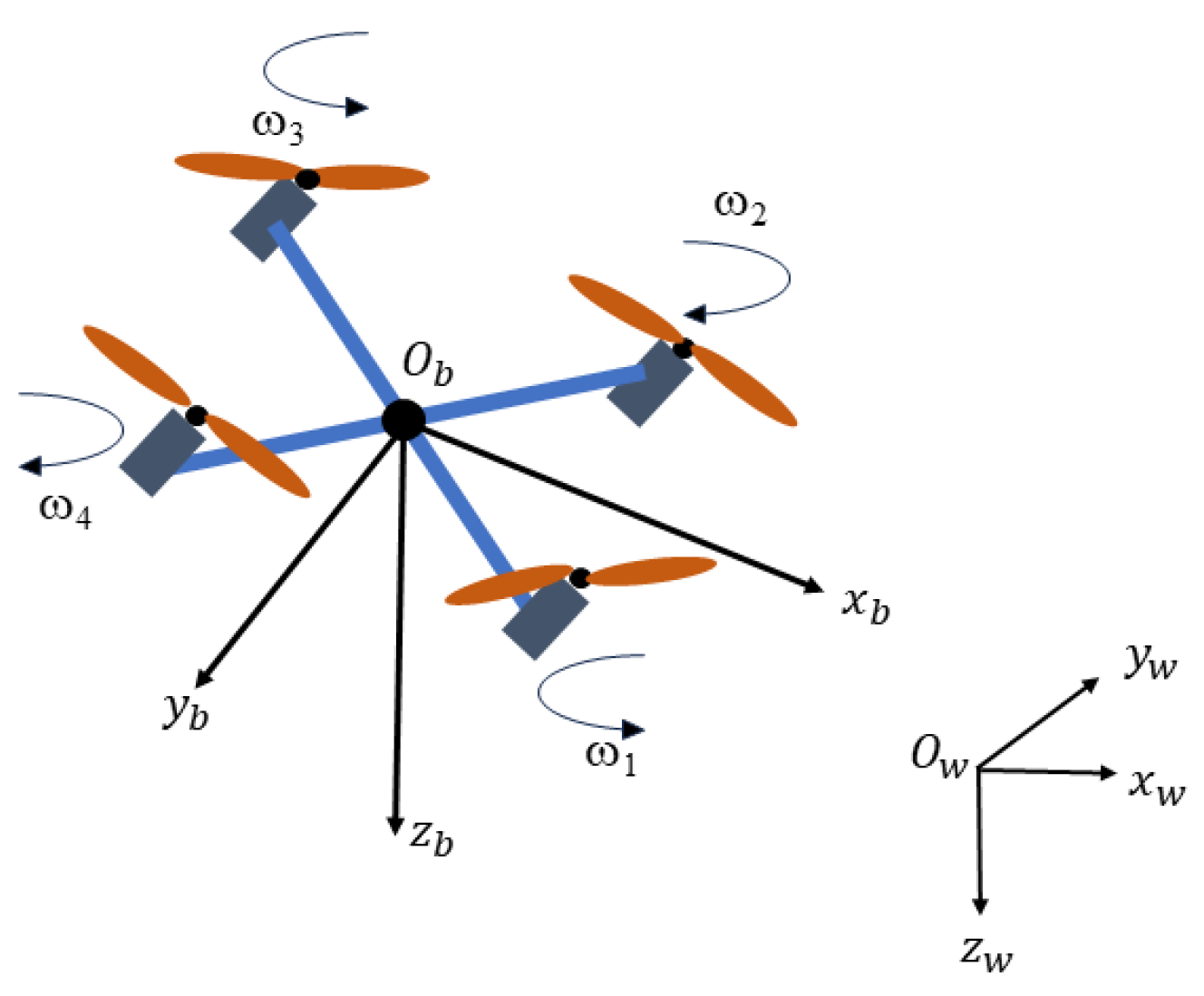
In this section, the dynamic model of the quadrotor with wind disturbances is described. The quadrotor is assumed as rigid so that we can focus on the expression forms of the position, velocity, attitude, and angular velocity only. An inertial reference frame $x_w,y_w,z_w$ is defined to represent the position and velocity of the quadrotor. A body-fixed reference frame $x_b,y_b,z_b$ is defined to model the forces and moments. Note that the quadrotor as shown in Figure 1 is symmetrical and the internal mass distribution is also symmetrical. Then the translational dynamics of the quadrotor are as follows:

$$\dot{p}=v,$$

(1)

$$m\dot{v}=mg+R{f}_T{e}_3+f_{ext},$$

(2)

where $m\in \mathbb{R}$ is the mass of the quadrotor; $g\in {\mathbb{R}}^3$ is the gravity vector; $p\in {\mathbb{R}}^3$ is the position vector, which expresses the quadrotor center of mass in the inertial frame; $v\in {\mathbb{R}}^3$ is the velocity vector; $f_T\in \mathbb{R}$ is the total thrust from four propellers; and $f_{ext}\in {\mathbb{R}}^3$ is the external disturbance force from unmodeled aerodynamic effects and wind gust conditions. The rotation matrix from the body-fixed reference frame to the inertial reference frame is $R\in {\mathbb{R}}^{3\times 3}$. On account of $f_T$ always only acts on the axes of the body-fixed reference frame, the quadrotor has to change its acceleration to reach the desired position.

Figure 1. A quadrotor schematic with an inertial reference frame and a body-fixed reference frame.

And the rotational dynamics are given by:

$$J\dot{\Omega }=J\Omega \times \Omega +M+M_{ext},$$

(3)

where $\Omega \in {\mathbb{R}}^3$ is the body angular velocity vector, $J\in {\mathbb{R}}^{3\times 3}$ is the moment of inertial matrix in the body fixed frame, $M\in {\mathbb{R}}^3$ represents the moment from propellers, and $M_{ext}\in {\mathbb{R}}^3$ represents the external disturbance moment.

In terms of control allocation of the quadrotor, the output consists of the total thrusts and moments acting on the quadrotor, while the input is determined by the speed of the four propellers. We can model $f_T$ and M as a quadratic function of four motors. Therefore, the moment M can be presented as

$$M=\left[\begin{array}{cccc}-l_y{k}_1& l_y{k}_1& l_y{k}_1& -l_y{k}_1\\ l_x{k}_1& -l_y{k}_1& l_x{k}_1& -l_x{k}_1\\ k_3& k_3& -k_3& -k_3\end{array}\right]\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right]+\left[\begin{array}{cccc}-l_y{k}_2& l_y{k}_2& l_y{k}_2& -l_y{k}_2\\ l_x{k}_2& -l_y{k}_2& l_x{k}_2& -l_x{k}_2\\ k_4& k_4& -k_4& -k_4\end{array}\right]\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\\ {\omega }_4\end{array}\right],$$

(4)

where $\omega ={\left[\begin{array}{cccc}{\omega }_1& {\omega }_2& {\omega }_3& {\omega }_4\end{array}\right]}^T$ is the vector of the motor speed, $l_x$ and $l_y$ are the quadrotor moment arms of the x-axis and y-axis, respectively, and $k_1,k_2,k_3,k_4$ are the quadratic coefficients [7]. We can obtain the control force $f_T$ and moment M and then directly distribute the signal to four motors.

As discussed in [13], the second item (the first degree) in (4) can be omitted in most cases. The thrust and the moment generated by the propellers can be represented as the quadratic terms of the motor speed. We can simplify it further by assuming that the ratio of the coefficient of rotor thrust and the moment is constant, which means $k_3/k_1=k_4/k_2=k$. This is reasonable when the yaw angle changes not radically. Then we can derive that

$$\left[\begin{array}{c}{f}_T\\ M\end{array}\right]=B\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right],$$

(5)

$$B=k_1\left[\begin{array}{cccc}1& 1& 1& 1\\ -l_y& l_y& l_y& -l_y\\ l_x& -l_x& l_x& -l_x\\ k& k& -k& -k\end{array}\right].$$

(6)

$B\in {\mathbb{R}}^{4\times 4}$ denotes the control matrix. We can obtain the command of the motor speed $u\in {\mathbb{R}}^4$ with the inversed mapping as follows:

$$\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right]=B^{-1}\left[\begin{array}{c}{f}_T\\ M\end{array}\right],$$

(7)

$$u=\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right].$$

(8)

Even though the matrix B is invertible, this may produce an infeasible motor speed, due to the hardware constraints [14]. So, the motor speed should subject to

$$0\le {\omega }_{min}\le {\omega }_i\le {\omega }_{max},i=1,2,3,4,$$

(9)

where ${\omega }_{min}$ and ${\omega }_{max}$ are the minimum and maximum motor speed limits, respectively. The inequality (9) defines a possible set of the motor speed.

As mentioned earlier, we assume that the internal mass distribution of the quadrotor is symmetric. Given that the quadrotor is geometrically distributed symmetrically and the measurement of the moment of inertia matrix J is quite accurate, this applies to most situations. However, some quadrotors cannot be naively considered as mass-symmetrical such as parcel delivery quadrotors. In these cases, J is a non-diagonal matrix, and the moment arms of the x-axis and y-axis are not equal. In Section 5, we will discuss how the lack of mass symmetry affects the results in detail.

3. Incremental Nonlinear Dynamic Inversion Control Design

3.1. Incremental Nonlinear Dynamic Inversion

The goal of INDI is to obtain an incremental form of the control input by inversing the nonlinear system at the present moment, after it has been linearized. The state space expression of a conventional nonlinear system can be written as:

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=f\left(x\left(t\right)\right)+g(x\left(t\right),u\left(t\right)),\hfill \\ y\left(t\right)=h\left(x\right(t\left)\right),\hfill \end{array}\right.$$

(10)

where $x\left(t\right)$ is the state vector, $u\left(t\right)$ is the control input vector, and $y\left(t\right)$ is the output vector. We rewrite (10) in the form of a Taylor expansion, ignoring higher-order terms as follows:

$$\left\{\begin{array}{c}\dot{x}={\dot{x}}_0+{\displaystyle \frac{\partial f\left(x\right)}{\partial x}}{|}_{x_0,u_0}(x-x_0)+{\displaystyle \frac{\partial g(x,u)}{\partial x}}{{|}_{x_0,u_0}(x-x_0)+{\displaystyle \frac{\partial g(x,u)}{\partial u}}|}_{x_0,u_0}(u-u_0)+\Delta ,\hfill \\ \dot{y}={\displaystyle \frac{dh}{dx}}\dot{x},\hfill \end{array}\right.$$

(11)

where $\Delta$ denotes the higher-order infinitesimal. Let $\Delta u$ and $\Delta x$ represent the increment of x and u, respectively. We assume that the flight control computer has a high sampling rate such that $\Delta u$ changes significantly faster than $\Delta x$. Therefore, we can ignore the contribution of $\Delta x$ to the output derivative and only keep $\Delta u$. It follows that

$$\begin{array}{cc}\hfill & \dot{y}\approx {\displaystyle \frac{dh}{dx}}[{\dot{x}}_0+{\displaystyle \frac{\partial g(x,u)}{\partial u}}{|}_{x_0,u_0}(u-u_0)]={\dot{y}}_0+H(x_0,u_0)\Delta u\hfill \end{array},$$

(12)

where $H(x_0,u_0)$ denotes the control matrix of the system. We can derive INDI control law as

$$\left\{\begin{array}{c}\Delta u=H^{-1}(x_0,u_0)({\dot{y}}_c-{\dot{y}}_0),\hfill \\ u=u_0+\Delta u,\hfill \end{array}\right.$$

(13)

where ${\dot{y}}_c$ is the desired output derivative, ${\dot{y}}_0$ is the output derivative at the current time, and $H^{-1}$ is the inverse matrix of the control matrix H. The input to the output dynamic of the system can be linearized as $\dot{y}={\dot{y}}_c$.

3.2. INDI Acceleration Controller

In this section, we design an INDI control law to track the desired trajectory. We define the state $x={\left[\begin{array}{cc}p& v\end{array}\right]}^T$. As given by (8), u is a vector composed of the squares of motor speeds. From (1) and (2) we can obtain:

$$\begin{array}{cc}\hfill \dot{x}& =\left[\begin{array}{c}\dot{p}\\ \dot{v}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}p\\ v\end{array}\right]+\left[\begin{array}{c}0\\ g+m^{-1}(R{f}_T{e}_3+f_{ext})\end{array}\right]\hfill \\ \hfill & =\underset{\mathit{f}\left(\mathit{x}\right)}{\underbrace{\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}p\\ v\end{array}\right]}}+\underset{\mathit{g}(\mathit{x},\mathit{u})}{\underbrace{\left[\begin{array}{c}0\\ g+m^{-1}(R\left[\begin{array}{c}0\\ 0\\ B(1:)\end{array}\right]\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right]+f_{ext})\end{array}\right]}}.\hfill \end{array}$$

(14)

We denote $F=R{f}_T{e}_3\in {\mathbb{R}}^3$. $F_0$ and $f_{ext0}\in {\mathbb{R}}^3$ denote the force from propellers and external disturbances at the current moment, respectively. $\Delta F=F-F_0$, $\Delta f_{ext}=f_{ext}-f_{ext0}$. To obtain a stable command signal while flying at a large attitude, the control command is designed as the control force in the inertial frame. Similar to (13) we can take a Taylor series expansion:

$$\dot{v}={\dot{v}}_0+m^{-1}(\Delta F+\Delta f_{ext}),$$

(15)

$${\dot{v}}_0=g+m^{-1}{F}_0+m^{-1}{f}_{ext0},$$

(16)

where ${\dot{v}}_0\in {\mathbb{R}}^3$ denotes the derivative of velocity at the current moment and can be measured directly. Defining $v_d\in {\mathbb{R}}^3$ as the reference velocity, the velocity error $e_v\in {\mathbb{R}}^3$ can be written as follows:

$$e_v=v-v_d.$$

(17)

Similarly, the position error is defined as $e_p\in {\mathbb{R}}^3$. The increment of the control force is designed as:

$$\Delta F=m(-k_x{e}_p-k_v{e}_v-{\dot{v}}_0+{\dot{v}}_d),$$

(18)

where $k_x\in {\mathbb{R}}^{3\times 3}$ is the diagonal gain matrix in the position loop and $k_v\in {\mathbb{R}}^{3\times 3}$ is the diagonal gain matrix in the velocity loop. Take the derivative of both sides of (17):

$$\dot{e_v}=-k_x{e}_p-k_v{e}_v+m^{-1}{f}_{ext0},$$

(19)

where $k_x$ and $k_v$ are chosen based on the conclusions in [15] to ensure that the system is asymptotically stable when it is free of disturbance. For instance, $k_x$ and $k_v$ are Hurwitz. Then the command force $F_c\in {\mathbb{R}}^3$ will be

$$F_c=F_0+\Delta F.$$

(20)

Once the force is determined, we can calculate the input motor speeds. The incremental property enables the controller to control the acceleration in the presence of disturbances or model errors.

4. Meta-Learning-Based INDI Control and Convergence Analysis

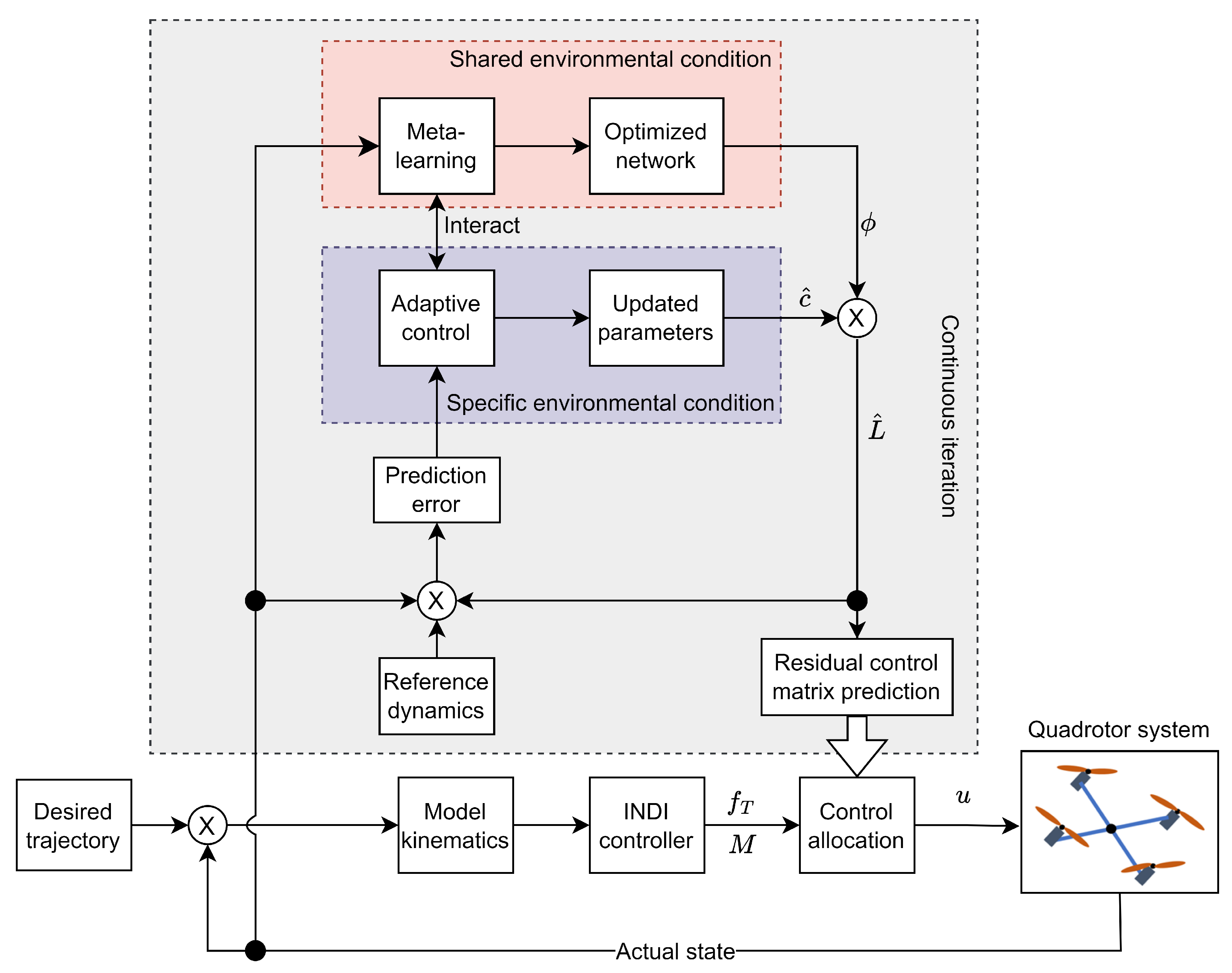
In this section, we discuss the design and implementation of the meta-learning-based INDI control method as shown in Figure 2. This method can effectively solve the adaptation issues of quadrotors in continuously changing disturbance environments (Section 4.1). We then proceed to present a comprehensive convergence analysis of the proposed approach, introducing the Average Control Error (ACE) [12] as a performance metric for evaluating the effectiveness of the proposed control framework (Section 4.2).

Figure 2. Meta-learning-based INDI control design. INDI controller calculates the control command. Meta-learning (the pink box) captures representation shared by all conditions. Adaptive control (the purple box) takes effect in each specific condition. The process in the gray box is conducted online and is continuously iterative.

Consider the dynamics model in (14). We suppose that the quadrotor encounters a sequence of N environments. Let $\delta \to$ 0, denoting the discretization step. In the ith environment the system dynamics are:

$$\begin{array}{cc}\hfill x_{t+1}^{\left(i\right)}& =\left[\begin{array}{c}{p}_{t+1}^{\left(i\right)}\\ v_{t+1}^{\left(i\right)}\end{array}\right]\hfill \\ \hfill & =\underset{\mathit{F}\left(\mathit{x}\right)}{\underbrace{\left[\begin{array}{cc}1& \delta \\ 0& 1\end{array}\right]\left[\begin{array}{c}{p}_t^{\left(i\right)}\\ v_t^{\left(i\right)}\end{array}\right]}}+\underset{\mathit{G}(\mathit{B},\mathit{u})}{\underbrace{\delta \left[\begin{array}{c}0\\ g+m^{-1}R\left[\begin{array}{c}0\\ 0\\ B(1:)\end{array}\right]\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right]\end{array}\right]}}+d_t^{\left(i\right)},1\le t\le T,\hfill \end{array}$$

(21)

where $d_t^{\left(i\right)}\in {\mathbb{R}}^6$ is the disturbance in the environment. In this paper, we apply meta-learning to the control allocation part. Let $L\in {\mathbb{R}}^{4\times 4}$ denote the unknown part of the control matrix B. We reformulate (21) as follows:

$$x_{t+1}^{\left(i\right)}=F\left(x_t^{\left(i\right)}\right)+G(B_t^{\left(i\right)},u_t^{\left(i\right)})-G(L_t^{\left(i\right)},u_t^{\left(i\right)})+d_t^{\left(i\right)},1\le t\le T.$$

(22)

4.1. Meta-Learning-Based INDI Control with Wind Disturbances

In this subsection we introduce how to use meta-learning combined with adaptive control to obtain the control matrix to resist the model uncertainties caused by wind disturbances.

One important issue is how to learn from the previous environments and behave better in the next environment. Motivated by the idea of OMAC [12], at the beginning of getting into the environment i, the controller estimates $\widehat{L}$ first, which is an estimation of $L_t^{\left(i\right)}$. And then the controller takes action $u_t^{\left(i\right)}$, premised on the assumption that the learned model faithfully represents the true system dynamics. i is incremented to $i+1$ and this process continues.

We define a function to describe $\widehat{L}$ as follows:

$$\widehat{L}=\varphi (x_t^{\left(i\right)},\widehat{\Theta }){\widehat{c}}^{\left(i\right)},$$

(23)

where $\varphi \in {\mathbb{R}}^{4\times h}$ is a state-related variable with weight $\widehat{\Theta }$ shared by all environments, and ${\widehat{c}}^{\left(i\right)}\in {\mathbb{R}}^{h\times 4}$ corresponds to a specific environmental condition. Here we represent $\varphi$ by a Deep Neural Network (DNN) to obtain the shared environmental representation, learning and retaining the distrubitions in various conditions. Spectral normalization [16] is integrated to stabilize the training process and enhance the performance of the models. We use Adam Optimizer [17] to update the network weights to minimize the prediction error [18]. This strategy embodies the fundamental concept of meta-learning.

In each specific environment, we keep the learned environmental representation $\varphi (·)$ fixed, and apply the online gradient descent method for adaptive control to adjust $\widehat{c}$ as follows:

$${\widehat{c}}^{(i+1)}={\widehat{c}}^{\left(i\right)}-2{\eta }_i{(\widehat{L}-B_d)}^T\varphi ,$$

(24)

where ${\eta }_i$ is the learning rate and $B_d\in {\mathbb{R}}^{4\times 4}$ is a measurement of the residual control matrix obtained from the reference dynamics. The learning rate ${\eta }_i$ decreases as the iteration proceeds, which leads to a convergence result. This is one of the defining characteristics of adaptive control. The adaptive approach attempts to update the model parameters by minimizing the prediction error. This rule is online, meaning that the controller parameters are updated immediately each time new data arrives.

Adaptive control focuses on adjusting controller parameters based on real-time performance, while meta-learning aims to improve the model’s generalization ability by learning from a set of tasks. Thus, the system state can iterate on each environmental condition and update the parameters to enhance the system performance as the number of environments increases.

4.2. Convergence Analysis

We define a metric termed ACE to evaluate the performance of learning and control:

$$ACE={\displaystyle \frac{1}{TN}}{\Sigma }_{i=1}^N{\Sigma }_{t=1}^T\Vert p_t^{\left(i\right)}-s_t^{\left(i\right)}\Vert ,$$

(25)

where $s_t^{\left(i\right)}\in {\mathbb{R}}^3$ denotes the desired position of the quadrotor at time t in the ith environment. ACE describes the tracking error under N iterations of environmental conditions, with each condition persisting for T time steps.

Assumption 1.

$\forall x_t^{\left(i\right)},d_t^{\left(i\right)}\le D$ and $s_t^{\left(i\right)}\le S$. D and S are finite constants.

Theorem 1.

Let constants $\gamma \ge 0$ and $0\le \rho <1$. The ACE has a non-asymptotic convergence guarantee as:

$$ACE\le {\displaystyle \frac{\gamma }{1-\rho }}\sqrt{{\displaystyle \frac{1}{TN}}}{\sqrt{{\Sigma }_{i=1}^N{\Sigma }_{t=1}^T{\Vert G(B_t^{\left(i\right)},u_t^{\left(i\right)})-G(L_t^{\left(i\right)},u_t^{\left(i\right)})+d_t^{\left(i\right)}-X_t^{\left(i\right)}\Vert }^2}}_{[1:3]}.$$

(26)

Proof. 

To prove the convergence of ACE, we replace the position vector in ACE with the state $x_t^{\left(i\right)}$. The desired state $X_t^{\left(i\right)}\in {\mathbb{R}}^6$ is bounded. Let constant $\beta \ge 0$. From the exponentially input to state stable property of (22) we can obtain:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{TN}}{\Sigma }_{i=1}^N{\Sigma }_{t=1}^T\Vert x_t^{\left(i\right)}-X_t^{\left(i\right)}\Vert \hfill \\ \hfill & \stackrel{\left(a\right)}{\le }{\displaystyle \frac{1}{TN}}{\Sigma }_{i=1}^N{\Sigma }_{t=1}^T(\beta {\rho }^{t-1}\Vert x_1^{\left(i\right)}\Vert +\gamma {\Sigma }_{k=1}^{t-1}{\rho }^{t-1-k}\Vert G(B_k^{\left(i\right)},u_k^{\left(i\right)})-G(L_k^{\left(i\right)},u_k^{\left(i\right)})+d_k^{\left(i\right)}-X_k^{\left(i\right)}\Vert )\hfill \\ \hfill & \stackrel{\left(b\right)}{=}{\displaystyle \frac{1}{TN}}{\Sigma }_{i=1}^N{\Sigma }_{t=1}^T\gamma {\Sigma }_{k=1}^{t-1}{\rho }^{t-1-k}\Vert G(B_k^{\left(i\right)},u_k^{\left(i\right)})-G(L_k^{\left(i\right)},u_k^{\left(i\right)})+d_k^{\left(i\right)}-X_k^{\left(i\right)}\Vert \hfill \\ \hfill & \stackrel{\left(c\right)}{\le }{\displaystyle \frac{\gamma }{1-\rho }}{\displaystyle \frac{1}{TN}}{\Sigma }_{i=1}^N{\Sigma }_{t=1}^{T-1}\Vert G(B_t^{\left(i\right)},u_t^{\left(i\right)})-G(L_t^{\left(i\right)},u_t^{\left(i\right)})+d_t^{\left(i\right)}-X_t^{\left(i\right)}\Vert \hfill \\ \hfill & \stackrel{\left(d\right)}{\le }{\displaystyle \frac{\gamma }{1-\rho }}\sqrt{{\displaystyle \frac{1}{TN}}}\sqrt{{\Sigma }_{i=1}^N{\Sigma }_{t=1}^T{\Vert G(B_t^{\left(i\right)},u_t^{\left(i\right)})-G(L_t^{\left(i\right)},u_t^{\left(i\right)})+d_t^{\left(i\right)}-X_t^{\left(i\right)}\Vert }^2}.\hfill \end{array}$$

(27)

(a) and (b) are based on the assumptions $X_1^{\left(i\right)}=0$ and $x_1^{\left(i\right)}=0$, respectively. (c) is from the geometric series and (d) is from the Cauchy–Schwarz inequality. $u_t^{\left(i\right)}$ is derived from

$$u={(R\left[\begin{array}{c}0\\ 0\\ B(1:)\end{array}\right])}^{†}(F_0+m(-k_x{e}_p-k_v{e}_v-{\dot{v}}_0+{\dot{v}}_d)),$$

(28)

and $L_t^{\left(i\right)}$ is related to the learned results $\varphi$ and ${\widehat{c}}^{\left(i\right)}$, which has a convergence guarantee. When the rotation angles are not large, it is evident that R is bounded. By appropriately setting the value of $k_x$ and $k_v$, we ensure that the error from $X_t^{\left(i\right)}$ in (27) is bounded. We can infer that ACE converges non-asymptotically. Further, we can also deduce that the improvement in the control law and learning performance significantly reduces ACE, as demonstrated in the subsequent section. □

5. Simulation Results

To validate the proposed framework, we conduct simulation experiments for a quadrotor with 3D wind disturbances. We utilize Visual Studio Code as the software environment and Python as the programming language. We perform the simulation with the proposed method by referencing the code from the paper [12]. The wind speed varies within a range of $-5$ m/s to 5 m/s along the x-axis, and $-2.5$ m/s to $2.5$ m/s along the z-axis. The wind condition randomly switches to the next one every 2 s. The parameters pertaining to the controller and the quadrotor platform are given in Table 1. The maximum motor speed is set to 1000 rad/s and the maximum quadrotor thrust is set to 125 N.

Table 1. Controller and quadrotor platform parameters.

Parameter	Value
$k_x$	$\left[\begin{array}{ccc}6& 0& 0\\ 0& 6& 0\\ 0& 0& 3\end{array}\right]$
$k_v$	$\left[\begin{array}{ccc}4& 0& 0\\ 0& 4& 0\\ 0& 0& 3\end{array}\right]$
g	9.81
m (kg)	2.4
J (kg· m2)	$\left[\begin{array}{ccc}0.0036& 0& 0\\ 0& 0.0036& 0\\ 0& 0& 0.0036\end{array}\right]$

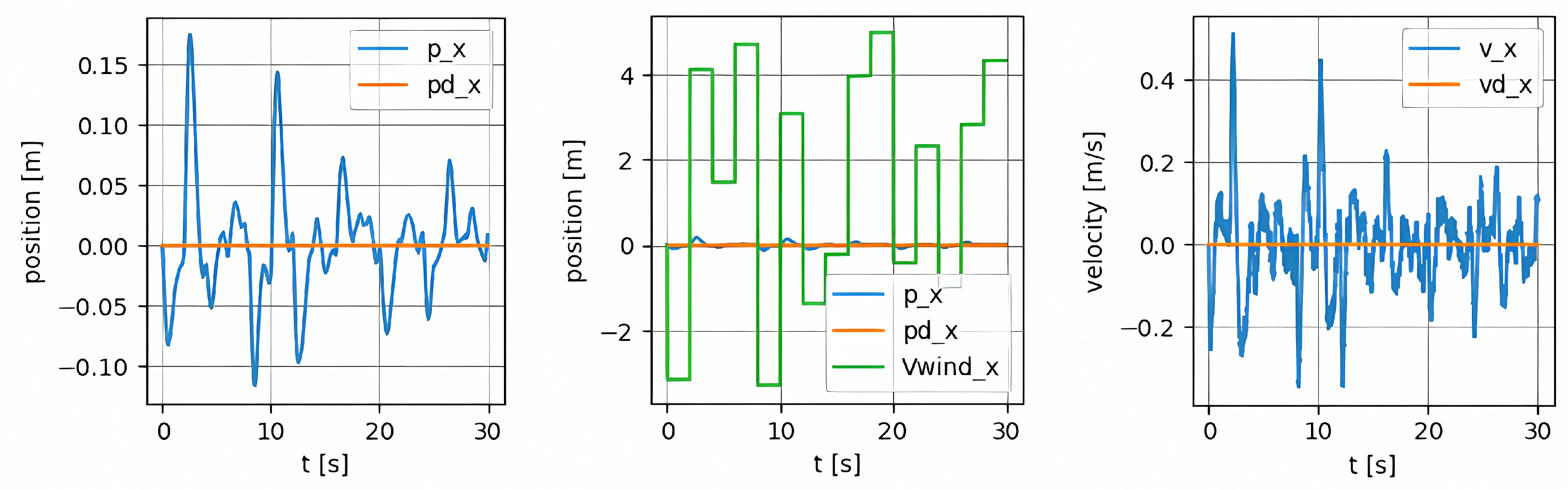
To verify the effectiveness of the meta-learning method on the control matrix, we utilize INDI control combined with the learned matrix for a quadrotor against wind disturbances. We can see in Figure 3 that as the system encounters more environments the controller performs better. This can be observed from the decreasing position and velocity errors along the x-axis over time.

Figure 3. Tracking errors along the x-axis. The first subfigure shows the actual position and the desired position along the x-axis. The position error is decreasing as the system encounters more situations. The second subfigure shows that in comparison with the wind disturbances, the size of position error is quite small. The third subfigure shows the actual velocity and the desired velocity along the x-axis. The velocity error is decreasing similarly.

We select three random situations and compare the control effectiveness of PID and INDI methods with the control matrix after meta-learning, respectively. We compare the Root Mean Square Error (RMSE), which represents the deviation of the quadrotor from the hover point under wind disturbances in these different situations. From Table 2 we can see that the proposed meta-learning-based INDI control method significantly outperforms the baseline INDI and it also performs considerably better than the meta-learning-based PID.

Table 2. The RMSE comparison from three random seeds.

Random Seed Number	PID Baseline	Meta-Learning-Based PID	INDI Baseline	Meta-Learning-Based INDI
1	0.303 m	0.225 m	0.054 m	0.043 m
2	0.282 m	0.217 m	0.054 m	0.047 m
3	0.320 m	0.230 m	0.069 m	0.057 m

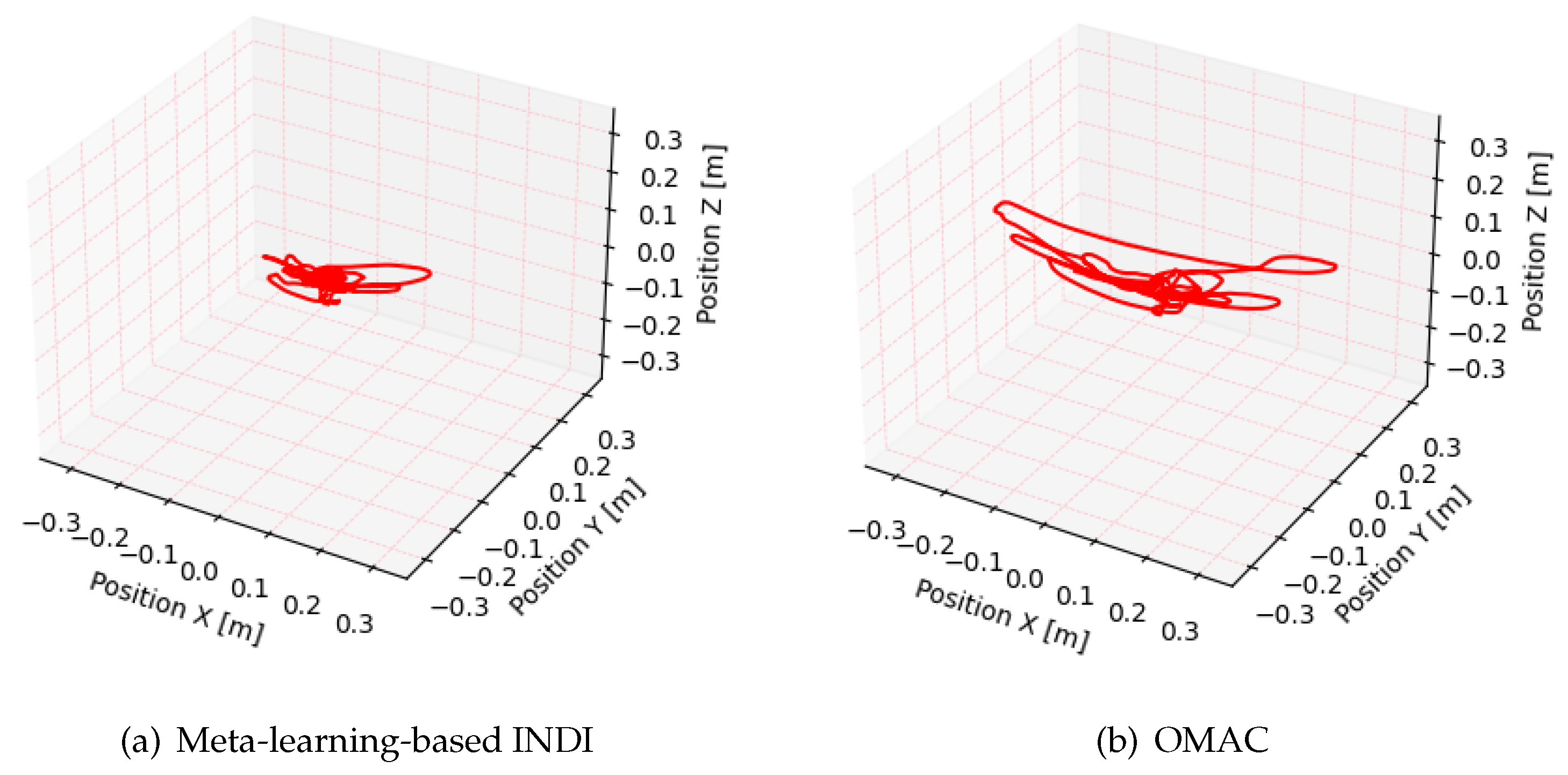
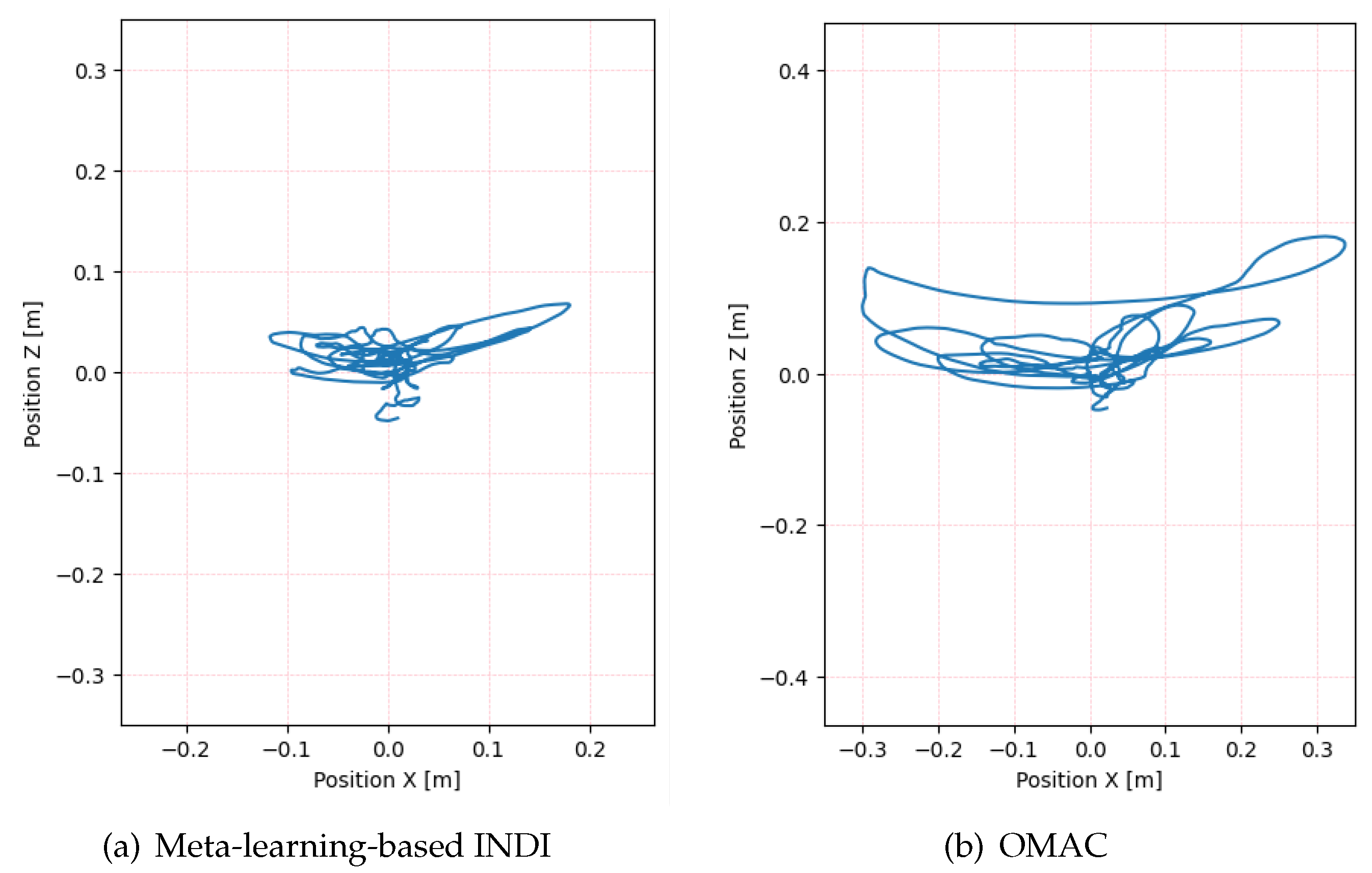
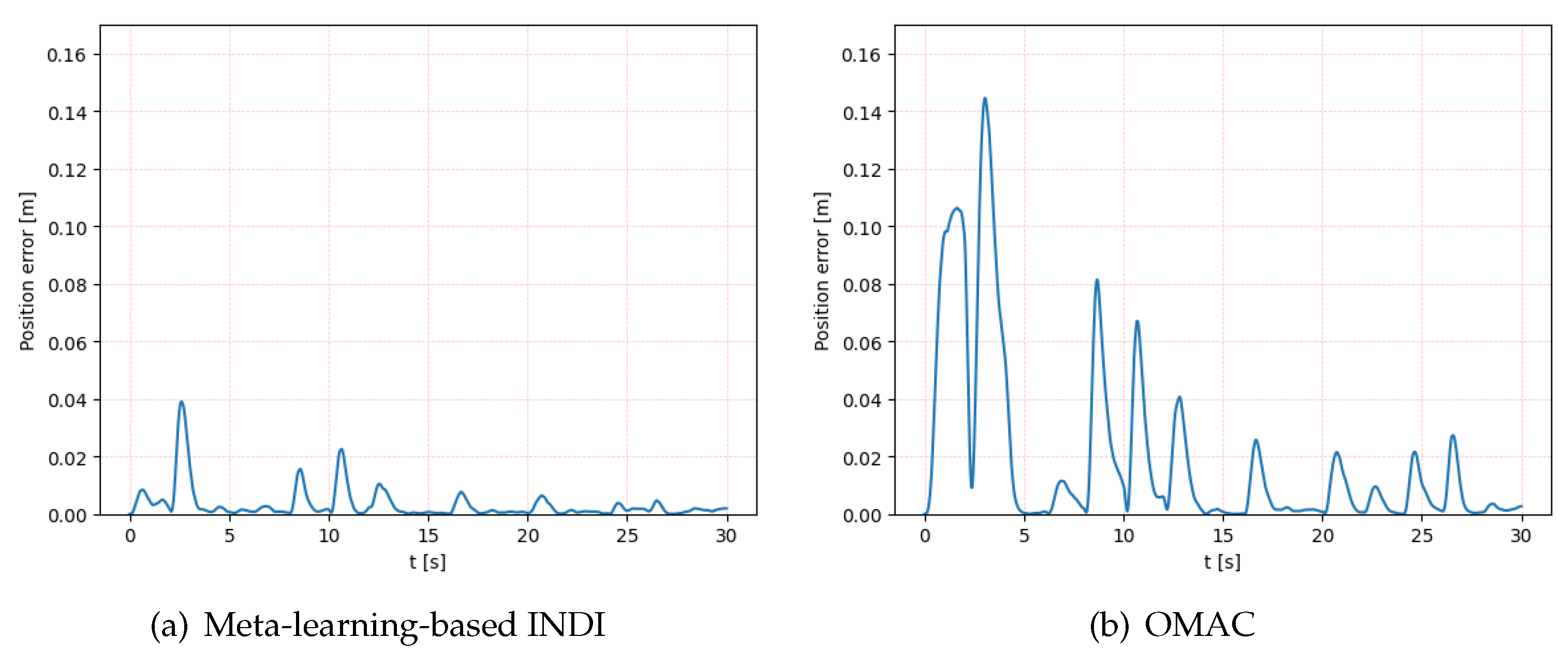
We compare the disturbance rejection capabilities of the proposed method and the OMAC method for quadrotors under a specific random wind condition to maintain a hovering state. The hover point is located at (0, 0, 0). As shown in Figure 4 and Figure 5, the flight trajectory of the quadrotor with the proposed method is closer to the desired hover point, indicating a better control performance. This is quantitatively reflected in the RMSE values, with the meta-learning-based INDI method yielding an RMSE of 0.057 m, significantly lower than 0.139 m observed with the OMAC method. The quadrotor operated by the proposed method exhibits a smaller position error diminishing progressively over time, as depicted in Figure 6, validating the effectiveness of the approach in minimizing discrepancies from the desired position. These results demonstrate the superiority of the proposed meta-learning-based INDI control method in enhancing the adaptability of quadrotors in continuously changing disturbance environments.

Figure 4. Flight trajectories of the proposed meta-learning-based INDI and OMAC in 3D space.

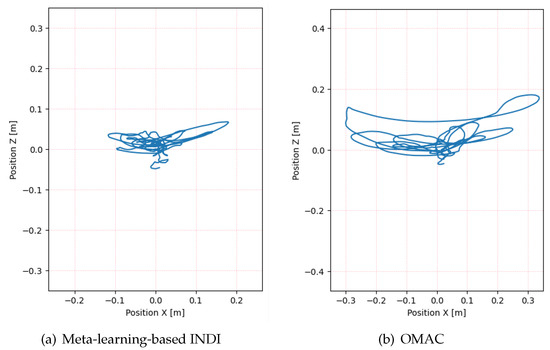
Figure 5. Flight trajectories of the proposed meta-learning-based INDI and OMAC in the X-Z plane.

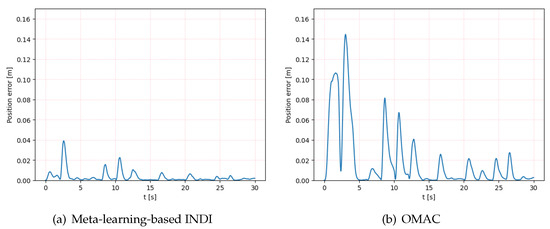
Figure 6. The position error in 3D space of the proposed meta-learning-based INDI and OMAC.

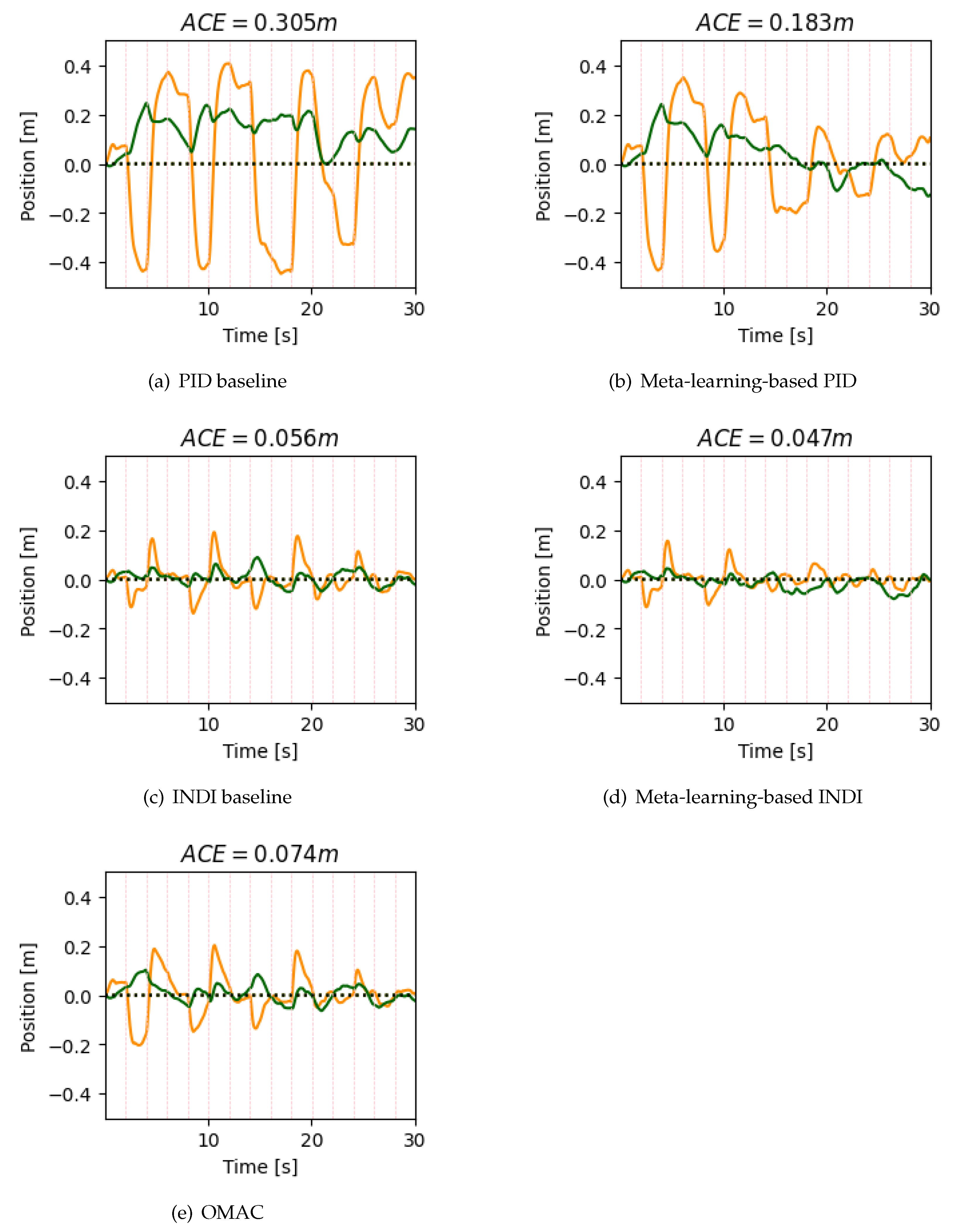
For one random situation the ACE values on the x-axis and z-axis are as shown in Figure 7. We consider the mass-asymmetric scenario first. Vertical lines in the figure indicate that the wind condition is switched. The performance of the meta-learning-based INDI method and the meta-learning-based PID method progressively improve in comparison with baseline, as they can benefit from prior experiences when they encounter more environments. Meta-learning-based INDI method reaches the best ACE value due to the representation power of DNN, adaptive capability, and the robust anti-interference performance of the INDI method. The ACE of the z-axis is smaller than that of the x-axis. As there is a relatively straightforward control along the z-axis, which usually refers to the vertical direction or altitude. This ease of control primarily stems from the fact that quadrotors modulate the speed of all motors to ascend or descend. The disturbances caused by the wind along the z-axis are also smaller.

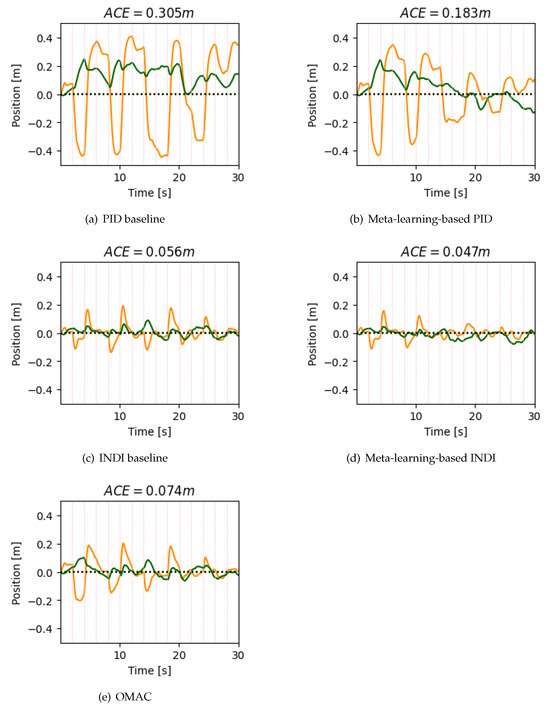
Figure 7. Trends of ACE values under different control methods in the mass-symmetric scenario. Meta-learning-based INDI yields the best outcomes.

To validate how the lack of mass symmetry affects the performance of the proposed method, we adjust the quadrotor model to be mass-asymmetric. The moment of inertial matrix is designed as a non-diagonal matrix as follows:

$$J=\left[\begin{array}{ccc}0.0036& 0.003& 0\\ 0.003& 0.0036& 0\\ 0& 0& 0.0036\end{array}\right].$$

(29)

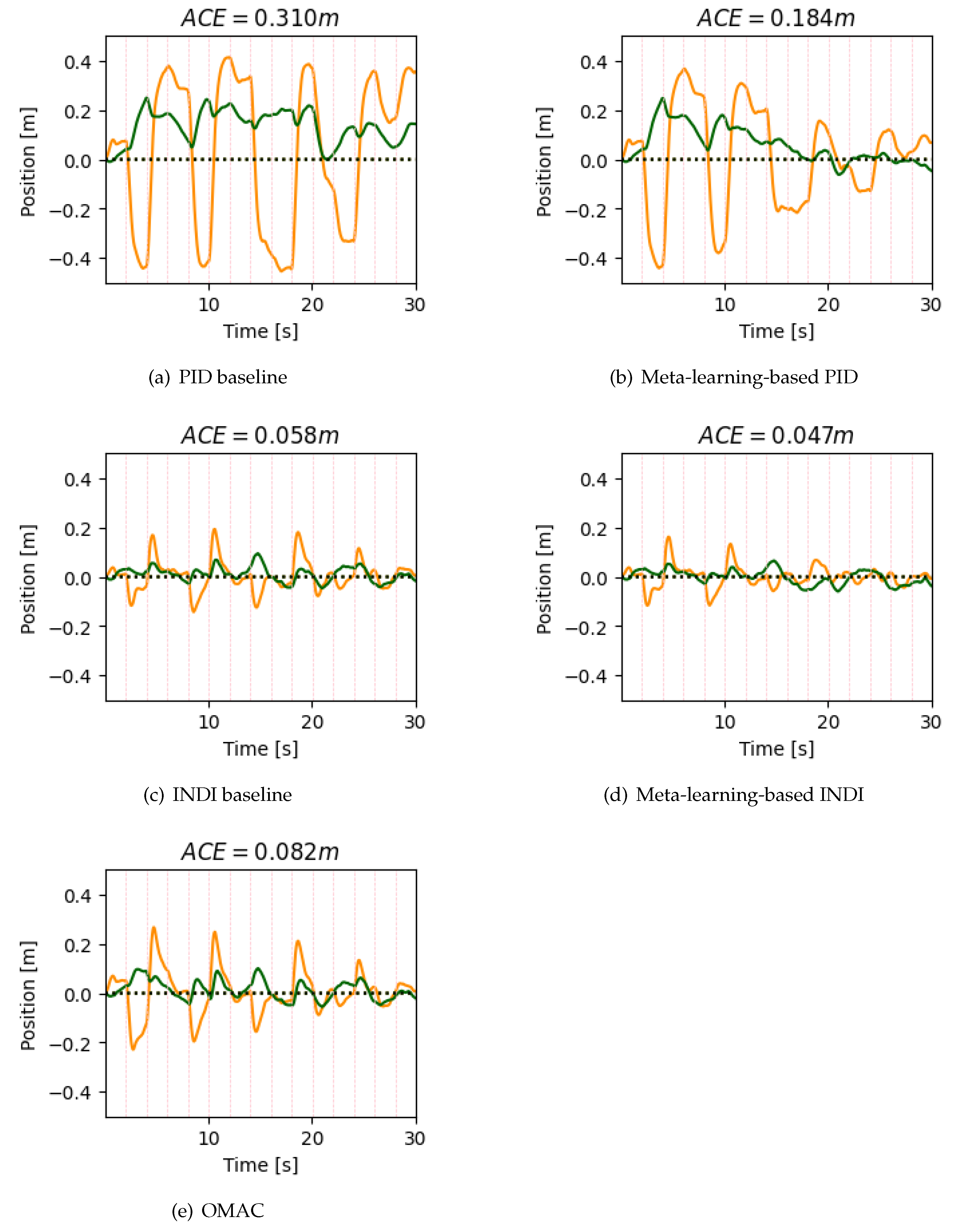
Another aspect worth noting is that the moment arms of the x-axis and the y-axis are incorporated in the control matrix, subject to optimization during the learning process. As a result, any effects stemming from discrepancies in the moment arms can be effectively mitigated. We apply the same environmental disturbance conditions as those set in Figure 7. The ACE values of the mass-asymmetric quadrotor are shown in Figure 8. The results indicate that, due to the lack of mass symmetry, the PID and INDI baseline methods perform somewhat inferiorly compared to the symmetrical case. However, the performance of the meta-learning-based PID and INDI methods approximate that observed in the mass-symmetric scenario. Therefore, we can conclude that the proposed method is capable of accommodating a certain degree of mass asymmetry.

Figure 8. Trends of ACE values under different control methods in the mass-asymmetric scenario. Meta-learning-based methods demonstrate satisfactory performance.

6. Discussion

The duration of the simulation is configured to 30 s. This timeframe is chosen as it sufficiently exhibits the convergence trend of positional control error with the meta-learning-based methods. Further, extending the simulation does not yield a significant reduction in error. We have configured the quadrotor with a diagonal length of 0.9 m, measured tip-to-tip across the opposing rotors. The meta-learning-based INDI method yields an ACE of approximately 0.05 m. The achieved accuracy is sufficient for applications such as environmental monitoring and parcel delivery. In the simulation, we compare the performance of the meta-learning-based PID and INDI methods, while both methodologies are effective in position control, the meta-learning-based INDI method outperforms in terms of ACE. This emphasizes the superior robustness and precision of the INDI control in controlling the position of quadrotors. However, this does not diminish the utility of the PID method. In fact, owing to its simplicity and ease of implementation, the PID control continues to find extensive applications in a variety of control systems.

In addition, certain equations are simplified to enhance the computational efficiency. For instance, we have overlooked some secondary dynamic effects, presumed the quadrotor to be a rigid body with its geometric center coinciding with its center of mass, assumed that the resistance and gravity experienced by the quadrotor are not influenced by factors such as flight altitude, and taken the thrust in all directions to be directly proportional to the square of the propeller rotation speed. In order to maintain a quadratic relationship of the pitch and roll channels, we also compromise the precision of the yaw channel. However, these simplifications are made with the aim of minimizing any compromise in model accuracy. The algorithm in this paper can operate in real-time on conventional embedded processors, negating the need for specialized hardware or elevated computational resources.

Our simulation encapsulates the principal dynamical characteristics of the quadrotor and environmental factors such as wind disturbances. Despite the fact that simulations cannot fully replicate the intricacies of the real world, we have reason to believe that the results should closely mirror those in practical implementation, given that the model captures the predominant behaviors of the system. We also compare our simulation results with [19], where experimental results were carried out with simple PD control law, and find that the error in position of the proposed method in this paper is significantly smaller than that in their results. In their flight tests where the quadrotor flies at a low speed, the discrepancy between the real experimental results and the simulation outcomes is modest, with the exception of some latency caused by the network link. Therefore, we expect that the actual flight performance of our method in hovering scenarios will also be satisfactory. In sum, we are confident in the accuracy of our simulations, and we believe the proposed approach to be viable in real-world implementations. Naturally, we are in the process of setting up the necessary experimental framework and look forward to sharing our experimental findings in future works. Our ultimate aim is to ensure that the proposed method is not just theoretically sound, but also practically feasible and effective in handling the complexities of real-world scenarios.

7. Conclusions

In conclusion, this paper proposes an online meta-learning-based INDI control method for quadrotors with unknown disturbances. This control framework not only addresses the inaccuracies of the control matrix often found in dynamic environments but also significantly enhances the system’s adaptability and performance. The INDI control technique provides superior tracking performance and robustness against uncertainties and disturbances, which is crucial for the stability of quadrotors. When combined with meta-learning, the controller can leverage prior information from different environments, thus accelerating its ability to adapt to new scenarios. Further, the inclusion of adaptive control for adjusting model parameters enables the system respond more effectively to specific environmental conditions. We also show that the proposed approach can achieve non-asymptotic convergence in certain conditions. The contribution in this paper supports quadrotors to perform a variety of complex tasks, including but not limited to navigation, obstacle avoidance, and payload transport. We plan to conduct experimental studies in the near future to validate our simulation results and enhance the applicability of our framework.The direction of future research is to refine the control framework, ensuring that even under high-speed flight states the quadrotor can maintain strong disturbance rejection capability. Further exploration can focus on the integration of machine learning techniques with other control theories such as active disturbance rejection control [20,21] to elevate the functional performance of the quadrotor system.