Concealed Conduit Routing in Building Slabs
Abstract
:Featured Application
Abstract
1. Introduction
1.1. Methodology Overview
1.2. Related Work
2. Materials and Methods
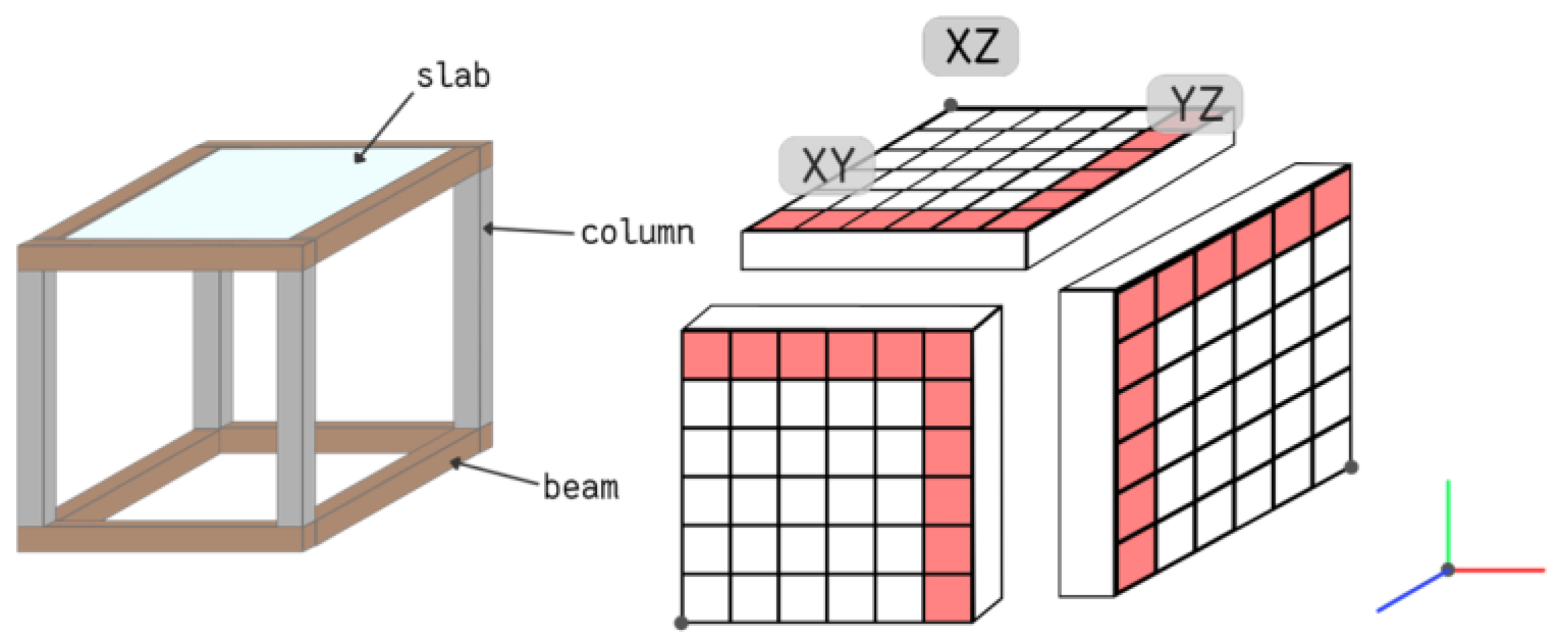
2.1. Workspace Representation
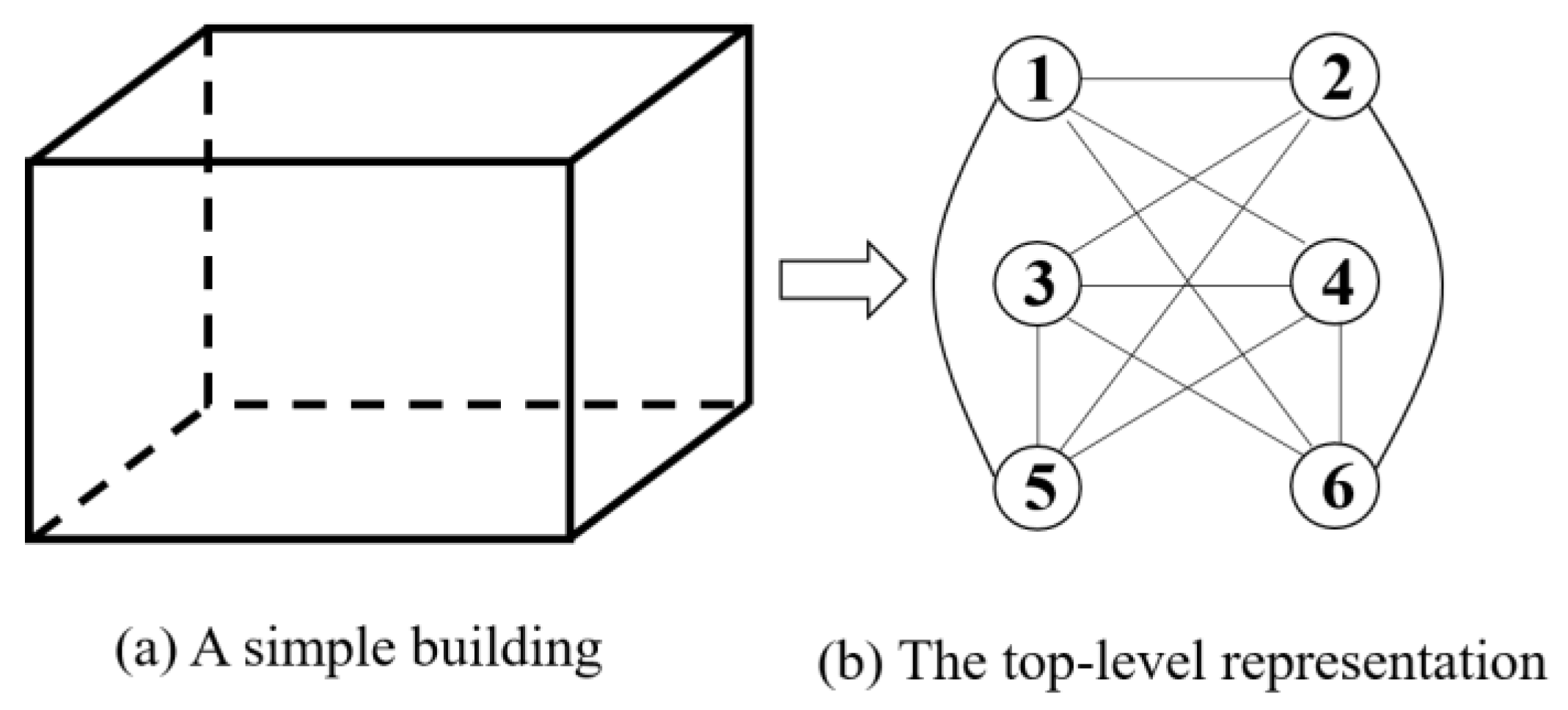
2.1.1. The Top-level Representation
- If S1 and S2 are coplanar, the edge weight is equal to the Manhattan distance between C1 and C2.
- Otherwise, the edge weight is set to 1.5 times the Manhattan distance between C1 and C2.
- Usage and limitation of the top-level representation
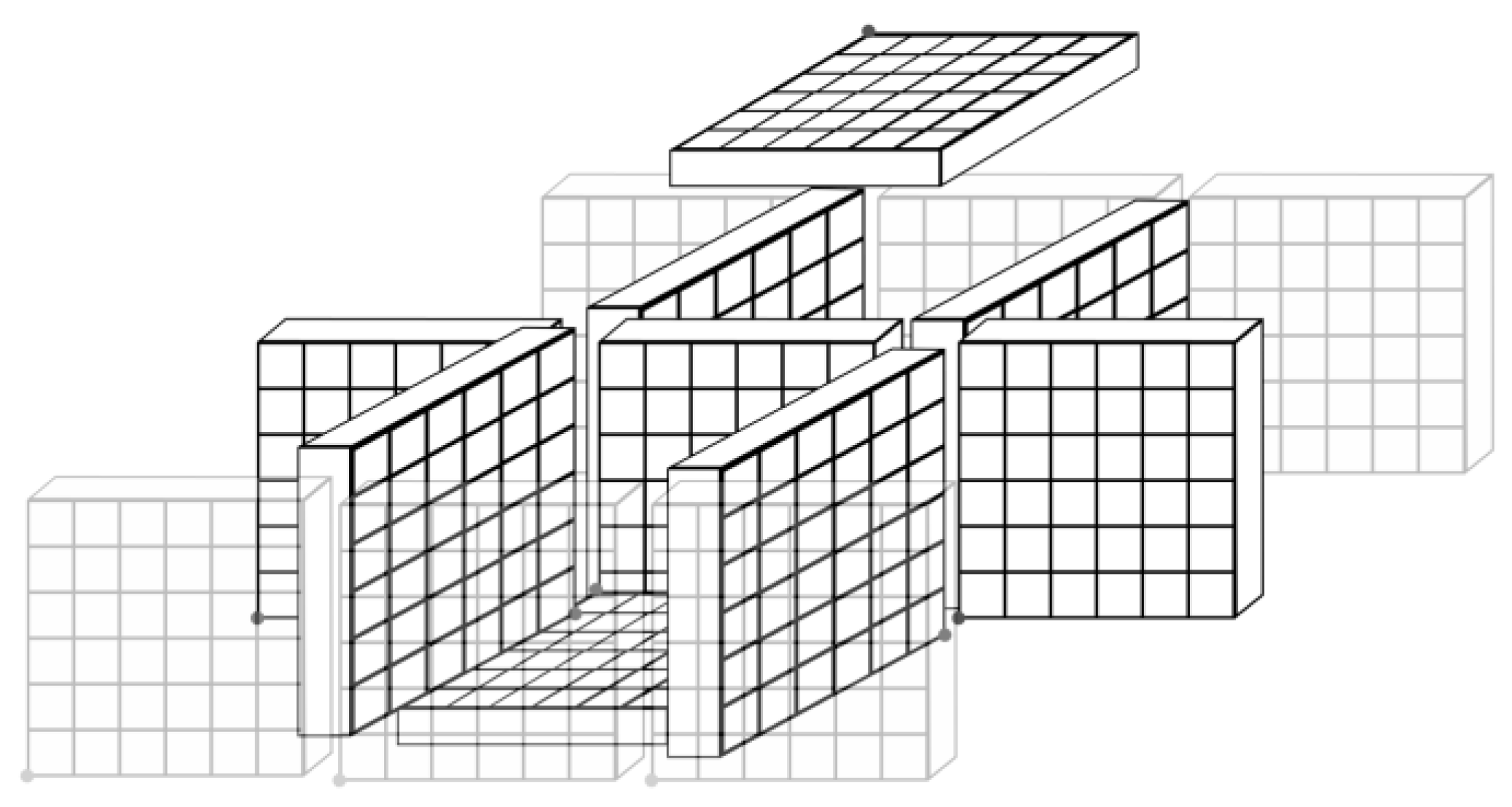
2.1.2. The Bottom-level Representation
- Obstacle voxel labelling
- Distance field computation
- The voxels adjacent to the open space or the obstacle voxels are identified. They form the boundaries of the distance field.
- The distance values in these boundary voxels are set to one-half of the voxel size.
- Then, the distance field is expanded by using a multiple-sweeping method until the distances of all the ordinary voxels have been computed.
- Peeling the slabs
- Bottom-level representation updating
2.2. Pipe Path Routing
2.2.1. Abstract Pipe Path Calculation
- Locate the vertices (slabs) in G, which contain the terminals of this pipe.
- Generate a shortest path to connect these vertices using Dijkstra’s algorithm.
- Duplicate the slabs containing multiple terminals: If a slab contains k terminals (k ≥ 2), the associated vertex is duplicated k times in the shortest path.
- Compute the path length by accumulating the weights of the edges in the shortest path. If the two ends of an edge are the same, its weight is set to one-half of the width of the slab. (We assume that the slab width > the slab height.)
- Output the length and vertices of this shortest path.
2.2.2. Pipe Ordering
2.2.3. Feasible Space Creation
- Usage of the distance field
- Connectivity of the terminals and safety gaps
2.2.4. Pipe Path Computation
- Branch scheduling
- Cost function of path-finding
2.2.5. Pipe Surface Generation and Workspace Update
3. Results
3.1. Implementation Issues
3.2. Methodology
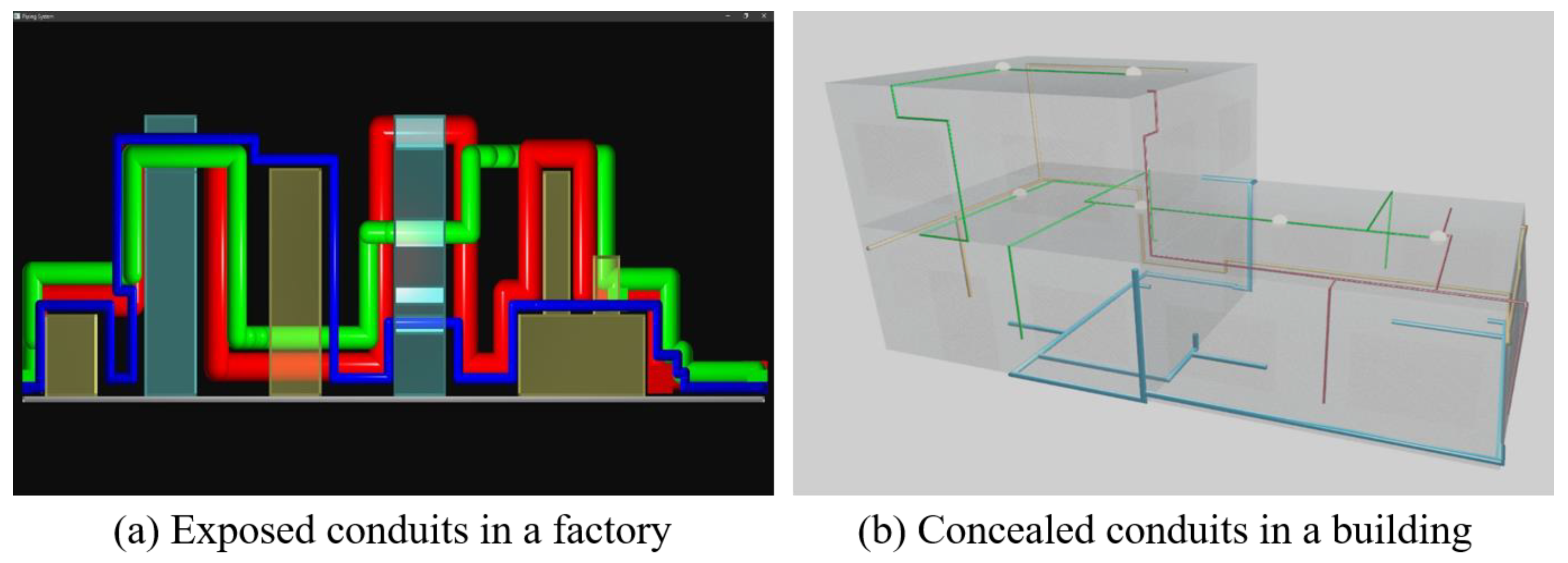
3.3. Test Case 1
3.4. Test Case 2
3.5. Quantitative Data of the Tests
4. Discussion and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, X.L.; Ren, T.; Wang, C.E. A Survey of pipe routing design. In Proceedings of the Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008; pp. 3994–3998. [Google Scholar]
- Lee, C.Y. An algorithm for path connections and its applications. IRE Trans. Electron. Comput. 1961, 3, 346–365. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; Choi, T.; Kwon, T.; Lee, T.H.; Lee, K. Automatic design system for generating routing layout of tubes, hoses, and cable harnesses in a commercial truck. J. Comput. Des. Eng. 2021, 8, 1098–1114. [Google Scholar] [CrossRef]
- Ueng, S.K.; Huang, H.K. A distance-field-based pipe-routing method. Materials 2022, 15, 5376. [Google Scholar] [CrossRef] [PubMed]
- Asmara, A.; Nienhuis, U. Automatic piping system in ship. In Proceedings of the International Conference on Computer and IT Application (COMPIT), Leiden, The Netherlands, 8–10 May 2006; pp. 269–280. [Google Scholar]
- Choi, W.; Kim, C.; Heo, S.; Na, S. The modification of A* pathfinding algorithm for building mechanical, electronic and plumbing (MEP) path. IEEE Access 2022, 10, 65784–65800. [Google Scholar] [CrossRef]
- Gao, H.; Koch, C.; Wu, Y. Building information modelling based building energy modelling: A review. Appl. Energy 2019, 238, 320–343. [Google Scholar] [CrossRef]
- Xie, H.; Tramel, J.M.; Shi, W. Building information modeling and simulation for the mechanical, electrical, and plumbing systems. In Proceedings of the IEEE International Conference on Computer Science and Automation Engineering, Shanghai, China, 10–12 June 2011; pp. 77–80. [Google Scholar]
- Horowitz, E.; Sahni, S.S.; Rajasekaran, S. Computer Algorithm; Computer Science Press: New York, NY, USA, 1998. [Google Scholar]
- Qu, Y.F.; Jiang, D.; Zhang, X.L. A new pipe routing approach for aero-engines by octree modeling and modified max-min ant system optimization algorithm. J. Mech. 2018, 34, 11–19. [Google Scholar] [CrossRef]
- Ito, T. A genetic algorithm approach to piping route path planning. J. Intell. Manuf. 1999, 10, 103–114. [Google Scholar] [CrossRef]
- Kang, S.S.; Sehyun, M.; Hah, S.H. A design expert system for auto-routing of ship pipes. J. Ship Prod. 1999, 15, 1–9. [Google Scholar] [CrossRef]
- Christodoulou, S.E.; Ellinas, G. Pipe routing through ant colony optimization. J. Infrastruct. Syst. 2010, 16, 149–159. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, J.; Al-Hussein, M.; Yin, X. BIM-based automated design of drainage systems for panelized residential buildings. Int. J. Constr. Manag. 2022, 1–16. [Google Scholar] [CrossRef]
- Samarasinghe, T.; Gunawardena, T.; Mendis, P.; Sofi, M.; Aye, L. Dependency Structure Matrix and Hierarchical Clustering based algorithm for optimum module identification in MEP systems. Autom. Constr. 2019, 104, 153–178. [Google Scholar] [CrossRef]
- Farooq, J.; Sharma, P. Applications of Building Information Modeling in Electrical Systems Design. J. Eng. Sci. Technol. Rev. 2017, 10, 119–128. [Google Scholar] [CrossRef]
- Teo, Y.H.; Yap, J.H.; An, H.; Yu, S.C.M.; Zhang, L.; Chang, J.; Cheong, K.H. Enhancing the MEP Coordination Process with BIM Technology and Management Strategies. Sensors 2022, 22, 4936. [Google Scholar] [CrossRef] [PubMed]
- Yue, Y.; Liu, Z.; Zuo, X. Integral layout optimization of subsea production control system considering three-dimensional space constraint. Processes 2021, 9, 1947. [Google Scholar] [CrossRef]
- Liu, M.Y.; Tuzel, O.; Veeraraghavan, A.; Chellappa, R. Fast directional chamfer matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1696–1703. [Google Scholar]
- Sethian, J.A. Fast marching methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
- Ueng, S.K.; Huang, H.C.; Chou, C.S.; Huang, H.K. Layered manufacturing for medical imaging data. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Kaufman, A.; Dachille, F.; Chen, B.; Bitter, I.; Kreeger, K.; Zhang, N.; Tang, Q. Real-time volume rendering. Int. J. Imaging Syst. Technol. 2000, 11, 44–52. [Google Scholar] [CrossRef]
- Tay, Y.W.D.; Panda, B.; Paul, S.C.; Noor Mohamed, N.A.; Tan, M.J.; Leong, K.F. 3D printing trends in building and construction industry: A review. Virtual Phys. Prototyp. 2017, 12, 261–276. [Google Scholar] [CrossRef]
- Szabó, L. Survey on applying 3D printing in manufacturing the cooling systems of electrical machines. In Proceedings of the 2022 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 19–21 May 2022; pp. 1–6. [Google Scholar]


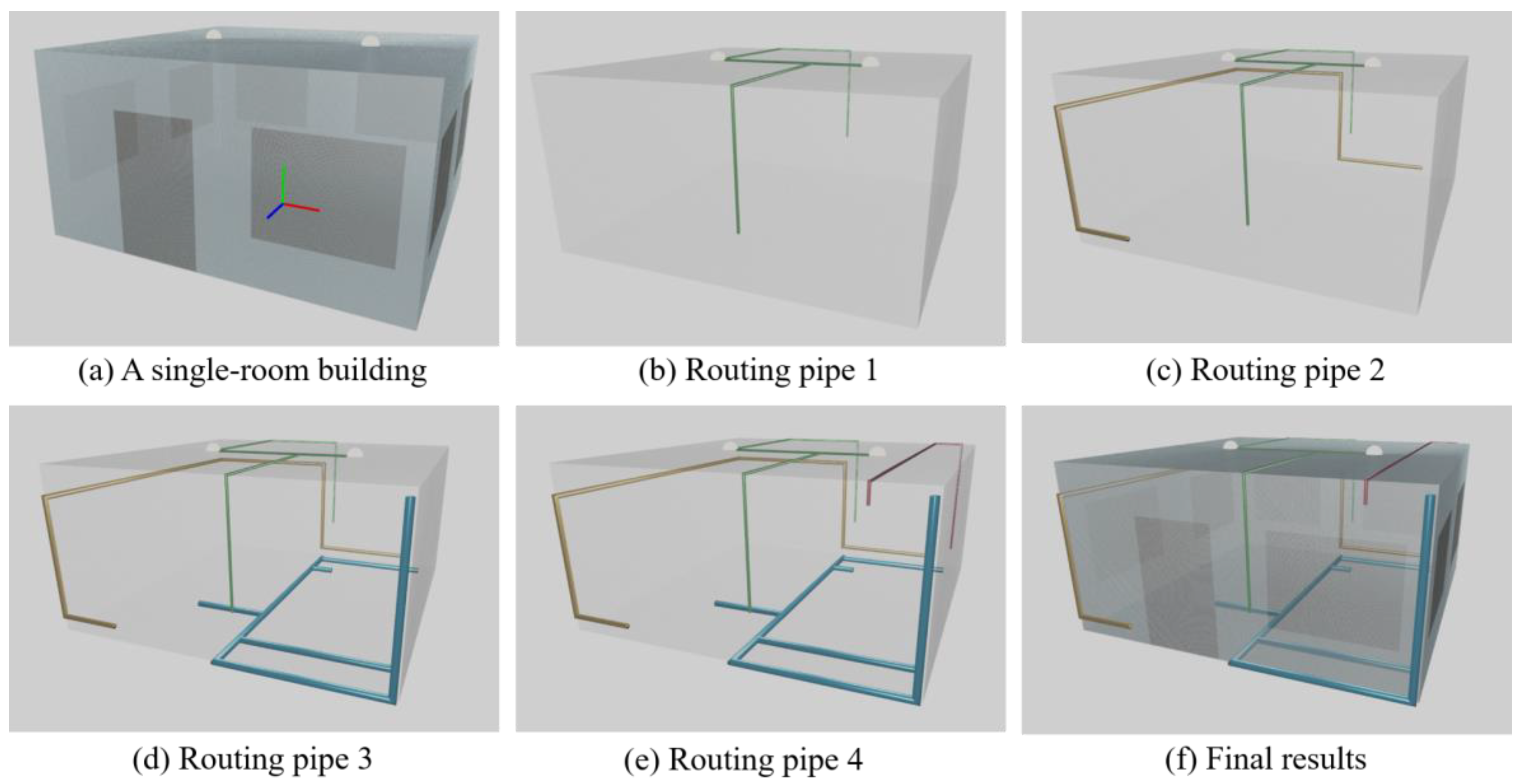
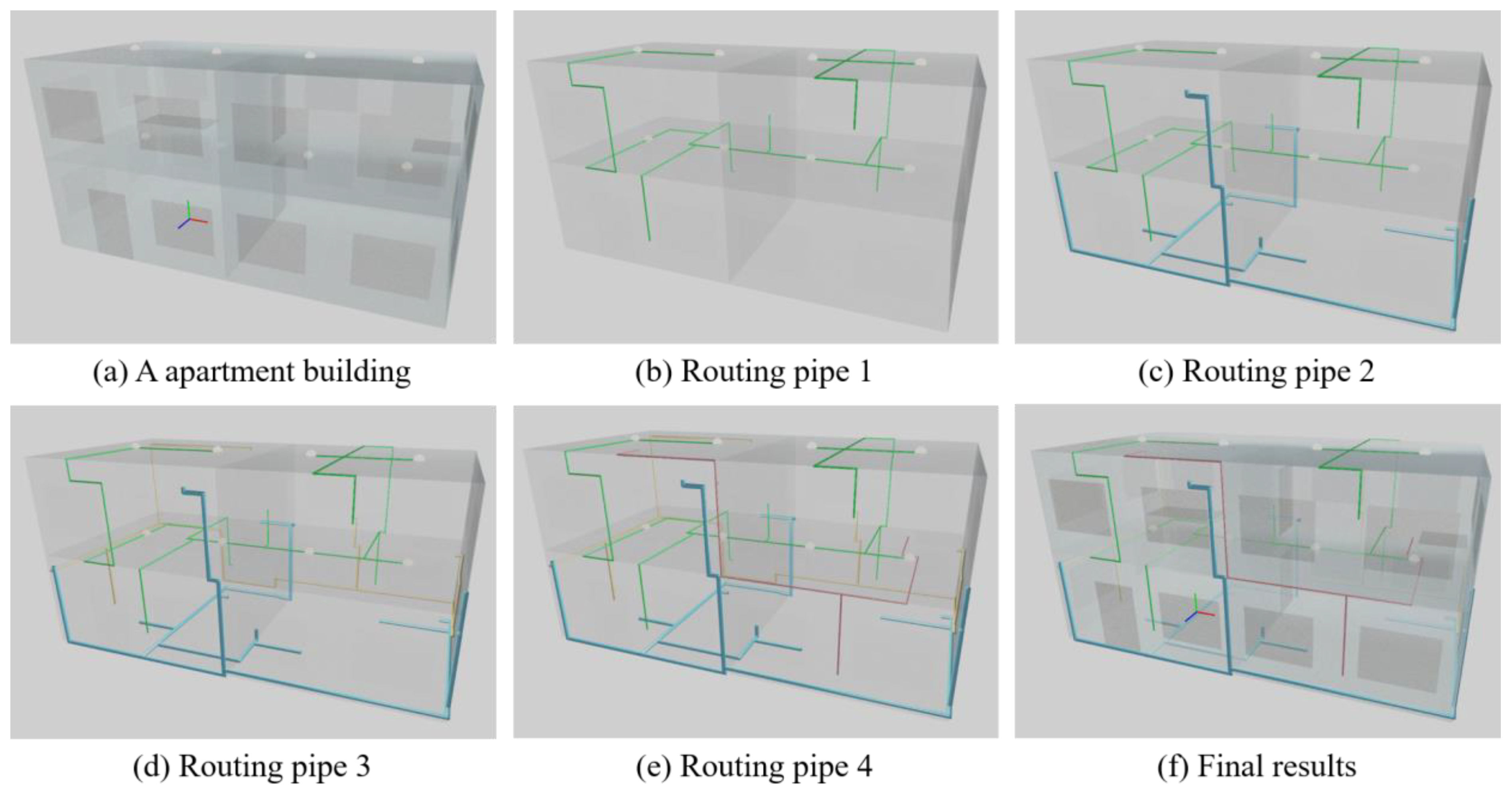
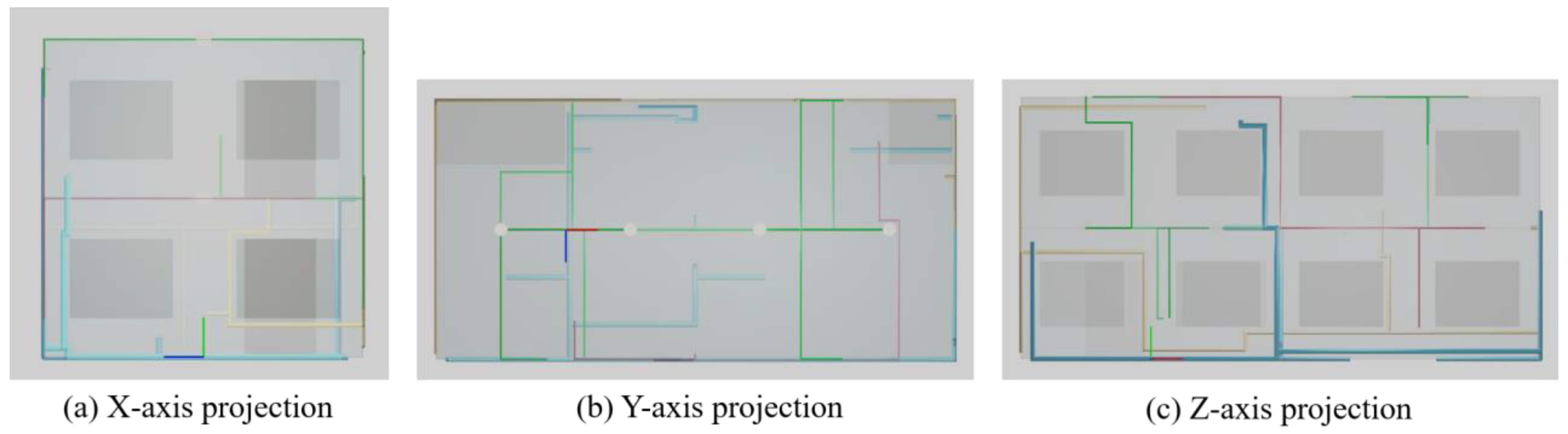
| Dimension | Slabs | Opening |
|---|---|---|
| Width = 8 m, Length = 8 m, Height = 4 m | 4 walls (8 m × 4 m), 1 floor (8 m × 8 m), 1 ceiling (8 m × 8 m) | 1 door (1.8 m × 3 m), 7 windows (2 m × 2.6 m) |
| Pipe | #(Terminals) | Diameter | Usage | Safe Gap | Color |
|---|---|---|---|---|---|
| 1 | 4 | 3 cm | Electricity | 20 cm | Green |
| 2 | 3 | 6 cm | Natural gas | 10 cm | Orange |
| 3 | 6 | 8 cm | Water | 5 cm | Blue |
| 4 | 2 | 3 cm | Air | 2 cm | Red |
| Components/Dimensions | Slabs | Opening |
|---|---|---|
| Apartment of 2 units, 2 stories in 1 unit, Width = 16 m, Length = 16 m, Height = 8 m, 4 rooms. | 20 slabs: 14 (8 m × 4 m) walls, 4 (8 m × 8 m) floors, 2 (8 m × 8 m) ceilings. Slab thickness = 30 cm. | 3 (1.8 m × 3 m) doors: 2 doors in 1st floor, 1 door in the 2nd floor. 23 (2 m × 2.6 m) windows: 11 windows in the 1st floor, 12 windows in the 2nd floor. 2 (4 m × 2 m) staircase openings, 1 opening in each unit. |
| Pipe | #(Terminals) | Diameter | Usage | Safe Gap | Color |
|---|---|---|---|---|---|
| 1 | 18 | 3 cm | Electricity | 20 cm | Green |
| 2 | 15 | 6 cm | Natural gas | 10 cm | Orange |
| 3 | 8 | 8 cm | Water | 5 cm | Blue |
| 4 | 4 | 3 cm | Air | 2 cm | Red |
| Pipe | Test 1 | Test 2 | ||||
|---|---|---|---|---|---|---|
| #(Terminals) | Length (m) | Cost (sec.) | #(Terminals) | Length (m) | Cost (sec.) | |
| 1 | 4 | 19.92 | 2.59 | 18 | 75.53 | 13.83 |
| 2 | 3 | 22.30 | 1.30 | 15 | 54.68 | 10.37 |
| 3 | 6 | 25.00 | 3.15 | 8 | 72.42 | 19.69 |
| 4 | 2 | 12.56 | 0.40 | 4 | 25.78 | 2.20 |
| Researches | Routing Algorithms | Data Structures | Working Environment | Applications |
|---|---|---|---|---|
| Kim et al. [3] | Genetic algorithm | Graph | Vehicles | Cables & pipes of vehicles |
| Choi et al. [6] | A* method | Graph | Buildings | MEB systems |
| Qu et al. [10] | ACO algorithm | Octree | Engine surfaces | Aero-engine pipes |
| Kang et al. [12] | Expert system | Graph | Ships | Pipes of ships |
| Christodoulou [15] | ACO algorithm | Graph | Communities | Water supply systems |
| Ours | Two-stage Dijkstra method | Graph + 3D voxel images | Building slabs | MEB systems |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ueng, S.-K.; Chang, C.-C. Concealed Conduit Routing in Building Slabs. Appl. Sci. 2023, 13, 10847. https://doi.org/10.3390/app131910847
Ueng S-K, Chang C-C. Concealed Conduit Routing in Building Slabs. Applied Sciences. 2023; 13(19):10847. https://doi.org/10.3390/app131910847
Chicago/Turabian StyleUeng, Shyh-Kuang, and Chun-Chieh Chang. 2023. "Concealed Conduit Routing in Building Slabs" Applied Sciences 13, no. 19: 10847. https://doi.org/10.3390/app131910847
APA StyleUeng, S.-K., & Chang, C.-C. (2023). Concealed Conduit Routing in Building Slabs. Applied Sciences, 13(19), 10847. https://doi.org/10.3390/app131910847





