PHCNet: Pyramid Hierarchical-Convolution-Based U-Net for Crack Detection with Mixed Global Attention Module and Edge Feature Extractor

Abstract

Crack detection plays a vital role in concrete surface maintenance. Deep-learning-based methods have achieved state-of-the-art results. However, these methods have some drawbacks. Firstly, a single-sized convolutional kernel in crack image segmentation tasks may result in feature information loss for small cracks. Secondly, only using linear interpolation or up-sampling to restore high-resolution features does not restore global information. Thirdly, these models are limited to learning edge features, causing edge feature information loss. Finally, various stains interfere with crack feature extraction. To solve these problems, a pyramid hierarchical convolution module (PHCM) is proposed by us to extract the features of cracks with different sizes. Furthermore, a mixed global attention module (MGAM) was used to fuse global feature information. Furthermore, an edge feature extractor module (EFEM) was designed by us to learn the edge features of cracks. In addition, a supplementary attention module (SAM) was used to resolv interference in stains in crack images. Finally, a pyramid hierarchical-convolution-based U-Net (PHCNet) with MGAM, EFEM, and SAM is proposed. The experimental results show that our PHCNet achieves accuracies of 0.929, 0.823, 0.989, and 0.801 on the Cracktree200, CRACK500, CFD, and OAD_CRACK datasets, respectively, which is higher than that of the traditional convolutional models.

1. Introduction

Concrete is an indispensable product in human society [1]. At present, most human buildings and bridges are made of concrete. However, with the increase in usage time or the impact of geological disasters, various cracks of varying sizes may appear on the surface of concrete, posing a safety hazard to buildings and bridges. Therefore, it is necessary to conduct crack detection on the surface of concrete in order to immediately repair these cracks. Usually, traditional methods involve manual detection, but these methods are time-consuming and labor-intensive. Thus, with the development of computer image processing technology, researchers have proposed using image detection methods for concrete crack detection.

Traditional computer image processing technology for detecting concrete cracks usually consists of the following steps: (1) using image detection vehicles to take photos of the concrete surface and collect images of the concrete to be tested; (2) using digital filters to extract crack features from concrete images, such as Sobel filters [2], Canny filters [3], or manually designed filters; (3) performing binarization on the extracted edge features to obtain the binary pixels of the crack area; (4) comparing the binary pixels of the crack area with the standard sample to evaluate the severity of the crack. However, this kind of method largely relies on handcrafted features extracted by the designed digital filters, and it is hard to design a perfect filter for crack feature extraction.

With the development of deep learning, image processing techniques based on deep learning have been widely applied in the fields of image classification, object detection, and image segmentation, and have achieved great results. The reason for this is that deep-learning-based methods can automatically extract features from images. Therefore, researchers have begun to apply these methods to concrete crack detection tasks. For example, the FCN [4] model was proposed by Wei for crack detection. In his model, a fully convolutional CNN was used as a crack feature extractor. This structure was able to extract high-level features and encode these features through hierarchical convolution. Then, the encoded features were restored with up-sampling layers. Finally, softmax [5] was used to calculate the category information of each pixel in crack images. However, the edge of the segmentation results generated by the FCN was not very smooth. To solve this problem, Cao [6] proposed using conditional random field (CRF) to improve the results. The CRF method is a graph model that can perform “smooth” segmentation based on the pixel intensity of the image. In CRF, points with similar pixel intensities are labeled as the same category. Thus, CRF could make the edge of the segmentation results smoother. Based on the methods proposed above, Fu [7] designed a DeepLab model to process the crack detection task for the purpose of expanding the receptive field of the model. In his design, cascaded expansion convolution was used to expand the receptive field. On the basis of DeepLab, Zhang [8] proposed a U-Net model. In U-Net, the feature encoder and decoder adopt a U-shaped symmetry structure, which is effective in the restoration of high-level features. In addition, skip connections were also used in the U-Net model, which can fuse features of the corresponding layers of the feature encoder and the feature decoder.

However, extension models based on U-Net above some obvious drawbacks:

(1)

Firstly, due to the varying shapes and sizes of cracks, using a single-sized convolutional kernel in crack image segmentation tasks may result in feature information loss for small cracks;

(2)

Secondly, these models only use linear interpolation and up-sampling operations to restore high-resolution features, and do not restore global information;

(3)

Thirdly, due to the variable shape of crack features, the accuracy of the model largely depends on the effectiveness of edge feature extraction. Therefore, it is necessary to strengthen the network’s ability to extract edge feature information. These models do not have a specialized structure to increase the model’s ability to learn edge features, which could cause some edge information loss;

(4)

Finally, various stains in crack images would interfere with the crack feature extraction, causing some crack areas to be ignored. The present methods often fuse output features from different layers or use attention mechanisms to solve this problem. However, as the characteristics of stains vary greatly, these methods cannot effectively solve the issue.

In this paper, a pyramid hierarchical convolution module (PHCM) is proposed by us to extract the features of cracks with different sizes, since PHCM contains series convolution kernels with different sizes. Meanwhile, a mixed global attention module (MGAM) was used to fuse global feature information, guiding the model to restore high-resolution features with global information. Furthermore, an edge feature extractor module (EFEM) was designed by us to learn the edge features of cracks through adding edge detection operators like Sobel, Laplacian, and Canny. In addition, a supplementary attention module (SAM) was used to solve the interference caused by stains in crack images.

The structure of this article is arranged as follows. Section 2 introduces the related works. Section 3 introduces our proposed methods. The model structure of our proposed PCHNet is also described. Additionally, the MGAM, EFEM, and SAM are illustrated in detail. Furthermore, we introduce the Swish activation function and our data augmentation strategies. Section 4 introduces the crack datasets and some experiments, and an analysis of results is presented. Section 5 provides the conclusion to the whole article.

2. Related Works

In this section, we present a brief introduction to related works on crack detection.

Earlier research about pavement detection was usually based on digital signal processing methods. For example, Wang [9] proposed a pavement detection method, which can be divided into following steps: Firstly, a new vehicle for collecting digital highway data was procured and four cameras were mounted at the rear of the vehicle to collect pavement surface images across a 4 m wide pavement. Secondly, the Direct Linear Transformation (DLT) method was used to correct camera distortion. Finally, the algorithm-based signal processing method was used to classify the crack area. Zou [10] proposed a probability-map-based crack detection method. In his method, firstly, a geodesic shadow-removal algorithm is used to remove the pavement shadows. Then, a crack probability map is used to enhance the connection between the crack fragments. Finally, a set of crack seeds from the crack probability map are represented by a graph model and used to generate the final result. These methods rely heavily on the manual design of digital filters and special algorithms, as well as on manual experience. They also have limited generalization and can only achieve good results on specific datasets. Thus, researchers began looking for a new approach.

Deep learning technology has been gradually developed since 2012. This technology can automatically extract high-level features from crack images, so there is no need to manually design features. Crack detection based on deep learning mainly focuses on semantic segmentation technology, which is mainly divided into the following categories:

Specialized CNN-based model: Anhtn [11] proposed a two-stage convolutional neural network (CNN) for road crack detection and segmentation in images at the pixel level. In his design, the first stage is to remove noise or artifacts in cracks; then, the second stage is to learn the contextual information of cracks in all detected areas. Lee [12] proposed a semantic segmentation model with an auto-encoder structure. In addition, he proposed a CNN-based image preprocessing model to deal with lighting conditions. However, these models have some common shortcomings: Firstly, the obtained results are still not fine enough, and the up-sampling results are still fuzzy and insensitive to the details in the image. Secondly, each pixel is directly classified without fully considering the relationship between pixels. Spatial feature fusion is neglected, resulting in a lack of spatial consistency.

DeepLab-based model: To solve the problems in these Specialized-CNN-based model. Wang [13] proposed a DeepLabv3+ model for crack detection. In his design, Deeplab v3+ uses the layer-fusing policy to process spatial feature fusion. The use of DeepLab v3+ with different backbones is compared, and the results show that DeepLab v3+ with the ResNet101 backbone could achieve the highest accuracy. Furthermore, Fu [7] introduced a densely connected atrous spatial pyramid pooling module to DeepLabv3+; thus, the network could obtain denser pixel sampling, which could solve the fuzzy segmentation problem. However, these DeepLab-based models have many parameters and require a large amount of calculation, which consumes a lot of training time. Moreover, this kind of model does not adopt the symmetric encoder–decoder structure, which could distort the detail of crack images.

UNet-based model: Based on the models above, researchers decided to improve the drawbacks of DeepLab-based models. Thus, they designed a segmentation model with a symmetric encoder–decoder structure named Unet. Di [14] proposed a UNet model. In his work, he desired to optimize the crack segmentation process through the implementation of a modified U-Net model-based algorithm. Experiments show that the U-Net based models could obtain a higher accuracy than traditional CNN models. In addition, Jiang [15] presented an extended version of the U-Net framework, named MSK-UNet. In his work, firstly, the UNet base model is used as the basic framework to extract hierarchical features. Secondly, he used selective kernel (SK) units to replace convolution blocks in UNet in order to obtain receptive fields with distinct scales. Finally, he used an image pyramid to maintain contextual feature information. However, extension models based on U-Net above have some obvious drawbacks. Firstly, the single-size convolutional kernels in crack image segmentation tasks may result in feature information loss for small cracks. Secondly, using only linear interpolation or up-sampling to restore high-resolution features will not restore global information. Thirdly, these models are limited to learning edge features, causing edge feature information loss. Finally, various stains would lead to interference in crack feature extraction.

Lightweight model: Along with the increase in accuracy for crack segmentation tasks, the computational complexity is also increased. Thus, some researchers decide designed lightweight models. For example, Zhang [16] designed a customized deep learning model architecture named the Efficient Crack Segmentation Neural Network (ECSNet) for accelerated real-time pavement crack detection and segmentation without compromising performance. The experimental results show that his model could obtain a similar performance to UNet, but his model has very low computational complexity. However, the reduction in the computational complexity of the model will always lead to a loss of accuracy. In addition, a large number of inexpensive edge-computing hardware have a quite powerful computing power, so accuracy is more important than speed in crack detection tasks. Therefore, this paper only focuses on improving the accuracy of crack detection.

3. Methods

To illustrate our proposed methods clearly, a list of abbreviations is shown as follows:

PCHNet: Pyramid Hierarchical-Convolution-based U-Net model with Mix Global Attention Module (MGAM), Edge Feature-Extractor Module (EFEM) and Supplementary Attention Module (SAM).

• PHCM: Pyramid Hierarchical Convolution Module.
• MGAM: Mix Global Attention Module.
• SAM: Supplementary Attention Module.
• EFEM: Edge Feature Extractor Module.

3.1. Model Structure

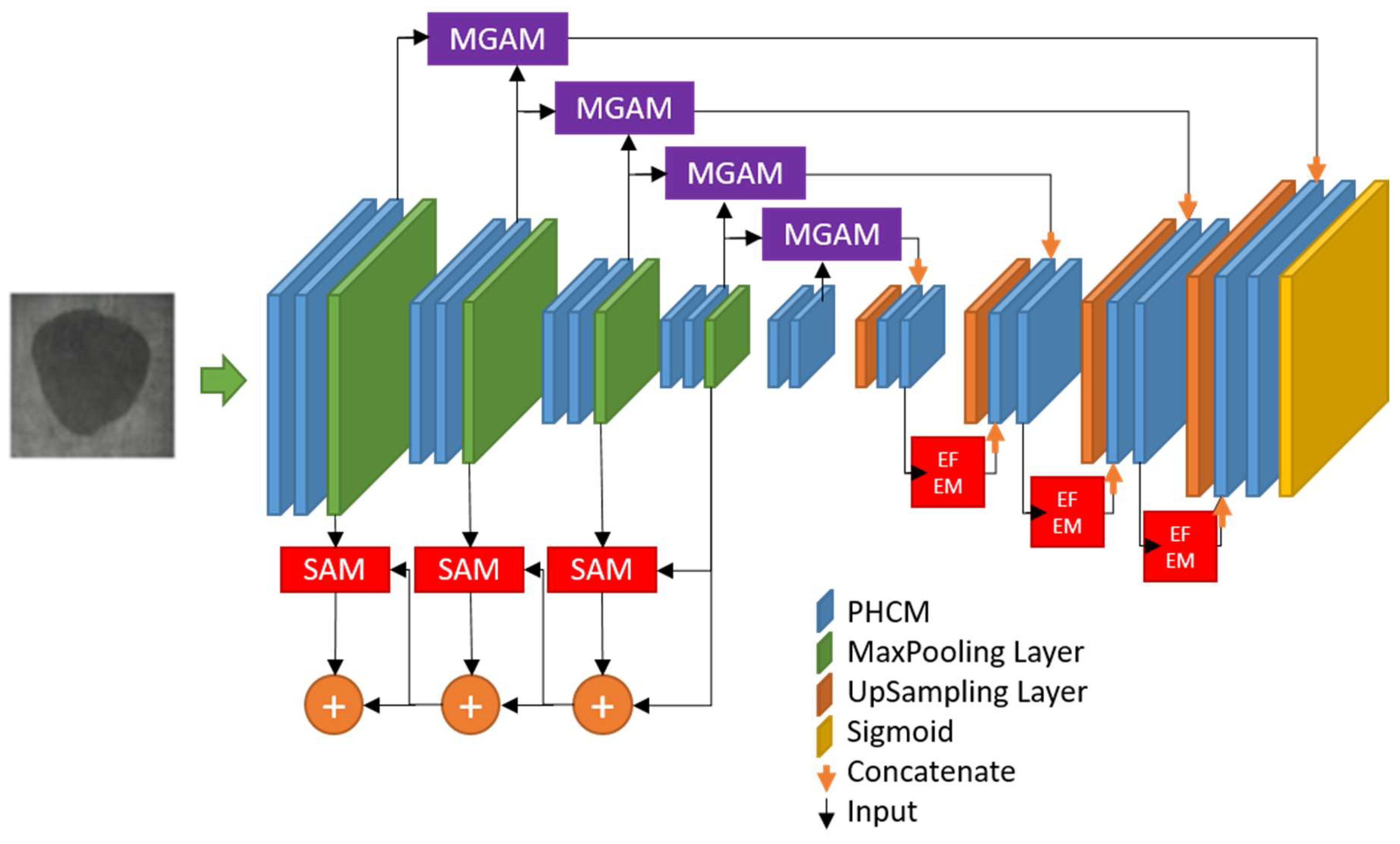
In this paper, we design a Pyramid Hierarchical-Convolution-based U-Net model with a Mix Global Attention Module (MGAM), Edge Feature-Extractor Module (EFEM) and Supplementary Attention Module (SAM), named PHCNet.

As shown in Figure 1, our proposed PHCNet is a fully convolutional neural network. It has a symmetric encoder (left side)–decoder (right side) structure like U-Net. We can see that the encoder includes several Pyramid Hierarchical Convolution Modules (PHCMs) and several max-pooling layers. The decoder also includes several PHCMs and several up-sampling layers. The PHCM is used to simultaneously extract features with different-size convolutions. In addition, several direct connections are used to concatenate feature maps from the encoder to the corresponding features of the decoder for the purpose of feature-fusion between layers. It is noted that feature maps generated from the encoder would input into the Mix Global Attention Module (MGAM) proposed by us before concatenating with the corresponding features of the decoder, since the MGAM is used to fuse global feature information, guiding the model to restore high-resolution features. These feature maps generated from the encoder would also be input into the Supplementary Attention Module (SAM) to solve the interference of various stains in crack images. In addition, the Edge Feature Extractor Module (EFEM) is used to increase the model’s ability to learn the edge features of cracks.

3.2. The Pyramid Hierarchical Convolution Module

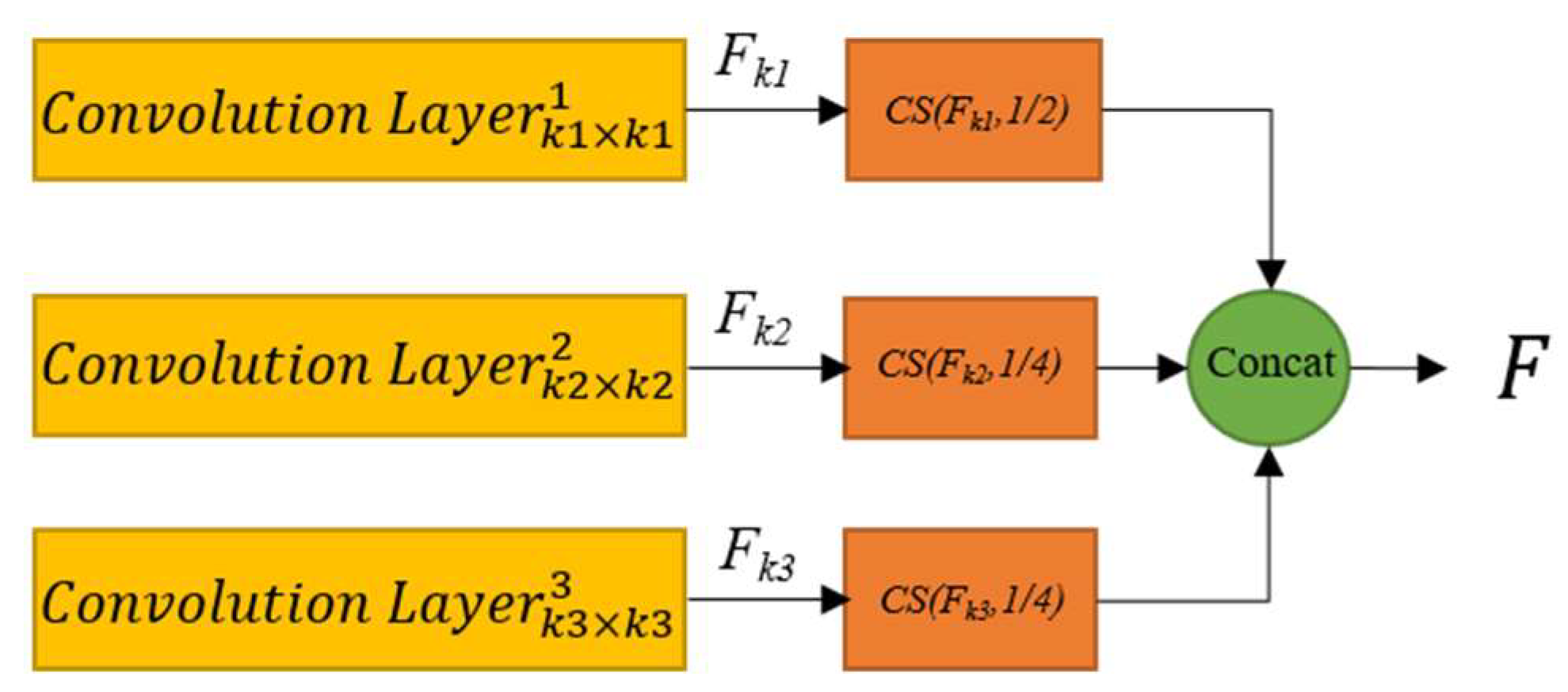
Due to the varying shapes and sizes of cracks, using a single size convolutional kernel in crack image segmentation tasks may result in some details being omitted, ultimately leading to poor performance. Therefore, we propose a Pyramid Hierarchical Convolution Module (PHCM), which contains three convolution layers with different kernel sizes.

As shown in Figure 2, the PHCM module includes three convolution layers with different kernel sizes. These convolution layers are mainly used for multi-scale feature extraction. Firstly the input features are input into these convolution layer. The above process can be expressed as follows:

$$\begin{array}{l}{F}_{k1}=Con{v}_{k1\times k1}^1(x)+b\\ F_{k2}=Con{v}_{k2\times k2}^2(x)+b\\ F_{k3}=Con{v}_{k3\times k3}^3(x)+b\end{array}$$

(1)

where k1, k2 and k3 represent three different convolution kernels with different sizes; F_k1, F_k2, and F_k3 represent the feature maps corresponding to the output of the three convolution layers. Conv() represents the convolution operation and b represents the trainable bias parameter.

Then, we randomly select 1/2 channel feature maps in F_k1, 1/4 channel feature maps in F_k2, and 1/4 channel feature maps in F_k3. After that, we concatenate these selected feature maps and randomly shuffle them. The above process could be expressed as:

$$F=Concatenate(CS(F_{k1},\frac{1}{2}),CS(F_{k2},\frac{1}{4}),CS(F_{k3},\frac{1}{4}))$$

(2)

where Concatenate(x) represents the channel concatenate operation, and CS(x,i) represents the operation of randomly selecting channel feature maps, that is, we randomly select i channel feature maps in x.

Through the above operations, we can see that the PHCM can extract multi-scale crack information without increasing the number of parameters and model complexity, since features generated from PHCM contain features with three kinds of scale.

3.3. The Mix Global Attention Module

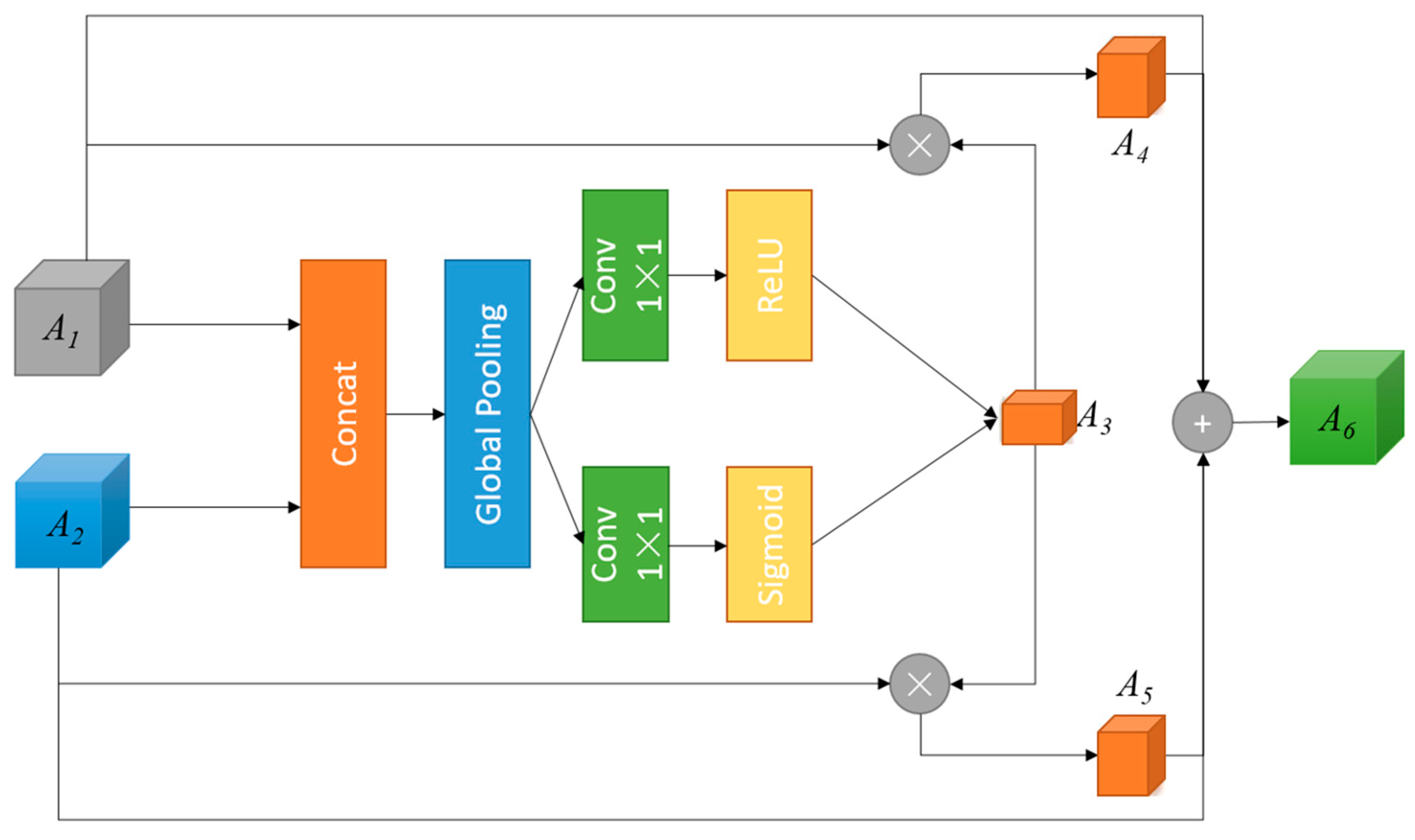
The decoding structure in semantic segmentation tasks is crucial for restoring high-resolution images. However, FCN [17], PSPNet [18], DeepLab v3+ [19] and other models only use linear interpolation or up-sampling operations to restore high-resolution features, without restoring global information. To solve this problem, we propose an efficient attention module based on the mixture of global information, guiding the model to restore high-resolution features, named the Mix Global Attention Module (MGAM), whose structure is shown in Figure 3.

Firstly, MGAM concatenates low-level feature A₁ with high-level feature A₂ to obtain mixed features. Then, the MGAM inputs the mixed features into global pooling to obtain global feature vectors. After that, the global feature vectors are input into the 1 × 1 convolutional layer with the Sigmoid and ReLU activation functions, respectively, obtaining two kinds of channel weight vectors, and these two channel weight vectors are combined to generate the mixed channel weight vector A₃. A₃ is multiplied with low-level feature A₁ and high-level feature A₂ to obtain the weighted feature A₄ and A₅. In addition, in order to obtain abstract features with mixed global information, A₄ and A₅ are added to A₁ and A₂ to obtain the final output A₆. Thus, feature A₆ includes three kinds of features: high-level features, low-level features, and global features. Figure 4 shows the entire process.

3.4. The Edge Feature Extractor Module

Due to the variable shape of crack features, the accuracy of the model largely depends on the effectiveness of edge feature extraction. Therefore, it is necessary to strengthen the network’s ability to extract edge feature information. We considered adding edge detection operators Sobel, Laplacian, and Canny to the network to enhance the image segmentation performance of the model; thus, we designed an Edge Feature Extractor Module (EFEM), which is shown in Figure 4.

In EFEM, the input feature G₁ is input into the convolution layers to obtain the output feature G₂ and G₆. At the same time, G₁ is input into the Sobel operator, Laplacian operator and the Canny operator to extract more detailed edge features: G₃, G₄, G₅. The Sobel operator could calculate the grayscale values of the top, bottom, left, and right pixels for each pixel in the image, and find the extreme value in images to detect edges. The Laplacian operator is a derivative operator, which has rotational invariance and could meet the requirements of edge enhancement of images in different directions. The Canny operator is used to find strong edges in the image and eliminate as much noise as possible. Therefore, by inputting the output features of the convolutional layer into these three edge detection operators, we can enhance the edge feature information of high-level features, thereby enhancing the model’s ability to extract edge feature information. Here, we also assign three adjustable weight parameter to the feature maps output by the three edge detection operators, and this weight parameter could be adjusted during the model training process. Finally, feature G₃, G₄, G₅ are added to feature G₆ to generate the final output G₇. The complete process is as follows:

$$\begin{array}{l}{G}_7=G_6+\alpha G_3+\beta G_4+\gamma G_5\\ G_6=Conv(Conv(G_1))\end{array}$$

(3)

where α, β, γ are the adjustable weight parameters; Conv(x) represents the convolution operation.

3.5. The Supplementary Attention Module

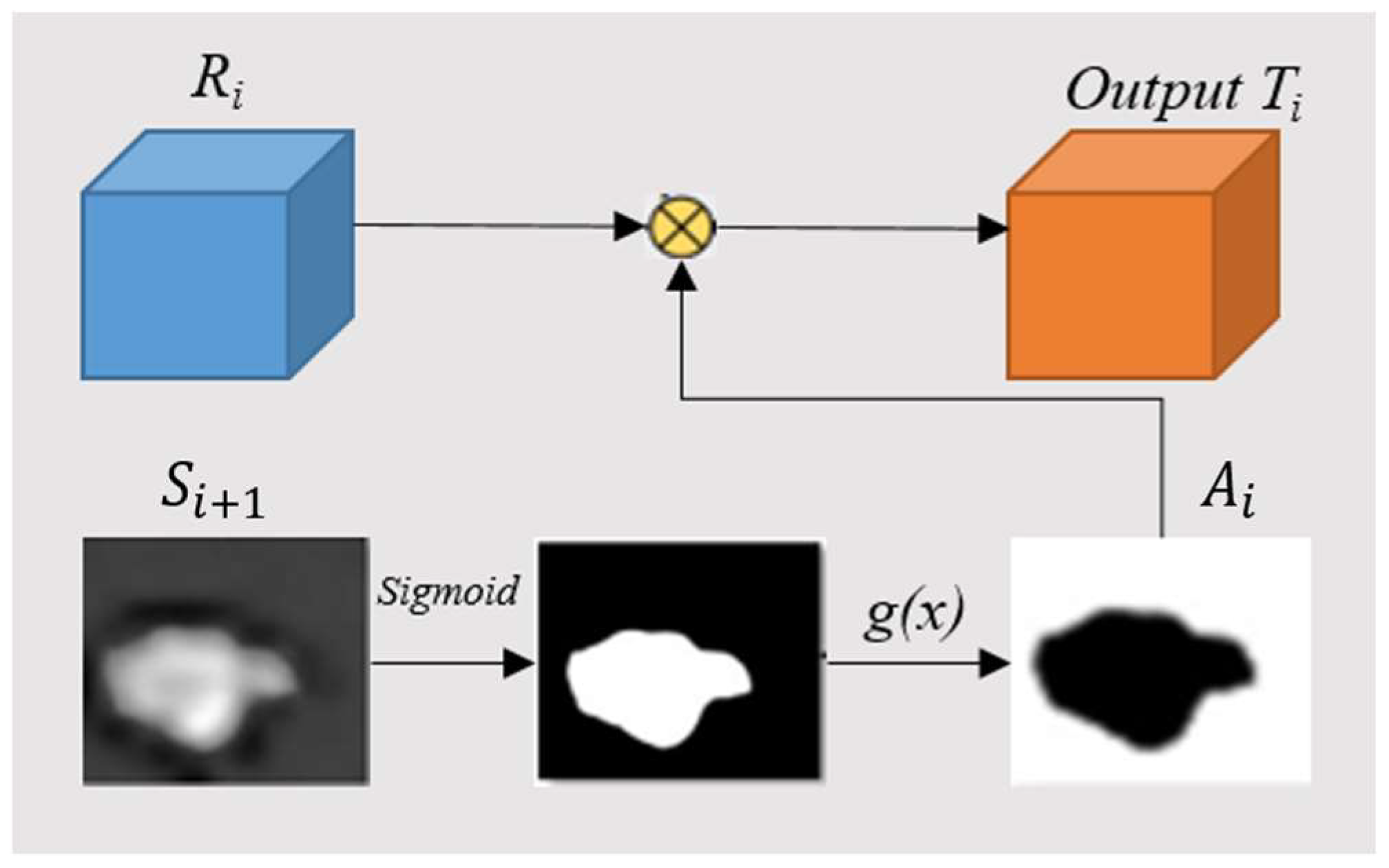
In current crack segmentation tasks, due to the presence of various stains in crack images, these stains cause interference in detailed feature extraction. Thus, some crack areas would be ignored. Present methods often fuse output features from different layers, or use attention mechanisms to solve this problem. However, the characteristics of stains vary greatly; these methods could not effectively solve the issue. Therefore, we propose a strategy to gradually extract the remaining crack features by gradually erasing the extracted crack features. That is, we propose a supplementary attention module (SAM) to remove the crack features that were extracted by the model from the high-level output to compel the model to learn new crack features, allowing for the model to automatically and continuously learn detailed supplementary features.

Specifically, we use an attention map A_i to filter the high-level features R_i continuously; it is noted that A_i is used to reverse feature maps for the purpose of removing the crack areas that were already calculated by the model. This process is shown as follows.

$$\begin{array}{l}{T}_i=R_i\odot A_i\\ A_i=g(sigmoid(up(S_{i+1})))\end{array}$$

(4)

where up(x) represents the up-sampling operation, while g(x) represents the reverse operation. S_i+1 represents the output from the following SAM, represents the multiply operation. Figure 5 shows the details of this process. It is encouraging to see that the model with SAM could ultimately refine imprecise and rough features into accurate and complete high-level features.

3.6. The Swish Activation Function

In the deep learning neural networks, the activation functions could transform linear transformations into nonlinear transformations. Current general activation functions include Sigmoid [20], Tanh [21] and ReLU [22]. The Sigmoid activation function is a common S-type function. Because of its single-increment properties, the Sigmoid activation function is often used as the activation function of neural networks, mapping the output into a value of 0–1. However, the Sigmoid activation function has some drawbacks. Firstly, it has the problem of gradient disappearance. Secondly, the computational complexity of the Sigmoid activation function is relatively high [23]. To solve the above problems, researchers designed the ReLU activation function. Due to the lack of complex mathematical operations, the computational complexity of ReLU is very low. Therefore, a network with ReLU can spend less time on training or prediction. It does not have a gradient-vanishing problem because it is an unbounded function on the positive half-axis. In addition, it could make the network sparser, since all negative parts of the ReLU function are not activated. However, this processing would cause feature information loss, as it drops all negative inputs. To solve the above problems, Google proposed a new activation function named Swish [24], whose original formula is:

$$f(x)=x\cdot sigmoid (x)$$

(5)

The formula of the deformed Swish-B activation function is:

$$f(x)=x\cdot sigmoid (b\cdot x)$$

(6)

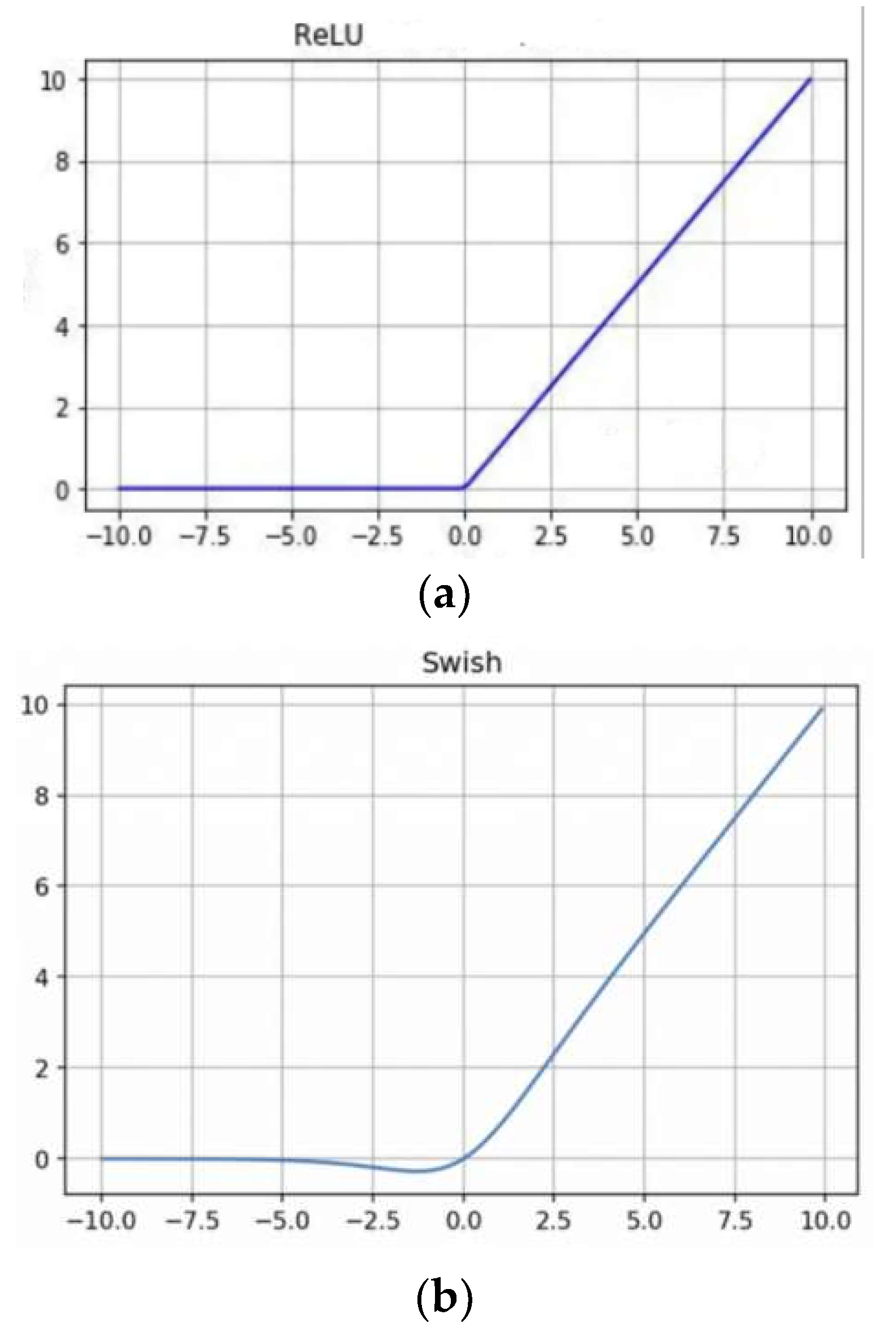
Figure 6 shows a comparison of the ReLU and Swish activation functions.

It could be seen that the Swish [24] function is similar to ReLU, the only difference is that the negative part of the ReLU is 0, while Swish has a small compressed output that retains some negative feature information. Thus, we decided to use the Swish activation function as a substitution of ReLU activation function in our proposed model.

3.7. Data Augmentation

Data augmentation could be effectively used to train the deep learning models in some applications. Generally, some of the simple transformations applied to the image of data augmentation are geometric transformations such as flipping, rotation, translation, cropping and scaling. Here, we use rotation and translation for our data augmentation strategies.

Angle Rotation: Traditionally, angle rotation is used to augment training datasets through rotating images into different angles. Usually, because crack images are invariant to random rotation, we rotate all images at the degree angle of 10, 30, 60, 90, 110, 140, 170 to generate new images.

Image Cropping: Generally, the image cropping method amplifies training datasets through cropping images. Usually, since crack images do not have regular shapes, we chose to randomly crop and recombine all images of the training datasets.

4. Datasets

In order to evaluate our proposed method, we tested our method on four datasets: the Cracktree200 dataset [25], the CFD dataset [26], the Crack500 dataset [27] and the OAD_CRACK dataset. Detailed descriptions of these datasets are provided as follows.

The Cracktree200 dataset: the Cracktree200 dataset is mainly collected on road pavement. This dataset is a visible light dataset containing various kinds of cracks in complex interference environments such as shadow, occlusion, low contrast, noise and other forms of interference. It contains 206 crack images of size 800 × 600. For the Cracktree200 dataset, 80% of the images are used for training and 20% of the images are used for testing.

The CFD dataset: The CFD dataset consists of 118 images of the size 480 × 320 pixels. Each image has manually labeled crack contours. The device used to acquire the images is an iPhone5 with a focus of 4mm, aperture of f/2.4 and exposure time of 1/135 s. For the CFD dataset, 80% of the images are used for training and 20% of the images are used for testing.

The Crack500 dataset: The Crack500 dataset is a pavement crack dataset including 3368 images captured by a cell phone on the main road of Temple University, which has the size of 1440 × 2560 or 2560 × 1440. This dataset was divided into a training dataset and testing dataset by the author. There are 1896 images in the training dataset and 1124 images in the testing dataset.

The OAD_CRACK dataset: Since there are too few crack images in the public datasets above, we collected a dataset by ourselves, named the OAD_CRACK dataset. This dataset has 5000 images with a 1920× 1080-pixel resolution. All images were taken by us with Huawei P30. Some sample images of the OAD_CRACK dataset are shown in Figure 7:

In this dataset, crack images were taken in Shenzhen, and ae divided into four classes: linear crack, circular crack, void and background. All images are manually annotated by the EISeg (an image segmentation labeling tool provided by Baidu) and labeled as 0, 1, 2, 3 respectively. For the purpose of preventing the over-fitting problem during the training process, these images were transformed with light and shadow to create more varied training data. Through this transformation, the whole dataset was extended into 30,000 images. Finally, we divided the whole dataset into two parts: 70% of the images were used for training and 30% of the images were used for testing.

5. Results and Discussion

5.1. Experimental Setup

In our experiment, firstly, the training images are normalized and augmented. Then, these images are input into our proposed PHCNet. In the PHCNet, we set the number of convolution filters in the encoder to 64, 64, 128, 128, 256, 256, 512, 512, 1024, and 1024, respectively, and we set the number of convolution filters in the decoder to 512, 512, 256, 256, 128, 128, 64, and 64, respectively. In the PHCM, the size of the filters in three convolution layers was set to 3 × 3, 5 × 5, 7 × 7, respectively. In addition, the Swish activation function was used in all convolution layers. A Stochastic Gradient Descent [25] (SGD) optimizer was used to train the PHCNet.

We used the accuracy as the evaluation criterion for our experiment. The definition of accuracy is the number of correct samples divided by the number of samples in the test datasets. The formula can be expressed as follows:

$$Acc=\frac{TP+TN}{S_{All}}$$

(7)

where Acc represents the accuracy criterion, TP represents the number of correctly identified positive samples, TN represents the number of correctly identified negative samples, and S_All represents the number of samples in the test datasets.

5.2. Comparison with the State-of-the-Art Methods

In order to evaluate the performance of our proposed PHCNet, we conducted an experiment. We used segmentation accuracy as the main indicator. For the purpose of demonstrating the effectiveness of our proposed model, we used several mainstream crack detection methods as our baseline.

Before our comparison, we provide some relevant explanations for these mainstream algorithms:

FCN [28]: a fully convolutional neural network.

ConvNet [29]: a deep convolutional neural network.

Split-Attention Network [30]: a channel-wise attention-based network.

Cascaded Attention DenseU-Net [31]: an attention-based network with global attention and core attention.

ECA-Net [32]: a lightweight-channel attention-based convolutional neural network.

DWTA-U-Net [33]: a U-Net based network with discrete wavelet-transformed image features.

U-Net proposed by Di without pretrained model [14]: a U-Net-based network proposed by Alessandro that was not pretrained with ImageNet. In order to make a fair comparison, the ResNet backbone of this model is not pre-trained by ImageNet.

Two-stage-CNN [34]: a two-stage CNN proposed by Nhung.

As shown in

Table 1. Comparison with the state-of-the-art methods.

Methods	Cracktree200	CRACK500	CFD	OAD_CRACK
CrackForest [35]	0.08	0.199	0.104	0.08
SVM [36]	0.382	0.418	0.32	0.215
FCN [28]	0.39	0.513	0.585	0.416
ConvNet [29]	0.471	0.591	0.579	0.422
U-Net by Jenkins [37]	0.75	0.681	0.851	0.681
U-Net by Nguyen [38]	0.763	0.695	0.856	0.683
Split-Attention Network [30]	0.851	0.73	0.963	0.696
Cascaded Attention DenseU-Net [31]	0.863	0.74	0.97	0.695
ECA-Net [32]	0.885	0.753	0.971	0.711
DWTA-U-Net [33]	0.90	0.77	0.973	0.729
U-Net proposed by Di without pretrained model [14]	0.791	0.732	0.887	0.715
Two-stage-CNN [34]	0.892	0.79	0.981	0.735
PHCNet	0.929	0.823	0.989	0.801

, compared with the mainstream extended U-Net models, (DWTA-U-Net, ECA-Net, Cascaded Attention DenseU-Net, Split-Attention Network, Alessandro-U-Net without pretrained model, two-stage-CNN), our proposed PCHNet could achieve much better segmentation accuracy on the four public datasets. This strongly proves the effectiveness of our proposed model.

Specifically, the Pyramid Hierarchical Convolution Module (PHCM) could extract features of cracks of different sizes since PHCM contains a series of convolution kernels with different sizes. Thus, the features extracted by PHCM could adapt varying shapes and sizes of cracks. Also, PHCM can extract multi-scale crack information without increasing the number of parameters and model complexity. Additionally, the Mix Global Attention Module (MGAM) is used to fuse global feature information, guiding the model in the restoration of high-resolution features with global information. Furthermore, the Edge Feature Extractor Module (EFEM) could learn the edge features of cracks by adding edge-detection operators Sobel, Laplacian, and Canny. Since these operators could provide a multi-view of edge features in our model. In addition, the Supplementary Attention Module (SAM) could solve the interference caused by stains in crack images, since it could continuously remove the crack features that have already been extracted by the model from the high-level output to compel the model to learn new crack features, allowing for the model to automatically and continuously learn supplementary detailed features.

Compared with the U-Net model, attention-based models such as ECA-Net, Cascaded Attention DenseU-Net, Split-Attention Network, DWTA-U-Net could achieve a better performance, since these models use attention block to decrease the interference caused by shadow and light. Compared with fully convolution neural networks such as FCN, ConvNet, the U-Net model could obtain a better performance, since U-Net not only has deeper layers, but also has a feature fusion policy that could be used to obtain more discriminative features. Compared with SVM and CrackForest, FCN could obtain a relatively better result, as deep learning models could automatically extract high-level features, which are more generalized than handcrafted features.

Here, we present some examples of our PHCNet’s detection results for crack images, which were taken from the CRACK500 datasets. These crack images and their detection results are shown in Figure 8.

5.3. Effects of Using Different Activation Functions

In order to compare the influence of using different activation functions in our model, we conducted an experiment. Here, we used some common activation functions as our baseline, such as Sigmoid, Tanh ReLU, PReLU, as shown in

Table 2. Effects of using different activation functions.

Activation Functions	Cracktree200	CRACK500	CFD	OAD_CRACK
Sigmoid [20]	0.887	0.768	0.959	0.731
Tanh [21]	0.891	0.772	0.965	0.734
ReLU [22]	0.912	0.803	0.981	0.787
PReLU [20]	0.915	0.807	0.982	0.792
Swish [24]	0.929	0.823	0.989	0.801

.

As shown in Table 2, compared with PReLU and ReLU, the Swish activation function could obtain a higher accuracy. Because Swish activation function uses a smooth curve to compress negative features, unlike PReLU and ReLU, which use a sharper curve, it can make the distribution of positive and negative features smoother.

In addition, we could see that PReLU could obtain better results compared with ReLU, since PReLU uses a linear function to compress negative features, avoiding feature information loss. However, the ReLU activation function outputs all negative features as 0, resulting in the loss of all negative features.

Finally, ReLU could obtain better results than Sigmoid and Tanh, as it solves the problem of gradient disappearance during the training process of deep networks.

5.4. Effects of Using Different Loss Function

For the purpose of evaluating the effect of using different loss functions, we conducted an experiment.

As shown in

Table 3. Effects of using different loss functions.

Loss Functions	Cracktree200	CRACK500	CFD	OAD_CRACK
Mean Square Error Loss Function [39]	0.903	0.785	0.962	0.736
Cross Entropy Loss Function [34]	0.917	0.795	0.973	0.772
Weights Cross Entropy Loss Function [40]	0.922	0.811	0.983	0.792
Focal Loss Function [41]	0.929	0.823	0.989	0.801

, we reached the conclusion that the Weights Cross Entropy Loss Function and the Focal Loss Function achieve a higher accuracy than the Mean Square Error Loss Function and Cross Entropy Loss Function, for the reason that category imbalance always exists in concrete crack datasets because the number of crack pixels is always much smaller than the number of normal pixels in a concrete crack image. However, the Weights Cross Entropy Loss Function and the Focal Loss Function uses special parameters to increase the weight of crack pixels in loss function to compel the model paying more attention on crack pixels. Compared with the Weights Cross Entropy Loss Function, the Focal Loss Function could achieve slightly better results, as the Focal Loss Function uses more adjustable parameters to adjust the category imbalance.

5.5. Effects of Using Different Numbers of MGAMs

For the purpose of evaluating the effect of using different numbers of Mix Global Attention Modules (MGAMs), we conducted an experiment.

As shown in

Table 4. Effects of using different numbers of MGAMs.

Numbers of MGAMs	Cracktree200	CRACK500	CFD	OAD_CRACK
2	0.903	0.791	0.974	0.735
3	0.912	0.815	0.982	0.786
4	0.929	0.823	0.989	0.801
5	0.925	0.812	0.981	0.788

, adjusting the numbers of MGAMs in our proposed PCHNet would affect the final segmentation accuracy. The accuracy of the model gradually increases and then slowly decreases, indicating that the MGAMs could extract more global features and these global features have a positive impact on the final segmentation accuracy. However, using too many MGAMs would bring redundant global features, and these features are interfering features. Thus, in the experiment, we used only four MGAMs in our PCHNet.

5.6. Effects of Using Different Numbers of SAMs

For the purpose of evaluating the effect of using different numbers of Supplementary Attention Modules (SAMs), we conducted an experiment.

As shown in

Table 5. Effects of using different numbers of SAMs.

Numbers of SAMs	Cracktree200	CRACK500	CFD	OAD_CRACK
2	0.901	0.786	0.972	0.773
3	0.929	0.823	0.989	0.801
4	0.919	0.817	0.981	0.789
5	0.906	0.805	0.972	0.776

, we could see that adjusting the numbers of SAMs in our proposed PCHNet would affect the final segmentation accuracy. The accuracy of the model gradually increases and then slowly decreases, indicating that, by continuously removing crack features that have already been extracted by the PCHNet from the high-level output, the SAMs could compel the PCHNet to learn new crack features, allowing the PCHNet to automatically and continuously learn supplementary detailed features. These supplementary detailed features could effectively enhance the feature expression of the PCHNet. However, using too many SAMs would bring redundant features. Thus, in the experiment, we used only three SAMs in our PCHNet.

5.7. Effects of Using Different Numbers of PHCMs

For the purpose of evaluating the effect of using Pyramid Hierarchical Convolution Modules (PHCMs), we conducted an experiment.

As shown in

Table 6. Effects of using PHCMs or traditional convolution layer.

Modules	Cracktree200	CRACK500	CFD	OAD_CRACK
Traditional Convolution Layers	0.921	0.812	0.979	0.793
PHCMs	0.929	0.823	0.989	0.801

, we could see that using PHCMs in our proposed PCHNet would affect the final segmentation accuracy. Compared with the use of traditional convolution layers, our proposed PHCMs could increase the segmentation performance. As PHCMs contains three convolution layers with different kernel sizes, the features extracted by PHCMs could adapt varying shapes and sizes of cracks. However, the traditional convolution layers only using one kernel size could not adapt varying shapes and sizes of cracks, meaning that some crack features of different scales were missed.

5.8. Effects of Using Different Numbers of EFEMs

For the purpose of evaluating the effect of using different numbers of Edge Feature Extractor Modules (EFEMs), we conducted an experiment.

As shown in

Table 7. Effects of using different numbers of EFEMs.

Numbers of EFEM	Cracktree200	CRACK500	CFD	OAD_CRACK
2	0.923	0.821	0.986	0.799
3	0.929	0.823	0.989	0.801
4	0.927	0.820	0.983	0.794

, we could see that adjusting the numbers of EFEMs in our proposed PCHNet would affect the final segmentation accuracy. The accuracy of the model gradually increases and then slowly decreases, indicating that adding edge detection operators like Sobel, Laplacian, and Canny could improve the model’s ability to extract edge features, and these edge features could increase the model’s feature expression in top layers. However, using too many EFEMs would lead to redundant features. Thus, according to the experiment, we used only three EFEMs in our PCHNet.

6. Conclusions

In this paper, a crack detection model named Pyramid Hierarchical-Convolution-based U-Net (PHCNet) with MGAM, EFEM and SAM is proposed by us. Firstly, the Pyramid Hierarchical Convolution Module (PHCM) is used to extract features of cracks with different sizes. Thus the features extracted by PHCM could adapt varying shapes and sizes of cracks. Secondly, the Mix Global Attention Module (MGAM) is used to fuse global feature information, guiding the model in the restoration of high-resolution features with global information. Thirdly, the Edge Feature Extractor Module (EFEM) is used to learn the edge features of cracks. Finally, the Supplementary Attention Module (SAM) is used to solve the interference caused by stains in crack images, since it can continuously remove the crack features that have already been extracted by the model from the high-level output to compel the model to learn new crack features. The experimental results show that our PCHNet could achieve an accuracy of 0.929, 0.823, 0.989 and 0.801 on the Cracktree200, CRACK500, CFD and OAD_CRACK datasets, respectively. This article improves the architecture of existing deep-learning-based crack detection models, solving the problems of multi-scale crack detection, insufficient refinement of crack edge feature extraction, and the influence of interference features in crack samples. However, the model size of the PCHNet is still very large; our future research would focus on lightweight models.