Generation of a Virtual Cohort of Patients for in Silico Trials of Acute Ischemic Stroke Treatments

Abstract

The development of in silico trials based on high-fidelity simulations of clinical procedures requires the availability of large cohorts of three-dimensional (3D) patient-specific anatomy models, which are often hard to collect due to limited availability and/or accessibility and imaging quality. Statistical shape modeling (SSM) allows one to identify the main modes of shape variation and to generate new samples based on the variability observed in a training dataset. In this work, a method for the automatic 3D reconstruction of vascular anatomies based on SSM is used for the generation of a virtual cohort of cerebrovascular models suitable for computational simulations, useful for in silico stroke trials. Starting from 88 cerebrovascular anatomies segmented from stroke patients’ images, an SSM algorithm was developed to generate a virtual population of 100 vascular anatomies, defined by centerlines and diameters. An acceptance criterion was defined based on geometric parameters, resulting in the acceptance of 83 generated anatomies. The 3D reconstruction method was validated by reconstructing a cerebrovascular phantom lumen and comparing the result with an STL geometry obtained from a computed tomography scan. In conclusion, the final 3D models of the generated anatomies show that the proposed methodology can produce a reliable cohort of cerebral arteries.

1. Introduction

The increasing credibility of computational models and simulations of medical treatments is encouraging the exploration of the use of in silico trials to support and refine traditional clinical trials. An in silico trial consists of using computational tools to simulate the use of a new treatment, device, or drug in a cohort of virtual patients, obtaining insights on the efficacy. Credible biomechanical models have the potential of reducing the overall time and costs of the process by estimating in advance the performance of the new devices and only letting the most promising ones move forward to actual clinical trials [1].

Many clinical applications would benefit from the development of in silico trials. Among these, an in silico trial may support the development of better treatments for acute ischemic stroke (AIS), the pathology occurring when a thrombus obstructs a cerebral artery causing the development of an infarct zone in brain tissues [2]. In the case of large vessel occlusion, i.e., occurring in the internal carotid artery (ICA), the middle cerebral artery (MCA) M1 or M2 segments, or the anterior cerebral artery (ACA), which form a bifurcation called the T-junction, the most effective treatment is endovascular thrombectomy [3], a minimally invasive treatment aiming at mechanically removing the thrombus with a stent-retriever and/or aspiration catheters.

High-fidelity in silico models of the thrombectomy procedure have been recently proposed in the literature [4,5,6,7]. The stent-retriever thrombectomy simulation developed in [4], used to replicate a patient-specific case, was integrated into a framework for running the first proof-of-concept in silico trial for stroke treatments [8]. The framework was validated by replicating a real clinical trial and then employed to compare treatment outcomes in different subpopulations and with different thrombectomy devices, demonstrating the potentiality of the in silico approach to support clinical stroke trials. Knowing that anatomy does impact thrombectomy outcome [9,10,11,12,13], two aspects are important to consider when developing in silico trials for stroke treatments: (i) patient stratification based on anatomical characteristics; (ii) the generation of a large cohort of patients. The latter aspect is important for building data-driven surrogate or reduced-order models to predict in silico trial outcomes.

Normally, in patient-specific modeling, the geometry domain is obtained from diagnostic images, e.g., computed tomography (CT) and Magnetic Resonance Imaging (MRI). In the AIS context, it is possible to automatically identify the centerlines and diameters of the vessels [14], while three-dimensional (3D) reconstruction from the segmentation process provides a non-smooth voxel representation and requires additional steps to be used in models [4]. Due to the limited accessibility, consistency, and quality of clinical images, the generation of virtual cohorts of patients is helpful to run in silico clinical trials. When an in silico trial is based solely on data-driven models, the cohort of patients can be represented by a set of metadata [8]. Differently, if the in silico trial pipeline includes high-fidelity modeling (e.g., [15,16]), the cohort of patients requires the collection of 3D domains. In [17], the authors provided a review of different virtual cohorts of cardiac models. They indicated three different methodologies for developing virtual patient cohorts: mapping virtual cohorts, sampling from inferred distributions, and random sampling with acceptance criteria. In the current literature, an acceptance criterion for a virtual patient cohort can be distinguished as data-driven or clinically driven: data-driven if the acceptance criterion relies on the geometrical variability of the training samples [18]; clinically driven if the acceptance criterion is defined by a clinical requirement, for example, a specific characteristic or phenotype [19]. In [19], the authors proposed a machine learning surrogate model to predict the outcome of the acceptance criteria in a clinically driven population of aortas. The authors demonstrated that the sampling strategy and the verification of the generated cases impacted the efficiency of the process and the quality of the resulting cohort. A centerline-based statistical shape model (SSM) was presented by [20] to generate a data-driven population of aortas; 154 real patient geometries were used to train an SSM that used a principal component analysis (PCA) to capture the morphological features in order to create a large virtual population (about 3000 patients).

Within this context, this work proposes an automatic procedure to generate a data-driven virtual cohort of AIS patients’ anatomies. The objective is the creation of a tool which enables the generation of large cohorts of virtual populations of cerebrovascular anatomies suitable for high-fidelity thrombectomy modeling. This will facilitate the development of in silico trial approaches, reducing the issues related to the availability of high-quality images of stroke patients and to privacy concerns when sharing patient data between hospitals and modelers. Moreover, the availability of large populations for in silico modeling is required in general when running in silico stroke trials, and in particular to train accurate and fast surrogate models like the one used in [8]. To this aim, first, (i) an SSM approach is used to generate cerebrovascular anatomies described by their centerlines and associated diameters, starting from a cohort of 88 real AIS patients. Then, (ii) an automatic 3D reconstruction of the vessels from the centerlines and associated diameters is implemented and (iii) validated.

2. Materials and Methods

2.1. Collection of Patient-Specific Data

The clinical data of 100 patients affected by an AIS due to an occlusion in the M1 segment of the MCA were retrospectively collected from the MR CLEAN Registry, a randomized clinical trial for stroke treatments involving several intervention centers in the Netherlands [21]. Images of the patients’ cerebral vasculature were acquired with non-contrast computed tomography (NCCT) and computed tomography angiography (CTA) before treatment. The image segmentation was performed with StrokeViewer (NICO.LAB, Amsterdam, The Netherlands), and the iCAFE V1.3.0 software [22] (© 2016–2018 University of Washington. Used with permission) was used to extract the centerlines and diameters of the cerebral vessels (a diameter associated with each point of the centerline) and to label the different segments. Thanks to the labeling of the vascular tracts, only the segments of interest for this work were collected, namely the ICA, ACA, M1, and M2. For each patient, the vessels on the contralateral side with respect to the occlusion were selected to gain a complete vascular representation (since in the occluded side the imaging is available only up to the proximal end of the occlusion).

For the purpose of creating a training dataset for the generation of virtual patients, exclusion criteria were imposed to select patients with a complete set of vessels of interest. Therefore, vascular segmentations not including the ACA or either of the M2 branches were excluded, resulting in a cohort of 88 patients in the training dataset.

2.2. Generation of Virtual Patients

A statistical shape modeling (SSM) approach was used for the generation of virtual patients. SSM generally relies on the application of a principal component analysis (PCA) to a set of anatomic representations to identify a mean anatomy and a number of modes of shape variation [23].

In this work, the training dataset was made of the cerebral anatomies of 88 patients, described by the vascular centerlines and the associated lumen diameter for each point of the centerline. The whole processing of the data was performed through a developed MATLAB (Math-Works, Natick, MA, USA) code. The centerlines were first smoothed and resampled such that each vascular segment was made of the same number of points for each patient. Linear interpolation was used to associate the diameter values to the new points. Segmentation artifacts frequently occurred at the extreme points. If a diameter value at the extreme point of a centerline was more than 50% bigger or smaller than the previous diameter, it was corrected by assigning the same diameter of the previous point.

To have homogeneous anatomies, and without evidence of significant anatomic differences between the two sides of the intracranial cerebral vasculature [24,25,26,27], the left-side anatomies were mirrored to obtain a right-side cerebrovasculature for all the training data. Subsequently, rigid registration was performed to align the anatomies. A PCA was conducted on the aligned centerlines with associated diameters to identify the principal modes of shape variation. The N modes which cumulatively represented 95% of the anatomy information were selected. The description of each vascular anatomy was then reduced to the first N principal dimensions.

One hundred virtual patients were generated by randomly sampling the values of the N principal dimensions following normal distributions fitted to each principal dimension in the training dataset. The Lilliefors test was used to test normality. An acceptance criterion was defined to reject unphysiological anatomic realizations. For this purpose, the vascular anatomies were analyzed to extract geometric parameters with the method described in [9]. Briefly, each ICA was divided into 4 bends (from the T-junction: superior, anterior, posterior, and inferior), and each bend was analyzed to extract the average diameter (D^sup, D^ant, D^pos, and D^inf), the curvature expressed as the radius of the fitting circle (r^sup, r^ant, r^pos, and r^inf), and the tortuosity, calculated as the ratio between the bend length along the centerline and the distance between the bend extremes (t^sup, t^ant, t^pos, and t^inf) (Figure 1). In addition, the three angles formed at the T-junction (α^ICA-ACA, α^ICA-M1, and α^M1-ACA) and the three angles at the M1 bifurcation (α^M1-M2a, α^M1-M2b, and α^M2a-M2b) were calculated. Finally, the average diameters of the ACA, M1, and M2 segments (D^ACA, D^M1, and D^M2) were stored. Since the inferior bend did not show significant variability among the analyzed cerebrovascular anatomies, r^inf and t^inf were excluded from the acceptance criteria. A total of 19 geometric parameters were calculated both for the anatomies in the training dataset to define their admissible ranges, and for the generated virtual patients, to evaluate the acceptability of the anatomy. If any of the parameters had a value outside the minimum–maximum range of the training dataset, the generated virtual patient was discarded. Finally, in order to validate the virtual cohort of patients, a comparison between cohort-level and training-population-level distributions of the geometric parameters was performed [17] by means of the Mann–Whitney U-test, where a two-sided p-value of less than 0.05 determined significance for rejecting the hypothesis that the two compared sets of data originated from distributions with equal medians.

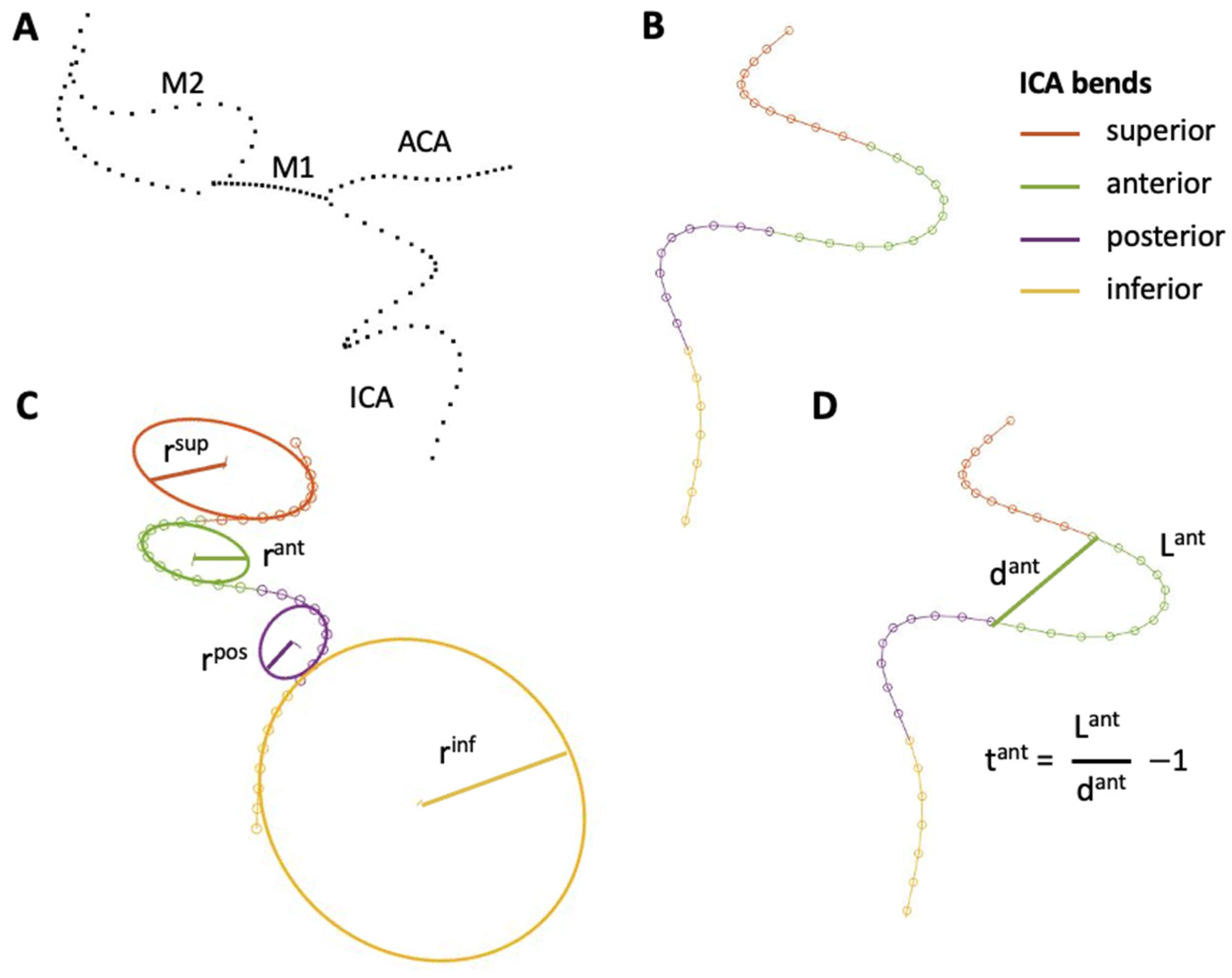
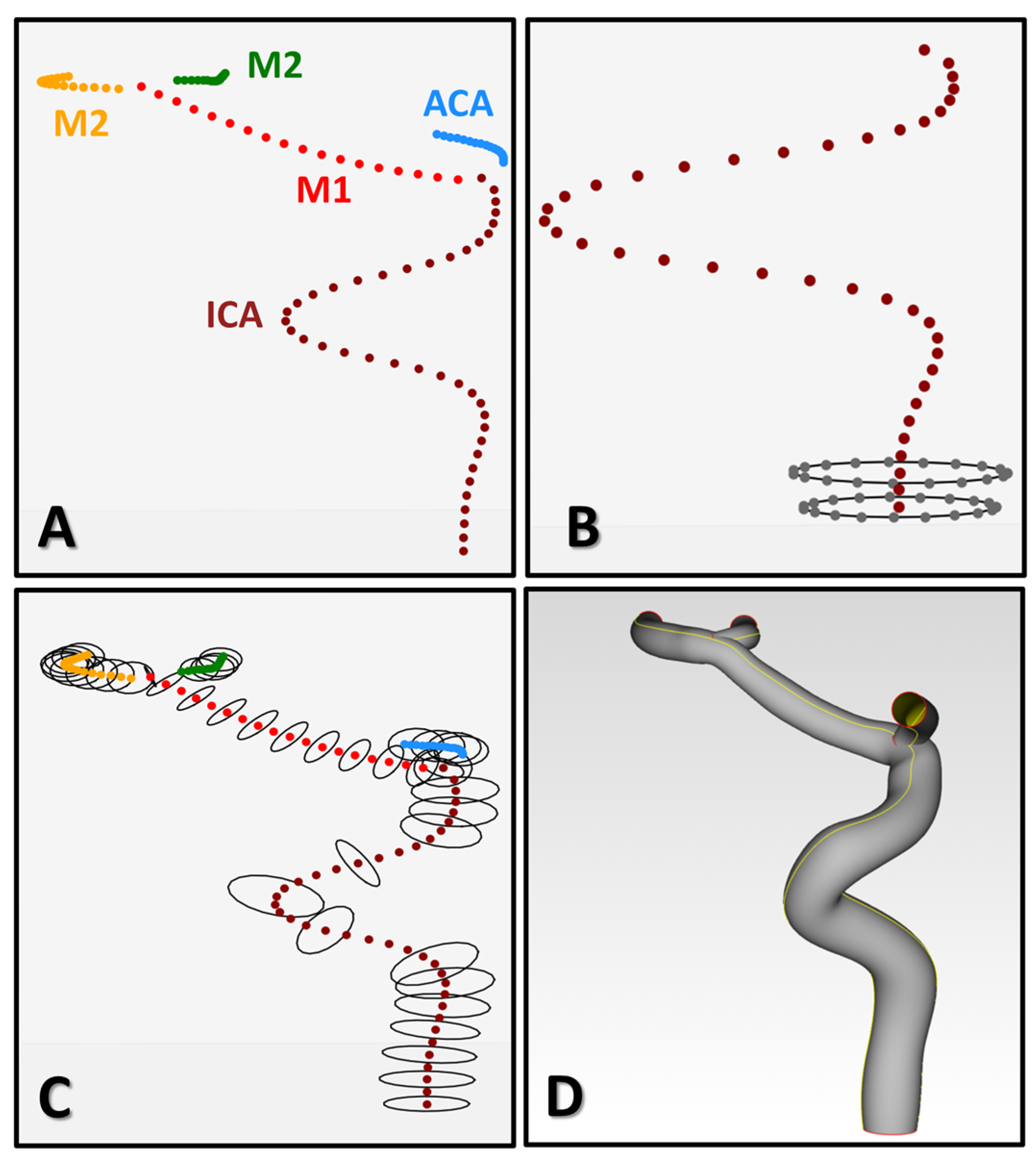
2.3. Automatic 3D Reconstruction of Cerebral Vessels

The proposed 3D reconstruction method requires the vascular centerlines with the associated diameters of the segment of interest to generate AIS patients. The Computer-Aided Design (CAD) software Creo Parametric (PTC, Boston, MA, USA) was used. In particular, within the software, an automatic procedure was implemented by creating blended surfaces from a text file containing cross-sections discretized by points. With a Python code, the ad hoc input files with the points-sections were created, starting from the generated vessels’ centerlines and diameters. The implemented Python code first recognized and combined the ICA, M1, and one M2 as a smooth and continuous line, the ACA in the T-junction, and the second M2 in the M1 bifurcation (Figure 2A). Then, the circular section for each node of the centerline was defined by considering the specific diameter and discretized with 20 nodes (Figure 2B). Only some sections were considered in the text files, based on the local curvature of the centerline (Figure 2C). In high-curvature points, few sections were considered in order to avoid the self-penetration of sections. More details about the local curvature calculation are presented in [9]. The final 3D reconstruction of the vascular anatomy was then automatically obtained in Creo Parametric (Figure 2D).

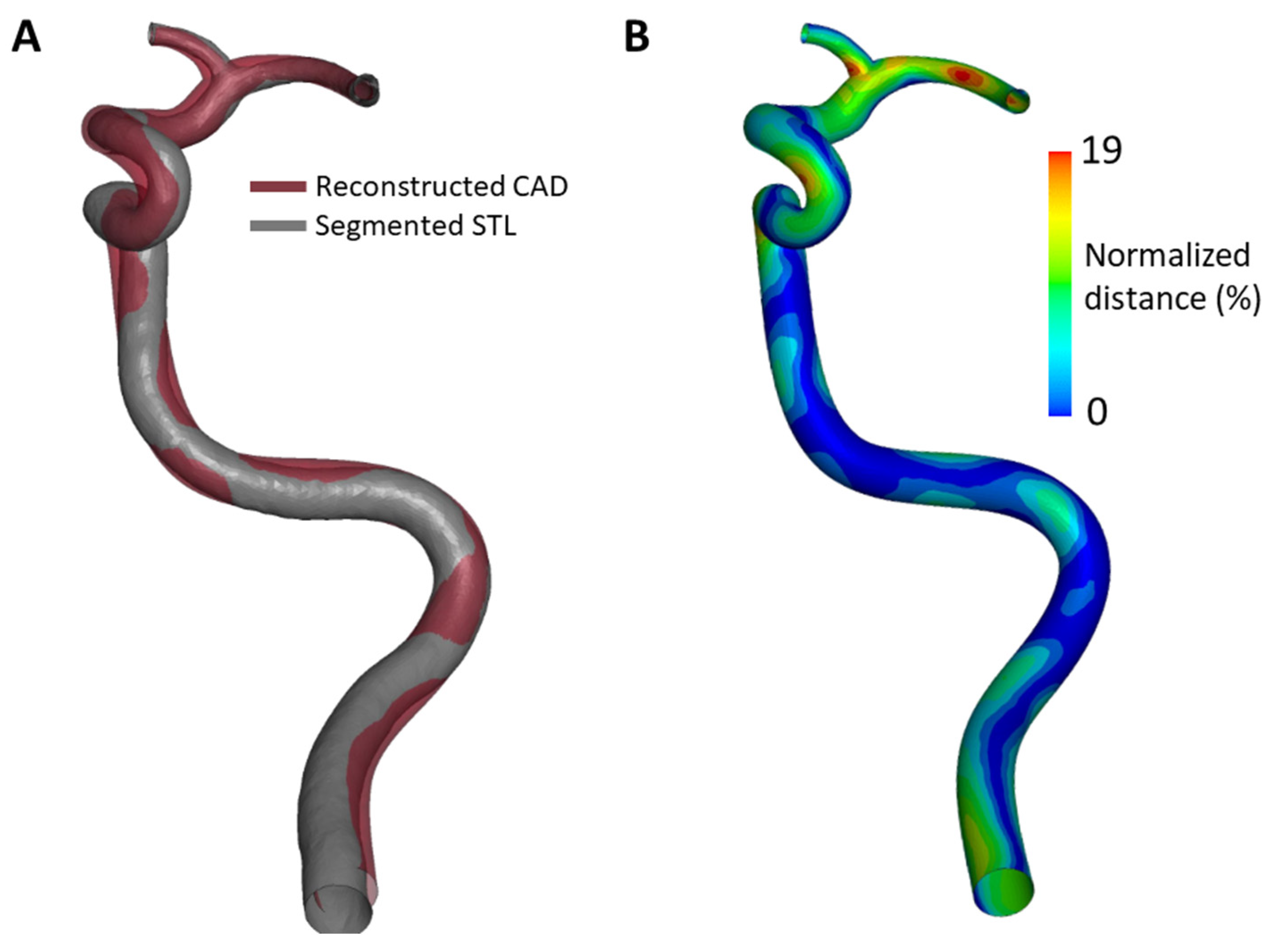
2.4. Reconstruction Validation

The quality of the proposed 3D reconstruction method was assessed by comparing the reconstructed CAD model with the STL geometry directly obtained from the segmentation process. For this purpose, a silicone phantom of the cerebral arteries with a complete circle of Willis anatomy was used (Figure 3A). The process of creating cerebrovascular phantoms from 3D-printed vessel lumina, which are derived from CTA scans, is described in [28].

The cerebral arteries phantom was segmented from CT images in a semi-automatic way with the open-source VMTK V1.4.0 (Orobix s.r.l.) software using the threshold method. In particular, all the pixels comprised within two specified thresholds were selected to obtain the final segmented domain (Figure 3B). The segmented domain, in particular the internal lumen, was triangulated to be exported in STL format (Figure 3C). To enable the quantification of the mismatch between the two models, the reconstructed CAD model was meshed in ANSA (BETA CAE Systems, Root, Switzerland) with triangular elements of the same average element size as in the STL model, i.e., 0.35 mm. In the post-processing software META (BETA CAE Systems), the CAD and STL models were superimposed and the mismatch between the two was evaluated by calculating, for each node of the CAD model, the Euclidean distance to the closest node of the STL model. The distances were then normalized by the local diameter value of the vascular model.

3. Results

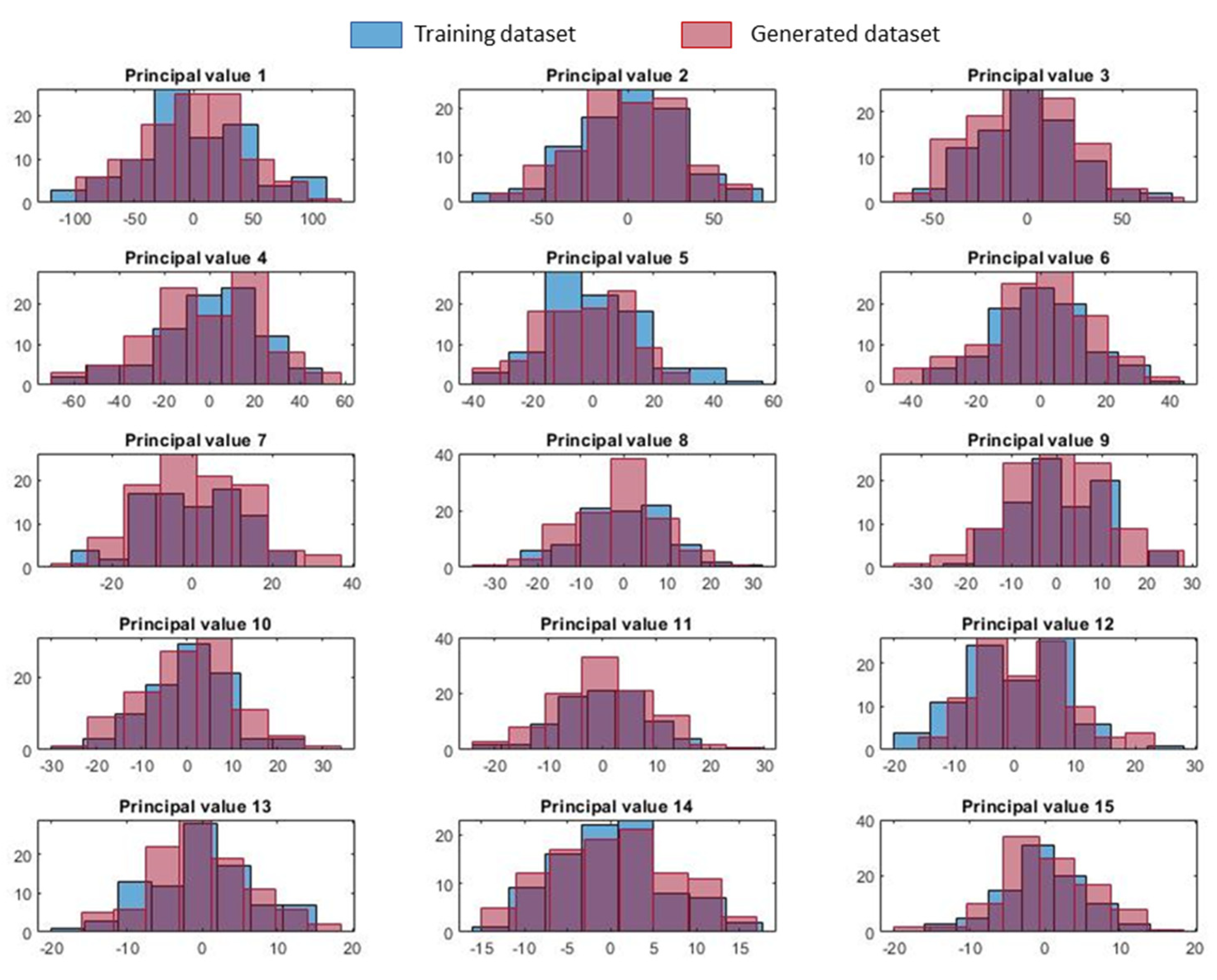
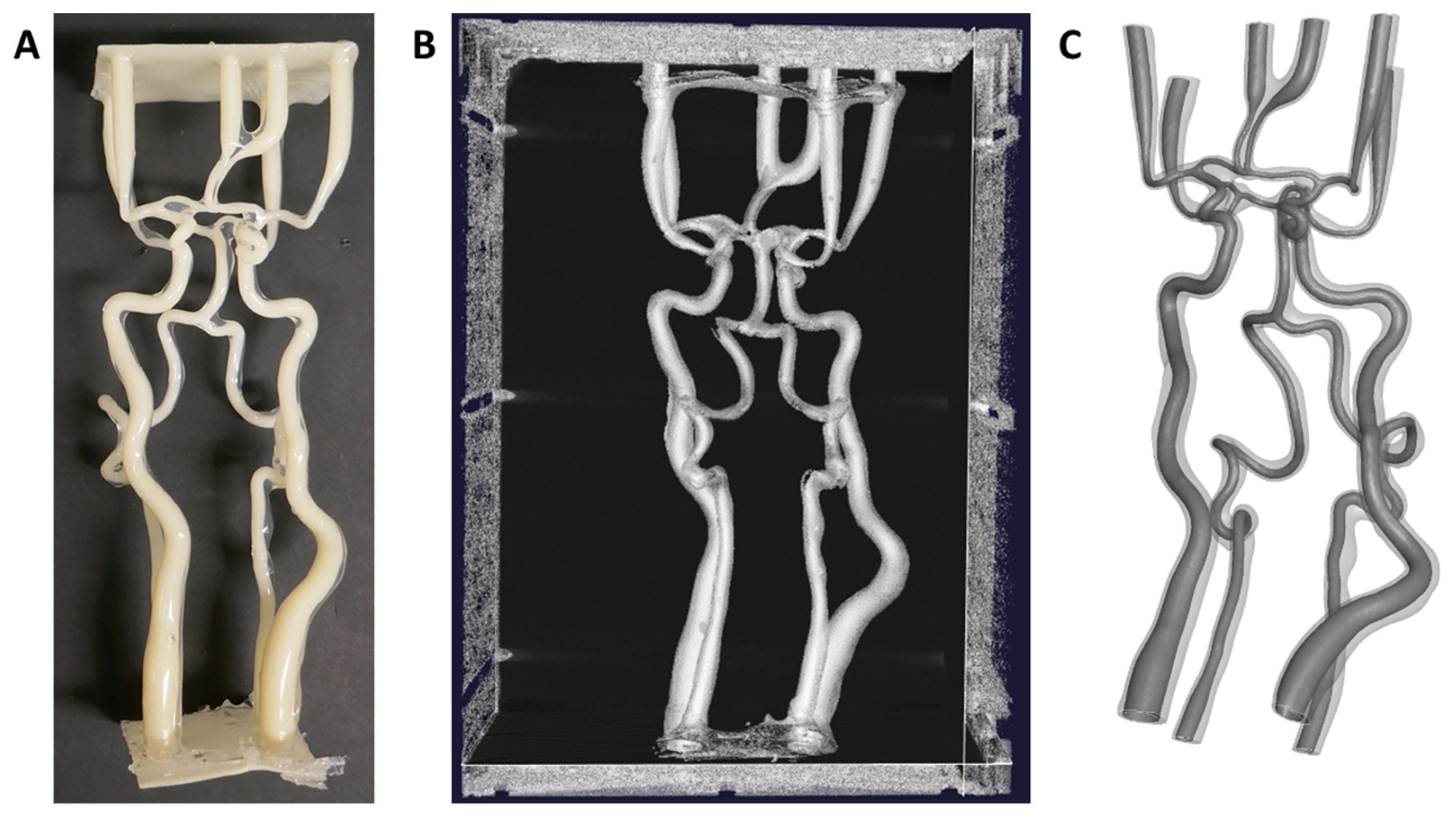
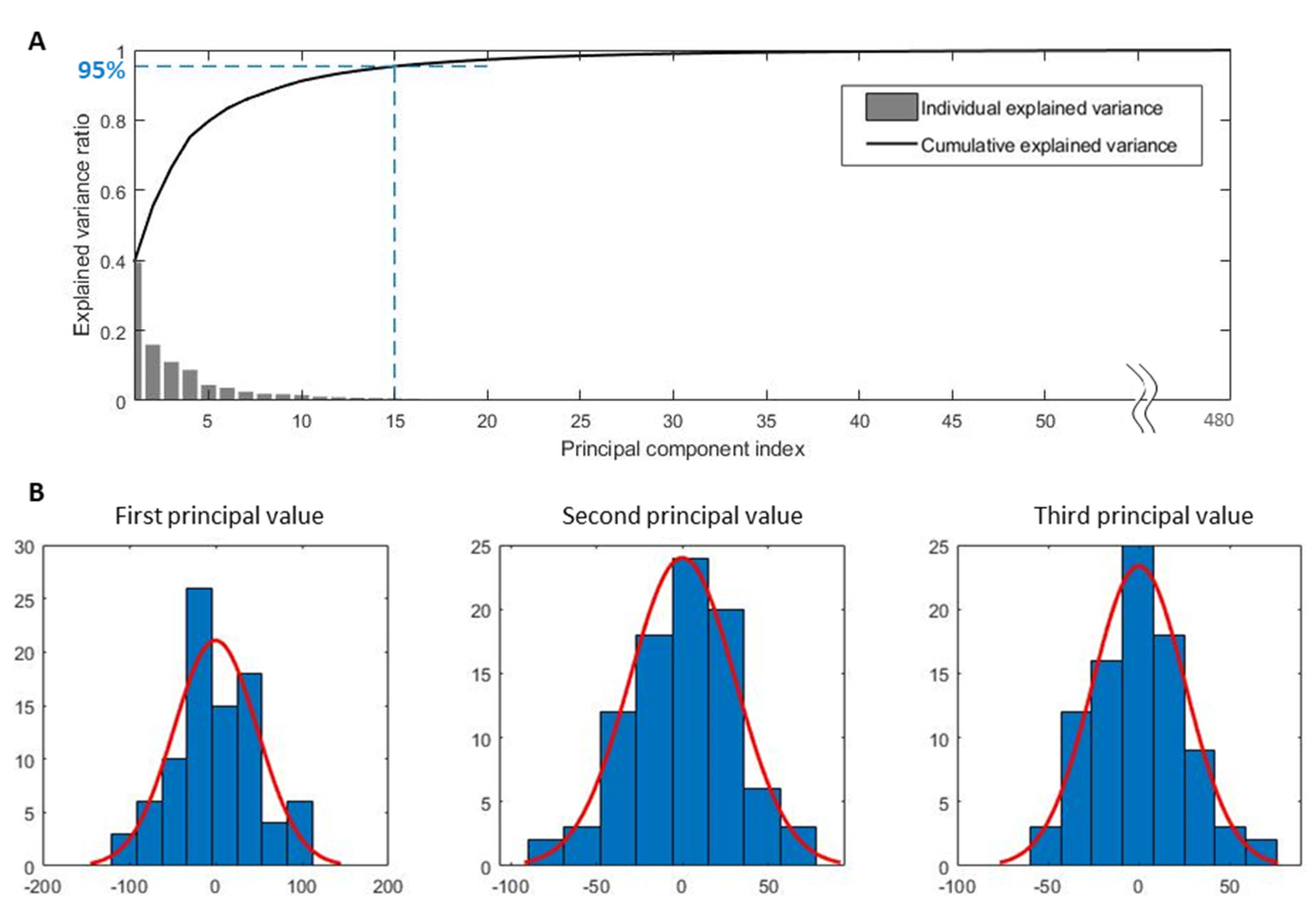
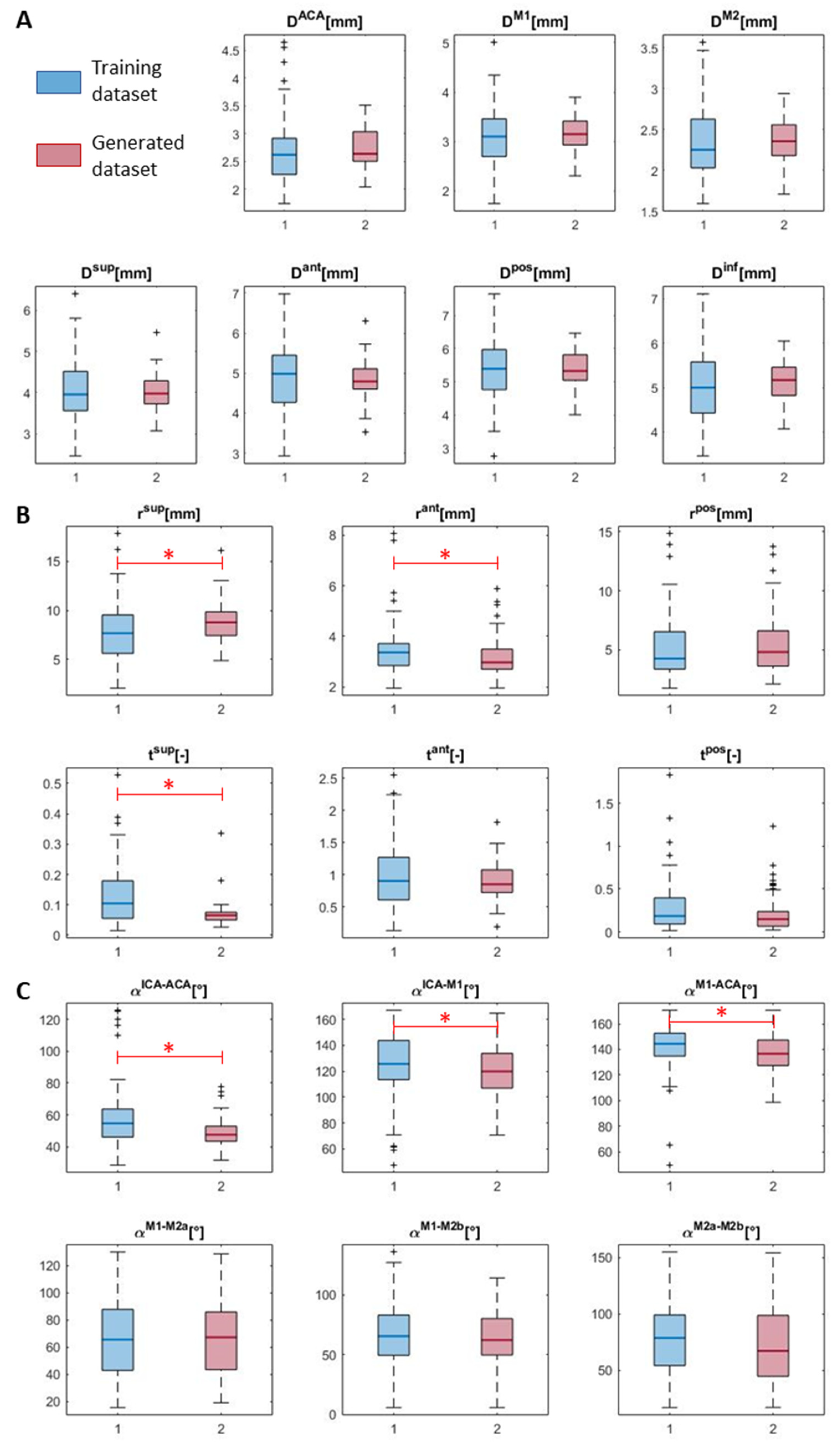
3.1. Generated Virtual Patients

Figure 4A shows the results of the PCA on the vascular anatomies in the training dataset. Fifteen modes were required to represent 95% of the variance of the anatomy shapes. Figure 4B shows as examples the distribution of the first three principal values and their fitting with normal distributions, which are subsequently used to sample new values of the principal modes for the generation of virtual anatomies. The Lilliefors test confirmed that 14 out of the 15 principal values were normally distributed. A comparison of the distributions of the 15 principal values in the training and generated datasets is shown in Appendix A.

Examples of 3D reconstructions of the generated virtual patients are shown in Figure 5. Of the 100 generated virtual anatomies, 17 were rejected due to the acceptance criteria, as one or more of the considered 19 geometric parameters were outside the range defined with the anatomies in the training dataset. Figure 6 shows the boxplots of the distributions of the geometric parameters in the training and generated dataset. The results of the Mann–Whitney U-test indicated that for 13 out of the 19 parameters, the values in the generated and training dataset could be described with distributions with equal medians (the red asterisks in Figure 6 indicate the parameters with different distributions between the generated and training dataset). More details on the calculated geometric parameters are collected in Appendix A.

3.2. Reconstruction Validation Analysis

A comparison between the STL geometry from segmentation and the corresponding 3D reconstruction geometry was carried out (Figure 7A), aiming at assessing the goodness of the developed 3D reconstruction method. In Figure 7B, the contour map of the distances normalized by the local diameter values is shown. Higher values with a maximum of 19% were detected at the T-junction and in the M1 segment with a maximum absolute distance of 0.36 mm and 0.33 mm, respectively.

4. Discussion

The availability of in silico models of patient cohorts is gaining importance due to the growing interest in the development of in silico trials for the assessment of the safety and efficacy of new medical devices and procedures. When the in silico trial is based on high-fidelity simulations of a clinical procedure, a large amount of high-quality Computerized Tomography or Magnetic Resonance Imaging data are required for the generation of patient-specific 3D anatomical domains, together with other clinical data needed as input for the procedure modeling. However, high-quality imaging is not always available, or accessible, for instance, due to patient privacy policies, and gathering a large number of such high-quality images may not be feasible in clinical practice.

In this regard, the implementation of methodologies for the generation of synthetic data, starting from a limited real patients’ dataset, can offer a solution for the creation of large virtual populations suitable for in silico trials. Statistical shape modeling is a well-established methodology [23,29,30,31] which, based on dimensionality reduction techniques and parameter sampling, allows one to identify the principal modes of shape variation of an object and to generate new samples. The SSM technique has been used in the literature for the generation of virtual cohorts of cardiac [17] and aortic [19,20] models.

This work proposed the use of the SSM approach for the generation of virtual populations of cerebrovascular anatomies, useful for the development of in silico trials for AIS treatments. In [8], the first proof-of-concept in silico stroke trial was implemented, based on a surrogate model of the thrombectomy procedure trained on a dataset of 94 high-fidelity thrombectomy simulations run in patient-specific vascular models. The methodology described in the present work would enable the creation of the desired number of virtual stroke patients for increasing the reliability of an in silico stroke trial. Moreover, this methodology also allows one to generate virtual patients with a variety of anatomic characteristics, which is important to assess the efficacy of a stroke treatment. In fact, several studies in the literature, based on the analysis of clinical data or on computational approaches, demonstrated the impact of geometric parameters, such as arterial diameters, curvatures and ICA tortuosity, on the outcome of thrombectomy procedures [9,10,11,12,13].

As a proof-of-concept of the methodology, a virtual population of 100 cerebrovascular anatomies was generated using an SSM methodology with random sampling of the principal shape modes following the normal distributions fitted to the principal values of the training dataset. The methodology allowed the generation of the centerlines of the main cerebral vessels (ICA, ACA, M1, and M2) and the associated diameters. Subsequently, an acceptance criterion was established, based on 19 geometric parameters. Of the 100 synthetic anatomies, 17 had at least one of the parameters outside the range allowed by the analysis of the data used for the training of SSM and were excluded from the final population. The comparison of the geometric parameters’ distribution (Figure 6 and Appendix A) demonstrated that the generated virtual population represents the data variability in the original training dataset well. The Mann–Whitney U-test assessed that, for 13 out of the 19 considered geometric parameters, the parameter distribution in the generated population had a median equal to the one in the training dataset, indicating that the generated population represents the characteristics observed in the training dataset well. Different sampling strategies may lead to different results on the distribution of the geometric parameters. For instance, uniform sampling of the principal values within the training set range would allow a broader coverage of the possible anatomy configurations, increasing the number of virtual anatomies with admissible geometric parameters but less represented in the training dataset.

Following the generation of vascular centerlines and diameters, a method for the automatic 3D reconstruction of the virtual anatomies was illustrated. More generally, the proposed 3D reconstruction method allows for the automatic reconstruction of patient-specific cerebral vessels starting from centerlines and diameters obtained from the segmentation of clinical images. The accuracy of the reconstruction was evaluated through a comparison with an STL model directly obtained after the segmentation of CT scans of a patient-like 3D-printed cerebrovascular phantom. The results indicated that the obtained CAD model replicates the STL model with good accuracy. Since the reconstruction method is built from the centerline and the associated diameters, circular lumen sections were assumed. In reality, non-circular and irregular sections could be observed. However, the relative distance calculated between CAD—with circular sections—and STL—with real non-circular sections—was less than 19%. The main mismatches were observed in vascular portions with critical shapes, e.g., tracts of high curvature, or at the extremes of the models, where segmentation artifacts were more frequent. In this regard, the accuracy of the vascular reconstruction was compared with the provided STL model to assess the overall agreement of the vascular shapes. Ultimately, the accuracy of the patient-specific vascular model will always depend on the resolution of the clinical imaging techniques.

5. Conclusions

This work proposed a method for automatically generating a virtual cohort of 3D cerebral arteries. The method allows one to reconstruct cerebral vessels with good accuracy and in a short time, allowing for the future generation of large cohorts of virtual patients for the in silico simulation of stroke treatments.