Abstract
In the context of noise reduction schemes for box-girder bridges (BGBs) used in high-speed railway, the thickened top plate design can effectively reduce the structural noise of the BGB, which has been widely recognized. However, it is difficult to obtain the optimum thickness of the top plate of the BGB without mastering the key mechanism of the noise reduction scheme. Therefore, this study took a 32 m simple-supported concrete BGB in the context of a high-speed railway as the research object and analyzed and compared the sound vibration characteristics of the entire thickened top plate versus the locally thickened top plate on BGB tracks, and the optimal noise reduction mechanism of the thickened top plate design scheme was studied in detail. The key issues of the thickened top plate noise reduction scheme are discussed. The results show that thickening the top plate can obviously reduce the bridge’s structural noise when subjected to severe vibration and high frequency bands because the vibration of the BGB is reduced. However, in the low frequency band, acoustic radiation can occur as a result of the small amplitude vibration, and this phenomenon is closely related to the vibrational distribution of the BGB. Therefore, it is necessary to focus on the vibrational distribution of the BGB as a priority when carrying out noise reduction using a thickened top plate. This paper points out the most significant factors affecting the acoustic radiation ability of the BGB in different frequency bands, especially the key problem of the strong acoustic radiation ability caused by small vibrations in low frequency band. The research results can provide an important theoretical basis for the optimal thickness design of the BGB.
1. Introduction
With the continuous increase in the speeds of high-speed train operation, the noise problem caused by high-speed railways is becoming increasingly prominent, aggravating the overall noise-related issue in various parts of the line. The noise of elevated high-speed railway lines covers the full frequency band; for example, wheel–track system noise, collector system noise, and aerodynamic noise are mainly concentrated in the middle and high-frequency bands, while the noise related to elevated concrete bridge sound radiation is mainly low-frequency. Therefore, elevated lines compared to other lines encounter a more prominent noise problem. In addition, due to the characteristics of low-frequency sound waves, acoustic waves will have a larger impact on human health and the ecological environment [1,2,3,4,5], so the problem of low-frequency acoustic radiation as associated with high-speed railway bridges is now a close concern of scholars from various countries.
Predicting the low-frequency acoustic radiation associated with high-speed railway bridges is difficult using analytical methods, so numerical calculation methods are widely used [6,7,8,9,10,11,12]. The main purpose of predicting the low-frequency acoustic radiation characteristics of elevated high-speed railway concrete bridges is to evaluate whether these acoustic waves are harmful to people and the ecological environment, investigate the key mechanisms of acoustic radiation, provide appropriate control targets for subsequent noise reduction designs, and finally realize the green and sustainable development of rail transportation. The authors here consider that noise reduction designs for high-speed railway bridges can be achieved in the following two ways. First, developing low-noise bridge types, i.e., low-noise-radiating bridges, in the early design stage, will reduce the capacity of bridges to radiate sound waves at the source. Second, designing and adopting suitable noise reduction measures for existing bridges, will limit the capacity for existing bridges to radiate sound. Both methods can to some extent reduce the low-frequency noise radiated by the bridge structure, helping to alleviate the noise impact.
At present, most scholars tend to focus on the development of vibration-reducing tracks [13,14,15,16,17,18] as a way to achieve noise reduction. Via controlling the vibration of the bridge, this design conforms to the general law of vibration-induced noise but can only affect the acoustic radiation caused by severe vibration in the bridge. In contrast, it is difficult to achieve a true noise-reducing design using vibration reduction in the low-frequency, small-amplitude vibration band, where the bridge’s characteristics determine its acoustic radiation capability [11,19]. This shows that the effect of using a vibration reduction track to control the low-frequency structural noise of the bridge will not be satisfactory but will cause the vibration in the vibration reduction track itself to be amplified and will also cause rail corrugation and many other problems [20]. Therefore, the use of a vibration reduction track in the control of bridge structural noise has severe limitations and will not achieve the same effect as vibration reduction. The most common noise-reducing bridge designs can be broadly divided into the following cases. First, the thickening of various parts of the bridge can achieve good results in both vibration and noise reduction [21,22,23,24,25]; however, the theoretical basis for the selection of the optimal thickness of each part is lacking. Second, installing tuned mass dampers (TMDs) or multi-tuned mass dampers (MTMDs) with enhanced robustness on bridges can effectively attenuate the vibration problems encountered in BGBs [26,27,28,29,30], and thus many scholars have conducted noise control studies related to this issue [31,32]. Third, many scholars have assessed the factors influencing noise in different bridges, such as BGB web openings [33], the laying of a constrained damping layer [34], the selection of bridge section type [35], and rail grinding [36].
Therefore, the top plate of the BGB is the main acoustic radiation component, which can obtain a good noise reduction effect when thickened. However, if the mechanism and related problems encountered in thickened top plate design schemes are not clearly understood, it will be difficult to determine the optimal design and thickness of the top plate. In this paper, firstly, design schemes for a BGB with a thickened top plate are described, including those wherein the whole top plate is thickened, and those featuring local top plate thickening under the track. Secondly, based on the train–track–bridge interaction theory and acoustic boundary element theory, the acoustic radiation characteristics of three BGBs are calculated, and the noise reduction effects of the design schemes are compared and analyzed. Finally, the noise reduction mechanism and key factors affecting the design scheme of the thickened top plate are systematically analyzed.
2. Two Kinds of Top Plate Thickening Low-Acoustic Radiation Bridge Design Scheme
Elevated high-speed railway bridges are the most common kind, and usually feature 32 m simple-supported concrete BGBs, so this bridge type has been selected as the object of study in this paper. Recent research results have shown that the top plate overwhelmingly determines the amount of overall noise radiated by BGBs [37,38,39], and thickening the whole top plate can reduce its acoustic radiation, making it a good design solution for low-acoustic radiation bridge types [23,24]. When a train passes through an elevated bridge, due to the contact between the wheels and the rails, the vibrational energy is transferred to the bridge through the rail structure, which causes the bridge to vibrate and radiate noise. As such, the vibrational energy generated by wheel–rail interaction is first transferred to the point of contact between the rail and the bridge deck. According to the requirements of the specific project, local thickening can be applied to the point of contact of the BGB and the rail to reduce the radiation noise of the BGB [25]. This design solution not only reduces the weight of the bridge, but also reduces costs by using prefabricated bridge components, compared to the process of thickening the top plate of the BGB.
According to the literature [11], the main reason for the radiation of soundwaves from the BGB is related to the resonance effect, its own modal acoustic radiation efficiency, and the violent vibration resulting from external excitation. The bridge type influences all of the above factors, especially the resonance effect and the modal acoustic radiation efficiency, both of which are most closely related to the BGB type. Therefore, the authors consider the following objectives when carrying out the design of a BGB with a thickened top plate in terms of noise control:
- (1)
- The design of the thickened BGB top plate can enhance key parameters, such as the bending stiffness of the BGB, and thus reduce its vibrational response;
- (2)
- The top plate of the BGB is the most important component contributing to its acoustic radiation, and local vibration within it significantly affects its acoustic radiation. Thickening the top plate can change the overall vibrational distribution of the BGB, especially in cases of the partial thickening of the top plate, which will not have a uniform thickness, and this has a stronger impact on the vibrational distribution. Resonance at certain frequencies can be avoided to a certain extent, and the change in vibrational pattern can affect the modal acoustic radiation efficiency of the BGB, thus weakening its acoustic radiation capacity.
In summary, this paper explores the key issues involved in designing bridge plate thickening as it relates to noise reduction by comparing and analyzing the acoustic vibrational characteristics of the initial BGB, the BGB with its whole top plate thickened, and the BGB with under-rail local thickening. The thicknesses of the top plates in both designs are twice that of the initial BGB, and the remaining parameters are kept the same. The initial BGB and the designs with top plate thickening are shown in Figure 1.

Figure 1.
Schematics of a BGB with a thickened top plate in a high-speed railway: (a) initial; (b) whole top plate thickened; (c) top plate locally thickened under the track.
3. Numerical Analysis
In this paper, firstly, based on the train-track-bridge interaction theory, the vehicle-track-bridge coupling dynamic models of three kinds of BGBs are established, which vibration characteristics by the external excitation are compared and analyzed. Secondly, taking the vibration response of three kinds of BGBs as acoustic boundary conditions, the acoustic boundary element method is adopted to predict the acoustic radiation characteristics of BGBs. Finally, the sound radiation mechanism of BGB is further analyzed by the vibration principle. The main research ideas are shown in Figure 2.
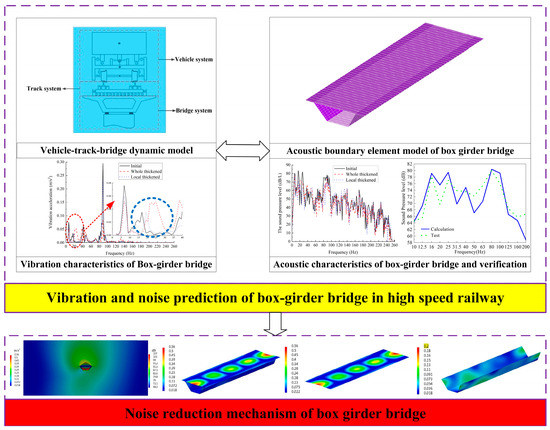
Figure 2.
Schematic representation of the vibration-acoustic radiation characteristics analysis of box-girder bridge.
The train runs on an elevated line, which can be divided into the vehicle subsystem, the track subsystem, and the bridge subsystem for theoretical analysis. The dynamic equations of the three can be expressed as follows:
The subscripts v, t, and b represent the vehicle, track, and bridge structures, respectively; M, C, and K are the mass, stiffness, and damping matrices, respectively; , and are the displacement, velocity, and acceleration vectors, respectively; and F is the generalized load. The vehicle–track–bridge interaction model is shown in Figure 3. In the overall system, the vehicle submodel uses the classical 35-degree-of-freedom model. Each vehicle section includes a vehicle body, two steering racks, and four wheels sets, all considered to be rigid-body structures, connected by the first and second suspension systems; the suspension system exhibits linear and nonlinear characteristics. Each rigid body comprises lateral, vertical, side-roll, rocker, and nodding degrees of freedom; the vehicle model dynamic equations and related parameters are described in the literature [40]. The finite element model is used for determining the structure of the elevated infrastructure. The theoretical finite element model of the track and the BGB structure is shown in Figure 3. The relevant parameters and finite element type are shown in Table 1.
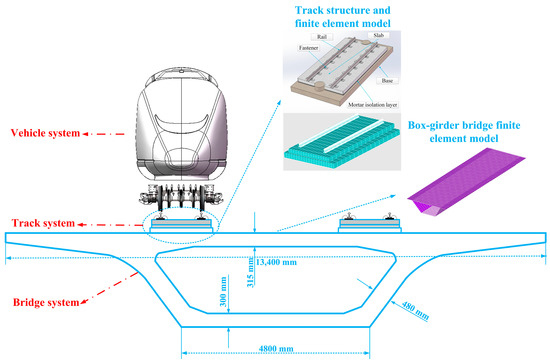
Figure 3.
High-speed train–slab ballastless track–BGB theoretical calculation model.

Table 1.
CRTS-I type plate ballastless track–BGB dynamics parameters.
When accurately predicting the noise radiated by the bridge due to the movement of trains, the determination of wheel–rail dynamic forces is important. In this study, we employ a dynamic wheel–rail interaction model [41], whose reliability and low computational burden have been verified, to calculate the wheel–rail forces. The wheel–rail normal force is calculated using the nonlinear Hertzian elastic contact theory. The tangential wheel–rail creep forces are first derived using Kalker’s linear creep theory, and then modified using the Shen–Hedrick–Elkins nonlinear modification theory. Because this study focuses on a bridge as a tangential railway segment, a single-point wheel–rail contact model is adopted. The entire system can be solved using the multi-step explicit–implicit time integration method [42,43] (i.e., the train–track system is solved by Zhai’s explicit method [44]) with a time step of 10−4 s, and the bridge system can be solved using the implicit Newmark-β method with a time step of 10−3 s. To calculate the vibrations of the BGB, the irregularity of the high-speed tracks is used to represent the excitation; the foregoing is also used as the acoustic boundary condition in the second step of the analysis. For these calculations, we assume that a CRH380B high-speed train under tare conditions is moving at a speed of 200 km/h.
Taking the vibration acceleration response of the BGB as the acoustic boundary condition, the acoustic boundary element method is adopted to determine the acoustic radiation characteristics of the BGB. The theory of the acoustic boundary element method can be seen in [45].
The sound pressure levels calculated and measured at a position 5 m directly below the bridge are shown in Figure 4. The results are in good agreement, and within the studied frequency band. Their trends of changing over time are consistent, and their peak values appear at similar frequencies. Therefore, the acoustic prediction model herein developed for BGBs is reliable.
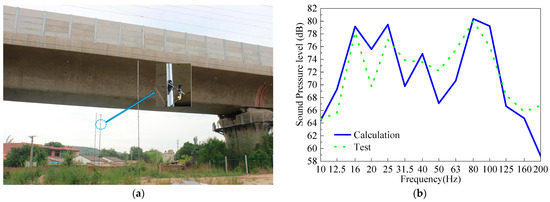
Figure 4.
In situ measurement of the noise radiation of high-speed railway BGB: (a) photograph of measurement site; (b) calculated and measured sound pressure levels.
4. Comparative Analysis of Acoustic Vibration Characteristics of BGBs for Three Working Conditions
The curves of the vibration acceleration spectrum taken at the center of the span of the top and bottom plates of the BGB are used to compare and analyze the vibrational characteristics of the two top plate-thickening design solutions. After this, the linear sound pressure levels at different points of the transverse sound field in the span of the BGB are selected, as shown in Figure 5, to analyze the noise reduction effects of the top plate-thickening design solutions, and the field points are selected as shown in Figure 5. The relationship between the two is used to infer the relationship between vibration reduction and noise reduction.
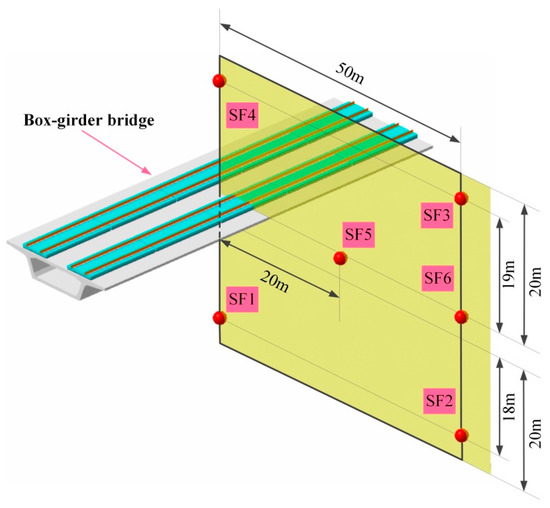
Figure 5.
Schematic diagram of sound field points to be used in the BGB sound radiation study.
As can be seen in Figure 6, under the same excitation, the vibration spectra of the three BGBs are similar. The severe vibration band is concentrated at 80–100 Hz, and the vibration at 0–80 Hz is the small-amplitude vibration. The difference is that the top plate-thickening design not only weakens the vibration amplitude of the BGB in this band, but the small-amplitude vibration band is also significantly shifted. The vibrational shift in the center of the bottom plate in the BGB with a thickened top plate is more obvious and is in the very low-frequency band of the initial BGB vibration. In the two BGB thickening designs, the vibrational amplitudes of different plates in the BGB are significantly reduced, and the reduction in the vibrational amplitude of the top plate is significantly greater than that seen in the rest of the plate, thus indicating that both designs will be very effective in vibration damping, with significant vibration reduction. Compared with the design with a partially thickened top plate under the rail, the vibration reduction effect of the whole top plate-thickening design is better, especially in the main vibrational frequency band. However, attention needs to be paid to the significant increase in vibration in the bottom plate at 20–40 Hz when the whole top plate of the BGB is thickened, so the effects of this phenomenon on acoustic radiation characteristics and noise reduction are studied in detail in the following.
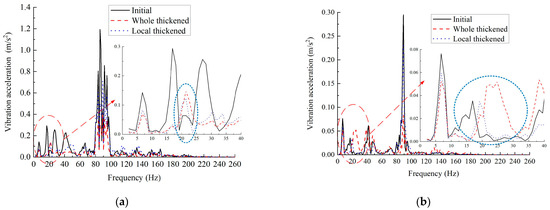
Figure 6.
The vibration acceleration comparison of the top plat-thickening design schemes: (a) top plate center point; (b) bottom plate center point.
Figure 7 shows a comparison of the linear sound pressure levels in three types of BGBs. From Figure 7, the acoustic radiation characteristics of BGBs can be summarized as follows:
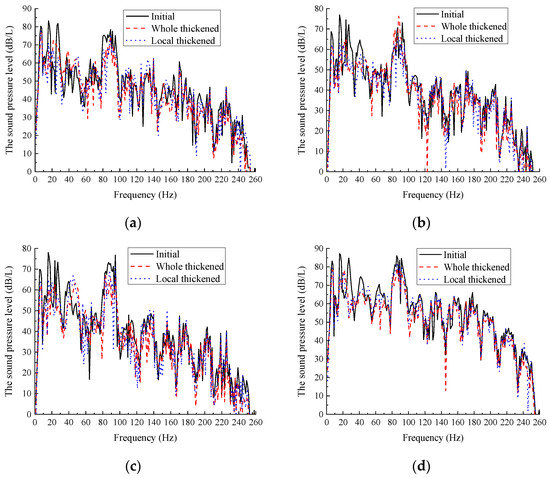
Figure 7.
Comparison of the sound pressure level at different sound field points in three kinds of BGBs: (a) SF1; (b) SF2; (c) SF3; (d) SF4.
- The stronger frequency band of BGB acoustic radiation can, in general, be divided into two bands, namely, the 0–40 Hz lower-frequency band and the 80–100 Hz severe vibration band. In these two bands, the BGB shows strong acoustic radiation characteristics. The phenomenon of concern is that the acoustic radiation of BGBs in the lower frequency band of different sound fields is very strong—even stronger than that seen in BGBs under the effects of severe external excitation. This phenomenon is contradictory to the general law of strong acoustic radiation caused by severe vibration. Therefore, the reasons for this phenomenon and the key issues to be addressed when designing a thickened top plate to reduce noise are analyzed in detail in the following, providing a basis for the further optimization of the subsequent design;
- The two noise reduction designs with top plate thickening have obvious noise reduction effects, the most significant being in the lower frequency bands, and there are also substantial reductions in sound pressure at certain frequencies. From the vibrational characteristics of the BGB, it can be seen that the vibration of the bottom plate intensifies at some frequencies in the lower frequency band, and so the sound pressure in the sound field directly below the BGB increases at the corresponding frequency (refer to the curve of the sound pressure spectrum of the sound field SF1). However, the noise reduction effect around 6.8 Hz is worse compared with those at other frequency bands, especially in the sound field under the bridge. Although the BGB has an obvious noise reduction effect in the main vibration band, the sound pressure in the sound field below the slope of the two BGBs with thickened top plates is enhanced (refer to the curve of the sound pressure spectrum of sound field SF2), and the reducing effect on the sound field above the bridge is poor compared with other sound fields (refer to the curve of the sound pressure spectrum of sound field SF4).
Different factors in the propagation process will affect the sound waves radiated by the BGB. The main principle is complicated. The sound pressure of different sound field receiving points is generated mainly by the superposition of the sound waves produced by the four plates of the BGB, and these are affected by noise reduction measures. Therefore, the overall acoustic radiation capacity of the BGB under different working conditions must be further analyzed. As such, the sound power is compared, from which the effectiveness of the top plate-thickening design aspiring towards low acoustic radiation can be judged, as shown in Figure 8. As can be seen from Figure 8, both design solutions involving thickening the top plates of the BGBs can significantly reduce the acoustic radiation capacity of the BGBs. In the lower frequency band, the noise reduction effects of the two design solutions are extremely close; however, with increased frequency, the noise reduction effect of the top plate-thickening design is better, but the difference is not obvious. Further, as the frequency increases, the effects of both solutions are also extremely similar in the severe vibration band.
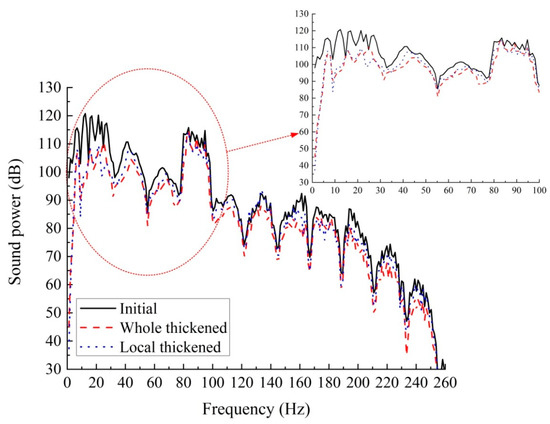
Figure 8.
Comparison of acoustic radiation power of the three working conditions.
In summary, in the two frequency bands where the acoustic radiation characteristics of the BGB are strongly expressed, the two design solutions are very effective in controlling the acoustic radiation capacity of the BGB. Still, thickening the whole top plate will have a better vibration reduction effect, especially with the violent vibration of the top plate.
To further analyze the noise reduction effects of the two design solutions, the maximum and minimum values of the radiated sound pressure of the initial BGB are used as the benchmark to compare the acoustic radiation patterns under the three operating conditions. This will enable us to further investigate the overall noise reduction effects of the two design solutions. As can be seen from Figure 9, the noise reduction effects of the two design solutions are better in the lower frequency band, and this greatly reduces the acoustic radiation range of the BGB. At the frequency where vibration shift occurs (24.8 Hz and 25.9 Hz), as shown in Figure 6, the acoustic radiation patterns change significantly. The main vibration band is severe, and although the acoustic radiation pattern also changes, the noise reduction effect is weaker compared with the lower frequency band. The vibroacoustic characteristics seen in the severe vibration band show that, for BGBs, simply reducing the vibration does not necessarily reduce the acoustic radiation, so the key effects of changing the vibration characteristics of BGBs in terms of reducing the acoustic radiation need to be studied in greater depth.
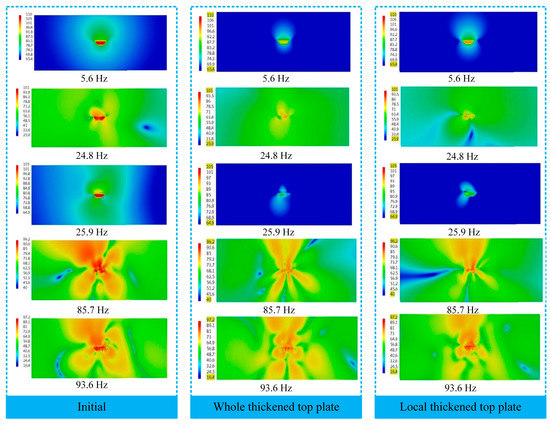
Figure 9.
The distribution of sound field patterns of BGBSs under the same reference values for three case conditions (Unit: dB).
5. Key Issues of BGB Top Plate Thickening Design in Acoustic Vibration Control
5.1. Analysis of Self-Vibration Characteristics of BGB under Three Working Conditions
Firstly, the self-vibration characteristics of the BGB before and after the design changes have been implemented are analyzed. Table 2 and Figure 10 give the partial self-vibrational characteristics and vibration patterns of the three types of BGBs, respectively, and analyze the effects of the two design options on the BGB’s self-vibration characteristics.

Table 2.
Comparison of self-vibration characteristics of three types of BGBs used in high-speed railways.
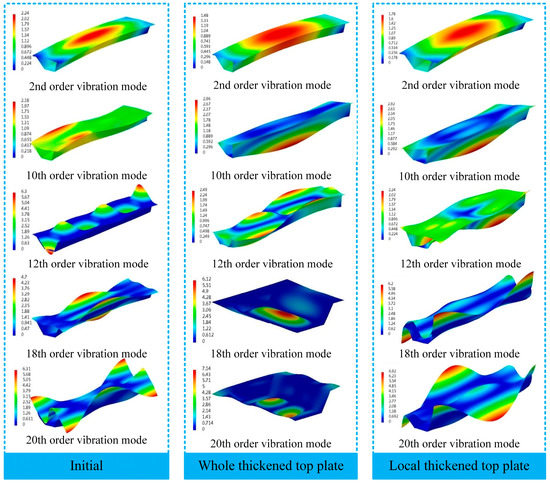
Figure 10.
Self-vibration model of BGBs (Unit mm).
From Table 2 and Figure 10, it can be seen that there is a certain increase in the natural frequency of the BGB with a thickened top plate and in that of the BGB with a locally thickened top plate, at the same order, between the initial and the natural frequency of the BGB with its whole top plate thickened. The modalities of the first two orders of the BGB under the three conditions give the overall self-oscillation characteristics; the initial BGB shows more local self-oscillation characteristics in the top plate, including the (m, n) order vibration patterns, which have a greater impact on the low-frequency acoustic radiation capability of the BGB. The whole and local self-oscillation characteristics in the higher-order modes occur simultaneously in most cases, forming the overall local self-oscillation characteristics of the BGB, and the local vibration characteristics of the top plate are more prominent in comparison. In regard to the design of BGB top plate thickening, the biggest change in the low-order vibration pattern is that the local self-oscillation characteristics of the top plate are weakened. In contrast, the bottom plate will show local self-oscillation characteristics, which will occur in both thickening designs. The local self-excitation of the wing plate will be enhanced in the process of vibrational energy transfer. At the same time, thickening the whole plate has less of an effect on the vibration of the wing plate, and a more significant effect on the vibration of the bottom plate, because the top plate under the rail that is being thickened is located above the BGB cavity and the wing plate, respectively.
In summary, the self-vibration characteristics of BGBs under all three operating conditions comprise the overall self-vibration characteristics, the local top plate self-vibration characteristics, and the overall local self-vibration characteristics of all plate members of the BGB. The top plate local vibration characteristics have the greatest influence on the acoustic radiation of the BGB. The top plate thickening design can reduce the probability of top plate local self-oscillation. This phenomenon plays a very important role in reducing the acoustic radiation of the BGB.
5.2. Vibration Acceleration Distribution Characteristics of BGB Subjected to External Excitation under Three Working Conditions
In order to reflect the overall vibration characteristics of the BGB subjected to external excitation at different frequencies under the three working conditions, the vibration acceleration distribution clouds of a BGB under external excitation are given in Figure 11.
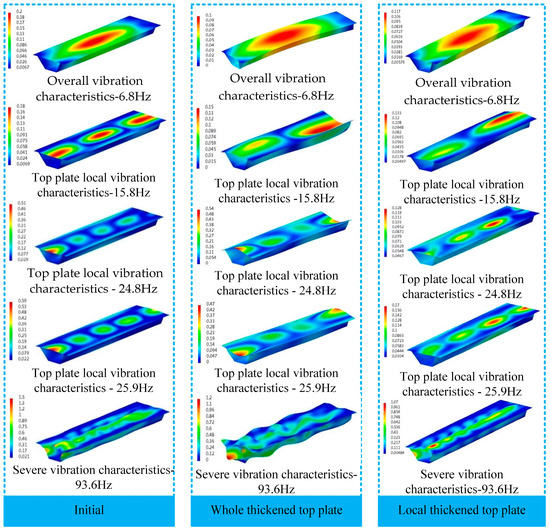
Figure 11.
Vibration acceleration characteristics and distribution under external excitation of three BGBs (Unit: m/s2).
From the comparison of the vibration acceleration clouds of the BGB shown in Figure 11, it can be seen that when thickening the top plate of the BGB, although the structure will still be dominated by the local vibration of the top plate subjected to external excitation, the bending vibration of the top plate will change significantly, i.e., the bending vibration characteristics of the BGB will be changed. At the same time, the vibration of the rest of the plate and of the wing plate of the BGB will be strengthened to a certain extent, and the vibrational amplitude will be significantly weakened. In the severe vibration frequency band, the vibration of the rest of the plate will be enhanced, reaching a state of vibration even stronger than that in the top plate. As shown in Figure 11 and Figure 12, the maximum vibration amplitudes of the entire BGB and the top plate at 93.6 Hz are 1.2 m/s2 and 0.72 m/s2, respectively, while the maximum amplitude of the improved BGB will be seen in the rest of the plate. That is, the vibration of the rest of the plate is obviously increased, and the vibration of the top plate is effectively suppressed. When thickening the top plate of the BGB, in addition to the overall vibration of the BGB, its vibration distribution will be changed, while in other cases, such as when applying 15.8 Hz, 24.8 Hz and 25.9 Hz, not only will the local vibration distribution of the top plate be changed, but that of the rest of the plate will be changed too.
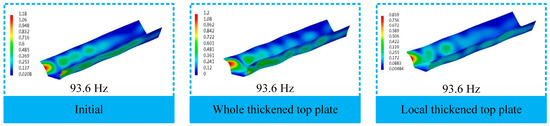
Figure 12.
Comparison of vibration acceleration clouds of the remaining plate members at 93.6 Hz (Unit: m/s2).
From the analysis of the self-vibration characteristics of the BGB and the vibration characteristics seen when it is subjected to external excitation, we can infer that the thickening of the top plate of the BGB significantly changes the vibrational distribution of the BGB. In terms of vibration reduction, although the overall vibration amplitude of the BGB will be weakened to a large extent, the vibration amplitude of the remaining plates will be strengthened. Ref. [11] shows that the acoustic radiation of a BGB is related to its capacity for resonance formation, its modal acoustic radiation efficiency, and the presence of violent vibration caused by external excitation. The first two are very closely related to the vibration distribution of the BGB. The above analysis shows that thickening the top plate of the BGB will result in a significant shift in the low-frequency small amplitude vibration frequencies in the center of the top and bottom plates. Secondly, the vibration acceleration distribution cloud shows that the local bending vibration characteristics of the top plate of the BGB will change significantly, and this will change the overall vibration distribution of the BGB, thus indicating that the vibration distribution plays a critical role in controlling the noise caused by low-frequency small amplitude vibration.
5.3. Exploration of the Key Influence of Vibration Distribution of BGB on Its Sound Radiation
Based on the effects of resonance and the modal acoustic radiation efficiency in the low-frequency band, Table 3 compares the acoustic vibration characteristics of the BGB at different frequencies under three different operating conditions. The natural vibration characteristics of the 2nd, 10th, 12th, and 18th orders are given in the low flutter magnet frequency band, vibration frequency, vibration pattern, maximum amplitude, and corresponding acoustic radiation characteristics of BGBs subjected to external excitation similar to their inherent frequencies, when under three working conditions, and also relate to the acoustic vibration characteristics of the severe vibration frequency band.

Table 3.
Comparison of acoustic vibration characteristics of BGBs used in a high-speed railway under three working conditions.
From the sound vibration characteristics of the BGB shown in Table 3, it can be seen that:
- (1)
- The BGBs under the three conditions have similar inherent frequencies at 6.8 Hz. The vibration pattern and external excitation vibration patterns take the form of first-order overall vertical bending, forming overall resonance in the BGBs. This vibration pattern does not correlate with strong acoustic radiation efficiency, and the BGBs under the three conditions show a high acoustic radiation capacity when subjected to very small vibration instead. This shows that, at this time, in the BGB subjected to resonance, a small vibration can give rise to a strong acoustic radiation capacity. Although the vibration of the BGB at 6.8 Hz is small, the thickened top plate also attenuates the vibration amplitude of the BGB, which can serve to reduce the acoustic radiation capacity of the BGB to a certain extent;
- (2)
- The 10th order vibration patterns of the BGBs under the three operating conditions change significantly, with the BGB with a thickened top plate showing bottom plate local self-oscillation characteristics. The acoustic radiation efficiency of the BGB with a thickened top plate is substantially reduced, which in turn reduces the acoustic radiation capacity of the BGB—for example, the maximum amplitudes of the initial BGB and that with a thickened top plate are 0.60 m/s2 and 0.54 m/s2, respectively, which is a smaller difference, but with a 9.6 dB sound power attenuation. Further, the sound radiation efficiency and the maximum vibration amplitude of the locally thickened BGB under the top rail plate have been reduced to a greater extent compared with the initial BGB, so the noise reduction effect is better. The comparison of the vibroacoustic characteristics between the two types of top plate-thickened BGBs and the initial BGB shows that the sound radiation efficiency of the attenuated BGBs in the low frequency band is better in terms of noise reduction as opposed to vibration reduction;
- (3)
- The vibroacoustic characteristics of the BGB in the 12th order mode under three operating conditions further affirm the results of the second analysis, and the significant reduction in sound radiation efficiency directly reduces the sound radiation capacity of the BGB. The web of locally thickened BGBs under the top rail plate also shows a certain resonance under these conditions, so the noise reduction effect of the design with the thickening of the whole top plate is better;
- (4)
- The natural vibration characteristics of the BGBs in the 18th order mode under the three operating conditions are quite different. As discussed above, the small-amplitude vibration of BGBs in this frequency band under external excitation will be shifted, and the maximum vibration amplitude of the two BGBs with thickened top plates will be increased substantially. Still, the problem is that the acoustic radiation capacity of the BGB with a thickened top plate under the rail will be slightly enhanced. In contrast, the sound radiation capacity of the BGB with a whole thickened top plate will be weakened. At this time, the natural vibration characteristics of the two top plate-thickened BGBs can be shown as the local natural vibration characteristics of the bottom plate and the top wing plate, respectively, and these affect the sound radiation efficiency of the BGB. This shows that the top plate of the BGB plays a particularly important role in its sound radiation and is a key area to control when aspiring to noise reduction. It also shows that, in the low-frequency band, the vibration of the BGB is not the most critical factor contributing to sound radiation;
- (5)
- The vibration patterns of the BGBs subjected to severe external excitation are similar under each of the three working conditions, and their acoustic radiation capacities decrease as the vibration is reduced. Therefore, the acoustic radiation of BGBs in the severe vibration band can be controlled mainly by reducing vibration.
From the above analysis, it can be seen that thickening the top plate changes the low-frequency oscillation distribution of the BGB, and so resonance can be avoided to a certain extent through the transfer of vibration frequency, thus weakening the resonance and the consequential sound radiation. The modal acoustic radiation efficiency of BGBs at lower frequency bands has a significant effect on their acoustic radiation capacity. According to the literature [11], when the local vibration in the top plate dominates the BGB’s overall vibration, the plate would ideally be thin. Therefore, by changing the (m, n) order vibration pattern of the top plate of the BGB, the modal acoustic radiation efficiency of the BGB is suppressed. Thus, the overall acoustic radiation efficiency of the BGB is weakened, as shown in Figure 13. Therefore, the vibration of the two kinds of top plate-thickened BGBs, as a result of small-vibration-peak sound radiation, can be limited to the lower frequency by changing the vibration distribution of the BGB in the noise control design. Changing the vibration distribution is the most critical factor in controlling the lower-frequency band noise of the BGB.
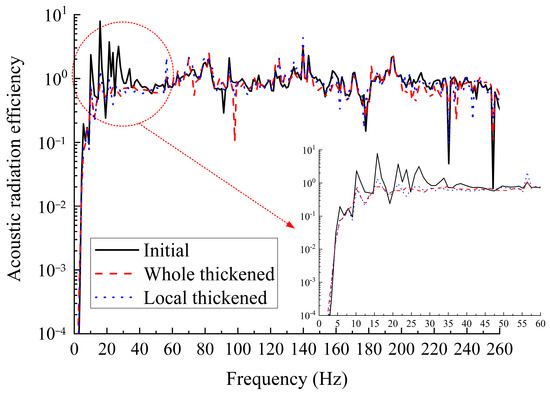
Figure 13.
Comparison of sound radiation efficiencies of the three types of BGBs.
In addition, changing the vibration distribution of the BGB will also greatly impact the propagation of sound radiation, and changing the sound radiation pattern of the BGB is very significant, as shown in Figure 14. The vibration characteristics of the whole top plate and the remaining three plates of the BGB when under the three operating conditions and subjected to 27.1 Hz show that the local bending vibration of the top plate is significantly changed at this time. The number of bending waves in the top plate is reduced under both top plate-thickening schemes. Analyses of the remaining three plates against the same benchmark show that, compared with the initial BGB, the vibration in most of the remaining plates is significantly enhanced, and the vibration area increases, resulting in a gradual increase in the area of radiated acoustic waves, but a narrowing of the area of concentrated acoustic radiation. The amplitude of the acoustic radiation in the area above the BGB is thus significantly weakened, but no obvious pattern of acoustic radiation arises as a result. This shows that the vibration distribution of the BGB also has a significant effect on its sound radiation pattern. When subjected to the severe vibration band, the vibration of the BGB will be more complex. The sound radiation distribution will show no obvious pattern because vibration damping reduces the overall sound radiation amplitude, as shown in Figure 15.
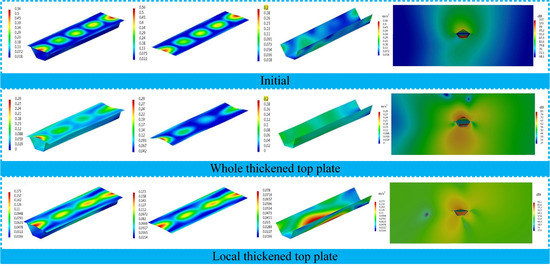
Figure 14.
Acoustic vibration characteristics of BGBs at 27.1 Hz under the three case conditions (unit of vibration: m/s2).

Figure 15.
Correspondence diagram of vibrational acoustic radiation of the BGB at 85.7 Hz under the three working conditions.
6. Conclusions
Based on the train–track–bridge interaction and acoustic boundary element theories, this study compared and analyzed the vibration and noise reduction effects of two design schemes involving thickening the top plate of a BGB. The relevant mechanisms and influencing factors of the design schemes were systematically analyzed. The main conclusions are as follows:
- (1)
- When designing a low-acoustic-radiation BGB, it is recommended to first focus on changing its vibration distribution. Thickening the top plate of the BGB can significantly change its vibration distribution—not only do the self-oscillation characteristics change significantly, but the vibrational frequency of similar vibration characteristics caused by external excitation will be shifted to the weaker frequency band of the initial BGB’s acoustic radiation. This evades the resonance effect caused by the small vibration resulting from the peak of acoustic radiation, and weakens the acoustic radiation efficiency of the BGB, thus reducing its acoustic radiation capacity. This will effectively reduce the acoustic radiation performance of a BGB in the lower frequency band;
- (2)
- Regarding the sound radiation, compared with the initial BGB, the two noise reduction schemes can limit the sound radiation to the weaker frequency band of the initial BGB, although the designs enhance the sound radiation characteristics and expand its range in this frequency band. Regarding the sound radiation in BGBs induced by severe vibration, compared to small vibration, it is entirely possible to achieve noise reduction by reducing vibration, and the implementation of noise reduction control measures is also easier under this approach. Therefore, thickening the top plate is a good solution for achieving low-sound-radiating BGBs, and the two design solutions involving top plate thickening described in this paper can contribute effectively to vibration and noise reduction;
- (3)
- Regarding the acoustic radiation characteristics of BGBs related to small-amplitude vibration in the lower frequency band, the design of vibration and noise reduction schemes is more difficult, and it is necessary to combine sound radiation mechanisms to formulate a more effective noise reduction scheme. If only a single damping measure is used, aiming at reducing the vibration, it is difficult to reduce the BGB radiation acoustic waves. The mechanisms involved in the two types of BGB noise reduction via top plate thickening and the key issues show that, by changing the vibration distribution of the BGB, the peak sound radiation, as determined by the characteristics of the BGB itself, can be reduced, so damping the vibration and changing the vibration distribution can be combined to achieve a better noise reduction effect.
The top plate of the BGB is the most important factor contributing to its acoustic radiation, and it should be considered in noise reduction design. Reducing the vibration characteristics of the top plate of the BGB (reducing the vibration amplitude and changing the vibration distribution) will directly determine the noise reduction effects of the design. Although the top plate thickening design scheme increases the vibration in the rest of the plate to a certain extent, it significantly affects the vibration suppression of the top plate of the BGB, so it can play a vital role in the noise reduction design.
The following problems with the current design model of using thickened top plates for noise reduction are worthy of further research:
- It is difficult in the current study to accurately determine the optimal thickness of the top plate of a low-noise-radiating BGB that meets all other requirements. An optimization algorithm can be adopted to determine the optimal top plate thickness for the low-frequency noise control of a BGB, the reference [46] maybe give us a great inspiration. Meanwhile, it is necessary to address all other engineering requirements.
- It will be difficult to use an optimization algorithm to determine the optimal thickness without mastering the key mechanisms of the noise reduction schemes.
Author Contributions
X.Z. (Xiaoan Zhang): Methodology. X.Z. (Xiaoyun Zhang): software. J.X.: validation. X.Z. (Xiaoyun Zhang), L.Y. and G.S.: formal analysis. G.S.: data curation. X.Z. (Xiaoan Zhang): writing—original draft preparation. J.X.: writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Gansu Province, grant numbers 22JR11RA152 and 22JR5RA344; the Young Doctor Foundation Education Department of Gansu Province, grant number 2022QB-063; Lanzhou Science and Technology Planning Project, grant number 2022-ZD-131; University Youth Fund Project of Lanzhou Jiaotong University, grant number 2021014; the Special Funds for Guiding Local Scientific and Technological Development by the Central Government, grant number 22ZY1QA005.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morata, T.C.; Themann, C.L.; Randolph, R.F.; Verbsky, B.L.; Byrne, D.C.; Reeves, E.R. Working in Noise with a Hearing Loss: Perceptions from Workers, Supervisors, and Hearing Conservation Program Managers. Ear Hear. 2005, 26, 529–545. [Google Scholar] [CrossRef]
- Babisch, W. Transportation noise and cardiovascular risk: Updated Review and synthesis of epidemiological studies indicate that the evidence has increased. Noise Health 2006, 8, 1–29. [Google Scholar] [CrossRef]
- Foglar, M.; Göringer, J. Influence of the structural arrangement of bridges on the noise induced by traffic. Eng. Struct. 2013, 56, 642–655. [Google Scholar] [CrossRef]
- Holt, D.E.; Johnston, C.E. Traffic noise masks acoustic signals of freshwater stream fish. Biol. Conserv. 2015, 187, 27–33. [Google Scholar] [CrossRef]
- Hauser, S.N.; Burton, J.A.; Mercer, E.T.; Ramachandran, R. Effects of noise overexposure on tone detection in noise in nonhuman primates. Hear. Res. 2017, 357, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.; Hemsworth, B.; Vincent, N. Experimental validation of the twins prediction program for rolling noise, part 1: Description of the model and method. J. Sound Vib. 1996, 193, 123–135. [Google Scholar] [CrossRef]
- Xie, X.; Wu, D.; Zhang, H.; Shen, Y.; Mikio, Y. Low-frequency noise radiation from traffic-induced vibration of steel double-box girder bridge. J. Vib. Control. 2011, 18, 373–384. [Google Scholar] [CrossRef]
- Li, X.; Liu, Q.; Pei, S.; Song, L.; Zhang, X. Structure-borne noise of railway composite bridge: Numerical simulation and experimental vali-dation. J. Sound Vib. 2015, 353, 378–394. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Song, L.; Su, B.; Li, Y. Vibrational and acoustical performance of concrete box-section bridges subjected to train wheel-rail excitation: Field test and numerical analysis. Noise Control. Eng. J. 2016, 64, 217–229. [Google Scholar] [CrossRef]
- Song, X.; Wu, D.; Li, Q.; Botteldooren, D. Structure-borne low-frequency noise from multi-span bridges: A prediction method and spatial distribution. J. Sound Vib. 2016, 367, 114–128. [Google Scholar] [CrossRef]
- Zhang, X.; Zhai, W.; Chen, Z.; Yang, J. Characteristic and mechanism of structural acoustic radiation for box girder bridge in urban rail transit. Sci. Total. Environ. 2018, 627, 1303–1314. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Thompson, D.J.; Xu, P.; Feng, Q.; Li, X. Investigation of train-induced vibration and noise from a steel-concrete composite railway bridge using a hybrid finite element-statistical energy analysis method. J. Sound Vib. 2020, 471, 115197. [Google Scholar] [CrossRef]
- Crockett, A.; Pyke, J. Viaduct design for minimization of direct and structure-radiated train niose. J. Sound Vib. 2000, 231, 883–897. [Google Scholar] [CrossRef]
- Ngai, K.; Ng, C.; Lee, Y. The control of structure-borne noise from a viaduct using floating honeycomb panel. JSME Int. J. Ser. C-Mech. Syst. Mach. Elem. Manuf. 2006, 49, 494–504. [Google Scholar] [CrossRef]
- Zhang, X.; Su, B.; Li, X. Study on the effect of fastener stiffness and damping on railroad box girder car-induced vibration noise. Vib. Shock 2015, 34, 150–155. (In Chinese) [Google Scholar]
- Wang, D.; Li, X.; Zhang, X.; Chen, G.; Yang, D. Study on the effect of track structure form on high frequency vibration in box girders. J. Civ. Eng. 2017, 50, 68–77. (In Chinese) [Google Scholar]
- Song, X.; Li, Q. Numerical analysis of vibration and noise reduction measures for concrete U-beams for rail transportation. J. Southeast Univ. (Nat. Sci. Ed.) 2019, 49, 460–466. (In Chinese) [Google Scholar]
- Liang, L.; Li, X.; Zheng, J.; Lei, K.; Gou, H. Structure-borne noise from long-span steel truss cable-stayed bridge under damping pad floating slab: Experimental and numerical analysis. Appl. Acoust. 2020, 157, 106988. [Google Scholar] [CrossRef]
- Zhang, X. Study on the Sound Generation Mechanism and Characteristics of Sound Radiation of Elevated Box Girder Bridge Structure for Rail Transportation. Ph.D. Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2019. (In Chinese). [Google Scholar]
- Zhai, W.; Zhao, C. Frontiers and challenges of modern rail transportation engineering science and technology. J. Southwest Jiaotong Univ. 2016, 51, 209–226. (In Chinese) [Google Scholar]
- Janssens, M.; Thompso, D.; Verheij, J. Application of a calculation model for low noise design of steel railway bridge. In Proceedings of the Internoise, Christchurch, New Zealand, 16–18 November 1998; pp. 1621–1625. [Google Scholar]
- Bos, J. Dutch group cuts steel bridge noise. Int. Railw. J. 1997, 38, 15–19. [Google Scholar]
- Han, J.; Wu, D.; Li, Q. Effect of plate thickness and ribbing on structural noise of slotted beams. J. Vib. Eng. 2012, 25, 589–594. (In Chinese) [Google Scholar]
- Zhang, X.; Li, X.; Liu, Q.; Wu, J.; Li, Y. Structural noise of concrete box girder and its influencing factors. J. Southwest Jiaotong Univ. 2013, 48, 409–414. (In Chinese) [Google Scholar]
- Zhang, X.; Zhai, W. Influences of local thickening top plate of high-speed railway box girder bridge on structure noise. In Proceedings of the 25th International Congress on Sound and Vibration (ICSV25), Hiroshima, Japan, 8 July 2018. [Google Scholar]
- Wang, J.; Lin, C.; Chen, B. Vibration suppression for high-speed railway bridges using tuned mass dampers. Int. J. Solids Struct. 2003, 40, 465–491. [Google Scholar] [CrossRef]
- Luu, M.; Zabel, C. An optimization method of multi-resonant response of high-speed train bridges using TMDs. Finite Elem. Anal. Des. 2012, 53, 13–23. [Google Scholar] [CrossRef]
- Miguel, L.F.; Lopez, R.H.; Torii, A.J.; Miguel, L.F.; Beck, A.T. Robust design optimization of TMDs in vehicle-bridge coupled vibration problems. Eng. Struct. 2016, 126, 703–711. [Google Scholar]
- Li, J.; Zhang, H.; Chen, S.; Zhu, D. Optimization and sensitivity of TMD parameters for mitigating bridge maximum vibration response under moving forces. Structures 2020, 28, 512–520. [Google Scholar] [CrossRef]
- Bai, X.; Liang, Q.; Huo, L. Vibration control of beam-model using tuned inerter enhanced TMD. J. Sound Vib. 2021, 510, 116304. [Google Scholar] [CrossRef]
- Poisson, F.; Margiocchi, F. The use of dynamic dampers on the rail to reduce the noise of steel railway bridges. J. Sound Vib. 2006, 293, 944–952. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, G.; Yang, J.; Zhang, X. MTMDs-based noise control for box-girder bridge of high speed railway. In Proceedings of the International Conference on Life System Modeling and Simulation (LSMS2017) and International Conference on Intelligent Computing for Sustainable Energy and Environment (ICSEE 2017), Nanjing, China, 22 September 2017. [Google Scholar]
- Zhang, X.; Li, X.; Liu, Q.; Zhang, Z.; Li, Y. Structure-borne noise control with MTMDs for a high-speed railway simply supported box-girder bridge. J. Vib. Shock. 2013, 32, 194–200. (In Chinese) [Google Scholar]
- Liu, L.; Xu, D. Analysis of noise radiation characteristics of box beam structures with open webs. J. Vib. Shock. 2016, 35, 204–210. (In Chinese) [Google Scholar]
- Liu, Q.; Li, X.; Zhang, X.; Liu, L. Study on vibration and noise reduction method of constrained damping layer of steel truss binding beam bridge. J. Railw. 2018, 40, 130–136. (In Chinese) [Google Scholar]
- Gu, M.; Li, W.; Li, Q. Effect of bridge section form on elevated noise of rail transit. J. Southwest Jiaotong Univ. 2019, 54, 715–723. (In Chinese) [Google Scholar]
- Alten, K.; Flesch, R. Finite element simulation prior to reconstruction of a steel railway bridge to reduce structure-borne noise. Eng. Struct. 2012, 35, 83–88. [Google Scholar] [CrossRef]
- Yin, Y.; Cai, C.; Chen, Z. Transient boundary element method based on acoustic radiation of box beam. J. Southwest Jiaotong Univ. 2015, 50, 1100–1105. (In Chinese) [Google Scholar]
- Zhang, T.; Zhou, L.; Luo, Y.; Wu, S. Low-frequency noise contribution sources and spatial distribution of concrete box girder for rail transit. J. Tongji Univ. (Nat. Sci. Ed.) 2020, 48, 332–339. (In Chinese) [Google Scholar]
- Zhang, X.; Zhai, W.; Shi, G.; Zhang, X. Influence of urban rail transit box girder bridge plates on their sound radiation. Noise Vib Control 2021, 41, 190–197. (In Chinese) [Google Scholar]
- Chen, G.; Zhai, W. A New Wheel/Rail Spatially Dynamic Coupling Model and its Verification. Veh. Syst. Dyn. 2004, 41, 301–322. [Google Scholar] [CrossRef]
- Zhai, W.; Xia, H.; Cai, C.; Gao, M.; Li, X.; Guo, X.; Zhang, N.; Wang, K. High-speed train-track-bridge dynamic interactions-Part I: Theoretical model and numerical simulation. Int. J. Rail Transp. 2013, 1, 3–24. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, S.; Zhai, W. A novel dynamics model for railway ballastless track with medium-thick slabs. Appl. Math. Model. 2019, 78, 907–931. [Google Scholar] [CrossRef]
- Zhai, W. Two simple fast integration methods for large-scale dynamic problems in engineering. Int. J. Numer. Meth. Eng. 1996, 39, 4199–4214. [Google Scholar]
- Hsiao, G.; Wendland, W. Boundary Integral Equations; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ghannadi, P.; Kourehli, S.S.; Mirjalili, S. A review of the application of the simulated annealing algorithm in structural health monitoring (1995–2021). Frat. Integrità Strutt. 2023, 17, 51–76. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).