Abstract
Efficiently modeling thin features using the finite-difference time-domain (FDTD) method involves a considerable reduction in the spatial mesh size. However, in real-world scenarios, such reductions can lead to unaffordable memory and CPU requirements. In this manuscript, we present two stable and efficient techniques in FDTD to handle narrow apertures on conductive thin panels. One technique employs conformal methods, while the other utilizes subgridding methods. We validate their performance compared to the classical Gilbert-Holland model and present experimental results in reverberation environments to shed light on these models’ actual confidence margins in real electromagnetic compatibility (EMC) scenarios.
1. Introduction
Modern on-board equipment is subject to aggressive electromagnetic environmental effects (E3) that impacts it directly and indirectly. As a paradigm, electromagnetic interference (EMI) and lightning indirect effects (LIE) are the main indirect threats to an aircraft from the EMC point-of-view [1]. EMC protection relies on shielded enclosures to safeguard sensitive equipment from disruptive E3 [2]. The shielding effectiveness (SE) parameter evaluates the protective capabilities of these enclosures by assessing their ability to shield the interior from external electromagnetic fields. Two main mechanisms affect enclosure shielding performance. Firstly, the conductive properties of enclosure walls play a vital role in mitigating electromagnetic wave penetration, reflecting or absorbing external electromagnetic radiation. Secondly, discontinuities in the enclosure walls, such as apertures (windows, slots, gaskets, junctions), can potentially facilitate electromagnetic wave propagation, posing vulnerabilities. This work proposes and evaluates three numerical models of slots on conductive panels to address both mechanisms, aiming to assess the overall enclosure shielding capabilities.
Numerical computational tools, including the finite-difference time-domain (FDTD) method, have become reliable tools for assessing EMC at all levels and scenarios. FDTD is formulated as an explicit method on a staggered time and space mesh known as Yee’s cube [3]. The FDTD method is conditionally stable and its analytical expression is determined by the causality Courant–Friedrichs–Lewy (CFL) criterion [4]. The CFL number (CFLN) bound the maximum allowable time step as a function of the minimum space step. Consequently, when dealing with small features, a refined space step is enforced in the usual FDTD, leading to a drastic decrease in the time step and, in turn, an increase in computer memory and CPU time required for the simulation.
An alternative approach to address these cases, is the Dispersive Magnetic Material Approximation (DMMA) method. These are a type of subcell model integrated into the FDTD method. Originally, it was proposed by Gilbert-Holland [5], and since then, numerous improvements have been done, e.g., [6]. The DMMA represents a robust method based on a capacitive approximation, wherein the narrow aperture is substituted with effective permittivity and permeability. Usually, these capacity models are frequency-dependent, but many authors use a static approximation to simplify the model and mitigate computational costs. Nonetheless, despite its strengths, DMMA exhibits certain drawbacks, which include:
- The finite-difference time-domain (FDTD) method typically uses a mesh size smaller than one-tenth of the wavelength, ; therefore, the width of a narrow slot is assumed to be (where is the wavelength, is the cell size of the mesh, and w is the width of the slot). Consequently, DMMA [7] is inherently applicable only when assuming a uniform field distribution on the slot;
- It assumes waves are perpendicularly impinging on the slot, with the electric field polarized in the direction across it;
- The magnetic condition must be placed on the dual grid, not matching the primary grid alignment used for PEC and dielectrics, thus making it tricky to implement in FDTD meshers.
Though DMMA proves to be robust even if these conditions are relaxed, in this paper, we show two full-wave computer-affordable alternatives allowing us to gain generality over the hypothesis of DMMA. They do not make any assumption either in the angle of incidence or in the electric polarization. The first one is the conformal approximation (CA) generalized from [8] and extended in ref. [9], which uses a locally conformal treatment embedded in the usual structured FDTD mesh. CA models the aperture and its bendings naturally and only assumes its width is smaller or almost equal to the FDTD cell size (). Similar to CA, there are other alternatives but based on the contour path [10]; these are used to treat overlapping joints and on metallic structures. The second method is based on a subgridding technique. In general, subgridding methods are very useful for solving multi-scale problems of general purpose, such as aperture problems [11,12]. In this paper, we use an orthogonalized integral subgridding (SG) technique based on ref. [13] and further proven in ref. [14]; this approach enables the utilization of a high cell resolution solely in the vicinity of the aperture, without any assumptions concerning the aperture width w, polarization, or angle of incidence. The proposed methods (CA and SG) are placed on the primary grid, unlike DMMA. This distinction offers several advantages, such as more natural and easier mesh generation in FDTD. These special characteristics make our approach promising for addressing problems in FDTD where the conductive surfaces are the mesher on the primary grid.
An essential aspect to consider in numerical EMC solutions is the preservation of ohmic connections between objects. In FDTD, structured meshers are not inherently capable of resolving details smaller than the cell size, which drastically compromises the accuracy of EMC problem resolution. This limitation leads to unwanted connections between meshed objects that do not exist in the original CAD model. To address this challenge, we propose the CA and SG methods, which enable the automation of this process, saving valuable time in the computer aided design (CAE) process and ensuring the reliability of electronic devices in diverse environments.
This work extends results shown in ref. [15], with three test cases. We first compare the proposed methods with a simple slot on an indefinite Perfect Electrically Conducting (PEC) or a CFC (modeled as a conductive thin panel). Then, we move to a PEC cage with one side either in PEC or CFC and a rectangular slot. Finally, we simulate a similar cage with curved slots, manufacture and test it in a reverberation chamber (RC) following the IEC 61000-4-21 standard [16]. Both limitations and robustness of DMMA are explored in each scenario.
2. Narrow Slots in FDTD
Let us first summarize, in short, the three numerical models used under FDTD for narrow slots compared in this work. Further details can be found in the references.
2.1. DMMA Model
The DMMA model does not directly address the geometry of the aperture. Instead, this method employs the slot admittance [17] as an equivalent model of its behavior. Through this formalism, the admittance is transformed into an artificial material with effective dispersive permittivity and permeability.
where C is the capacity per unit of length [5,18]. Generally, C depends on the frequency. However, for reducing the computational cost and simplicity, the capacity is taken as constant in frequency and, as a result, the relative effective parameter is also constant in frequency [7,19].
The aperture is determined by the cells centered on the magnetic-field components. Consequently, the electric fields are aligned across the slot (), and the magnetic fields are arranged transverse to its gap (), as depicted in Figure 1.
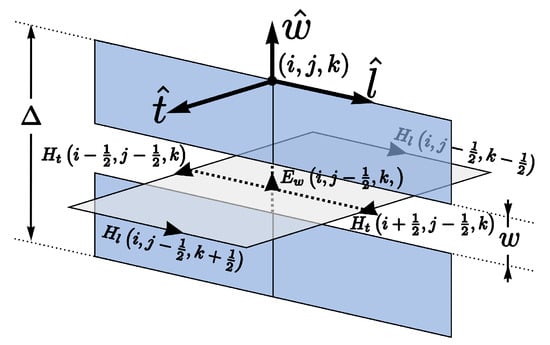
Figure 1.
FDTD cells with a narrow slot centered on the dual grid (magnetic cell).
2.2. Conformal Approximation (CA) Model
The CA method uses conformal techniques to manage the geometry of the aperture [9]. In this method, the aperture is placed within an FDTD cell. This approach simply assumes that the aperture size is smaller than the cell size, i.e., . Figure 2 (left) displays a narrow aperture embedded in a staircase surface mesh aligned with the tangential electric FDTD discretization lines, and Figure 2 (right) depicted a conformal mesh generated according to the aperture geometry and the orientation of the cells that contain the slot. The staircase cells, which initially contain the slot, are substituted with conformal cells. The geometry of these cells is adjusted to account for half of the slot surface lying on each conformal patch. The magnetic field in each zone is updated by computing the closed line integral of the tangential electric fields (, ) along its contour (see Figure 3), following Faraday’s law,
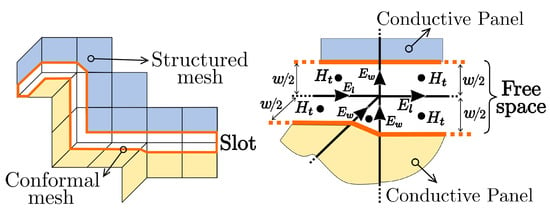
Figure 2.
FDTD cells with a narrow slot centered on the primary grid (electric edges). Furthermore, details of the fields that are involved in the CA model.
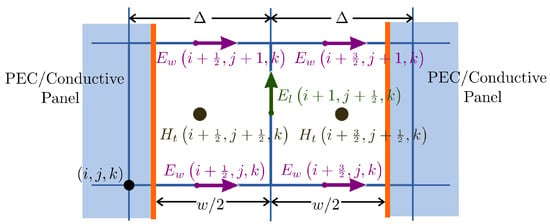
Figure 3.
Cross-section of a conformal cell used for aperture treatment using the CA procedure. Detail of the electric (E) and magnetic (H) fields involved in the method.
It shall be noted that the components are not meaningful with respect to , and can be removed in the last equation.
2.3. Subgridding Approximation Model
In general terms, SG methods involve progressively subdividing cells into finer cells. This approach enables an increase in resolution only where it is necessary to resolve fine geometric details, such as apertures. Most SG methods employ recursive division, successively reducing the cell size according to a specific aspect ratio (refinement ratio), from coarsest to finest. This results in a set of regions where the conventional Yee method can be used, except at the boundaries between two regions of different sizes, which require a specific procedure. The complexity of these algorithms lies in the transitions between different levels of subgrid, and each SG algorithm offers various solution approaches based on its particular algorithm.
The SG method used in this work [13,14] is based on dividing each FDTD cell using a 1:2 refinement ratio, which is applied recursively, resulting in multiple subgrid levels. Each subgrid level consists of cells with half cell size of the adjacent level (see Figure 4). To handle narrow apertures, the aim of this method is to position the aperture within the finest grid (with higher resolution). With a number of subgrid divisions, the aperture is resolved with a cell size times finer than the coarsest one.
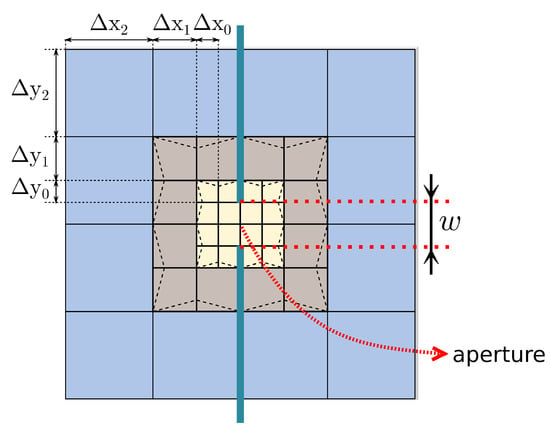
Figure 4.
Cross-section of a subgridded region with a refinement ratio of 1:2 and 3 subgrid divisions, . Each color corresponds to cells at the same subgrid level. The aperture of the slot is located in the finest grid.
This technique allows us to reduce the cell size within and around the aperture, where the field variations are significant. All of the field components are computed to naturally consider every polarization and propagation direction. Though more costly computationally than DMMA and CA, this method is more accurate and allows us to handle arbitrarily-sized apertures. Furthermore, the algorithm is globally much more efficient than the usual FDTD when combined with causal local time stepping technique, only requiring reductions of the CFL by a factor of [14].
It should be noted that, as a disadvantage compared to CA and DMMA, the SG method requires adjusting the size of the slot aperture to fit an integer multiple of the cell size. This adjustment may result in an error equal to or less than half of the cell size in the finest grid. However, this error is mitigated when using a high number of subgrid levels.
3. CFC Numerical Modeling: SGBC for Lossy Thin Panels
This paper employs DMMA, CA, and SG to analyze slots drilled in PEC plates and carbon fiber composite (CFC) panels. For the CFC panels, a convenient subcell model is assumed, treating them as finite-conductivity bulk thin panels (typically tens of kS/m) with a thickness smaller than the cell size. In this work, we have used the Subgridding Boundary Condition (SGBC) techniques described in ref. [20] to model this situation. However, it is worth noting that there are other different techniques based on an impedance model that are equally valid for the same purpose, as presented in the articles [21,22]. The SGBC method calculates the fields on both faces of the panel by conducting a full-wave 1D simulation inside the panel. For this purpose, the panel is meshed with a fine spatial step only along the direction normal to the panel. The size of this fine mesh is chosen to ensure a precise resolution of the wavelength and skin depth at the maximum frequency of interest within the panel [23,24]. Details for the extension of SGBC to CA can also be found in ref. [15].
4. Results
DMMA, CA, and SG have been analyzed in three scenarios, and we have taken the standard FDTD results with a dense space resolution and without any additional sub-algorithm as reference.
- A.
- A classical validation consisting of a narrow slot placed on an indefinite PEC or CFC, aiming to examine the limits of the normal propagation hypothesis and the field homogeneity along the slot when the thickness is the same as the FDTD cell size;
- B.
- A typical PEC cage with one of its sides covered either by PEC or CFC, including a rectangular slot with the same width as the FDTD cell size. We evaluate the SE at the center of the cage when a tilted plane wave illuminates it. Here, we seek to assess the actual robustness of DMMA in a highly resonant scenario;
- C.
- Finally, a real PEC cage with one side, either in PEC or CFC, is tested in an RC, and experimental results are known. To mimic the experimental RC in FDTD simulations, we employ a stochastic plane-wave incidence [25]. Results aim to show a typical EMC real scenario to illustrate the expected differences in simulation versus measurements.
4.1. Slot on Indefinite Plate
We have used a setup where:
- The effects of non-normal propagation are relevant: we illuminate one side of the slot with a dipole source and observe the field on the other side at a point where there is no straight line of vision to the source (Figure 5 shows the positions of the dipole and probe with respect to the slot);
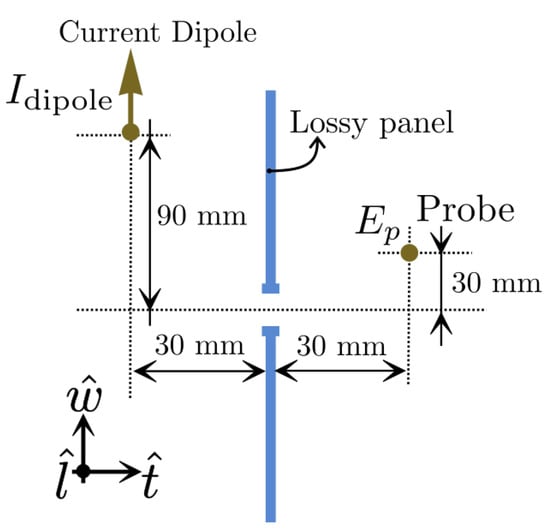 Figure 5. Dipole in front of a narrow slot on an indefinite conductive plane panel.
Figure 5. Dipole in front of a narrow slot on an indefinite conductive plane panel. - The slot width is not thin with respect to the FDTD space step, specifically .
The insertion loss (IL) function of the electric field is found by
We use a Hertzian dipole along , excited with a current excitation having a Gaussian time profile with a decay in amplitude at a frequency of 5 GHz. The slot has a width of and is placed on a plane aligned with the grid. We compare the results obtained using CA and DMMA with a spatial resolution of to FDTD with a higher spatial resolution of .
Figure 6 shows the results of the IL function for both a PEC and a conductive plane. The conductive plane is modeled using the SGBC method, with a conductivity of and a thickness of 1 mm. Note that the tendency of the conductive panel at low frequency (LF) (when the skin depth is greater than the thickness of the panel) is similar with and without the slot. However, above the first resonance, the slot response dominates the results. The convergence of the CA model and brute force at LF is similar to the conductive panel case. In our view, the observed differences with the DMMA model may be attributed to the fact that the DMMA model does not modify the surfaces affected by the slot, whereas the CA method naturally handles them in a conformal integral manner. This difference becomes particularly relevant when the slot dimensions are similar to the cell size. Notably, it is worth noting that this drawback does not appear for PEC panels, as the tangential electric fields are directly zero.
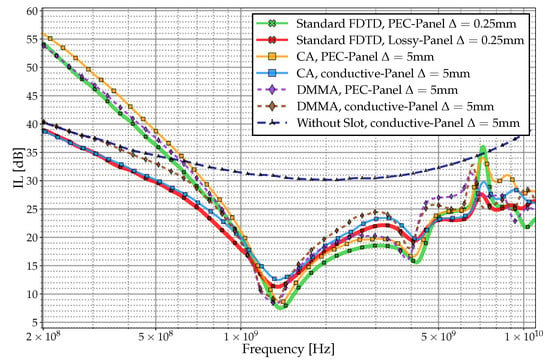
Figure 6.
Comparison of the IL results of CA and DMMA methods for a narrow slot on a conductive indefinite plane.
Though DMMA agrees with full-wave methods at LF, we observe that CA outperforms DMMA over the first resonance when the DMMA method loses precision because the assumption that the fields are uniform on it begins to be false.
4.2. Enclosure under Plane Wave Incidence
In this test case, we evaluated the SE of a rectangular PEC cavity with dimensions . The cavity has a slot on one of its rectangular faces, which can be either PEC or made of a CFC material. For the CFC case, we use a SGBC numerical model with an equivalent conductivity of 200 S/m and a thickness of 1 mm. The cavity is illuminated with a non-normal plane wave at an angle of (see Figure 7). The SE is evaluated at the center point of the cavity for both the electric fields and the magnetic field ,
where and are the electric and magnetic fields evaluated in free space at a location coinciding with the center of the original cavity, is the field generated by the plane wave, and is the intrinsic impedance of free space.
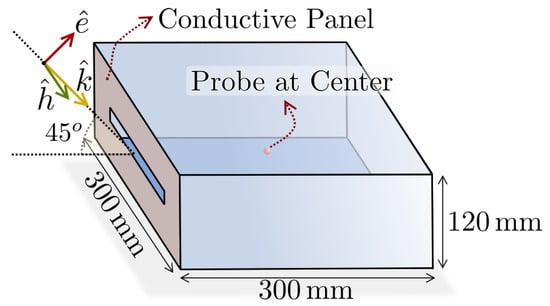
Figure 7.
Geometry of a rectangular PEC cavity with slot mounted on conductive face. The slot dimensions are 100 mm × 5 mm.
Several setups for the cage are compared: a slot on the PEC cover, a slot on the conductive panel cover, an open box (without conductive panel), and a conductive panel without a slot. The aim is to compare and understand the contributions of each of the different propagation ways. We also include an analytical formulation of the slot on the PEC panel given in ref. [26].
The SE behavior of an enclosed entity can be determined by three main variables: the size of the object, the presence of any apertures, and the conductivity properties of its wall materials. Two regions can be considered for each: LF and high frequency HF. The SE behavior is a function of a combination of the three variables mentioned above, thereby delineating distinct regions.
The proposed cage, which includes a conductive panel and slot, exhibits three distinct regions. At LF, before the cutoff frequency of the slot and the cage, the is characterized by an attenuation of , while remains constant (assuming that the cage is made using electrically conductive materials for its walls). In this region, the dominant factor influencing both SE is the largest opening in the cage, determined by the size of the conductive panel, as depicted in Figure 8 and Figure 9. The trend is similar to the “open box” curve (without a conductive panel). At medium frequencies (MF), currents start to be induced around the openings following Lenz’s law. This inductive behavior results in an increase of SE with a slope of per decade in the LF region. Consequently, the remains constant, while the experiences a gain of . The resonant zone occurs at HF where the slot size becomes comparable to the wavelength. In this regime, the finite conductivity of the material does not have any influence, and the resonances are determined by both the slot and the cage size.
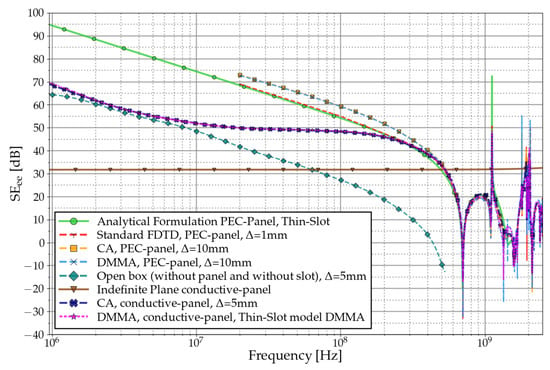
Figure 8.
Electric field shielding effectiveness () evaluated at the central position of the rectangular enclosure. These results correspond to the Test Case shown in Figure 7.
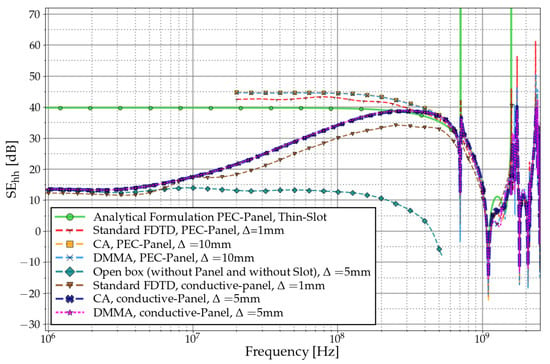
Figure 9.
Magnetic field shielding effectiveness () evaluated at the central position of the rectangular enclosure. These results correspond to the Test Case shown in Figure 7.
4.3. Cage with Curved Slots: Numerical and Experimental Data
The final test setup evaluates the shielding effectiveness in a real test case proposed in ref. [27], measured at INTA facilities in an RC, following the standards [16,28]. The box used in the experiments has dimensions of m (width), m (height), and 1 m (length), and it is primarily made of galvanized steel. One face of the box is removable, allowing for different material panels to be placed inside (Figure 10). In the first test case, the removable panel is made of aluminum and features two semicircular slots, as indicated in Figure 11. In the second test case (Figure 12), the panel is made of CFC material (referred to as CFC-“blue” in ref. [27,29]), and it has two pairs of semicircular slots. The box has been tested in the reverberation chamber at INTA facilities. This setup exposes the apertures to waves with all possible polarizations and directions of incidence. The metals like aluminum and galvanized steel are considered as PEC. The CFC material has a thickness of 2 mm, and we use a SGBC numerical model with an equivalent conductivity of at the frequencies of interest. To simulate the reverberating environment, we use a statistical superposition of plane waves, with random propagation and polarization [25].

Figure 10.
Experimental setup of a rectangular enclosure with a semicircular slot on the front panel.
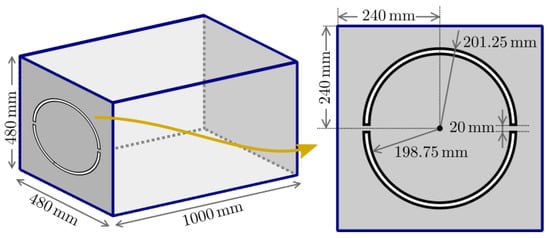
Figure 11.
Sketch of the rectangular enclosure with two semicircular centered slots.
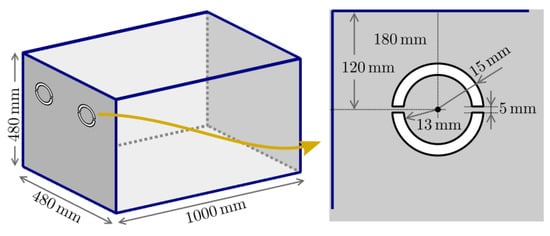
Figure 12.
Sketch of a rectangular enclosure with a pair of semicircular slots.
Figure 13 and Figure 14 compare results for these configurations using DMMA, CA, standard FDTD, and SG. The minimal cell size for SG is , and the maximum is mm. Results show that DMMA underestimates the SE, significantly below the first resonance. We can attribute it to the stochastic nature of the incident waves, making the DMMA fail to cope with non-normal incidence relevant.
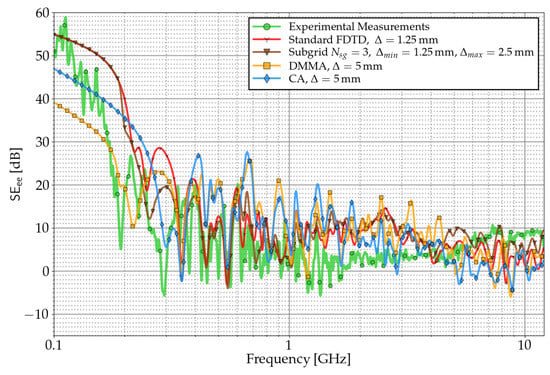
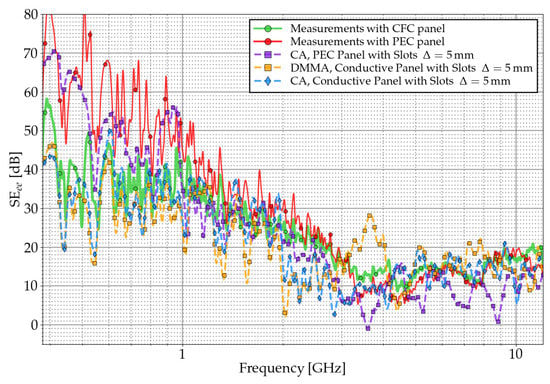
Table 1 Shows the required computational resources. DMMA and CA have employed a cell size of . For SG, only the box walls and apertures lie within the finest grid region with two refinement levels = 1, 3. Note that the test case proposed here is where the subcell method for narrow slots (CA and DMMA) is already computationally very efficient. In this sense, SG is less competitive in computing performance than subcell techniques.

Table 1.
Efficiency results.
5. Conclusions
This paper proposes and evaluates two subcell full-wave alternatives to the classical capacitive Gilbert-Holland DMMA FDTD model for analyzing the coupling through narrow slots on conducting thin panels: a conformal one (CA) and a subgridding (SG) one. The DMMA method exhibits deficiencies when normal propagation and uniformity of the fields around the slot are not fulfilled. On the other hand, SG and CA do not have this limitation, since they consider all the field components around the slot. Therefore, when the polarization or the incidence angle is relevant, subgridding and CA present better results than DMMA. Three test cases are presented:
- A classical validation consisting of a narrow slot on PEC and conductive panel, where DMMA assumptions of the normal propagation and uniform field distribution across it produce worse results than CA at HF;
- A PEC cage with one of its sides covered either by PEC or conductive panel with a rectangular slot under plane wave incidence. There, the actual robustness of DMMA is shown compared to the full-wave CA method since the cage resonances dominate over the slot ones at HF;
- A real PEC cage with one side, either in PEC or in CFC, in a RC compared with experimental results. Results show a typical EMC real scenario and help the engineer understand the margins in the differences in simulation versus measurements. Results show that DMMA underestimates the SE, especially below the first resonance. This effect does not appear in the well-controlled cage of the previous test case, and we have attributed it to the stochastic nature of the incident waves. For higher frequencies, no clear conclusions can be drawn since the cage resonances clutter the results, and only worst-case margins could be extracted by an EMC practitioner.
Next, we will explore the integration of the Conformal Approximation (CA) method and the subgridding technique proposed in this work for Electromagnetic Compatibility (EMC) applications. By combining these two approaches, we aim to effectively address more complex EMC scenarios, especially in conductive structures with overlapping joints. This integration could lead us to develop a stable and computational efficient method, surpassing the limitations of each method individually, and opening up new possibilities for EMC solutions in various engineering and applied sciences contexts.
Author Contributions
Conceptualization, M.R.C., A.J.M.V., B.P., M.F., D.P., A.R.B., A.G.B. and S.G.G.; methodology, M.R.C., A.J.M.V., B.P. and A.G.B.; software, M.R.C., A.J.M.V. and A.G.B.; validation, M.R.C., B.P., M.F. and D.P.; formal analysis, M.R.C., A.J.M.V., A.R.B., A.G.B. and S.G.G.; investigation, M.R.C., A.J.M.V., A.R.B., A.G.B. and S.G.G.; resources, B.P., M.F., D.P. and S.G.G.; data curation, B.P., M.F., D.P. and A.G.B.; writing—original draft preparation, M.R.C., B.P. and S.G.G.; writing—review and editing, M.R.C., A.J.M.V., M.F., D.P., A.R.B. and A.G.B.; visualization, A.J.M.V., B.P., M.F. and A.G.B.; supervision, S.G.G.; project administration, D.P., A.R.B. and S.G.G.; funding acquisition, D.P., A.R.B. and S.G.G. All authors have read and agreed to the published version of the manuscript.
Funding
Funded by the European Union under GA no 101101961—HECATE. Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or Clean Aviation Joint Undertaking. Neither the European Union nor the granting authority can be held responsible for them. The project is supported by the Clean Aviation Joint Undertaking and its Members and, by Spanish Ministry of Science and Innovation (MICINN) under projects eSAFE-UAV PID2019-106120RB-C32; PID2019-106120RB-C33.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FDTD | Finite-difference time-domain |
| EMC | Electromagnetic compatibility |
| EMI | Electromagnetic interference |
| LIE | Lightning indirect effects |
| CFC | Carbon Fiber Composites |
| CFL | Courant–Friedrichs–Lewy |
| DMMA | Dispersive magnetic material approximation |
| PEC | Perfect electrically conducting |
| CA | Conformal approximation |
| SG | Subgridding |
| RC | Reverberating chamber |
| SE | Shielding effectiveness |
| IL | Insertion loss |
| HF | High frequencies |
| MF | Medium frequencies |
| LF | Low frequencies |
References
- Radasky, W.A.; Baum, C.E.; Wik, M.W. Introduction to the special issue on high-power electromagnetics (hpem) and intentional electromagnetic interference (iemi). IEEE Trans. Electromagn. Compat. 2004, 46, 314–321. [Google Scholar] [CrossRef]
- EUROCAE ED-107A/SAE ARP5583A Std; Guide to Certification of Aircraft in a High-Intensity Radiated Field (HIRF) Environment. SAE International: Warrendale, PA, USA, 2010.
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics the Finite-Differences Time Domain Method; Artech House: Debham, MA, USA, 2005. [Google Scholar]
- Gilbert, J.; Holland, R. Implementation of the thin-slot formalism in the finite-difference emp code thredii. IEEE Trans. Nucl. Sci. 1981, 28, 4269–4274. [Google Scholar] [CrossRef]
- Wu, C.T.; Pang, Y.H.; Wu, R.B. An improved formalism for FDTD analysis of thin-slot problems by conformal mapping technique. IEEE Trans. Antennas Propag. 2003, 51, 2530–2533. [Google Scholar]
- Gkatzianas, M.; Tsiboukis, T. Thin-slot/thin-layer subcell fdtd algorithms for em penetration through apertures. Electromagnetics 2003, 23, 119–133. [Google Scholar] [CrossRef]
- Dey, S.; Mittra, R. A locally conformal finite-difference time-domain (FDTD) algorithm for modeling three-dimensional perfectly conducting objects. IEEE Microw. Guid. Wave Lett. 1997, 7, 273–275. [Google Scholar] [CrossRef]
- Cabello, M.R.; Angulo, L.D.; Alvarez, J.; Bretones, A.R.; Gutierrez, G.G.; Garcia, S.G. A new efficient and stable 3D conformal FDTD. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 553–555. [Google Scholar] [CrossRef][Green Version]
- Yan, L.; Fang, M.; Zhao, X.; Feng, B.; Li, J.; Liu, Q.; Zhou, H. Efficient shielding effectiveness prediction of metallic structures with three-dimensional arbitrary thin slots using extended CP-FDTD. IEEE Trans. Electromagn. Compat. 2019, 61, 1353–1361. [Google Scholar] [CrossRef]
- Kuo, C.W.; Kuo, C.M. Finite-difference time-domain analysis of the shielding effectiveness of metallic enclosures with apertures using a novel subgridding algorithm. IEEE Trans. Electromagn. Compat. 2016, 58, 1595–1601. [Google Scholar] [CrossRef]
- Bekmambetova, F.; Zhang, X.; Triverio, P. Acceleration of shielding effectiveness analysis using stable FDTD subgridding. In Proceedings of the IEEE 26th Conference on Electrical Performance of Electronic Packaging and Systems (EPEPS), San Jose, CA, USA, 15–18 October 2017; pp. 1–3. [Google Scholar]
- Ritter, J.; Arndt, F. A generalized 3d subgrid technique for the finite-difference time domain method. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Denver, CO, USA, 8–13 June 1997; Volume 3, pp. 1563–1566. [Google Scholar]
- Valverde, A.M.; Cabello, M.R.; Sánchez, C.C.; Bretones, A.R.; Garcia, S.G. On the effect of grid orthogonalization in stability and accuracy of a fdtd subgridding method. IEEE Trans. Antennas Propag. 2022, 70, 10769–10776. [Google Scholar] [CrossRef]
- Cabello, M.R.; Martín Valverde, A.J.; Plaza Gallardo, B.; Frövel, M.; Poyatos Martínez, D.; Rubio Bretones, A.; González García, S. A subcell fdtd scheme implementation for thin slot modeling. In Numerical Electromagnetic and Multiphysics Modeling and Optimization for RF, Microwave, and Terahertz Applications (NEMO); IEEE: New York, NY, USA, 2022. [Google Scholar]
- IEC 61000-4-21:2011; Electromagnetic Compatibility (EMC): Testing and Measurement Techniques—Reverberation Chamber Test Methods. International Electrotechnical Commission: Geneva, Switzerland, 2011.
- Harrington, R.F. Time-Harmonic Electromagnetic Fields; IEEE Press Series on Electromagnetic Wave Theory; Wiley: Hoboken, NJ, USA, 2001; ISBN 9780470546710. [Google Scholar]
- Smythe, W.B. Static and Dynamic Electricity; OSTI: Oak Ridge, TN, USA, 1988. [Google Scholar]
- Gkatzianas, M.A.; Balanis, C.A.; Diaz, R.E. The gilbert-holland fdtd thin slot model revisited: An alternative expression for the in-cell capacitance. IEEE Microw. Wirel. Compon. Lett. 2004, 14, 219–221. [Google Scholar] [CrossRef]
- Cabello, M.R.; Angulo, L.D.; Bretones, A.R.; Martin, R.G.; Garcia, S.G.; Alvarez, J. A new fdtd subgridding boundary condition for fdtd subcell lossy thin-layer modeling. In Proceedings of the IEEE International Symposium on Antennas and Propagation (APSURSI), Fajardo, PR, USA, 26 June–1 July 2016; pp. 2031–2032. [Google Scholar]
- Beggs, J.H.; Luebbers, R.J.; Yee, K.S.; Kunz, K.S. Finite-difference time-domain implementation of surface impedance boundary conditions. IEEE Trans. Antennas Propag. 1992, 40, 49–56. [Google Scholar] [CrossRef]
- Sarto, M. A new model for the FDTD analysis of the shielding performances of thin composite structures. IEEE Trans. Electromagn. Compat. 1999, 41, 298–306. [Google Scholar] [CrossRef]
- Cabello, M.R.; Angulo, L.D.; Alvarez, J.; Flintoft, I.D.; Bourke, S.; Dawson, J.F.; Martín, R.G.; Garcia, S.G. A hybrid crank-nicolson fdtd subgridding boundary condition for lossy thin-layer modeling. IEEE Trans. Microw. Theory Tech. 2017, 65, 1397–1406. [Google Scholar] [CrossRef]
- Cabello, M.R.; Angulo, L.D.; Alvarez, J.; Bretones, A.R.; Garcia, S.G. A new conformal fdtd for lossy thin panels. IEEE Trans. Antennas Propag. 2019, 67, 7433–7439. [Google Scholar] [CrossRef]
- Moglie, F.; Pastore, A.P. Fdtd analysis of plane wave superposition to simulate susceptibility tests in reverberation chambers. IEEE Trans. Electromagn. Compat. 2006, 48, 195–202. [Google Scholar] [CrossRef]
- Robinson, M.P.; Benson, T.M.; Christopoulos, C.; Dawson, J.F.; Ganley, M.D.; Marvin, A.C.; Porter, S.J.; Thomas, D.W. Analytical formulation for the shielding effectiveness of enclosures with apertures. IEEE Trans. Electromagn. Compat. 1998, 40, 240–248. [Google Scholar] [CrossRef]
- de Francisco, P.G.; Martinez, D.P.; Gallardo, B.P.; Bocanegra, D.E.; Romero, S.F. Limitations in the measurement of the shielding effectiveness of aeronautical multi-ply cfc laminates. In Proceedings of the 2019 International Symposium on Electromagnetic Compatibility-EMC EUROPE, Barcelona, Spain, 2–6 September 2019; pp. 662–667. [Google Scholar]
- 299.1-2013; IEEE Standard Method for Measuring the Shielding Effectiveness of Enclosures and Boxes Having All Dimensions between 0.1 m and 2 m. The Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2014.
- Ramos, D.; Cidrás, J.; Plaza, B.; Moravec, C.; de la Torre, A.; Frövel, M.R.K.; Poyatos, D. Novel electromagnetic characterization methods for new materials and structures in aerospace platforms. Materials 2022, 15, 5128. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).