Mission and Reliability Driven Fleet-Level Selective Maintenance Planning and Scheduling Two-Stage Method
Abstract
1. Introduction
2. Equipment Group Maintenance Planning Model Based on Service Age Regression Model
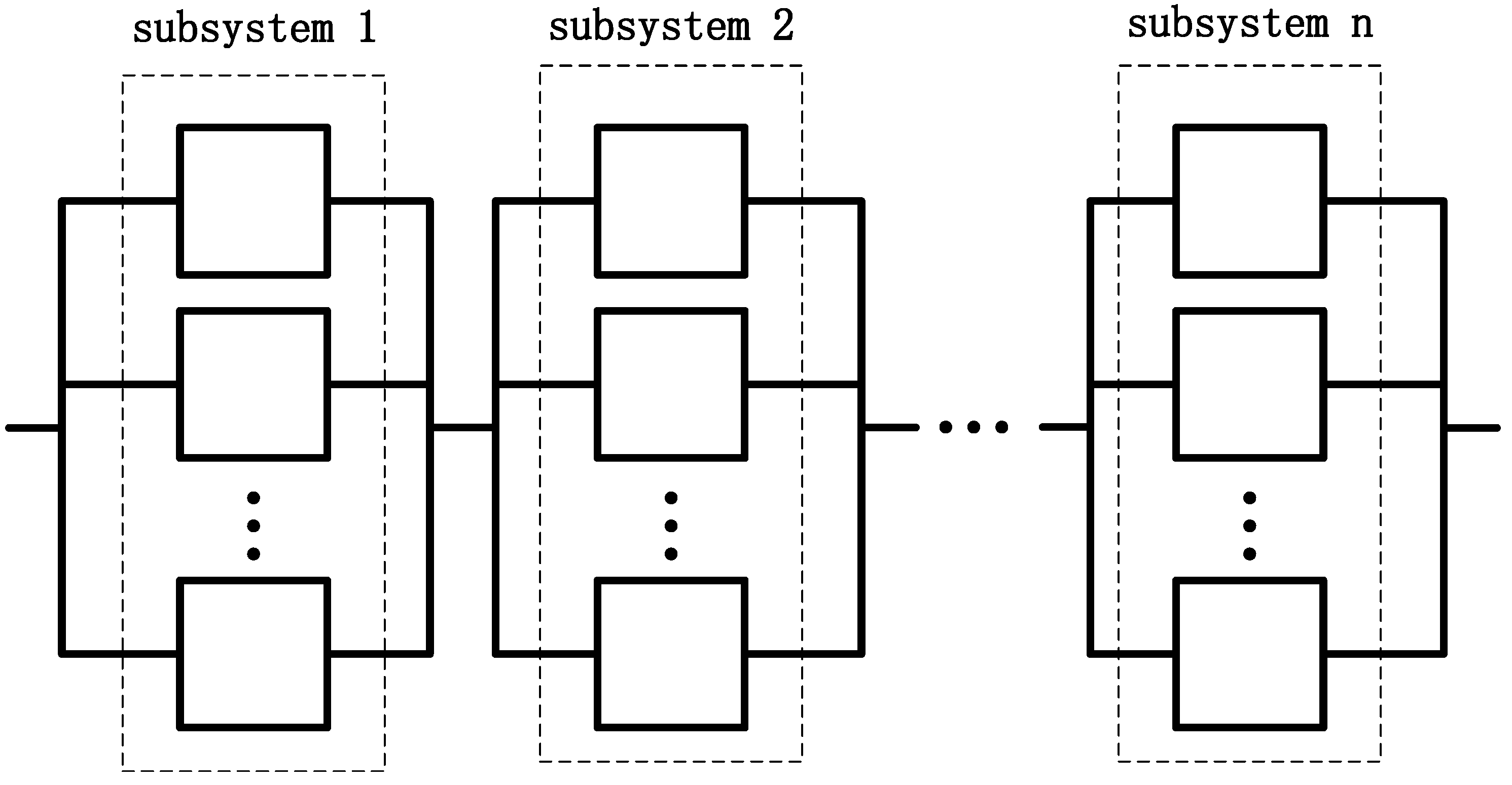
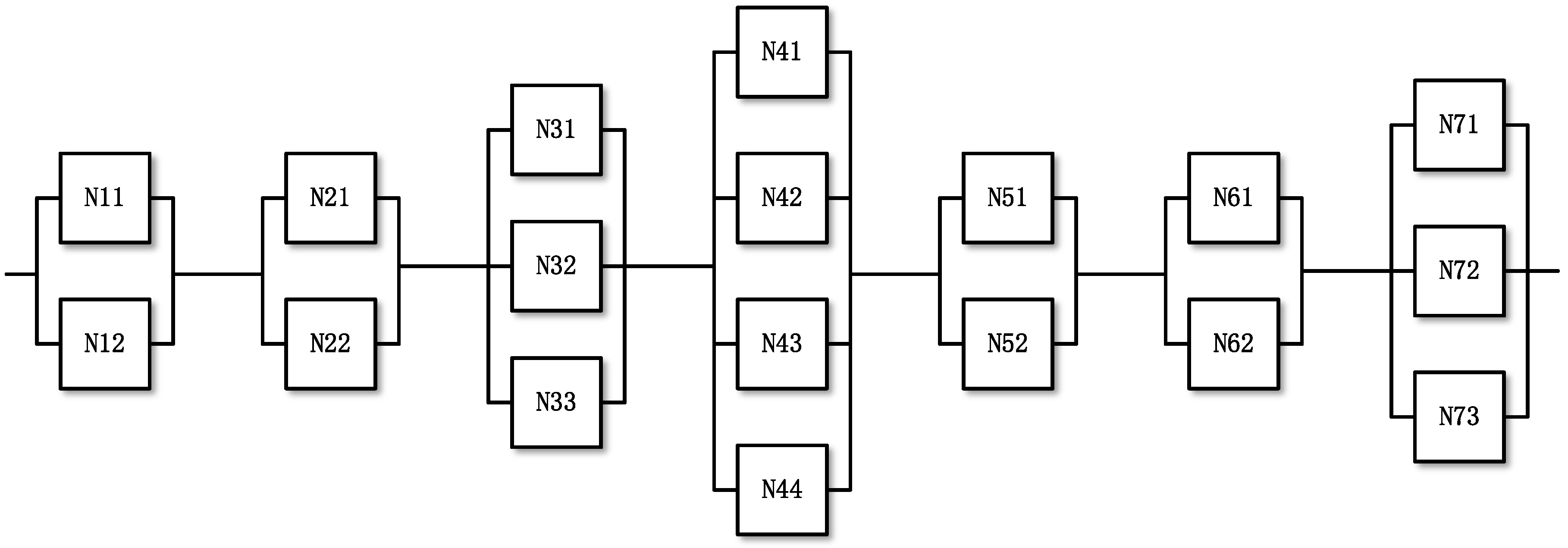
2.1. Problem Description and Model Assumptions
2.2. Optimization Objective
2.2.1. The Probability of the Fleet to Satisfy the Requirement in the Next Mission
2.2.2. Maintenance Cost of Equipment Group
2.2.3. Constraints in the Maintenance Task
2.2.4. Optimization Model
3. Mission and Reliability Driven Fleet Selective Maintenance Planning Two-Stage Method
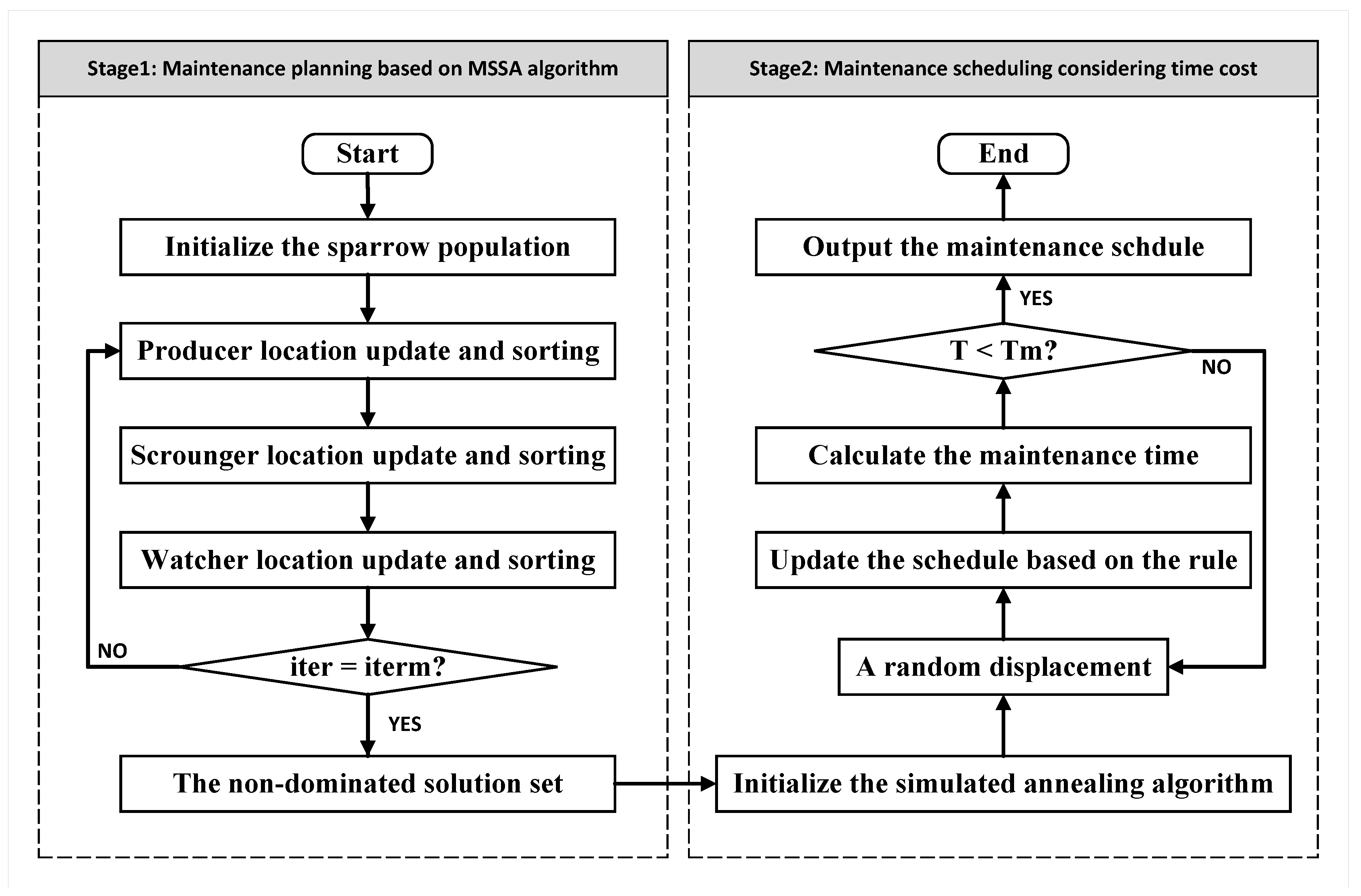
3.1. A Two-Stage Method Considering Multiple Optimization Objectives and Maintenance Time Constraints
3.2. Algorithm Design
3.2.1. An Improved Sparrow Search Algorithm Used for Solving Selective Maintenance Planning
- (1)
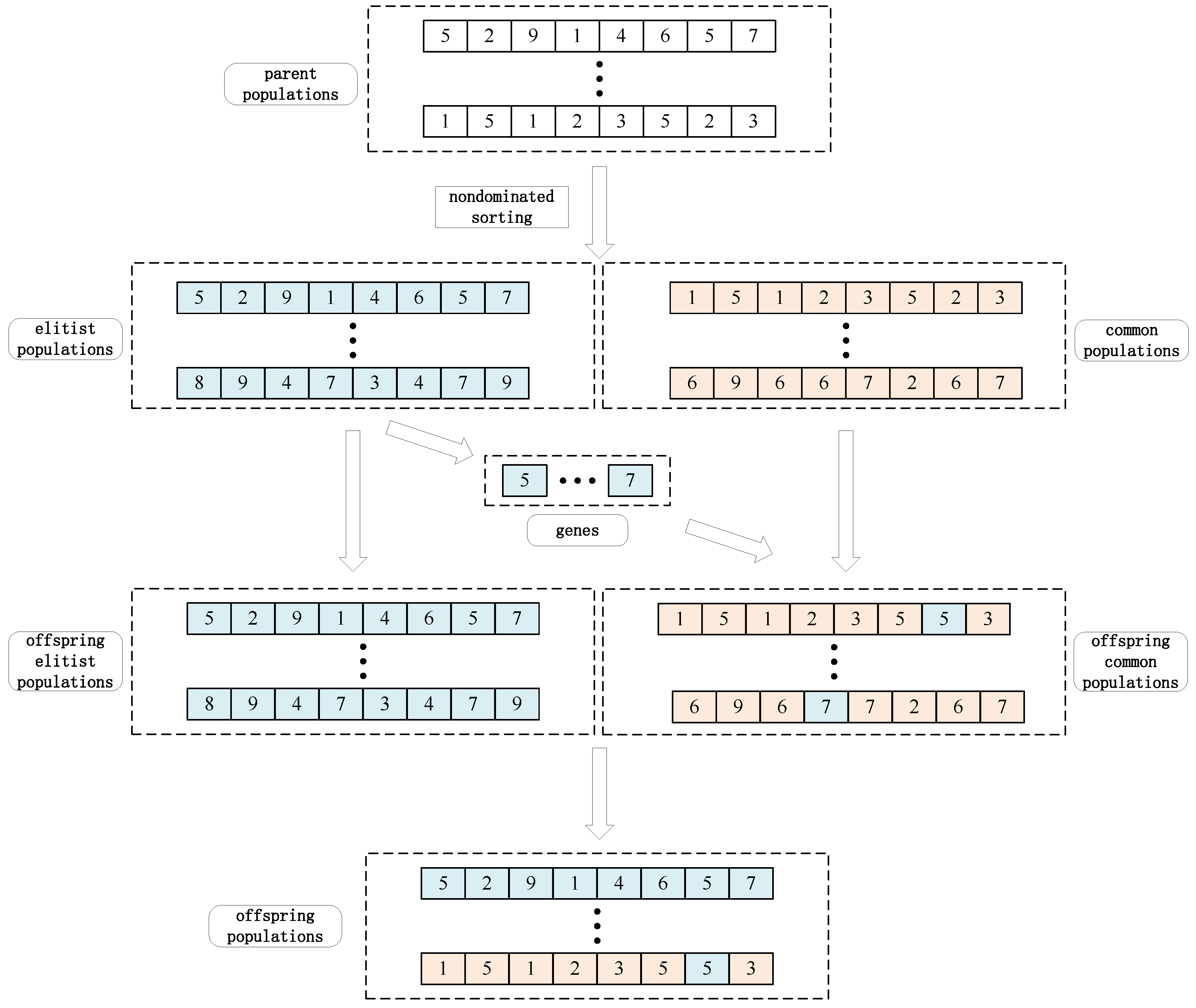
- Coding method
- (2)
- Nondominant sorting method
- (3)
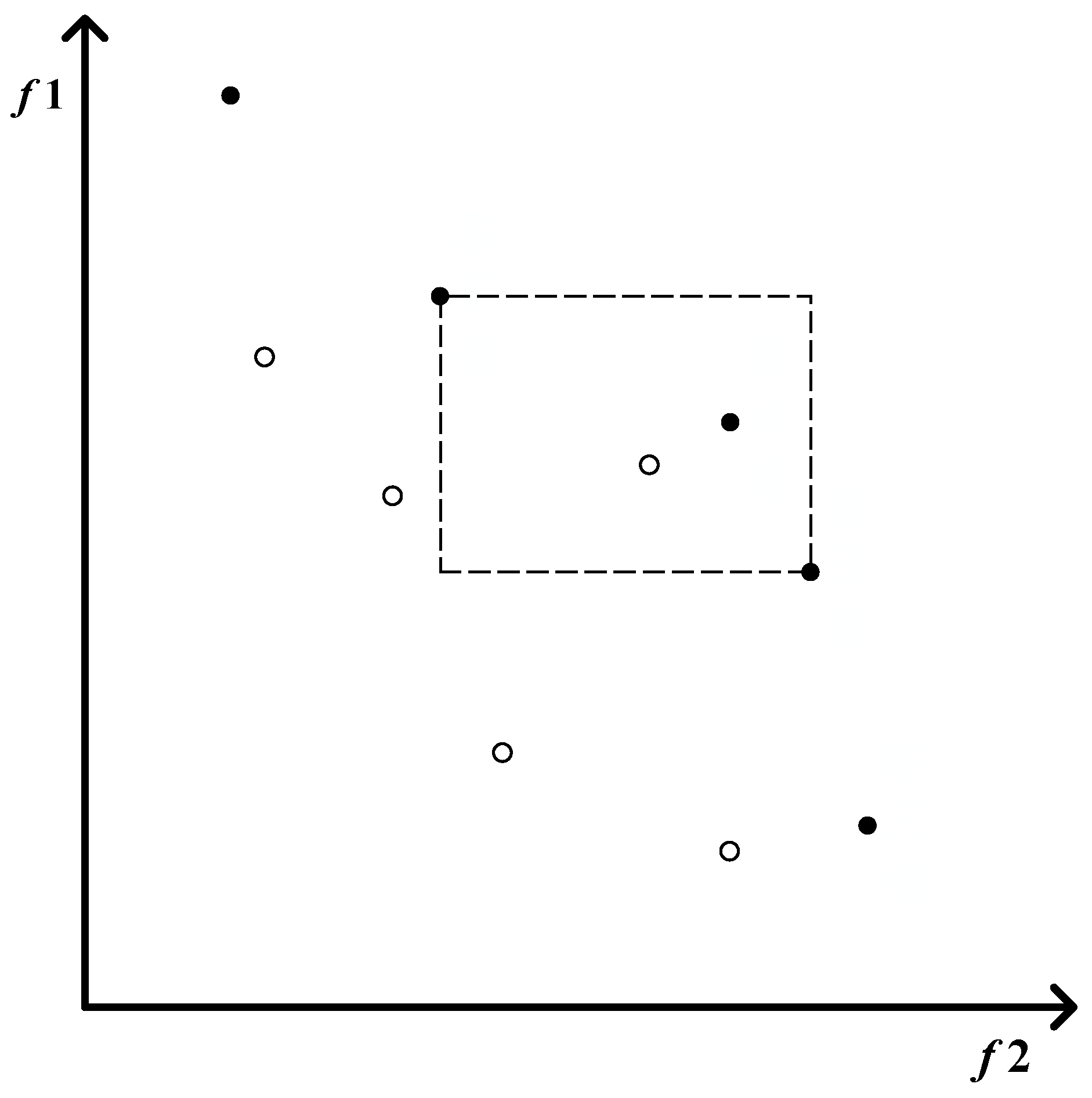
- Nondominated solution set update strategy
- (4)
- Location update procedure
| Algorithm 1: The framework of MSSA | |
| Input: | |
| N: population of sparrows | |
| iterm: maximum iterations | |
| Output: | |
| nondominated solution set | |
| 1: | Initialize a population of N sparrows and define its relevant parameters |
| 2: | while iter < iterm do |
| 3: | rank the population with nondominated sorting approach; |
| 4: | for condition do |
| 5: | Using Equation (24) update the producers’ location; |
| 6: | set producers’ location as integer |
| 7: | Sort the population with nondominated sorting approach; |
| 8: | Genetic recombination between elitist swarms and basic swarms; |
| 9: | Sort the population with nondominated sorting approach; |
| 10: | Save the nondominated solution to the external archive; |
| 11: | Using Equation (25) update the guards’ location; |
| 12: | Sort the population with nondominated sorting approach; |
| 13: | Save the nondominated solution to the external archive; |
| 14: | iter = iter + 1; |
| 15: | Sort the external archive with crowding distance; |
| 16: | return nondominated solution set. |
3.2.2. A Simulated Annealing Algorithm Used to Solve Maintenance Scheduling
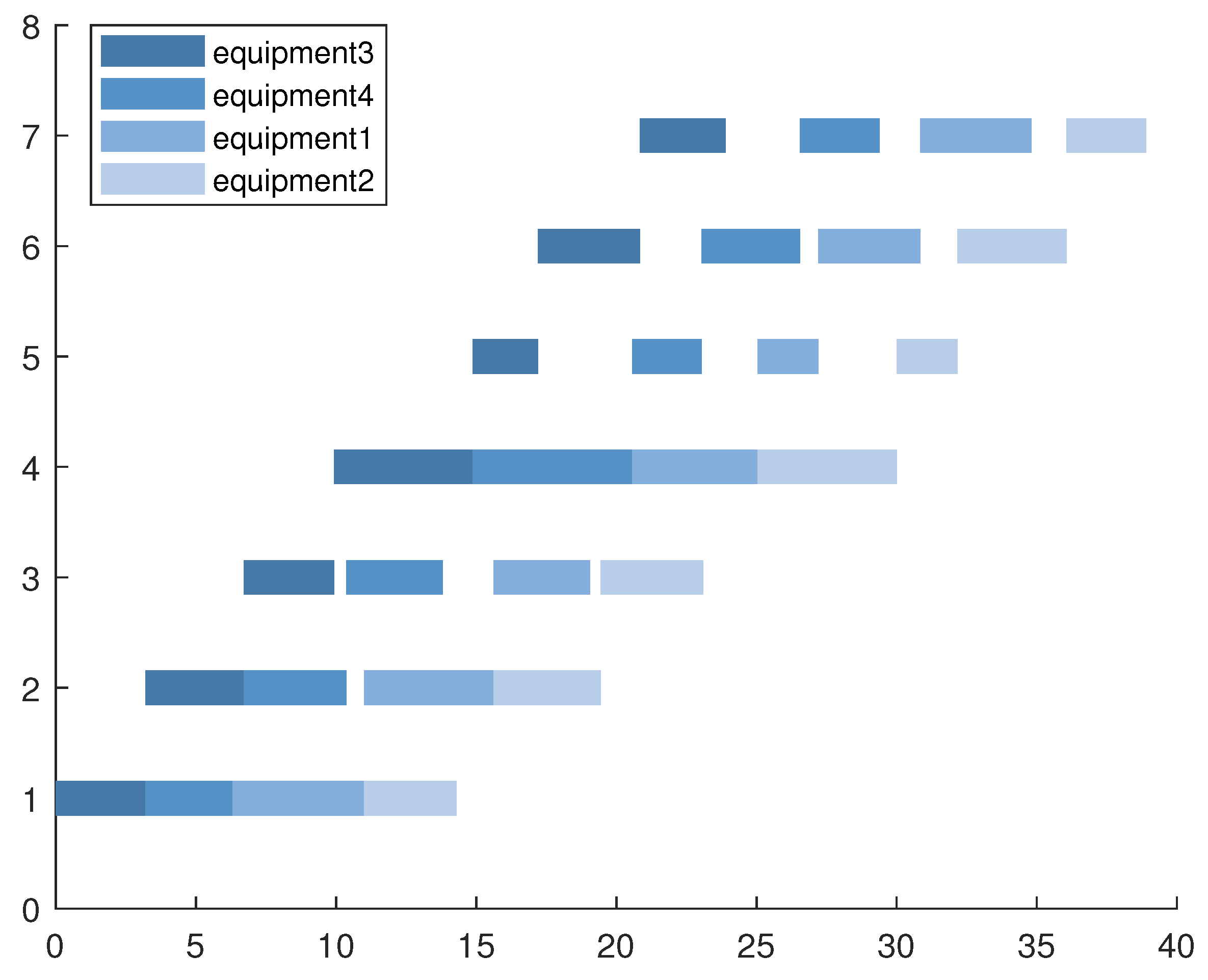
3.3. Process of Selective Maintenance Planning for Equipment Cluster Based on Two-Stage Algorithm Driven by Task and Reliability
4. Case Verification and Result Analysis
4.1. Case Verification
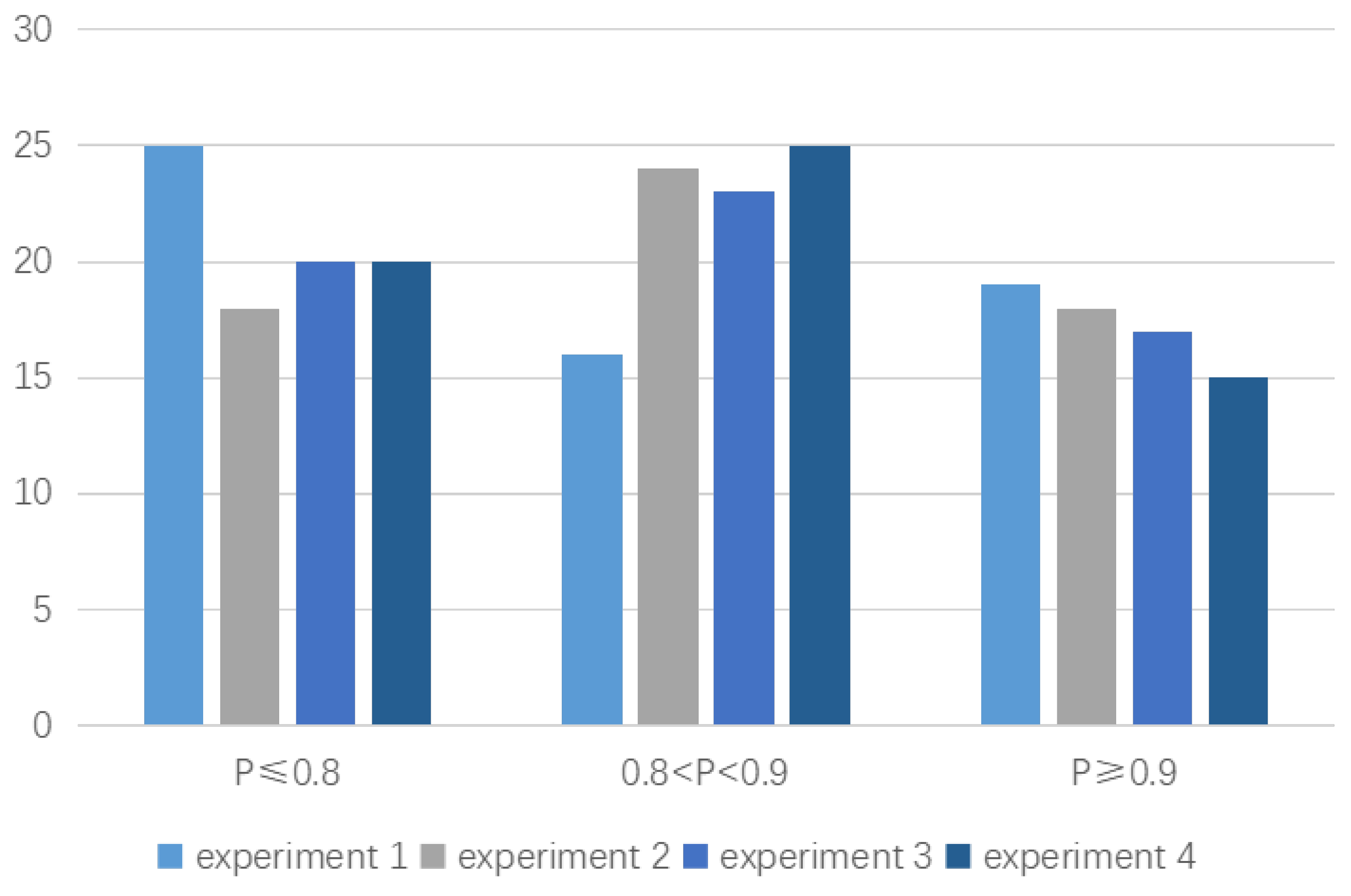
4.2. Result Analysis
- (1)
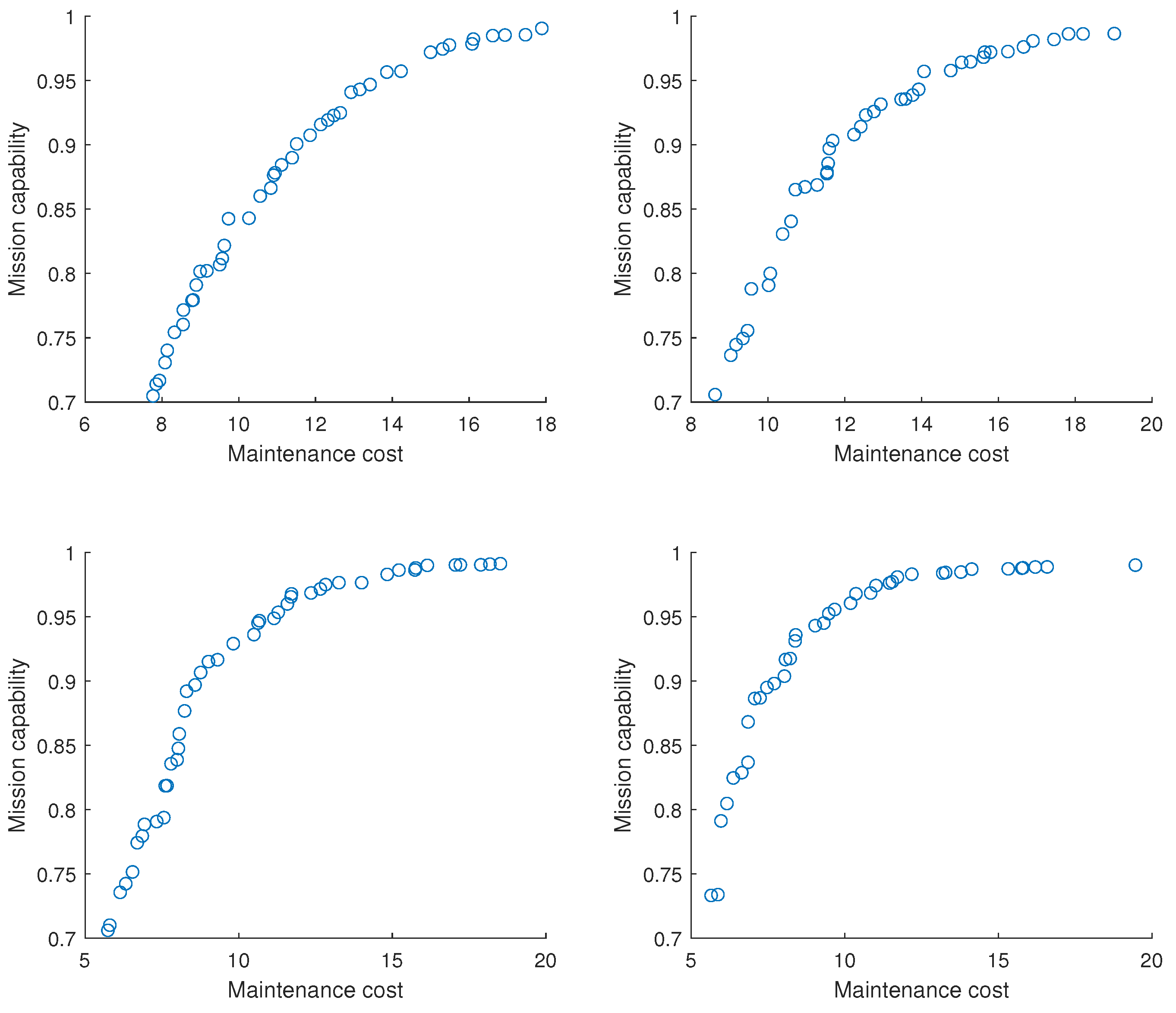
- Fleet mission satisfied capability has a high correlation with the cost of maintenance tasks invested, and the benefit of unit maintenance cost invested decreases with the increase in fleet mission satisfied capability. The mission satisfied capability of the equipment cluster is determined by the health status of each equipment unit. The higher mission satisfied capability has higher requirements on the health status of each equipment; so, it needs to invest a lot in maintenance costs. In the case of a high requirement of mission satisfied capability and sufficient budget, more cost should be invested in exchange for higher mission success rate. In the case of low mission satisfied capability requirements and tight budgets, maintenance strategies with slightly lower mission satisfied capability can be selected to reduce costs.
- (2)
- There is little difference in maintenance hours corresponding to different maintenance strategies. Since a reasonable maintenance schedule is established to maximize the use of maintenance time, when the fixed maintenance hours are longer than the hours associated with the maintenance level, the corresponding maintenance hours of different maintenance strategies are not different; so, the maintenance hours can be considered as a supernumerary optimization objective.
5. Conclusions
- (1)
- A selective maintenance decision model of fleets based on virtual age reduction was constructed. In the process of model establishment, the traditional research structure of “unit–system” in maintenance planning was extended to the three-level research structure of “unit–system–fleet”, considering the cooperation of different equipment in missions. Based on the Kijima II imperfect maintenance model, this model uses virtual age to evaluate the health condition of equipment. A cost-based maintenance evaluation method is proposed considering the service age improvement coefficient, and the mission satisfied capability of a fleet is described by the survival probability.
- (2)
- The two-stage problem-solving framework of “decision–evaluation” and the corresponding solution method were proposed. The problem is decomposed into two parts: the multiobjective optimization decision of mission satisfied capability and maintenance cost and the strategy evaluation based on maintenance hours considering the convergence rate of the algorithm so as to simplify the difficulty of solving the problem. Based on the sparrow search algorithm, the discrete and multiobjective improvement is made, and the NSGA-II nondominated sorting method and elitist strategy are integrated so that the solution set of nondominated maintenance strategy distributed uniformly in the target space can be quickly obtained. Then, the SA algorithm is used to evaluate the maintenance strategy and give the corresponding optimal maintenance schedule and the minimized maintenance time so as to obtain a series of optimal maintenance strategies that satisfy the mission requirements.
- (3)
- In terms of the application of the method, we verified the case of a vehicle fleet, established its selective maintenance decision model and solved it by using the two-stage algorithm proposed in this chapter. A series of selective maintenance schemes of the vehicle fleet uniformly distributed in the target space were obtained, and the effectiveness of the method was verified. The above research methods can be applied to the dynamic selective maintenance decision problem of repairable fleets driven by mission and reliability, optimize maintenance task planning, reduce maintenance cost, improve availability and mission success probability and provide guidance for other similar problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Verhoeff, M.; Verhagen, W.J.C. Component Maintenance Planning Optimization in Defense Aviation. Aerospace 2023, 10, 255. [Google Scholar] [CrossRef]
- De Jonge, B.; Scarf, P.A. A review on maintenance optimization. Eur. J. Oper. Res. 2020, 285, 805–824. [Google Scholar] [CrossRef]
- Álvarez, C.; López-Campos, M.; Stegmaier, R.; Mancilla-David, F.; Schurch, R.; Angulo, A. A Condition-Based Maintenance Model Including Resource Constraints on the Number of Inspections. IEEE Trans. Reliab. 2020, 59, 1165–1176. [Google Scholar] [CrossRef]
- You, M.-Y. A generalized three-type lifetime probabilistic models-based hybrid maintenance policy with a practical switcher for time-based preventive maintenance and condition-based maintenance. Proc. Inst. Mech. Eng. Part J. Process. Mech. Eng. 2019, 233, 1231–1244. [Google Scholar] [CrossRef]
- Jiang, T.; Liu, Y. Selective maintenance strategy for systems executing multiple consecutive missions with uncertainty. Reliab. Eng. Syst. Saf. 2020, 193, 106632. [Google Scholar] [CrossRef]
- Yuan, P.; Han, W.; Su, X.; Liu, J.; Song, J. A Dynamic Scheduling Method for Carrier Aircraft Support Operation under Uncertain Conditions Based on Rolling Horizon Strategy. Appl. Sci. 2018, 8, 1546. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, Y.; Zhao, X.; Song, X. A timed colored petri net simulation-based self-adaptive collaboration method for production-logistics systems. Appl. Sci. 2017, 7, 235. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, Y.; Zhao, X.; Song, X. CPS-based self-adaptive collaborative control for smart production-logistics systems. IEEE Trans. Cybern. 2020, 51, 188–198. [Google Scholar] [CrossRef]
- Keizer, M.C.O.; Flapper, S.D.P.; Teunter, R.H. Condition-based maintenance policies for systems with multiple dependent components: A review. Eur. J. Oper. Res. 2017, 261, 405–420. [Google Scholar] [CrossRef]
- Ali, A.; Abdelhadi, A. Condition-Based Monitoring and Maintenance: State of the Art Review. Appl. Sci. 2022, 12, 688. [Google Scholar]
- Koopmans, M.; De Jonge, B. Condition-based maintenance and production speed optimization under limited maintenance capacity. Comput. Ind. Eng. 2023, 179, 109155. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X. Piecewise deterministic Markov process for condition-based imperfect maintenance models. Reliab. Eng. Syst. Saf. 2023, 236, 109271. [Google Scholar]
- Pham, H.; Wang, H. Imperfect maintenance. Eur. J. Oper. Res. 1996, 94, 425–438. [Google Scholar]
- Yang, L.; Ye, Z.S.; Lee, C.G.; Yang, S.F.; Peng, R. A two-phase preventive maintenance policy considering imperfect repair and postponed replacement. Eur. J. Oper. Res. 2019, 274, 966–977. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, P.; Zhang, C. Fleet-Level Selective Dispatch and Imperfect Maintenance Strategy Optimization Based on Evolutionary Co-Petition Game Theory. IEEE Access 2020, 8, 148689–148701. [Google Scholar] [CrossRef]
- Cheng, W.; Zhao, X. Maintenance Optimization for Dependent Two-Unit Systems Considering Stochastic Degradation and Imperfect Maintenance. In Proceedings of the 2022 IEEE 22nd International Conference on Software Quality, Reliability, and Security Companion (QRS-C), Guangzhou, China, 30 March 2023. [Google Scholar]
- Shahraki, A.F.; Yadav, O.P.; Vogiatzis, C. Selective maintenance optimization for multi-state systems considering stochastically dependent components and stochastic imperfect maintenance actions. Reliab. Eng. Syst. Saf. 2020, 196, 106738. [Google Scholar]
- Liu, Y.; Chen, Y.; Jiang, T. On sequence planning for selective maintenance of multi-state systems under stochastic maintenance durations. Eur. J. Oper. Res. 2018, 268, 113–127. [Google Scholar] [CrossRef]
- Cao, W.; Jia, X.; Hu, Q.; Zhao, J.; Wu, Y. A literature review on selective maintenance for multi-unit systems. Qual. Reliab. Eng. Int. 2018, 34, 824–845. [Google Scholar] [CrossRef]
- Lust, T.; Roux, O.; Riane, F. Exact and heuristic methods for the selective maintenance problem. Eur. J. Oper. Res. 2009, 197, 1166–1177. [Google Scholar] [CrossRef]
- Vu, H.C.; Do, P.; Barros, A.; Bérenguer, C. Maintenance grouping strategy for multi-component systems with dynamic contexts. Reliab. Eng. Syst. Saf. 2014, 132, 233–249. [Google Scholar] [CrossRef]
- Duan, C.; Deng, C.; Gharaei, A.; Wu, J.; Wang, B. Selective maintenance scheduling under stochastic maintenance quality with multiple maintenance actions. Int. J. Prod. Res. 2018, 56, 7160–7178. [Google Scholar] [CrossRef]
- Xu, E.B.; Yang, M.S.; Li, Y.; Gao, X.Q.; Wang, Z.Y.; Ren, L.J. A multi-objective selective maintenance optimization method for series-parallel systems using NSGA-III and NSGA-II evolutionary algorithms. Adv. Prod. Eng. Manag. 2021, 16, 372–384. [Google Scholar]
- Urbani, M.; Brunelli, M.; Punkka, A. An approach for bi-objective maintenance scheduling on a networked system with limited resources. Eur. J. Oper. Res. 2023, 305, 101–113. [Google Scholar]
- Maillart, L.M.; Cassady, C.R.; Rainwater, C.; Schneider, K. Selective Maintenance Decision-Making Over Extended Planning Horizons. IEEE Trans. Reliab. 2009, 58, 462–469. [Google Scholar]
- Kijima, M. Some results for repairable systems with general repair. J. Appl. Probab. 1989, 26, 89–102. [Google Scholar] [CrossRef]
- Kang, J.; Sobral, J.; Soares, C.G. Review of condition-based maintenance strategies for offshore wind energy. J. Mar. Sci. Appl. 2019, 18, 1–16. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar]
- Zhang, C.; Ding, S. A stochastic configuration network based on chaotic sparrow search algorithm. Knowl.-Based Syst. 2021, 220, 106924. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, Y. Discrete sparrow search algorithm for symmetric traveling salesman problem. Appl. Soft Comput. 2022, 118, 108469. [Google Scholar]
- Li, Y.; Wang, S.; Chen, Q.; Wang, X. Comparative study of several new swarm intelligence optimization algorithms. Comput. Eng. Appl. 2020, 56, 1–12. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
| S | T | ||||||
|---|---|---|---|---|---|---|---|
| 2 | 1.20 | 94 | 0.05 | 0.52 | 1.5 | 3 | |
| 2 | 1.40 | 70 | 0.04 | 2.40 | 2.4 | 3.5 | |
| 3 | 2.00 | 98 | 0.07 | 1.60 | 3.3 | 3 | |
| 4 | 1.50 | 105 | 0.08 | 0.80 | 3.6 | 4 | |
| 2 | 1.80 | 112 | 1.20 | 1.20 | 2.4 | 2 | |
| 2 | 1.15 | 89 | 1.41 | 1.41 | 2.0 | 3.5 | |
| 3 | 1.64 | 92 | 0.87 | 0.87 | 1.7 | 2.5 |
| Option 1 | Option 2 | Option 3 | |
|---|---|---|---|
| Maintenance cost | 9.28 | 14.38 | 22.63 |
| Mission capability | 0.72 | 0.83 | 0.91 |
| Maintenance hour | 40.27 | 42.21 | 42.69 |
| Maintenance schedule | 3-4-1-2 | 1-2-3-4 | 4-1-2-3 |
| Cost-effectiveness ratio | 0.0776 | 0.0577 | 0.0402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Wang, P.; Yang, L.; Wang, J.; Yi, X. Mission and Reliability Driven Fleet-Level Selective Maintenance Planning and Scheduling Two-Stage Method. Appl. Sci. 2023, 13, 8600. https://doi.org/10.3390/app13158600
Chen Q, Wang P, Yang L, Wang J, Yi X. Mission and Reliability Driven Fleet-Level Selective Maintenance Planning and Scheduling Two-Stage Method. Applied Sciences. 2023; 13(15):8600. https://doi.org/10.3390/app13158600
Chicago/Turabian StyleChen, Qinghua, Pengxiang Wang, Lin Yang, Jiangshan Wang, and Xiaojian Yi. 2023. "Mission and Reliability Driven Fleet-Level Selective Maintenance Planning and Scheduling Two-Stage Method" Applied Sciences 13, no. 15: 8600. https://doi.org/10.3390/app13158600
APA StyleChen, Q., Wang, P., Yang, L., Wang, J., & Yi, X. (2023). Mission and Reliability Driven Fleet-Level Selective Maintenance Planning and Scheduling Two-Stage Method. Applied Sciences, 13(15), 8600. https://doi.org/10.3390/app13158600







