A Numerical Analysis for Ball End Milling Due to Coupling Effects of a Flexible Rotor-Bearing System Using GPEM
Abstract
1. Introduction
1.1. Three Principal Methods for Rotor System
1.1.1. Transfer Matrix Method
1.1.2. Finite Element Method
1.1.3. Generalized Polynomial Expansion Method
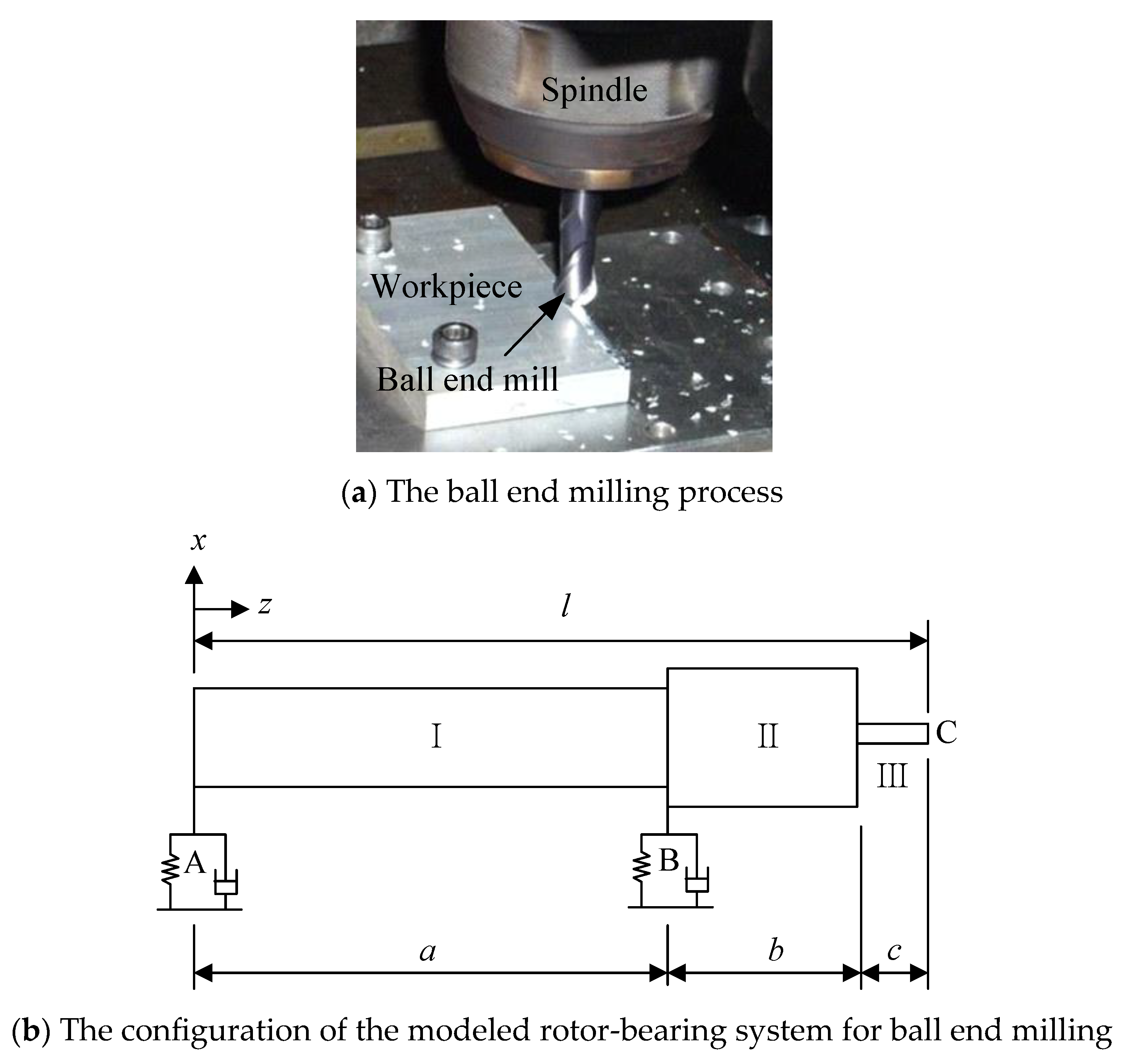
1.2. Ball End Milling
1.3. The Purpose and Novelty of This Work
2. Equation Formulation Using GPEM
3. Dynamic Responses for Ball End Milling
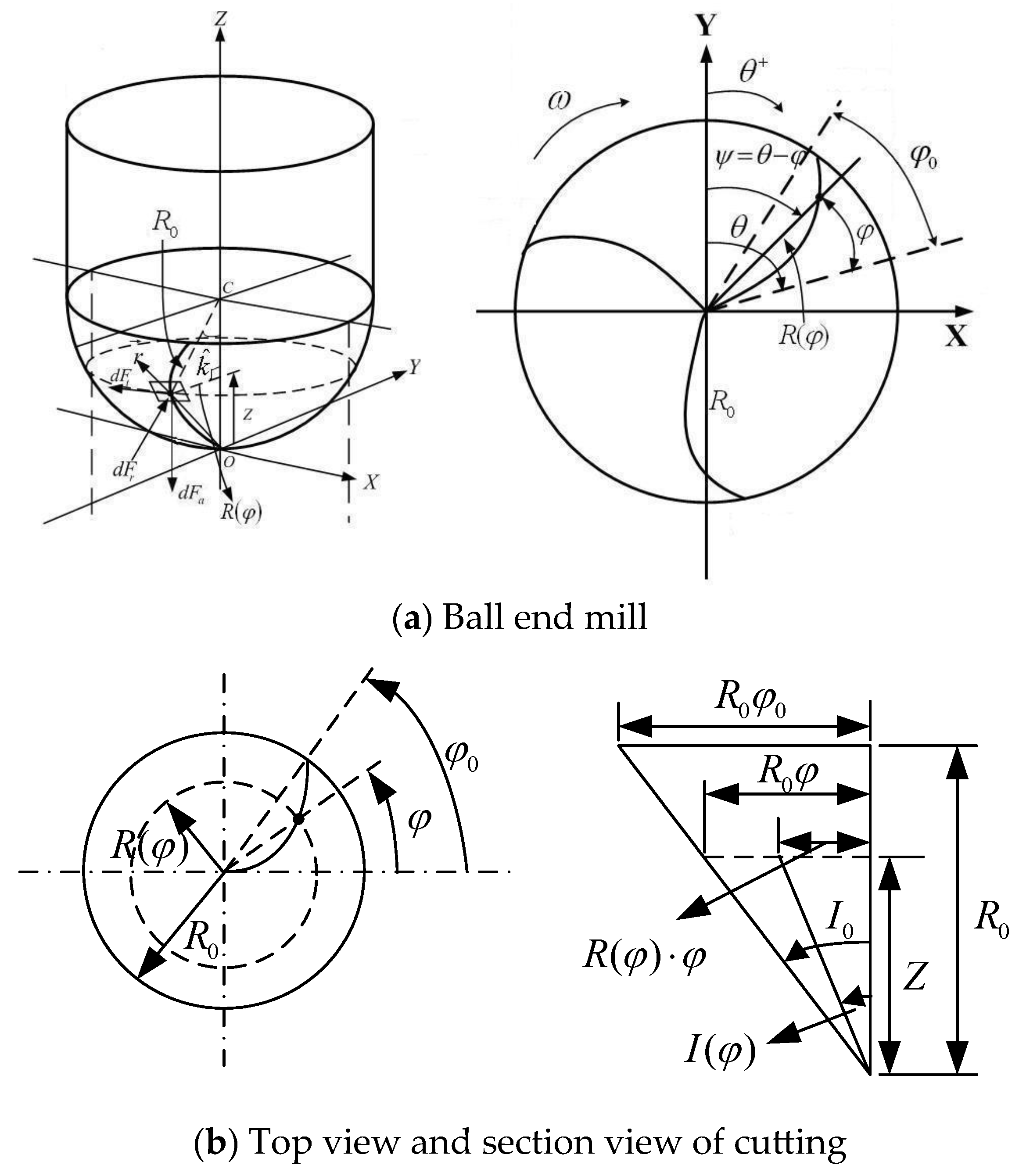
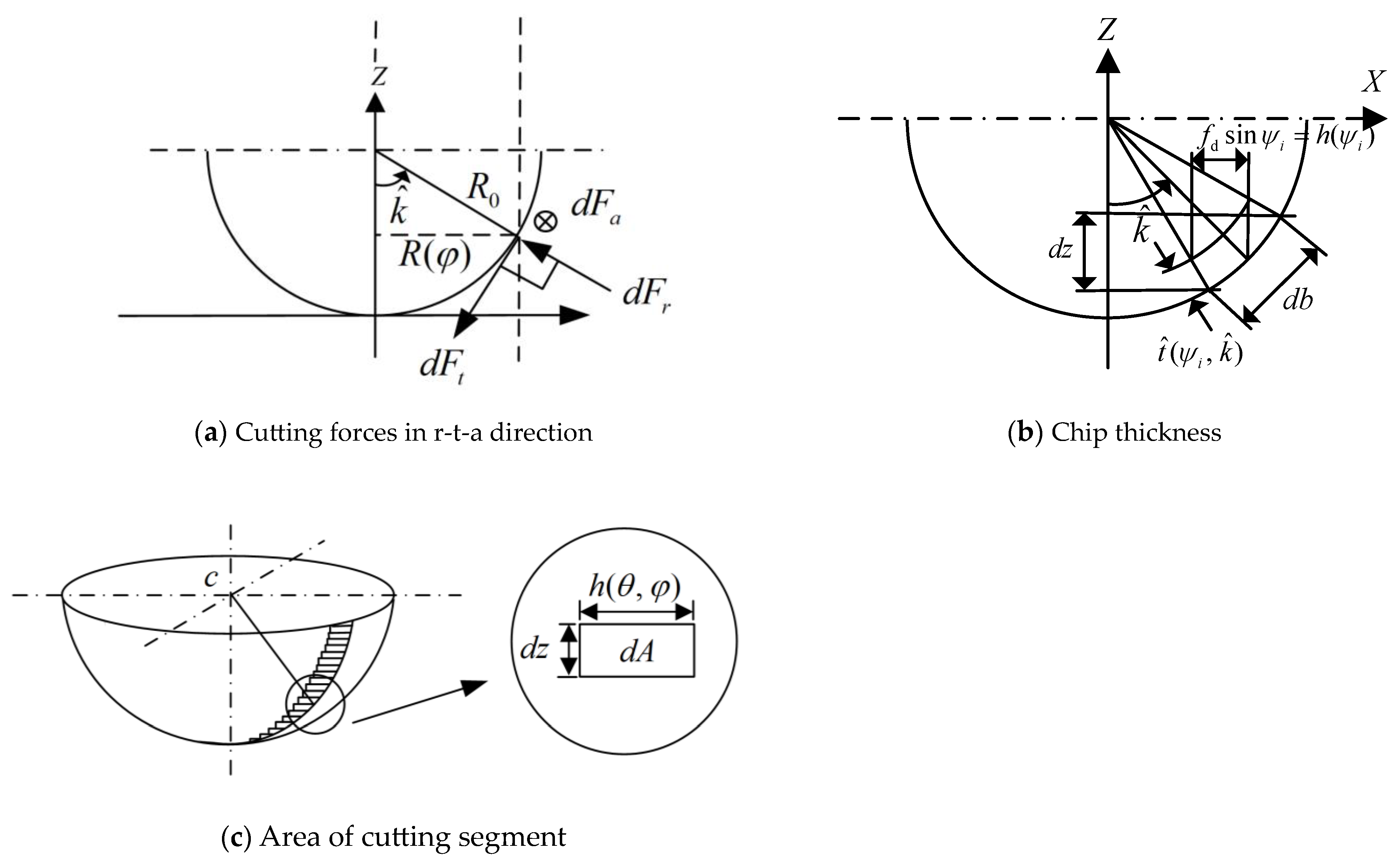
3.1. Dynamic Cutting Forces
3.2. Responses of System Using GPEM
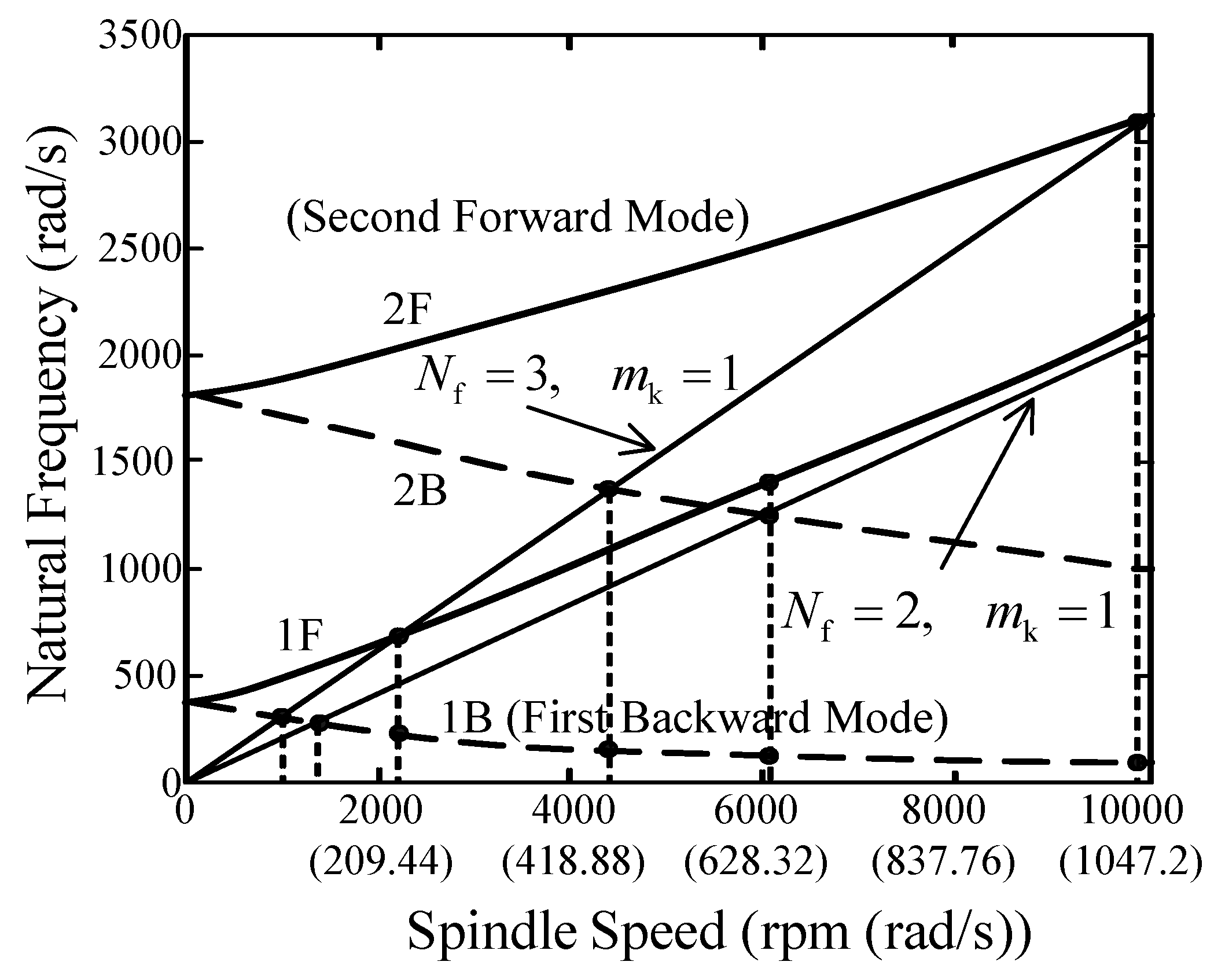
3.3. Numerical Results and Discussion
4. Conclusions
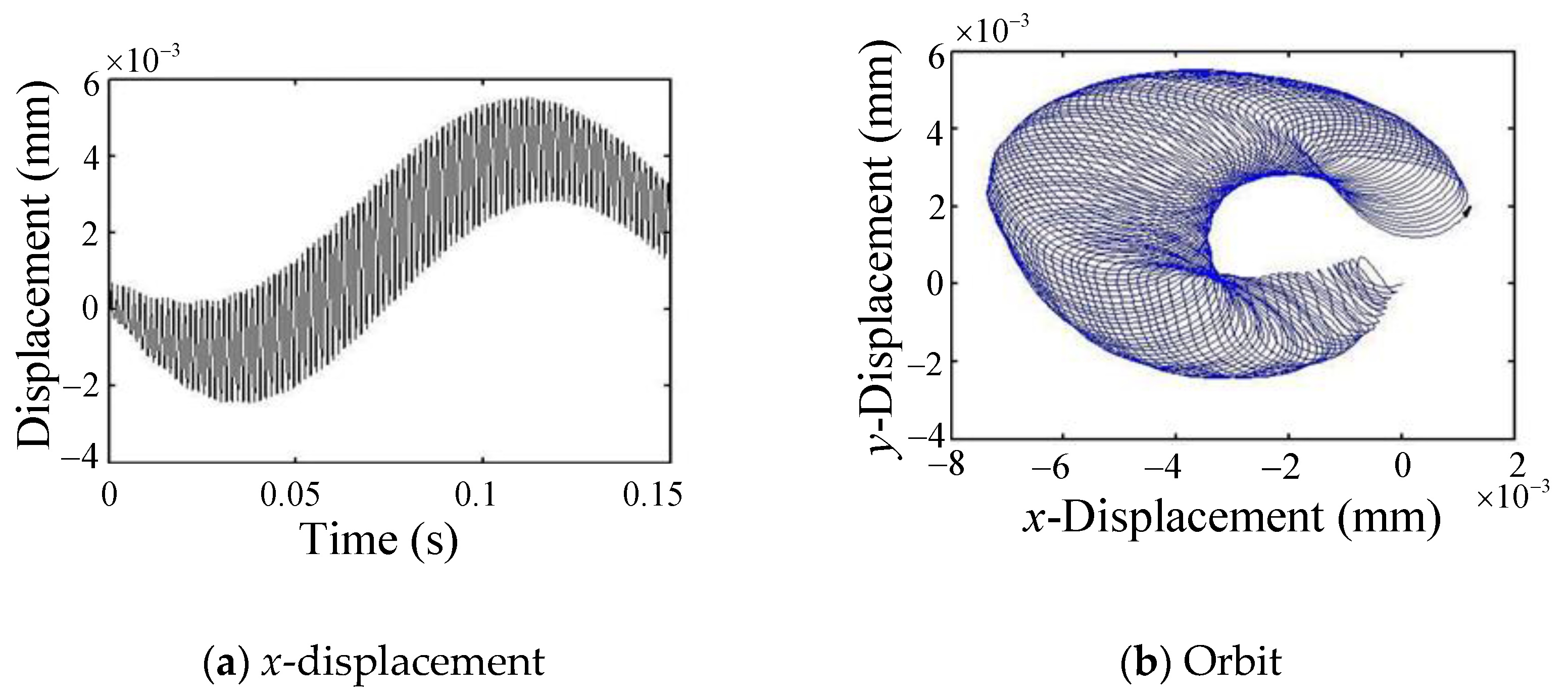
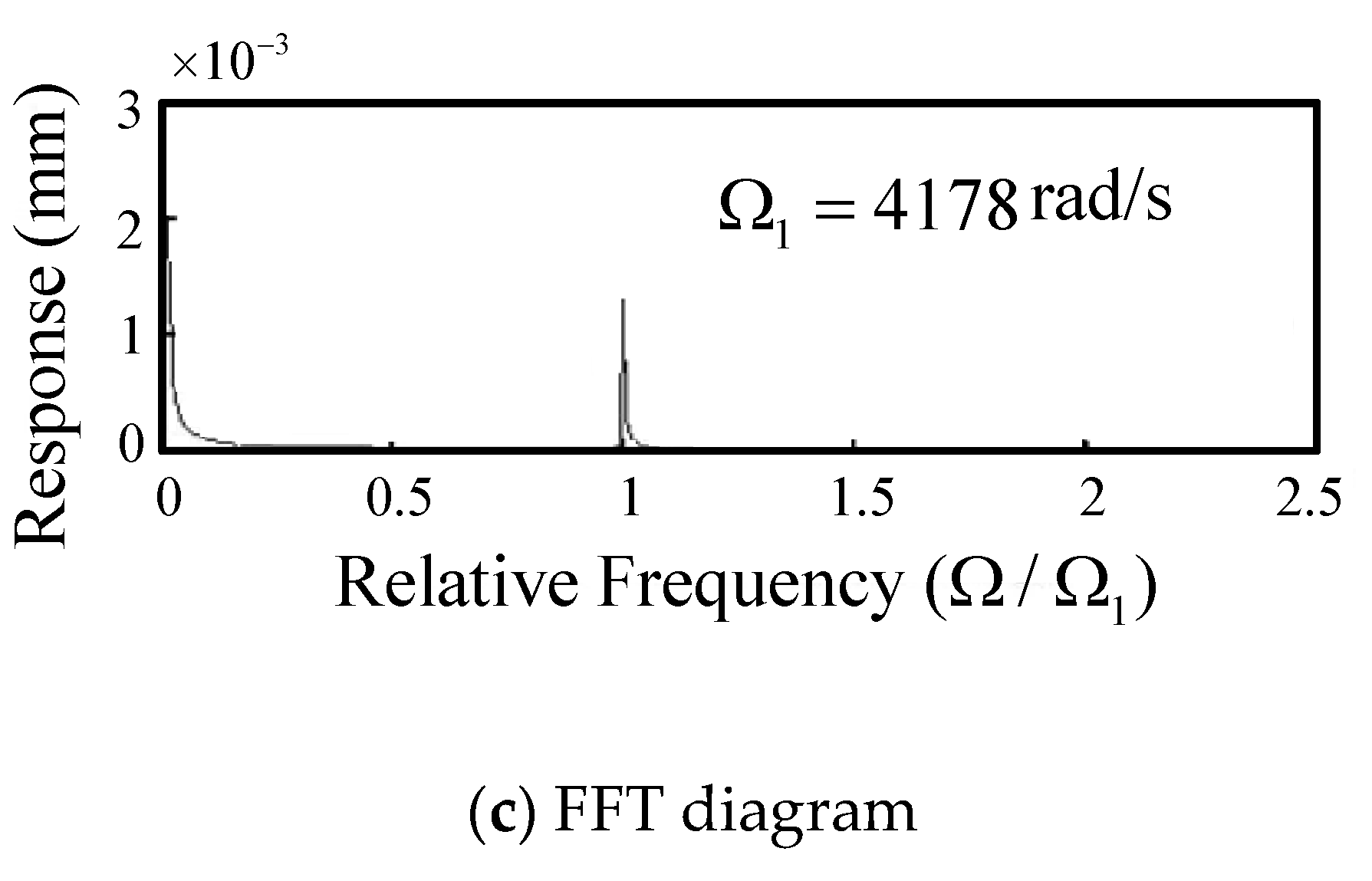
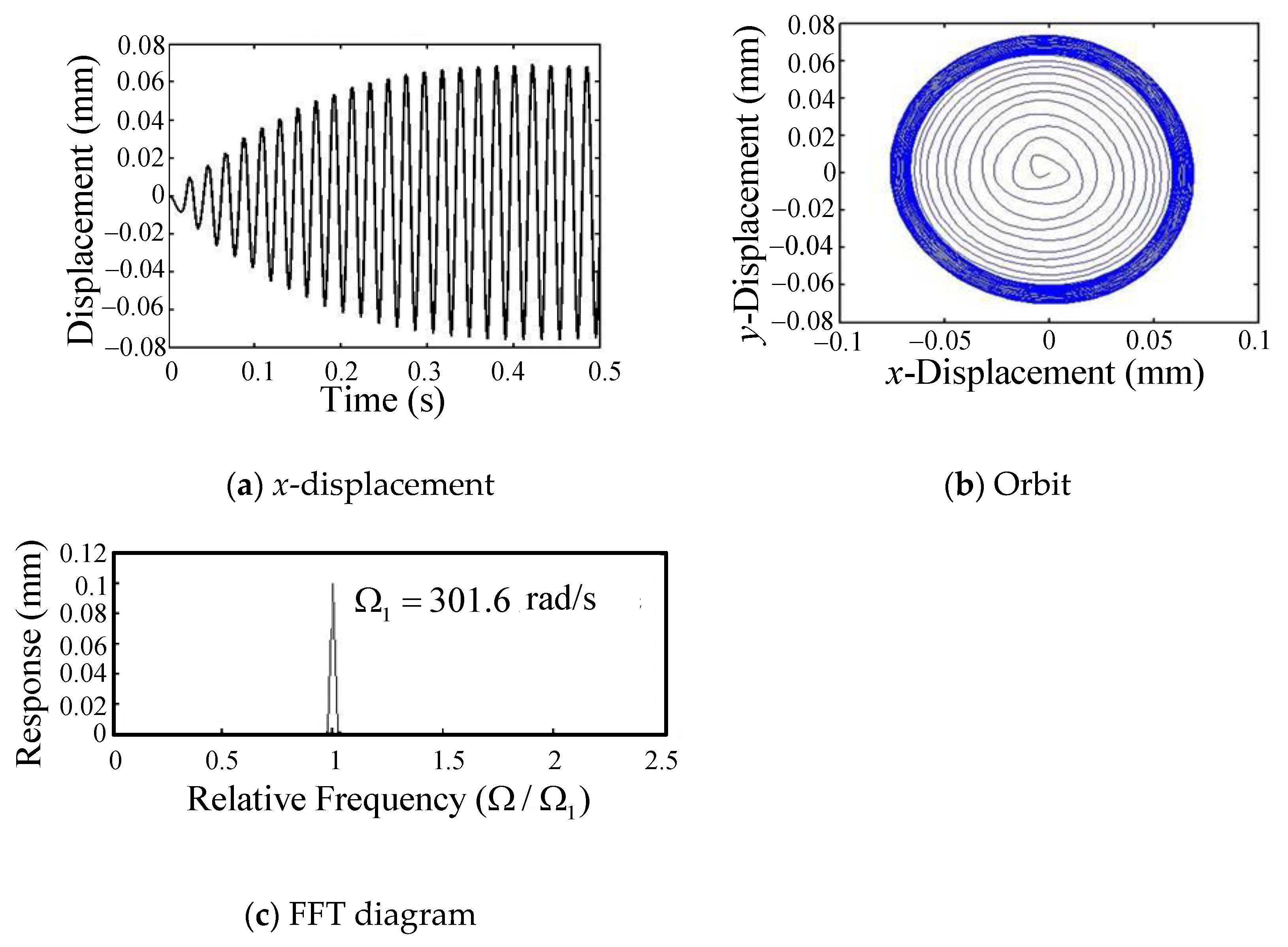
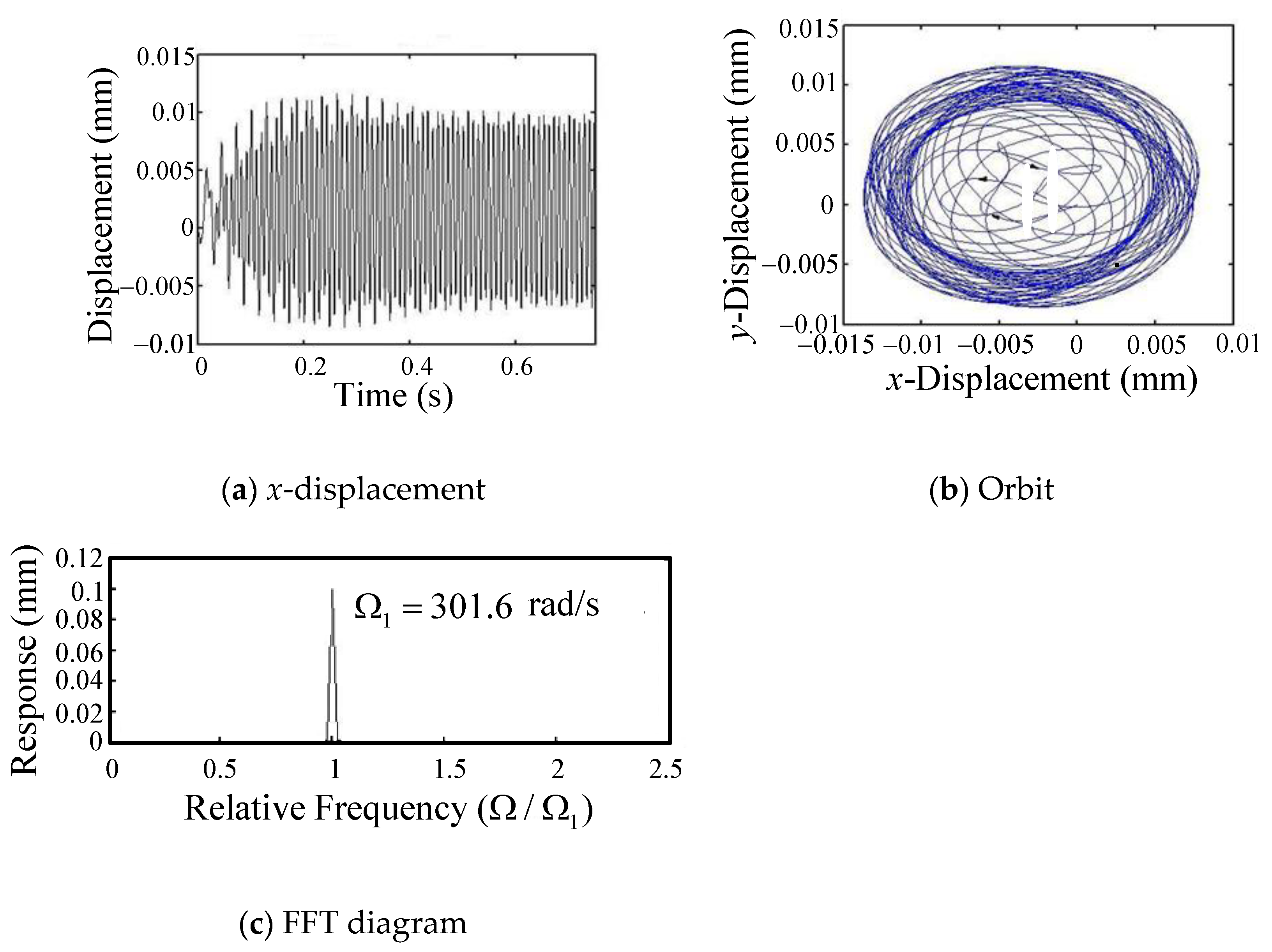
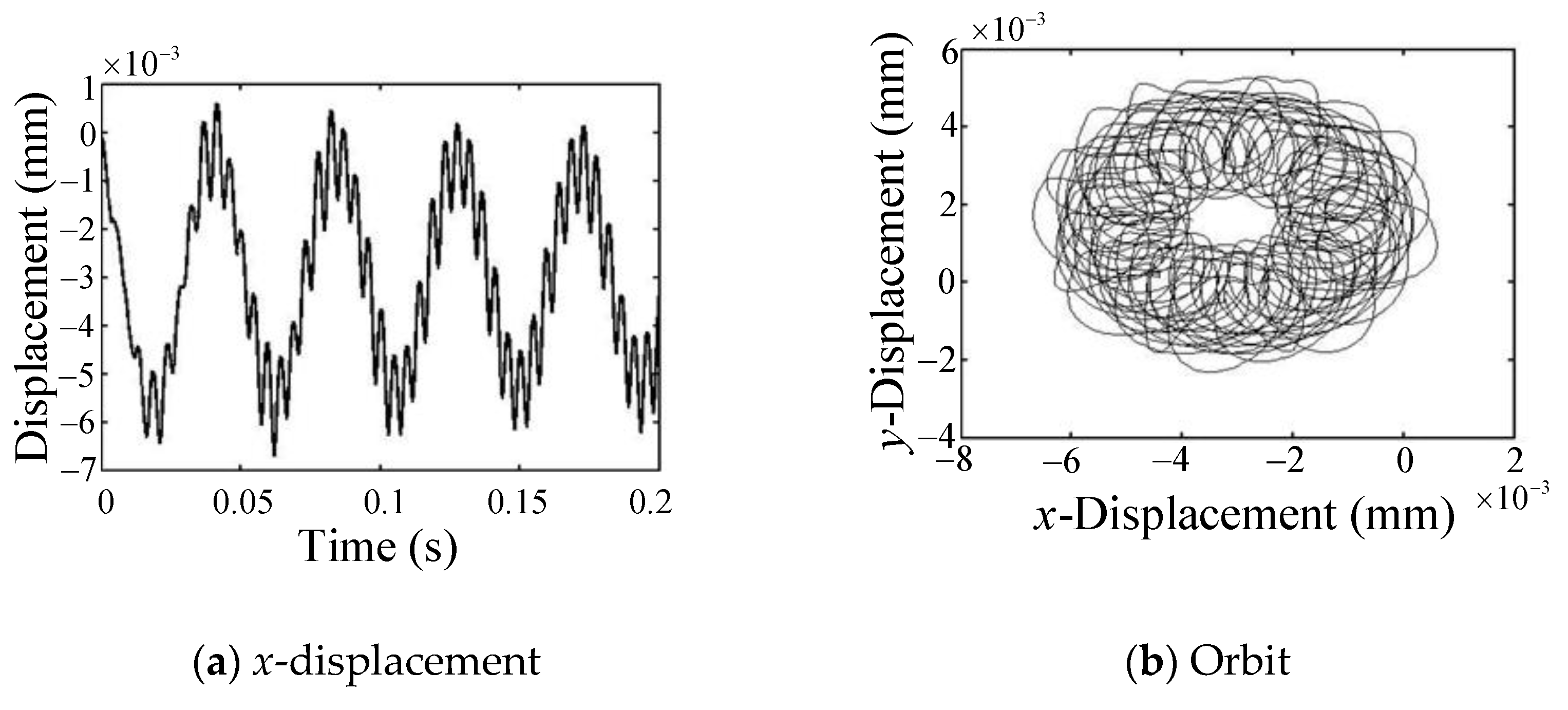
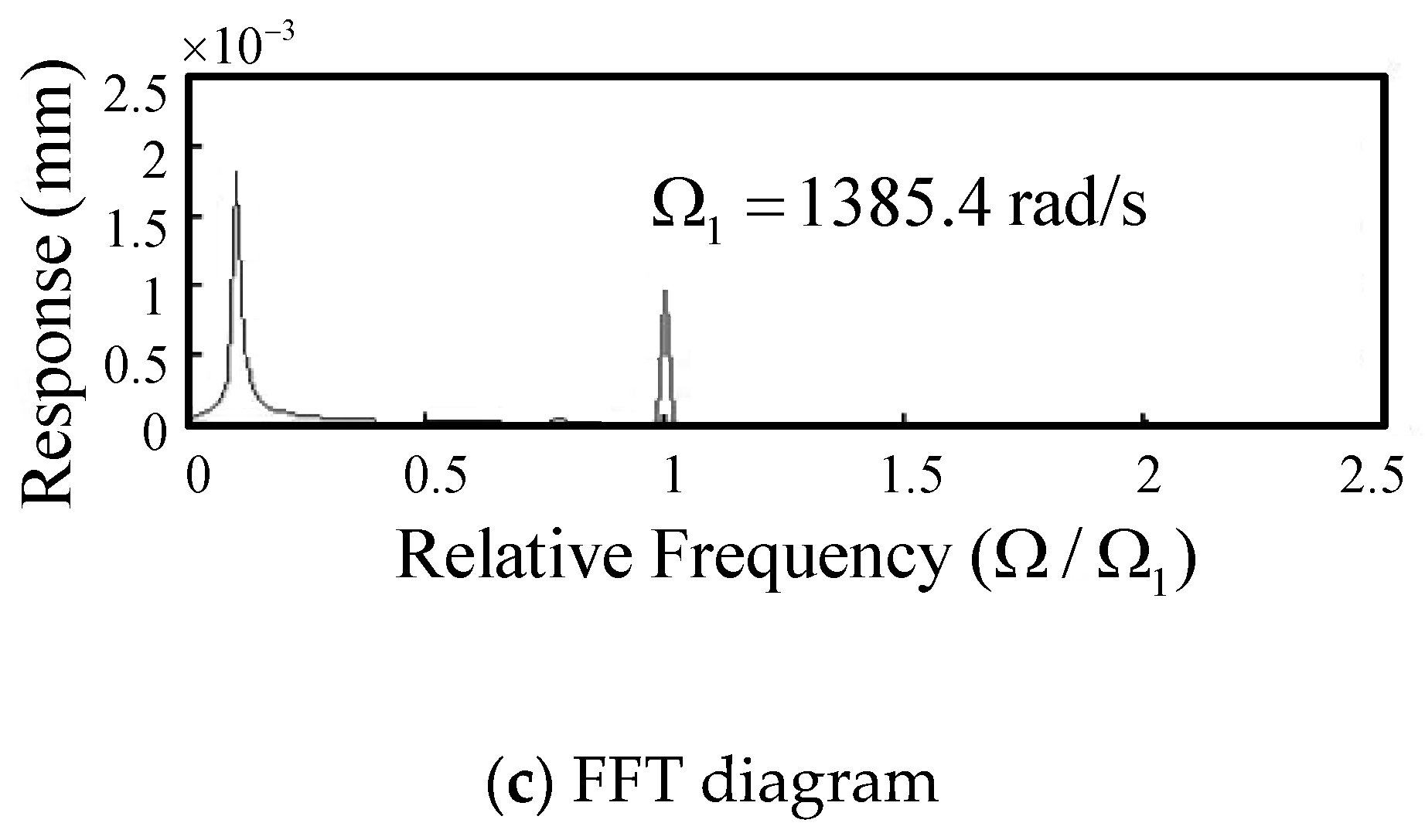
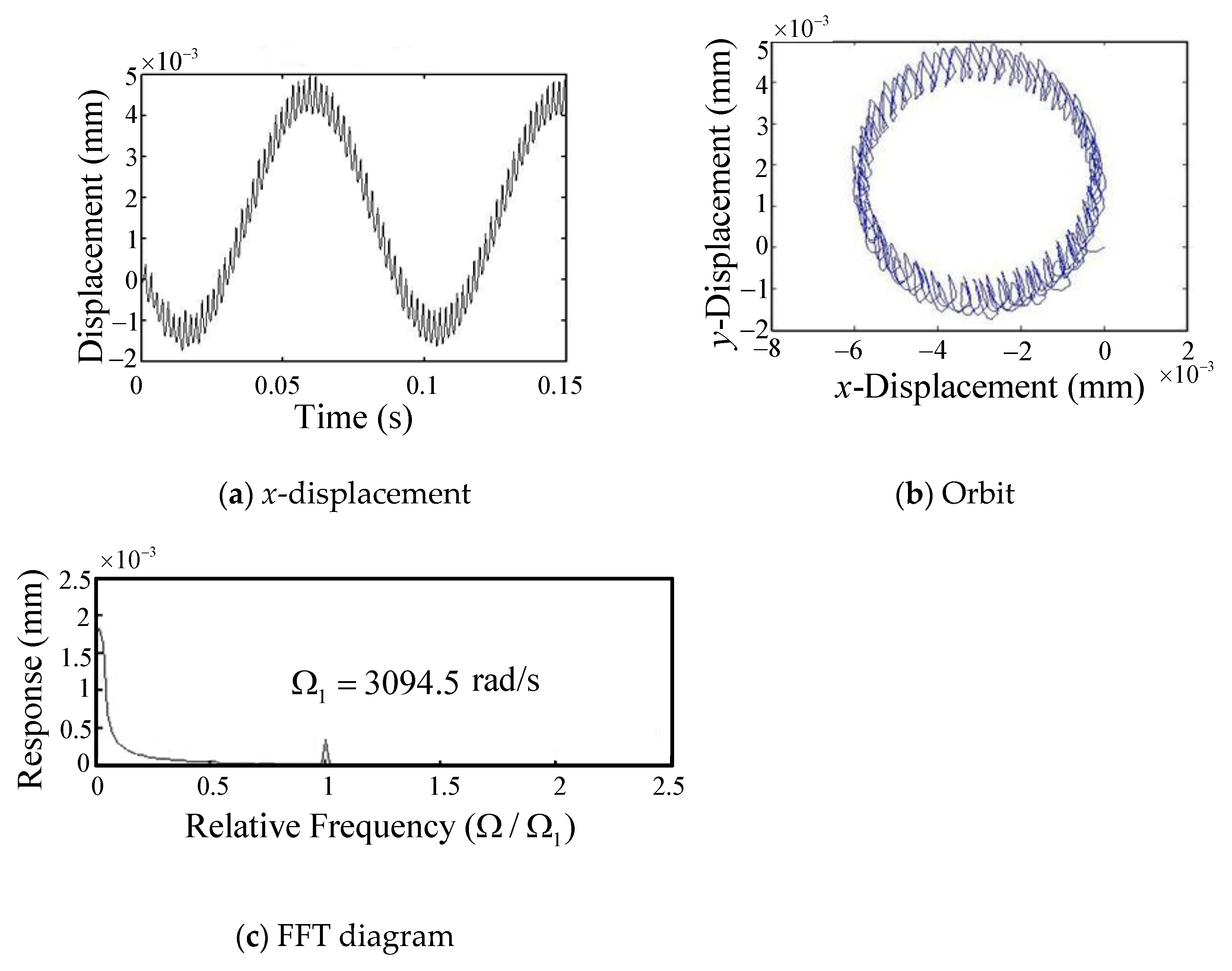
- In milling at a higher spindle speed (2160–19,950 rpm), the tool-tip oscillates with the cutting-force frequency combined with a longer cycle vibration of the first backward mode due to the coupling effects of the flexible rotor-bearing system, and the period of the long cycle vibration enlarges as the spindle speed increases. From the FFT plot, it can be seen that as the spindle speed becomes larger, the peak amplitude at the first backward mode (long-period vibration) becomes larger compared to the peak at the cutting force frequency.
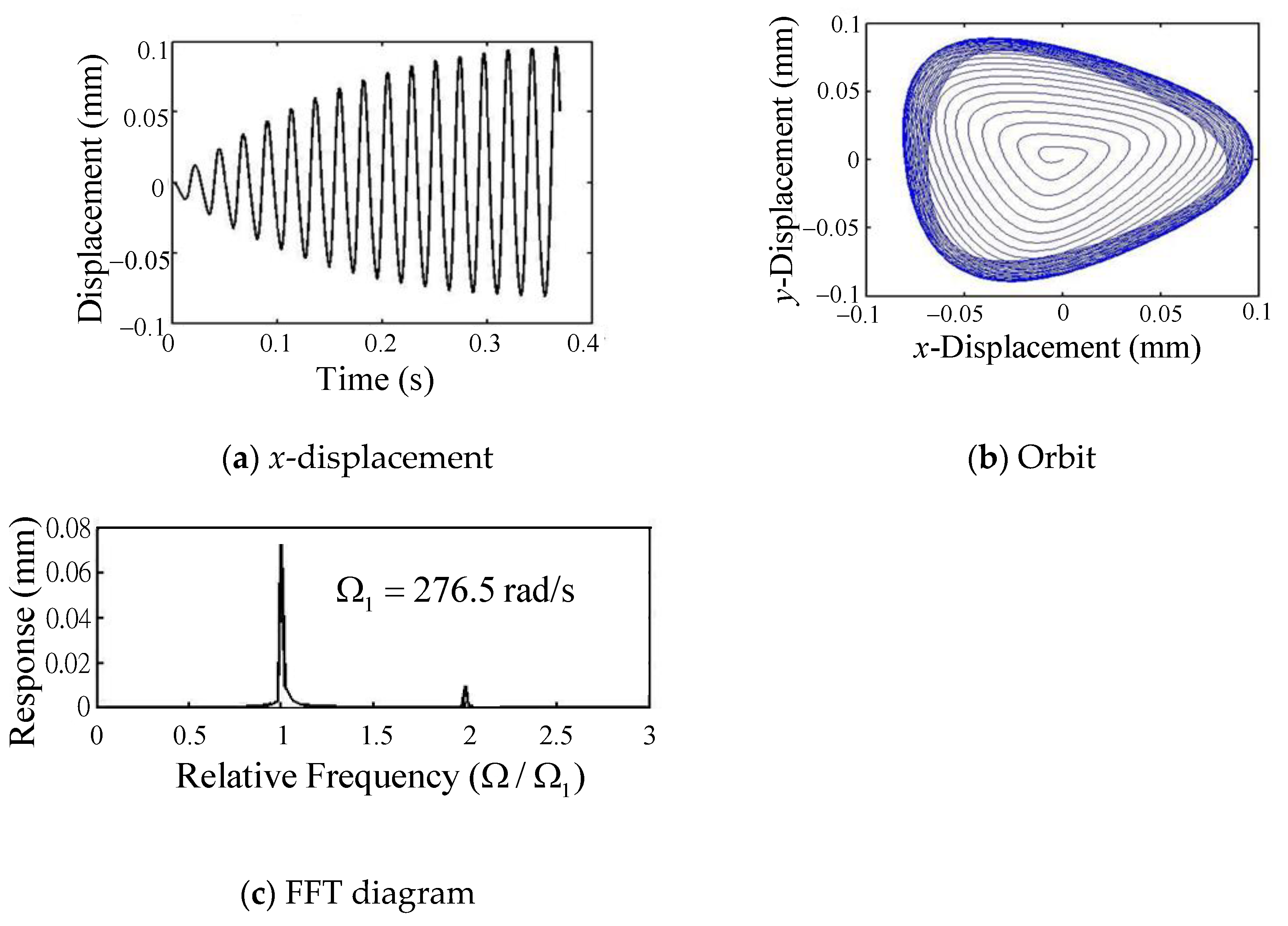
- Under lower spindle speed milling (960, 1320 rpm), the vibration trajectory of the tool-tip in the co-plane expands clockwise gradually around the origin until arriving at a stable loop. This is because only the first backward mode of the rotor-bearing system is excited.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| section length of tool spindle | |
| axial depth of cut | |
| generalized coordinates | |
| cross-sectional area of the shaft | |
| tool length | |
| damping matrix of the bearing using GPEM | |
| damping coefficients of the j-th bearing | |
| outer and inner diameter of the shaft and tool | |
| area of cutting segment | |
| differential cutting edge length | |
| differential cutting forces in tangential, radial, and axial direction | |
| differential milling force in Cartesian coordinate | |
| differential length of the curved cutting edge segment | |
| differential height in axial direction | |
| elastic modulus of the shaft and tool | |
| feed per tooth () | |
| natural frequency () | |
| coefficients of cutting force | |
| gyroscopic matrix of the rotor using GPEM | |
| chip thickness | |
| helix angle at meeting boundary between the ball and shank | |
| diametral and polar mass moment of inertia of the shaft | |
| diametral and polar mass moment of inertia of the i-th disk | |
| stiffness matrix of the shaft using GPEM | |
| tangential, radial, and axial cutting force coefficients | |
| tangential, radial, and axial edge force coefficients | |
| stiffness matrix of the bearing using GPEM | |
| elastic constant of the j-th bearing | |
| angle in a vertical plane between a point on the flute and the z-axis | |
| total length of the tool spindle | |
| mass matrix of the rotor using GPEM | |
| mass of the i-th disk | |
| vibration cycle number of tool during the cutting time from one flute to another | |
| total number of the disk | |
| total number of the flutes | |
| total number of the bearing | |
| total number of polynomial | |
| number of flute | |
| critical speed in rpm | |
| ball radius of tool | |
| tool radius in x-y plane at a point defined by | |
| uncut chip thickness normal to cutting edge in milling | |
| deflections of tool-tip at the present time | |
| rake angle of cutting parameter | |
| friction angle of cutting parameter | |
| chip compression ratio of cutting parameter | |
| density of the shaft and tool | |
| tool rotation angle, measured from y-axis (CW) | |
| , | the start and exit angles in the milling process |
| lag angle between the tip (z = 0) and a point on the helical flute at height z | |
| instantaneous angular immersion in the global coordinate system | |
| shear stress of cutting parameter | |
| spindle speed |
Appendix A
Appendix B
Appendix C
References
- Lund, J.W.; Orcutt, F.K. Calculations and experiments on the unbalance response of a flexible rotor. J. Eng. Ind. 1967, 89, 785–796. [Google Scholar] [CrossRef]
- Lund, J.W. Stability and damped critical speeds of a flexible rotor in fluid-film bearings. J. Eng. Ind. 1974, 96, 509–517. [Google Scholar] [CrossRef]
- Chu, F.H.; Pilkey, W.D. A direct integration technique for the transient analysis of rotating shafts. J. Mech. Des. 1982, 104, 384–388. [Google Scholar] [CrossRef]
- Gu, J. An Improved Transfer matrix-direct integration method for rotor dynamics. J. Vib. Acoust. 1986, 108, 182–188. [Google Scholar] [CrossRef]
- Nelson, H.D. A finite rotating shaft element using Timoshenko beam theory. J. Mech. Des. 1980, 102, 793–803. [Google Scholar] [CrossRef]
- Ruhl, R.L.; Booker, J.F. A finite element model for distributed parameter turborotor systems. J. Eng. Ind. 1972, 94, 126–132. [Google Scholar] [CrossRef]
- Nelson, H.D.; McVaugh, J.M. The dynamics of rotor-bearing systems using finite elements. J. Eng. Ind. 1976, 98, 593–600. [Google Scholar] [CrossRef]
- Subbiah, R.; Kumar, A.S.; Sankar, T.S. Transient dynamic analysis of rotors using the combined methodologies of finite elements and transfer matrix. J. Appl. Mech. 1988, 55, 448–452. [Google Scholar] [CrossRef]
- Shiau, T.N.; Hwang, J.L. A new approach to the dynamic characteristic of undamped rotor-bearing systems. J. Vib. Acoust. 1989, 111, 379–385. [Google Scholar] [CrossRef]
- Shiau, T.N.; Hwang, J.L. Generalized polynomial expansion method for the dynamic analysis of rotor-bearing systems. J. Eng. Gas Turbines Power 1993, 115, 209–217. [Google Scholar] [CrossRef]
- Shiau, T.N.; Hwang, J.L.; Chang, Y.B. A study on stability and response analysis of a nonlinear rotor system with mass unbalance and side load. J. Eng. Gas Turbines Power 1993, 115, 218–226. [Google Scholar] [CrossRef]
- Shiau, T.N.; Chen, E.C.; Huang, K.H.; Hsu, W.C. Dynamic response of a spinning Timoshenko beam with general boundary conditions under a moving skew force using global assumed mode method. JSME Int. J. Ser. C 2006, 49, 401–410. [Google Scholar] [CrossRef]
- Shiau, T.N.; Huang, K.H.; Hsu, W.C. Dynamic response and stability of a rotating ball screw under a moving skew load. J. CSME 2006, 27, 297–305. [Google Scholar]
- Lee, P.; Altintas, Y. Prediction of ball-end milling forces from orthogonal cutting data. Int. J. Mach. Tools Manuf. 1996, 36, 1059–1072. [Google Scholar] [CrossRef]
- Altintas, Y.; Lee, P. Mechanics and dynamics of ball end milling. J. Manuf. Sci. Eng. Trans. 1998, 120, 684–692. [Google Scholar] [CrossRef]
- Stepan, G.; Szalai, R.; Mann, B.P.; Bayly, P.V.; Insperger, T.; Gradisek, J.; Govekar, E. Nonlinear dynamics of high-speed milling—Analyses, Numerics, and Experiments. J. Vib. Acoust. 2005, 127, 197–203. [Google Scholar] [CrossRef]
- Shiau, T.N.; Chen, K.H.; Chang, J.R.; Huang, M.H. Identification of system parameters for ball end milling. J. CSME 2009, 30, 95–105. [Google Scholar]
- Shiau, T.N.; Chen, K.H.; Chang, J.R. Critical speed analysis for nonlinear effects of rotor system and ball end milling. Int. J. Adv. Manuf. Technol. 2009, 44, 463–475. [Google Scholar] [CrossRef]
- Cao, H.; Li, B.; He, Z. Chatter stability of milling with speed-varying dynamics of spindles. Int. J. Mach. Tools Manuf. 2012, 52, 50–58. [Google Scholar] [CrossRef]
- Kalinski, K.J.; Galewski, M.A. Optimal spindle speed determination for vibration reduction during ball-end milling of flexible details. Int. J. Mach. Tools Manuf. 2015, 92, 19–30. [Google Scholar] [CrossRef]
- Yao, Q.; Wu, B.; Luo, M.; Zhang, D. On-line cutting force coefficients identification for bull-end milling process with vibration. Measurement 2018, 125, 243–253. [Google Scholar] [CrossRef]
- Zhan, D.; Jiang, S.; Niu, J.; Sun, Y. Dynamics modeling and stability analysis of five-axis ball-end milling system with variable pitch tools. Int. J. Mech. Sci. 2020, 182, 105774. [Google Scholar] [CrossRef]
- Cai, S.; Cai, Z.; Yao, B.; Shen, Z.; Ma, X. Identifying the transient milling force coefficient of a slender end-milling cutter with vibrations. J. Manuf. Process. 2021, 67, 262–274. [Google Scholar] [CrossRef]
- Miao, H.; Li, C.; Wang, C.; Xu, M.; Zhang, Y. The vibration analysis of the CNC vertical milling machine spindle system considering nonlinear and nonsmooth bearing restoring force. Mech. Syst. Signal Process. 2021, 161, 107970. [Google Scholar] [CrossRef]
- Li, B.; Liu, T.; Liao, J.; Feng, C.; Yao, L.; Zhang, J. Non-invasive milling force monitoring through spindle vibration with LSTM and DNN in CNC machine tools. Measurement 2023, 210, 112554. [Google Scholar] [CrossRef]
- Dai, Y.; Li, H.; Liu, H.; Yong, J.; Yang, C.; Wang, C.; Liu, S. Dynamics and stability analysis of five-axis ball end milling with low radial immersion considering cutter runout. J. Manuf. Process. 2023, 92, 479–499. [Google Scholar] [CrossRef]
- Qin, S.; Hao, Y.; Zhu, L.; Wiercigroch, M.; Yuan, Z.; Shi, C.; Cui, D. CWE identification and cutting force prediction in ball-end milling process. Int. J. Mech. Sci. 2023, 239, 107863. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Krajewska-Spiewak, J.; Maruda, R.W.; Krolczyk, G.M.; Nieslony, P.; Wieczorowski, M.; Gawlik, J. Study on ploughing phenomena in tool flank face—Workpiece interface including tool wear effect during ball-end milling. Tribol. Int. 2023, 181, 108313. [Google Scholar] [CrossRef]
- Lv, B.; Lin, B.; Cao, Z.; Liu, W.; Wang, G. Numerical simulation and experimental investigation of structured surface generated by 3D vibration-assisted milling. J. Manuf. Process. 2023, 89, 371–383. [Google Scholar] [CrossRef]

| Cutting Condition | ||
|---|---|---|
| Carbide Ball End Mills | ||
| Tool radius | R3 | Workpiece material: Ti6Al4V Cutting coefficient Shear stress MPa Friction angle Chip compression ratio , Rake angle, Chip thickness Edge force coefficients: , , Cutting force coefficients: given in Appendix C |
| Tool length | 30 mm | |
| Axial depth of cut | 1 mm | |
| Feed per tooth | 0.3 mm (2 flutes) | |
| 0.2 mm (3 flutes) | ||
| Rake angle | ||
| Helix angle | ||
| Spindle Section | E (N/mm2) | ρ (kg/mm3) | do (mm) | dI (mm) | Length |
|---|---|---|---|---|---|
| I | 100 | 60 | |||
| II | 160 | 60 | |||
| III | 6 | 0 | |||
| Bearing A: , , Bearing B: , , | |||||
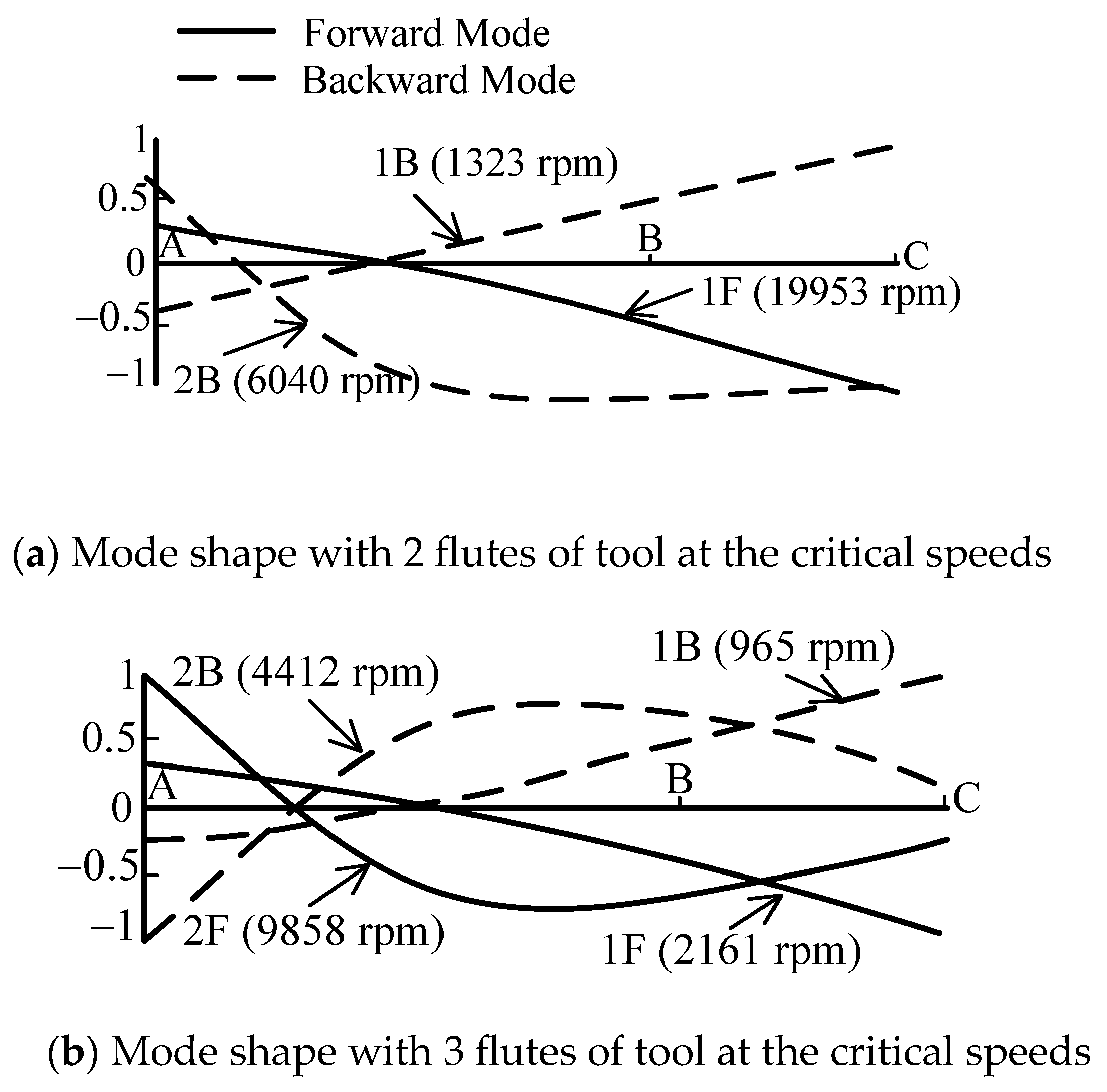
| Mode | Type | Flutes | Ncr (rpm) | fn (rad/s) |
|---|---|---|---|---|
| 1 | Backward Mode | 2 | 1323 | 277 |
| 3 | 965 | 303 | ||
| Forward Mode | 2 | 19,953 | 4179 | |
| 3 | 2161 | 679 | ||
| 2 | Backward Mode | 2 | 6040 | 1265 |
| 3 | 4412 | 1386 | ||
| Forward Mode | 2 | - | - | |
| 3 | 9858 | 3097 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-J.; Chang, J.-R.; Shiau, T.-N.; Chen, K.-H. A Numerical Analysis for Ball End Milling Due to Coupling Effects of a Flexible Rotor-Bearing System Using GPEM. Appl. Sci. 2023, 13, 7252. https://doi.org/10.3390/app13127252
Huang C-J, Chang J-R, Shiau T-N, Chen K-H. A Numerical Analysis for Ball End Milling Due to Coupling Effects of a Flexible Rotor-Bearing System Using GPEM. Applied Sciences. 2023; 13(12):7252. https://doi.org/10.3390/app13127252
Chicago/Turabian StyleHuang, Chun-Jung, Jer-Rong Chang, Ting-Nung Shiau, and Kuan-Hung Chen. 2023. "A Numerical Analysis for Ball End Milling Due to Coupling Effects of a Flexible Rotor-Bearing System Using GPEM" Applied Sciences 13, no. 12: 7252. https://doi.org/10.3390/app13127252
APA StyleHuang, C.-J., Chang, J.-R., Shiau, T.-N., & Chen, K.-H. (2023). A Numerical Analysis for Ball End Milling Due to Coupling Effects of a Flexible Rotor-Bearing System Using GPEM. Applied Sciences, 13(12), 7252. https://doi.org/10.3390/app13127252






