Methods and Tools Supporting the Learning and Teaching of Mathematics Dedicated to Students with Blindness
Abstract
1. Introduction
2. Related Works
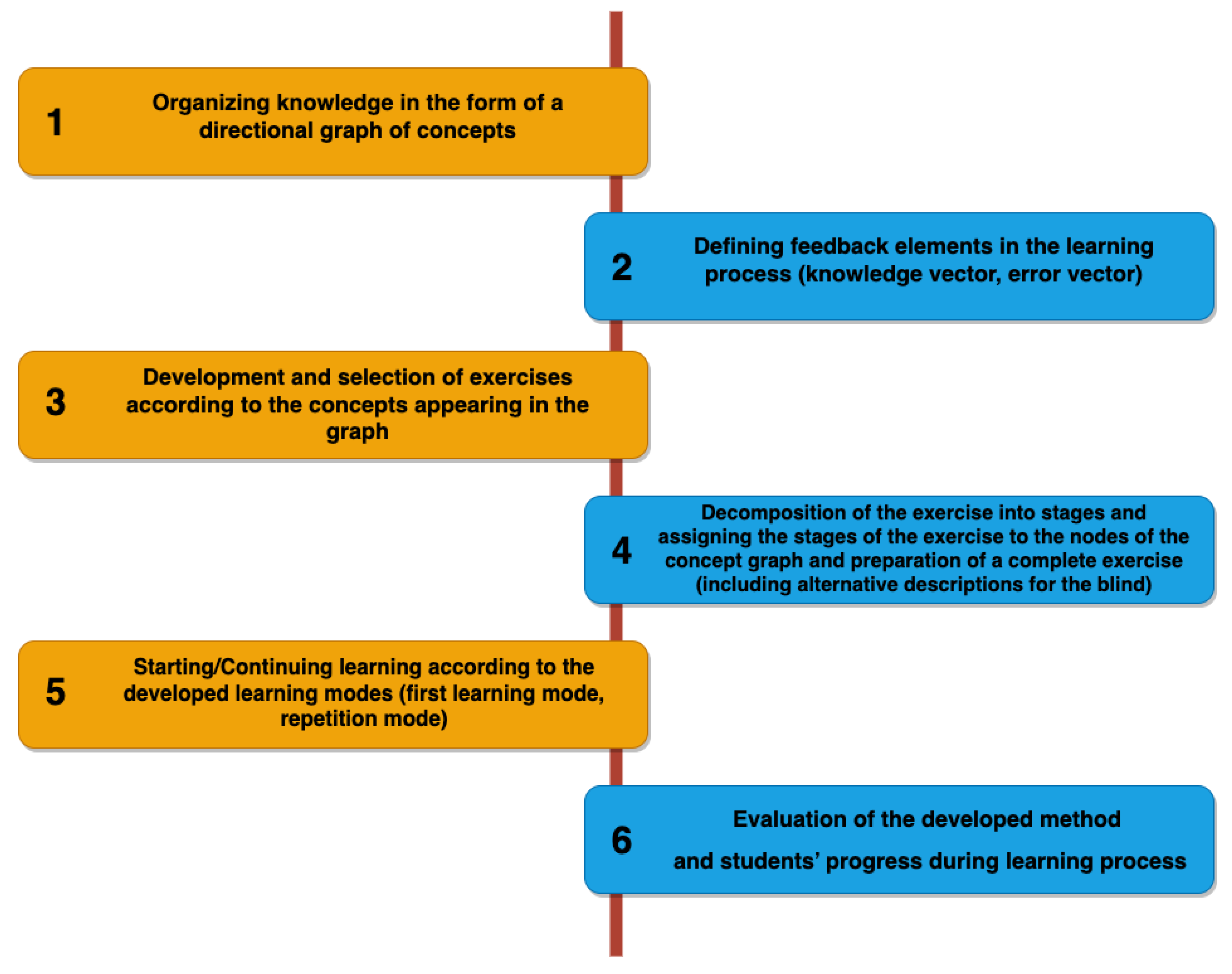
3. Materials and Methods
- Multiple choice lists;
- Drop-down lists;
- Text fields/boxes to enter values.
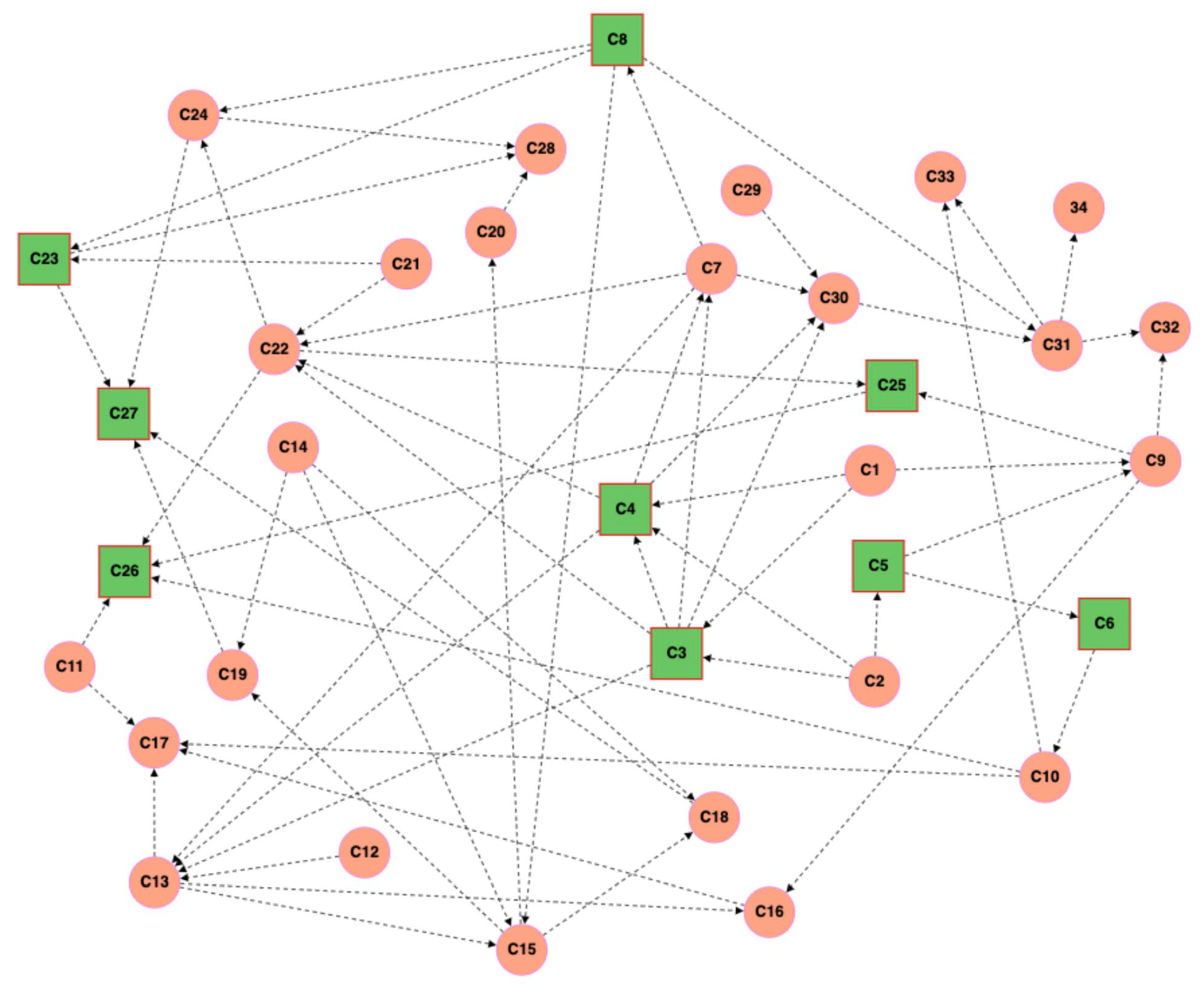
3.1. Structuring Knowledge into a Graph of Concepts
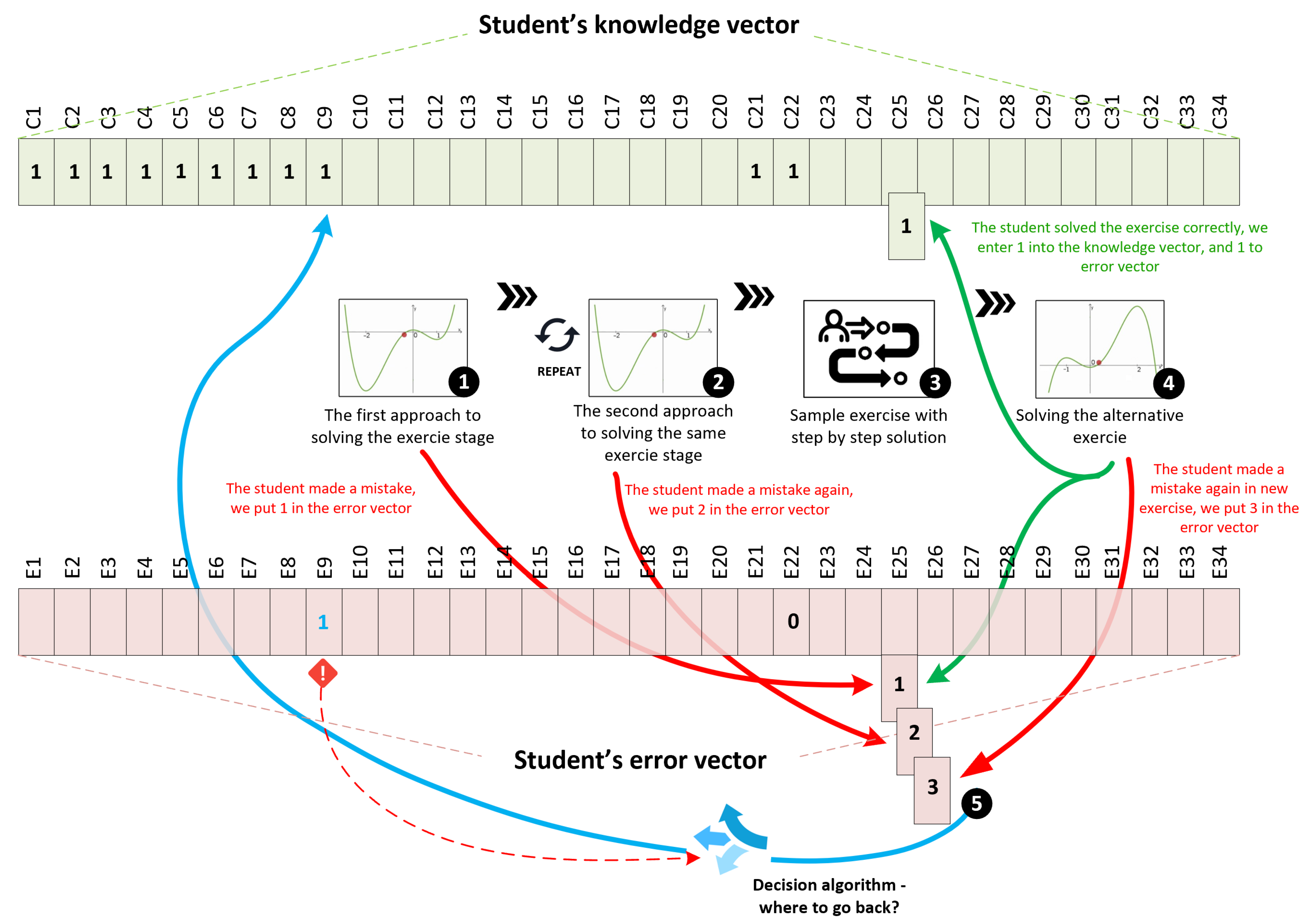
3.2. Elements of Feedback Used during Learning in the Developed Platform
- Error vector: Creates a learning history for a given student and accumulates mistakes that are grouped into classes. With a given node in the concept graph, multiple types of defined errors can be associated.
- Knowledge vector: stores information about the concepts mastered by the student based on correctly solved exercises.
| Algorithm 1 Pseudocode of exercise selection during learning mode | |
| 1: | require: concept graph C, knowledge_vector, error_vector |
| 2: | require: list of all exercises E corresponding for each element in graph C |
| 3: | |
| 4: | input: current node N in concept graph C |
| 5: | |
| 6: | M = C.get_predecessors(N) |
| 7: | W[] = 0 |
| 8: | M_predecessor = None |
| 9: | for Mi in M: |
| 10: | Wi = error_vector[Mi] |
| 11: | end for |
| 12: | if all Wi in W == 0: |
| 13: | M_predecessor = select Mi from M where min(knowledge_vector[Mi].time_stamp) |
| 14: | |
| 15: | else: |
| 16: | maxW = max(W[]) |
| 17: | M_temp = select all Mi from M where Wi == maxW |
| 18: | M_predecessor = select Mi from M_temp where max(error_vector[Mi].time_stamp) |
| 19: | |
| 20: | Z = select random exercise from E corresponding to M_predecessor |
| 21: | |
| 22: | output: Z |
3.3. Selection/Development of a Set of Exercises
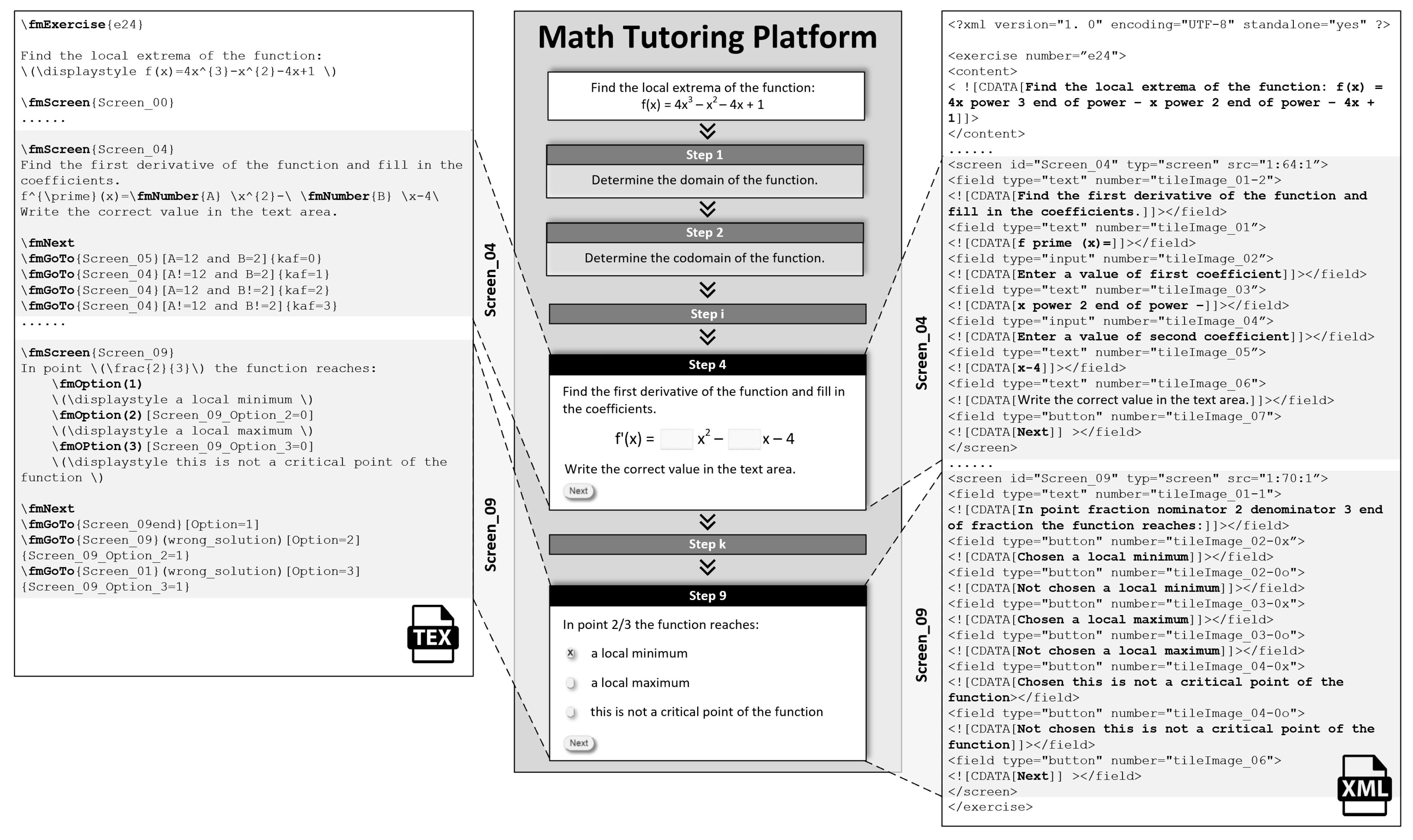
3.4. Decomposition of the Exercise into Phases
3.5. Starting/Continuing Learning
3.5.1. Learning Mode 1—Mastering New Material
3.5.2. Learning Mode 2—Material Review
| Algorithm 2 Pseudocode of exercise selection during revision mode. | |
| 1: | require: student’s error_vector instance—E |
| 2: | require: list of exercises Z = [Z1, Z2, Z3 …] with information about covered concept nodes |
| 3: | where: Zi = [z1, z2, …, zn] is a binary vector of length n equals to the length of error vector. Every exercise Zi is represented as a vector, where each non zero component represents the corresponding covered concept node. E = [e1, e2, …, en] is a vector of length n equals to the length of error vector, where each non zero component represents the number of errors made by the student in a particular concept. |
| 4: | |
| 5: | input: E |
| 6: | |
| 7: | n = E.length() |
| 8: | E_repetition[] = 0 |
| 9: | Z_selected[] = None |
| 10: | Z_copy = Z |
| 11: | for j in n: |
| 12: | if E[j] > 0: |
| 13: | E_repetition[j] = 1 |
| 14: | end for |
| 15: | while (E_repetition.contains(1)): |
| 16: | for Zi in Z_copy: |
| 17: | covered_concepts[] = 0 |
| 18: | for j in n: |
| 19: | if zj * ej == 1: covered_concepts[i]++ |
| 20: | end for |
| 21: | end for |
| 22: | |
| 23: | Z_temp = Z_copy[index of max(covered_concepts[])] |
| 24: | Z_selcted.append(Z_temp) |
| 25: | Z_copy.remove(Z_temp) |
| 26: | |
| 27: | E_covered[] = 0 |
| 28: | for j in n: |
| 29: | E_covered[j] = E_covered[j] * Z_temp[j] |
| 30: | E_repetition[j] = E_repetition[j] − E_covered[j] |
| 31: | end for |
| 32: | end while |
| 33: | |
| 34: | outuput: Z_selected |
3.6. Experiments and Evaluation Method
- Selection of the scope of the material—the evaluation covered the correctness of the preparation of the concept graph.
- Selection or design of new exercises—the evaluation included the preparation of exercises in the extended syntax of the TEX compiler.
- Division of the exercises into stages—the evaluation included the assignment stages of exercise to concepts in the graph.
- Creating alternative descriptions—the evaluation included applying the developed rules for generating alternative descriptions.
- 5.
- Using the system for learning—the evaluation included verifying the feedback mechanisms: the error vector and the knowledge vector in the process of mastering the developed material by students.
- Additional teacher time needed to prepare the course:
- Preparation of the concept graph.
- Selection of the exercise.
- Division of exercises into stages, assignment of every exercise stage to the node in the concept graph, and preparation of alternative descriptions.
- Evaluation of the impact of the developed method on students’ progress through the average grades of students in mastering the developed material:
- Comparison of grades between two classes in the final test (one using the developed method and one not using it).
- Evaluation of the possibility of knowledge consolidation by blind students through assisting less advanced peers in learning a new topic—the percentage of students who attempted to support their peers.
4. Results
- Preparation of the concept graph (average time of preparing a graph of concepts for the teacher’s course)—between 10 and 18 h, with an average value of 15.2 h.
- Selection of a set of exercises that cover all of the concepts from the concept graph within the chosen branch of mathematics. The exercises should represent different difficulty levels, and each element of the graph should be associated with five different exercises (average time for a teacher to choose or prepare an exercise)—between 8 and 16 h, with an average value of 9.7 h.
- Dividing the exercises into stages, assigning stages to the nodes in the concept graph, and preparing alternative descriptions (average time per exercise)—from 2 to 8 h, with an average of value 5.3 h.
5. Discussion and Conclusions
- Standardization of the educational material and the phases of its acquisition;
- The possibility of a quantitative assessment of the student’s knowledge;
- The possibility of a detailed assessment of challenging elements;
- The ability to easily compare the knowledge of students;
- The ability to choose lesson materials corresponding to the level of knowledge of students in the class;
- The possibility of cooperation between students via individual consultations;
- The development of various ways of navigation and presentation of the exercise content, as well as the formula itself, in visual forms and alternative audio presentations, depending on the stage of the exercise and its context;
- Semi-automatic generation of alternative presentations of mathematical formulas, including additional structural information based on the TEX notation, which is a standard used for writing mathematical expressions; the choice of widely used TEX notation serves as a bridge between the commonly used presentation and the proposed alternative presentation. The developed method of alternative presentation can be used in different languages. It requires adapting the alternative descriptions to the rules of a specific language, while the TEX syntax modifications remain unchanged. The paper presents the method and demonstrates its application with alternative descriptions in the Polish language.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Node Number | Concept (Math Term) | Successor Node | Mistake Node 1 | Mistake Type and Description |
|---|---|---|---|---|
| C1 | Number intervals | C3, C4, C9 | E1 | Number set type definition error; range boundary definition error; range boundary type error |
| C2 | Function definition | C3, C4, C5 | E2 | Function definition understanding error; function definition error |
| C3 | Definition of the domain of a function | C4, C7, C13, C22, C30 | E3 | Determination of value constraints in the domain of the function error; determination of the boundary of the range of the domain of the function error |
| C4 | Definition of the codomain of a function | C7, C13, C22, C30 | E4 | Determination of value constraints in the counter domain of the function error; determination of the boundary of the range of the counter domain of the function error |
| C5 | Definition of the derivative of a function | C6, C9 | E5 | Function derivative definition error; function derivative definition understanding error |
| C6 | Definition of the second derivative of the function | C10 | E6 | Second function derivative definition error; second function derivative understanding error |
| C7 | Definition of the function graph | C8, C13, C22, C30 | E7 | Determination of the value of the function for the specified value of the argument error; inability to determine the shape of the function graph error |
| C8 | Definition of a root of a function | C15, C23, C24, C31 | E8 | Inability to understand the definition of zero error; inability to calculate zero error |
| C9 | Definition of monotonicity interval | C16, C25, C32 | E9 | Inability to understand the idea of monotonicity error; inability to calculate the interval error; calculation of monotonicity interval error |
| C10 | Definition of the inflection point of a function | C11, C17, C26, C33 | E10 | Inability to understand the idea of an inflection point error; inability to calculate inflection point error; inflection point calculation error |
| C11 | Definition of the extreme of a function | C17, C26 | E11 | Inability to understand the function extreme error; distinguishing the type of extreme error; inability to calculate the extreme of a function error; function extreme calculation error |
| C12 | Quadratic function | C13 | E12 | Inability to understand the formula of a quadratic function error; formula of a quadratic function writing error |
| C13 | Quadratic function graph | C15, C16, C17 | E13 | Inability to determine the shape of the graph of a quadratic function error; inability to determine the properties of the graph of a quadratic function error (vertex, direction of parabola arms) |
| C14 | Quadratic equation | C15, C18, C19 | E14 | Inability to understand the ways used to solve quadratic equation error; quadratic equation calculation error |
| C15 | Roots of a quadratic function | C18, C19, C20 | E15 | Inability to understand the formulas for the roots of a quadratic function error; quadratic equation root calculation error |
| C16 | Monotonicity intervals of a quadratic function | C17 | E16 | Inability to understand how to calculate monotonicity intervals of a quadratic function error; monotonicity intervals of a quadratic function calculation error |
| C17 | The extreme of a quadratic function | - | E17 | Extreme of a quadratic function calculation error |
| C18 | Square root equations | C27 | E18 | Inability to understand how to solve an equation with a square root error; root equation calculation error |
| C19 | Equations to be solved by square substitution | C27 | E19 | Inability to understand how to solve an equation with substitution error; solving an equation with substitution calculation error |
| C20 | Quadratic inequalities | C28 | E20 | Inability to understand how to solve a quadratic inequality error; square inequality calculation error |
| C21 | Polynomial | C22, C23 | E21 | Inability to understand the formula of polynomial function error; polynomial function formula writing error |
| C22 | Polynomial graph | C24, C25, C26 | E22 | Inability to determine the shape of the graph of a polynomial function error; inability to determine the properties of a polynomial graph error |
| C23 | Division of polynomials | C27, C28 | E23 | Inability to understand the method of dividing polynomial error; polynomial dividing error |
| C24 | Roots of a polynomial | C27, C28 | E24 | Inability to understand the formulas for polynomial root error; polynomial root calculation error |
| C25 | Monotonicity intervals of a polynomial | C26 | E25 | Inability to understand how to calculate polynomial monotonicity interval error; polynomial monotonicity interval calculation error |
| C26 | The extreme of a polynomial | - | E26 | Polynomial extreme calculation error |
| C27 | Polynomial equation | - | E27 | Inability to understand how to solve a polynomial equation error; polynomial equation calculation error |
| C28 | Polynomial inequalities | - | E28 | Inability to understand how to solve a polynomial inequality error; polynomial inequality calculation error |
| C29 | Trigonometric function—types | C30 | E29 | Inability to understand the types of trigonometric function error; inability to determine the period of trigonometric function error |
| C30 | Graphs of trigonometric functions | C31 | E30 | Inability to distinguish the type of trigonometric function based on the graph error; period of trigonometric function determination error |
| C31 | The zero of the trigonometric function | C32, C33, C34 | E31 | Inability to understand inverse trigonometric function error; zero calculation error |
| C32 | Monotonicity intervals of trigonometric functions | - | E32 | Inability to understand the properties of graphs of trigonometric function error; trigonometric function monotonicity interval determination error |
| C33 | Trigonometric equations | - | E33 | Inability to understand how to solve trigonometric equation error; trigonometric equation calculation error |
| C34 | Trigonometric inequalities | - | E34 | Inability to understand how to solve trigonometric inequality error; trigonometric inequality calculation error |
References
- Rodriguez-Ascaso, A.; Letón, E.; Muñoz-Carenas, J.; Finat, C. Accessible Mathematics Videos for Non-Disabled Students in Primary Education. PLoS ONE 2018, 13, e0208117. [Google Scholar] [CrossRef]
- Karshmer, A.I.; Bledsoe, C. Access to Mathematics by Blind Students: Introduction to the Special Thematic Session. In Computers Helping People with Special Needs, Proceedings of the 8th International Conference on Computers for Handicapped Persons, ICCHP 2002, Linz, Austria, 15–20 July 2002; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2398, pp. 471–476. [Google Scholar]
- Mountapmbeme, A.; Ludi, S. Investigating Challenges Faced by Learners with Visual Impairments Using Block-Based Programming/Hybrid Environments. In Proceedings of the 22nd International ACM SIGACCESS Conference on Computers and Accessibility, Virtual Event, Greece, 26–28 October 2020; Association for Computing Machinery: New York, NY, USA, 2020. [Google Scholar]
- Brawand, A.C.; Johnson, N.M. Effective Methods for Delivering Mathematics Instruction to Students with Visual Impairments. J. Blind. Innov. Res. 2016, 6. [Google Scholar] [CrossRef]
- Rule, A.C.; Stefanich, G.P.; Boody, R.M.; Peiffer, B. Impact of Adaptive Materials on Teachers and Their Students with Visual Impairments in Secondary Science and Mathematics Classes. Int. J. Sci. Educ. 2011, 33, 865–887. [Google Scholar] [CrossRef]
- Klingenberg, O.G.; Holkesvik, A.H.; Augestad, L.B. Research Evidence for Mathematics Education for Students with Visual Impairment: A Systematic Review. Cogent Educ. 2019, 6, 1626322. [Google Scholar] [CrossRef]
- van Leendert, A.; Doorman, M.; Drijvers, P.; Pel, J.; van der Steen, J. Towards a Universal Mathematical Braille Notation. J. Vis. Impair. Blind. 2022, 116, 141–153. [Google Scholar] [CrossRef]
- White, J.G. The Accessibility of Mathematical Notation on the Web and Beyond. J. Sci. Educ. Stud. Disabil. 2020, 23, 9. [Google Scholar] [CrossRef]
- Souza, A.; Freitas, D. Technologies in Mathematics Teaching: A Transcript of the Voices of Visually Impaired Students, Braille Teachers, and Screen Readers. In Proceedings of the 2019 International Symposium on Computers in Education (SIIE), Tomar, Portugal, 21–23 November 2019; pp. 1–6. [Google Scholar]
- Gulley, A.P.; Smith, L.A.; Price, J.A.; Prickett, L.C.; Ragland, M.F. Process-Driven Math: An Auditory Method of Mathematics Instruction and Assessment for Students Who Are Blind or Have Low Vision. J. Vis. Impair. Blind. 2017, 111, 465–471. [Google Scholar] [CrossRef]
- Manitsa, I.; Doikou, M. Social Support for Students with Visual Impairments in Educational Institutions: An Integrative Literature Review. Br. J. Vis. Impair. 2022, 40, 29–47. [Google Scholar] [CrossRef]
- Almeida, A.M.P.; Beja, J.; Pedro, L.; Rodrigues, F.; Clemente, M.; Vieira, R.; Neves, R. Development of an Online Digital Resource Accessible for Students with Visual Impairment or Blindness: Challenges and Strategies. Work 2020, 65, 333–342. [Google Scholar] [CrossRef]
- Klingenberg, O.G.; Holkesvik, A.H.; Augestad, L.B. Digital Learning in Mathematics for Students with Severe Visual Impairment: A Systematic Review. Br. J. Vis. Impair. 2020, 38, 38–57. [Google Scholar] [CrossRef]
- Nazemi, A.; Murray, I.; Mohammadi, N. Mathspeak: An Audio Method for Presenting Mathematical Formulae to Blind Students. In Proceedings of the 2012 5th International Conference on Human System Interactions, Perth, Australia, 6–8 June 2012; pp. 48–52. [Google Scholar]
- Bier, A.; Sroczyński, Z. Rule Based Intelligent System Verbalizing Mathematical Notation. Multimed. Tools Appl. 2019, 78, 28089–28110. [Google Scholar] [CrossRef]
- Salamonczyk, A.; Brzostek-Pawlowska, J. Translation of MathML Formulas to Polish Text, Example Applications in Teaching the Blind. In Proceedings of the 2015 IEEE 2nd International Conference on Cybernetics (CYBCONF), Gdynia, Poland, 24–26 June 2015; pp. 240–244. [Google Scholar]
- Fichten, C.S.; Asuncion, J.V.; Barile, M.; Ferraro, V.; Wolforth, J. Accessibility of E-Learning and Computer and Information Technologies for Students with Visual Impairments in Postsecondary Education. J. Vis. Impair. Blind. 2009, 103, 543–557. [Google Scholar] [CrossRef]
- Maćkowski, M.; Brzoza, P.; Żabka, M.; Spinczyk, D. Multimedia Platform for Mathematics’ Interactive Learning Accessible to Blind People. Multimed. Tools Appl. 2018, 77, 6191–6208. [Google Scholar] [CrossRef]
- Azure Immersive Reader Documentation|Microsoft Learn. Available online: https://learn.microsoft.com/en-us/azure/applied-ai-services/immersive-reader/ (accessed on 13 June 2023).
- Da Paixão Silva, L.F.; de Barbosa, A.A.O.; Freire, E.R.C.G.; Cardoso, P.C.F.; Durelli, R.S.; Freire, A.P. Content-Based Navigation Within Mathematical Formulae On the Web For Blind Users and Its Impact On Expected User Effort. In Proceedings of the 8th International Conference on Software Development and Technologies for Enhancing Accessibility and Fighting Info-Exclusion, Thessaloniki, Greece, 20–22 June 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 23–32. [Google Scholar]
- Dabi, G.K.; Golga, D.N. The Role of Assistive Technology in Supporting the Engagement of Students with Visual Impairment in Learning Mathematics: An Integrative Literature Review. Br. J. Vis. Impair. 2023. [Google Scholar] [CrossRef]
- Ruipérez-Valiente, J.A.; Muñoz-Merino, P.J.; Kloos, C.D. A Demonstration of ALAS-KA: A Learning Analytics Tool for the Khan Academy Platform. Lect. Notes Comput. Sci. 2014, 8719, 518–521. [Google Scholar] [CrossRef]
- Essa, A. A Possible Future for next Generation Adaptive Learning Systems. Smart Learn. Environ. 2016, 3, 16. [Google Scholar] [CrossRef]
- Web Content Accessibility Guidelines (WCAG) Overview|Web Accessibility Initiative (WAI)|W3C. Available online: https://www.w3.org/WAI/standards-guidelines/wcag/ (accessed on 2 September 2022).
- Amponsah, S.; Bekele, T.A. Exploring Strategies for Including Visually Impaired Students in Online Learning. Educ. Inf. Technol. 2022. [Google Scholar] [CrossRef]
- Borba, M.C.; Askar, P.; Engelbrecht, J.; Gadanidis, G.; Llinares, S.; Aguilar, M.S. Blended Learning, e-Learning and Mobile Learning in Mathematics Education. ZDM 2016, 48, 589–610. [Google Scholar] [CrossRef]
- Moreno-Guerrero, A.J.; Aznar-Díaz, I.; Cáceres-Reche, P.; Alonso-García, S. E-Learning in the Teaching of Mathematics: An Educational Experience in Adult High School. Mathematics 2020, 8, 840. [Google Scholar] [CrossRef]
- Bell, E.C.; Silverman, A.M. Access to Math and Science Content for Youth Who Are Blind or Visually Impaired. J. Blind. Innov. Res. 2019, 9. [Google Scholar] [CrossRef]
- Shoaib, M.; Khan, S.; Fitzpatrick, D.; Pitt, I. A Mobile E-Learning Application for Enhancement of Basic Mathematical Skills in Visually Impaired Children. Univers. Access Inf. Soc. 2023, 1–11. [Google Scholar] [CrossRef]
- Mattheiss, E.; Regal, G.; Sellitsch, D.; Tscheligi, M. User-Centred Design with Visually Impaired Pupils: A Case Study of a Game Editor for Orientation and Mobility Training. Int. J. Child-Comput. Interact. 2017, 11, 12–18. [Google Scholar] [CrossRef]
- Kruger, R.; De Wet, F.; Niesler, T. Mathematical Content Browsing for Print-Disabled Readers Based on Virtual-World Exploration and Audio-Visual Sensory Substitution. ACM Trans. Access. Comput. 2023, 16, 1–27. [Google Scholar] [CrossRef]
- Brzoza, P.; Maćkowski, M. Intelligent Tutoring Math Platform Accessible for Visually Impaired People; Springer Nature: Cham, Switzerland, 2014; Volume 8547, ISBN 9783319085951. [Google Scholar]
- Spinczyk, D.; Maćkowski, M.; Kempa, W.; Rojewska, K. Factors Influencing the Process of Learning Mathematics among Visually Impaired and Blind People. Comput. Biol. Med. 2019, 104, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Maćkowski, M.S.; Brzoza, P.F.; Spinczyk, D.R. Tutoring Math Platform Accessible for Visually Impaired People. Comput. Biol. Med. 2018, 95, 298–306. [Google Scholar] [CrossRef]
- Mavrikis, M.; Holmes, W. Intelligent Learning Environments: Design, Usage and Analytics for Future Schools. In Shaping Future Schools with Digital Technology; Springer Nature: Singapore, 2019; pp. 57–73. ISBN 978-981-13-9438-6. [Google Scholar]
- Mikułowski, D.; Brzostek-Pawłowska, J. Multi-Sensual Augmented Reality in Interactive Accessible Math Tutoring System for Flipped Classroom. Intell. Tutoring Syst. 2020, 12149, 1–10. [Google Scholar] [CrossRef]
- Drachsler, H.; Verbert, K.; Santos, O.C.; Manouselis, N. Panorama of Recommender Systems to Support Learning BT—Recommender Systems Handbook; Ricci, F., Rokach, L., Shapira, B., Eds.; Springer: Boston, MA, USA, 2015; pp. 421–451. ISBN 978-1-4899-7637-6. [Google Scholar]
- Good, J.; Robertson, J. CARSS: A Framework for Learner-Centred Design with Children. Int. J. Artif. Intell. Educ. 2006, 16, 381–413. [Google Scholar]
- Lynch, D.; Howlin, C.P. Real World Usage of an Adaptive Testing Algorithm to Uncover Latent Knowledge. In Proceedings of the 7th International Conference of Education, Seville, Spain, 17–19 November 2014; pp. 504–511. [Google Scholar]
- Maćkowski, M.; Kawulok, M.; Brzoza, P.; Spinczyk, D. Method and Tools to Supporting Math Learning in Inclusive Education of Blind Students. In Augmented Intelligence and Intelligent Tutoring Systems, Proceedings of the International Conference on Intelligent Tutoring Systems, Corfu, Greece, 2–5 June 2023; Frasson, C., Mylonas, P., Troussas, C., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 42–53. [Google Scholar] [CrossRef]
- Brzoza, P.; Łobos, E.; Macura, J.; Sikora, B.; Żabka, M. ForMath Intelligent Tutoring System in Mathematics. In Proceedings of the 4th International Conference on Computer Supported Education, Porto, Portugal, 16–18 April 2012; SciTePress: Setúbal, Portugal, 2012; pp. 118–122. [Google Scholar]
- Maćkowski, M.; Rojewska, K.; Dzieciątko, M.; Spinczyk, D. Initial Motivation as a Factor Predicting the Progress of Learning Mathematics for the Blind. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1011, pp. 349–357. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maćkowski, M.; Kawulok, M.; Brzoza, P.; Spinczyk, D. Methods and Tools Supporting the Learning and Teaching of Mathematics Dedicated to Students with Blindness. Appl. Sci. 2023, 13, 7240. https://doi.org/10.3390/app13127240
Maćkowski M, Kawulok M, Brzoza P, Spinczyk D. Methods and Tools Supporting the Learning and Teaching of Mathematics Dedicated to Students with Blindness. Applied Sciences. 2023; 13(12):7240. https://doi.org/10.3390/app13127240
Chicago/Turabian StyleMaćkowski, Michał, Mateusz Kawulok, Piotr Brzoza, and Dominik Spinczyk. 2023. "Methods and Tools Supporting the Learning and Teaching of Mathematics Dedicated to Students with Blindness" Applied Sciences 13, no. 12: 7240. https://doi.org/10.3390/app13127240
APA StyleMaćkowski, M., Kawulok, M., Brzoza, P., & Spinczyk, D. (2023). Methods and Tools Supporting the Learning and Teaching of Mathematics Dedicated to Students with Blindness. Applied Sciences, 13(12), 7240. https://doi.org/10.3390/app13127240









