Modification of Nonlinear Controller for Asymmetric Marine Vehicles Moving in Horizontal Plane
Abstract
1. Introduction
- (1)
- Decomposition of the inertia matrix enabling description of the use of velocity transformation for an underactuated underwater vehicle moving in the horizontal plane, obtaining diagonal equations of motion, and testing of the modified control algorithm.
- (2)
- Showing some of the information available from the trajectory-tracking controller when a dynamic description containing quasi-velocities (QV) is used.
- (3)
- Proposal of an algorithm for trajectory tracking in horizontal motion when the center of mass lies outside both axes of symmetry of the vehicle. This controller is generalized in the sense that the previously known controllers from [38,52] are special cases of it and apply only when the center of mass is shifted in the longitudinal direction. In contrast, this scheme also considers shift in the center of mass in the lateral direction. A simulation test of the modified control algorithm was performed for two models of different vehicles and three desired trajectories based on intuitive selection of controller parameters.
- (1)
- First, the algorithm presented is applicable to vehicles whose center of mass lies outside the coordinate axes and is not symmetrical on the longitudinal axis.
- (2)
- Second, the theoretical contribution is that the vehicle dynamics model is more realistic and this has been taken into account in the control algorithm.
- (3)
- Third, the controller contains more dynamic couplings due to the more complex dynamic model. Therefore, it is possible to assess their influence on the movement of the vehicle along the selected desired trajectory.
- (4)
- Fourth, a motion analysis for the cycloid–like trajectory is included in the simulation study, which provides a deeper understanding of the vehicle dynamics using the proposed controller. Instead of a sine trajectory, a sine-cosine trajectory was applied. In addition, quantities that are crucial for coupling evaluation are added.
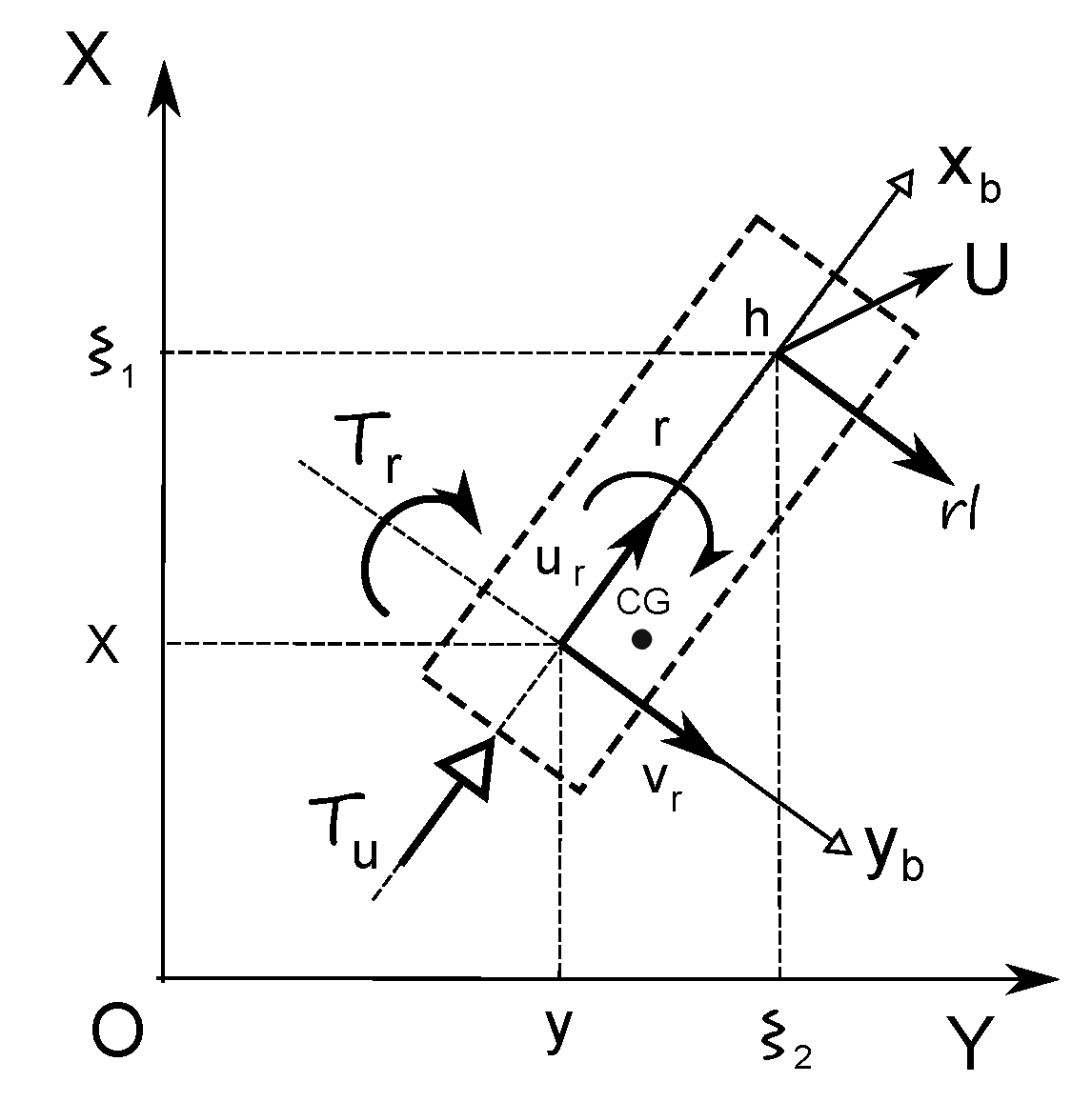
2. Marine Vehicle Model
2.1. Transformed Equations of Motion
2.2. Additional Information Obtained by Using QV
- (1)
- Norm of the matrix representing the normalized value of the couplings in the dynamic vehicle model. The matrix is calculated from the symmetric matrix M and depends on the dynamic and geometric parameters.
- (2)
- The kinetic energy dissipated by each vector variable (and its sum concerning the whole vehicle) following the formula: .
- (3)
- The mean value of kinetic energy related to each variable and the sum of the mean kinetic energy: .
- (4)
- The distortion of each velocity due to couplings resulting from the formula: . The QV includes couplings between itself and the other velocities because .
2.3. Relationship to Original Description of Dynamics
3. Controller in Terms of Quasi-Velocities
3.1. Differences Compared to the Original Trajectory-Tracking Algorithm
3.2. Advantages and Limitation of Using the Proposed Tracking Controller
- It can be used to control fully asymmetric vehicles, making the dynamics model more realistic than a model with a diagonal inertia matrix. Simplifying the dynamics model still allows the algorithm to work, but loses some information about the effects of dynamic coupling.
- The resulting equations employed in the algorithm are decoupled because of the diagonalization of the inertia matrix instead of calculating the inverse inertia matrix. The equations of motion are in diagonal form. From the dynamics equations, it can be determined which values of mass correspond to the quasi-accelerations when couplings are included.
- Insights into vehicle dynamics with the controller are available.
- Each quasi-velocity is controlled separately. The time history provides information about the deformation of the velocity during vehicle movement.
- Control signals are related to the vehicle dynamics because they are scaled by and the set of parameters is included in the algorithm.
- Compared to other algorithms, additional information hidden in the inertia matrix can be obtained after the velocity transformation from the modified controller.
- suitable for fully asymmetrical vehicle models (about both axes of symmetry), e.g., the proposed QV controller;
4. Numerical Simulations
4.1. Vehicles and Test Conditions
- (1)
- The starting points were selected taking into account the dynamics of each vehicle model.
- (2)
- The simulation time s was chosen to show the effects of the use of the controller.
- (3)
- The disturbances were assumed to be close to [38], i.e., m/s, m/s. The forces and torques were limited to reduce their initial values, that is, N and Nm.
- (4)
- The test was performed based on the software referred to in [56], modified to obtain results using the equations expressed in QV.
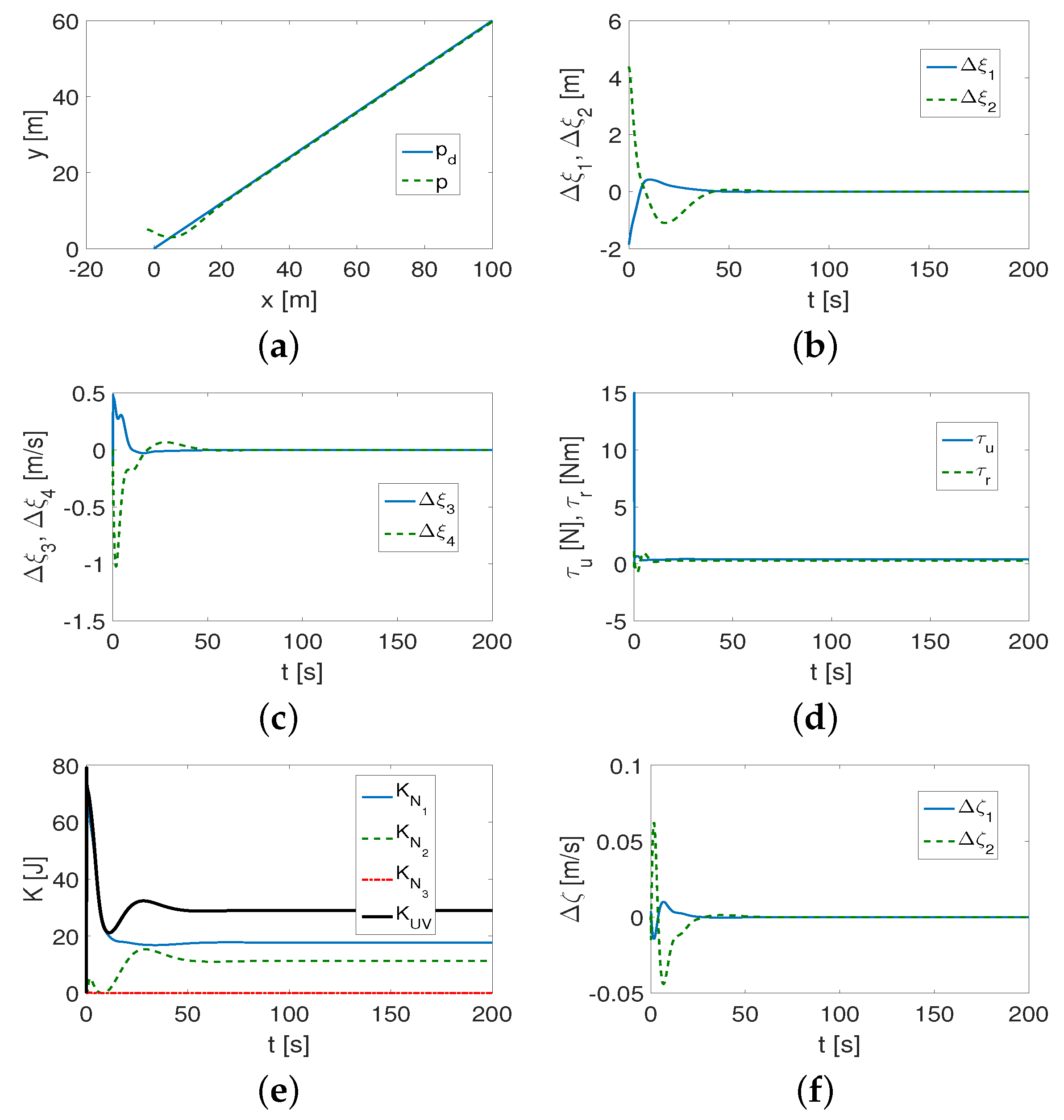
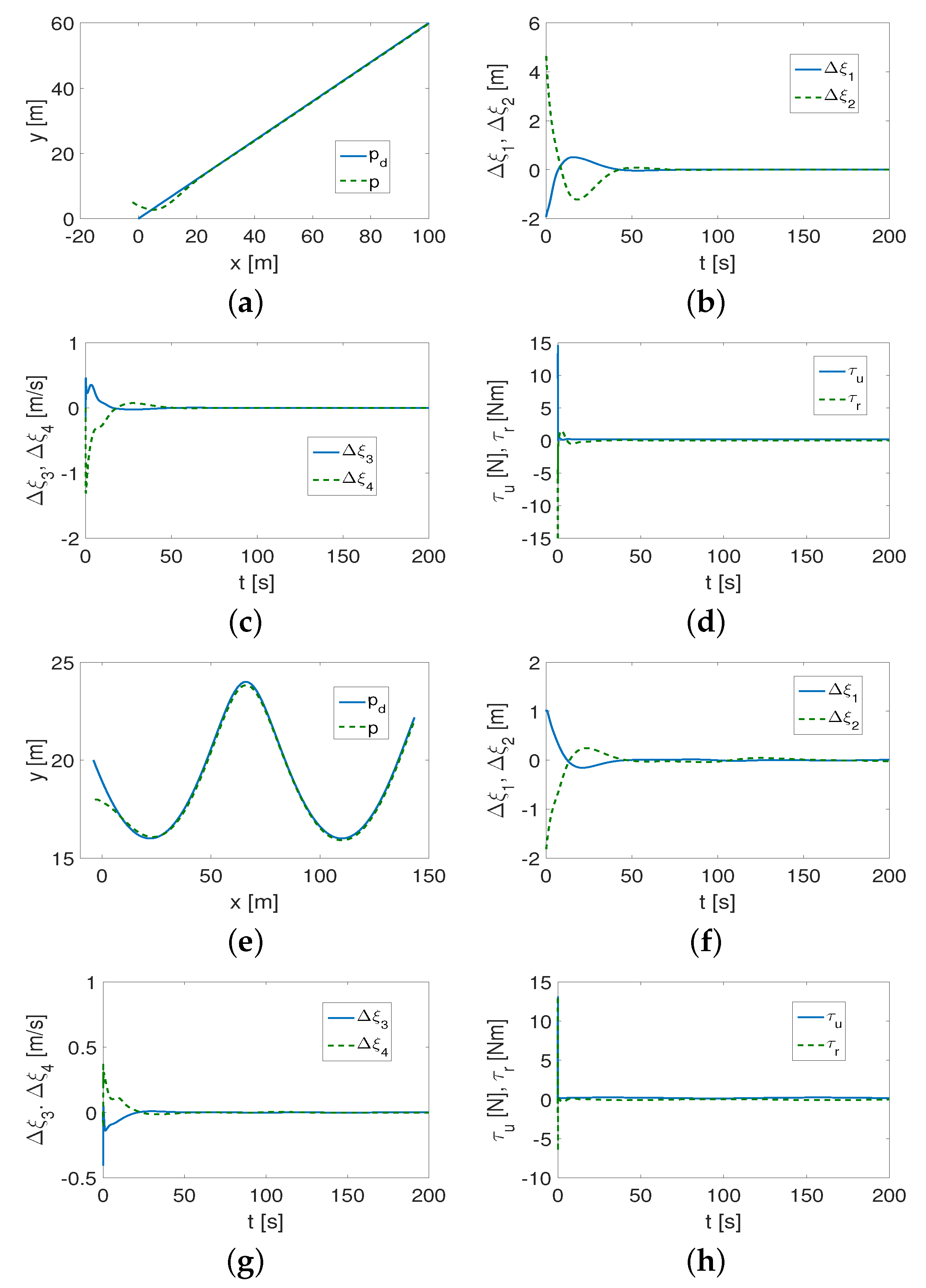
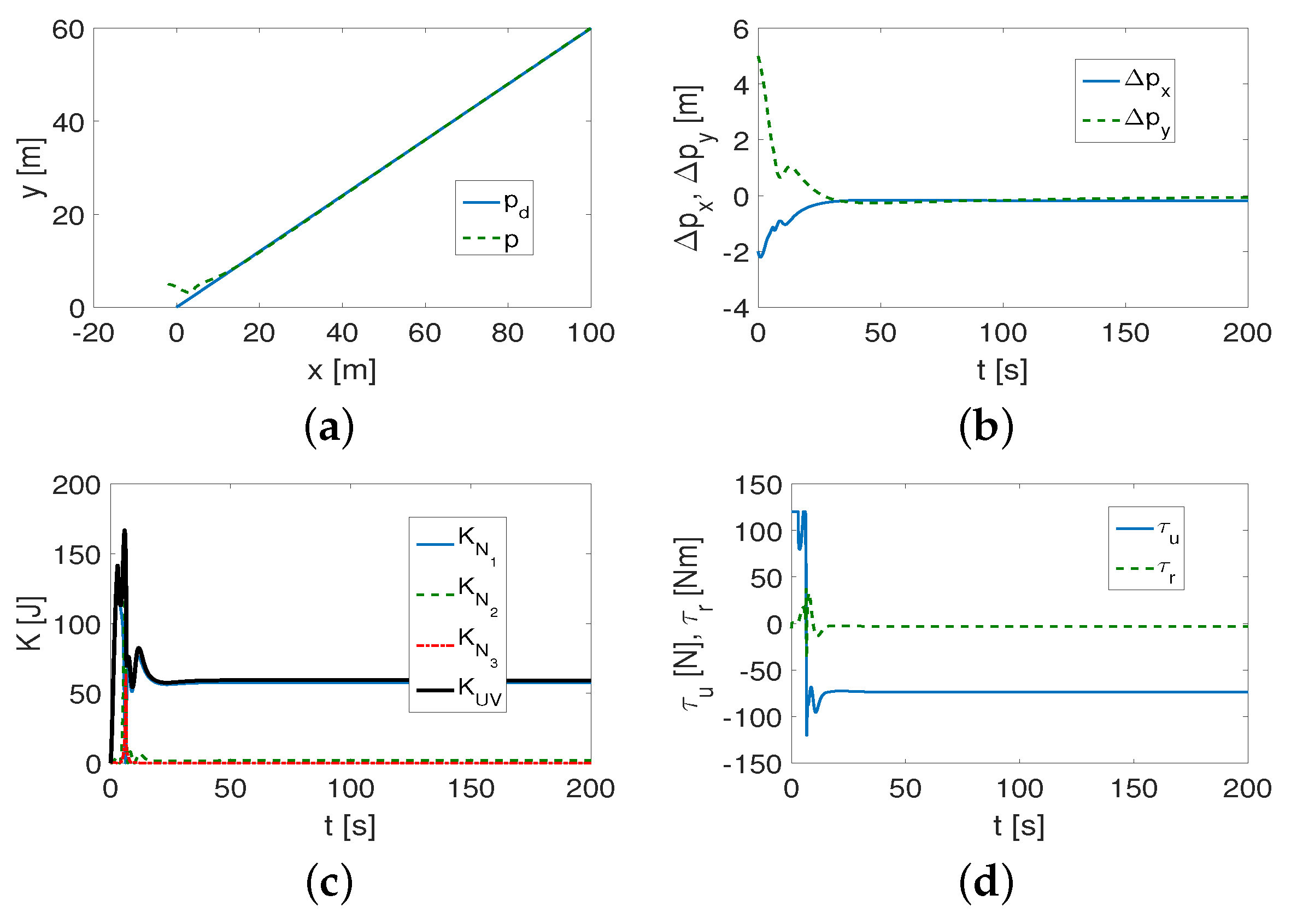
4.1.1. Results for QV Control Algorithm
- mean of the elements (mean), i.e., mean(), where ; mean(), where ; mean(), where ;
- the standard deviation of the elements (std), i.e., std(), std(), std();
- root mean square of the tracking error, i.e., ,with (, —the position errors in the reference frame);
- mean integrated absolute control, i.e., , where .
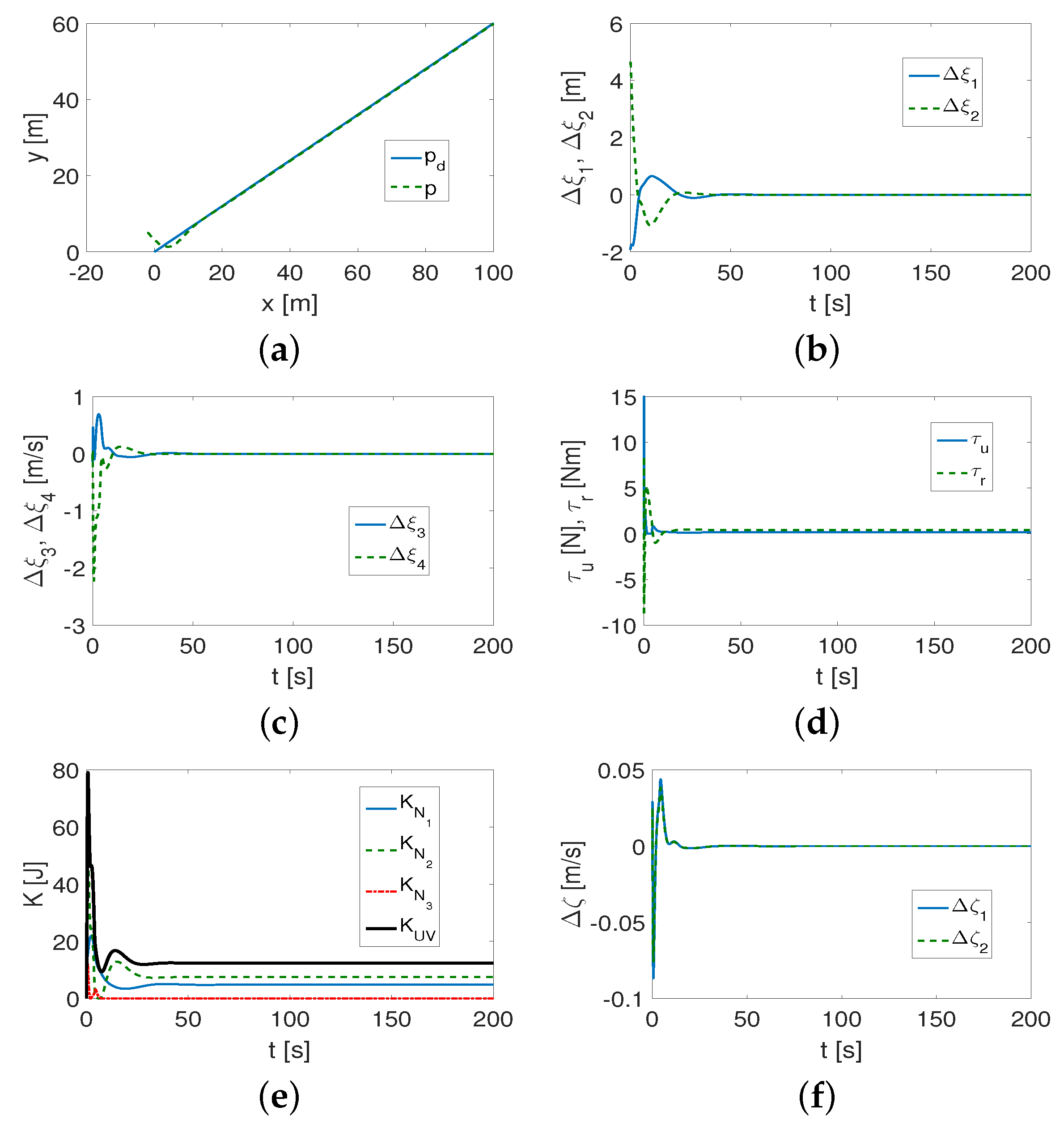
4.1.2. Comparison with Classic Controller
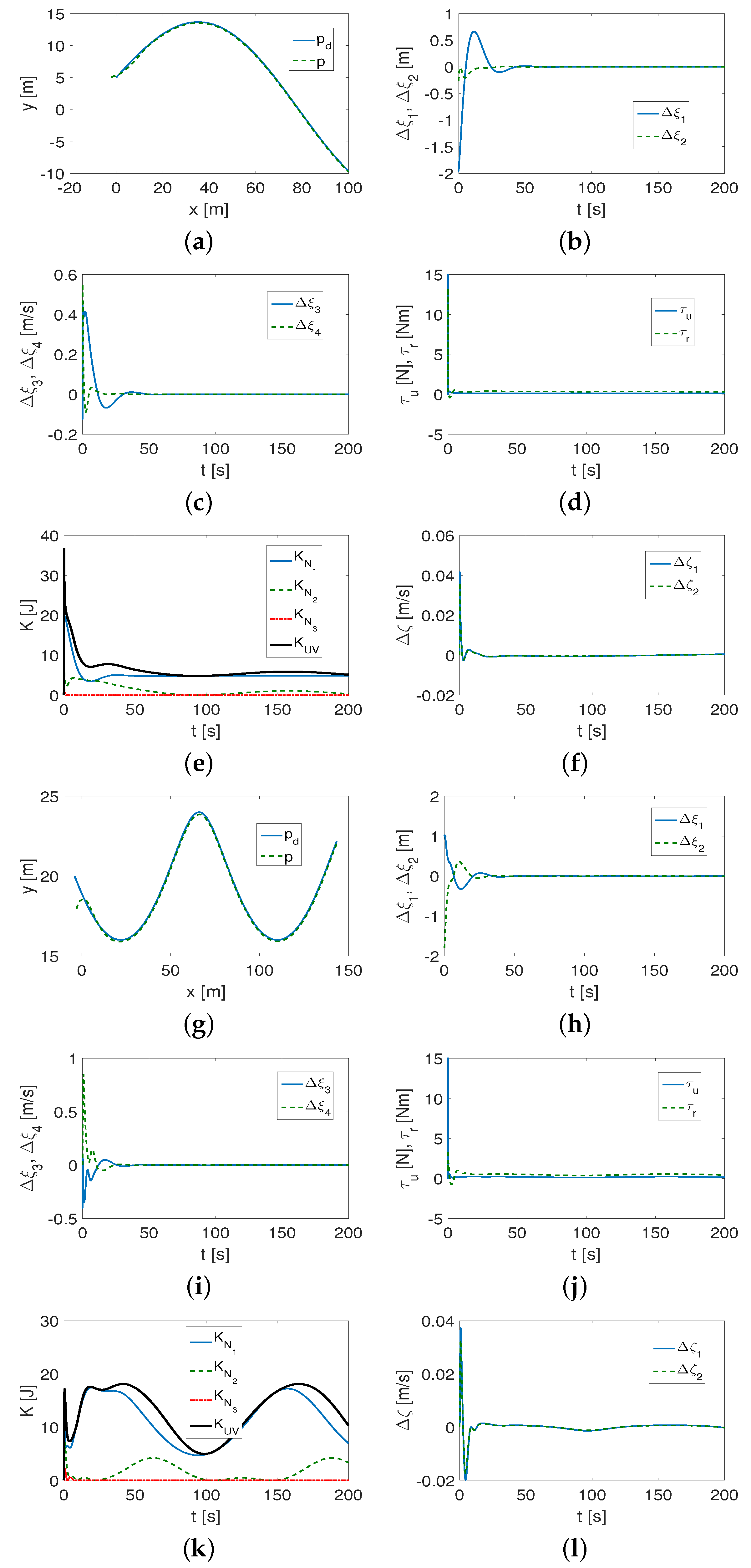
4.1.3. Comparison with Algorithm Based on Velocity Transformations
4.2. Discussion of Results
- (1)
- It was found that the performance of the control algorithm is affected by both vehicle dynamics and the selection of the desired trajectory.
- (2)
- The curvature of the trajectory (smaller radius of curvature) causes more interference at the beginning of the vehicle movement, and this, in turn, forces the controller to increase the control signals. The result can be a reduction in the trajectory-tracking accuracy unless the value of the coefficient l is reduced.
- (3)
- Not only are the gains of the controllers , , important for tracking the desired trajectory, but the value of the l parameter is also essential. If l has a large value (), then, in the case of trajectories with small curvature (which should be determined after performing a simulation to check the accuracy of trajectory tracking), tracking occurs after a short time, but is inaccurate during movement (tracking errors in the x-y plane increase). The value of the coefficient depends on the weight of the vehicle, and, more specifically, on its dynamic parameters.
- (4)
- It turned out that the algorithm is somehow robust to changes in the appropriately selected set of control gains. This means that the same set of gains can be applied to different trajectories and only slightly modified to track trajectories with sufficiently small curvature.
- (5)
- Investigating the distribution of kinetic energy consumption across variables representing quasi-velocities and velocity deformations caused by dynamic couplings in the vehicle provides additional insight into its dynamics. The time history of this energy indicates for which QV the reduction is greatest (in which direction of motion), and how the changes occur for different shapes of the desired trajectory.
- (6)
- The variables also reflect the shape of the trajectory because they can change as the vehicle moves.
- (1)
- Comparative observations of the figures show that both the QV and CL controllers work correctly, although, in some cases, the error convergence time may be shorter for the QV controller than for the CL controller. This may be due to the fact that coupling in the lateral direction is included in the control equation.
- (2)
- The proposed performance indexes provide more information. It can be seen that, for both algorithms, their effectiveness depends on the parameters of the vehicle model and the trajectory being tracked.
- (3)
- After applying the CL algorithm, the smaller index values are not determined by the dynamic parameters of the vehicle because some of the smaller index values apply to the Kambara vehicle and some to XX AUV. Therefore, it is difficult to identify the relationship between the performance and the vehicle dynamics. Having applied the algorithm using QV, it is clear that smaller index values were obtained more often for the XX AUV vehicle than for the Kambara. From this it can be concluded that the effectiveness of the proposed controller depends, to some extent, on the dynamic parameters of the vehicle, which is not seen for the CL one.
- The calculated index values show that both algorithms track linear trajectories with less accuracy than curvilinear trajectories.
- The base indexes (that is, without force and torque) are mostly lower for each vehicle after using the QV controller when we compare them with the indexes obtained from the CL algorithm. The advantage is more evident for the actual errors (mean() and RMS()). It is worth noting that the errors in the position and velocity states indicate whether the algorithm correctly performs the tracking task, but the actual errors are larger, which is, however, in line with the assumptions of both the original (CL controller) and the modified (QV controller) methods. Since the QV-based control scheme takes into account both the longitudinal and lateral asymmetry of the vehicle, while CL only takes into account the longitudinal asymmetry, it would seem that it is the CL algorithm that should be more effective in performing the task of trajectory tracking. The fact that this is very often not the case can be explained by modifications to the controller that use the dynamic parameters of the vehicle.
- Both controllers, i.e., QV and CL, primarily use the driving force, but smaller values are provided by the QV algorithm. In contrast, the average torque is much lower (close to zero) for the CL controller. The reason for this is the taking of vehicle dynamics into account, as it is necessary to provide larger values of this torque.
- Compared to the other control scheme tested, here denoted VT, it turned out that, for the assumed operating conditions and desired trajectories, the considered QV algorithm gave slightly better performance with respect to the tracking errors with significantly lower values of the control signals.
- (4)
- It is worth noting that a properly selected set of control coefficients allows some flexibility because it can be applied to different trajectories (at most with a slight change in value).
- (5)
- Using the QV controller, more information is obtained on the dynamics of the vehicle than the CL controller. This is one of the essential differences between the two control schemes.
- According to the idea presented in [38] and used to design the QV-based controller, only the convergence of the position and velocity state errors to zero is guaranteed. This means that the real position errors (represented by the values of RMS() and mean()) can tend to certain constant values. This is what would explain their larger values than the values of the state errors.
- In addition to the controller parameters , , and the l parameter, the quality of the results is also affected by the value of the additional factor , so the total number of parameters is one more than for a classic controller. However, the advantage of is that it is adopted according to the dynamic parameters of the vehicle and can be tuned even if the algorithm does not work properly with another set of gains.
- It takes quite a long time to reach the convergence values of the position and velocity states, even with the correct choice of controller gains. This time can be reduced by decreasing the values of , but then oscillations and rapid changes in the error values will occur. To avoid this phenomenon, the values of can be increased, but this will increase the convergence time of the state errors to zero. Therefore, a compromise between all gain values is important.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles; Springer: London, UK, 2009. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley and Sons: Chichester, UK, 1994. [Google Scholar]
- Aguiar, A.P.; Hespanha, J.P. Trajectory-Tracking and Path-Following of Underactuated Autonomous Vehicles with Parametric Modeling Uncertainty. IEEE Trans. Autom. Control 2007, 528, 1362–1379. [Google Scholar] [CrossRef]
- Zhang, L.J.; Qi, X.; Pang, Y.J. Adaptive output feedback control based on DRFNN for AUV. Ocean Eng. 2009, 36, 716–722. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Karras, G.C.; Heshmati-Alamdari, S.; Kyriakopoulos, K.J. Trajectory Tracking with Prescribed Performance for Underactuated Underwater Vehicles Under Model Uncertainties and External Disturbances. IEEE Trans. Control Syst. Technol. 2017, 25, 429–440. [Google Scholar] [CrossRef]
- Fetzer, K.L.; Nersesov, S.; Ashrafiuon, H. Nonlinear control of three-dimensional underactuated vehicles. Int. J. Robust Nonlinear Control 2020, 30, 1607–1621. [Google Scholar] [CrossRef]
- Fang, K.; Fang, H.; Zhang, J.; Yao, J.; Li, J. Neural adaptive output feedback tracking control of underactuated AUVs. Ocean Eng. 2021, 234, 109211. [Google Scholar] [CrossRef]
- Huang, B.; Zhou, B.; Zhang, S.; Zhu, C. Adaptive prescribed performance tracking control for underactuated autonomous underwater vehicles with input quantization. Ocean Eng. 2021, 221, 108549. [Google Scholar] [CrossRef]
- Liu, J.; Du, J. Composite learning tracking control for underactuated autonomous underwater vehicle with unknown dynamics and disturbances in three-dimension space. Appl. Ocean Res. 2021, 112, 102686. [Google Scholar] [CrossRef]
- Behal, A.; Dawson, D.M.; Dixon, W.E.; Fang, Y. Tracking and Regulation Control of an Underactuated Surface Vessel with Nonintegrable Dynamics. IEEE Trans. Autom. Control 2002, 47, 495–500. [Google Scholar] [CrossRef]
- Lefeber, E.; Pettersen, K.Y.; Nijmeijer, H. Tracking Control of an Underactuated Ship. IEEE Trans. Control Syst. Technol. 2003, 11, 52–61. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding-Mode Tracking Control of Surface Vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, B.; Liao, Y.; Wang, B. Finite-Time Trajectory Tracking Control for Uncertain Underactuated Marine Surface Vessels. IEEE Access 2019, 7, 102321–102330. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Sun, Y.; Lewis, F.L. Robust adaptive trajectory tracking control of underactuated autonomous underwater vehicles with prescribed performance. Int. J. Robust Nonlinear Control 2019, 29, 4629–4643. [Google Scholar] [CrossRef]
- Zhang, J.X.; Chai, T. Singularity-Free Continuous Adaptive Control of Uncertain Underactuated Surface Vessels With Prescribed Performance. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5646–5655. [Google Scholar] [CrossRef]
- Pan, C.Z.; Lai, X.Z.; Wang, S.X.; Wu, M. An efficient neural network approach to tracking control of an autonomous surface vehicle with unknown dynamics. Expert Syst. Appl. 2013, 40, 1629–1635. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Chen, P. Fuzzy observer-based tracking control of an underactuated underwater vehicle with linear velocity estimation. IET Control Theory Appl. 2020, 14, 584–593. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles. Ocean Eng. 2017, 129, 613–625. [Google Scholar] [CrossRef]
- Do, K.D.; Jiang, Z.P.; Pan, J.; Nijmeijer, H. A global output-feedback controller for stabilization and tracking of underactuated ODIN: A spherical underwater vehicle. Automatica 2004, 40, 117–124. [Google Scholar] [CrossRef]
- Serrano, M.E.; Scaglia, G.J.E.; Godoy, S.A.; Mut, V.; Ortiz, O.A. Trajectory Tracking of Underactuated Surface Vessels: A Linear Algebra Approach. IEEE Trans. Control Syst. Technol. 2014, 22, 1103–1111. [Google Scholar] [CrossRef]
- Do, K.D. Robust adaptive tracking control of underactuated ODINs under stochastic sea loads. Robot. Auton. Syst. 2015, 72, 152–163. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.; Qiao, L.; Zhang, W. Robust adaptive trajectory tracking control of underactuated surface vessel in fields of marine practice. J. Mar. Sci. Technol. 2018, 23, 950–957. [Google Scholar] [CrossRef]
- Xu, J.; Wang, M.; Qiao, L. Dynamical sliding mode control for the trajectory tracking of underactuated unmanned underwater vehicles. Ocean Eng. 2015, 105, 54–63. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y. Trajectory tracking control for underactuated unmanned surface vehicle subject to uncertain dynamics and input saturation. Neural Comput. Appl. 2021, 33, 12777–12789. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, Y.; Huang, B.; Su, Y. Finite-time trajectory tracking control for under-actuated unmanned surface vessels with saturation constraint. Ocean Eng. 2022, 249, 110745. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, C.; Wei, Y.; Wang, J. Neural-Based Command Filtered Backstepping Control for Trajectory Tracking of Underactuated Autonomous Surface Vehicles. IEEE Access 2020, 8, 42482–42490. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, X.; Chen, T.; Yan, Z.; Yang, Z. Trajectory Tracking Control of an Underactuated AUV Based on Backstepping Sliding Mode with State Prediction. IEEE Access 2019, 7, 181983–181993. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, C.; Wang, J.; Li, C. Neuro-adaptive trajectory tracking control of underactuated autonomous surface vehicles with high-gain observer. Appl. Ocean Res. 2020, 97, 102051. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, Z.; Gong, M.; Ni, T. Event-Triggered Asymptotic Tracking Control of Underactuated Ships with Prescribed Performance. IEEE Trans. Intell. Transp. Syst. 2023, 24, 645–656. [Google Scholar] [CrossRef]
- Sun, X.; Wang, G.; Fan, Y. Trajectory Tracking Control for Vector Propulsion Unmanned Surface Vehicle with Incomplete Underactuated Inputs. IEEE J. Ocean Eng. 2023, 48, 80–92. [Google Scholar] [CrossRef]
- Liu, W.; Ye, H.; Yang, X. Super-Twisting Sliding Mode Control for the Trajectory Tracking of Underactuated USVs with Disturbances. J. Mar. Sci. Eng. 2023, 11, 636. [Google Scholar] [CrossRef]
- Mu, D.; Li, L.; Wang, G.; Fan, Y.; Zhao, Y; Sun, X. State constrained control strategy for unmanned surface vehicle trajectory tracking based on improved barrier Lyapunov function. Ocean Eng. 2023, 277, 114276. [Google Scholar] [CrossRef]
- Pan, B.; Chen, C.; Zhu, G.; Su, Y. Event-Triggered Composite Learning Finite-Time Trajectory Tracking Control for Underactuated MSVs Subject to Uncertainties. IEEE Access 2022, 10, 14440–14449. [Google Scholar] [CrossRef]
- Dong, Z.; Wan, L.; Liu, T.; Zeng, J. Horizontal-plane Trajectory-tracking Control of an Underactuated Unmanned Marine Vehicle in the Presence of Ocean Currents. Int. J. Adv. Robot. Syst. 2016, 13, 83. [Google Scholar] [CrossRef]
- Wang, N.; Xie, G.; Pan, X.; Su, S.F. Full-State Regulation Control of Asymmetric Underactuated Surface Vehicles. IEEE Trans. Ind. Electron. 2019, 66, 8741–8750. [Google Scholar] [CrossRef]
- Do, K.D. Practical control of underactuated ships. Ocean Eng. 2010, 37, 1111–1119. [Google Scholar] [CrossRef]
- Wang, C.; Xie, S.; Chen, H.; Peng, Y.; Zhang, D. A decoupling controller by hierarchical backstepping method for straight-line tracking of unmanned surface vehicle. Syst. Sci. Control Eng. 2019, 7, 379–388. [Google Scholar] [CrossRef]
- Paliotta, C.; Lefeber, E.; Pettersen, K.Y.; Pinto, J.; Costa, M.; Borges de Sousa, J.Td.F. Trajectory Tracking and Path Following for Underactuated Marine Vehicles. IEEE Trans. Control Syst. Technol. 2019, 27, 1423–1437. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Nersesov, S.; Clayton, G. Trajectory Tracking Control of Planar Underactuated Vehicles. IEEE Trans. Autom. Control 2017, 62, 1959–1965. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Li, Y.; Xu, G.; Xiang, X. Improved line-of-sight trajectory tracking control of under-actuated AUV subjects to ocean currents and input saturation. Ocean Eng. 2019, 174, 14–30. [Google Scholar] [CrossRef]
- Wang, N.; Su, S.F.; Pan, X.; Yu, X.; Xie, G. Yaw-Guided Trajectory Tracking Control of an Asymmetric Underactuated Surface Vehicle. IEEE Trans. Ind. Inform. 2019, 15, 3502–3513. [Google Scholar] [CrossRef]
- Qu, Y.; Cai, L. Simultaneous planning and executing trajectory tracking control for underactuated unmanned surface vehicles from theory to practice. Ocean Eng. 2023, 270, 113665. [Google Scholar] [CrossRef]
- Park, B.S. Neural Network-Based Tracking Control of Underactuated Autonomous Underwater Vehicles with Model Uncertainties. J. Dyn. Syst. Meas. Control Trans. 2015, 137, 021004. [Google Scholar] [CrossRef]
- Chen, L.; Cui, R.; Yang, Ch.; Yan, W. Adaptive Neural Network Control of Underactuated Surface Vessels with Guaranteed Transient Performance: Theory and Experimental Results. IEEE Trans. Ind. Electron. 2020, 67, 4024–4035. [Google Scholar] [CrossRef]
- Jia, Z.; Hu, Z.; Zhang, W. Adaptive output-feedback control with prescribed performance for trajectory tracking of underactuated surface vessels. Isa Trans. 2019, 95, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.L.; He, S.; Lin, H. Transverse function control with prescribed performance guarantees for underactuated marine surface vehicles. Int. J. Robust Nonlinear Control 2019, 29, 1577–1596. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. Robust trajectory tracking with adjustable performance of underactuated surface vessels via quantized state feedback. Ocean Eng. 2022, 246, 110475. [Google Scholar] [CrossRef]
- Herman, P. Trajectory Tracking Nonlinear Controller for Underactuated Underwater Vehicles Based on Velocity Transformation. J. Mar. Sci. Eng. 2023, 11, 509. [Google Scholar] [CrossRef]
- Loduha, T.A.; Ravani, B. On First-Order Decoupling of Equations of Motion for Constrained Dynamical Systems. J. Appl. Mech. 1995, 62, 216–222. [Google Scholar] [CrossRef]
- Herman, P. Application of nonlinear controller for dynamics evaluation of underwater vehicles. Ocean Eng. 2019, 179, 59–66. [Google Scholar] [CrossRef]
- Herman, P. Vehicle Dynamics Study Based on Nonlinear Controllers Conclusions and Perspectives. In Inertial Quasi-Velocity Based Controllers for a Class of Vehicles; Springer Tracts in Mechanical Engineering; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Herman, P. Application of a Trajectory Tracking Algorithm for Underactuated Underwater Vehicles Using Quasi-Velocities. Appl. Sci. 2022, 12, 3496. [Google Scholar] [CrossRef]
- Silpa-Anan, C. Autonomous Underwater Robot: Vision and Control. Master’s Thesis, The Australian National University, Canberra, Australia, 2001. [Google Scholar]
- Silpa-Anan, C.; Abdallah, S.; Wettergreen, D. Development of autonomous underwater vehicle towards visual servo control. In Proceedings of the Australian Conference on Robotics and Automation, Melbourne, Australia, 30 August–1 September 2000; pp. 105–110. [Google Scholar]
- Dong, Z.; Wan, L.; Li, Y.; Liu, T.; Zhuang, J.; Zhang, G. Point Stabilization for an Underactuated AUV in the Presence of Ocean Currents. Int. J. Adv. Robot. Syst. 2015, 12, 100. [Google Scholar] [CrossRef]
- Lesniak, J.; Stachowiak, M. Simulation Analysis of Selected Vehicle Control Methods with Incomplete Input Signals. Engineering Thesis, Poznan University of Technology, Poznan, Poland, 2020. [Google Scholar]


| Source | Asymmetry | Disturbances | ||
|---|---|---|---|---|
| No | y Axis | x y Axis | ||
| Behal et al. [10] | + | − | − | none |
| Zhang et al. [13] | + | − | − | variable |
| Sun et al. [22] | + | − | − | variable |
| Xu et al. [23] | + | − | − | variable |
| Zhang et al. [25] | + | − | − | variable |
| Zhou et al. [27] | + | − | − | variable |
| Deng et al. [29] | + | − | − | variable |
| Liu et al. [31] | + | − | − | variable |
| Mu et al. [32] | + | − | − | variable |
| Pan et al. [33] | + | − | − | variable |
| Dong et al. [34] | + | + | − | variable |
| Paliotta et al. [38] | + | + | − | constant |
| Ashrafiuon et al. [39] | + | + | − | variable |
| Wang et al. [41] | + | + | − | variable |
| Park [43] | + | + | − | none |
| Chen et al. [44] | + | + | − | variable |
| Dai et al. [46] | + | + | − | variable |
| Park and Yoo [47] | + | + | − | variable |
| Herman [48] | + | + | + | variable |
| Kambara | XX AUV | ||
|---|---|---|---|
| Parameter | Value | Value | Unit |
| 175.4 | 47.5 | kg | |
| 10 | 3.0 | kg m | |
| 140.8 | 94.1 | kg | |
| −35 | 5.2 | kg m | |
| 16.07 | 13.6 | kg m | |
| 120 | 13.5 | kg/s | |
| 10 | 10.0 | kg/s | |
| 90 | 50.2 | kg/s | |
| 10 | 41.4 | kg m/s | |
| 10 | 10.0 | kg m/s | |
| 10 | 17.3 | kg m/s | |
| 18 | 27.2 | kg m/s |
| Vehicle | Kambara | XX AUV | ||||
|---|---|---|---|---|---|---|
| 1.000 | <1.047 | <1.186 | <1.326 | <1.466 | ≤1.932 | |
| Couplings | no | very weak | weak | average | strong | very strong |
| 0 % | <5 % | <20 % | <35 % | <50 % | ≥50 % |
| Kambara | XX AUV | |||||
|---|---|---|---|---|---|---|
| Trajectory | L | SC | C | L | SC | C |
| mean() | 0.2343 | 0.0992 | 0.1056 | 0.1652 | 0.0794 | 0.0704 |
| std() | 0.6691 | 0.2615 | 0.3077 | 0.6071 | 0.2359 | 0.2489 |
| mean() | 0.0472 | 0.0188 | 0.0198 | 0.0525 | 0.0210 | 0.0233 |
| std() | 0.1776 | 0.0728 | 0.0644 | 0.2403 | 0.0795 | 0.1018 |
| mean() | 0.5564 | 0.3556 | 0.2863 | 0.3472 | 0.2207 | 0.1921 |
| std() | 0.7640 | 0.2460 | 0.3462 | 0.6740 | 0.0795 | 0.3003 |
| RMS() | 0.7466 | 0.3436 | 0.3591 | 0.5674 | 0.2747 | 0.2647 |
| MIAC() | 0.4029 | 0.3220 | 0.4669 | 0.1674 | 0.1203 | 0.1776 |
| MIAC() | 0.2913 | 0.2278 | 0.3380 | 0.4865 | 0.3386 | 0.4870 |
| Kambara | XX AUV | |||||
|---|---|---|---|---|---|---|
| L | SC | C | L | SC | C | |
| mean() | 0.2342 | 0.1131 | 0.1227 | 0.2808 | 0.1266 | 0.1345 |
| std() | 0.6366 | 0.2799 | 0.2993 | 0.7391 | 0.2945 | 0.3528 |
| mean() | 0.0495 | 0.0294 | 0.0261 | 0.0514 | 0.0204 | 0.0197 |
| std() | 0.1955 | 0.1084 | 0.0625 | 0.1752 | 0.0657 | 0.0575 |
| mean() | 0.5491 | 0.3600 | 0.2910 | 0.4617 | 0.2613 | 0.2251 |
| std() | 0.7363 | 0.2612 | 0.3527 | 0.8204 | 0.3006 | 0.3820 |
| RMS() | 0.7120 | 0.3551 | 0.3588 | 0.7225 | 0.3183 | 0.3360 |
| MIAC() | 0.4236 | 0.3365 | 0.4858 | 0.1784 | 0.1414 | 0.2083 |
| MIAC() | 0.0679 | 0.0439 | 0.0396 | 0.0548 | 0.0347 | 0.0600 |
| Kambara | ||
|---|---|---|
| L | SC | |
| mean() | 0.5750 | 0.2750 |
| std() | 0.9292 | 0.3243 |
| RMS() | 0.8065 | 0.3726 |
| MIAC() | 75.174 | 68.921 |
| MIAC() | 3.7864 | 3.9702 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herman, P. Modification of Nonlinear Controller for Asymmetric Marine Vehicles Moving in Horizontal Plane. Appl. Sci. 2023, 13, 7242. https://doi.org/10.3390/app13127242
Herman P. Modification of Nonlinear Controller for Asymmetric Marine Vehicles Moving in Horizontal Plane. Applied Sciences. 2023; 13(12):7242. https://doi.org/10.3390/app13127242
Chicago/Turabian StyleHerman, Przemyslaw. 2023. "Modification of Nonlinear Controller for Asymmetric Marine Vehicles Moving in Horizontal Plane" Applied Sciences 13, no. 12: 7242. https://doi.org/10.3390/app13127242
APA StyleHerman, P. (2023). Modification of Nonlinear Controller for Asymmetric Marine Vehicles Moving in Horizontal Plane. Applied Sciences, 13(12), 7242. https://doi.org/10.3390/app13127242






