Abstract
The design of the implant and osseointegration play an important role in the long-term stability of implants. This study aims to investigate the impact of porous implants on full and partial osseointegration in varying bone qualities. Finite element models of porous implants were modeled and assembled with normal and weak bones considering full and partial osseointegration. These assemblies were simulated under an occlusal load of 200 N when the outer surfaces of bones were fixed in all directions. The results showed that in the case of full osseointegration, the stresses in surrounding bones were increased with decreasing implant stiffness, while decreased in partial osseointegration. Moreover, the maximum octahedral shear strain in the weak bone exceeded 3000 µε in all the cases but decreased (from 7256 to 3632 µε) with decreasing implant stiffness. According to the mechanostat hypothesis, using porous implants in normal bone may enhance bone density in full osseointegration, while susceptivity of bone damage may reduce in weak bones using porous implants. Thus, careful selection of implant material and design based on the patient’s specific bone quality is crucial for successful outcomes.
1. Introduction
Dental implants made of dense titanium alloys (Ti) are widely used to restore damaged tooth functionality due to their excellent biocompatibility [,]. Despite numerous advantages of these implants, such as natural appearance, improved speech and comfort, and ability to prevent bone loss in the jaw [], they may cause stress shielding and bone resorption which depends on many factors such as bone quality, mechanical stimulus, implant design, and so on. Bone quality refers to the overall health of bone tissue and is determined by several factors, including bone volume fraction and microarchitecture. The mechanical properties of bone, such as elasticity modulus and yield strength, are also important indicators of bone quality. Sandino et al. [] have used high-resolution micro-CT images and micro-finite-element analysis to examine the microarchitecture of trabecular bone and its effect on mechanical stimuli. They have quantified the changes in the apparent Young’s modulus of bone tissue with varying levels of porosities and found that as porosity increases, there is a decrease in the apparent Young’s modulus. Another study comparing osteoporotic and healthy bone elastic properties [] has shown that the yield strength of osteoporotic bone tissue is lower than that of healthy bone tissue. This indicates that the bone tissue of individuals with osteoporosis may be weaker and more susceptible to fractures. These studies provide insights into the complex relationship between bone microarchitecture, including porosity and mechanical properties []. So dense implant designs are not the best choice for different bone qualities.
After implantation, osseointegration (fusion of the dental implant with the surrounding bone) occurs at peri-implant which depends on the bone health, design of the implant, loadings, and other biological factors. Osseointegration, the process of direct structural and functional connection between living bone and the surface of the implant, is a critical factor in the long-term success of dental implants. Although full osseointegration, where the implant becomes completely integrated with the surrounding bone tissue, is the desired outcome. A previous study showed that partial osseointegration can pose a potential risk that may compromise implant stability and reliability [] and that unfavorable changes in trabecular bone architecture due to bone remodeling can lead to implant failure as well. Dental implants present challenges for researchers and clinicians due to their high mismatch material properties between implant and host bones. One of the most significant complications is stress shielding [,], which occurs when the high Young’s modulus of the dense Ti implant does not match the lower Young’s modulus of the surrounding bone, leading to a reduced load on the bone and a subsequent decrease in bone density [,].
To overcome these challenges, researchers are continuously exploring innovative strategies to minimize the risk of stress shielding and improve the longevity and success of implants [,]. One potential solution is the use of materials with lower Young’s modulus, such as porous Ti, which could provide a better match with the bone and reduce the risk of implant failure [,]. Porous Ti has become increasingly important in modern dentistry due to its low Young’s modulus, strong biocompatibility, great corrosion resistance, and highly interconnected porous structure to aid osseointegration []. The advancement of additive manufacturing (AM) has paved the way for the creation of complex-shaped architectures from CAD data [], enabling the production of topologically optimized porous implants []. The impact of porosity and osseointegration on mechanical performance (i.e., strength and stiffness) of topologically optimal designs of implants has been assessed in numerous studies [,]. Porosity and performance are crucial design parameters that affect the overall performance of implants []. This approach can effectively lower the effective Young’s modulus of the implants [,]. But still, an appropriate design of the implant is required for different bone qualities and specific patient needs.
To investigate and understand the implant biomechanical performance and remodeling process around the implant, the mechanostat hypothesis based on Wolff’s law [] and updated by Frost [] is commonly used. This hypothesis describes the bone response to mechanical loading based on different levels of mechanical strain (atrophy, adapted state, overload, and fracture). Bone remodeling is a complex and unclear process that maintains bone homeostasis [,] which is time-consuming and expensive to investigate experimentally. Thus, finite element methods have been used to study and simulate bone remodeling phenomena [,,,,]. This tool is increasingly popular in biomechanics [,,,,,] for obtaining stress and strain prediction in the host bones.
By addressing these research questions, the study aims to contribute to the existing body of knowledge on dental implants and provide insights that could inform the development of more effective implant designs. This study investigates the effect of implant stiffness on surrounding bones when simulated with full and partial osseointegrations in normal and weak bones. Stresses and strains in implants and bones were estimated to understand bone remodeling based on mechanostat criteria which gave us an insight into selecting an appropriate implant stiffness for a specific case.
2. Materials and Methods
2.1. Construction of 3D Models
The bone sections and implants were created using Solidworks software (V2020, Dassault Systemes, Vélizy-Villacoublay, France). The first step was to create a sketch of the internal geometry of the bone in a sectional view using the available drawing tools. The extrude feature was then used to create a solid body that represented the cancellous bone. In the case of the mandibular bone section, the model was composed of a 2 mm thick cortical bone layer around the cancellous bone, with a height of 32 mm, length of 22 mm, and width of 20 mm, as shown in Figure 1a. The sectional view provided a simplified representation of the internal structure of the bone, allowing for easier visualization and calculation. The implant model used in this study was designed as a one-piece cylinder (similar to Straumann® pure ceramic implant monotype, Villeret, Switzerland), which combined with implant and abutment. This design was chosen for its simplicity and ease of use in clinical applications. The implant featured a thread depth of 0.2 mm, a pitch of 1.2 mm, a total length of 18 mm, and a diameter of 3.5 mm, which are typical dimensions for dental implants. The dental crown was created with the same software using a spline line, which is a smooth and continuous curve without any predefined dimensions. The location of the implant was the lower first molar, which was replaced before performing the simulation. To create the assembly of the implant bone, the “combine” feature in Solidworks was used. This feature allowed the implant and the mandibular bone section to be merged, which could then be exported as STEP format for simulation in ABAQUS 6.14 (Dassault Systemes, Vélizy-Villacoublay, France).
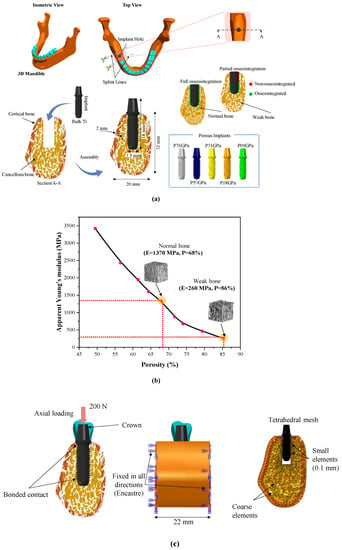
Figure 1.
Bone-implant models; (a) CAD modeling of bone and dental implants, (b) the correlation between cancellous bone apparent Young’s modulus and porosity, and (c) load, boundary conditions, and mesh.
2.2. Material Properties
The implant materials used in this study were bulk titanium alloy (Ti-6Al-4V) and effective porous titanium properties. The effective material properties of porous titanium were investigated in the previous study [] with a body-centered cubic (BCC) structure and had a porosity ranging from 18.1 to 77.65%. Five porosities (77.65%, 62.8%, 47.3%, 29.9%, and 18.1%) of BCC cubes were modeled and simulated under compression test. The elastoplastic material properties of bulk titanium alloy (Ti-6Al-4V) were assigned to porous cubes. The stress-strain curves of these cubes were plotted to obtain effective Young’s moduli of all porous cubes which are reported in Table 1. In this study, the effective Young’s moduli were utilized to define five porous implants. The labels for porous implants were selected based on their porosity (represented by “P”) and Young’s modulus. For instance, a porous implant with Young’s modulus of 76.71 GPa was labeled as P76 as listed in Table 1. Similarly, P53, P31, P18, and P9 correspond to 53.84 GPa, 31.49 GPa, 18.33 GPa, and 9.11 GPa of Young’s moduli. Two distinct bone models were investigated, the normal bone model represents healthy bone, while the osteoporotic bone represents weak bone. Both models exhibited different apparent Young’s modulus, as shown in Figure 1b []. In finite element models, bone is modeled as a solid with effective material properties of normal and weak cancellous bones. All models were assumed to be homogeneous, isotropic, and linearly elastic. The mechanical properties of the porous titanium (Ti) used in this study, Young’s modulus, Poisson’s ratio, and titanium porosity, have been reported in previous studies [,] and are summarized in Table 1.

Table 1.
Material properties used in finite element analysis [,,,].
2.3. Load, Boundary Conditions, and Mesh
After importing the STEP files of models into the ABAQUS 6.14 software (Dassault Systemes, Vélizy-Villacoublay, France), a mesh convergence was carried out by using a technique called “h-refinement”. This involved refining the mesh in zones of interest by increasing the number of elements from a coarse mesh to a finer mesh until the results converged. The convergence was evaluated by monitoring the changes in the maximum von Mises stress with respect to the number of elements. The convergence was met when the relative error in the maximum von Mises stress between two consecutive mesh refinements was below a specified tolerance value. This tolerance value was set to 2% in this study, as it provided a good balance between accuracy and computational efficiency. After mesh convergence, we achieved a total number of 208,685 (C3D10) elements. In our study, the cortical bone was represented by 10,834 (C3D10) tetrahedral elements, and the cancellous bone was meshed using 13,891 (C3D10) tetrahedral elements. The crown was modeled with 2056 (C3D10) tetrahedral elements, and the dental implant required a total of 181,904 (C3D10) tetrahedral elements. To ensure that the mesh had a high quality and met the necessary criteria for accurate and reliable results, the “Mesh Verify” feature in ABAQUS was used to evaluate the element distortion, aspect ratios, and skewness. The bone-implant interfaces were meshed with smaller element sizes (0.1 mm) and other regions with coarse element sizes (varying between 0.5 and 1 mm). A static load of 200 N was applied to the occlusal surface of the crown. This chewing force of 200 N was reported on the first premolar and first molars [,]. The bone’s side surfaces were fixed (zero degrees-of-freedom, (U1 = U2 = U3 = UR1 = UR2 = UR3 = 0)) in all directions as shown in Figure 1c. Two scenarios of osseointegration were investigated: full osseointegration, where the full implant and bone interfaces were assumed to be perfectly bonded (100% osseointegration), and this was achieved by using a tied contact as shown in Figure 1c (in green color). For partially osseointegrated cases, a frictionless contact was assigned between the upper part of the implant (upper half) and the bone interface to allow the relative movement between the implant and surrounding bone as shown in Figure 1c (in red color). The lower part of the implant and the bone interface was tied perfectly to mimic the osseointegration in the lower part (lower half) as shown in Figure 1c (in green color).
3. Results
3.1. Stress in Implants
Figure 2 displays the distribution of von Mises stress (in MPa) in the implants that have contact with cancellous bone and the highest values of the stresses acting on the implants are reported in Table 2. It was observed that the cervical area next to the cortical bone was found to have the highest concentration of stresses. Additionally, it was noticed that the weak bone generated more stress in the implants than the normal bone. Furthermore, it was observed that the maximum stresses obtained for the implants of partial osseointegration were lower than those of full osseointegration. The maximum stresses ranging between 13.07 MPa and 19.90 MPa, were observed in the weak bone with full osseointegration case. The minimum stresses were observed in normal bone with partial osseointegration, ranging from 10 MPa to 15.90 MPa. Moreover, the stress in bulk Ti implants was higher than in porous implants. However, the magnitudes of the highest stresses (Table 2 and Figure 2) were below the yield stress in all cases (P76 with a yield stress of 760 MPa, P53 with 528 MPa, P31 with 305 MPa, P18 with 176 MPa, and P9 with 88 MPa) as reported in []). It was also observed that the stress distribution in the axial direction of implants was reduced as the porosity of implants was increased in the case of normal bone. However, in weak bone, the stresses remained similar.
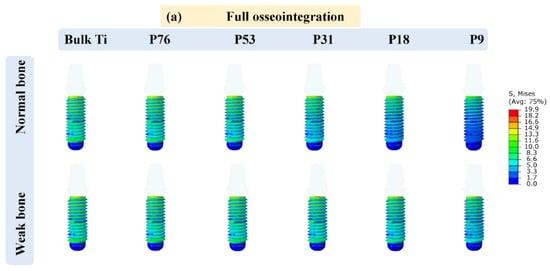
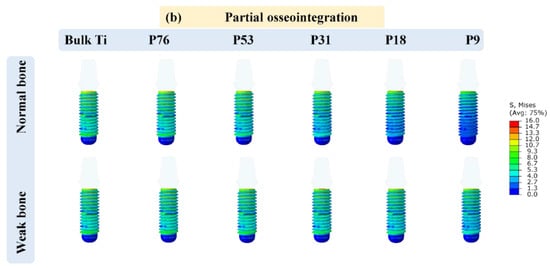
Figure 2.
Von Mises stress distribution in the implants; (a) full osseointegration and (b) partial osseointegration.

Table 2.
Maximum von Mises stress (MPa) in implants.
3.2. Displacement in Cancellous Bone
The displacements in cancellous bone in all cases were calculated when the load of 200 N was applied at the top of the crown. The vertical micro-displacement in the case of full and partial osseointegration for normal and weak bones is depicted in Figure 3, and the maximum values are shown in Figure 4. The maximum displacement was observed in weak bone for the P76 implant, with a value of 26.48 µm in the case of full osseointegration and 24.51 µm in the case of partial osseointegration. The minimum displacement reached a value of 5.67 µm in normal bone for bulk Ti implant in the case of full osseointegration, and 5.38 µm in the case of partial osseointegration. Therefore, the low stiffness of the implant (porous implants) produces more displacement in cancellous bone than the Bulk Ti implant, which has higher stiffness. Moreover, weak bone is more susceptible to higher displacement than normal bone.
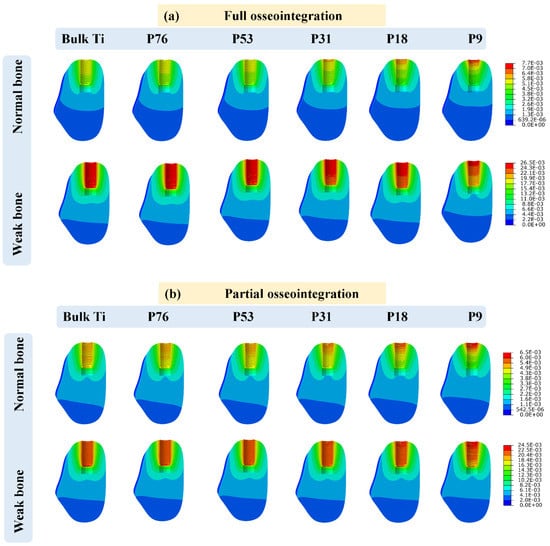
Figure 3.
Implant displacement (measured in micrometers) in cancellous bone for (a) full osseointegration and (b) partial osseointegration.
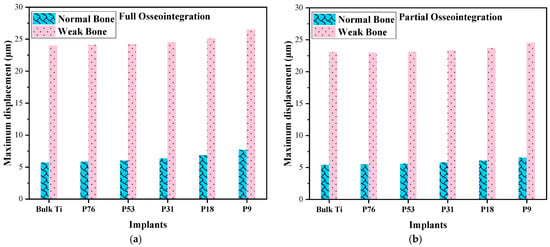
Figure 4.
Comparison of displacements in normal and weak bone; (a) full osseointegration and (b) partial osseointegration.
3.3. Stress in Cancellous Bone
The stress distribution in cancellous bone is shown in Figure 5. It could be observed that the mechanical stresses are transmitted to the surrounding bone closest to the dental implant and decrease towards the other outer regions. It was also observed that the maximum stress was generated at the apical region in normal bone with 4.47 MPa with the Bulk Ti implant and 6.12 MPa with the P9 implant. In weak bone, when bulk Ti and P9 implants were used then the stresses were 4.18 MPa and 4.24 MPa, respectively, and that is in the case of full osseointegration, as shown in Figure 6a. In the case of partial osseointegration, the maximum von Mises stress was observed in normal bone for bulk Ti and it decreases with decreasing the Young’s modulus of the implant, the same pattern follows for weak bone, as shown in Figure 6b. The compressive strength of normal bone is typically around 15 MPa, whereas for individuals with osteoporosis, the compressive strength decreases to around 6 MPa []. In the case of full osseointegration, where the implant is fully bonded to the surrounding bone tissue, the stresses exerted on the cancellous bone were typically below the compressive strength for both normal and weak bones. However, in the cases of partial osseointegration, where the implant is not fully integrated with the bone tissue, the stresses on the bone were higher, especially for weak bone with denser implants such as Bulk Ti, P76, P53, and P31. This increased stress can make the cancellous bone more prone to fracture.
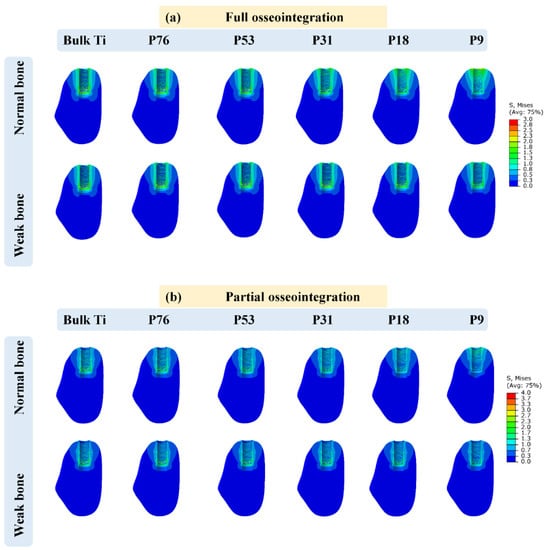
Figure 5.
Graphical representation of stress (MPa) in cancellous bone for; (a) full osseointegration and (b) partial osseointegration.
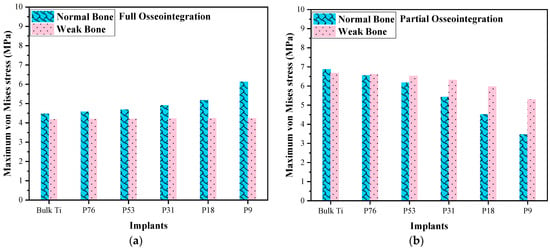
Figure 6.
Comparison of von Mises stresses in normal and weak bone; (a) full osseointegration and (b) partial osseointegration.
3.4. Octahedral Shear Strain in Cancellous Bone
In the context of mechanostat theory and bone remodeling, the octahedral shear strain has been used as a relevant strain measure to describe the mechanical state of bone. It provides a measure of the deformation experienced by bone tissue, taking into account both axial and shear strains. Researchers have studied the relationship between octahedral shear strain and bone adaptation or remodeling to understand the mechanical stimuli that influence bone behavior. The octahedral shear strain was determined by Piccinini et al. [] as the most significant strain for the mechanostat hypothesis. The mechanostat distinguishes five major strain levels [], as shown in Figure 7. Strain below 1000 µɛ leads to bone atrophy, and the strain between 1000 µɛ and 1500 µɛ is the adapted state for which bone is maintained. The physiological overload level is between 1500 µɛ and 3000 µɛ, where bone modeling takes place. The pathologic overload above 3000 µɛ leads to bone damage and absorption. For strain levels over 25,000 µɛ, resulting in spontaneous fracture.
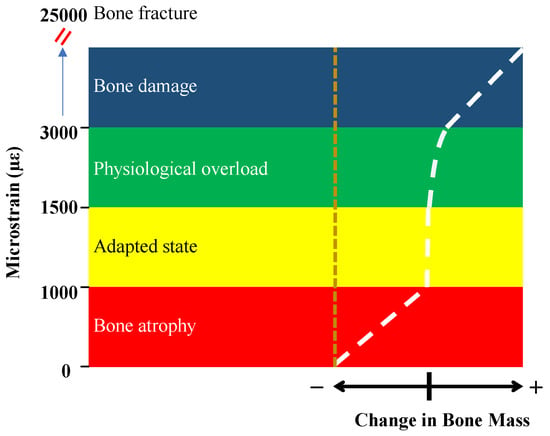
Figure 7.
The mechanostat hypothesis shows different levels of strains and corresponding bone remodeling [].
The octahedral shear strain was calculated by Equation (1).
where εoct is the octahedral shear strain (mm/mm) and ε1, ε2, and ε3 are the principal strains in directions x, y, and z, respectively.
εoct = 2/3 [(ε1 − ε2)² + (ε2 − ε3)² +(ε3 − ε1)²]½
Figure 8 shows the maximum octahedral shear strain in cancellous bone. It can be observed that higher strain was in normal bone compared to weak bone in all cases. In the case of full osseointegration for normal bone, the minimum octahedral shear strain was observed in bulk Ti implants, compared to the porous Ti implants. However, for the weak bone, the octahedral shear strain decreased with increasing the porosity of the implant. In the case of partial osseointegration, the octahedral shear strains were higher compared to the full osseointegration. In all cases of weak bone (see Figure 8), where the octahedral shear strains were above 3000 µɛ, it is expected that bone damage may occur. Such high levels of strain put significant stress on the weakened bone, making it prone to damage according to the mechanostat in Figure 7. When considering full osseointegration with P76, P53, and P31 implants in normal bone, where the maximum octahedral shear strains ranged between 700 µɛ and 1500 µɛ, the bone experiences an adaptive strain state. This range of strain stimulates bone adaptation to the implant, enhancing stability and integration which does not change the mass or density of the bone. In the case of full osseointegration in normal bone with bulk Ti, P76, and P53 implants, where the strain was less than 1000 µɛ, the bone may experience some degree of atrophy. Strain levels within this range indicate that the mechanical stimulus provided by the implant is relatively low, which can result in bone resorption. However, in the case of partial osseointegration with the same set of implants of normal bone, where the strain ranged between 1500 and 3000 µɛ, the bone faces physiological overload.
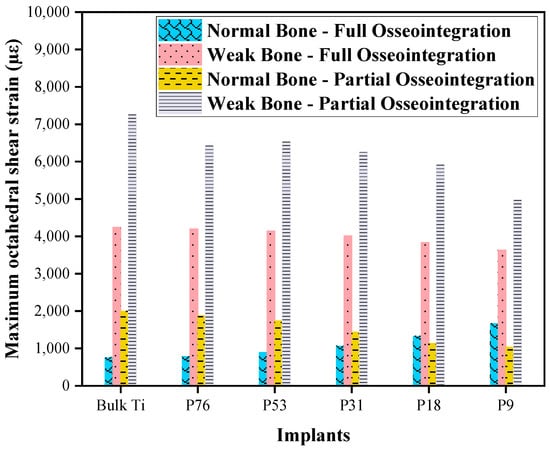
Figure 8.
Comparison of octahedral shear strain in normal and weak bones with different implants.
4. Discussion
The current study evaluates the stress and strain with the patient’s bone condition in the case of full and partial osseointegration using the finite element method. Based on Wolff’s law, it is well known that bone adapts to stress generated by the load transmission from the implant which induces strain surrounding the bone. The magnitude of the strain is affected by several biomechanical factors, such as the implant material, the design of the implant, and the magnitude of the load applied. The two most common complications that currently exist in the field of implants are stress shielding and loss of osseointegration. Therefore, porous implants were designed with full and partial osseointegration, and their performances were investigated in normal and weak bones.
The von Mises stresses of the implants are often calculated as they represent a good measure of the stress experienced by the implant. The results of such calculations demonstrate that the quality of a patient’s bone can have a significant effect on the success of dental implants, with weaker bone resulting in higher levels of stress. Additionally, the stage of osseointegration (the process by which the implant fuses with the surrounding bone) is a key factor in determining the effectiveness of dental implants. It is worth noting that while dental implant failure is rare [], it can still occur, particularly during the first five years after the implant is placed. However, modern dental implant technologies, particularly those made of titanium alloys, are considered to be the best option due to their superior biomechanical strength and biocompatibility []. Overall, while dental implants are generally a safe and effective option for replacing missing teeth, it is important to consider all factors that can affect their success and to seek out experienced and qualified dental professionals to perform the procedure.
The analysis of implant displacements in cancellous bone has shown that increasing the porosity of the implant generates more micromovement in the surrounding bone. The stiffness of the implant also plays a role in determining the amount of displacement, with porous implants allowing for more displacement compared to dense titanium implants. While considering the distribution of stress in cancellous bone, the results indicate that in the case of full osseointegration (where the implant is fully fused with the surrounding bone), increasing the porosity of the implant leads to higher stresses being transferred to the surrounding bone. This means that decreasing the stiffness of the implant can result in the implant transferring more stress to the surrounding bone. However, in the case of partial osseointegration (where the implant is only partially fused with the surrounding bone), the opposite effect is observed. Decreasing the stiffness of the implant leads to lower stresses being transferred to the surrounding bone. Bulk titanium implants transfer more load to the surrounding bone compared to porous titanium implants. Moreover, there has been ongoing research in developing new implant materials and designs that can improve the osseointegration process and minimize the risk of implant failure []. For instance, new implant designs are being developed to promote faster and stronger bone ingrowth []. Overall, the stiffness and porosity of implants play a role in determining the stress distribution and implant displacement in cancellous bone.
The octahedral shear strain was calculated in this study to determine the bone response to dental implants, and the mechanostat hypothesis was used to interpret the results. The adapted state, which is the optimal state of bone adaptation to the implant, was found to include P31, P18, and P9 implants in normal bone for both partial and full osseointegration. The range of strain observed in this state was between 1000 µε and 1500 µε, which is the range where the balance of bone resorption and formation becomes equal and the bone remodeling process occurs. However, in the cases of weak bone, the octahedral shear strain was observed to be above 3000 µε, which is the pathologic overload stage that may lead to bone damage. It is important to note that weak bone can be a result of various factors [] such as age, disease, or previous trauma, and it can significantly affect the success of dental implants. Additionally, the atrophied state, which is the state of bone that is not well adapted to the implant, was found to include the bulk Ti, P76, and P53 implants with the lower octahedral shear strain of less than 1000 µε. In this case, the stress shielding phenomenon may occur, where the implant takes on most of the load and the surrounding bone experiences reduced stress. This can lead to bone resorption and implant loosening over time. It’s important to keep in mind that the mechanostat hypothesis is just one theory for explaining bone remodeling, and other factors such as hormonal changes and local cytokine signaling can also influence bone adaptation to implants []. Further research is needed to fully understand the complex interplay between these factors and how they affect the long-term success of dental implants.
Bulk Ti implants have a significantly higher elastic modulus (114 GPa) than human bones, which can result in stress shielding and eventually lead to bone resorption and aseptic loosening of the implants []. It is essential to consider the stiffness of implants when planning implant procedures, as using implants with low stiffness can improve long-term implant stability and prevent complications.
It’s important to take into consideration the state of osseointegration and bone quality, as partial osseointegration can pose a potential risk to the longevity of dental implants and may cause damage to the surrounding bone tissue []. People who suffer from osteoporosis will inevitably have less bone stiffness, are more prone to fracture []. Bone quality has been examined in many studies using finite element methods [,,]. Our findings concur with their conclusion that deterioration in bone quality precedes a worsening of stress and strain. Recent studies have suggested that 3D-printed porous titanium implants can be a suitable choice for improving osseointegration capacity and prolonging the functional life of the implant [,]. This is mainly due to the ability of porous implants to promote bone ingrowth and osseointegration, leading to better long-term outcomes. With the advances in computer-assisted design and topological optimization technologies, 3D printing has become a revolutionary process that allows for the precise fabrication of porous titanium implants with tailored porosity and pore size, which can further enhance their performance. However, it’s important to note that enhancing secondary stability at the bone-implant interface remains a challenge in implant dentistry. Several approaches have been proposed to improve implant stability, including surface modifications and coating techniques, as well as the use of growth factors and stem cells to promote bone regeneration []. Further research is needed to fully understand the mechanisms underlying implant stability and to develop more effective strategies for enhancing osseointegration and reducing implant failures. Selecting the appropriate implant material and design is critical for ensuring the long-term success of dental implants. The use of porous implants with low stiffness can be an effective approach for improving implant stability and promoting osseointegration. Advances in 3D printing technology have enabled the precise fabrication of such implants, opening up new possibilities for improving the outcomes of implant procedures.
While FEA is a useful tool for predicting the behavior of dental implants, it has some limitations that should be considered when interpreting the results. For example, in this study, the complex forces that are applied to dental implants by the oral cavity muscles were not considered. Additionally, bone properties are highly complex and their behavior was assumed to be isotropic and homogeneous, but in reality, they have anisotropic properties that can influence implant stability. To accurately model bone tissue mechanical properties, it is important to consider the orthotropic and non-linear properties of biological tissues, which could be better characterized with data from material science experiments. Another limitation of our study is that we modeled the bone tissue as a solid model, whereas in real conditions the bone is a porous tissue. Despite these limitations, this study provides important insights into the role of octahedral shear strain in bone response to dental implants. By considering factors such as bone quality and implant stiffness when planning and performing implant procedures, dental professionals can help ensure the best possible outcomes for their patients.
In future studies, machine learning algorithms could be utilized to optimize dental implant design. To support Wolff’s and Frost’s law, strain or stress trajectories of the main bones of the mandible could be described. A theory of stimulators of bone remodeling can be developed to provide a better understanding of the biological processes involved in successful dental implant integration.
5. Conclusions
The results of this study provide valuable insights into the biomechanical responses of bone conditions to varying porous implant structures. The findings suggest that 3D-printed porous implants have the potential to form sufficient osseointegration with normal bone tissue, while an improvement in bone quality can reduce stress in the bone and lower the risk of implant failure in patients with osteoporosis. These findings could have significant practical implications for the development and use of 3D-printed orthopedic and dental implants in clinics, as they offer a promising approach for improving implant success rates and patient outcomes. Overall, the study’s findings can guide dental and orthopedic surgeons in selecting the appropriate implant type and design for each patient’s specific condition, taking into account factors such as bone quality, and implant stiffness. This can lead to better clinical outcomes, fewer complications, and improved patient satisfaction.
Author Contributions
Conceptualization, H.M., A.O. and M.F.I.; Methodology, H.M. and A.O.; Software, H.M., A.O. and M.F.I.; Validation, H.M. and A.O.; Formal analysis, A.O.; Investigation, H.M.; Writing—original draft, H.M.; Writing—review & editing, M.F.I.; Supervision, M.F.I.; Project administration, M.F.I.; Funding acquisition, M.F.I. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the King Salman Center For Disability Research for funding this work through Research Group no KSRG-2022-033.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the authors upon reasonable request.
Acknowledgments
The authors extend their appreciation to the King Salman Center For Disability Research for funding this work through Research Group no KSRG-2022-033.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saha, S.; Roy, S. Metallic Dental Implants Wear Mechanisms, Materials, and Manufacturing Processes: A Literature Review. Materials 2022, 16, 161. [Google Scholar] [CrossRef]
- Barrak, F.; Li, S.; Muntane, A.; Bhatia, M.; Crossthwaite, K.; Jones, J. Particle Release from Dental Implants Immediately after Placement—An Ex Vivo Comparison of Different Implant Systems. Dent. Mater. 2022, 38, 1004–1014. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xiao, T.; Yang, L.; Ning, C.; Guan, S.; Li, X. Application of a Vascularized Bone Free Flap and Survival Rate of Dental Implants after Transplantation: A Systematic Review and Meta-Analysis. J. Stomatol. Oral Maxillofac. Surg. 2023, 124, 101401. [Google Scholar] [CrossRef] [PubMed]
- Sandino, C.; McErlain, D.D.; Schipilow, J.; Boyd, S.K. Mechanical Stimuli of Trabecular Bone in Osteoporosis: A Numerical Simulation by Finite Element Analysis of Microarchitecture. J. Mech. Behav. Biomed. Mater. 2017, 66, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Rieger, R.; Auregan, J.C.; Hoc, T. Micro-Finite-Element Method to Assess Elastic Properties of Trabecular Bone at Micro- and Macroscopic Level. Morphologie 2018, 102, 12–20. [Google Scholar] [CrossRef]
- Calvo-Gallego, J.L.; Gutiérrez-Millán, F.; Ojeda, J.; Pérez, M.Á.; Martínez-Reina, J. The Correlation between Bone Density and Mechanical Variables in Bone Remodelling Models: Insights from a Case Study Corresponding to the Femur of a Healthy Adult. Mathematics 2022, 10, 3367. [Google Scholar] [CrossRef]
- Marcián, P.; Wolff, J.; Horáčková, L.; Kaiser, J.; Zikmund, T.; Borák, L. Micro Finite Element Analysis of Dental Implants under Different Loading Conditions. Comput. Biol. Med. 2018, 96, 157–165. [Google Scholar] [CrossRef]
- Liverani, E.; Rogati, G.; Pagani, S.; Brogini, S.; Fortunato, A.; Caravaggi, P. Mechanical Interaction between Additive-Manufactured Metal Lattice Structures and Bone in Compression: Implications for Stress Shielding of Orthopaedic Implants. J. Mech. Behav. Biomed. Mater. 2021, 121, 104608. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Shi, Y.; Wang, H.; Li, R.; Tu, J.; Jin, G. In Vitro and in Vivo Comparisons of the Porous Ti6Al4V Alloys Fabricated by the Selective Laser Melting Technique and a New Sintering Technique. J. Mech. Behav. Biomed. Mater. 2019, 91, 149–158. [Google Scholar] [CrossRef]
- Cehreli, M.C.; Akca, K. Mechanobiology of Bone and Mechanocoupling of Endosseous Titanium Oral Implants. J. Long Term Eff. Med. Implant. 2005, 15, 139–152. [Google Scholar] [CrossRef]
- Liang, S. Review of the Design of Titanium Alloys with Low Elastic Modulus as Implant Materials. Adv. Eng. Mater. 2020, 22, 2000555. [Google Scholar] [CrossRef]
- Alcudia, A.; Begines, B.; Rodriguez-Lejarraga, P.; Greyer, V.; Godinho, V.C.F.; Pajuelo, E.; Torres, Y. Development of Porous Silver Nanoparticle/Polycaprolactone/Polyvinyl Alcohol Coatings for Prophylaxis in Titanium Interconnected Samples for Dental Implants. Colloid Interface Sci. Commun. 2022, 48, 100621. [Google Scholar] [CrossRef]
- Yaqoob, K.; Amjad, I.; Awan, M.A.M.; Liaqat, U.; Zahoor, M.; Kashif, M. Novel Method for the Production of Titanium Foams to Reduce Stress Shielding in Implants. ACS Omega 2023, 8, 1876–1884. [Google Scholar] [CrossRef]
- Delgado-Pujol, E.J.; Alcudia, A.; Elhadad, A.A.; Rodríguez-Albelo, L.M.; Navarro, P.; Begines, B.; Torres, Y. Porous Beta Titanium Alloy Coated with a Therapeutic Biopolymeric Composite to Improve Tribomechanical and Biofunctional Balance. Mater. Chem. Phys. 2023, 300, 127559. [Google Scholar] [CrossRef]
- Song, C.; Liu, L.; Deng, Z.; Lei, H.; Yuan, F.; Yang, Y.; Li, Y.; Yu, J. Research Progress on the Design and Performance of Porous Titanium Alloy Bone Implants. J. Mater. Res. Technol. 2023, 23, 2626–2641. [Google Scholar] [CrossRef]
- Xiong, Y.; Han, Z.; Qin, J.; Dong, L.; Zhang, H.; Wang, Y.; Chen, H.; Li, X. Effects of Porosity Gradient Pattern on Mechanical Performance of Additive Manufactured Ti-6Al-4V Functionally Graded Porous Structure. Mater. Des. 2021, 208, 109911. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive Manufacturing (3D Printing): A Review of Materials, Methods, Applications and Challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Chao, L.; He, Y.; Gu, J.; Xie, D.; Yang, Y.; Shen, L.; Wu, G.; Wang, L.; Tian, Z. Evaluation of Compressive and Permeability Behaviors of Trabecular-Like Porous Structure with Mixed Porosity Based on Mechanical Topology. J. Funct. Biomater. 2023, 14, 28. [Google Scholar] [CrossRef]
- Hou, C.; Liu, Y.; Xu, W.; Lu, X.; Guo, L.; Liu, Y.; Tian, S.; Liu, B.; Zhang, J.; Wen, C. Additive Manufacturing of Functionally Graded Porous Titanium Scaffolds for Dental Applications. Biomater. Adv. 2022, 139, 213018. [Google Scholar] [CrossRef]
- Gu, Y.; Sun, Y.; Shujaat, S.; Braem, A.; Politis, C.; Jacobs, R. 3D-Printed Porous Ti6Al4V Scaffolds for Long Bone Repair in Animal Models: A Systematic Review. J. Orthop. Surg. Res. 2022, 17, 68. [Google Scholar] [CrossRef]
- Kelly, C.N.; Wang, T.; Crowley, J.; Wills, D.; Pelletier, M.H.; Westrick, E.R.; Adams, S.B.; Gall, K.; Walsh, W.R. High-Strength, Porous Additively Manufactured Implants with Optimized Mechanical Osseointegration. Biomaterials 2021, 279, 121206. [Google Scholar] [CrossRef] [PubMed]
- Al Zoubi, N.F.; Tarlochan, F.; Mehboob, H.; Jarrar, F. Design of Titanium Alloy Femoral Stem Cellular Structure for Stress Shielding and Stem Stability: Computational Analysis. Appl. Sci. 2022, 12, 1548. [Google Scholar] [CrossRef]
- Mehboob, H.; Tarlochan, F.; Mehboob, A.; Chang, S.-H. Finite Element Modelling and Characterization of 3D Cellular Microstructures for the Design of a Cementless Biomimetic Porous Hip Stem. Mater. Des. 2018, 149, 101–112. [Google Scholar] [CrossRef]
- Wolff, J. Das Gesetz Der Transformation Der Knochen. DMW—Dtsch. Med. Wochenschr. 1893, 19, 1222–1224. [Google Scholar] [CrossRef]
- Frost, H.M. A 2003 Update of Bone Physiology and Wolff’s Law for Clinicians. Angle Orthod. 2004, 74, 3–15. [Google Scholar]
- Nishimura, I. Genetic Networks in Osseointegration. J. Dent. Res. 2013, 92, 109S–118S. [Google Scholar] [CrossRef]
- Gomathi, K.; Akshaya, N.; Srinaath, N.; Rohini, M.; Selvamurugan, N. Histone Acetyl Transferases and Their Epigenetic Impact on Bone Remodeling. Int. J. Biol. Macromol. 2021, 170, 326–335. [Google Scholar] [CrossRef]
- Peyroteo, M.M.A.; Belinha, J.; Jorge, R.M.N. Predicting Bone Remodeling Using a Mechano-Biological Mathematical Model Combined with a Natural Neighbor Meshless Method. Eng. Anal. Bound. Elem. 2021, 132, 437–445. [Google Scholar] [CrossRef]
- Cheong, V.S.; Fromme, P.; Mumith, A.; Coathup, M.J.; Blunn, G.W. Novel Adaptive Finite Element Algorithms to Predict Bone Ingrowth in Additive Manufactured Porous Implants. J. Mech. Behav. Biomed. Mater. 2018, 87, 230–239. [Google Scholar] [CrossRef]
- Cheong, V.S.; Marin, A.C.; Lacroix, D.; Dall’Ara, E. A Novel Algorithm to Predict Bone Changes in the Mouse Tibia Properties under Physiological Conditions. Biomech. Model. Mechanobiol. 2020, 19, 985–1001. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, W.; Ajmera, D.H.; Zhang, Y.; Fan, Y.; Ji, P. Simulated Bone Remodeling around Tilted Dental Implants in the Anterior Maxilla. Biomech. Model. Mechanobiol. 2016, 15, 701–712. [Google Scholar] [CrossRef] [PubMed]
- Cheong, V.S.; Fromme, P.; Coathup, M.J.; Mumith, A.; Blunn, G.W. Partial Bone Formation in Additive Manufactured Porous Implants Reduces Predicted Stress and Danger of Fatigue Failure. Ann. Biomed. Eng. 2020, 48, 502–514. [Google Scholar] [CrossRef] [PubMed]
- Al-Tamimi, A.A. Topology Optimization of Patient-Specific Custom-Fit Distal Tibia Plate: A Spiral Distal Tibia Bone Fracture. Appl. Sci. 2022, 12, 10569. [Google Scholar] [CrossRef]
- Ouldyerou, A.; Merdji, A.; Aminallah, L.; Mehboob, H.; Mehboob, A.; Roy, S.; Goswami, T.; Mukdadi, O.M.; Tarlochan, F. Functionally Graded Ceramics (FGC) Dental Abutment with Implant-Supported Cantilever Crown: Finite Element Analysis. Compos. Commun. 2023, 38, 101514. [Google Scholar] [CrossRef]
- Ouldyerou, A.; Mehboob, H.; Merdji, A.; Aminallah, L.; Mehboob, A.; Mukdadi, O.M. Biomechanical Analysis of Printable Functionally Graded Material (FGM) Dental Implants for Different Bone Densities. Comput. Biol. Med. 2022, 150, 106111. [Google Scholar] [CrossRef]
- Tatarciuc, M.; Maftei, G.A.; Vitalariu, A.; Luchian, I.; Martu, I.; Diaconu-Popa, D. Inlay-Retained Dental Bridges—A Finite Element Analysis. Appl. Sci. 2021, 11, 3770. [Google Scholar] [CrossRef]
- Messias, A.; Neto, M.A.; Amaro, A.M.; Lopes, V.M.; Nicolau, P. Mechanical Evaluation of Implant-Assisted Removable Partial Dentures in Kennedy Class I Patients: Finite Element Design Considerations. Appl. Sci. 2021, 11, 659. [Google Scholar] [CrossRef]
- Lin, P.-J.; Su, K.-C. Biomechanical Design Application on the Effect of Different Occlusion Conditions on Dental Implants with Different Positions—A Finite Element Analysis. Appl. Sci. 2020, 10, 5826. [Google Scholar] [CrossRef]
- Mehboob, H.; Mehboob, A.; Abbassi, F.; Ahmad, F.; Khan, A.S.; Miran, S. Bioinspired Porous Dental Implants Using the Concept of 3D Printing to Investigate the Effect of Implant Type and Porosity on Patient’s Bone Condition. Mech. Adv. Mater. Struct. 2021, 29, 6011–6025. [Google Scholar] [CrossRef]
- Celik, H.K.; Koc, S.; Kustarci, A.; Rennie, A.E.W. A Literature Review on the Linear Elastic Material Properties Assigned in Finite Element Analyses in Dental Research. Mater. Today Commun. 2022, 30, 103087. [Google Scholar] [CrossRef]
- Darwich, A.; Alammar, A.; Heshmeh, O.; Szabolcs, S.; Nazha, H. Fatigue Loading Effect in Custom-Made All-on-4 Implants System: A 3D Finite Elements Analysis. IRBM 2021, 43, 372–379. [Google Scholar] [CrossRef]
- Gao, H.; Li, X.; Wang, C.; Ji, P.; Wang, C. Mechanobiologically Optimization of a 3D Titanium-Mesh Implant for Mandibular Large Defect: A Simulated Study. Mater. Sci. Eng. C 2019, 104, 109934. [Google Scholar] [CrossRef] [PubMed]
- Metzner, F.; Neupetsch, C.; Fischer, J.-P.; Drossel, W.-G.; Heyde, C.-E.; Schleifenbaum, S. Influence of Osteoporosis on the Compressive Properties of Femoral Cancellous Bone and Its Dependence on Various Density Parameters. Sci. Rep. 2021, 11, 13284. [Google Scholar] [CrossRef]
- Piccinini, M.; Cugnoni, J.; Botsis, J.; Ammann, P.; Wiskott, A. Numerical Prediction of Peri-Implant Bone Adaptation: Comparison of Mechanical Stimuli and Sensitivity to Modeling Parameters. Med. Eng. Phys. 2016, 38, 1348–1359. [Google Scholar] [CrossRef]
- Korabi, R.; Shemtov-Yona, K.; Dorogoy, A.; Rittel, D. The Failure Envelope Concept Applied to the Bone-Dental Implant System. Sci. Rep. 2017, 7, 2051. [Google Scholar] [CrossRef]
- Ouldyerou, A.; Aminallah, L.; Merdji, A.; Mehboob, A.; Mehboob, H. Finite Element Analyses of Porous Dental Implant Designs Based on 3D Printing Concept to Evaluate Biomechanical Behaviors of Healthy and Osteoporotic Bones. Mech. Adv. Mater. Struct. 2022, 30, 2328–2340. [Google Scholar] [CrossRef]
- Berglundh, T.; Persson, L.; Klinge, B. A Systematic Review of the Incidence of Biological and Technical Complications in Implant Dentistry Reported in Prospective Longitudinal Studies of at Least 5 Years. J. Clin. Periodontol. 2002, 29, 197–212. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, J.W. Titanium Alloys for Dental Implants: A Review. Prosthesis 2020, 2, 100–116. [Google Scholar] [CrossRef]
- Wally, Z.J.; van Grunsven, W.; Claeyssens, F.; Goodall, R.; Reilly, G.C. Porous Titanium for Dental Implant Applications. Metals 2015, 5, 1902–1920. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Yang, X.; Xie, Q.; Wang, C. Comparison of Bone Ingrowth between Two Porous Titanium Alloy Rods with Biogenic Lamellar Structures and Diamond Crystal Lattice on Femoral Condyles in Rabbits. Biochem. Biophys. Res. Commun. 2023, 641, 155–161. [Google Scholar] [CrossRef]
- Masri, D.; Masri-Iraqi, H.; Nissan, J.; Naishlos, S.; Ben-Zvi, Y.; Rosenfeld, E.; Avishai, G.; Chaushu, L. On the Association between Dental Implants, Osteoporosis and Bone Modulating Therapy. Appl. Sci. 2023, 13, 3398. [Google Scholar] [CrossRef]
- Jakovljevic, A.; Nikolic, N.; Holtzman, L.P.; Tournier, P.; Gaudin, A.; Cordaro, L.; Milinkovic, I. Involvement of the Notch Signaling System in Alveolar Bone Resorption. Jpn. Dent. Sci. Rev. 2023, 59, 38–47. [Google Scholar] [CrossRef]
- Huang, G.; Pan, S.-T.; Qiu, J.-X. The Osteogenic Effects of Porous Tantalum and Titanium Alloy Scaffolds with Different Unit Cell Structure. Colloids Surf. B Biointerfaces 2022, 210, 112229. [Google Scholar] [CrossRef] [PubMed]
- Triantafyllopoulos, G.; Mitsea, A.; Rontogianni, A.; Korres, D. Osteoporosis Screening Using Dental Panoramic Radiographs and Age at Menarche. Diagnostics 2023, 13, 881. [Google Scholar] [CrossRef] [PubMed]
- Lemos, C.A.A.; Verri, F.R.; Noritomi, P.Y.; Kemmoku, D.T.; de Souza Batista, V.E.; Cruz, R.S.; de Luna Gomes, J.M.; Pellizzer, E.P. Effect of Bone Quality and Bone Loss Level around Internal and External Connection Implants: A Finite Element Analysis Study. J. Prosthet. Dent. 2021, 125, 137.e1–137.e10. [Google Scholar] [CrossRef]
- Didier, P.; Piotrowski, B.; Le Coz, G.; Joseph, D.; Bravetti, P.; Laheurte, P. Finite Element Analysis of the Stress Field in Peri—Implant Bone: A Parametric Study of Influencing Parameters and Their Interactions for Multi-Objective Optimization. Appl. Sci. 2020, 10, 5973. [Google Scholar] [CrossRef]
- Azcarate-Velázquez, F.; Castillo-Oyagüe, R.; Oliveros-López, L.-G.; Torres-Lagares, D.; Martínez-González, Á.-J.; Pérez-Velasco, A.; Lynch, C.D.; Gutiérrez-Pérez, J.-L.; Serrera-Figallo, M.-Á. Influence of Bone Quality on the Mechanical Interaction between Implant and Bone: A Finite Element Analysis. J. Dent. 2019, 88, 103161. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, T.; Wei, Q.; Cai, H.; Cheng, Y.; Tian, Y.; Leng, H.; Wang, C.; Feng, S.; Liu, Z. Surface Treatment of 3D Printed Porous Ti6Al4V Implants by Ultraviolet Photofunctionalization for Improved Osseointegration. Bioact. Mater. 2022, 7, 26–38. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Wu, Z.; Dai, Y.; Wang, X.; Ye, R.; Huang, H.; Xie, X. Biofunctional Micro/Nanostructured “Volcano-like” Layer-Coated 3D Porous Ti-10Ta-2Nb-2Zr Scaffolds Improve Osteogenesis and Osseointegration for Dental Implants In Vitro and In Vivo. Surf. Coat. Technol. 2021, 427, 127852. [Google Scholar] [CrossRef]
- Deering, J.; Presas, A.; Yu, B.; Valentin, D.; Heiss, C.; Bosbach, W.A.; Grandfield, K. Implant Resonance and the Mechanostat Theory: Applications of Therapeutic Ultrasound for Porous Metallic Scaffolds. Mater. Sci. Eng. C 2021, 125, 112070. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).