Influence of Joint Stiffness and Motion Time on the Trajectories of Underactuated Robots
Abstract
1. Introduction
1.1. State of the Art
1.2. Contributions of This Work
- The effect of motion time on the trajectories and on the swept area of the robot;
- The need of via-points to generate specific trajectories and avoid collisions with obstacles;
- The effect of friction in the nonactuated joint;
- The effect of spring stiffness on the generated trajectories and on the swept area;
- The energy consumed by the robot to perform the task.
- The introduction of friction in the mechanical model of the nonactuated joint;
- The analysis of the influence of torsional stiffness on trajectories;
- The analysis of the influence of motion time on trajectories;
- The development of an algorithm for the calculation of the area swept by the robot;
- The calculation of motor torques as functions of torsional stiffness and motion time.
2. Mathematical Model
3. Effect of Joint Stiffness on Trajectories
4. Effect of Motion Time on Trajectories
5. Optimal Combination of Stiffness and Motion Time
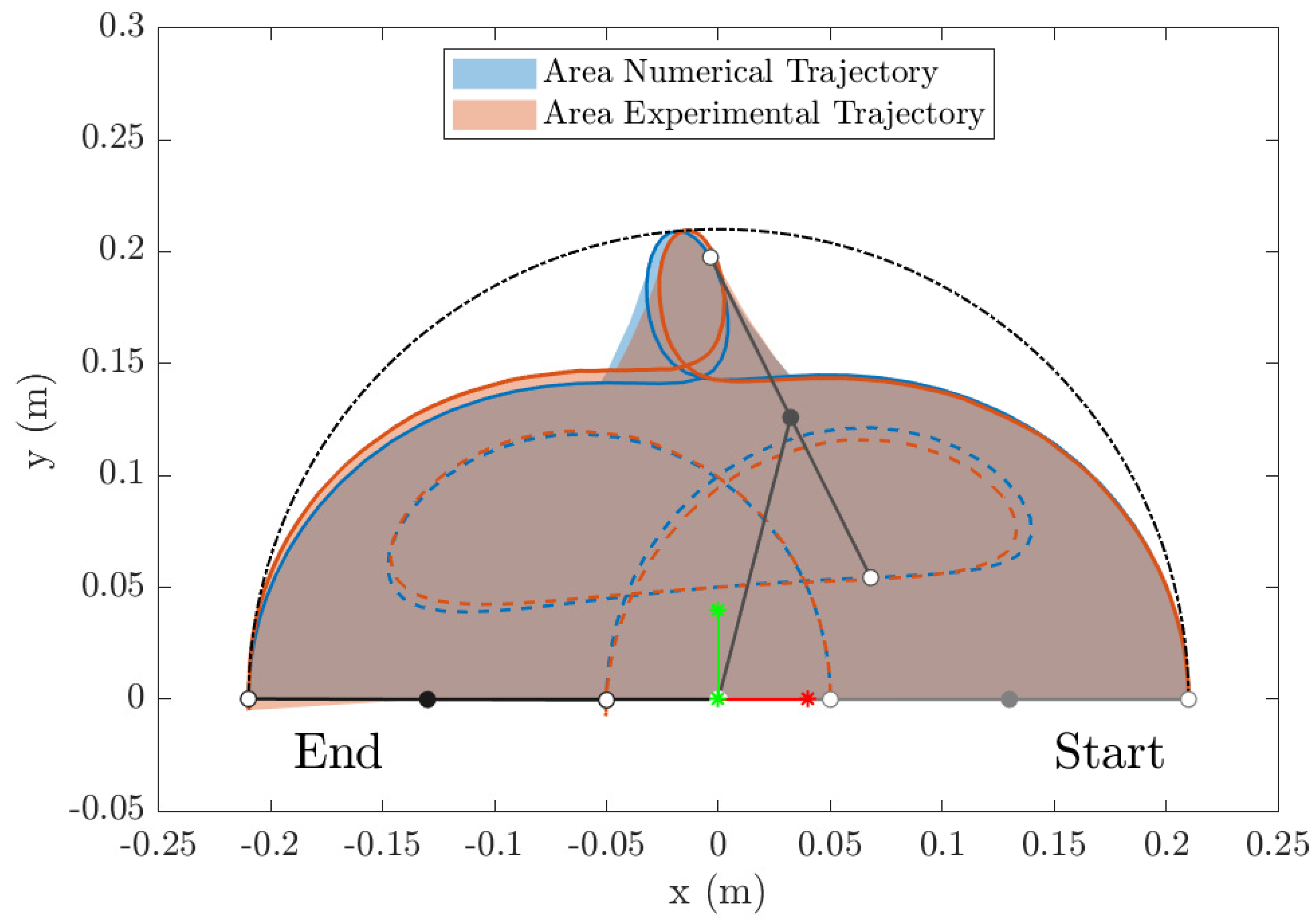
6. Experimental Validation
6.1. Mathematical Model of a Simplified 2-DOF Robot
6.2. Experimental Setup
6.3. Experimental Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, B.; Wang, S.; Liu, Y. Underactuated robotics: A review. Int. J. Adv. Robot. Syst. 2019, 16, 1–29. [Google Scholar] [CrossRef]
- Barbazza, L.; Zanotto, D.; Rosati, G.; Agrawal, S. Design and Optimal Control of an Underactuated Cable-Driven Micro-Macro Robot. IEEE Robot. Autom. Lett. 2017, 2, 896–903. [Google Scholar] [CrossRef]
- Berkemeier, M.D.; Fearing, R.S. Tracking fast inverted trajectories of the underactuated Acrobot. IEEE Trans. Robot. Autom. 1999, 15, 740–750. [Google Scholar] [CrossRef]
- Nakanishi, J.; Fukuda, T.; Koditschek, D.E. A brachiating robot controller. IEEE Trans. Robot. Autom. 2000, 16, 109–123. [Google Scholar] [CrossRef]
- De Luca, A.; Oriolo, G. Trajectory planning and control for planar robots with passive last joint. Int. J. Robot. Res. 2002, 21, 575–590. [Google Scholar] [CrossRef]
- Shoji, T.; Katsumata, S.; Nakaura, S.; Sampei, M. Throwing motion control of the springed pendubot. IEEE Trans. Control Syst. Technol. 2012, 21, 950–957. [Google Scholar] [CrossRef]
- Ren, M.; Chen, J.; Wang, C.; Zhang, C.; Chen, M.; Ma, J.; Zhang, D. Design of Three-Phalange Underactuated Adaptive Lsdh Finger. SSRN 4402140. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4402140 (accessed on 27 March 2023).
- Liu, S.; Chen, C.; Angeles, J. A novel framework for the analysis of underactuated fingers. Mech. Mach. Theory 2023, 182, 105238. [Google Scholar] [CrossRef]
- Xu, H.; Yu, G.; Niu, C.; Zhao, X.; Wang, Y.; Chen, Y. Design and Experiment of an Underactuated Broccoli-Picking Manipulator. Agriculture 2023, 13, 848. [Google Scholar] [CrossRef]
- ur Rehman, F.; Shah, I.; Abbasi, W. Smooth Second Order Sliding Mode Stabilization of Underactuated Two-Link Manipulators: The Acrobot and Pendubot Examples. Int. J. iRobotics 2021, 4, 1–13. [Google Scholar]
- Spong, M.W. Partial feedback linearization of underactuated mechanical systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Munich, Germany, 12–16 September 1994; Volume 1, pp. 314–321. [Google Scholar]
- Yu, C.; Xiang, X.; Lapierre, L.; Zhang, Q. Nonlinear guidance and fuzzy control for three-dimensional path following of an underactuated autonomous underwater vehicle. Ocean Eng. 2017, 146, 457–467. [Google Scholar] [CrossRef]
- Li, Y.; Wei, C.; Wu, Q.; Chen, P.; Jiang, Y.; Li, Y. Study of 3 dimension trajectory tracking of underactuated autonomous underwater vehicle. Ocean Eng. 2015, 105, 270–274. [Google Scholar] [CrossRef]
- Duleba, I.; Sasiadek, J.Z. Nonholonomic motion planning based on Newton algorithm with energy optimization. IEEE Trans. Control Syst. Technol. 2003, 11, 355–363. [Google Scholar] [CrossRef]
- Yang, E.C.Y.; Chao, P.C.P.; Sung, C.K. Optimal control of an under-actuated system for landing with desired postures. IEEE Trans. Control Syst. Technol. 2010, 19, 248–255. [Google Scholar] [CrossRef]
- Massaro, M.; Lovato, S.; Limebeer, D.J. The Optimal Erection of the Inverted Pendulum. Appl. Sci. 2022, 12, 8112. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y. Online Trajectory Planning Control for a Class of Underactuated Mechanical Systems. IEEE Trans. Autom. Control 2023, 1–8. [Google Scholar] [CrossRef]
- Huang, Z.; Hou, M.; Hua, Y.; Yu, C.; Wang, L. A General Stable Control Method for R-Type Underactuated Robot with Three Different Initial Situations. Appl. Sci. 2023, 13, 5565. [Google Scholar] [CrossRef]
- Acuña-Bravo, W.; Molano-Jiménez, A.G.; Canuto, E. Embedded model control for underactuated systems: An application to Furuta pendulum. Control Eng. Pract. 2021, 113, 104854. [Google Scholar] [CrossRef]
- Olivares, M.; Albertos, P. Linear control of the flywheel inverted pendulum. ISA Trans. 2014, 53, 1396–1403. [Google Scholar] [CrossRef]
- Hou, M.; Zhang, X.; Chen, D.; Xu, Z. Hierarchical Sliding Mode Control Combined with Nonlinear Disturbance Observer for Wheeled Inverted Pendulum Robot Trajectory Tracking. Appl. Sci. 2023, 13, 4350. [Google Scholar] [CrossRef]
- Gritli, H.; Belghith, S. Robust feedback control of the underactuated Inertia Wheel Inverted Pendulum under parametric uncertainties and subject to external disturbances: LMI formulation. J. Frankl. Inst. 2018, 355, 9150–9191. [Google Scholar] [CrossRef]
- Murray, R.M.; Rathinam, M.; Sluis, W. Differential flatness of mechanical control systems: A catalog of prototype systems. In Proceedings of the American Society of Mechanical Engineers, Dynamic Systems and Control Division (Publication) DSC, San Francisco, CA, USA, 12–17 November 1995; Volume 57-1, pp. 349–357. [Google Scholar]
- Sira-Ramirez, H.; Agrawal, S.K. Differentially Flat Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Agrawal, S.; Sangwan, V. Design of under-actuated open-chain planar robots for repetitive cyclic motions. In Proceedings of the ASME Design Engineering Technical Conference, Philadelphia, PA, USA, 10–13 September 2006; Volume 2006. [Google Scholar]
- Agrawal, S.; Sangwan, V. Differentially flat designs of underactuated open-chain planar robots. IEEE Trans. Robot. 2008, 24, 1445–1451. [Google Scholar] [CrossRef]
- Franch, J.; Reyes, A.; Agrawal, S. Differential flatness of a class of n-DOF planar manipulators driven by an arbitrary number of actuators. In Proceedings of the 2013 European Control Conference, ECC 2013, Zurich, Switzerland, 17–19 July 2013; pp. 161–166. [Google Scholar]
- Franch, J.; Agrawal, S.; Sangwan, V. Differential flatness of a class of n-DOF planar manipulators driven by 1 or 2 actuators. IEEE Trans. Autom. Control 2010, 55, 548–554. [Google Scholar] [CrossRef]
- Boscariol, P.; Richiedei, D. Robust point-to-point trajectory planning for nonlinear underactuated systems: Theory and experimental assessment. Robot. Comput.-Integr. Manuf. 2018, 50, 256–265. [Google Scholar] [CrossRef]
- Bottin, M.; Rosati, G. Comparison of Under-Actuated and Fully Actuated Serial Robotic Arms: A Case Study. J. Mech. Robot. 2022, 14, 034503. [Google Scholar] [CrossRef]
- Huang, A.C.; Chen, Y.F.; Kai, C.Y. Adaptive Control of Underactuated Mechanical Systems; World Scientific: Singapore, 2015. [Google Scholar]
- Mareczek, J.; Buss, M.; Schmidt, G. Robust global stabilization of the underactuated 2-DOF manipulator R2D1. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No. 98CH36146), Leuven, Belgium, 20 May 1998; Volume 3, pp. 2640–2645. [Google Scholar]
- Nuchkrua, T.; Chen, S.L. Precision contouring control of five degree of freedom robot manipulators with uncertainty. Int. J. Adv. Robot. Syst. 2016, 14, 1729881416682703. [Google Scholar] [CrossRef]
- Mareczek, J.; Buss, M.; Schmidt, G. Robust control of a non-holonomic underactuated SCARA robot. In Progress in System and Robot Analysis and Control Design; Springer: Berlin/Heidelberg, Germany, 1999; pp. 381–396. [Google Scholar]
- Bettega, J.; Richiedei, D. Trajectory tracking in an underactuated, non-minimum phase two-link multibody system through model predictive control with embedded reference dynamics. Mech. Mach. Theory 2023, 180, 105165. [Google Scholar] [CrossRef]
- Mottard, A.; Laliberté, T.; Gosselin, C. Underactuated tendon-driven robotic/prosthetic hands: Design issues. In Proceedings of the Robotics: Science and Systems, Cambridge, MA, USA, 12–16 July 2017. [Google Scholar]
- Teng, Z.; Xu, G.; Liang, R.; Li, M.; Zhang, S.; Chen, J.; Han, C. Design of an underactuated prosthetic hand with flexible multi-joint fingers and eeg-based control. In Proceedings of the 2018 IEEE International Conference on Cyborg and Bionic Systems (CBS), Shenzhen, China, 25–27 October 2018; pp. 647–651. [Google Scholar]
- Rao, S.S. Vibration of Continuous Systems; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2004; pp. 1–720. [Google Scholar]
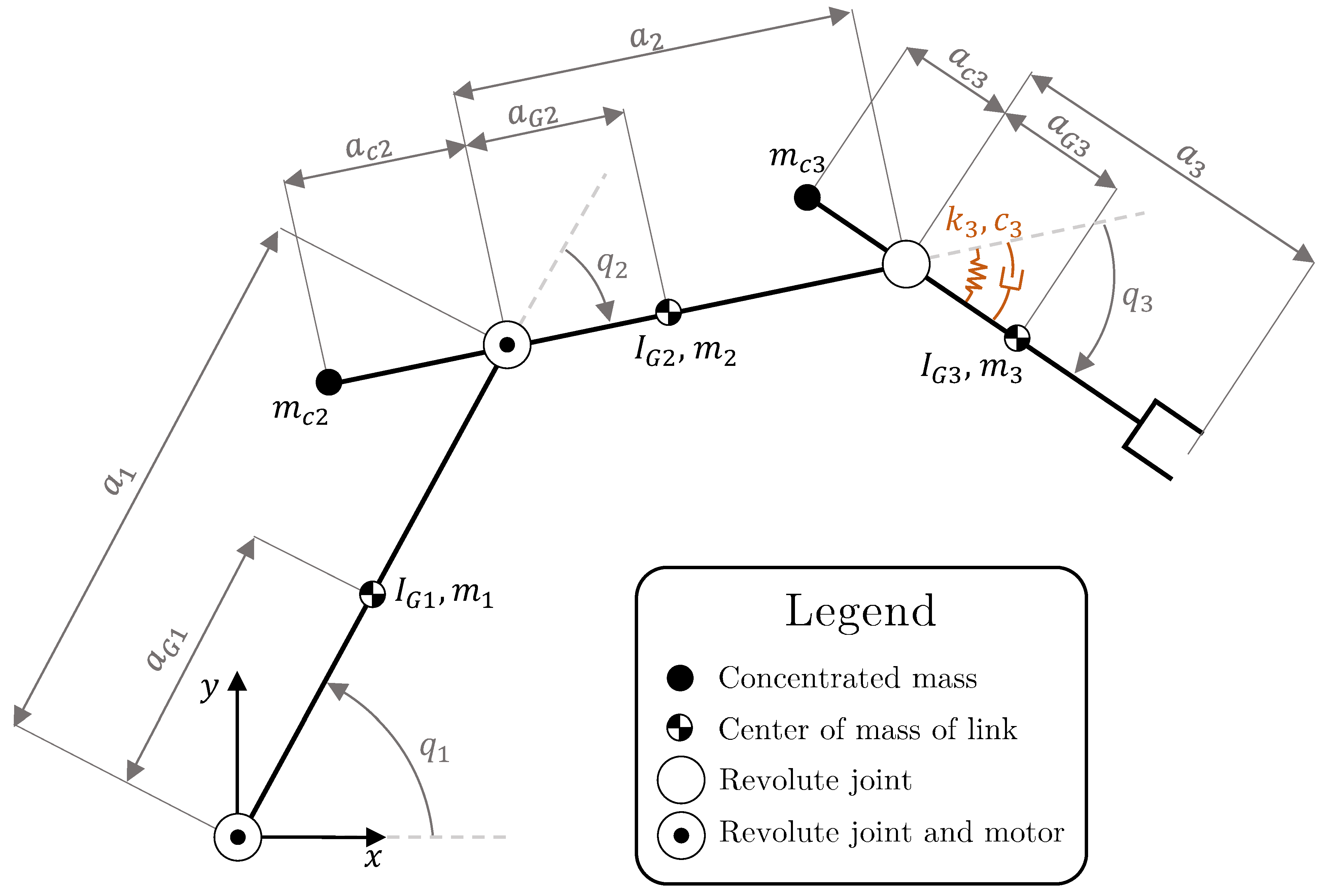

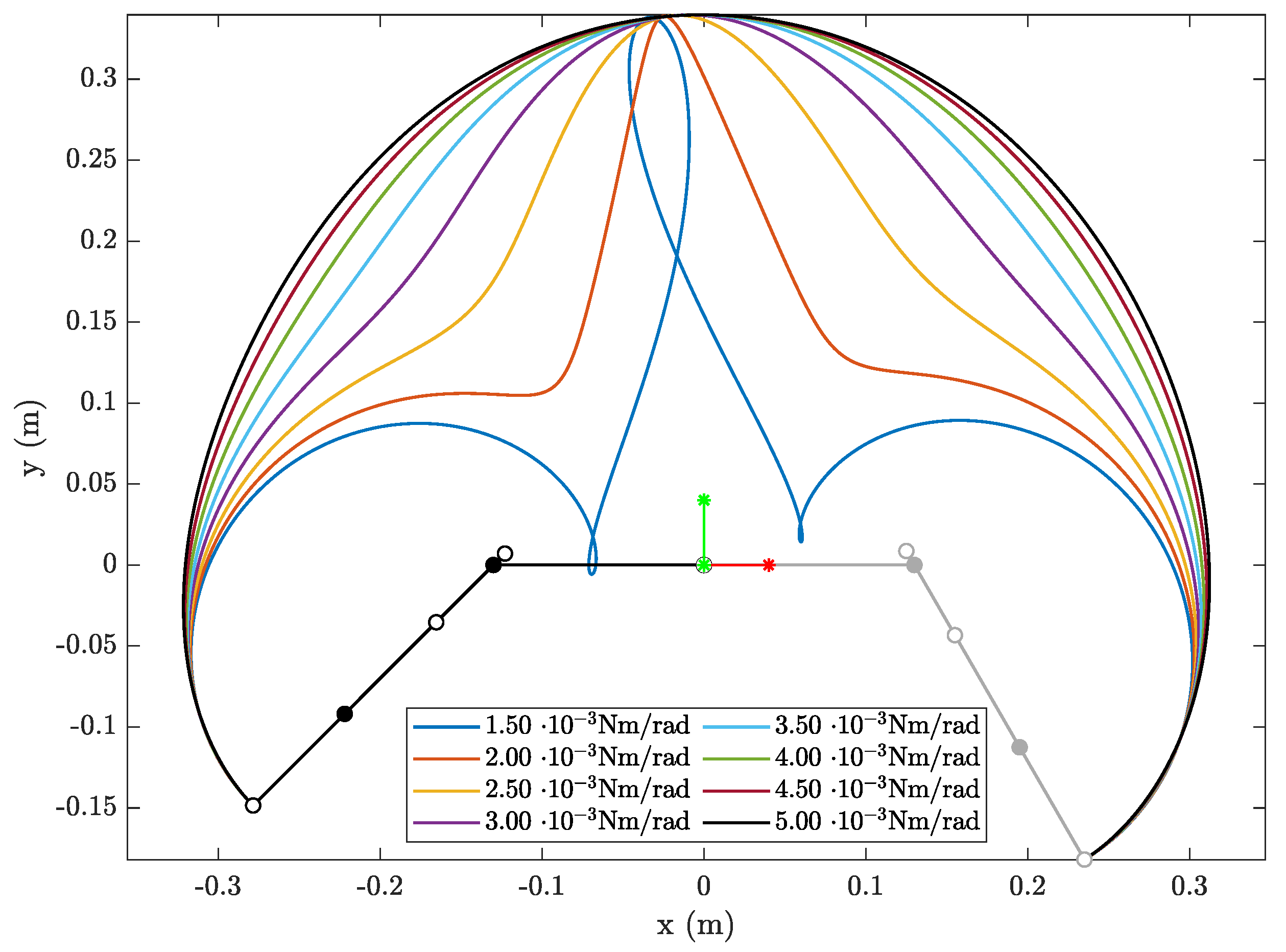

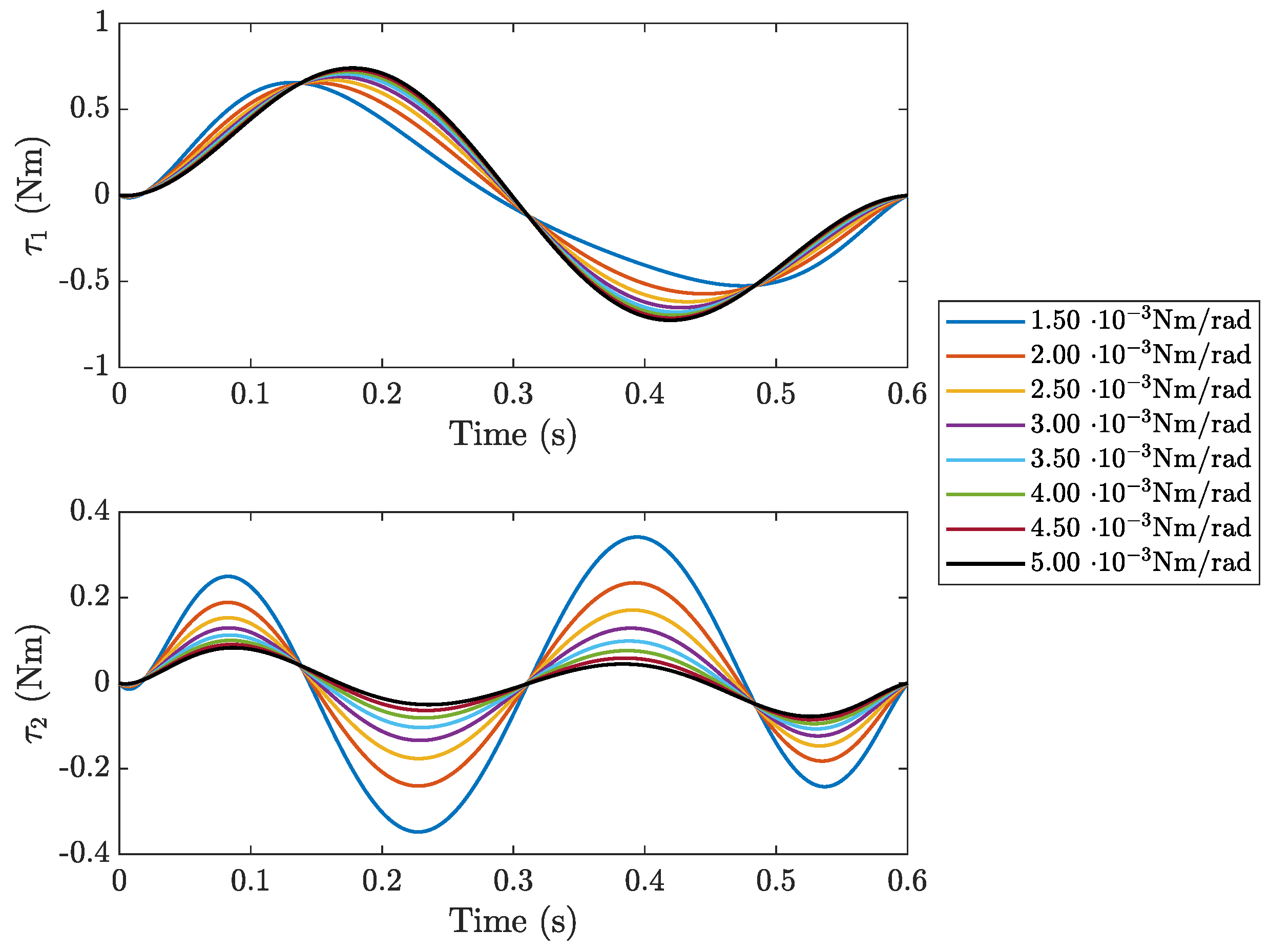
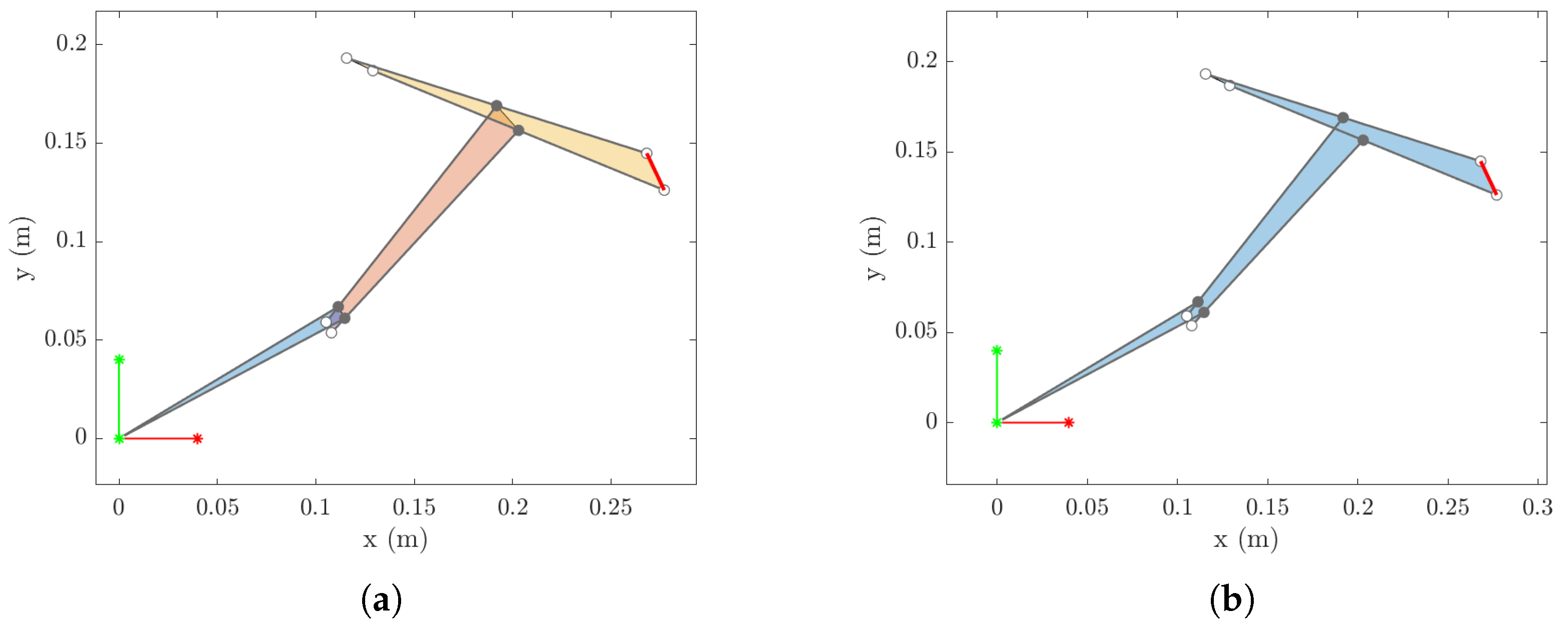

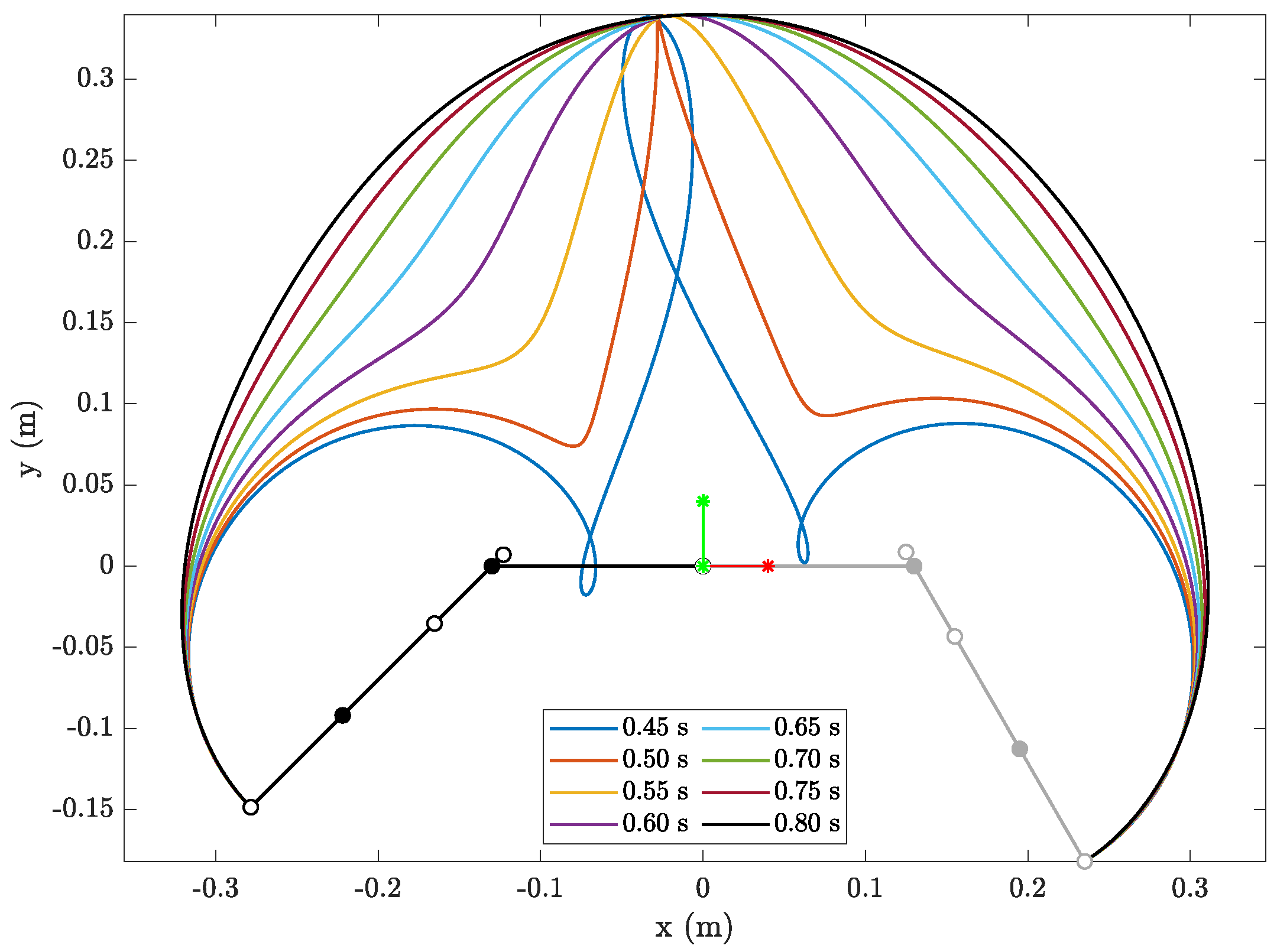

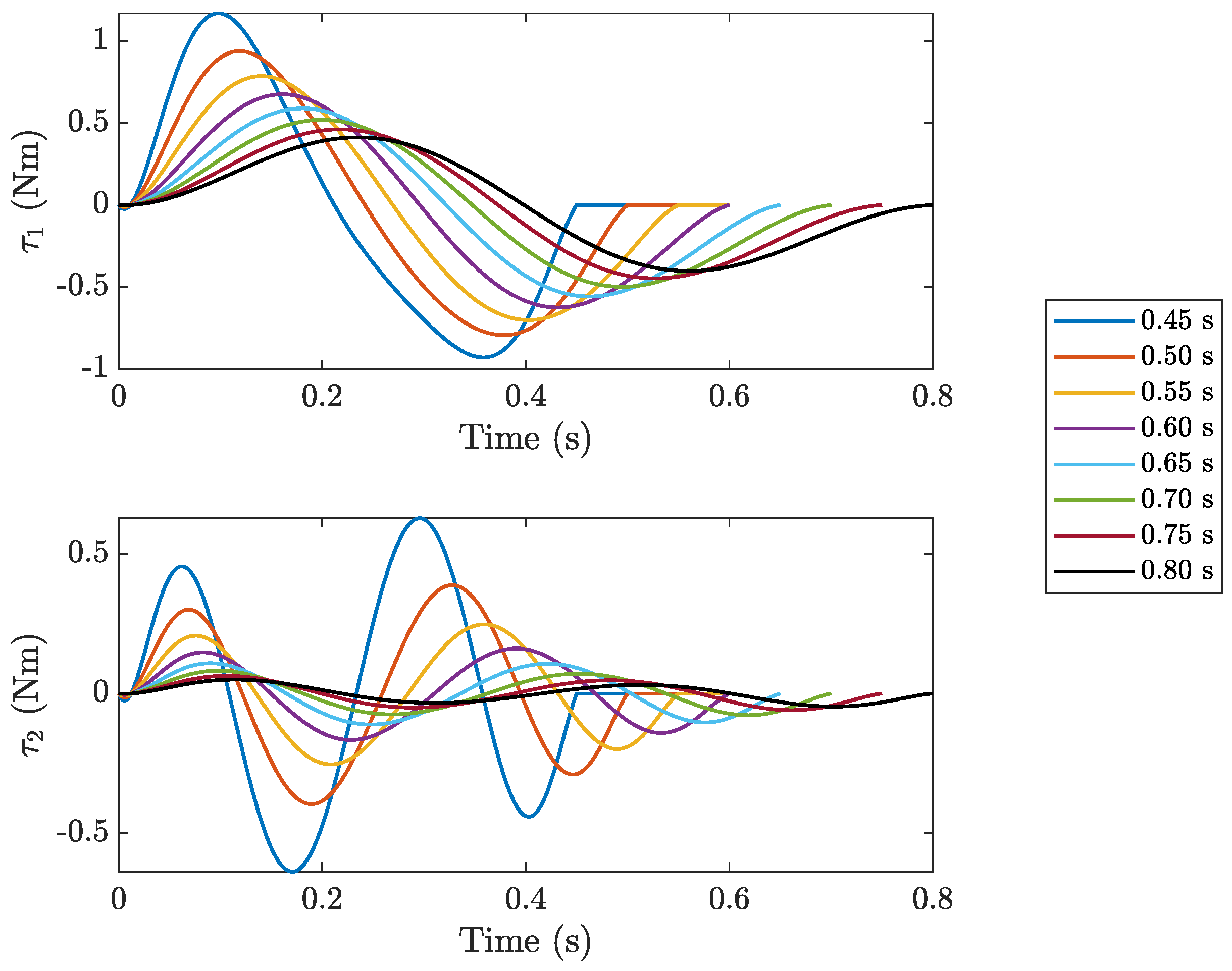
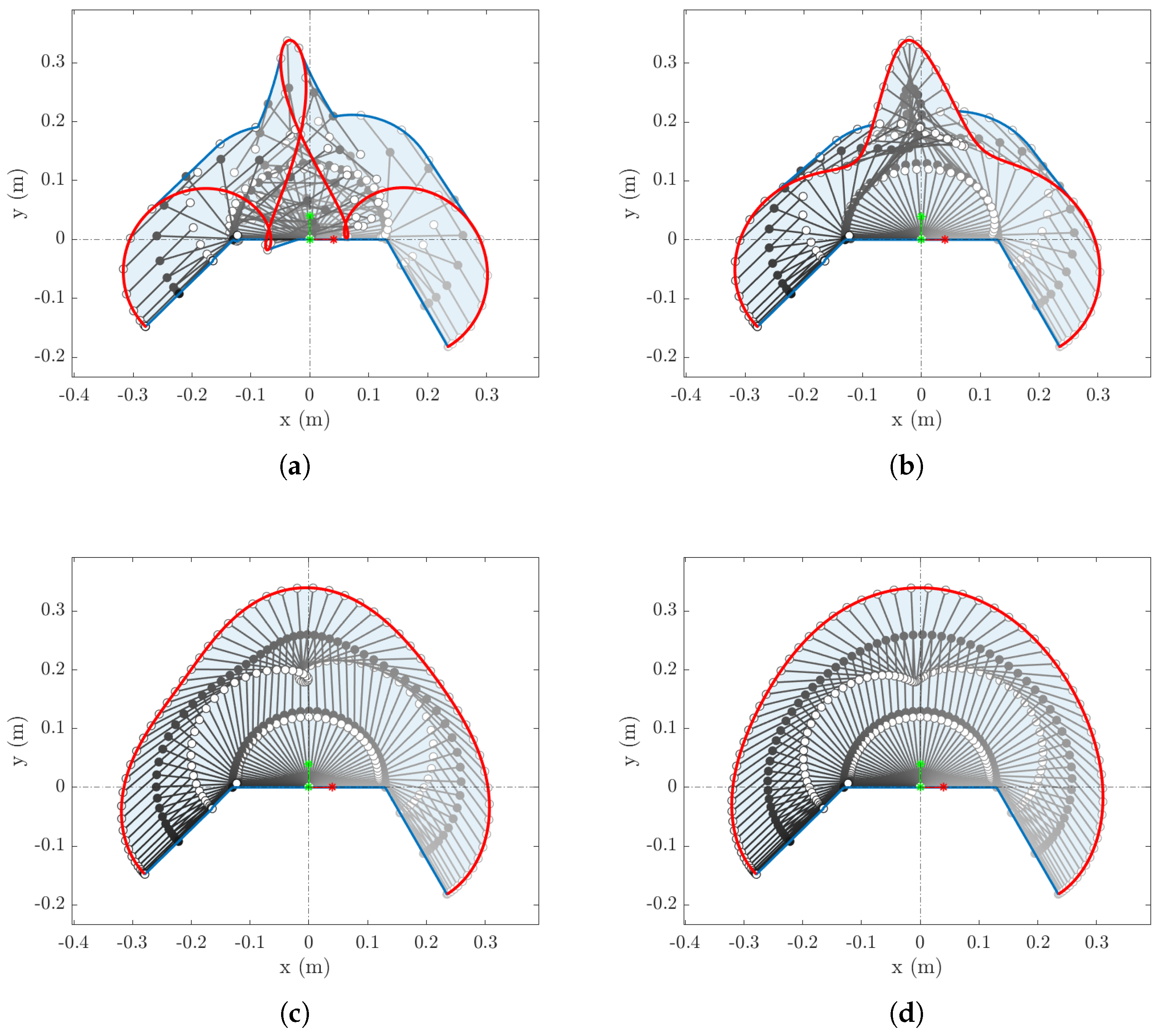
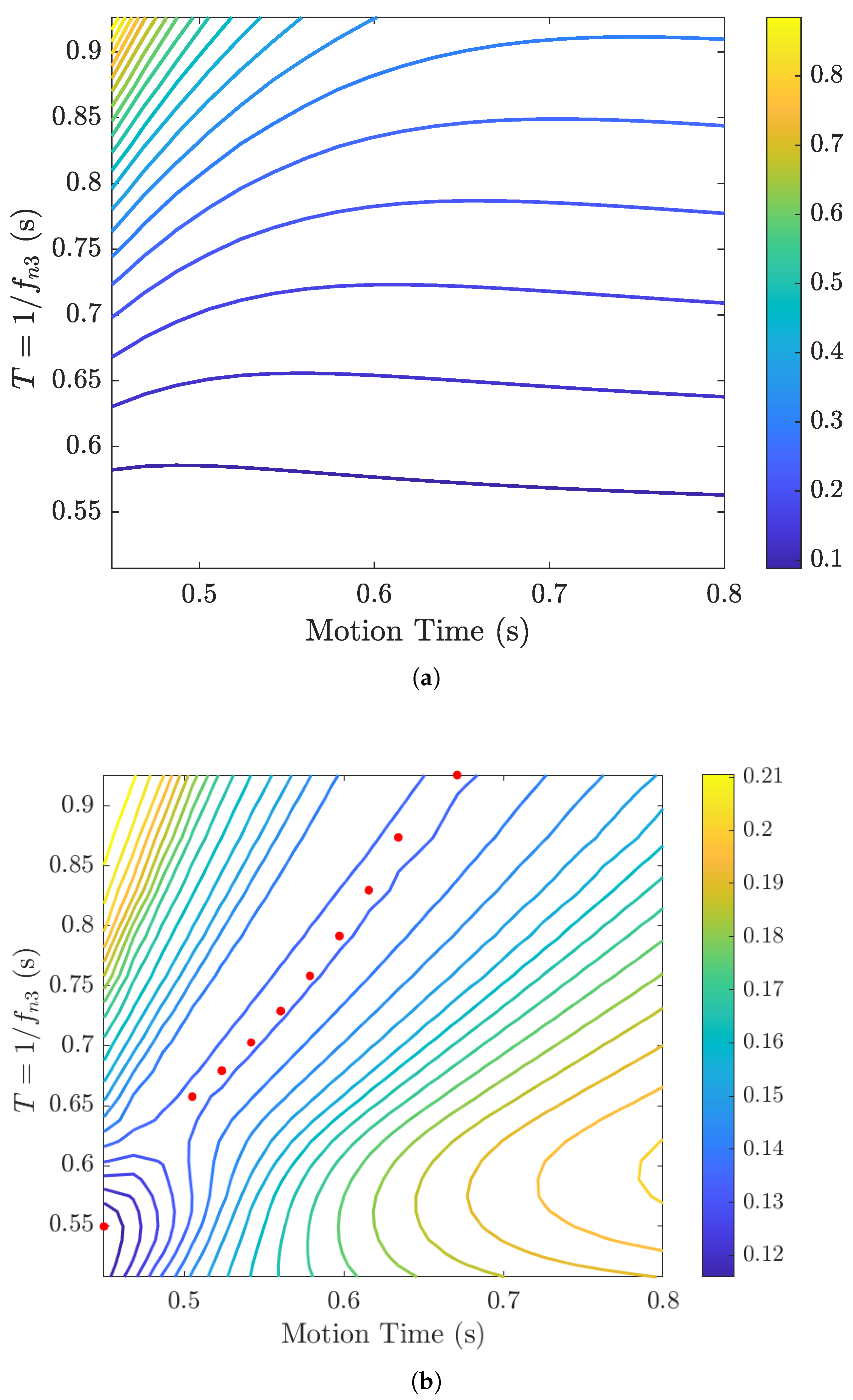



| Link (i) | (kg) | (kg) | (kgm2) | (m) | (m) | (m) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | ||||
| 2 | ||||||
| 3 | 0 |
| (Nm/rad) | (kgm2) | (kgm2) | (kgm2) | (Hz) |
|---|---|---|---|---|
| 1.5 | ||||
| 5 |
| Stiffness Value (Nm/rad) | 2-DOF Area (m2) | 3-DOF Area (m2) | Reduction (%) |
|---|---|---|---|
| 0.2065 | 0.1320 | 36.08 | |
| 0.2065 | 0.1468 | 28.91 | |
| 0.2065 | 0.1884 | 8.77 | |
| 0.2065 | 0.1989 | 3.68 |
| Motion Time (s) | 2-DOF Area (m2) | 3-DOF Area (m2) | Reduction (%) |
|---|---|---|---|
| 0.45 | 0.2065 | 0.1329 | 35.64 |
| 0.55 | 0.2065 | 0.1379 | 33.22 |
| 0.7 | 0.2065 | 0.1801 | 12.78 |
| 0.8 | 0.2065 | 0.1958 | 5.18 |
| Motion Time (s) | Numerical Area (m2) | Experimental Area (m2) | Error (%) |
|---|---|---|---|
| 0.55 | 0.0537 | 0.0544 | 1.28 |
| 0.6 | 0.0564 | 0.0558 | 1.07 |
| 0.7 | 0.0605 | 0.0611 | 0.95 |
| Motion Time (s) | 1-DOF Area (m2) | 2-DOF Area (m2) | Reduction (%) |
|---|---|---|---|
| 0.55 | 0.0693 | 0.0544 | 21.50 |
| 0.6 | 0.0693 | 0.0558 | 19.48 |
| 0.7 | 0.0693 | 0.0611 | 11.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tonan, M.; Doria, A.; Bottin, M.; Rosati, G. Influence of Joint Stiffness and Motion Time on the Trajectories of Underactuated Robots. Appl. Sci. 2023, 13, 6939. https://doi.org/10.3390/app13126939
Tonan M, Doria A, Bottin M, Rosati G. Influence of Joint Stiffness and Motion Time on the Trajectories of Underactuated Robots. Applied Sciences. 2023; 13(12):6939. https://doi.org/10.3390/app13126939
Chicago/Turabian StyleTonan, Michele, Alberto Doria, Matteo Bottin, and Giulio Rosati. 2023. "Influence of Joint Stiffness and Motion Time on the Trajectories of Underactuated Robots" Applied Sciences 13, no. 12: 6939. https://doi.org/10.3390/app13126939
APA StyleTonan, M., Doria, A., Bottin, M., & Rosati, G. (2023). Influence of Joint Stiffness and Motion Time on the Trajectories of Underactuated Robots. Applied Sciences, 13(12), 6939. https://doi.org/10.3390/app13126939











