Fully Homomorphic Encryption with Optimal Key Generation Secure Group Communication in Internet of Things Environment

Abstract

The Internet of Things or “IoT” determines the highly interconnected network of heterogeneous devices where each type of communication seems to be possible, even unauthorized. Consequently, the security requirement for these networks became crucial, while conventional Internet security protocol was identified as unusable in these types of networks, especially because of some classes of IoT devices with constrained resources. Secure group communication (SGC) in the IoT environment is vital to ensure the confidentiality, integrity, and availability (CIA) of data swapped within a collection of IoT devices. Typically, IoT devices were resource-constrained with limited memory, processing, energy, and power, which makes SGC a difficult task. This article designs a Fully Homomorphic Encryption with Optimal Key Generation Secure Group Communication (FHEOKG-SGC) technique in the IoT environment. The presented FHEOKG-SGC technique mainly focuses on the encryption and routing of data securely in the IoT environment via group communication. To accomplish this, the presented FHEOKG-SGC technique initially designs an FHE-based encryption technique to secure the data in the IoT environment. Next, the keys in the FHE technique are chosen optimally using the sine cosine algorithm (SCA). At the same time, the plum tree algorithm (PTA) is applied for the identification of the routes in the IoT network. Finally, the FHEOKG-SGC technique employs a trust model to improve the secure communication process, and the key management center is used for optimal handling of the keys. The simulation analysis of the FHEOKG-SGC technique is tested using a series of experiments, and the outcomes are studied under various measures. An extensive comparative study highlighted the improvement of the FHEOKG-SGC algorithm over other recent approaches.

1. Introduction

The number of devices connected to the Internet has been continuously increasing since it appeared [1]. This developing technology paves the way for revolutionary applications such as autonomous vehicles, health care, smart homes, smart city, environment monitoring, etc. To attain this, the IoT gadgets automatically interact with one another in two different ways: Device-to-Device and group communications [2]. In group communication, a device communicates with many others simultaneously. Such gadgets have common interests and generally participate in the same service. This device can tackle others in a Peer-to-Peer (P2P) manner [3]. This is known as Device-to-Device communication. An example of this is Vehicle-to-Everything communication. Technology allows vehicles to interact with nearby devices (public lighting, cars, and so on). The objective is to cause the vehicle to sense its environment and thus take the correct decision [4]. On the other hand, Vehicle-to-Vehicle communication lets two particular vehicles interchange data, in a P2P manner, regarding their position and speed. Hence, it could improve the environment, avoid crashes, and ease traffic congestion [5]. Securing the interaction between its devices has been a significant challenge faced by the IoT. It is a challenging problem since IoT gadgets have the particularity of being heterogeneous.

Various contemporary scenarios necessitate communication to and data acquisition from several devices with the same functionalities [6], e.g., nodes, medical sensors, and industrial Wireless Sensor Network (WSN) nodes installed in smart homes. For this scenario, group communication has proven to be potentially one in the form of broadcasting and multicasting. In a communication network, Group Key Management (GKM) includes the updating, handling, distribution, and revocation of cryptographic keys to different group members [7]. GKM is adopted in a distributed or centralized manner. The centralized GKM technique includes a centralized entity, such as a Key Distribution Center, which performs and produces keys for the above-mentioned functions. On the other, in dispersed GKM techniques, nodes were clustered into groups and various cluster heads (CHs) were allocated to manage keys locally [8]. However, the latter method has higher computational costs; as a result, much research is based on the centralized method. Nowadays, traditional GKM methods execute ineffectually in dynamic IoT environments, i.e., those nodes often join or leave a network or migrate over a period [9]. In this scenario, if changes happen in the network, keys should be distributed and updated so that forward and backward privacy is maintained. Other than this, the overall scalability of the system can be limited by using asymmetric cryptography in dynamic IoT environments [10]. Therefore, a GKM technique based on symmetric cryptography that can effectively scale in dynamic settings was in demand.

This article designs a Fully Homomorphic Encryption with Optimal Key Generation Secure Group Communication (FHEOKG-SGC) technique in the IoT environment. The proposed FHEOKG-SGC algorithm mainly focuses on the encryption and routing of data securely in the IoT environment via group communication. To accomplish this, the presented FHEOKG-SGC technique initially designs an FHE-based encryption technique to secure the data in the IoT environment. Next, the keys in the FHE technique are chosen optimally using the sine cosine algorithm (SCA). At the same time, the plum tree algorithm (PTA) is applied for the identification of the routes in the IoT network. Finally, the FHEOKG-SGC technique employs a trust model to improve the secure communication process, and the key management center is used for optimal handling of the keys. The simulation analysis of the FHEOKG-SGC technique is tested using a series of experiments, and the outcomes are studied under various measures.

The rest of the paper is organized as follows. Section 2 provides the related works, and Section 3 offers the proposed model. Then, Section 4 presents the results and analysis, and Section 5 concludes the paper.

2. Literature Review

Dammak et al. [11] established a new Decentralized Lightweight Group Key Management for Access Control (DLGKM-AC) from the IoT platform. According to a hierarchical design, collected of many Sub Key Distribution Centers (SKDCs) and one Key Distribution Center (KDC), the presented method improves the management of subscriber groups and improves the re-keying above on KDC. Kandi et al. [12] presented a new Blockchain-based decentralized key management (KM) protocol. It is resilient, dynamic, and scalable, and the presented technique utilizes the Blockchain (BC) for securely distributing the KM to many entities. Wang et al. [13] examined a BC-based mutual authentication and key agreement procedure for edge computing-based smart grid schemes. The authors of [14] introduced a BC-based secure key management (BC-EKM) method. Primarily, the stake BC was generated dependent upon the hybrid sensor network. In addition, the author’s proposal shows a secured cluster development technique and secured node movement technique for implementing key management, whereas staking BC as a trust machine exchanges the popular functions of BS.

Ma et al. [15] resolved these problems by presenting a new BC-based distributed key management architecture (BDKMA) with fog computing to reduce latency and multi-BCs performed from the cloud to achieve cross-domain access. The presented technique employs BC technology to satisfy the fine-grained auditability, maximum scalability, decentralization, extensibility necessities, and privacy-preserving rules for hierarchical access control from the IoT. A system operations approach with various authorization assignment modes and group access patterns is introduced to reinforce the extensibility. In [16], dependent upon (t,n) confidential sharing, a SIN-specific lightweight group key agreement protocol was presented for SD-SIN to ensure either applicability or security. In addition, assuming the extremely dynamic network topology, the authors also propose a group key-based secured handover authentication method for reducing the overhead. In [17], de Ree et al. examined the proposal of a decentralized and effectual key management system termed the DECENT method. During the threshold confidential sharing systems, the network node performs as a distributed trusted third party (TTP), so a threshold count of nodes cooperates for executing key management functions.

Choudhury et al. [18] present a DTLS (Datagram Transport Layer Security)-based SGC technique. The presented technique was scalable, lightweight, and robust against member compromise. In addition, the presented method verifies all the group members and is also appropriate for dynamic groups. Wang et al. [19] present a novel method to offer FHE service, namely by utilizing garbled circuits. From a high-level perspective, garbled circuit and FHE both function by executing difficult computations on the ciphertext. The author determines a novel cryptographic primitive termed reusable garbled gate that develops in the region of garbled circuits; afterwards, dependent upon this novel primitive, the author depicts that it is very simple to construct FHE. Naresh et al. [20] presented a BC-IOTA sharding-based smart contract-centric group key agreement (GKA) for SGC in a huge VANET. In the elliptic curve decision Diffie–Hellman (ECDDH) and group-elliptic curve Diffie–Hellman (GECCDH), the presented method was established to be secure. Raj et al. [21] concentrated on website page dataset security with the support of optimizer and encrypted approaches for Web of Things platforms. Primarily, the chosen queries from the webpage application can be introduced as a Discrete Bee Colony Optimizer (DBCO) technique. In addition, an effectual FHE encryption was presented in the case.

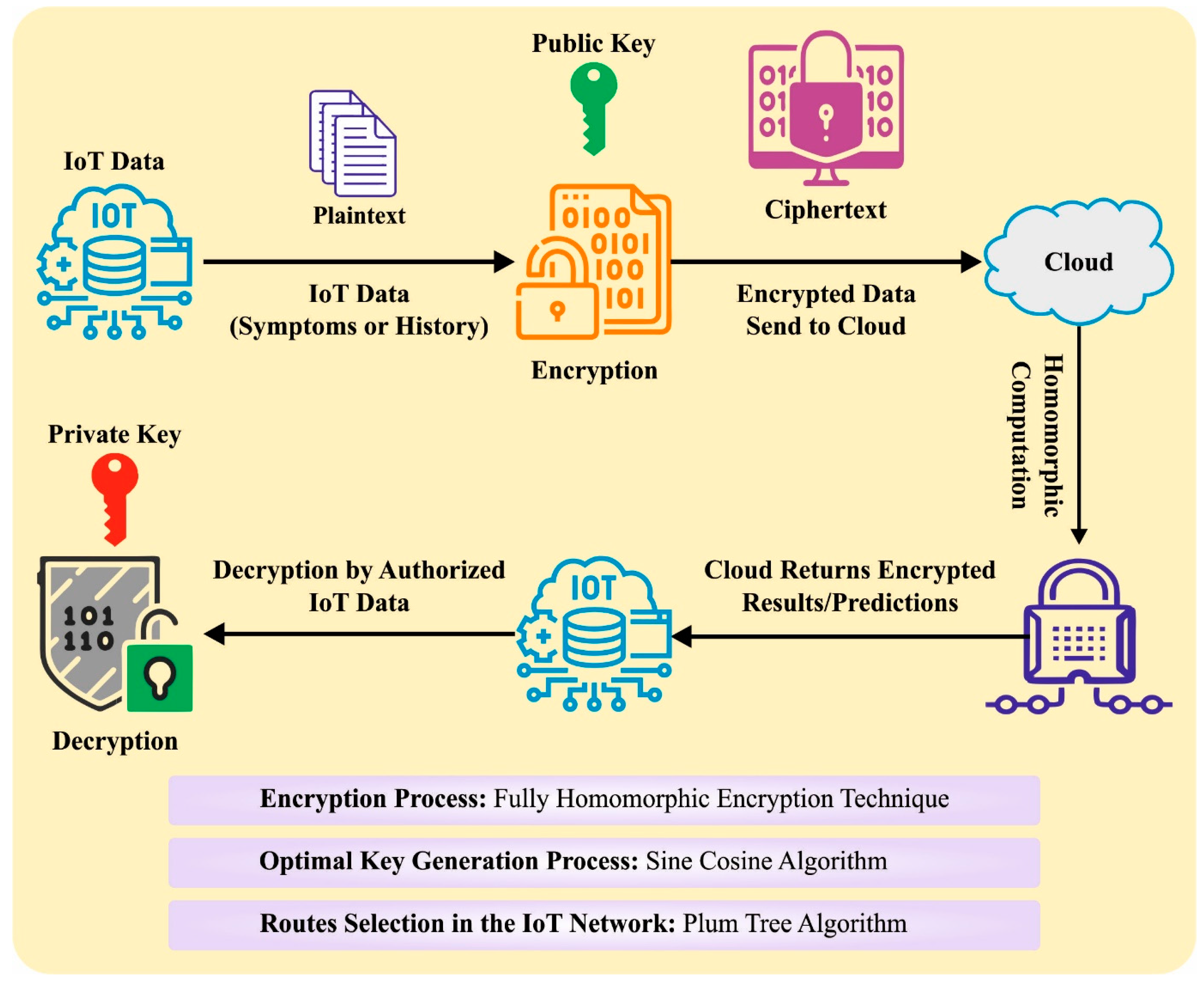
3. The Proposed Model

In this paper, we have designed a new FHEOKG-SGC algorithm for the encryption and key generation process in the IoT environment. The proposed FHEOKG-SGC technique concentrated on the encryption and routing of data securely in the IoT environment via group communication. To achieve this, the presented FHEOKG-SGC technique primarily focused on the design of an FHE-based encryption technique to secure the data in the IoT environment. Following this, the SCA helps to choose the optimal keys related to the FHE technique. Meanwhile, the PTA is applied for the identification of the routes in the IoT network. Figure 1 represents the workflow of the FHEOKG-SGC approach.

3.1. Fully Homomorphic Encryption

An explanation of the homomorphic encryption (HE) method is provided as follows [22]:

Definition 1.

(HE): a group of methods$\{{\epsilon }_k{\}}_{k\in {\mathbb{Z}}_{+}}$ is considered homomorphic in terms of the operator  $\circ$ if there occur decrypt techniques  $\{D_k{\}}_{k\in {\mathbb{Z}}_{+}}$, so that for any 2 ciphertexts  $c_1,c_2\in C$ , the subsequent equality was fulfilled as follows:

$$D_k\left({\epsilon }_k\left(m_1,r_1\right)\circ {\epsilon }_k\left(m_2,r_2\right)\right)=m_1\circ m_2,\forall m_1,m_2\in M,$$

(1)

where $r_1,r_2\in \mathcal{R}$ denotes the equivalent randomness.

The HE method is a pair of methods, $Enc$ and $Dec$, with the subsequent features:

• Enc obtains as input a plaintext $m\in {\mathbb{Z}}_N$ and outputs a c ciphertext so that c refers to the homomorphic image of m, viz., $Dec\left(c\right)=m$;
• Dec proceeds to input a c ciphertext and output a plaintext m so that m denotes the homomorphic image of c;
• Enc and Dec are calculated as effective.

There are 2 categories of HE: multiplicatively HE and additively HE.

Additively HE comprises a pair of techniques, Enc and Dec, to ensure that for each $m_1,m_2\in {\mathbb{Z}}_N,$ $c_1=Enc\left(m_1\right),c_2=Enc\left(m_2\right)$, and $c_3=c_1+c_2$, ensure that $Dec\left(c_3\right)=m_1+m_2$.

Multiplicatively HE involves a pair of methods, Enc and Dec, to ensure that for every $m_1,m_2\in {\mathbb{Z}}_N,$ $c_1=Enc\left(m_1\right),c_2=Enc\left(m_2\right)$, and $c_3=c_1{c}_2$, ensure that $Dec\left(c_3\right)=m_1{m}_2$.

Partially HE is different from HE, but homomorphism is only partially assisted, viz., the encrypt method was homomorphic for some operations but not homomorphic for others.

Partially HE is different from fully HE, but homomorphism is only restricted and maintained, i.e., the encryption scheme is homomorphic for some operations while not homomorphic for others.

FHE is a kind of HE that permits homomorphism on every function; for instance, the encryption method was homomorphic for every operation. Specifically, an FHE method contains a pair of methods, Enc and Dec, so that for every $m_1,m_2\in {\mathbb{Z}}_N,$ $c_1=Enc\left(m_1\right),c_2=Enc\left(m_2\right)$, and $c_3=c_1{c}_2$, ensure that $Dec\left(c_3\right)=m_1{m}_2.$

3.2. Optimal Key Generation Process

To optimally choose the keys related to the FHE technique, the SCA is exploited in this work. Mirjalili introduced an SCA based on the population-based optimization technique [23]. The SCA produces the initial choice and enables it to alter towards a better solution by applying sin and cos functions.

The optimization-based algorithm was separated into exploration and exploitation stages. Two stages of exploration and exploitation are defined as follows:

$$X_i^{t+1}=X_i^t+r_1\ast \mathrm{s}\mathrm{i}\mathrm{n}\left(r_2\right)\ast \left|r_3\ast P-X_i^t\right|,$$

(2)

$$X_i^{t+1}=X_i^t+r_1\ast \mathrm{c}\mathrm{o}\mathrm{s}\left(r_2\right)\ast \left|r_3\ast P-X_i^t\right|.$$

(3)

Combine Equations (2) and (3) by using the following expression:

$$X_i^{t+1}=\{\frac{X_i^t+r_1\ast \sin \left(r_2\right)\ast \left|r_3\ast P-X_i^t\right|;r_4\le 0.5}{X_i^t+r_1\ast \cos \left(r_2\right)\ast \left|r_3\ast P-X_i^t\right|;r_4\ge 0.5},$$

(4)

In Equation (4), $r_4$ refers to the random integer within $[0,1]$.

The key variables in Equations (2)–$\left(4\right)$ are $r_1,r_2,r_3,$ and $r_4.$

i.

r₁ determines the direction within the space among the solution and the space outside the solution or the destination.

ii.

r₂ gives the distance to travel toward or outward from the target.

iii.

r₃ shows random weight to highlight the weight of exploitation (r₃ < 1) or exploration (r₃ > 1).

The effects of $\mathrm{s}\mathrm{i}\mathrm{n}$ and $\mathrm{c}\mathrm{o}\mathrm{s}$ in Equations (2) and (3) determined the spatial region among 2 solutions from the search range. The cyclic model of $\mathrm{s}\mathrm{i}\mathrm{n}$ and $\mathrm{c}\mathrm{o}\mathrm{s}$ functions enables relocating around the different solutions. Moreover, to prevent local optimization, solutions should be explored outside the space among the destination and solutions.

The effects of $\mathrm{s}\mathrm{i}\mathrm{n}$ and $\mathrm{c}\mathrm{o}\mathrm{s}$ functions are within $(-2,2)$. Changing the scope of $\mathrm{s}\mathrm{i}\mathrm{n}$ and $\mathrm{c}\mathrm{o}\mathrm{s}$ functions would result in one solution that itself changes the location of the solutions with one another. Figure 2 demonstrates the steps included in the SCA.

For a better algorithm, a balance of the two stages of exploitation and exploration is needed to discover potential areas of searching space to reach the global optimizer.

For the SCA, to balance both exploitation and exploration, the scope of $\mathrm{s}\mathrm{i}\mathrm{n}$ and $\mathrm{c}\mathrm{o}\mathrm{s}$ functions in Equations (2)–(4) is changed as follows:

$$r_1=a-t\frac{a}{T},$$

(5)

where $t$ refers to the existing iteration, $T$ signifies the maximal iteration counts, and $a$ represents the constant. The above equation decreases the scope of $sin$ and $cos$ functions over iterations. It should be noted that the SCA explores the search range once the $\mathrm{s}\mathrm{i}\mathrm{n}$ and $\mathrm{c}\mathrm{o}\mathrm{s}$ functions range within (1, 2] and [−2, −1). However, this method uses the searching space once the range is within (−1, 1).

The SCA process begins the optimizer with a series of random solutions. This technique stores the better solution, allocates it as the destination, and upgrades other solutions. In the meantime, the scope of $\mathrm{s}\mathrm{i}\mathrm{n}$ and $\mathrm{c}\mathrm{o}\mathrm{s}$ functions are upgraded to emphasize the exploitation of the search range as the iteration count rises. The SCA technique ends the optimizer technique once the iteration count becomes greater than the maximal number of iterations. The ending criteria are regarded as the accuracy of the global optimum or evaluation of the maximal amount of function.

Figure 2. Flowchart of SCA.

Figure 2. Flowchart of SCA.

3.3. PTA-Based Route Selection in Group Communication

In our proposed research work, the PTA is applied for the effective election of routes related to the group communication process. The plum is a fruit of the Prunus species, a genus of trees which also includes peach, cherry, nectarine, almond, and apricot trees [24]. Plum fruit has many health benefits. The proposed PTA was based on the CSO technique in the usage of Gaussian distribution to upgrade the flower location and the usage of random integers from the range between $the\left(F{R}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$ maximum fruitiness rate and the $\left(F{R}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)$ minimum fruitiness rate. The PTA was stimulated using the PSO technique in the expansion of the formula that updates the flower location. Another reason for inspiration is the GWO because of the fact that this equation considers the best and second-best place obtained. The PTA defines this position as the ripe and unripe locations, correspondingly. The input of PTA can be given as follows: D—the number of dimensions, I—the amount of iterations, FT—the fruitiness threshold, N—the amount of plums, $F{R}_{in}$—the minimal fruitiness rate, $X_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and $X_{\mathrm{m}\mathrm{a}\mathrm{x}}$—the maximal and minimum potential value of the location, RT—the ripeness threshold,$ϵ—a$ constant used to prevent division by zero, $F{R}_{ax}$—the maximal fruitiness rate, and OF—the objective function. The output of PTA is $p_{gbest}$, the global better plum location. $N$ flower is initialized in $D$-dimensional search space with value ranges within [$X_{\mathrm{m}\mathrm{i}\mathrm{n}},X_{\mathrm{m}\mathrm{a}\mathrm{x}}]$:

$$flowers=\left[\begin{array}{ccc}{F}_{1,1}^0& \cdots & F_{1,D}^0\\ \cdots & \cdots & \cdots \\ F_{N,1}^0& \cdots & F_{N,D}^0\end{array}\right],$$

(6)

and $N$ plums are initialized with the value of flower:

$$plums=\left[\begin{array}{ccc}{P}_{1,1}^0& \cdots & P_{1,D}^0\\ \cdots & \cdots & \cdots \\ P_{N,1}^0& \cdots & P_{N,D}^0\end{array}\right]=flowers.$$

(7)

The fitness value of flowers and plums is calculated using $\mathrm{O}\mathrm{F}$, and the value of global better plum $p_{gbest}$ is upgraded to the plum location that has a better fitness value.

The instruction is implemented $I$ times so that $iter$ defines the values of the existing iteration. The ripe location Pipe is upgraded to the plum location with better fitness value, while the unripe location $P_{unripe}$ is upgraded to the plum location with second better fitness value. The flower location can be represented as $F_i^{iter}$, where $i=\overline{1,N}$ is upgraded. Consider the value of random integer $r$ in $[0,1]$.

When the $r$ value is larger than or equivalent to $FT$, the flower location can be upgraded as follows:

$$F_i^{iter}=F_i^{iter-1}+random\left(P{R}_{\mathrm{m}\mathrm{i}\mathrm{n}},P{R}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\times \left(P_i^{iter-1}-F_i^{iter-1}\right),$$

(8)

so that random $(F{R}_{in},F{R}_{ax})$ uniformly return a number ranging from $F{R}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ to $F{R}_{\mathrm{m}\mathrm{a}\mathrm{x}}.$ When the $r$ value is lesser than $FT$ and larger than or equivalent to $RT$, the flower location can be upgraded as follows:

$$F_i^{iter}=F_i^{iter-1}+2\times r_1\times \left(P_{ripe}-F_i^{iter-1}\right)+2\times r_2\times \left(P_{unripe}-F_i^{iter-1}\right),$$

(9)

where $r_1$ and $r_2$ denote a random number within $\left[\mathrm{0,1}\right]$, and $P_{ripe}$ and $P_{unripe}$ show the ripe and the unripe location, correspondingly. When the $r$ value is lesser than $RT$, the flower location can be upgraded using the following equation:

$$F_i^{iter}=P_i^{iter-1}\times \left(1+\mathcal{N}\left(0,{\sigma }^2\right)\right),$$

(10)

so that $\mathcal{N}(0,{\sigma }^2)$ is a Gaussian distribution that has the standard deviation ${\sigma }^2$ and mean $0$ as follows:

$${\sigma }^2=\left\{\begin{array}{c}1,if OF(P_i^{iter-1}<OF(P_{ripe})\\ \frac{OP\left(P_{ripe}\right)-OP\left(P_i^{iter-1}\right),if OP\left(P_i^{iter-e}\right)}{\left|OF\right(P_i^{iter-1}\left)\right|+e}\end{array},\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\right.$$

(11)

where $e$ denotes the constant to prevent division by 0.

The flower is modified to the $[X_{\mathrm{m}\mathrm{i}\mathrm{n}},X_{\mathrm{m}\mathrm{a}\mathrm{x}}]$ interval so that when $F_{i,j}^{iter}<X_{\mathrm{m}\mathrm{i}\mathrm{n}},$ the $F_{i,j}^{iter}=X_{\mathrm{m}\mathrm{i}\mathrm{n}},$ and if $F_{i,j}^{iter}>x_{\mathrm{m}\mathrm{a}\mathrm{x}}$, then $F_{i,j}^{iter}=X_{\mathrm{m}\mathrm{a}\mathrm{x}}$, where $j=\overline{1,D}.$ Every plum location can be upgraded using the following equation:

$$P_i^{iter}=\left\{\begin{array}{l}{F}_i^{iter},ifOF\left(F_i^{iter}\right)<OF\left(P_i^{iter-1}\right)\\ P_i^{iier-1},otherwise.\end{array}\right.,$$

(12)

The value of global better plum $p_{gbest}$ is upgraded to the plum location that has the better fitness value based on the objective function OF. Lastly, return the $p_{gbesi}$ value. In this work, the PTA is applied for the identification of the routes in the IoT network. The latency and power consumption of the method was determined in the subsequent equations [25]. The latency of the IoT has been contained in 3 portions.

$$T_{\mathrm{a}\mathrm{l}\mathrm{l}}=T_1+T_2+T_3$$

(13)

where T₁ refers to the data communication latency between IoT devices and the data center. T₃ simulates the delay of IoT in the data center to the last node. The T₂ comprises 2 portions.

$$T_2=T_{21}+T_{\mathrm{i}\mathrm{j}}$$

(14)

in which $T_{\mathrm{i}\mathrm{j}}$ represents the latency in node $i$ to node j, and $T_{21}$ stands for the latency of residence time for IoT (time of reception and data transmission, and time of establishing the transmission connection amongst IoT and node). At this point, $R_{\mathrm{i}}$ implies the broadcast range of node $i.$ $H$ signifies the height of IoT overground. $L_{\mathrm{c}}$ showcases the connection to make a transmission among $i$ and IoT. $T_{\mathrm{c}}$ denotes the latency of the evolving transmission link in $\mathrm{i}$-$\mathrm{t}\mathrm{h}$ node to the IoT. Because of the length of data transferred $\left(f_{\mathrm{d}}\right)$ and bit per second $\left(V_{\mathrm{c}}\right)$, the kind of transmission chip remains similar, and $T_{\mathrm{c}}$ is signified as follows:

$${\tau }_{\mathrm{c}=l_{\mathrm{d}}l{V}_{\mathrm{c}}}$$

(15)

In addition, the speed $\left(V_{\mathrm{U}}\right)$ of the IoT has to meet the provided condition in the subsequent:

$$V_{\mathrm{U}}<=L_{\mathrm{C}}/T_{\mathrm{C}}$$

(16)

$$T_{21}=T_{\mathrm{C}}+T_S$$

(17)

in which $T_{\mathrm{s}}$ represents the latency of data forwarded amongst nodes as well as the IoT. If the visited nodes are $n$ that is dependent on Equations (14)–(17), $T_{\mathrm{a}\mathrm{l}\mathrm{l}}$ is written as

$$T_{all},=T_1+{\displaystyle \sum }_1^n\left(T_C+T_S+T_{ij}\right)+T_3$$

(18)

where $T_{\mathrm{i}\mathrm{j}}$ demonstrates the time in $i$-$th$ to jth nodes. The energy utilization of the IoT is contained in three portions.

$$P_{\mathrm{a}\mathrm{l}\mathrm{l}}=P_1+P_2+P_3$$

(19)

in which $P_1$ illustrates the power consumption in CHs to the data center. $T_3$ signifies the power application in the resultant node to the data center. The $P_2$ has 2 portions.

$$P_2=P_{21}+P_{\mathrm{i}\mathrm{j}}$$

(20)

where $P_{21}$ implies the power consumption of the IoT, and $P_{\mathrm{i}\mathrm{j}}$ showcases the energy consumption of IoT devices from $i$ to j nodes.

$$P_{oll}=P_1+{\displaystyle \sum }_1^n\left(P_C+P_S+P_{ij}\right)+P_3$$

(21)

Consider that the speed $V_{\mathrm{U}}$ was considerable; therefore, the T₁, T₃, P₁, and P₃ were also considerable. $T_{\mathrm{C}},T_{\mathrm{S}},P_{\mathrm{C}},{andP}_{\mathrm{S}}$ are maximum because of the data length of data maximum. The objective function of the PTA technique is to decrease power utilization along with delay. The power consumption or delay are selected by a frequent visit to the IoT device, and it is represented as follows:

$$\mathrm{m}\mathrm{i}\mathrm{n}f\left(L\right)={\displaystyle \sum }_{l=1}^{n-1}{d}_{L_i{L}_{i+1}}$$

(22)

where $\mathrm{L}$ denotes the sequence of nodes. The NP-hard problem can be resolved by using the PTA technique. The overall process involved in PTA is shown in Algorithm 1.

Algorithm 1: Pseudocode of PTA

Input $I,$ $N,$ $D,$ $RT,FT,$ $F{R}_{\mathrm{m}\mathrm{a}\mathrm{x}},$ $F{R}_{\mathrm{m}\mathrm{i}\mathrm{n}},e,$ OF, $X_{\mathrm{m}\mathrm{a}\mathrm{x}},X_{\mathrm{m}\mathrm{i}\mathrm{n}}$ Output $p_{gbest}$ $N$ flowers initialized in the $D$-dimension space with ranges from $[X_{\mathrm{m}\mathrm{i}\mathrm{n}},X_{\mathrm{m}\mathrm{a}\mathrm{x}}]$ $N$ plums are initialized to the locations of the $N$ flowers Apply OF to calculate the plum’s fitness and the flowers and upgrade $p_{gbest}$ For $iter=1to$, $I$ do     Calculate the ripe location of $P_{ripe}$     Calculate the unripe location $P_{unripe}$     For every flower, do       Upgrade $r$ to a random integer ranging from $\left[\mathrm{0,1}\right]$       If $r\ge FT$, then        Upgrade the flower based on Equation (8)       Else if $r\ge RT$, then         Upgrade the flower based on Equation (9)         Else         Upgrade the flower based on Equations (10) and (11)         End if         Adjust the flower to be in the $[X_{\mathrm{m}\mathrm{i}\mathrm{n}},X_{\mathrm{m}\mathrm{a}\mathrm{x}}]$ interval         End for         For every plum, do          Upgrade the plum based on Equation (12)         End for         Upgrade the $p_{gbest}$   End for Return $p_{gbest}$

3.4. Security and Group Key Management Center

The security manager coordinates with a cluster-based secure routing method by decrypting the information at the receiver end and encrypting the information at the transmission side [26]. Now, the key is produced by combining the SCA- and FHE-based key generation system to provide secure transmission. By using the root agents, a novel specialized agent has been generated to manage security activities. The security agent employs the rule and makes the decision to select the proper encryption technique to secure the information before it is transmitted. Its interaction with the trust management model exists from the security manager to compute the privacy level of the node. Through the neighbor feedback-based trust values, historical trust, and current behavioral trust, the trust manager calculated the entire trust. When any data transmission node attempts to decrypt the information, the trust management model monitors them. Lastly, the security manager interacts with the group key management and distribution center for re-keying, key generation, and key distribution. The group key management center is accountable for key generation, re-keying, and key distribution activities owing to the existence of change in the group size and group members. Once the gathered information is only decrypted, it forms extremely secure groups with 2 members, such as the source and target. Then, multicast transmission will be implemented once the information is utilized by the intermediate node for data analysis or aggregation. The multicast group key was produced and only distributed securely by the key distribution center to consider the group member. Similarly, due to the existence of member leave and member join operations, it is accountable to maintain the forward and backward privacies that are required. The group key manager constructed by the root agent is accountable for making communication within these components and all other components, such as the routing and security managers.

4. Results and Discussion

In this section, the experimental validation of the FHEOKG-SGC technique is examined in detail.

Table 1. Comparative outcome of the FHEOKG-SGC approach with other protocols under varying file sizes.

File Size (Bytes)	AES Protocol	FGECDH Protocol	EESRA Protocol	FHEOKG-SGC
Key Generation Time (ms)
1024	1696	1678	1661	1616
2048	1773	1753	1739	1678
4096	1951	1886	1825	1802
8192	2216	2160	2124	2105
Encryption Time (ms)
1024	2264	2182	2171	2107
2048	2338	2312	2283	2245
4096	2511	2461	2443	2431
8192	3020	2947	2916	2903
Decryption Time (ms)
1024	2676	2238	1831	1625
2048	2665	2196	1817	1621
4096	2654	2125	1766	1592
8192	2541	2026	1725	1558
Encrypted File Size (Bytes)
1024	1912	1780	1584	1531
2048	3624	1893	1829	1812
4096	5757	2060	2026	2107
8192	13246	8273	8794	8170

provides a detailed comparative study of the FHEOKG-SGC system with recent models under varying file sizes [26]. The comparative key generation time (KGT) inspection of the FHEOKG-SGC technique with other protocols demonstrated that the FHEOKG-SGC technique gains effectual performance with minimal KGT values. For instance, with a 1024 bytes file, the FHEOKG-SGC technique reaches a reduced KGT of 1616 ms, while the AES, FGECDH, and EESRA approaches obtain increased KGT values of 1696 ms, 1678 ms, and 1661 ms, respectively. Next, the comparative encryption time (ENT) inspection of the FHEOKG-SGC technique with other protocols illustrated that the FHEOKG-SGC technique gains effectual performance with minimal ENT values. For example, with a 1024 bytes file, the FHEOKG-SGC method reaches a reduced ENT of 2107 ms, whereas the AES, FGECDH, and EESRA approaches attain increased ENT values of 2264 ms, 2182 ms, and 2171 ms, respectively. Based on decryption time (DET) examination of the FHEOKG-SGC technique, the experimental values illustrate that the FHEOKG-SGC method attains effectual performance with minimal DET values. For instance, with a 1024 bytes file, the FHEOKG-SGC technique achieves a decreased DET of 1625 ms, while the AES, FGECDH, and EESRA methods attain increased DET values of 2676 ms, 2238 ms, and 1831 ms, respectively.

Figure 3 demonstrates the comparative encrypted file size (EFS) inspection of the FHEOKG-SGC method with other protocols. The experimental values show that the FHEOKG-SGC technique attains effectual performance with minimal EFS values.

For instance, with a 1024 bytes file, the FHEOKG-SGC method obtains a reduced EFS of 1531 bytes, while the AES, FGECDH, and EESRA approaches obtain increased EFS values of 1912 bytes, 1780 bytes, and 1584 bytes, respectively. Furthermore, with an 8170 bytes file, the FHEOKG-SGC method reaches a reduced EFS of 2105 bytes, while the AES, FGECDH, and EESRA approaches obtain increased EFS values of 13,246 bytes, 8273 bytes, and 8794 bytes, respectively.

Table 2. PLR outcome of the FHEOKG-SGC approach with other protocols under varying counts of tests.

Packet Loss Rate (%)
No. of Tests	LEACH	AES Protocol	FGECDH Protocol	EESRA Protocol	FHEOKG-SGC
Test-1	26.75	27.35	24.59	22.72	19.45
Test-2	25.23	26.32	22.37	21.67	19.1
Test-3	23.89	24.68	22.12	20.97	19.48
Test-4	24.16	25.74	23.87	19.51	18.98
Test-5	26.09	23.65	21.47	18.34	17.69

demonstrates the comparative packet loss rate (PLR) inspection of the FHEOKG-SGC technique with other protocols. The experimental values illustrate that the FHEOKG-SGC method obtains effectual performance with minimal PLR values. For instance, in Test-1, the FHEOKG-SGC method attained a reduced PLR of 19.45%, while the LEACH, AES, FGECDH, and EESRA methods obtained increased PLR values of 26.75%, 27.35%, 24.59%, and 22.72%, respectively. Furthermore, in Test-5, the FHEOKG-SGC technique attained a reduced PLR of 17.69%, while the LEACH, AES, FGECDH, and EESRA approaches gained increased PLR values of 26.09%, 23.65%, 21.47%, and 18.34%, respectively.

Figure 4 demonstrates the comparative delay (DEL) inspection of the FHEOKG-SGC technique with other protocols. The experimental values demonstrate that the FHEOKG-SGC method gains effectual performance with minimal DEL values. For example, in Test-1, the FHEOKG-SGC technique attained a reduced DEL of 0.096 ms, while the LEACH, AES, FGECDH, and EESRA approaches obtained increased DEL values of 0.504 ms, 0.478 ms, 0.401 ms, and 0.245 ms, respectively.

Moreover, in Test-5, the FHEOKG-SGC technique attained a reduced DEL of 2.387 ms, while the LEACH, AES, FGECDH, and EESRA approaches gained increased DEL values of 5.968 ms, 5.632 ms, 4.512 ms, and 3.326 ms, respectively. These results highlighted the supremacy of the FHEOKG-SGC method over the other approaches.

5. Conclusions

In this article, we have designed a novel FHEOKG-SGC technique for the encryption and key generation process in the IoT environment. The presented FHEOKG-SGC technique accomplishes secure communication in the IoT network via group communication. To achieve this, the presented FHEOKG-SGC technique follows different processes such as FHE-based encryption, SCA-based optimal key generation, and PTA-based route identification in the IoT network. In addition, the FHEOKG-SGC technique employs a trust model to improve the secure communication process and key management center, which is used for the optimal handling of the keys. The simulation validation of the FHEOKG-SGC system was tested using a series of experiments, and the outcomes were studied under several measures. An extensive comparative study highlighted the improvement of the FHEOKG-SGC algorithm over other recent approaches, with a minimum encryption time of 2107 ms, decryption time of 1558 ms, and encrypted file size of 1531 kb. In the future, lightweight cryptographic algorithms can improve the performance of the FHEOKG-SGC technique.