Thermal Management of Fuel Cells Based on Diploid Genetic Algorithm and Fuzzy PID
Abstract
1. Development Status and Research Content of Fuel Cell
1.1. Prospect of Fuel Cell
1.2. The Importance of Thermal Management Systems
1.3. Advances in Fuel Cell Research
1.4. Research Content of This Paper
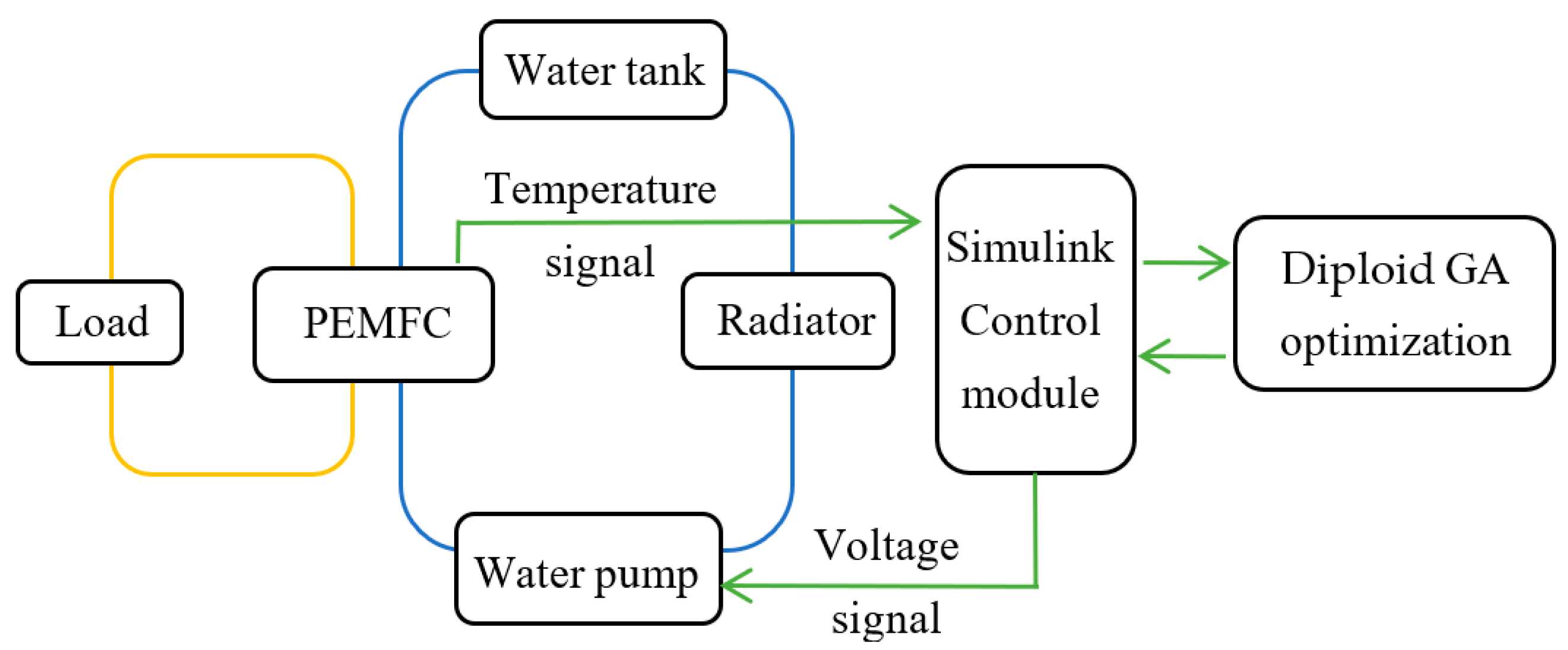
2. Modeling of Fuel Cell Systems
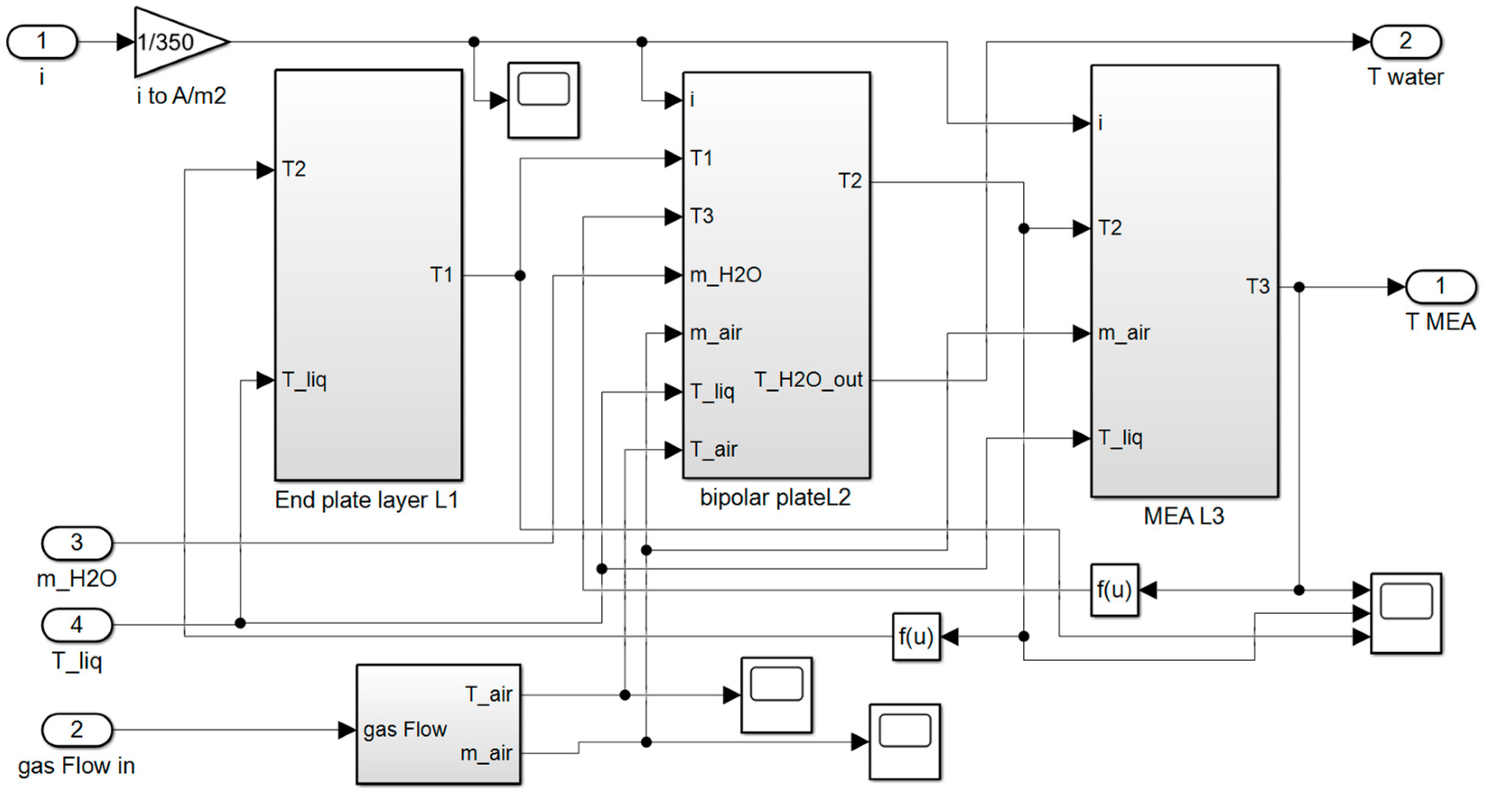
2.1. Fuel Cell Single Cell Modeling
2.1.1. End-Plate Temperature Model
2.1.2. Bipolar Plate Temperature Model
2.1.3. MEA Temperature Model
2.2. Tank Model and Radiator Model
- The temperature of the condensate at the outlet of the unit is the same as that at the inlet of the next unit;
- Heat from condensed water entering the tank from the fuel cell spreads rapidly through the tank;
- In the radiator, air and condensed water exchange heat, and the air temperature is always room temperature.
- The conservation equation of the water tank energy is:
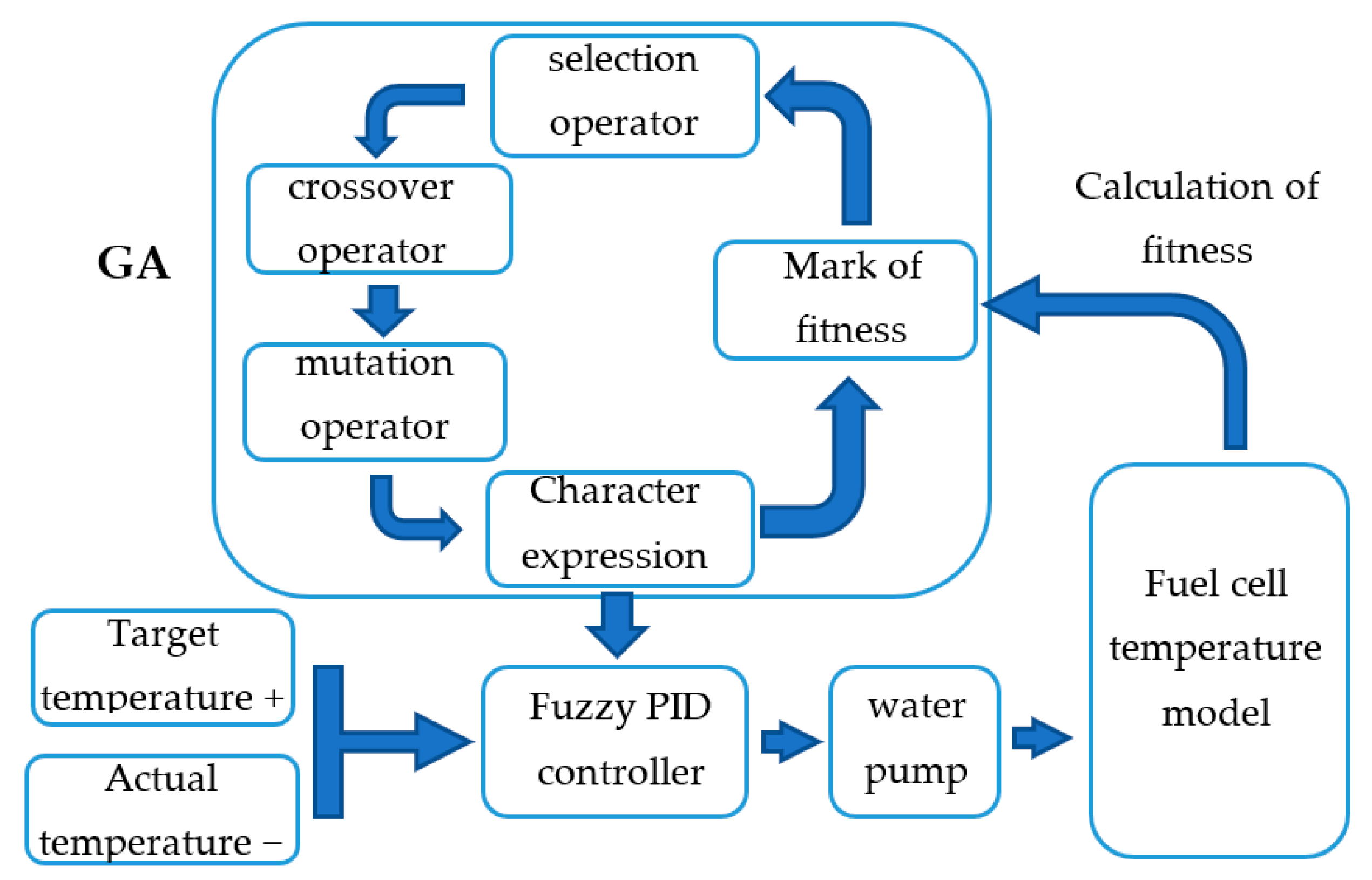
3. Design of Thermal Management Control Strategy for Fuel Cells
3.1. Design of Fuzzy PID Control Strategy
3.2. Parameter Optimization of Diploid Genetic Algorithm
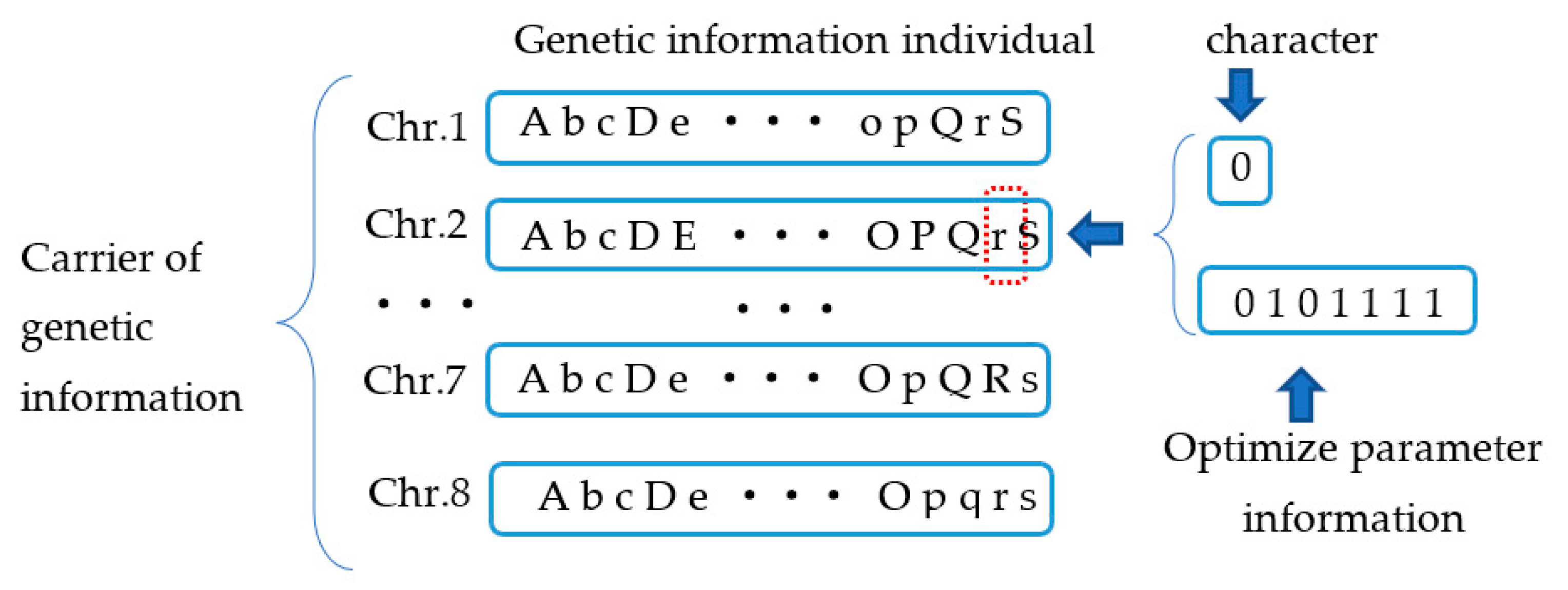
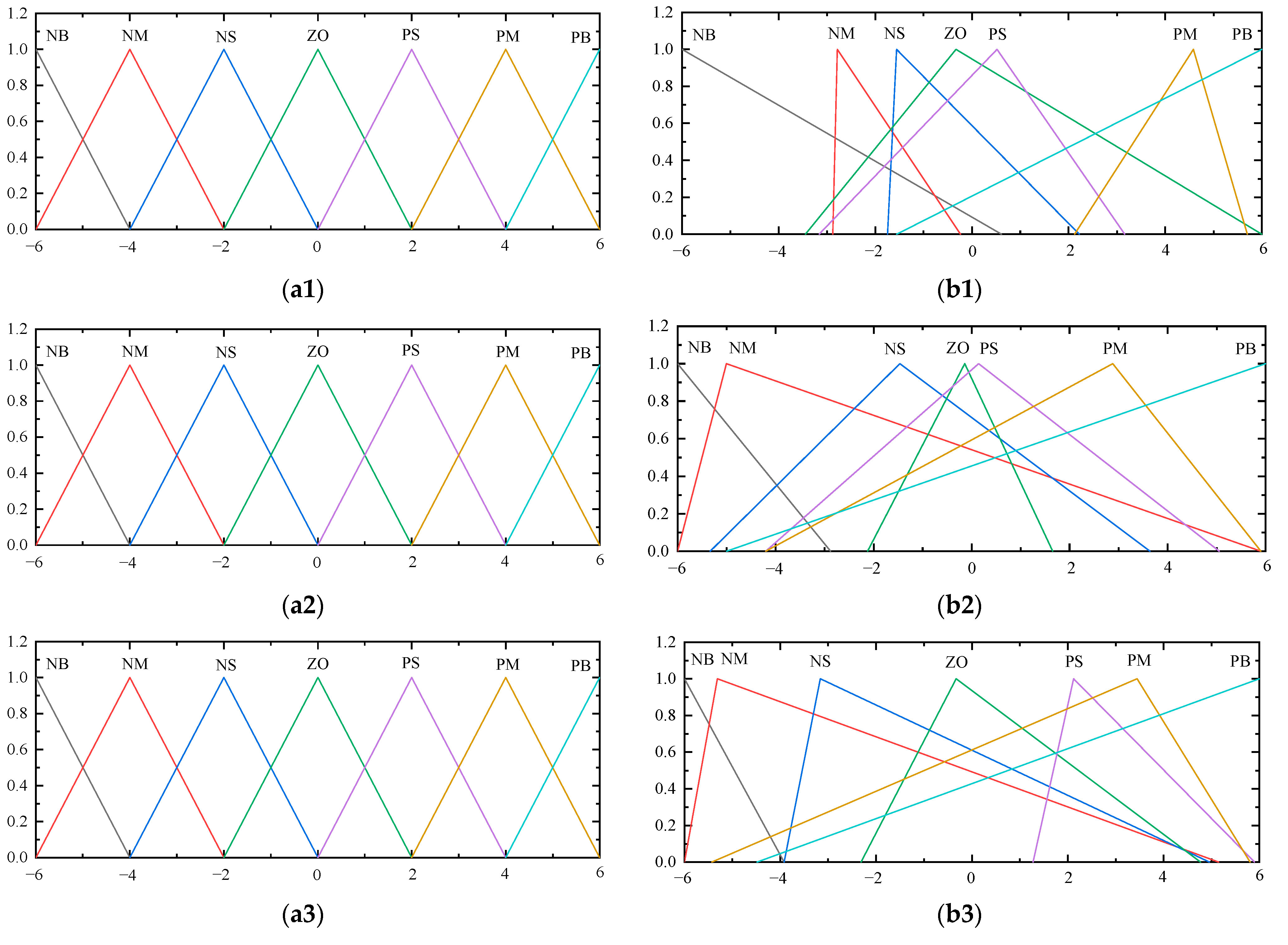
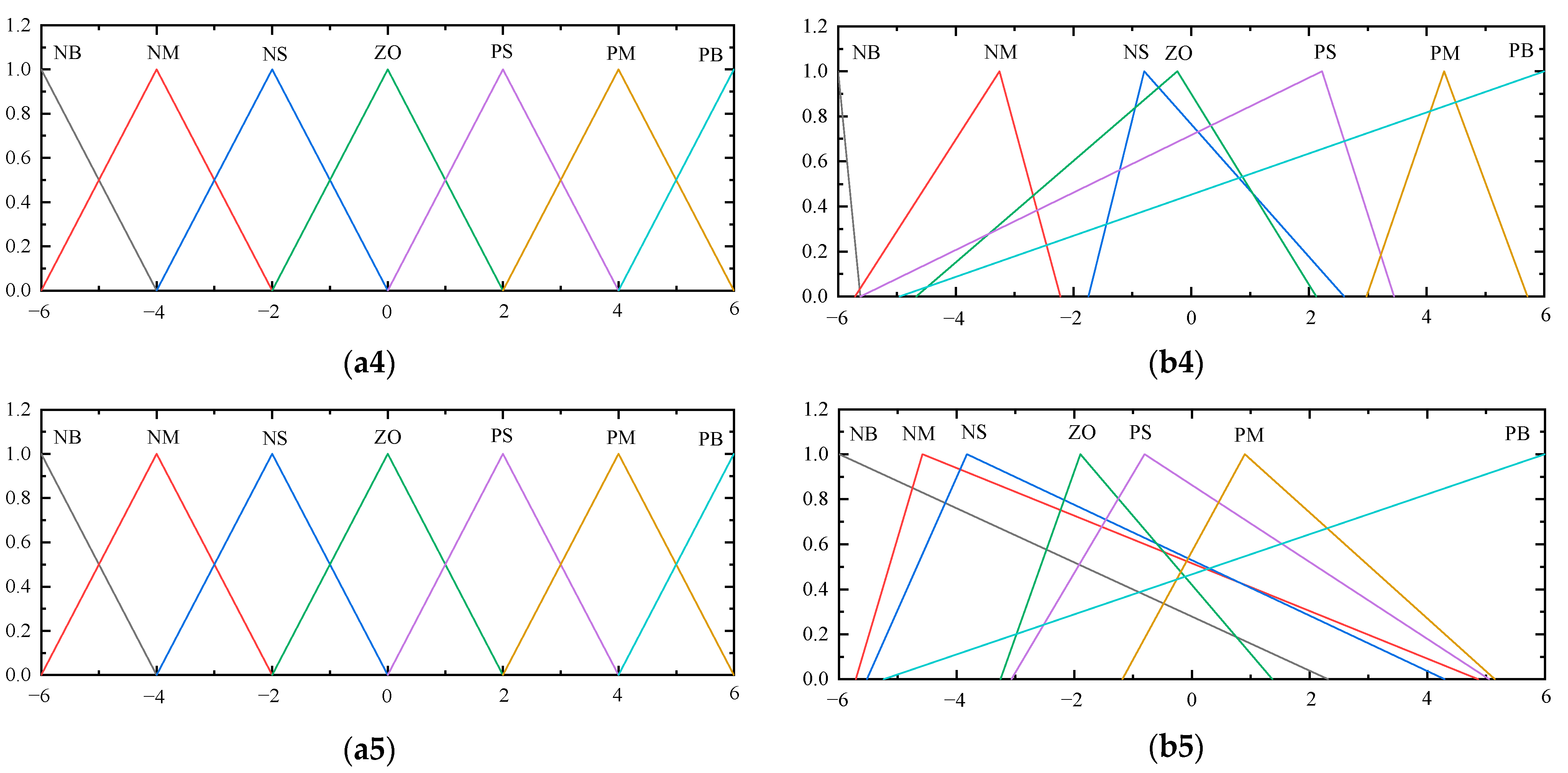
3.2.1. Genetic Coding and Trait Expression
3.2.2. Calculation of Fitness
3.2.3. Selection Operator
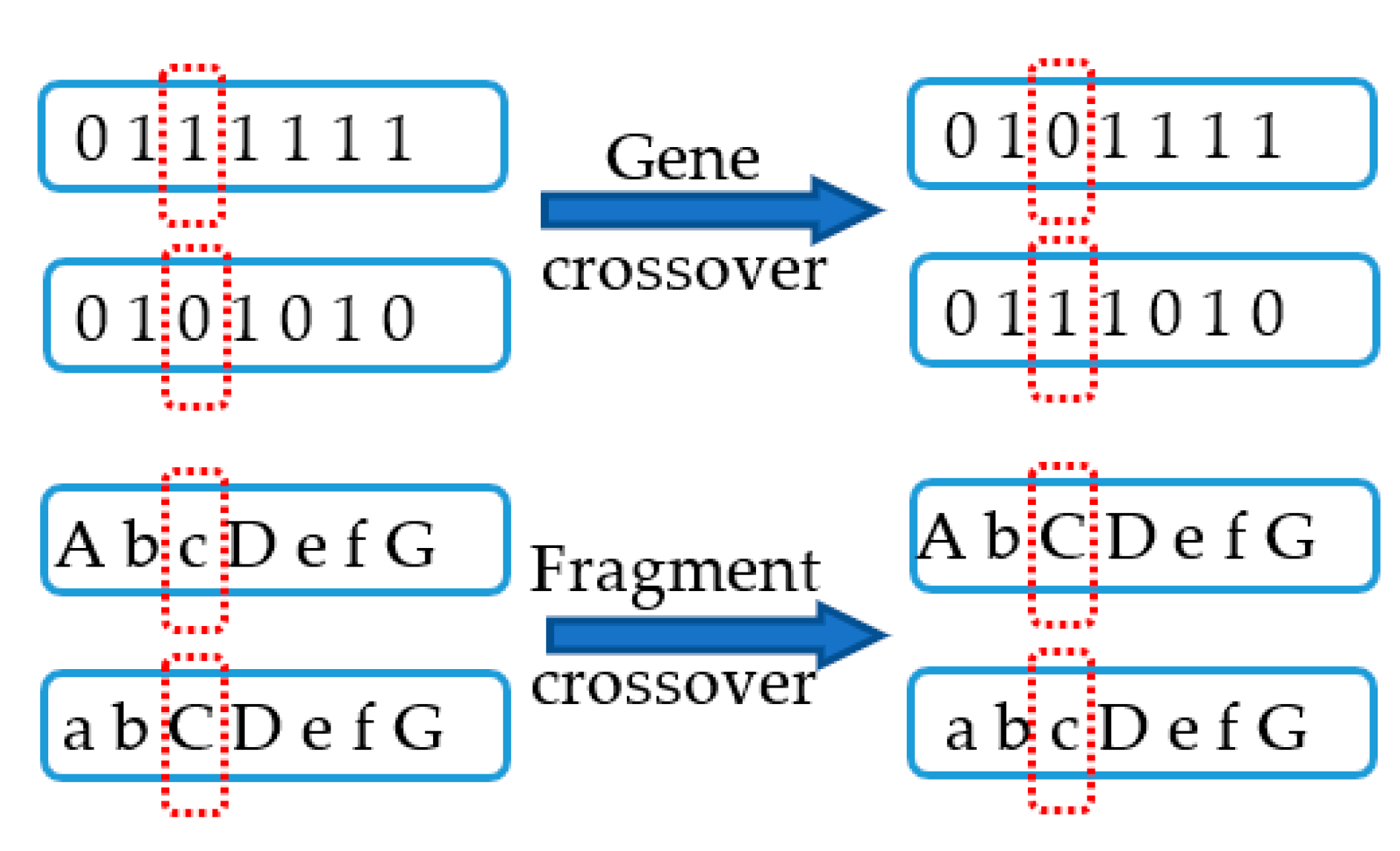
3.2.4. Crossover Operator
- Gene crossover. The same position of the 7-bit binary code of two “gene fragments” will be exchanged under a certain probability;
- Fragment crossover. All the genetic information carried by the two “gene segments” is exchanged together with a certain probability, including the “traits” of the parameters.
3.2.5. Mutation Operator
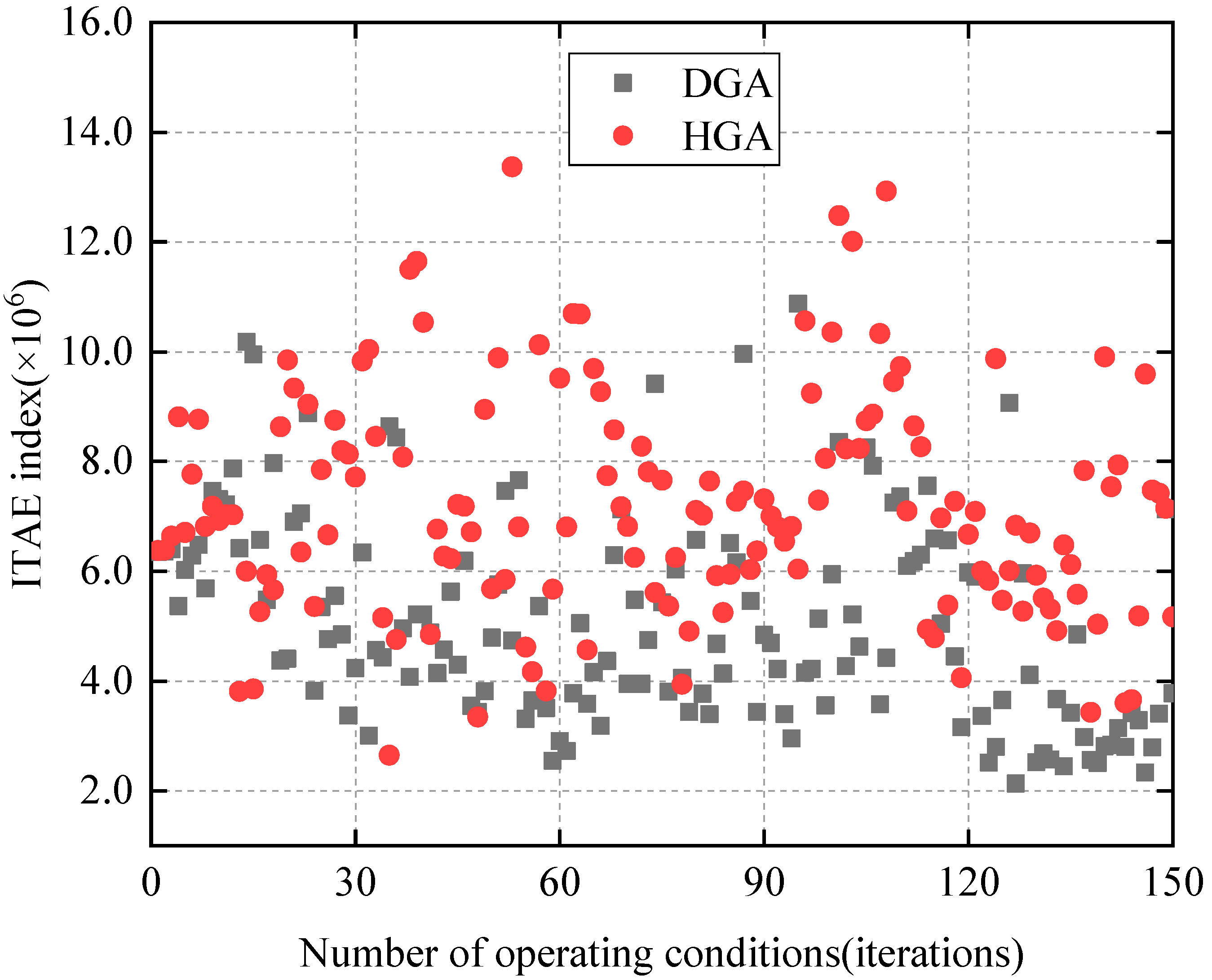
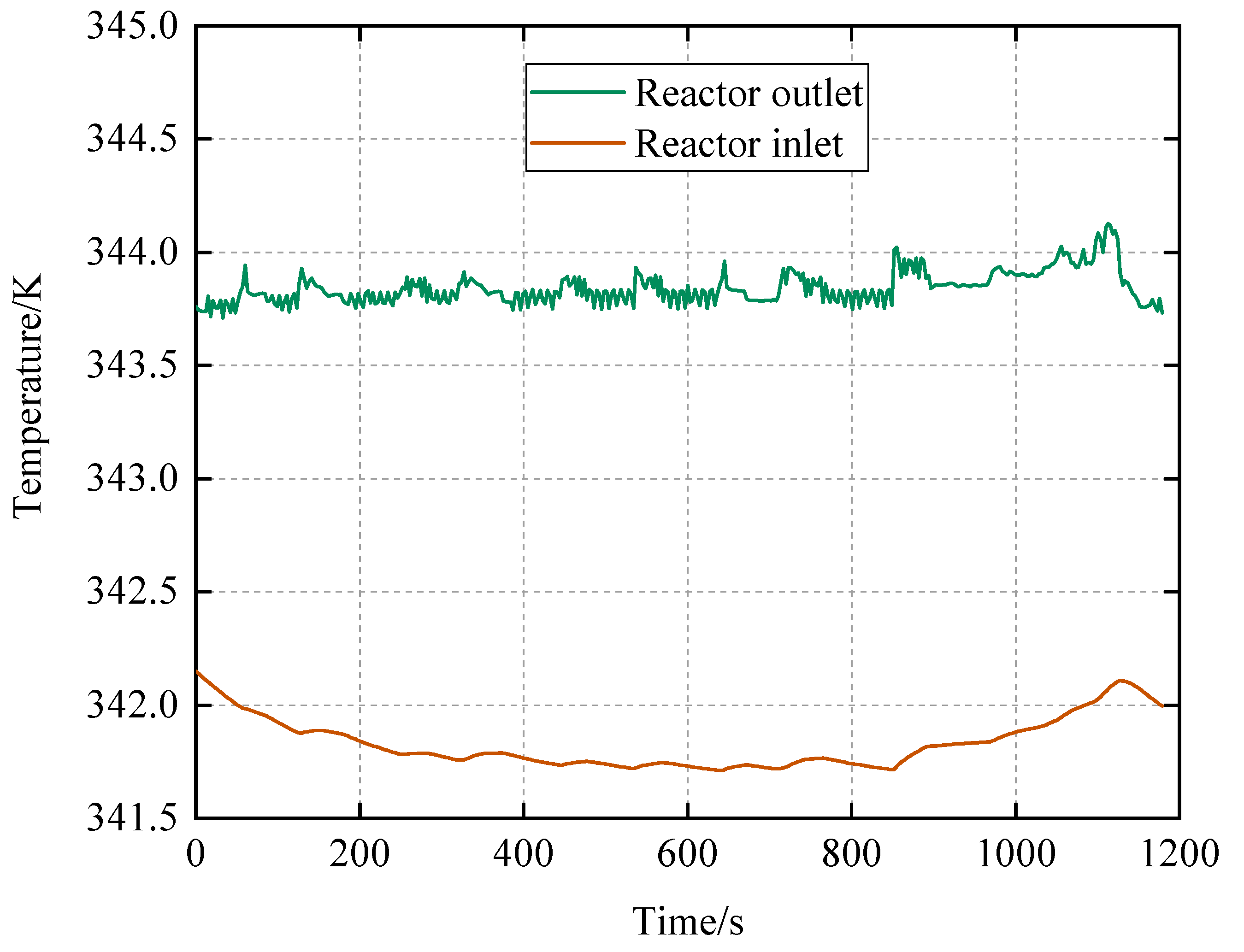
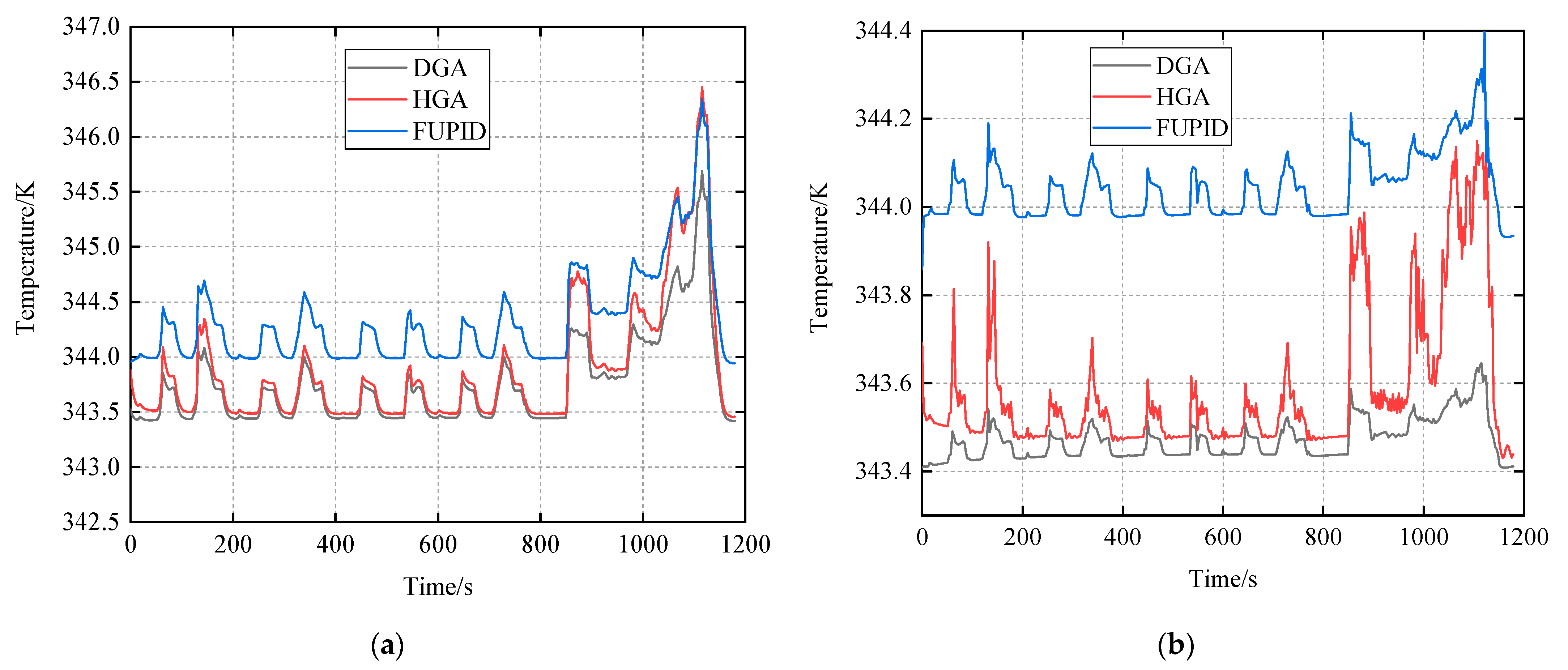
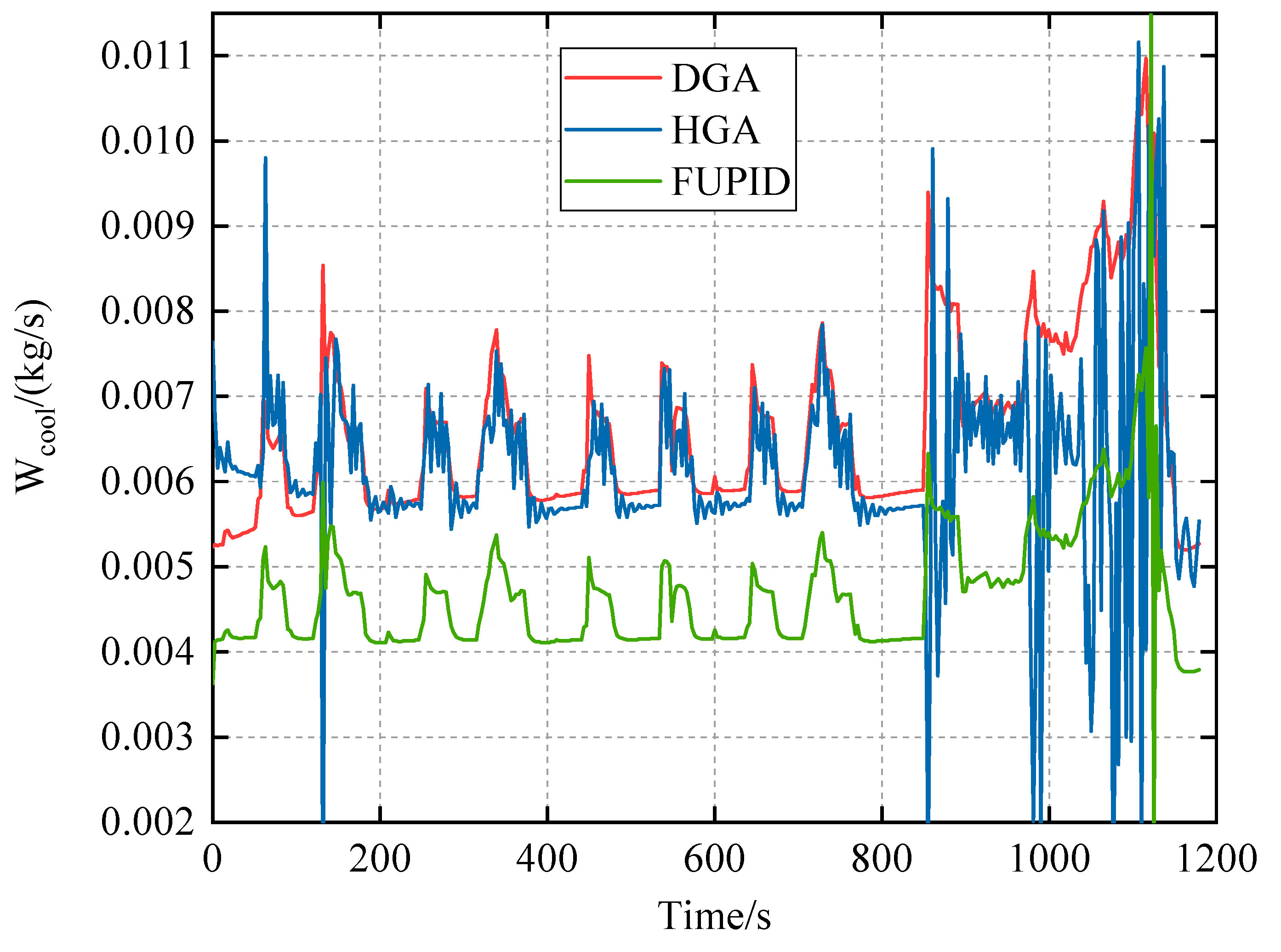
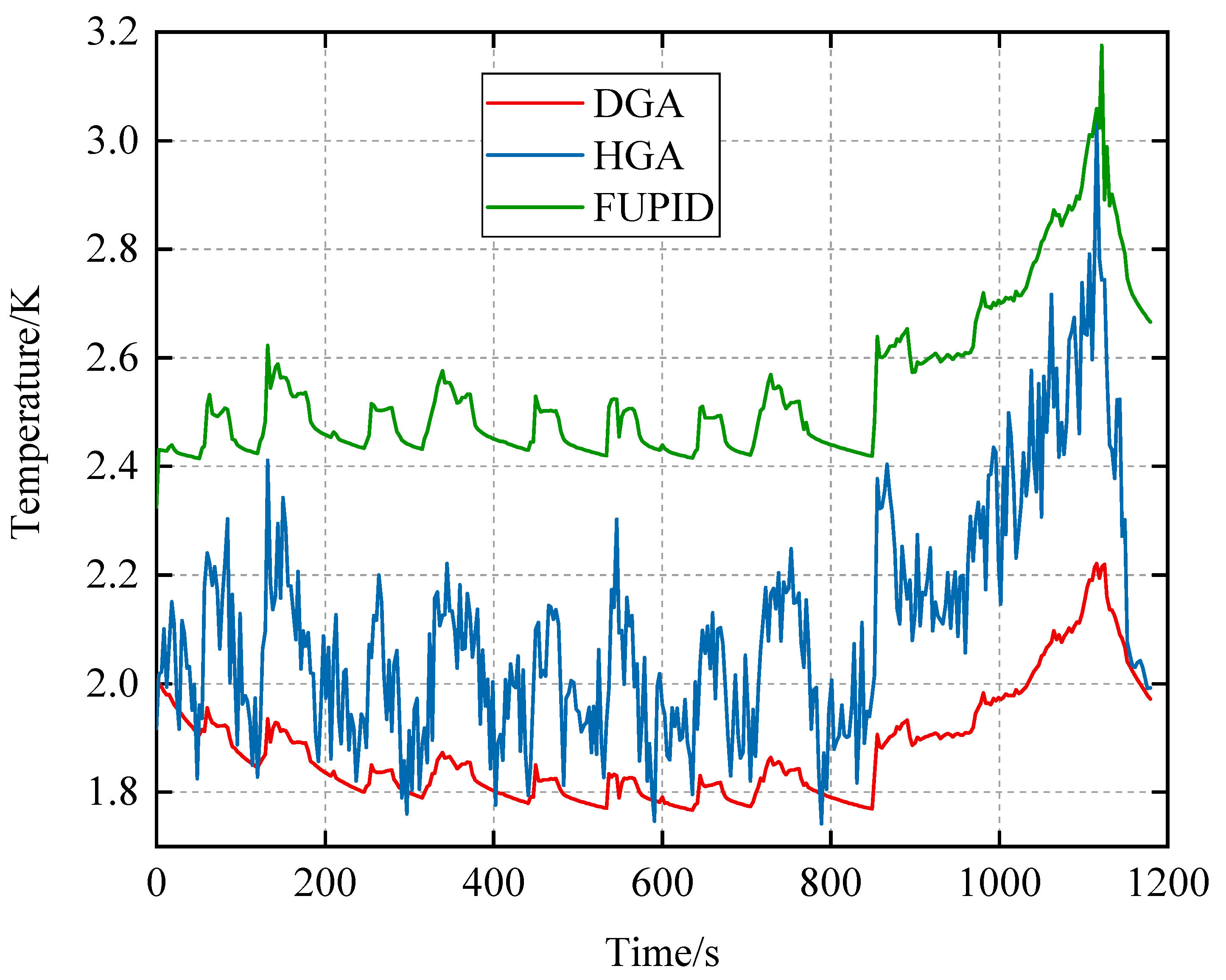
4. Simulation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEMFC | Proton exchange membrane fuel cell |
| MEA | Membrane electrode assembly |
| GA | Genetic algorithm |
| HGA | Haploid genetic algorithm |
| DGA | Diploid genetic algorithm |
| GDL | Gas diffusion layer |
| FEA | Finite element analysis |
| CFD | Computational fluid dynamics |
| LSA | Lightning search algorithm |
| FTT | Finite time thermodynamic |
| HT-PEMFC | High temperature proton exchange membrane fuel cell |
| PID | Proportional integral differential |
| LQR | Linear quadratic regulator |
| MPL | Micro-porous layer |
| ITAE | Integral of Time and Absolute Error |
| NEDC | New European Driving Cycle |
References
- Silaa, M.Y.; Barambones, O.; Derbeli, M.; Napole, C.; Bencherif, A. Fractional Order PID Design for a Proton Exchange Membrane Fuel Cell System Using an Extended Grey Wolf Optimizer. Processes 2022, 10, 450. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, H. Review of the Development of First-Generation Redox Flow Batteries: Iron-Chromium System. ChemSusChem 2022, 15, e202101798. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Al-Shankiti, I.; Ziani, A.; Idriss, H. Demonstration of green hydrogen production using solar energy at 28% efficiency and evaluation of its economic viability. Sustain. Energy Fuels 2021, 5, 1085–1094. [Google Scholar] [CrossRef]
- Agyekum, E.B.; Ampah, J.D.; Wilberforce, T.; Afrane, S.; Nutakor, C. Research Progress, Trends, and Current State of Development on PEMFC-New Insights from a Bibliometric Analysis and Characteristics of Two Decades of Research Output. Membranes 2022, 12, 1103. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Negro, E.; Nale, A.; Pagot, G.; Vezzu, K.; Zawodzinski, T.A.; Meda, L.; Gambaro, C.; Di Noto, V. An efficient barrier toward vanadium crossover in redox flow batteries: The bilayer [Nafion/(WO3)x] hybrid inorganic-organic membrane. Electrochim. Acta 2021, 378, 138133. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, S.; Li, K.; Zhou, J.; Zhang, C.; Wang, G.; Zhang, T. An Effective Force-Temperature-Humidity Coupled Modeling for PEMFC Performance Parameter Matching by Using CFD and FEA Co-Simulation. Sustainability 2022, 14, 14416. [Google Scholar] [CrossRef]
- Mohanty, B.; Madurai Elavarasan, R.; Hasanien, H.M.; Devaraj, E.; Turky, R.A.; Pugazhendhi, R. Parameters Identification of Proton Exchange Membrane Fuel Cell Model Based on the Lightning Search Algorithm. Energies 2022, 15, 7893. [Google Scholar] [CrossRef]
- Li, D.; Ma, Z.; Shao, W.; Li, Y.; Guo, X. Finite Time Thermodynamic Modeling and Performance Analysis of High-Temperature Proton Exchange Membrane Fuel Cells. Int. J. Mol. Sci. 2022, 23, 9157. [Google Scholar] [CrossRef]
- San Martín, I.; Ursúa, A.; Sanchis, P. Modelling of PEM Fuel Cell Performance: Steady-State and Dynamic Experimental Validation. Energies 2014, 7, 670–700. [Google Scholar] [CrossRef]
- O’Keefe, D.; El-Sharkh, M.Y.; Telotte, J.C.; Palanki, S. Temperature dynamics and control of a water-cooled fuel cell stack. J. Power Sources 2014, 256, 470–478. [Google Scholar] [CrossRef]
- Cheng, S.; Fang, C.; Xu, L.; Li, J.; Ouyang, M. Model-based temperature regulation of a PEM fuel cell system on a city bus. Int. J. Hydrog. Energy 2015, 40, 13566–13575. [Google Scholar] [CrossRef]
- Wang, Y.X.; Qin, F.F.; Ou, K.; Kim, Y.B. Temperature Control for a Polymer Electrolyte Membrane Fuel Cell by Using Fuzzy Rule. Energy Convers. 2016, 31, 667–675. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Silaa, M.Y.; Napole, C. Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System. Actuators 2020, 9, 105. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Derbeli, M.; Barambones, O.; Cheknane, A. Design and Implementation of High Order Sliding Mode Control for PEMFC Power System. Energies 2020, 13, 4317. [Google Scholar] [CrossRef]
- Qin, Y.; Sun, L.; Hua, Q.; Liu, P. A Fuzzy Adaptive PID Controller Design for Fuel Cell Power Plant. Sustainability 2018, 10, 2438. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Tao, Q.; Bargal, M.H.S.; Yu, M.; Yuan, X.; Su, C. Thermal Management System Modeling and Simulation of a Full-Powered Fuel Cell Vehicle. J. Energy Resour. 2020, 142, 061304. [Google Scholar] [CrossRef]
- Chen, M.; Zhao, C.; Sun, F.; Fan, J.; Li, H.; Wang, H. Research progress of catalyst layer and interlayer interface structures in membrane electrode assembly (MEA) for proton exchange membrane fuel cell (PEMFC) system. eTransportation 2020, 5, 100075. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Barambones, O.; Bencherif, A. A Novel Adaptive PID Controller Design for a PEM Fuel Cell Using Stochastic Gradient Descent with Momentum Enhanced by Whale Optimizer. Electronics 2022, 11, 2610. [Google Scholar] [CrossRef]
- Park, D.; Ham, S.; Sohn, Y.; Choi, Y.; Kim, M. Mass transfer characteristics according to flow field and gas diffusion layer of a PEMFC metallic bipolar plate for stationary applications. Int. J. Hydrog. Energy 2022, 48, 304–317. [Google Scholar] [CrossRef]
- Frano, B. PEM Fuel Cells: Theory and Practice, 2nd ed.; Elsevier Academic Press: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Silaa, M.Y.; Derbeli, M.; Barambones, O.; Napole, C.; Cheknane, A.; Gonzalez De Durana, J.M. An Efficient and Robust Current Control for Polymer Electrolyte Membrane Fuel Cell Power System. Sustainability 2021, 13, 2360. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Y.; Han, C.; Zhang, H. Stress response and contact behavior of PEMFC during the assembly and working condition. Int. J. Hydrog. Energy 2021, 46, 30467. [Google Scholar] [CrossRef]
- Roudgar Saffari, P.; Salarian, H.; Lohrasbi, A.; Salehi, G.; Khoshgoftar Manesh, M.H. Optimization of a Thermal Cracking Reactor Using Genetic Algorithm and Water Cycle Algorithm. ACS Omega 2022, 7, 12493–12508. [Google Scholar] [CrossRef] [PubMed]
- Chatrattanawet, N.; Hakhen, T.; Kheawhom, S.; Arpornwichanop, A. Control structure design and robust model predictive control for controlling a proton exchange membrane fuel cell. Clean. Prod. 2017, 148, 934. [Google Scholar] [CrossRef]
- Hu, P.; Cao, G.; Zhu, X.; Hu, M. Coolant circuit modeling and temperature fuzzy control of proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2010, 35, 9110. [Google Scholar] [CrossRef]
- Kandi, D.M.; Soleymani, M.; Ghadimi, A.A. Designing an Optimal Fuzzy Controller for a Fuel Cell Vehicle Considering Driving Patterns. Sci. Iran. 2016, 23, 218–227. [Google Scholar] [CrossRef]
- Hu, D.; Wang, Y.; Li, J.; Yang, Q.; Wang, J. Investigation of optimal operating temperature for the PEMFC and its tracking control for energy saving in vehicle applications. Energy Convers. Manag. 2021, 249, 114842. [Google Scholar] [CrossRef]
- AbouOmar, M.S.; Su, Y.; Zhang, H.; Shi, B.; Wan, L. Observer-based interval type-2 fuzzy PID controller for PEMFC air feeding system using novel hybrid neural network algorithm-differential evolution optimizer. Alex. Eng. J. 2022, 61, 7353. [Google Scholar] [CrossRef]






| Parameter | Name | Value |
|---|---|---|
| The end plate density | 1300 kg/m3 | |
| The end plate area | 0.0064 m2 | |
| The end plate thickness | 0.01 m | |
| Specific heat capacity of the end plate | 1200 J/(kg·K) | |
| Heat transfer coefficient (L1, air) | 16.44 W/m2·K | |
| Heat transfer coefficient (L1, L2) | 481.18 W/m2·K | |
| Specific heat capacity of mixing (air, liq) | 1395 J/(kg·K) | |
| Density of the bipolar plate | 8000 kg/m3 | |
| Area of the bipolar plate | 0.0049 m2 | |
| Thickness of the bipolar plate | 0.005 m | |
| Specific heat capacity of the bipolar plate | 500 J/(kg·K) | |
| The MEA layer density | 1300 kg/m3 | |
| The MEA layer area | 0.0036 m2 | |
| The MEA layer thickness | 0.0015 m | |
| Specific heat capacity of the bipolar plate | 864 J/(kg·K) | |
| Specific heat capacity (water) | 4200 J/(kg·K) | |
| Length of gas passage | 1768.8 mm | |
| Gas passage section perimeter | 5.69 mm | |
| Gas passage section area | 2.00 mm2 | |
| Gas density (air) | 1.24 kg/m3 | |
| Aerodynamic viscosity (air) | 1.71 × 10−5 Pa·s | |
| Prandtl constant (air) | 0.708 | |
| Conductivity coefficient (air) | 0.0263 W/m2·K | |
| Length of liquid runner | 381 mm | |
| Liquid runner section perimeter | 7.62 mm | |
| Section area of liquid runner | 3.23 mm2 | |
| Liquid density (water) | 1000 kg/m3 | |
| Hydrodynamic viscosity (water) | 3.79 × 10−4 Pa·s | |
| Prandtl constant (water) | 7 | |
| Conductivity coefficient (water) | 0.602 W/m2·K | |
| The number of electrons exchanged by chemical reactions | 2 | |
| Faraday constant | 96485 C/mol | |
| Coolant mass (Water tank) | 2.5 kg | |
| Heat transfer coefficient (coolant, Tank wall) | 0.64 W/m2·K | |
| Coolant mass (radiator) | 0.2 kg |
| Working Parameter | Value Range |
|---|---|
| Current density | 0~0.7 A/cm2 |
| Air and hydrogen flow | 1~20/min, 1~5 L/min |
| Initial coolant temperature | 60 °C |
| Gas pressure | 1.5 bar |
| Gas humidity | 90% |
| e | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| ec | ||||||||
| NB | PB | PB | PM | PM | PM | ZO | ZO | |
| NM | PB | PM | PM | PM | PS | ZO | ZO | |
| NS | PM | PM | PS | PS | ZO | NS | NS | |
| ZO | PM | PS | PS | ZO | NS | NS | NM | |
| PS | PS | ZO | ZO | NS | NM | NM | NM | |
| PM | PS | NS | NS | NS | NM | NM | NB | |
| PB | ZO | NS | NS | NM | NM | NB | NB | |
| e | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| ec | ||||||||
| NB | NB | NB | NM | NM | NS | NS | ZO | |
| NM | NM | NM | NM | NS | NS | ZO | ZO | |
| NS | NM | NM | NS | ZO | ZO | ZO | PS | |
| ZO | NS | NS | NS | ZO | PS | PM | PM | |
| PS | NS | NS | ZO | PS | PS | PM | PB | |
| PM | ZO | ZO | ZO | PS | PM | PB | PB | |
| PB | ZO | ZO | PS | PM | PM | PB | PB | |
| e | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| ec | ||||||||
| NB | NB | NB | NM | NM | NS | NS | ZO | |
| NM | NM | NM | NM | NS | NS | ZO | ZO | |
| NS | NM | NM | NS | ZO | ZO | ZO | PS | |
| ZO | NS | NS | NS | ZO | PS | PM | PM | |
| PS | NS | NS | ZO | PS | PS | PM | PB | |
| PM | ZO | ZO | ZO | PS | PM | PB | PB | |
| PB | ZO | ZO | PS | PM | PM | PB | PB | |
| Number of Iterations | GA | Excellent | Good | Bad | Max | Min |
|---|---|---|---|---|---|---|
| 1~30 | haploid | 2 | 6 | 22 | 9.8 | 3.80 |
| diploid | 2 | 14 | 14 | 10.1 | 3.37 | |
| 31~60 | haploid | 3 | 10 | 17 | 13.3 | 2.64 |
| diploid | 9 | 17 | 4 | 8.64 | 2.54 | |
| 61~90 | haploid | 1 | 10 | 19 | 10.6 | 3.94 |
| diploid | 11 | 18 | 1 | 9.95 | 2.72 | |
| 91~120 | haploid | 0 | 5 | 25 | 12.9 | 4.05 |
| diploid | 5 | 16 | 9 | 10.8 | 2.94 | |
| 121~150 | haploid | 2 | 15 | 13 | 9.90 | 3.42 |
| diploid | 24 | 3 | 3 | 9.06 | 2.13 | |
| 1~150 | haploid | 8 | 46 | 96 | 13.3 | 2.64 |
| diploid | 51 | 68 | 31 | 10.8 | 2.13 |
| Maximum Temperature Difference | Mean Temperature Difference | Variance | |
|---|---|---|---|
| DGA | 2.22 | 1.87 | 0.010 |
| HGA | 3.03 | 2.09 | 0.046 |
| FUPID | 3.17 | 2.54 | 0.020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; Qin, D.; Chen, B.; Wang, T.; Wu, H. Thermal Management of Fuel Cells Based on Diploid Genetic Algorithm and Fuzzy PID. Appl. Sci. 2023, 13, 520. https://doi.org/10.3390/app13010520
Zhao R, Qin D, Chen B, Wang T, Wu H. Thermal Management of Fuel Cells Based on Diploid Genetic Algorithm and Fuzzy PID. Applied Sciences. 2023; 13(1):520. https://doi.org/10.3390/app13010520
Chicago/Turabian StyleZhao, Ruikang, Dongchen Qin, Benhai Chen, Tingting Wang, and Hongxia Wu. 2023. "Thermal Management of Fuel Cells Based on Diploid Genetic Algorithm and Fuzzy PID" Applied Sciences 13, no. 1: 520. https://doi.org/10.3390/app13010520
APA StyleZhao, R., Qin, D., Chen, B., Wang, T., & Wu, H. (2023). Thermal Management of Fuel Cells Based on Diploid Genetic Algorithm and Fuzzy PID. Applied Sciences, 13(1), 520. https://doi.org/10.3390/app13010520





