Abstract
Dexterous object manipulation using anthropomorphic robot hands is of great interest for natural object manipulations across the areas of healthcare, smart homes, and smart factories. Deep reinforcement learning (DRL) is a particularly promising approach to solving dexterous manipulation tasks with five-fingered robot hands. Yet, controlling an anthropomorphic robot hand via DRL in order to obtain natural, human-like object manipulation with high dexterity remains a challenging task in the current robotic field. Previous studies have utilized some predefined human hand poses to control the robot hand’s movements for successful object-grasping. However, the hand poses derived from these grasping taxonomies are limited to a partial range of adaptability that could be performed by the robot hand. In this work, we propose a combinatory approach of a deep transformer network which produces a wider range of natural hand poses to configure the robot hand’s movements, and an adaptive DRL to control the movements of an anthropomorphic robot hand according to these natural hand poses. The transformer network learns and infers the natural robot hand poses according to the object affordance. Then, DRL trains a policy using the transformer output to grasp and relocate the object to the designated target location. Our proposed transformer-based DRL (T-DRL) has been tested using various objects, such as an apple, a banana, a light bulb, a camera, a hammer, and a bottle. Additionally, its performance is compared with a baseline DRL model via natural policy gradient (NPG). The results demonstrate that our T-DRL achieved an average manipulation success rate of 90.1% for object manipulation and outperformed NPG by 24.8%.
1. Introduction
Dexterous object manipulation via anthropomorphic robot hands has recently gained lots of interest in the field of natural object manipulations across the areas of healthcare, smart homes, and smart factories [,,,,,]. However, it is challenging for robots to achieve the dexterity of grasping and manipulation seen in human movements [,,,,,]. The complexity of these movements is difficult to grasp naturally due to the high Degree of Freedom (DoF) of an anthropomorphic robot hand. In nature, before grasping an object, humans consider its shape, orientation, and position (i.e., object affordance) in the environment. Humans naturally grasp objects through an intelligence that estimates suitable hand poses based on the object affordance. Humans perform natural object-grasping by controlling finger movements from learned hand poses. Thus, natural hand pose estimation is an important factor for manipulating intelligence by providing proper guidelines that enable the robot hand to learn and imitate human finger movements. Therefore, to attain such a level of complex, dexterous manipulation over tasks, the robot hand pose estimation should be incorporated into the robot intelligence.
In recent studies, Deep Reinforcement Learning-based (DRL) techniques have demonstrated their capability in controlling the robot fingers for dexterous manipulations of various objects, utilizing the databases of human hand poses and object affordances [,,,,]. In [,,,,], the authors presented supervised learning techniques with large-scale hand pose datasets to train the robot hand controller, achieving object manipulation. However, these approaches require collecting hand pose demonstrations for each object. Extending the knowledge of these approaches for all possible objects remains a challenging task and the generalization of these approaches is difficult [,,]. For dexterous manipulation with the anthropomorphic robot hand, it is essential to have a natural hand pose estimator without relying on human demonstrations. The robot hand needs intelligence to estimate high-dimensional information (i.e., 24-DoF hand poses) from low-dimensional information (i.e., 6-DoF object affordance for location and orientation).
Natural hand pose estimation for an anthropomorphic robot hand has been generally derived from a grasping taxonomy with predefined hand poses (e.g., top-down or lateral grasps) []. This hand pose estimation has been shown as a helpful control technique for finger movement for some objects [,,,,,]. For instance, in [], the object affordance information of shape, pose, and orientation from a partial point cloud was used in a DRL policy to derive the best grasping poses for either the top-down or parallel-side grasping. To cover the variability of human grasping movements, deep learning techniques have been recently proposed to estimate the natural hand poses according to the various object shapes [,,,,,]. In [], an autoencoder network was used to estimate the natural hand poses from the point clouds of the object. In [,], a GAN approach was used to estimate the natural hand pose in which the encoder- and decoder-based neural networks were adopted to estimate natural hand poses. However, the estimated hand poses were upside down or unnatural and, therefore, not much associated with the object affordance. For autonomous grasping and manipulation that simulates human movements, a robust estimation of natural hand pose is essential.
Recently, deep transformer networks have been actively used in areas of data estimation, including natural language processing, bioinformatics, and hand pose estimation in which the transformer network was used to estimate hand joints from 3D hand mesh data [,,,,,,,,]. The transformer network has typically shown better performance in estimating high-dimensional information from low-dimensional information, in comparison to various deep neural networks (i.e., autoencoder, GAN, and LSTM) []. The transformer network estimates the output by modeling the information between the input and output through learning the inherent dependencies of each. The attention mechanism in the transformer demonstrates particularly excellent performance in exploring the dependency of the input and output data by modeling the correlation between them []. In this work, the transformer network estimates the high-dimensional natural hand poses from the low-dimensional object affordances.
Recently, reinforcement learning approaches were introduced to train an anthropomorphic robot hand with the estimated natural hand poses [,]. Furthermore, Demo Augmented Policy Gradient (DAPG) was introduced []. Previous works estimated hand poses and used them to initialize finger parameters at the beginning of DRL training through imitation learning. In [], an object grasping intelligence framework was proposed and trained for three objects (an apple, a potato, and a mustard bottle) for an anthropomorphic robot hand. Grasping of both the apple and potato was successful but grasping of the mustard bottle failed since the thumb and other fingers of the robot hand could not close properly, due to the estimation of an unnatural hand pose. In previous studies it is noted that a DRL methodology with a robust transformer network has not yet been reported.
A transformer network incorporated into a DRL policy should improve dexterous object manipulation with an anthropomorphic robot hand. Furthermore, in the policy training phase of DRL, imitation learning and reward function are used to train the robot’s grasping intelligence through demonstrations. Imitation learning can help in early-stage learning, and the reward function carries out the learning process until its completion. In the design of the reward function, reward shaping was employed by utilizing various categories of information, such as object location, robot hand location, and hand pose.
In this work, we propose a novel methodology of dexterous object manipulation with an anthropomorphic robot hand via a transformer-based DRL with a novel reward shaping-function. The proposed transformer network estimates natural hand poses from object affordance to guide the learning process of DRL. The transformer network estimates high-dimensional information (i.e., 24-DoF hand poses) from low-dimensional information (i.e., 6-DoF object affordance for location and orientation). This reduction provides natural hand poses for the movement of an anthropomorphic robot hand. Then, the DRL algorithm utilizes the estimated natural hand poses in the reward-shaping function and learns dexterous object manipulation.
2. Methods
The proposed T-DRL intelligent framework for object grasping is composed of two main components illustrated in Figure 1. First, the transformer network estimates an optimal natural hand pose for the given object’s 3D point cloud. Second, the DRL policy learns to control the movements of an anthropomorphic robot hand for object manipulation.
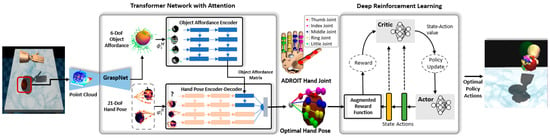
Figure 1.
Overview of the proposed T-DRL. The DRL training for object manipulation using the estimated optimal hand pose from the transformer network.
We leverage the capabilities of the transformer network to infer the optimal natural hand pose from the object affordance. The object affordance is represented by a 3-DoF position and orientation (roll, yaw, and pitch) of an anthropomorphic robot hand. The optimal grasping hand pose from the transformer network had 21-DoF joint positions, corresponding to a five-fingered anthropomorphic hand. We leverage the DRL to train the anthropomorphic robot hand for object manipulation with a natural hand pose. The DRL is composed of a policy that performs robot actions and a reward function that evaluates and updates the policy parameters. The proposed DRL uses the estimated optimal hand pose to achieve natural grasping and relocation of various objects. The reward function is configured such that the estimated hand pose is set as a goal, and the reward increases as the joints of the anthropomorphic robot hand are aligned with the estimated hand pose. The policy updates the hand poses (i.e., actions) of the anthropomorphic robot hand (i.e., agent) so that the value of the reward function increases for natural grasping. The proposed T-DRL is trained to achieve natural grasping and relocation for six objects. In our work, we selected objects based on the shape property representing most of the 24 objects in the ContactPose DB. Therefore, the proposed T-DRL trained in this work can be generalized for objects with similar shapes.
2.1. Databases for T-DRL Trainings
To derive the optimal hand poses from the transformer network and incorporate them into the proposed DRL, this work utilizes the databases of a 6-DoF object affordance and 21-DoF hand pose.
The information of the 6-DoF object affordance is derived from GraspNet [] which computes the point clouds of an object and produces 6-DoF affordance information. The probability of possible grasping success rates is determined according to the object shape and hand pose with a parallel gripper, as shown in Figure 1. GraspNet [] is trained with 206 objects of five categories (boxes, cylinders, mugs, bottles, and bowls) and trained based on a variational autoencoder, which estimates a predefined number of grasping poses in the Cartesian coordinates. The 6-DoF object affordance is denoted as in this study, where , with denotes the number of grasps and each ϕi ∊ ℝ6 denotes the position and orientation of an anthropomorphic robot hand attempting to grasp the object.
The information of the 21-DoF hand pose, corresponding to the joint angles of a five-fingered anthropomorphic hand, is derived from the ContactPose database []. This database consists of grasping demonstrations made by human hands, holding various household objects. The database also includes the point clouds of objects with the corresponding 3D coordinates of the 21 finger joints used in a human hand pose. The grasping data was collected with two intentional grasps of ‘use’ (i.e., using the object after grasping) and ‘handoff’ (i.e., handing over the object after grasping) for fifty different objects. We selected objects representing six geometric shapes (spherical, rod, cube, oval, cylindrical, and curved) from the available 24 objects, including: apple, banana, camera, hammer, bottle, and light bulb. Each object has a total of 25 grasping demonstrations that were reduced to 10 corresponding to the right hand, with their functional intent being ‘use’. Henceforth, the extracted 21-DoF joints that coordinate the hand poses are denoted as () where denotes the number of demonstrations and each φi ∊ ℝ21 denotes the joint angles in the hand pose reference system.
As input to the transformer network, we need a data tuple containing five 21-DoF hand poses and five 6-DoF object affordances. Two of the ten 21-DoF hand pose data for each object were classified for testing and eight for training. One tuple was formed by matching with the 6-DoF generated at the exact same location as the center position of the 21-DoF. By randomly selecting five of the eight tuples, a list of approximately 16,500 unique tuples is generated from the combination of 6-DoF object affordance and 21-DoF hand poses for the six objects.
2.2. Object Manipulation T-DRL
In Figure 2, we have illustrated the two stages for training and testing of the proposed method. For training, Figure 2a illustrates the inputs for the transformer network, including a set of 6-DoF object affordances and 21-DoF hand poses. The network estimates the optimal hand pose by computing the attention value between the two inputs. Attention value indicates the similarity between information in the input and is used to estimate the 21-DoF hand pose in the decoder. In the testing phase, Figure 2b illustrates the process of estimating hand pose corresponding to the 6-DoF object affordance generated from the environment. In testing, a Mask R-CNN [] with a ResNet-50-FPN backbone pre-trained with the COCO object dataset [] estimates a pixel-level mask for the object in the captured RGBD image. Then, this mask is used to segment the image and extract a point cloud with a partial view of the object. The point cloud goes through GraspNet to obtain the object affordance and, combined with a set of hand poses from the ContactPose database, the pre-trained transformer network estimates the optimal hand pose of 21-DoF .
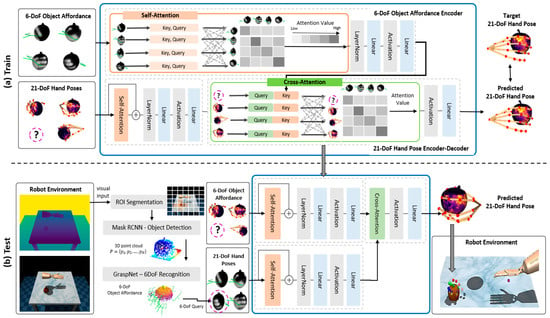
Figure 2.
The architecture of the transformer Network. (a) In Training, it takes both 6-DoF object affordance and 21-DoF hand pose as input to estimate an optimal 21-DoF hand pose for grasping the object. (b) At test time, 6-DoF object affordance is generated through GraspNet from an RGB-D image taken in the environment. Then, the trained transformer network estimates the optimal hand pose for generated object affordance.
2.2.1. Transformer Network with Attention Mechanism
The transformer network illustrated in Figure 2a is composed of two modules to derive an optimal hand pose for natural grasping: the 6-DoF object affordance encoder and the 21-DoF hand pose encoder–decoder.
The object affordance encoder first uses a self-attention mechanism to discover the local relationship between every element in the source input of 6-DoF object affordance. The attention layer in the encoder uses three independent feedforward networks to transform the input (i.e., the hand pose of 21-DoF and object affordance of 6-DoF) into query (Q), key (K), and value (V) tensors of dimension dq, dv and , respectively. In the self-attention layer, Q, K, and V are calculated from each encoder input. Then, the self-attention layer finds the correlation between encoder inputs. Then, calculating the attention value, the query and key tensors are dot-produced and scaled. A SoftMax function then obtains the attention probabilities and the resulting tensor takes a linear projection using the value tensor. The attention is then computed with the following equation []:
The computed attention weights represent the relative importance of the input in the sequence (keys) for each particular output (query) and multiply it by a dynamic weight (value). To improve the range of input features that could be learned via attention, the multi-head attention runs multiple self-attention layers in parallel and learns different projections of the input data. These are expressed as:
where linear transformations , , , and are parameter matrices. The parameter represents the number of subspaces we compute with . Therefore, the two self-attention layers shown in Figure 2 compute the attention matrix to find similarity within the 6-DoF object affordance and 21-DoF hand pose individually. The self-attention output is an embedding of dimension that carries the mutual information of each element in the input. Then, a residual connection expands this embedding, concatenating with the original object affordance. Later, a normalization layer and two feedforward networks, both with a non-linear activation function, output the encoded representation (attention value) of the object affordance from the encoder. The hand pose encoder does the same job as the object affordance encoder, with the target input of the hand pose being 21-DoF. The output of the hand pose encoder is an embedding vector of dimension , which computed the mutual information of the input elements through a self-attention mechanism, using a residual connection and two feedforward layers.
The outputs of both encoders are used as input for the hand pose decoder. The cross-attention layer learns to map between the encoded values of the hand pose of 21-DoF and the object affordance of 6-DoF. Through this mapping the network can estimate the optimal hand pose for the object affordance . The decoder uses the cross-attention mechanism. In the cross-attention mechanism, K and V are calculated from 6-DoF object affordances and Q is calculated from 21-DoF hand poses. Then, the cross-attention layer discovers the relationship between 6-DoF object affordances and 21-DoF hand poses. The multi-head attention expands the ability of the model to focus on different elements from the object affordances of 6-DoF and hand poses of 21-DoF in parallel. It does this by estimating from 6-DoF to 21-DoF through the attention value calculated in the decoder. Later, this output will be used in the shaping-reward funtion for training the DRL policy.
2.2.2. DRL with Reward Shaping
The DRL policy illustrated in Figure 1 is trained to control the robot’s movements for generating a natural grasping hand pose for object manipulation. The model-free DRL policy πθ(at,st) describes the control problem of the robot hand as a Markov Decision Process , where s ∊ S, S ⊆ ℝn is an observation vector describing the current location of the robot hand and object in Cartesian coordinates. The agent’s actions a ∊ A, A ⊆ ℝm control the robot hand’s movements to interact with the object. A reward function evaluates the completeness of the manipulation task.
To optimize the parameters of the DRL policy we follow the implementation of natural policy gradient (NPG) in [], which computes the policy gradient as:
Then, it pre-conditions the gradient with the Fisher Information Matrix, and makes the following normalized gradient ascent update:
where is the step size. The advantage function Aπ is the difference between the value for the given state–action pair and the value function of the state. The NPG in [] uses the general advantage estimator (GAE), which is defined as:
where, = rt + γV(st+1) − V(st) defines the temporal difference residual between consecutive predictions, assuming a value function that approximates the true value function, . Both the policy and value networks share the same architecture and were defined by a three-layer neural network with 64 units in the hidden layers.
The reward function maximizes the sum of the expected rewards at the end of each training episode. This function measures the similarity of the robot hand’s pose to the optimal hand pose estimated by the transformer network. It also evaluates how close the object is to the target location at the end of an episode. Defining the reward function to solve the manipulation tasks is expressed as follows:
where is the mean squared error between the hand pose of 21-DoF, derived from the transformer network, and the robot hand’s pose after following the policy actions. Empirically, we found that by optimizing for during the first 150 timesteps of each iteration, the policy could learn how to shape the robot hand before grasping an object. The second term of the reward function minimizes the distance between the hand and the object and the distance of the object to the target location . The values of are constant weights to balance the total reward, , which measures the completeness of the task. The value of gives a larger reward when at the end of the episode the object finishes near the target location.
2.3. Training and Validation of T-DRL
The proposed method is trained for natural object manipulation, including grasping and relocating of the randomly located object to a random target position.
2.3.1. Training and Validation of Transformer Network
For each training step, a minibatch was sampled from the tuples. More specifically, we defined the input tuple as and hand pose output as . We minimized the MSE loss function between the ground truth and predicted hand pose using the Adam optimizer with a learning rate of , . The model was trained until the MSE error for every joint between the predicted and ground truth hand pose was lower than 5%. We validated the transformer network by MSE between the estimated hand joint and the ContactPose hand joint. Additionally, we compared the joint angle’s range distribution with the dataset and the estimated hand pose.
2.3.2. Training and Validation of T-DRL
The T-DRL policy updates its parameters by computing the sum of the rewards from Equation (6). Learning is optimized using the natural policy gradient (NPG) described in []. First, for each object two policies were initialized with a random normal distribution and trained for 5000 iterations, each iteration with episodes, and a time horizon of time steps. At the start of each episode the transformer network computes the 21-DoF hand pose for grasping the object in the simulation environment.
We have compared our approach with a baseline DRL (i.e., the NPG algorithm) in Section 2.2.2 using a sparse reward of the reward function . After training, we compared the probability of success of successful grasping and relocation (i.e., over a threshold that indicates the policy has learned to grasp and move the object to the target location) among 100 trials of NPG and T-DRL.
3. Results
3.1. Simulation Environments
The experiments were conducted in a simulation environment based on the MuJoCo physics engine. MuJoCo is a robotics simulation package providing tools for research and development, such as robotic kinematics, objects models, and articulated structures interacting with the environment for machine learning applications []. The simulated anthropomorphic robot hand is modeled after the ADROIT robot hand [] and has a 3-DoF wrist and 21-DoF hand pose with five fingers for dynamic and dexterous manipulations. The first, middle, ring, and little fingers have 4-DoF, meanwhile the thumb has 5-DoF. Each joint is equipped with a joint angle sensor and a haptic sensor. The movements are controlled via a position control actuator.
3.2. Hand Pose Estimation via Transformer Network
After training the transformer network, it was tested on 250 tuples generated from the combination of 6-DoF object affordance and 21-DoF hand poses for the six objects. Figure 3 shows the distribution range of the joint angles alongside the estimated hand pose and ground truth. For each finger in the anthropomorphic robot hand, the ground truth distribution of 21 joint angles from the ContactPose database hand poses is illustrated in Figure 3a. The distribution of 21 joint angles as estimated by the transformer network is shown in Figure 3b. Visual difference between the hand poses is within range in MSE in the joints for all fingers. To visualize the difference between the ground and estimated hand pose, MSE was computed between both hand poses as shown in Figure 3c.
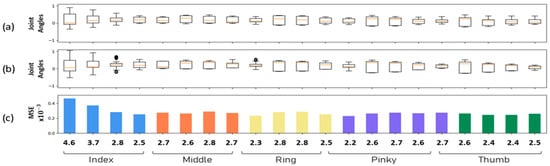
Figure 3.
The mean squared error (c) between the joint angle distributions of the ContactPose dataset (a) and the angles’ distributions as estimated by the transformer network (b) for each finger in the anthropomorphic hand. A lower error indicates higher confidence in estimation.
The error is located in the first joint of the index finger. However, considering the range of motion for each joint, the angular error of every finger DoF in the anthropomorphic hand is lower than 5%. These results show that the hand pose estimated by the transformer network has a similar joint angle distribution with a similar hand pose.
3.3. Object Manipulation Performance by T-DRL
The average success rates of T-DRL and NPG for grasping and relocation tasks of the six objects are shown in Table 1. The success rate achieved by our T-DRL was 90.1%, outperforming the 65.3% achieved by NPG. For the objects, such as light bulb, bottle, and camera, the baseline policy could not learn a proper grasping strategy, resulting in a low success rate. However, for objects such as the bottle and camera (those with values under 50%), we noticed the policy achieved to increase the reward by hitting the object and lifting it in the air. This is not a desired behavior that we expected the DRL policy to learn without proper guidance. The results for each object reported in Table 1 are the averaged success rate for policies trained by T-DRL and NPG, which were trained with three random initializations per object. In total, we trained 36 different DRL policies (18 T-DRL and 18 NPG) for grasping and relocation in a workstation with two RTX-2080 GPU for more than 100 h.

Table 1.
Success rate (%) of natural manipulation tasks using NPG and T-DRL.
In the left column of Figure 4, the average cumulative reward for all objects is shown, where the solid line represents the mean and the shadow area the standard deviation of the rewards. Overall, the cumulative reward from T-DRL achieves a higher success rate under 1000 iterations with 70% of the maximum return. This increment in speed is significant compared to NPG. The right column of Figure 4 illustrates the time-series frames of the DRL policies during grasping and relocation. Without shaped rewards, the resulting actions were unnatural and failed to grasp the object. This is shown in the row frames of Figure 4g, where the light bulb was hit and thrown into the air with force. In Figure 4i, the robot hand merely pushed the bottle off the table and did not learn to lift it. In Figure 4k, a similar behavior is shown with the light bulb. This phenomenon is all part of the learning process as DRL continues to explore the environment. By T-DRL, we were able to minimize these errors and prevent unnatural behaviors, manipulating the objects in a manner that resembled human-like actions.
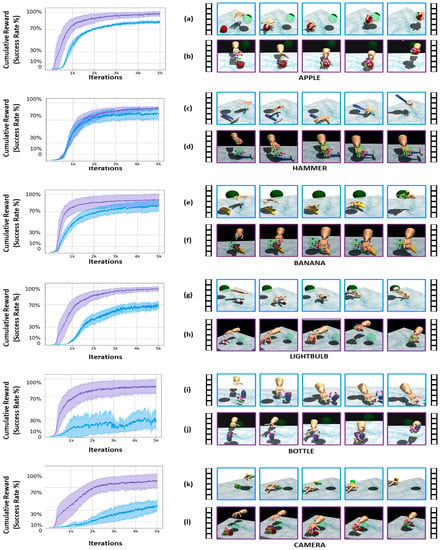
Figure 4.
On the left, the average sum of rewards for object manipulation by NPG (blue, top) and T-DRL (purple, bottom). On the right, the evaluation time-series frames from grasping and relocation of each object using the best policies of NPG (blue, top) vs. T-DRL (purple, bottom) for apple (a) vs. (b), hammer (c) vs. (d), banana (e) vs. (f), light bulb (g) vs. (h), bottle (i) vs. (j), and camera (k) vs. (l).
The NPG policy grasps the hammerhead and reaches the target location with a similar success ratio compared to T-DRL, as shown in Figure 4c,d. While it achieves a high success rate, this hand pose does not comply with the object affordance that is inferred when using hand pose priors in the training loop. T-DRL reduces the expectation that the policy learns these behaviors. More importantly, T-DRL generated a pre-shape of the hand by extending the fingers, as seen in the row frames of Figure 4h,j, and then proceeded to close the hand grasping the object.
4. Discussion
For dexterous object manipulation, using natural hand poses has a significant impact on the success of natural object grasping. Several previous studies have conducted dexterous object manipulation with hand pose estimation and DRL [,]. Yueh-Hua Wu et al. [] used GraspCVAE and DRL to manipulate objects with an ADROIT robot hand. GraspCVAE is based on a variational autoencoder that estimates the natural hand pose from the object affordance. In this work, DRL imitated the estimated hand pose without reward shaping and manipulated five objects (a bottle, a remote, a mug, a can, and a camera), achieving an average manipulation success rate of 80%. Similarly, Priyanka Mandikal et al. [] used the FrankMocap regressor and DRL to manipulate objects with an ADROIT robot hand. They utilized the FrankMocap regressor to estimate natural hand poses according to object affordance. The six objects (a pan, a mug, a teapot, a knife, a cup, and a hammer) were manipulated, achieving an average success rate of 60%. The low success rate was mainly due to the FrankMocap regressor, which has shown poor performance in generating novel natural hand poses without object and hand pose data. In our study, we incorporated the transformer network into DRL with reward shaping for object manipulation. Our T-DRL outperforms the object manipulation of similar objects with an average success rate of 90.1%. We believe DRL’s transformer network and reward shaping contributes to this performance.
In T-DRL, dexterous object manipulation of an anthropomorphic robot hand is possible through natural hand poses produced by the transformer network. For instance, NPG without natural hand poses grasps only a few objects, such as an apple, a hammer, a banana, and a light bulb as shown in Figure 4. For the bottle and camera, NPG fails to grasp them. The results demonstrate that for complex shaped objects, proper guidance through natural hand poses plays a critical role in grasping them. In contrast, the proposed T-DRL with natural hand poses successfully grasps all six objects. Unlike NPG, when grasping each object with T-DRL, we noticed that each object gets grasped in a hand pose that suits the object affordance. This is because of the natural hand pose produced by the transformer network according to the object affordance. Accordingly, T-DRL utilizes the natural hand pose in learning via reward shaping. The reward curves in Figure 4 show that the proposed reward function performs effective exploitation of the object grasping space in comparison to NPG. For example, when manipulating the objects of the hammer and banana, NPG and T-DRL obtain high rewards, but only T-DRL grasps objects with natural hand poses. This suggests that the proposed reward function provides better guidance for natural object manipulation in comparison to the NPG reward function. In general, the reward of T-DRL increases much faster than that of NPG. This suggests that unnecessary exploration for object grasping is reduced for the anthropomorphic robot hand, while the useful experience for successful grasping is gained much more quickly. The proposed reward-shaping function in T-DRL results in improving the grasping success rates from 65.3% by NPG to 90.1% by T-DRL. Using natural hand poses and reward shaping in T-DRL seems to play a significant role in training the anthropomorphic robot hand for dexterous object manipulation, especially considering the high-DoF of the five fingers.
5. Conclusions
In this paper, we present the T-DRL intelligence of an anthropomorphic robot hand for dexterous manipulation of various objects with natural hand poses. The transformer network improves the performance of object manipulation by the robot hand pose, providing natural hand poses from object affordance to DRL. The reward function via reward shaping in T-DRL efficiently trains the high-DoF anthropomorphic robot hand via estimated natural hand poses. An extension of this work in the future could include estimating natural hand poses to manipulate novel unseen objects with T-DRL.
Author Contributions
Conceptualization, W.H.L. and T.-S.K.; Formal analysis, J.G.J., I.E.J., J.H.L., H.J. and C.C.; Funding acquisition, T.-S.K.; Investigation, P.R.L. and J.-H.O.; Methodology, P.R.L. and J.-H.O.; Project administration, T.-S.K.; Software, P.R.L. and J.-H.O.; Supervision, W.H.L. and T.-S.K.; Validation, W.H.L. and T.-S.K.; Visualization, P.R.L. and J.-H.O.; Writing—original draft, P.R.L. and J.-H.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) (No. 2017-0-00655).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van Hoof, H.; Hermans, T.; Neumann, G.; Peters, J. Learning robot in-hand manipulation with tactile features. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015; pp. 121–127. [Google Scholar]
- Pinto, L.; Gupta, A. Supersizing self-supervision: Learning to grasp from 50K tries and 700 robot hours. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3406–3413. [Google Scholar]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Ibarz, J.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2018, 37, 421–436. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Baker, B.; Chociej, M.; Jozefowicz, R.; McGrew, B.; Pachocki, J.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning dexterous in-hand manipulation. Int. J. Robot. Res. 2020, 39, 3–20. [Google Scholar] [CrossRef]
- Valarezo Anazco, E.; Rivera Lopez, P.; Park, N.; Oh, J.H.; Ryu, G.; Al-antari, M.A.; Kim, T.S. Natural hand object manipulation using anthropomorphic robotic hand through deep reinforcement learning and deep grasping probability network. Appl. Sci. 2021, 51, 1041–1055. [Google Scholar] [CrossRef]
- Lu, Q.; Rojas, N. On Soft Fingertips for In-Hand Manipulation: Modeling and Implications for Robot Hand Design. IEEE Robot. Autom. Lett. 2019, 4, 2471–2478. [Google Scholar] [CrossRef]
- Erol, A.; Bebis, G.; Nicolescu, M.; Boyle, R.D.; Twombly, X. Vision-based hand pose estimation: A review. Computer Vision and Image Understanding 2007, 108, 52–73. [Google Scholar] [CrossRef]
- Du, G.; Wang, K.; Lian, S.; Zhao, K. Vision-based Robotic Grasping from Object Localization, Pose Estimation, Grasp Detection to Motion Planning: A Review. Int. J. Robot. Res. 2020, 54, 1677–1734. [Google Scholar]
- Abdal Shafi Rasel, A.; Abu Yousuf, M. An Efficient Framework for Hand Gesture Recognition based on Histogram of Oriented Gradients and Support Vector Machine. I.J. Inf. Technol. Comput. Sci. 2019, 12, 50–56. [Google Scholar]
- Feix, T.; Romero, J.; Schmiedmayer, H.-B.; Dollar, A.M.; Kragic, D. The GRASP Taxonomy of Human Grasp Types. IEEE Trans. Hum. Mach. Syst. 2016, 46, 66–77. [Google Scholar] [CrossRef]
- Hampali, S.; Sarkar, S.; Rad, M.; Lepetit, V. HandsFormer: Keypoint Transformer for Monocular 3D Pose Estimation of Hands and Object in Interaction. arXiv 2021, arXiv:2104.14639. Available online: https://arxiv.org/abs/2104.14639 (accessed on 6 August 2021).
- Bohg, J.; Morales, A.; Asfour, T.; Kragic, D. Data-Driven Grasp Synthesis—A Survey. IEEE Trans. Robot. 2014, 30, 289–309. [Google Scholar] [CrossRef]
- Caldera, S.; Rassau, A.; Chai, D. Review of Deep Learning Methods in Robotic Grasp Detection. MTI 2018, 2, 57. [Google Scholar] [CrossRef]
- Abondance, S.; Teeple, C.B.; Wood, R.J. A Dexterous Soft Robotic Hand for Delicate In-Hand Manipulation. IEEE Robot. Autom. Lett. 2020, 5, 5502–5509. [Google Scholar] [CrossRef]
- Osa, T.; Peters, J.; Neumann, G. Hierarchical reinforcement learning of multiple grasping strategies with human instructions. Adv. Robot. 2018, 32, 955–968. [Google Scholar] [CrossRef]
- Ji, S.-Q.; Huang, M.-B.; Huang, H.-P. Robot Intelligent Grasp of Unknown Objects Based on Multi-Sensor Information. Sensors 2019, 19, 1595. [Google Scholar] [CrossRef]
- Karunratanakul, K.; Yang, J.; Zhang, Y.; Black, M.J.; Muandet, K.; Tang, S. Grasping Field: Learning Implicit Representations for Human Grasps. arXiv 2020, arXiv:2008.04451. Available online: https://arxiv.org/abs/2008.04451 (accessed on 10 August 2020).
- Qin, Y.; Su, H.; Wang, X. From One Hand to Multiple Hands: Imitation Learning for Dexterous Manipulation from Single-Camera Teleoperation. arXiv 2022, arXiv:2204.12490. Available online: https://arxiv.org/abs/2204.12490 (accessed on 26 April 2022). [CrossRef]
- Corona, E.; Pumarola, A.; Alenya, G.; Moreno-Noguer, F.; Rogez, G. GanHand: Predicting Human Grasp Affordance in Multi-Object Scenes. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–15 June 2020; pp. 5030–5040. [Google Scholar]
- Lundell, J.; Corona, E.; Le, T.N.; Verdoja, F.; Weinzaepfel, P.; Rogez, G.; Moreno-Noguer, F.; Kyrki, V. Multi-FinGAN: Generative Coarse-To-Fine Sampling of Multi-Finger Grasps. arXiv 2020, arXiv:2012.09696. Available online: https://arxiv.org/abs/2012.09696 (accessed on 17 December 2020).
- Varley, J.; Weisz, J.; Weiss, J.; Allen, P. Generating multi-fingered robotic grasps via deep learning. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4415–4420. [Google Scholar]
- Jiang, H.; Liu, S.; Wang, J.; Wang, X. Hand-Object Contact Consistency Reasoning for Human Grasps Generation. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 11087–11096. [Google Scholar]
- Lin, K.; Wang, L.; Liu, Z. End-to-End Human Pose and Mesh Reconstruction with Transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 1954–1963. [Google Scholar]
- Huang, L.; Tan, J.; Liu, J.; Yuan, J. Hand-Transformer: Non-Autoregressive Structured Modeling for 3D Hand Pose Estimation. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; pp. 17–33. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the 31th Conference on Neural Information Processing Systems (NeuralIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 3–5 June 2019; pp. 4171–4186. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. Available online: https://arxiv.org/abs/2010.11929 (accessed on 22 October 2021).
- Kaiser, L.; Gomez, A.N.; Shazeer, N.; Vaswani, A.; Parmar, N.; Jones, N.; Uszkoreit, J. One Model to Learn Them All. arXiv 2017, arXiv:1706.05137. Available online: https://arxiv.org/abs/1706.05137 (accessed on 16 June 2017).
- Khatun, A.; Abu Yousuf, M.; Ahmed, S.; Uddin, M.D.Z.; Alyami, A.S.; Al-Ashhab, S.; F. Akhdar, H.; Kahn, A.; Azad, A.; Ali Moni, M. Deep CNN-LSTM With Self-Attention Model for Human Activity Recognition Using Wearable Sensor. IEEE J. Transl. Eng. Health Med. 2022, 10, 1–16. [Google Scholar] [CrossRef]
- Cachet, T.; Perez, J.; Kim, S. Transformer-based Meta-Imitation Learning for Robotic Manipulation. In Proceedings of the 3rd Workshop on Robot Learning, Thirty-Fourth Conference on Neural Information Processing Systems (NeurlIPS), Virtual Only Conference, 6–12 December 2020. [Google Scholar]
- Huang, L.; Tan, J.; Meng, J.; Liu, J.; Yuan, J. HOT-Net Non-Autoregressive Transformer for 3D Hand-Object Pose Estimation. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 3136–3145. [Google Scholar]
- Wu, Y.-H.; Wang, J.; Wang, W. Learning Generalizable Dexterous Manipulation from Human Grasp Affordance. arXiv 2022, arXiv:2204.02320. Available online: https://arxiv.org/abs/2204.02320 (accessed on 5 April 2022).
- Rajeswaran, A.; Kumar, V.; Gupta, A.; Vezzani, G.; Schulman, J.; Todorov, E.; Levine, S. Learning Complex Dexterous Manipulation with Deep Reinforcement Learning and Demonstrations. arXiv 2017, arXiv:1709.10087. Available online: https://arxiv.org/abs/1709.10087 (accessed on 28 September 2017).
- Mousavian, A.; Eppner, C.; Fox, D. 6-DOF GraspNet: Variational Grasp Generation for Object Manipulation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 2901–2910. [Google Scholar]
- Brahmbhatt, S.; Tang, C.; Twigg, C.D.; Kemp, C.C.; Hays, J. ContactPose: A Dataset of Grasps with Object Contact and Hand Pose. arXiv 2020, arXiv:2007.09545. Available online: https://arxiv.org/abs/2007.09545 (accessed on 19 July 2020).
- Johnson, J.W. Adapting Mask-RCNN for Automatic Nucleus Segmentation. arXiv 2018, arXiv:1805.00500. Available online: https://arxiv.org/abs/1805.00500 (accessed on 1 May 2018).
- Lin, T.-Y.; Maire, M.; Belongie, S.; Bourdev, L.; Grishick, R.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L.; Dollar, P. Microsoft COCO: Common Objects in Context. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Kakade, S.M. A Natural Policy Gradient. In Proceedings of the International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, BC, Canada, 3–8 December 2001; pp. 1531–1538. [Google Scholar]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar]
- Kumar, V.; Xu, Z.; Todorov, E. Fast, strong and compliant pneumatic actuation for dexterous tendon-driven hands. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 1512–1519. [Google Scholar]
- Mandikal, P.; Grauman, K. DexVIP: Learning Dexterous Grasping with Human Hand Pose Priors from Video. arXiv 2022, arXiv:2022.00164. Available online: https://arxiv.org/abs/2202.00164 (accessed on 1 February 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).