Modeling Locations with Enhanced Earth’s Crust Deformation during Earthquake Preparation near the Kamchatka Peninsula
Abstract
1. Introduction
2. Research Significance
3. Research Methods
4. Simulation of Stress and Strain Fields
5. The Results of Computational Experiment
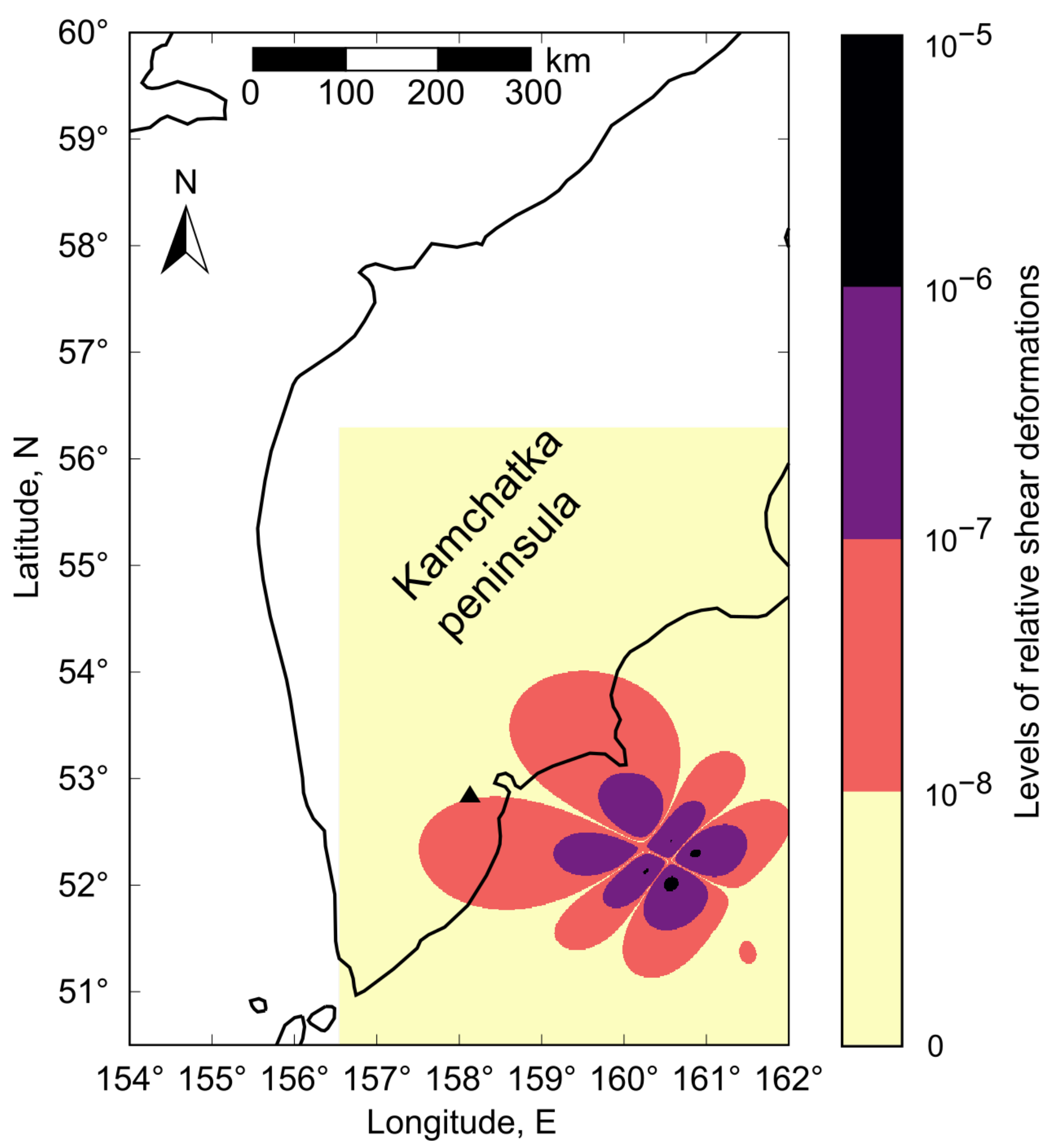
5.1. Earthquake No. 1
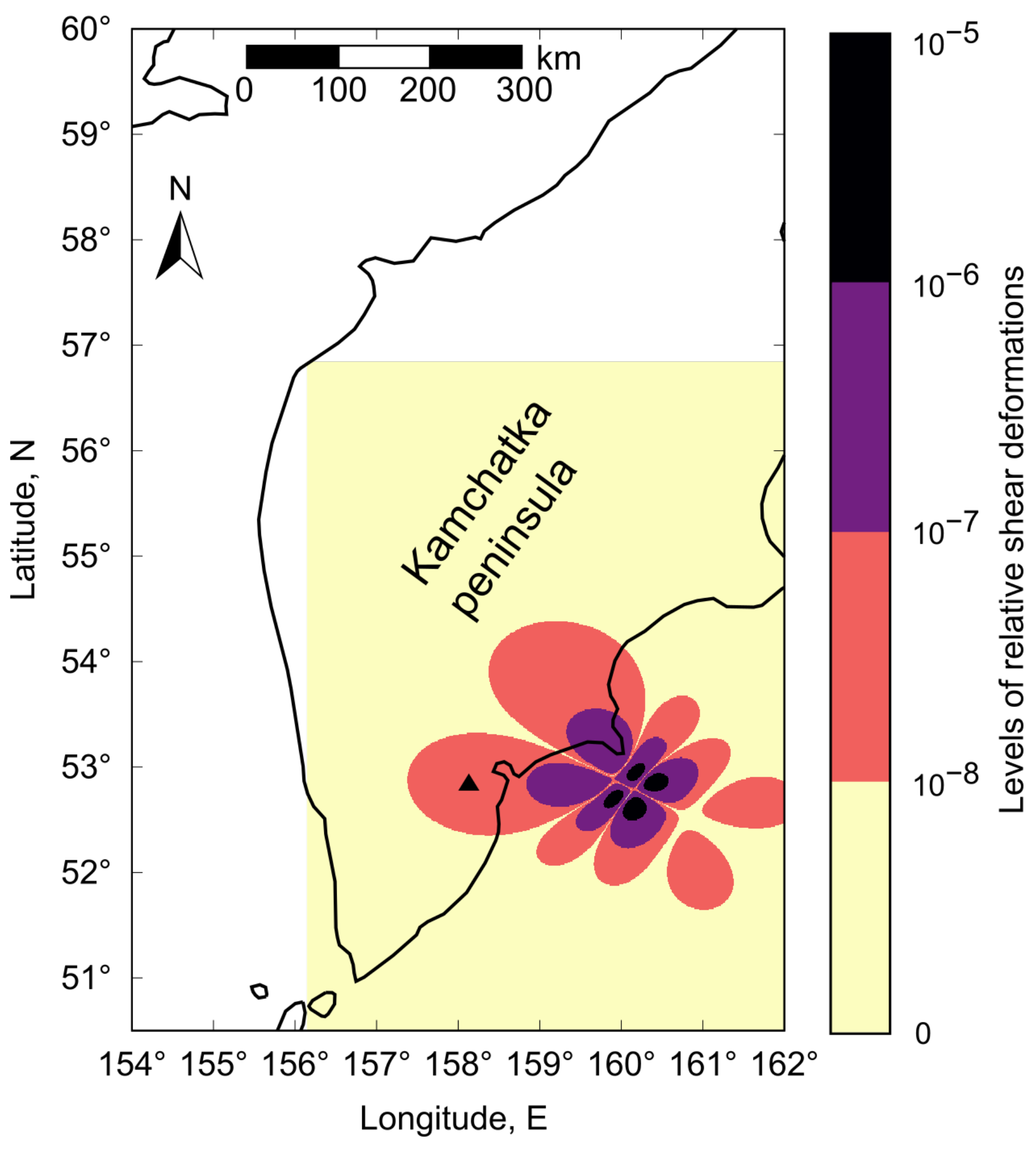
5.2. Earthquake No. 2
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sholz, C. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019; p. 512. [Google Scholar]
- Kocharyan, G.G.; Kishkina, S.B. The physical mesomechanics of the earthquake source. Phys. Mesomech. 2021, 24, 343–356. [Google Scholar] [CrossRef]
- Shah, M.; Abbas, A.; Adil, M.A.; Ashraf, U.; Oliveira-Junior, J.F.; Tariq, M.A.; Ahmed, J.; Ehsan, M.; Ali, A. Possible seismo-ionospheric anomalies associated with Mw > 5.0 earthquakes during 2000–2020 from GNSS TEC. Adv. Space Res. 2022, 70, 179–187. [Google Scholar] [CrossRef]
- Cicerone, R.D.; Ebel, J.E.; Britton, J. A systematic compilation of earthquake precursors. Tectonophysics 2009, 476, 371–396. [Google Scholar] [CrossRef]
- Marapulets, Y.; Rulenko, O. Joint anomalies of high-frequency geoacoustic emission and atmospheric electric field by the ground-atmosphere boundary in a seismically active region (Kamchatka). Atmosphere 2019, 10, 267. [Google Scholar] [CrossRef]
- Riaz, M.S.; Bin, S.; Naeem, S.; Kai, W.; Xie, Z.; Gilani, S.M.; Ashraf, U. Over 100 years of faults interaction, stress accumulation, and creeping implications, on Chaman Fault System, Pakistan. Int. J. Earth Sci. 2019, 108, 1351–1359. [Google Scholar] [CrossRef]
- Ashraf, U.; Zhang, H.; Anees, A.; Mangi, H.N.; Ali, M.; Zhang, X.; Imraz, M.; Abbasi, S.S.; Abbas, A.; Ullah, Z.; et al. A Core Logging, Machine Learning and Geostatistical Modeling Interactive Approach for Subsurface Imaging of Lenticular Geobodies in a Clastic Depositional System, SE Pakistan. Nat. Resour. Res. 2021, 30, 2807–2830. [Google Scholar] [CrossRef]
- Ullah, J.; Luo, M.; Ashraf, U.; Pan, H.; Anees, A.; Li, D.; Ali, M.; Ali, J. Evaluation of the geothermal parameters to decipher the thermal structure of the upper crust of the Longmenshan fault zone derived from borehole data. Geothermics 2022, 98, 102268. [Google Scholar] [CrossRef]
- Kopylova, G.; Kasimova, V.; Lyubushin, A.; Boldina, S. Variability in the Statistical Properties of Continuous Seismic Records on a Network of Stations and Strong Earthquakes: A Case Study from the Kamchatka Peninsula, 2011–2021. Appl. Sci. 2022, 12, 8658. [Google Scholar] [CrossRef]
- Morgunov, V.A.; Lyuboshevskij, M.N.; Fabricius, V.Z. Geoacoustic precursor of the Spitak earthquake. Vulkanol. Seismol. 1991, 4, 104–106. (In Russian) [Google Scholar]
- Gregori, G.P.; Poscolieri, M.; Paparo, G.; DeSimone, S.; Rafanelli, C.; Ventrice, G. “Storms of crustal stress” and AE earthquake precursors. Nat. Hazards Earth Syst. Sci. 2010, 10, 319–337. [Google Scholar] [CrossRef]
- Kuptsov, A.V. Variations in the geoacoustic emission pattern related to earthquakes on Kamchatka. Izv. Phys. Solid Earth 2005, 41, 825–831. [Google Scholar]
- Marapulets, Y.; Shevtsov, B. Mesoscale Acoustic Emission; Dal’nauka: Vladivostok, Russia, 2012; p. 125. (In Russian) [Google Scholar]
- Rulenko, O.P.; Marapulets, Y.V.; Kuz’min, Y.D.; Solodchuk, A.A. Joint perturbation in geoacoustic emission, radon, thoron, and atmospheric electric field based on observations in Kamchatka. Izv. Phys. Solid Earth 2019, 55, 76–78. [Google Scholar] [CrossRef]
- Marapulets, Y.V. High-frequency acoustic emission effect. Bull. KRASEC. Phys. Math. Sci. 2015, 10, 39–48. [Google Scholar]
- Marapulets, Y.V.; Shevtsov, B.M.; Larionov, I.A.; Mishchenko, M.A.; Shcherbina, A.O.; Solodchuk, A.A. Geoacoustic emission response to deformation processes activation during earthquake preparation. Russ. J. Pac. Geol. 2012, 6, 457–464. [Google Scholar] [CrossRef]
- Dolgikh, G.I.; Shvets, V.A.; Chupin, V.A.; Yakovenko, S.V.; Kuptsov, A.V.; Larionov, I.A.; Marapulets, Y.V.; Shevtsov, B.M.; Shirokov, O.P. Deformation and acoustic precursors of earthquakes. Dokl. Earth Sci. 2007, 413, 281–285. [Google Scholar] [CrossRef]
- Larionov, I.A.; Marapulets, Y.V.; Shevtsov, B.M. Features of the Earth surface deformations in the Kamchatka peninsula and their relation to geoacoustic emission. J. Geophys. Res. Solid Earth 2014, 5, 1293–1300. [Google Scholar] [CrossRef]
- Turcotte, D.; Schubert, G. Geodynamics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2014; p. 636. [Google Scholar]
- Nikolaevsky, V. Mechanics of Porous and Fractured Media; Nedra: Moscow, Russia, 1984; p. 232. (In Russian) [Google Scholar]
- Aki, K.; Richards, P. Quantitative Seismology, 2nd ed.; University Science Books: Cambridge, UK, 2002; p. 704. [Google Scholar]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Dobrovolsky, I. Mathematical Theory of Preparation and Prediction of a Tectonic Earthquake; Fizmatlit: Moscow, Russia, 2009; p. 235. (In Russian) [Google Scholar]
- Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Alekseev, A.S.; Belonosov, A.S.; Petrenko, V.E. On the concept of multidisciplinary earthquake prediction using an integral predictor. Vych. Seismol. 2001, 32, 81–97. (In Russian) [Google Scholar]
- Li, Y.; Liu, M.; Li, Y.; Chen, L. Active crustal deformation in southeastern Tibetan Plateau: The kinematics and dynamics. Earth Planet. Sci. Lett. 2019, 523, 115708. [Google Scholar] [CrossRef]
- Dansereau, V.; Shapiro, N.; Campillo, M.; Weiss, J. A Burgers-Brittle model for the seismic-aseismic, brittle-ductile transition within the Earth crust. In Proceedings of the EGU General Assembly Conference Abstracts, vEGU21: Gather Online, Vienna, Austria, 19–30 April 2021. EGU21–7547. [Google Scholar]
- Pollitz, F. Viscoelastic Fault-Based Model of Crustal Deformation for the 2023 Update to the U.S. National Seismic Hazard Model. Seismol. Res. Lett. 2022, 93, 3087–3099. [Google Scholar] [CrossRef]
- Takagi, Y.; Okubo, S. Internal deformation caused by a point dislocation in a uniform elastic sphere. Geophys. J. Int. 2017, 208, 973–991. [Google Scholar] [CrossRef][Green Version]
- Liu, T.; Fu, G.; She, Y.; Zhao, C. Co-seismic internal deformations in a spherical layered earth model. Geophys. J. Int. 2020, 221, 1515–1531. [Google Scholar] [CrossRef]
- Zhu, S. Inter-and pre-seismic deformations in the 2011 MW 9.0 Tohoku-Oki earthquake: Implications for earthquake prediction. Chin. J. Geophys. 2020, 63, 427–439. [Google Scholar]
- Chen, C.H.; Su, X.; Cheng, K.C.; Meng, G.; Wen, S.; Han, P. Seismo-deformation anomalies associated with the M 6.1 Ludian earthquake on August 3, 2014. Remote Sens. 2020, 12, 1067. [Google Scholar] [CrossRef]
- Lv, X.; Shao, Y. Rheology of the Northern Tibetan Plateau Lithosphere Inferred from the Post-Seismic Deformation Resulting from the 2001 Mw 7.8 Kokoxili Earthquake. Remote Sens. 2022, 14, 1207. [Google Scholar] [CrossRef]
- Jiao, Z.H.; Zhao, J.; Shan, X. Pre-seismic anomalies from optical satellite observations: A review. Nat. Hazards Earth Syst. Sci. 2018, 18, 1013–1036. [Google Scholar] [CrossRef]
- Perezhogin, A.S.; Shevtsov, B.M.; Sagitova, R.N.; Vodinchar, G.M. Geoacoustic emission’s zones modeling. Math. Models Comput. Simul. 2007, 19, 59–64. [Google Scholar]
- Perezhogin, A.S. Geoacoustic emission zones in an elastic model of continuum. Bull. KRASEC Earth Sci. 2009, 13, 198–201. (In Russian) [Google Scholar]
- Perezhogin, A.S.; Shevtsov, B.M. Models of an intense-deformed condition of rocks before earthquakes and their correlation with geo-acoustic emission. Comput. Technol. 2009, 14, 48–57. (In Russian) [Google Scholar]
- Saltykov, V.A.; Kugaenko, Y.A. Development of near-surface dilatancy zones as a possible cause for seismic emission anomalies before strong earthquakes. Russ. J. Pac. Geol. 2012, 6, 86–95. [Google Scholar] [CrossRef]
- Gapeev, M.I.; Marapulets, Y.V. Modeling of relative shear deformation zones before strong earthquakes in Kamchatka from 2018–2021. Vestn. KRAUNC Fiz.-Mat. Nauki 2021, 37, 53–66. (In Russian) [Google Scholar]
- The Global Centroid-Moment-Tensor (CMT) Project. Available online: https://www.globalcmt.org/ (accessed on 27 June 2022).
- Gusev, A.A.; Melnikova, V.N. Relations between magnitudes: Global and Kamchatka data. J. Volcanol. Seismol. 1990, 6, 55–63. [Google Scholar]
- Kanamori, H. The radiated energy of the 2004 Sumatra-Andaman earthquake. In Earthquakes: Radiated Energy and the Physics of Faulting (Geophysical Monograph Series); Abercrombie, R., McGarr, A., Kanomari, H., Di Toro, G., Eds.; American Geophysical Union: Washington, DC, USA, 2006; pp. 59–60. [Google Scholar]
- Bath, M.; Duda, S. Earthquake volume, fault plane area, seismic energy, strain, deformation and related quantities. Ann. Geophys. 1964, 17, 353–368. [Google Scholar]
- Rebetsky, Y. Tectonic Stresses and Strength of Natural Massifs; IKC ”Akademkniga”: Moscow, Russia, 2007; p. 406. (In Russian) [Google Scholar]
- Mindlin, R. Force at a point in the interior of a Semi-Infinite solid. J. Appl. Phys. 1936, 195, 195–292. [Google Scholar] [CrossRef]
- Mindlin, R.; Cheng, D. Nuclei of Strain in the Semi-Infinite Solid. J. Appl. Phys. 1950, 21, 926–930. [Google Scholar] [CrossRef]
- Kamchatka Branch of Geophysical Service Russian Academy of Science. Available online: http://sdis.emsd.ru/info/earthquakes/catalogue.php (accessed on 5 June 2022).
- Gusev, A.A.; Skorkina, A.A.; Pavlov, V.M.; Abubakirov, I.R. Obtaining mass estimates of regional moment magnitudes MW and establishing their relationship with ML3 for subduction Kamchatka earthquakes. In Proceedings of the Materials of the XX Regional Scientific Conference dedicated to the Day of Volcanologist, XX Regional Scientific Conference dedicated to the Day of Volcanologist, Petropavlovsk-Kamchatsky, Russia, 30–31 March 2017; Institute of Volcanology and Seismology FEB RAS: Petropavlovsk-Kamchatsky, Russia, 2017. (In Russian). [Google Scholar]
- Mondal, D.; Debnath, P. An application of fractional calculus to geophysics: Effect of a strike-slip fault on displacement, stresses and strains in a fractional order Maxwell type visco-elastic half space. Int. J. Appl. Math. 2021, 34, 873–888. [Google Scholar] [CrossRef]
- Rebetsky, Y.L.; Lermontova, A.S. On the long-range Influence of earthquake rupture zones. J. Volcanol. Seismol. 2018, 12, 341–352. [Google Scholar] [CrossRef]
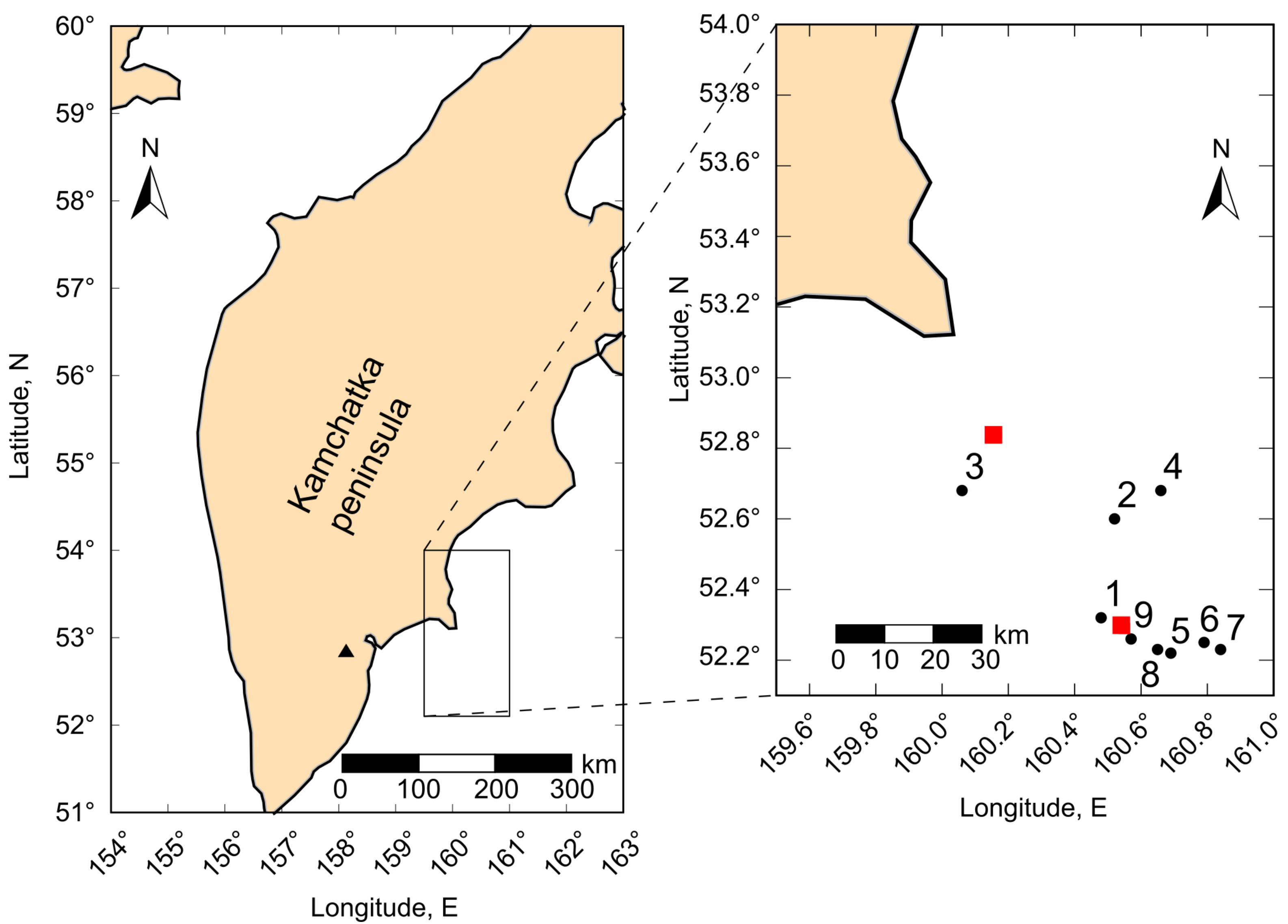
| No | Date, Time | Coordinates of the Epicenter | Depth, km | Strike Angle 1, | Dip Angle 1, | Angle of Displacement 1, | Focal Mechanism | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1977/12/2, 12:57:22.6 | 52.32 N, 160.48 E | 40.0 | 5.6 | 217 | 35 | 96 |  |
| 2 | 1977/12/21, 16:39:40.9 | 52.60 N, 160.52 E | 55.6 | 5.6 | 218 | 38 | 93 |  |
| 3 | 1979/6/25, 18:45:57.2 | 52.68 N, 160.06 E | 57.3 | 5.0 | 210 | 19 | 76 |  |
| 4 | 1979/9/1, 17:54:59.9 | 52.86 N, 160.66 E | 15.0 | 5.5 | 309 | 25 | −150 |  |
| 5 | 1980/1/23, 1:51:49.8 | 52.22 N, 160.69 E | 20.3 | 5.8 | 213 | 26 | 86 |  |
| 6 | 1980/1/23, 2:34:17.6 | 52.25 N, 160.79 E | 15.0 | 5.7 | 192 | 21 | 57 |  |
| 7 | 1980/1/23, 6:52:53.7 | 52.23 N, 160.84 E | 19.6 | 5.5 | 216 | 28 | 90 |  |
| 8 | 1980/1/23, 8:12:31.6 | 52.23 N, 160.65 E | 15.0 | 5.6 | 219 | 21 | 92 |  |
| 9 | 1980/1/23, 10:7:17.1 | 52.26 N, 160.57 E | 17.2 | 5.2 | 205 | 22 | 77 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gapeev, M.; Marapulets, Y. Modeling Locations with Enhanced Earth’s Crust Deformation during Earthquake Preparation near the Kamchatka Peninsula. Appl. Sci. 2023, 13, 290. https://doi.org/10.3390/app13010290
Gapeev M, Marapulets Y. Modeling Locations with Enhanced Earth’s Crust Deformation during Earthquake Preparation near the Kamchatka Peninsula. Applied Sciences. 2023; 13(1):290. https://doi.org/10.3390/app13010290
Chicago/Turabian StyleGapeev, Maksim, and Yuri Marapulets. 2023. "Modeling Locations with Enhanced Earth’s Crust Deformation during Earthquake Preparation near the Kamchatka Peninsula" Applied Sciences 13, no. 1: 290. https://doi.org/10.3390/app13010290
APA StyleGapeev, M., & Marapulets, Y. (2023). Modeling Locations with Enhanced Earth’s Crust Deformation during Earthquake Preparation near the Kamchatka Peninsula. Applied Sciences, 13(1), 290. https://doi.org/10.3390/app13010290






