Deformations of Image Blocks in Photogrammetric Documentation of Cultural Heritage—Case Study: Saint James’s Chapel in Bratislava, Slovakia
Abstract
Featured Application
Abstract
1. Introduction
- Manual—point clouds from photogrammetry are transformed into the reference coordinate system based on manually selected identical points or GCPs. This approach is used, for example, in ContextCapture software by Bentley Systems [14]. If only the spatial similarity transformation of the finished photogrammetric point clouds is used, it is not possible to remove the already existing deformations. On the contrary, if a sufficient number of identical points is used during bundle adjustment before point cloud generation, the photogrammetrically obtained geometry can be improved and the possible deformations adjusted relatively to the GCPs [15,16].
- Semi-automatically—most often with the support of the Iterative Closest Point (ICP) algorithm [17]. The approximately oriented point clouds are automatically transformed to each other. However, this method does not allow the removal of deformations that already exist in the cloud, it only tries to minimize deviations from the reference point cloud by adjusting the translations, rotations, or scale [18,19]. The ICP algorithm is used, e.g., in 3DF Zephyr photogrammetric software [20].
- Automatic—the most progressive method, which enables fully-automated orientation of photogrammetric images against geometrically reliable laser scans based on the identification of significant elements in the texture [21]. A prerequisite for a successful result is laser scanning in color; information only about the intensity may not be sufficient. The differences between the features on intensity images from TLS and photogrammetric RGB images can be too large for successful matching. This functionality is currently supported by photogrammetric software, e.g., Metashape Professional by Agisoft LLC [22] and RealityCapture by Capturing Reality [23].
2. Materials and Methods
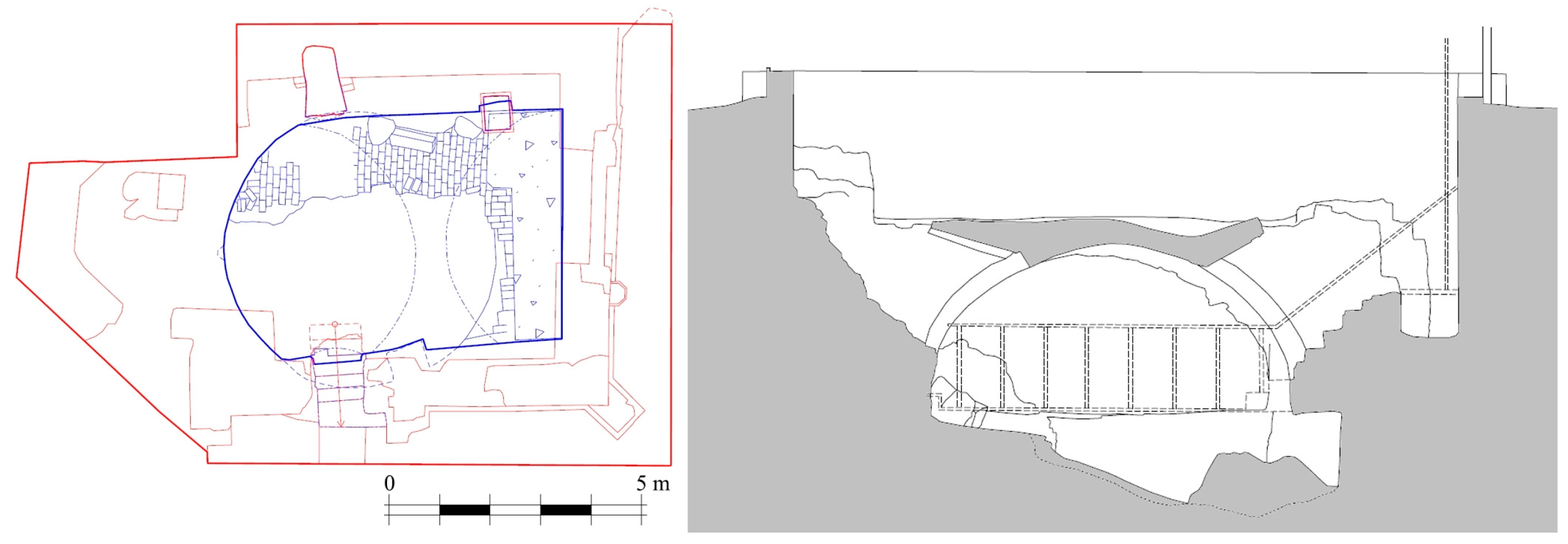
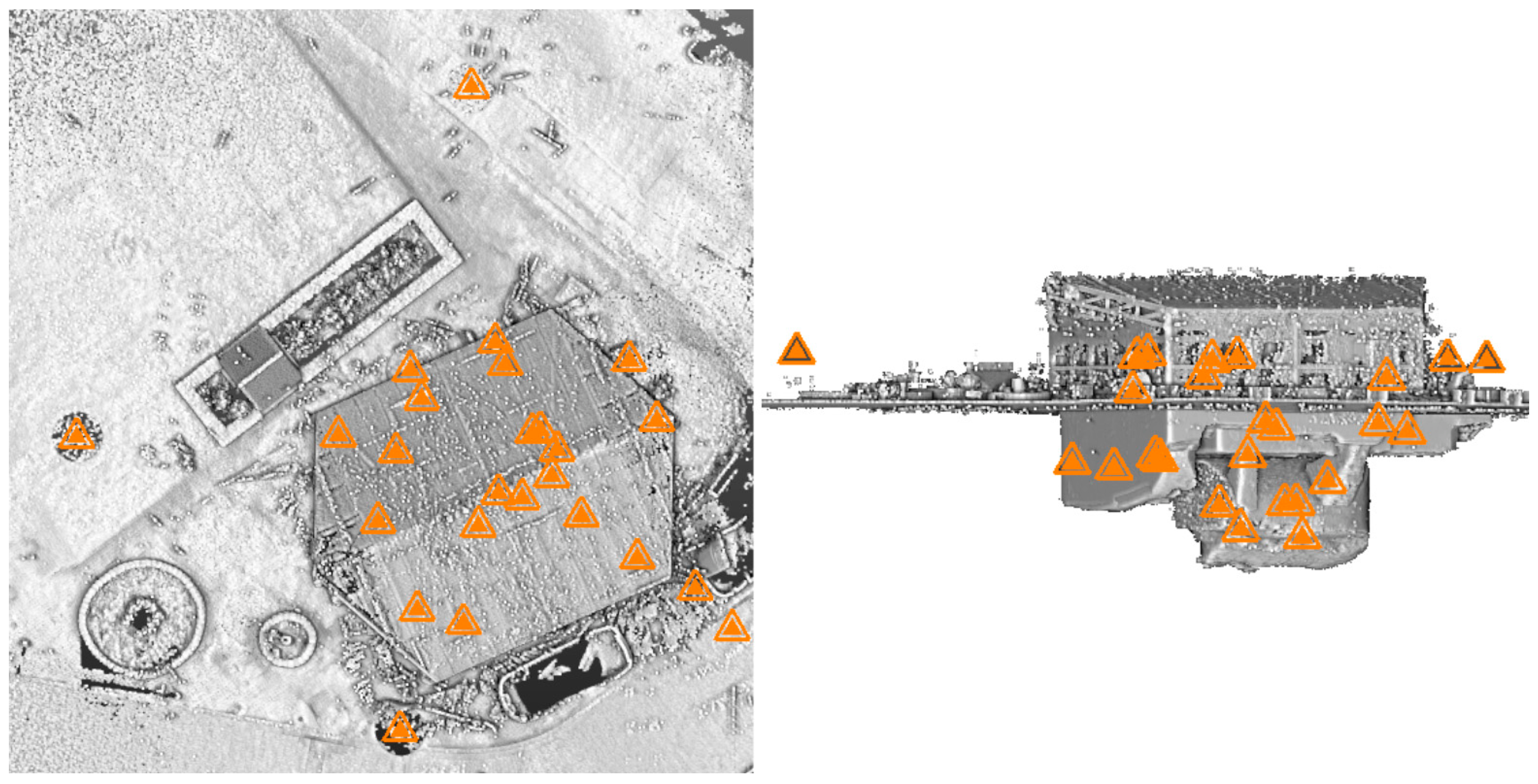
2.1. TLS and Photogrammetry—Field Work
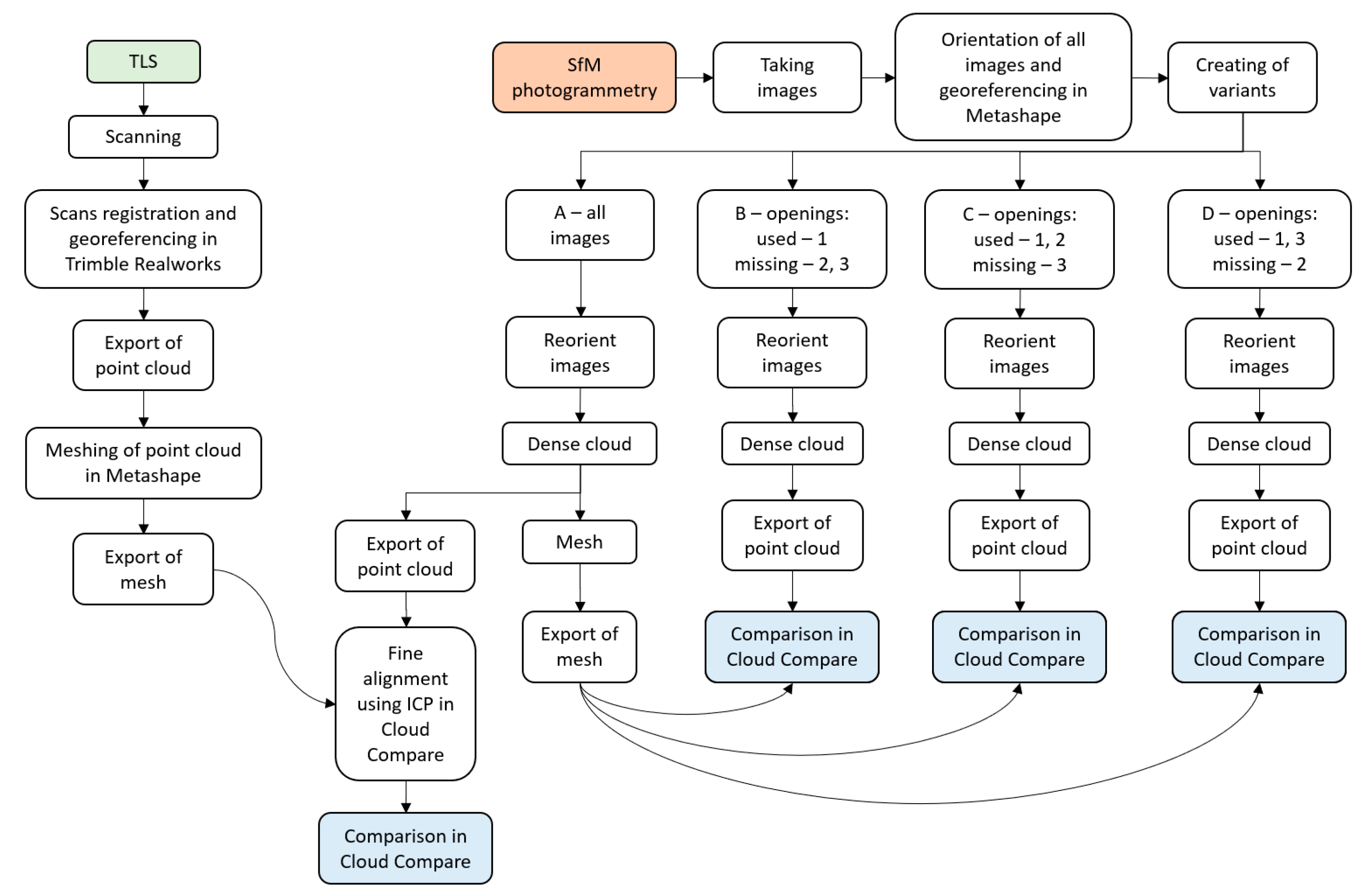
2.2. Experiment Methodology
- (A)
- A photogrammetric point cloud was generated in “medium” quality after orienting all 789 images. Subsequently, it was compared to the reference model from TLS. This was created by meshing a cloud of points from TLS in Metashape software. Since photogrammetry georeferencing relied only on four manually measured identical points extracted from laser scans, the photogrammetric cloud was finely aligned to the TLS model using the ICP algorithm in the Cloud Compare software. During the transformation, not only translations and rotations were allowed, but also the adjustment of scale.
- (B)
- The image strips through openings 2 and 3 were excluded from the image alignment (Figure 4 right). To speed up the calculations for variants B, C, and D, the point cloud was generated in “low” quality, as we did not need such high detail and we were mainly interested in cloud deformations of larger areas. Since we were also mainly interested in the relative changes between individual photogrammetric variants, the resulting clouds in variants B, C, and D were compared with the reference photogrammetric model from variant A. Therefore, the resulting relative changes were better read than if they were compared only with TLS.
- (C)
- The image strips through opening 3 were excluded from the processing (Figure 6).
- (D)
- The image strips through opening 2 were excluded from the processing (Figure 5).
3. Data Processing
3.1. TLS—Processing of Measurements
3.2. Photogrammetry—Processing of Measurements
4. Results
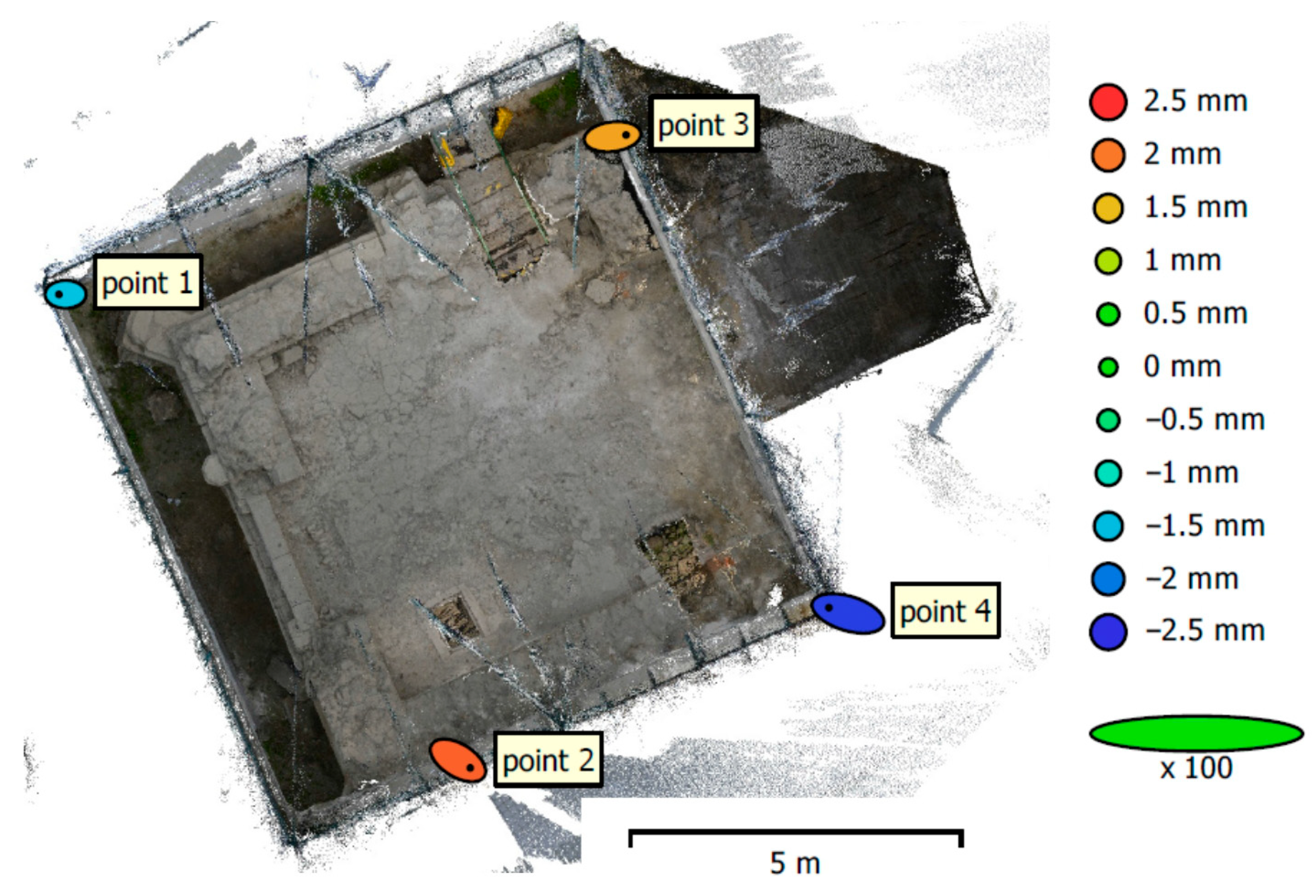
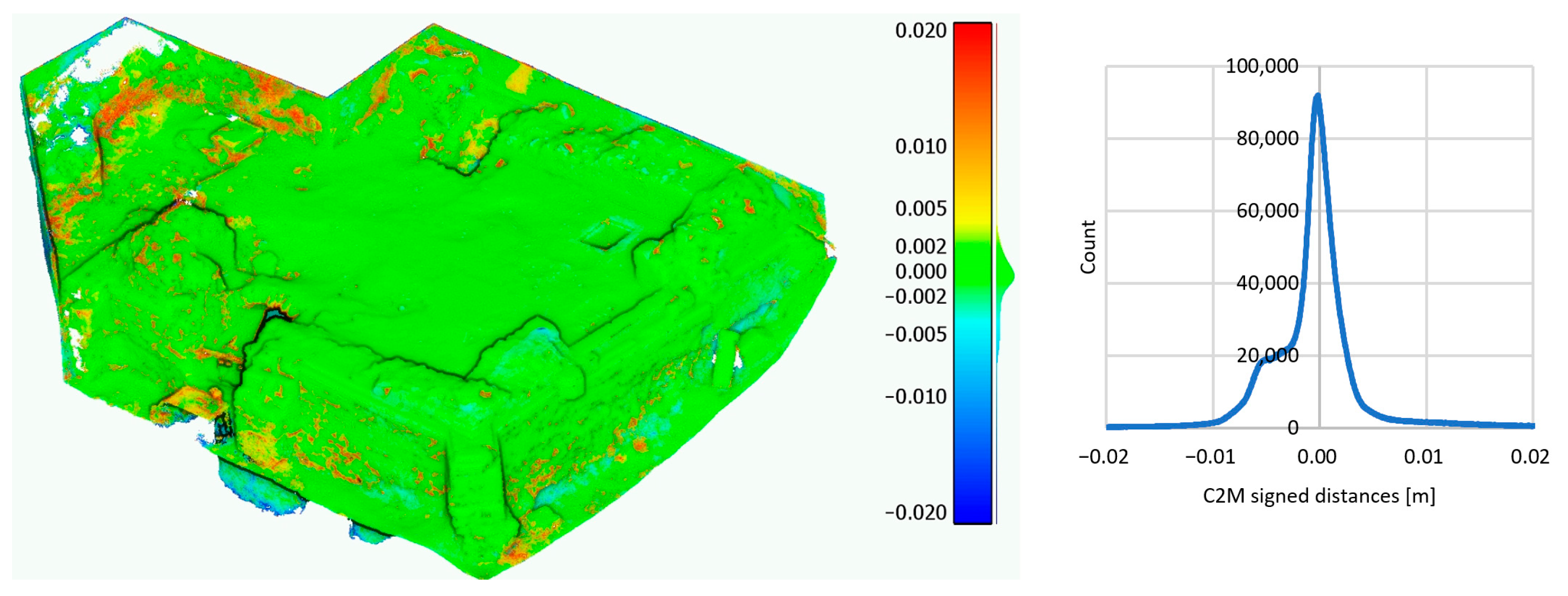
4.1. Photogrammetric Variant A (with All Images) vs. TLS
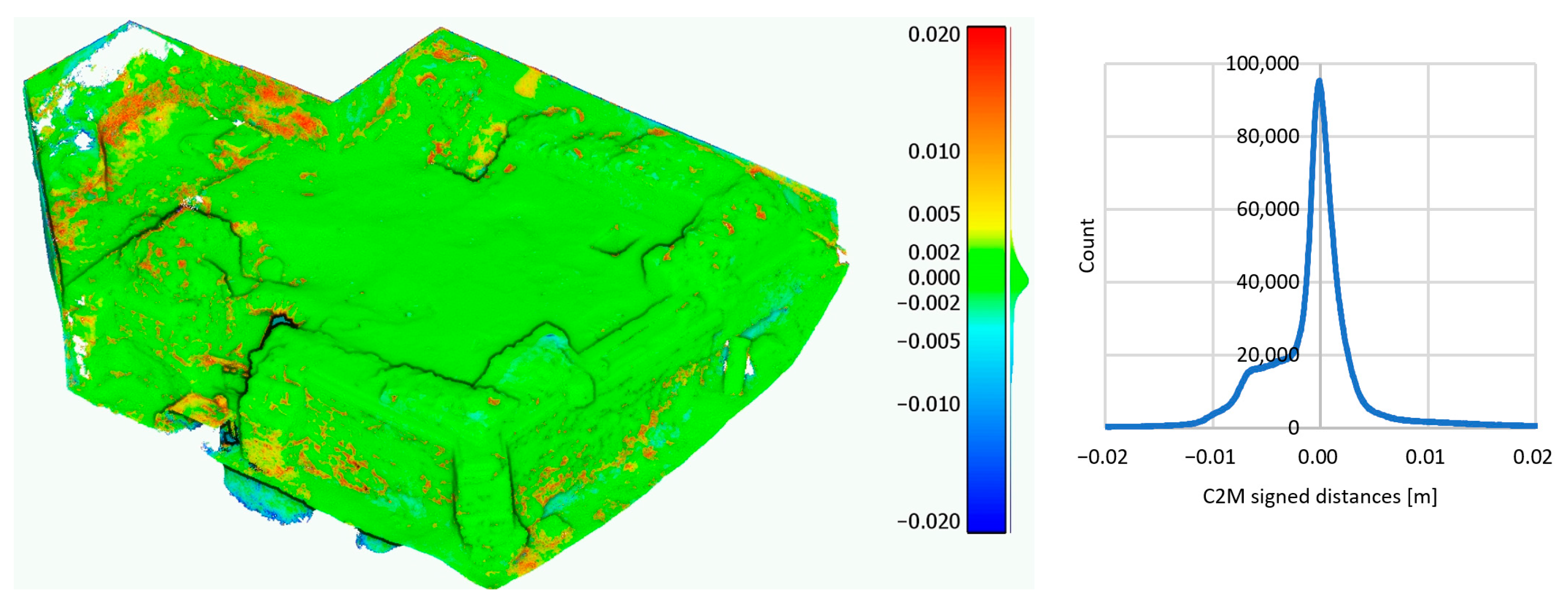
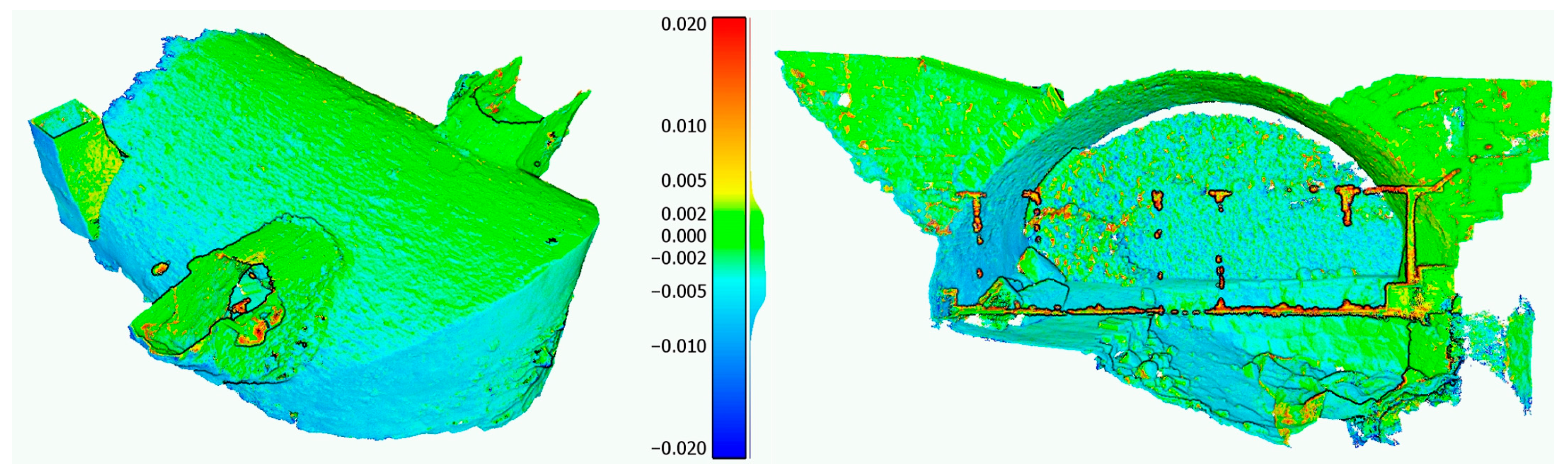
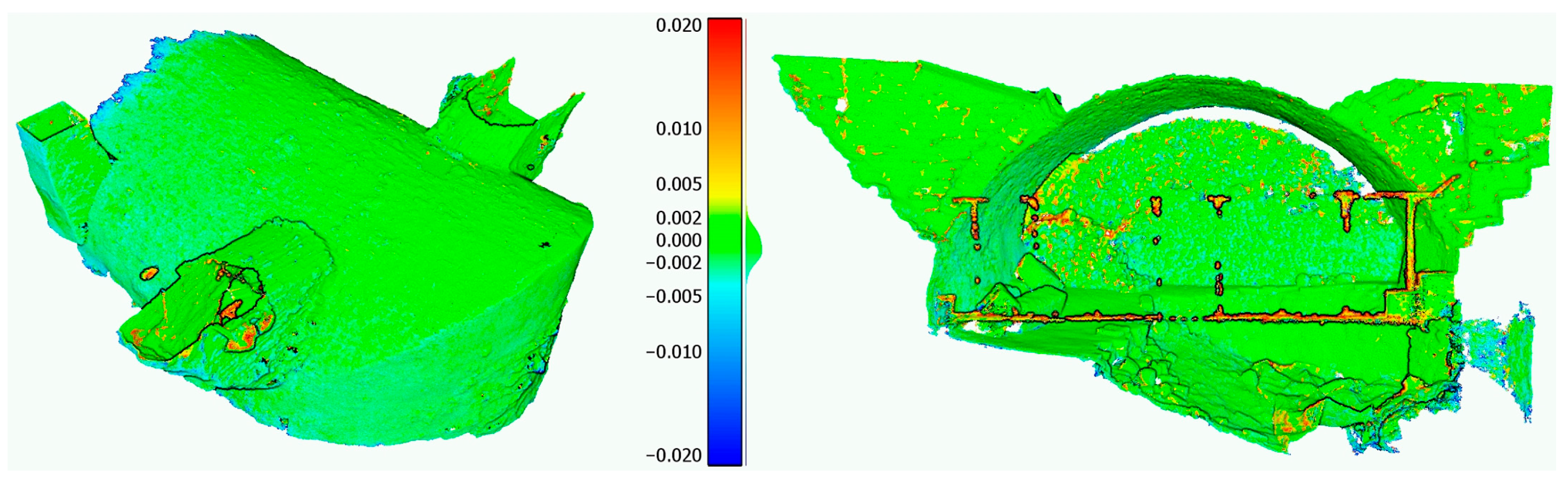
4.2. Photogrammetric Variants B, C, and D vs. the Reference Photogrammetric Variant A
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brandolini, F.; Patrucco, G. Structure-from-motion (SFM) photogrammetry as a non-invasive methodology to digitalize historical documents: A highly flexible and low-cost approach? Heritage 2019, 2, 2124–2136. [Google Scholar] [CrossRef]
- Caroti, G.; Martinez Espejo Zaragoza, I.; Piemonte, A. Historical data of laser scanning and photogrammetry for the knowledge and memory plan of Cultural Heritage. In Proceedings of the IMEKO TC-4 International Conference on Metrology for Archaeology and Cultural Heritage, Florence, Italy, 4–6 December 2019; pp. 136–141. [Google Scholar]
- Lowe, G. Sift-the scale invariant feature transform. Int. J. 2004, 2, 91–110. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Ullman, S. The interpretation of structure from motion. Proc. R. Soc. London. Ser. B Biol. Sci. 1979, 203, 405–426. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J.-M. Structure-from-motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar] [CrossRef]
- Wu, C. Towards linear-time incremental structure from motion. In Proceedings of the 2013 International Conference on 3D Vision-3DV 2013, Washington, DC, USA, 29 June–1 July 2013; IEEE: New York, NY, USA, 2013; pp. 127–134. [Google Scholar] [CrossRef]
- Gherardi, R.; Farenzena, M.; Fusiello, A. Improving the Efficiency of Hierarchical Structure-and-motion. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; IEEE: New York, NY, USA, 2010; pp. 1594–1600. [Google Scholar] [CrossRef]
- Crandall, D.; Owens, A.; Snavely, N.; Huttenlocher, D. Discrete-continuous optimization for large-scale structure from motion. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; IEEE: New York, NY, USA, 2011; pp. 3001–3008. [Google Scholar] [CrossRef]
- Förstner, W.; Wrobel, B.P. Photogrammetric Computer Vision; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Pavelka, K.; Raeva, P.; Pavelka, K., Jr.; Kýhos, M.; Veselý, Z. Analysis of data joining from different instruments for object modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 853–860. [Google Scholar] [CrossRef]
- Laasch, H.; Ryter, N.; Steffen, I.; Reske, A.; Friedli, E.; Frangez, V. Automated Inspection within Galleries of Large Dams. Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2022/papers/ts04d/TS04D_laasch_ryter_et_al_11349.pdf (accessed on 10 December 2022).
- Piniotis, G.; Soile, S.; Bourexis, F.; Tsakiri, M.; Ioannidis, C. Experimental assessment of 3D narrow space mapping technologies. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 149–156. [Google Scholar] [CrossRef]
- ContextCapture. Available online: https://www.bentley.com/software/contextcapture/ (accessed on 10 December 2022).
- Lerma, J.L.; Navarro, S.; Cabrelles, M.; Villaverde, V. Terrestrial laser scanning and close range photogrammetry for 3D archaeological documentation: The Upper Palaeolithic Cave of Parpalló as a case study. J. Archaeol. Sci. 2010, 37, 499–507. [Google Scholar] [CrossRef]
- Hatzopoulos, J.N.; Stefanakis, D.; Georgopoulos, A.; Tapinaki, S.; Volonakis, S.; Volonakis, P.; Liritzis, I. Use of various surveying technologies to 3D digital mapping and modelling of cultural heritage structures for maintenance and restoration purposes: The Tholos in Delphi, Greece. Mediterr. Archaeol. Archaeom. 2017, 17, 311–336. [Google Scholar] [CrossRef]
- Li, P.; Wang, R.; Wang, Y.; Tao, W. Evaluation of the ICP algorithm in 3D point cloud registration. IEEE Access 2020, 8, 68030–68048. [Google Scholar] [CrossRef]
- Grussenmeyer, P.; Alby, E.; Assali, P.; Poitevin, V.; Hullo, J.F.; Smigiel, E. Accurate Documentation in Cultural Heritage by Merging TLS and High-resolution Photogrammetric Data. In Videometrics, Range Imaging, and Applications XI; SPIE: Bellingham, WD, USA, 2011; pp. 79–91. [Google Scholar] [CrossRef]
- Andaru, R.; Cahyono, B.K.; Riyadi, G.; Ramadhan, G.R.; Tuntas, S.; Istarno. The combination of terrestrial lidar and UAV photogrammetry for interactive architectural heritage visualization using Unity 3D game engine. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W17, 39–44. [Google Scholar] [CrossRef]
- 3DF Zephyr. Available online: https://www.3dflow.net/3df-zephyr-photogrammetry-software/ (accessed on 15 September 2022).
- Luhmann, T.; Chizhova, M.; Gorkovchuk, D.; Hastedt, H.; Chachava, N.; Lekveishvili, N. Combination of terrestrial laserscanning, UAV and close range photogrammertry for 3D reconstruction of complex churches in Georgia. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, XLII-2/W11, 753–761. [Google Scholar] [CrossRef]
- Agisoft Metashape: Professional Edition. Available online: https://www.agisoft.com/features/professional-edition/ (accessed on 15 September 2022).
- RealityCapture—Photogrammetry Software. Available online: https://www.capturingreality.com/realitycapture (accessed on 15 September 2022).
- Teza, G.; Pesci, A.; Ninfo, A. Morphological analysis for architectural applications: Comparison between laser scanning and structure-from-motion photogrammetry. J. Surv. Eng. 2016, 142, 04016004. [Google Scholar] [CrossRef]
- Wilkinson, M.; Jones, R.; Woods, C.; Gilment, S.; McCaffrey, K.; Kokkalas, S.; Long, J. A comparison of terrestrial laser scanning and structure-from-motion photogrammetry as methods for digital outcrop acquisition. Geosphere 2016, 12, 1865–1880. [Google Scholar] [CrossRef]
- Masiero, A.; Fissore, F.; Guarnieri, A.; Piragnolo, M.; Vettore, A. Comparison of low cost photogrammetric survey with TLS and Leica pegasus backpack 3d modelss. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 147. [Google Scholar] [CrossRef]
- Marín-Buzón, C.; Pérez-Romero, A.M.; León-Bonillo, M.J.; Martínez-Álvarez, R.; Mejías-García, J.C.; Manzano-Agugliaro, F. Photogrammetry (SfM) vs. Terrestrial Laser Scanning (TLS) for Archaeological Excavations: Mosaic of Cantillana (Spain) as a Case Study. Appl. Sci. 2021, 11, 11994. [Google Scholar] [CrossRef]
- Šimončičová Koóšová, P.; Lesák, B.; Pivko, D. Kamenárske značky z Kaplnky sv. Jakuba v Bratislave. Archaeol. Hist. 2015, 711–731. [Google Scholar] [CrossRef][Green Version]
- Masnicová, S.; Beňuš, R. The Health Status and Lifestyle of Historic Bratislava Inhabitants: I. Pilot Study of Long Bone Lesions from Gothic Part (XVth–XVIIIth Cent. AD) of the Ossuary in St. Jacob Chapel (Bratislava, Slovakia). Anthropologie 2001, 39, 63–68. [Google Scholar]
- Alsadik, B.; Gerke, M.; Vosselman, G.; Daham, A.; Jasim, L. Minimal camera networks for 3D image based modeling of cultural heritage objects. Sensors 2014, 14, 5785–5804. [Google Scholar] [CrossRef] [PubMed]
- Uffenkamp, V. State of the Art of High Precision Industrial Photogrammetry. In Third International Workshop on Accelerator Alignment; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Urban, R.; Braun, J.; Štroner, M. Precise deformation measurement of prestressed concrete beam during a strain test using the combination of intersection photogrammetry and micro-network measurement. In Videometrics, Range Imaging, and Applications XIII; SPIE: Bellingham, WD, USA, 2015; pp. 305–312. [Google Scholar] [CrossRef]
- Amiri, P.J.; Gruen, A.; Cozzani, A. High accuracy space structures monitoring by a close-range photogrammetric network. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 236–241. [Google Scholar] [CrossRef]










| Max. scan speed | 976,000 pts/s |
| Range | 0.6–120 m |
| Field of view (vertical/horizontal) | 300°/360° |
| Ranging error | ±2 mm at 25 m |
| Ranging noise | 0.95 mm at 25 m and 90% reflectivity |
| Sensor size | 36 × 24 mm |
| Image size | 7360 × 4912 pixels |
| Lens 1 | AF-S Nikkor 20 mm f/1.8 G ED |
| Lens 2 | Nikkor 16 mm f2.8 D AF Fisheye |
| Variant | A | B, C, and D |
|---|---|---|
| Max. features per image | 40,000 | |
| Image downscale factor | 1 (high accuracy) | |
| Max. tie points per image | 10,000 | |
| Dense cloud quality | Medium | Low |
| Distortion model for fisheye lens | Fisheye | |
| Distortion model for 20 mm lens | Frame (Brown distortion model) | |
| Variant | A | B | C | D |
|---|---|---|---|---|
| Number of aligned images | 789 | 737 | 754 | 771 |
| Number of tie points | 1.74 mil. | 1.63 mil. | 1.66 mil. | 1.71 mil. |
| RMS Reprojection error | 0.18 pix | 0.18 pix | 0.18 pix | 0.18 pix |
| Number of points in dense cloud | 58.9 mil. | 24.5 mil. | 26.1 mil. | 27.3 mil. |
| Number of faces in mesh | 14.7 mil. | - | - | - |
| Comparison | Standard Deviation (mm) | Points with Dev. <10 mm (%) | Points with Dev. <5 mm (%) |
|---|---|---|---|
| TLS vs. A after ICP | 7.0 | 95.5 | 85.6 |
| A vs. B | 8.0 | 94.4 | 82.1 |
| A vs. C | 7.8 | 93.6 | 90.3 |
| A vs. D | 8.2 | 93.6 | 78.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marčiš, M.; Fraštia, M.; Kovanič, Ľ.; Blišťan, P. Deformations of Image Blocks in Photogrammetric Documentation of Cultural Heritage—Case Study: Saint James’s Chapel in Bratislava, Slovakia. Appl. Sci. 2023, 13, 261. https://doi.org/10.3390/app13010261
Marčiš M, Fraštia M, Kovanič Ľ, Blišťan P. Deformations of Image Blocks in Photogrammetric Documentation of Cultural Heritage—Case Study: Saint James’s Chapel in Bratislava, Slovakia. Applied Sciences. 2023; 13(1):261. https://doi.org/10.3390/app13010261
Chicago/Turabian StyleMarčiš, Marián, Marek Fraštia, Ľudovít Kovanič, and Peter Blišťan. 2023. "Deformations of Image Blocks in Photogrammetric Documentation of Cultural Heritage—Case Study: Saint James’s Chapel in Bratislava, Slovakia" Applied Sciences 13, no. 1: 261. https://doi.org/10.3390/app13010261
APA StyleMarčiš, M., Fraštia, M., Kovanič, Ľ., & Blišťan, P. (2023). Deformations of Image Blocks in Photogrammetric Documentation of Cultural Heritage—Case Study: Saint James’s Chapel in Bratislava, Slovakia. Applied Sciences, 13(1), 261. https://doi.org/10.3390/app13010261









