Quasi-Shor Algorithms for Global Benchmarking of Universal Quantum Processors
Abstract
1. Introduction
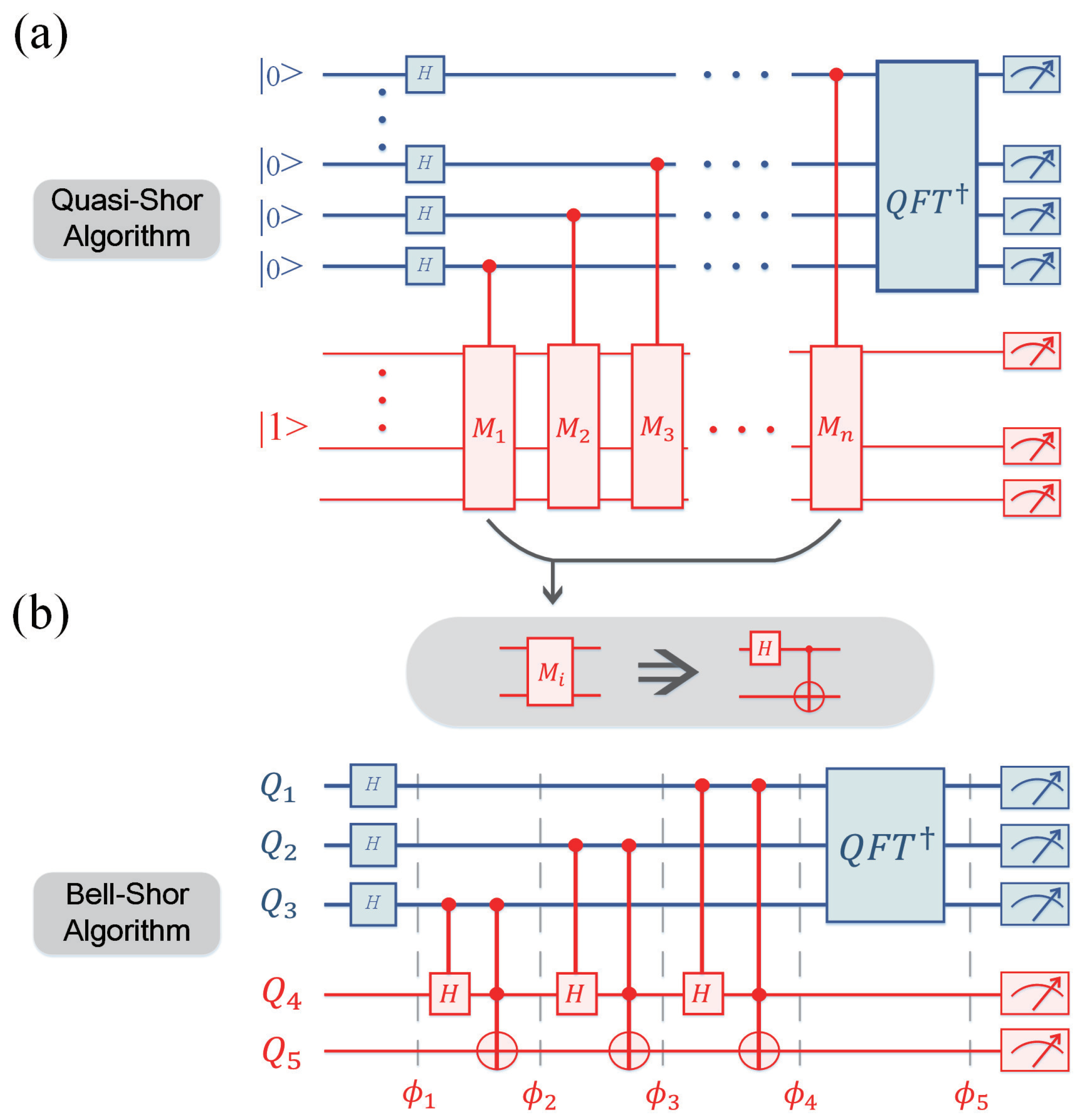
2. Quasi-Shor and Bell–Shor Algorithms
3. Witness the Density Matrices
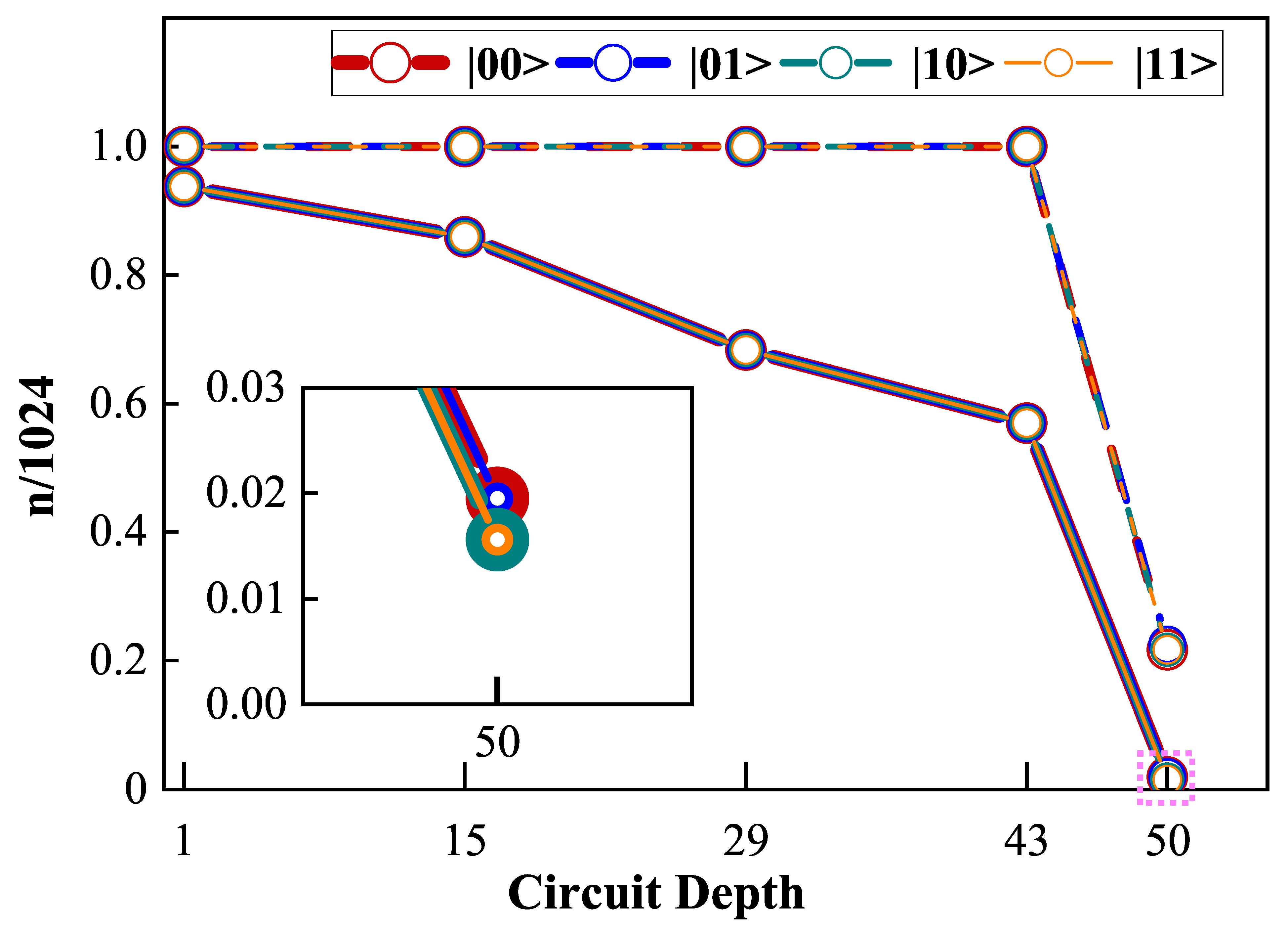
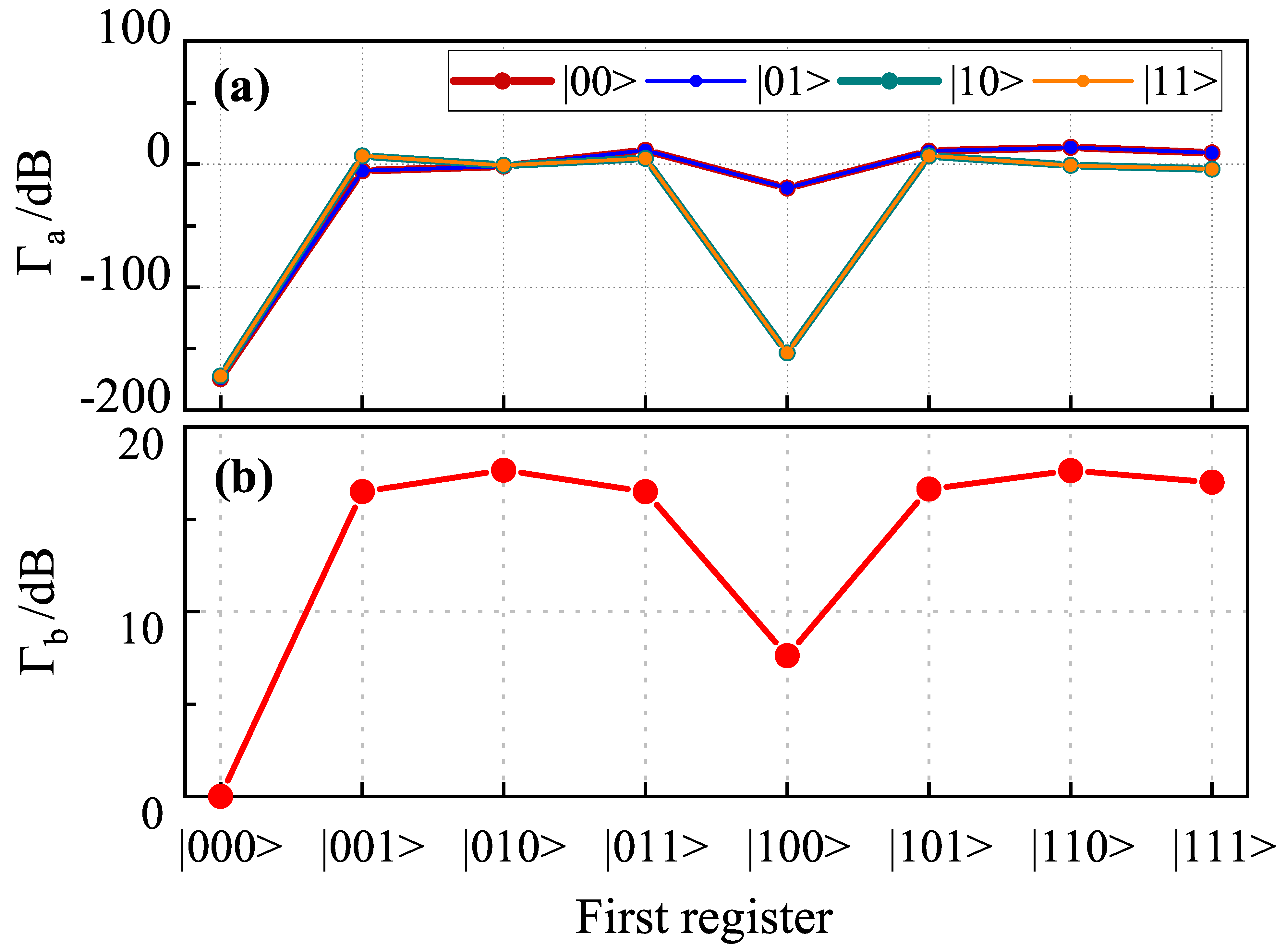
4. Error Metrics for Benchmarking
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
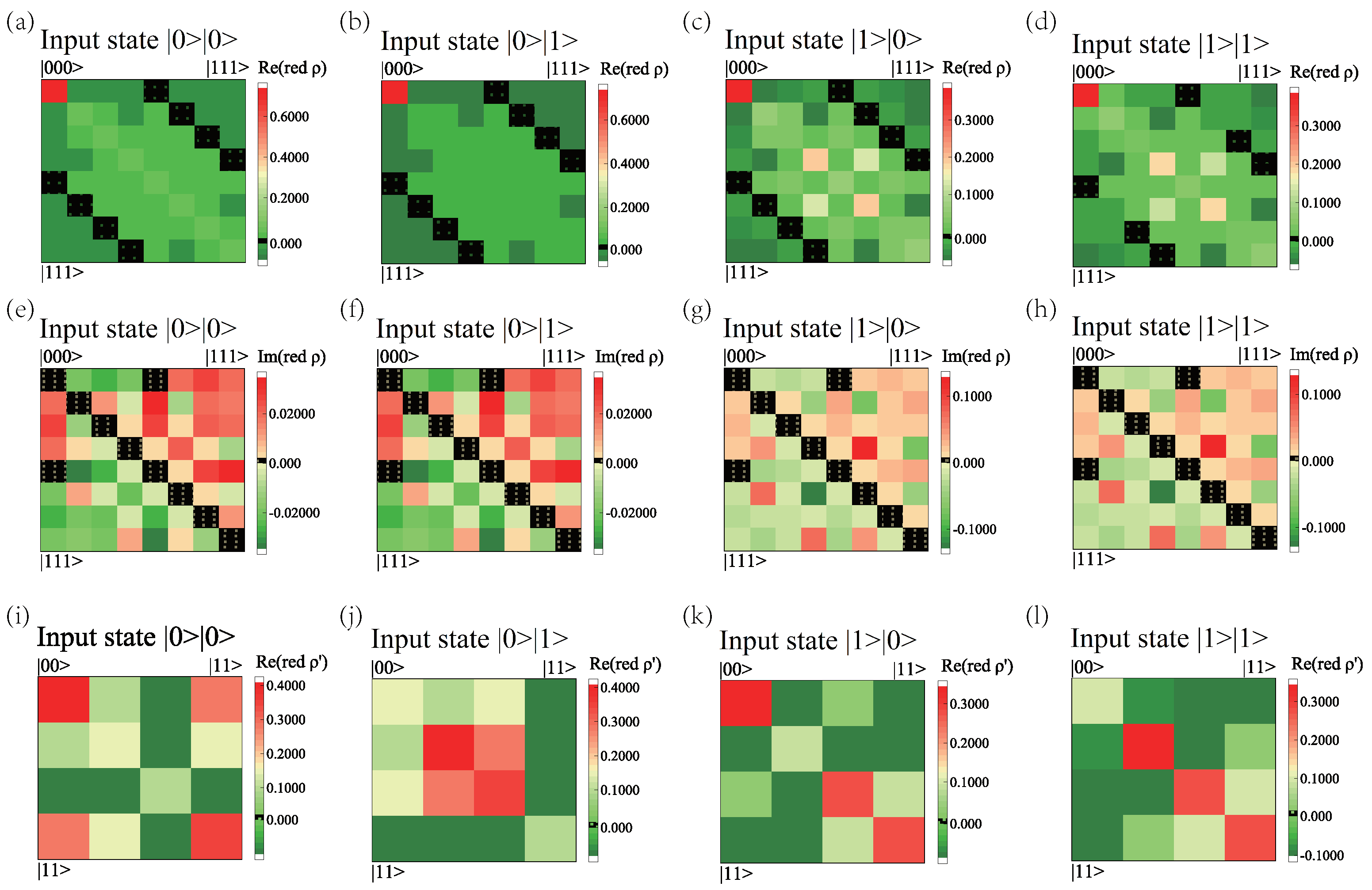
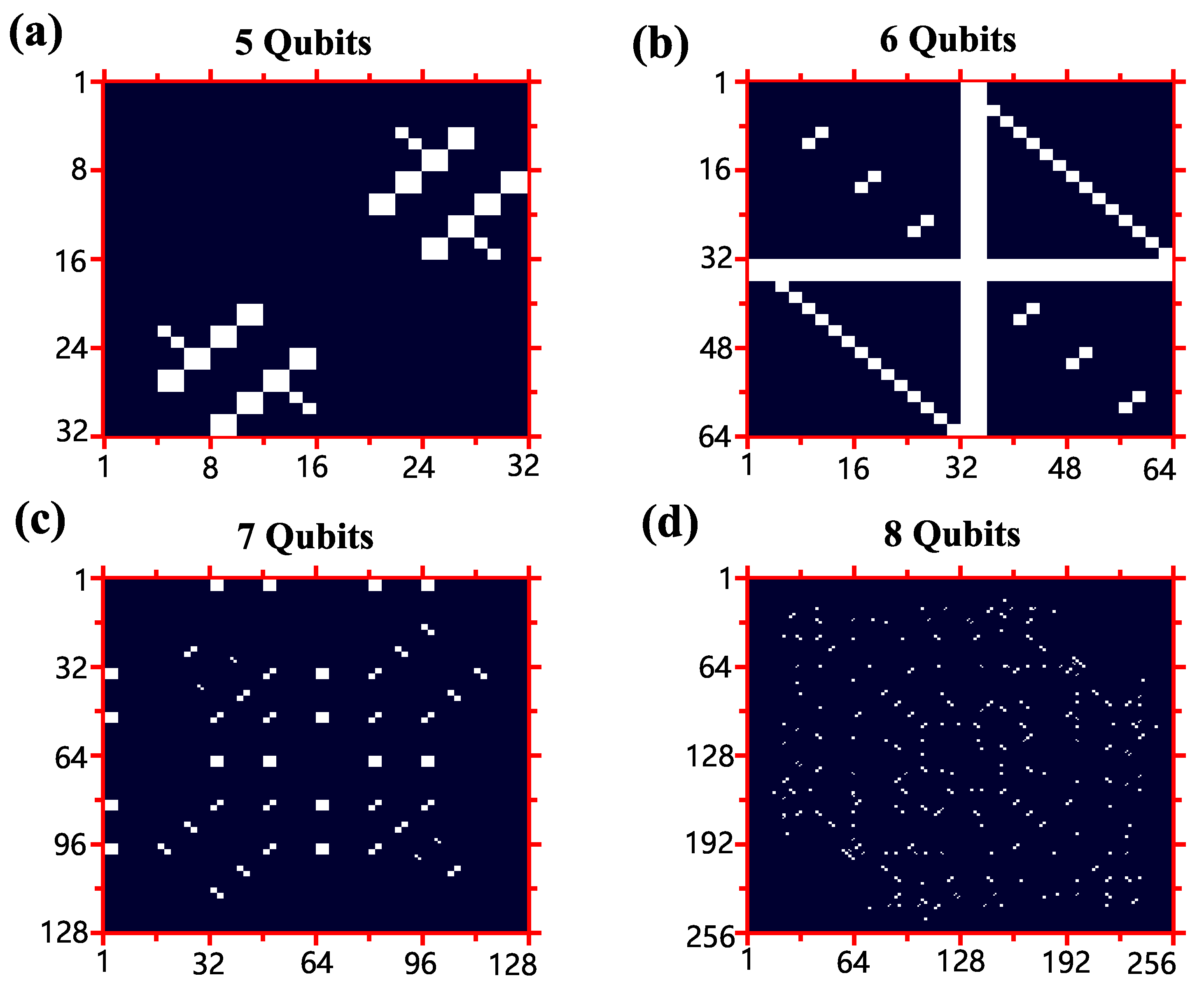
Appendix A. Visualization of Density Matrices
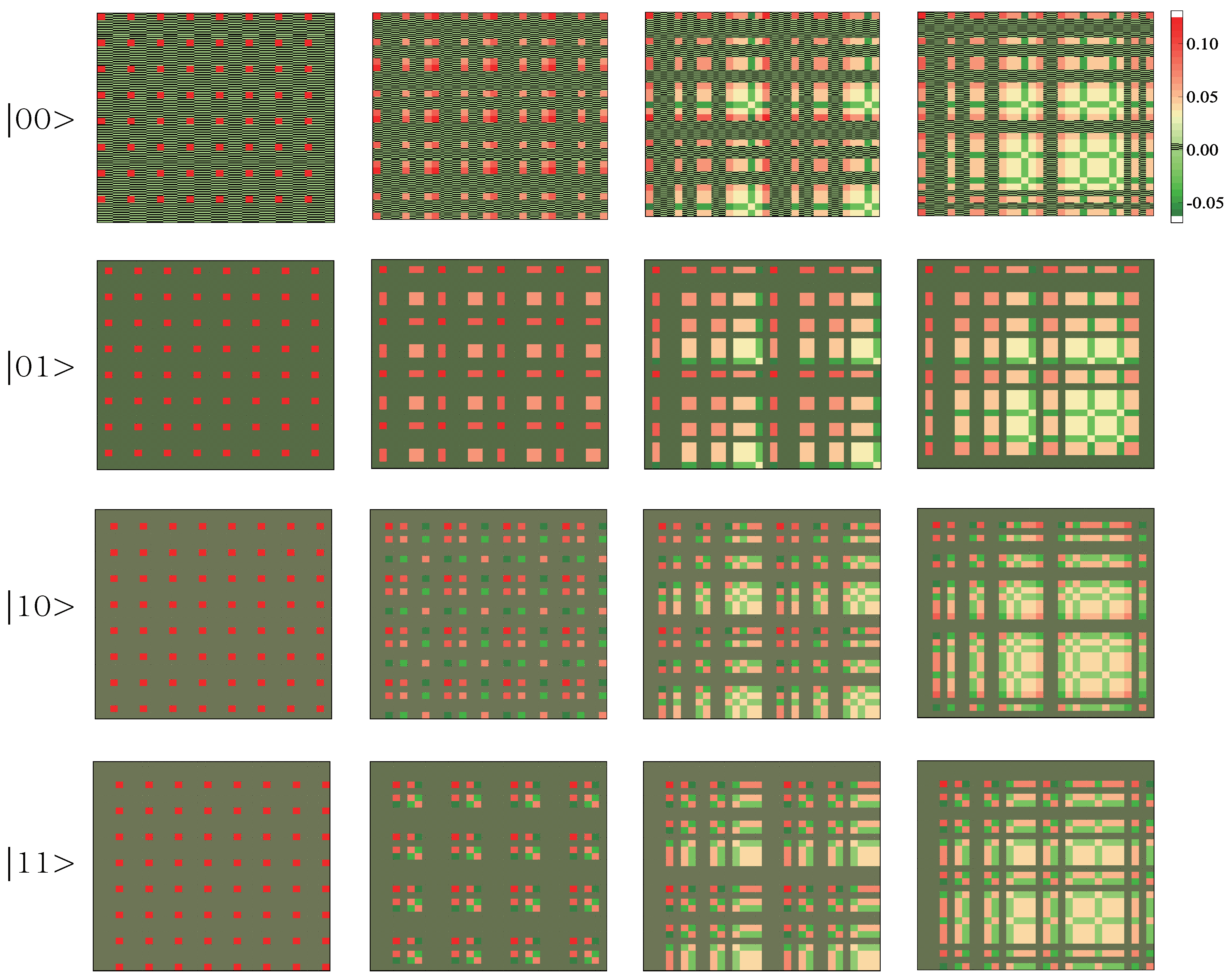
| Quantum States | Standard | Real Part | Imaginary Part |
|---|---|---|---|
| (1,1) | (2,5);(5,2);(5,8);(8,5) | ||
| ) | Absolute Zero | (1,5);(2,6);(3,7);(4,8); (5,1);(6,2);(7,3);(8,4) | (1,1);(2,2);(3,3);(4,4);(5,5); (6,6);(7,7);(8,8);(1,5);(5,1) |
| (1,1) | (2,5);(5,2);(5,8);(8,5) | ||
| Absolute Zero | (1,5);(2,6);(3,7);(4,8); (5,1);(6,2);(7,3);(8,4) | (1,1);(2,2);(3,3);(4,4);(5,5); (6,6);(7,7);(8,8);(1,5);(5,1) | |
| (1,1) | (6,4);(4,6) | ||
| Absolute Zero | (1,5);(2,6);(3,7);(4,8); (5,1);(6,2);(7,3);(8,4) | (1,1);(2,2);(3,3);(4,4);(5,5); (6,6);(7,7);(8,8);(1,5);(5,1) | |
| (1,1) | (6,4);(4,6) | ||
| ) | Absolute Zero | (1,5);(3,7);(4,8); (5,1);(7,3);(8,4) | (1,1);(2,2);(3,3);(4,4);(5,5); (6,6);(7,7);(8,8);(1,5);(5,1) |
| (1,1) | None | ||
| ) | Absolute Zero | None | All |
| (2,2) | None | ||
| ) | Absolute Zero | None | All |
| (1,1) | None | ||
| ) | Absolute Zero | None | All |
| (2,2) | (2,3);(3,2) | ||
| ) | Absolute Zero | None | (1,1);(1,3);(1,4);(2,2);(2,4);(3,1); (3,3);(3,4);(4,1);(4,2);(4,3);(4,4) |
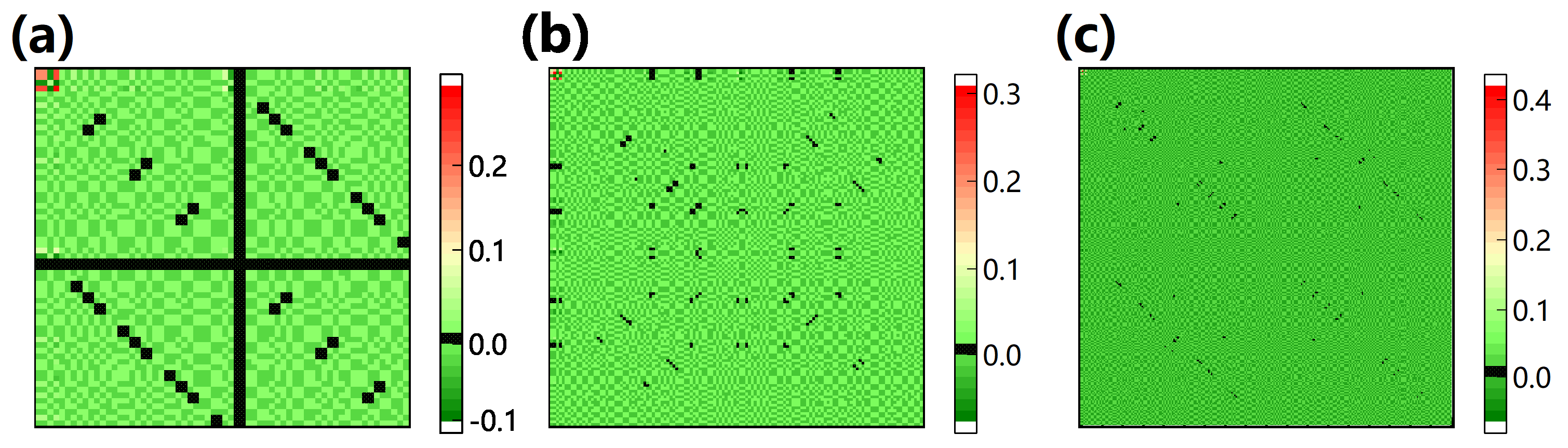
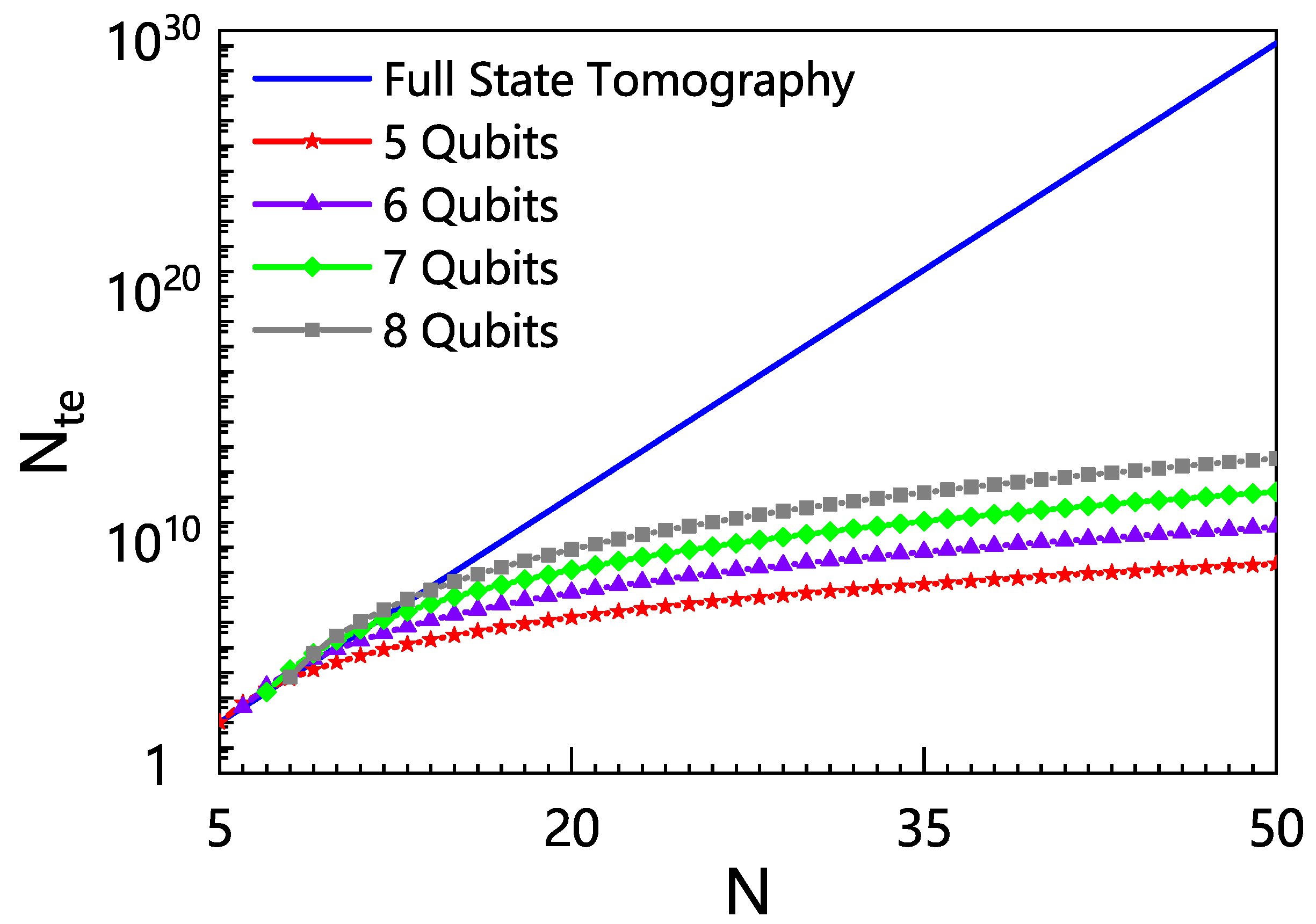
Appendix B. Bell–Shor Algorithm with Larger Numbers of Qubits
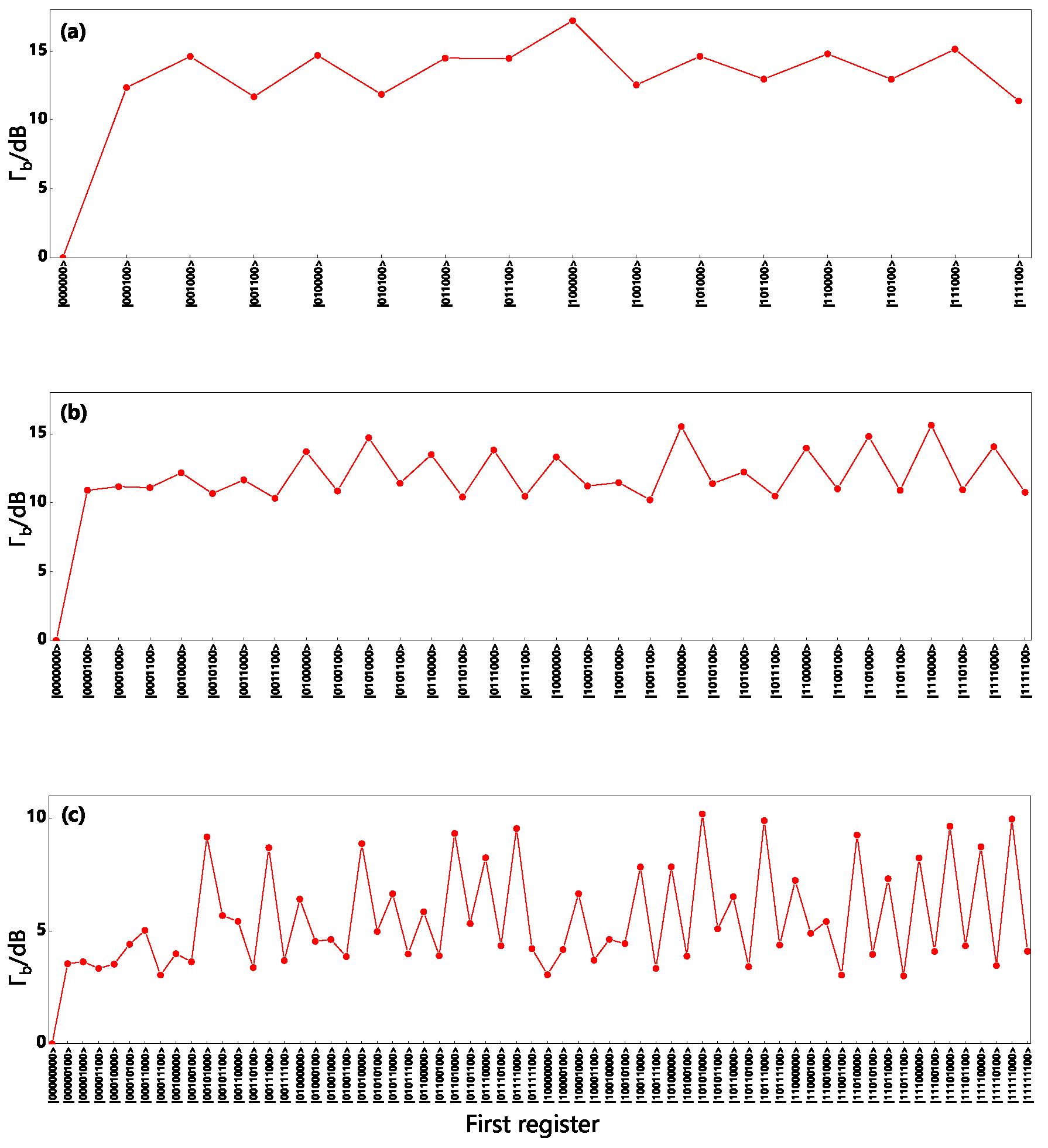
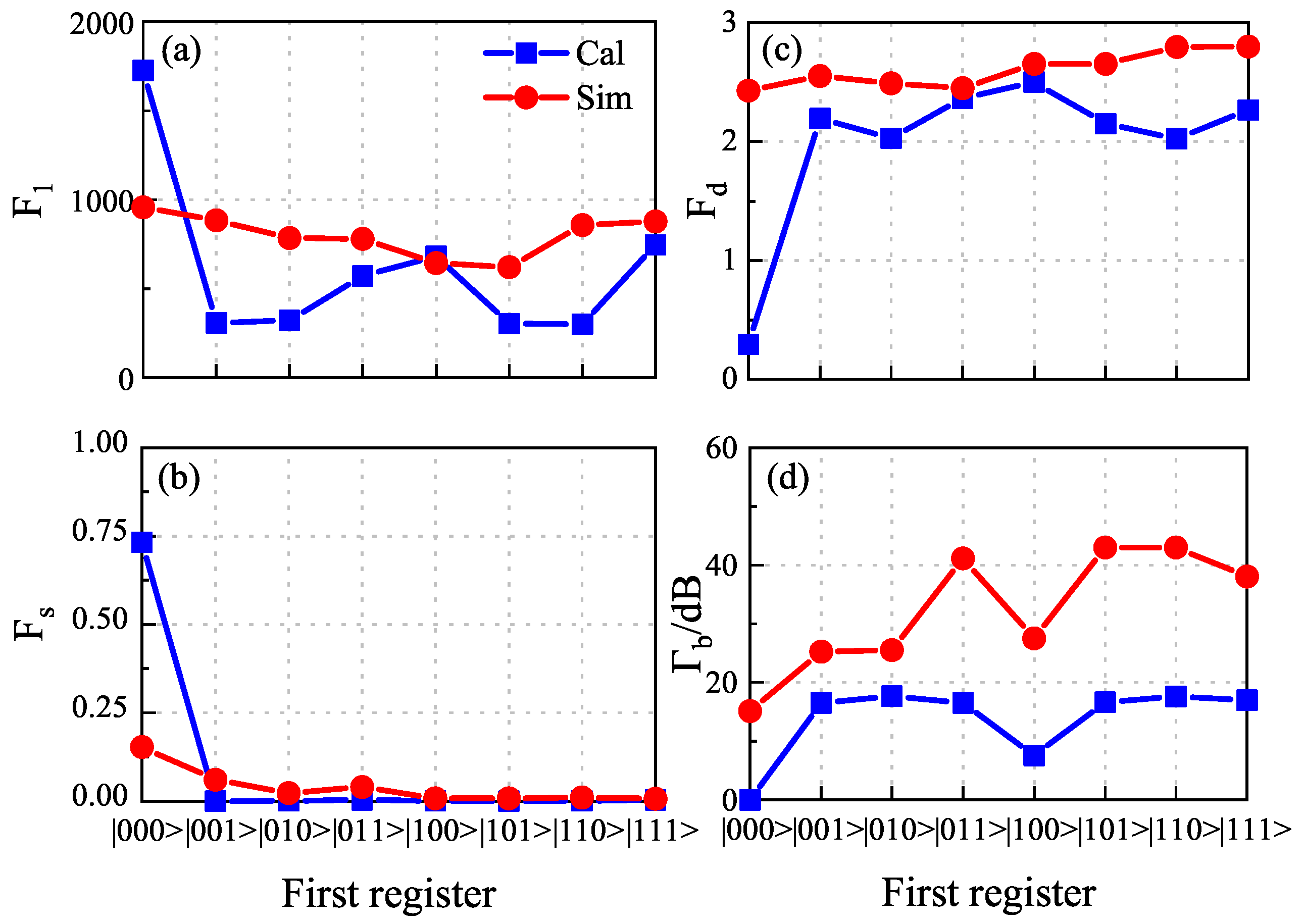
Appendix C. Calculation and Simulation of Γb and Fidelity
References
- Devoret, M.H.; Schoelkopf, R.J. Superconducting Circuits for Quantum Information: An Outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, S.; Christensen, K.; Pedersen, S.; Kristensen, L.; Bækkegaard, T.; Loft, N.; Zinner, N. Superconducting Circuit Companion—An Introduction with Worked Examples. PRX Quantum 2021, 2, 040204. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Wright, K.; Beck, K.M.; Debnath, S.; Amini, J.M.; Nam, Y.; Grzesiak, N.; Chen, J.-S.; Pisenti, N.C.; Chmielewski, M.; Collins, C.; et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 2019, 10, 5464. [Google Scholar] [CrossRef] [PubMed]
- Zu, C.; Wang, W.-B.; He, L.; Zhang, W.-G.; Dai, C.-Y.; Wang, F.; Duan, L.-M. Experimental realization of universal geometric quantum gates with solid-state spins. Nature 2014, 514, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Lekitsch, B.; Weidt, S.; Fowler, A.G.; Mølmer, K.; Devitt, S.J.; Wunderlich, C.; Hensinger, W.K. Blueprint for a microwave trapped ion quantum computer. Nature 2017, 3, 2. [Google Scholar] [CrossRef]
- Mong, R.S.K.; Clarke, D.J.; Alicea, J.; Lindner, N.H.; Fendley, P.; Nayak, C.; Oreg, Y.; Stern, A.; Berg, E.; Shtengel, K.; et al. Universal Topological Quantum Computation from a Superconductor-Abelian Quantum Hall Heterostructure. Phys. Rev. X 2014, 4, 011036. [Google Scholar] [CrossRef]
- Terhal, B.M. Quantum error correction for quantum memories. Rev. Mod. Phys. 2015, 87, 307–346. [Google Scholar] [CrossRef]
- Harrow, A.W.; Montanaro, A. Quantum computational supremacy. Nature 2017, 549, 203–209. [Google Scholar] [CrossRef]
- Campbell, E.T.; Terhal, B.M.; Vuillot, C. Roads towards fault-tolerant universal quantum computation. Nature 2017, 549, 172–179. [Google Scholar] [CrossRef]
- Moll, N.; Barkoutsos, P.; Bishop, L.S.; Chow, J.M.; Cross, A.; Egger, D.J.; Filipp, S.; Fuhrer, A.; Gambetta, J.M.; Ganzhorn, M.; et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Sci. Technol. 2018, 3, 030503. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A 1985, 400, 97–117. [Google Scholar]
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Math. Phys. Eng. Sci. 1992, 439, 553–558. [Google Scholar]
- DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.R.; Schuster, D.I.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.M.; et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240–244. [Google Scholar] [CrossRef]
- Sangskriti, S.; Nag, P.; Haque, S. Fundamental Machine Learning Routines as Quantum Algorithms on a Superconducting Quantum Computer. arXiv 2021, arXiv:2109.09522. [Google Scholar]
- Lee, Y.; Joo, J.; Lee, S. Hybrid quantum linear equation algorithm and its experimental test on IBM Quantum Experience. Sci. Rep. 2019, 9, 4778. [Google Scholar] [CrossRef] [PubMed]
- Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef]
- Chen, C.-C.; Shiau, S.-Y.; Wu, M.-F.; Wu, Y.-R. Hybrid classical-quantum linear solver using Noisy Intermediate-Scale Quantum machines. Sci. Rep. 2019, 9, 16251. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Logarithms on a Quantum Computer. Siam J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Skosana, U.; Tame, M. Demonstration of Shor’s factoring algorithm for N = 21 on IBM quantum processors. Sci. Rep. 2021, 11, 16599. [Google Scholar] [CrossRef]
- Figgatt, C.; Maslov, D.; Landsman, K.; Linke, N.M.; Debnath, S.; Monroe, C.R. Complete 3-Qubit Grover search on a programmable quantum computer. Nat. Commun. 2017, 8, 1918. [Google Scholar] [CrossRef] [PubMed]
- Damm, W.V.; Hayden, P. Universal entanglement transformations without communication. Phys. Rev. A 2003, 67, 060302. [Google Scholar]
- Zhou, X.-Q.; Kalasuwan, P.; Ralph, T.; O’Brien, J. Calculating unknown eigenvalues with a quantum algorithm. Nat. Photon. 2013, 7, 223–228. [Google Scholar] [CrossRef]
- Vandersypen, L.M.K.; Steffen, M.; Breyta, G.; Yannoni, C.S.; Sherwood, M.H.; Chuang, I.L. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 2001, 414, 883–887. [Google Scholar] [CrossRef] [PubMed]
- López, E.M.; Laing, A.; Lawson, T.; Alvarez, R.; Zhou, X.Q.; O’Biren, J.L. Experimental realization of Shor’s quantum factoring algorithm using qubit recycling. Nat. Photon. 2012, 6, 773–776. [Google Scholar] [CrossRef]
- Greganti, C.; Demarie, T.F.; Ringbauer, M.; Jones, J.A.; Saggio, V.; Calafell, I.A.; Rozema, L.A.; Erhard, A.; Meth, M.; Postler, L.; et al. Cross-verification of independent quantum devices. In Proceedings of the 2021 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 21–25 June 2021. [Google Scholar]
- Chen, Y.-T.; Farquhar, C.; Parrish, R.M. Low-rank density-matrix evolution for noisy quantum circuits. NPJ Quantum Inf. 2021, 7, 61. [Google Scholar] [CrossRef]
- Roulet, J.; Vanicek, J. An implicit split-operator algorithm for the nonlinear time-dependent Schrödinger equation. J. Chem. Phys. 2021, 155, 204109. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, B.; Wang, X. Variational Quantum Algorithm for Schmidt Decomposition. arXiv 2021, arXiv:2109.10785v1. [Google Scholar]
- Wang, B.; Hu, F.; Yao, H.; Wang, C. Prime factorization algorithm based on parameter optimization of Ising model. Sci. Rep. 2020, 10, 7106. [Google Scholar] [CrossRef]
- Shor, P.W. Progress in Quantum Algorithms. In Experimental Aspects of Quantum Computing; Springer: Berlin/Heidelberg, Germany, 2007; pp. 5–13. [Google Scholar]
- He, Y.C.; Zhao, C.H.; Dai, G.T.; He, K.Y.; Geng, X.; Liu, J.S.; Chen, W. Quantum modular multiplier via binary-exponent-based recombination. Quantum Inf. Process. 2022, 21, 391. [Google Scholar] [CrossRef]
- Ferraro, E.; Michielis, M.D. On the robustness of the hybrid qubit computational gates through simulated randomized benchmarking protocols. Sci. Rep. 2020, 10, 17780. [Google Scholar] [CrossRef] [PubMed]
- Onorati, E.; Werner, A.H.; Eisert, J. Randomized Benchmarking for Individual Quantum Gates. Phys. Rev. Lett. 2019, 123, 060501. [Google Scholar] [CrossRef]
- Benedetti, M.; Pintos, D.G.; Perdomo, O.; Ortega, V.L.; Nam, Y.; Ortiz, A.P. A generative modeling approach for benchmarking and training shallow quantum circuits. Npj Quantum Inform. 2019, 5, 45. [Google Scholar] [CrossRef]
- Chasseur, T.; Reich, D.M.; Koch, C.; Wilhelm, F.K. Hybrid benchmarking of arbitrary quantum gates. Phys. Rev. A 2017, 95, 062335. [Google Scholar] [CrossRef]
- Knill, E.; Leibfried, D.; Reichle, R.; Britton, J.; Blakestad, R.B.; Jost, J.D.; Langer, C.; Ozeri, R.; Seidelin, S.; Wineland, D.J. Randomized benchmarking of quantum gates. Phys. Rev. A 2008, 77, 012307. [Google Scholar] [CrossRef]
- Huang, Y.-T.; Lin, J.-D.; Ku, H.-Y.; Chen, Y.-N. Benchmarking quantum state transfer on quantum devices. Phys. Rev. Res. 2021, 3, 023038. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, Y.; Zhao, Q.; Regula, B.; Thompson, J.; Gu, M. Universal and operational benchmarking of quantum memories. NPJ Quantum Inf. 2021, 7, 108. [Google Scholar] [CrossRef]
- Eisert, J.; Hangleiter, D.; Walk, N.; Roth, I.; Markham, D.; Parekh, R.; Chabaud, U.; Kashefi, E. Quantum certification and benchmarking. Nat. Rev. Phys. 2020, 2, 382–390. [Google Scholar] [CrossRef]
- Eisert, J.; Hangleiter, D.; Walk, N.; Roth, I.; Markham, D.; Parekh, R.; Chabaud, U.; Kashefi, E. Quantum benchmarking with realistic states of light. Phys. Rev. A 2012, 86, 022331. [Google Scholar]
- Nakata, Y.; Zhao, D.; Okuda, T.; Bannai, E.; Suzuki, Y.; Tamiya, S.; Heya, K.; Yan, Z.G.; Zuo, K.; Tamate, S.H.; et al. Quantum Circuits for Exact Unitary t-Designs and Applications to Higher-Order Randomized Benchmarking. PRX Quantum 2021, 2, 030339. [Google Scholar] [CrossRef]
- Subires, D.; Ruiz, F.J.G.; García, A.R.; Alonso, D.; Campo, A.D. Benchmarking quantum annealing dynamics: The spin-vector Langevin model. Phys. Rev. Res. 2022, 4, 023104. [Google Scholar] [CrossRef]
- Song, C.; Cui, J.; Wang, H.; Hao, J.; Feng, H.; Li, Y. Quantum computation with universal error mitigation on a superconducting quantum processor. Sci. Adv. 2019, 5, 9. [Google Scholar] [CrossRef] [PubMed]
- Erhard, A.; Wallman, J.J.; Postler, L.; Meth, M.; Stricker, R.; Martinez, E.A.; Schindler, P.; Monz, T.; Emerson, J.; Blatt, R. Characterizing large-scale quantum computers via cycle benchmarking. Nat. Commun. 2019, 10, 5347. [Google Scholar] [CrossRef] [PubMed]
- Flamini, F.; Spagnolo, N.; Viggianiello, N.; Crespi, A.; Osellame, R.; Sciarrino, F. Benchmarking integrated linear-optical architectures for quantum information processing. Sci. Rep. 2017, 7, 15133. [Google Scholar] [CrossRef]
- Magesan, E.; Gambetta, J.M.; Emerson, J. Scalable and Robust Randomized Benchmarking of Quantum Processes. Phys. Rev. Lett. 2011, 106, 180504. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Martinez, R.; Negrevergne, C. Benchmarking Quantum Computers: The Five-Qubit Error Correcting Code. Phys. Rev. Lett. 2001, 86, 5811–5814. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Martinez, R.; Negrevergne, C. Sampling Strategy Optimization for Randomized Benchmarking. arXiv 2019, arXiv:2109.07653. [Google Scholar]
- Grant, E.; Humble, T.S.; Stump, B. Benchmarking Quantum Annealing Controls with Portfolio Optimization. Phys. Rev. Appl. 2021, 15, 014012. [Google Scholar] [CrossRef]
- Regula, B.; Bu, K.; Takagi, R.; Liu, Z.-W. Benchmarking one-shot distillation in general quantum resource theories. Phys. Rev. A 2020, 101, 062315. [Google Scholar] [CrossRef]
- Lathiotakis, N.N.; Marques, M.A.L. Benchmark calculations for reduced density-matrix functional theory. J. Chem. Phys. 2008, 128, 184103. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.L.; Bao, W.S.; Cao, S.R.; Chen, F.S.; Chen, M.C.; Chen, X.W.; Chung, T.H.; Deng, H.; Du, Y.J.; Fan, D.J.; et al. Benchmark calculations for reduced density-matrix functional theory. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef] [PubMed]
- Jafferis, D.; Zlokapa, A.; Lykken, J.D.; Kolchmeyer, D.K.; Davis, S.I.; Lauk, N.; Neven, H.; Spiropulu, M. Traversable wormhole dynamics on a quantum processor. Nature 2022, 612, 51–55. [Google Scholar] [CrossRef]
- Corcoles, A.D.; Gambetta, J.M.; Chow, J.M.; Smolin, J.A.; Ware, M.; Strand, J.; Plourde, B.L.; Steffen, M. Process verification of two-qubit quantum gates by randomized benchmarking. Phys. Rev. A 2013, 87, 030301. [Google Scholar] [CrossRef]
- Barends, R.; Kelly, J.; Megrant, A.; Veitia, A.; Sank, D.; Jeffrey, E.; White, T.; Mutus, J.; Fowler, A.; Campbell, B.; et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500–503. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Xu, K.; Liu, W.; Yang, C.-P.; Zheng, S.-B.; Deng, H.; Xie, Q.; Huang, K.; Guo, Q.; Zhang, L.; et al. 10-Qubit Entanglement and Parallel Logic Operations with a Superconducting Circuit. Phys. Rev. Lett. 2017, 119, 180511. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.; Grover, L.K. Quantum Computation and Quantum Information. Am. J. Phys. 2002, 70, 558–559. [Google Scholar] [CrossRef]
- Erhard, M.; Malik, M.; Krenn, M.; Zeilinger, A. Experimental Greenberger–Horne–Zeilinger entanglement beyond qubits. Nat. Photon. 2018, 12, 759–764. [Google Scholar] [CrossRef]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Reed, M.D.; DiCarlo, L.; Nigg, S.E.; Sun, L.; Frunzio, L.; Girvin, S.M.; Schoelkopf, R.J. Realization of three-qubit quantum error correction with superconducting circuits. Nature 2012, 482, 382–385. [Google Scholar] [CrossRef]
- Reed, M.D. Entanglement and Quantum Error Correction with Superconducting Qubits. arXiv 2013, arXiv:1311.6759v1. [Google Scholar]
- Available online: https://qiskit.org/ (accessed on 30 May 2021).
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying Entanglement. Phys. Rev. Lett. 1997, 78, 2275–2279. [Google Scholar] [CrossRef]
- Wei, T.-C.; Goldbart, P.M. Geometric measure of entanglement and applications to bipartite and multipartite quantum states. Phys. Rev. A 2003, 68, 042307. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S.; Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046–2052. [Google Scholar] [CrossRef] [PubMed]
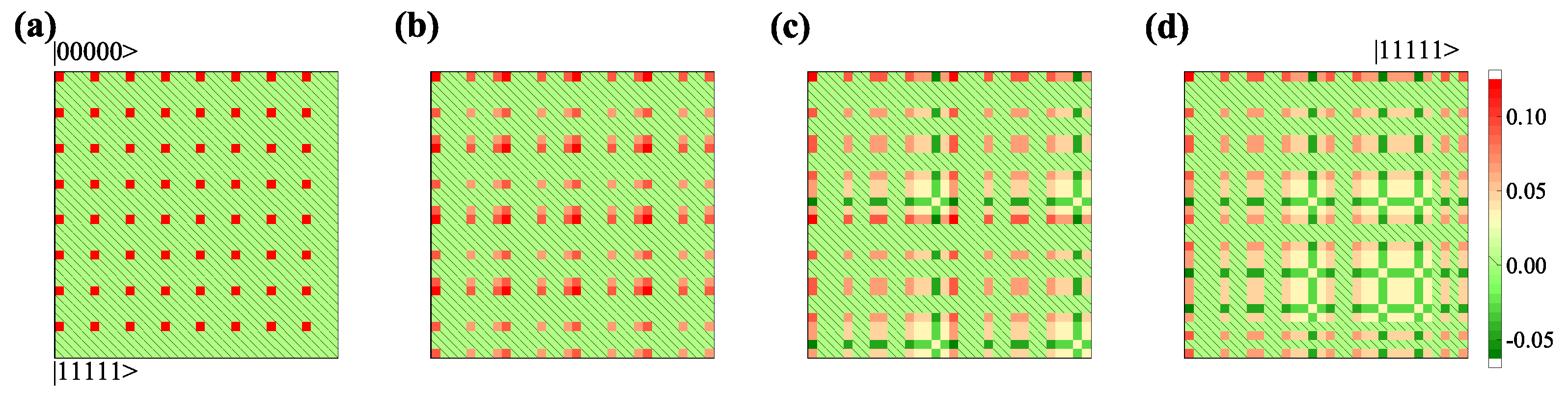
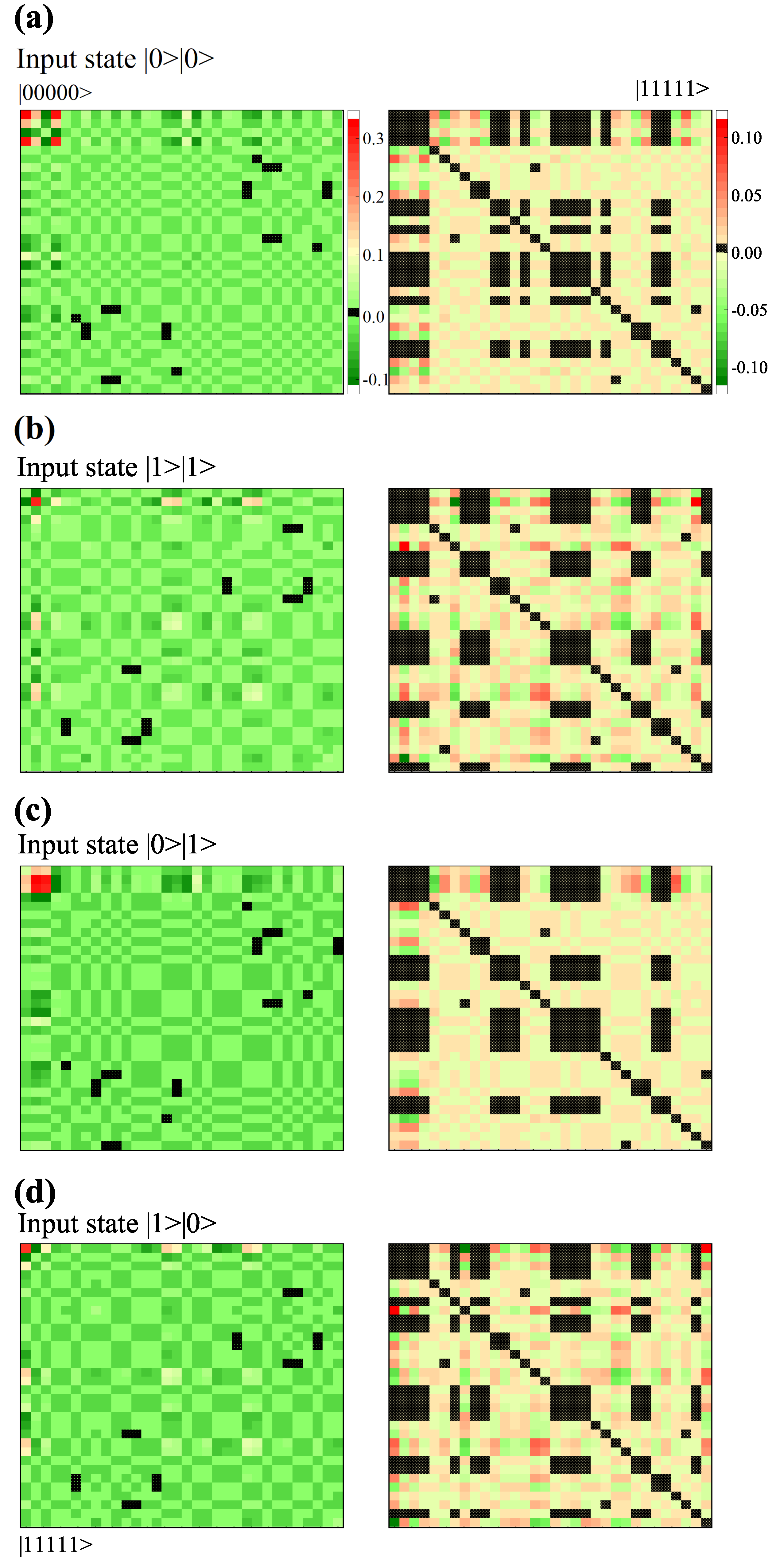
| Input States | Absolute Zero | |
|---|---|---|
| (1,1) | (6,24);(7,25);(7,26);(9,23); | |
| (9,31);(10,23);(10,31);(15,25); | ||
| (15,26);(16,30);(23,9);(23,10); | ||
| (24,6);(25,7);(25,15);(26,7); | ||
| (26,15);(30,16);(31,9);(31,10) | ||
| (2,2) | (5,23);(8,25);(8,26);(9,24); | |
| (9,32);(10,24);(10,32);(15,29); | ||
| (16,25);(16,26);(23,5);(24,9); | ||
| (24,10);(25,8);(25,16);(26,8); | ||
| (26,16);(29,15);(32,9);(32,10) | ||
| (1,1) | (6,27);(6,28);(11,22);(11,30); | |
| (12,22);(12,30);(14,27);(14,28); | ||
| (22,11);(22,12);(27,6);(27,14); | ||
| (28,6);(28,14);(30,11);(30,12) | ||
| (2,2) | (5,27);(5,28);(11,21);(11,29); | |
| (12,21);(12,29);(13,27);(13,28); | ||
| (27,5);(28,5);(21,12);(21,11); | ||
| (29,11);(29,12);(27,13);(28,13) |
| Number of Qubits k | Total Number of Elements | Total Number of Zero Elements | Percentage (%) |
|---|---|---|---|
| 5 | 4 × 1024 | 72 | 1.758 |
| 6 | 4 × 4096 | 1520 | 9.277 |
| 7 | 4 × 16,384 | 1096 | 1.672 |
| 8 | 4 × 65,536 | 1916 | 0.731 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, G.; He, K.; Zhao, C.; He, Y.; Liu, J.; Chen, W. Quasi-Shor Algorithms for Global Benchmarking of Universal Quantum Processors. Appl. Sci. 2023, 13, 139. https://doi.org/10.3390/app13010139
Dai G, He K, Zhao C, He Y, Liu J, Chen W. Quasi-Shor Algorithms for Global Benchmarking of Universal Quantum Processors. Applied Sciences. 2023; 13(1):139. https://doi.org/10.3390/app13010139
Chicago/Turabian StyleDai, Genting, Kaiyong He, Changhao Zhao, Yongcheng He, Jianshe Liu, and Wei Chen. 2023. "Quasi-Shor Algorithms for Global Benchmarking of Universal Quantum Processors" Applied Sciences 13, no. 1: 139. https://doi.org/10.3390/app13010139
APA StyleDai, G., He, K., Zhao, C., He, Y., Liu, J., & Chen, W. (2023). Quasi-Shor Algorithms for Global Benchmarking of Universal Quantum Processors. Applied Sciences, 13(1), 139. https://doi.org/10.3390/app13010139





