Dimensional Reduction-Based Moment Model for Probabilistic Slope Stability Analysis

Abstract

Uncertainty is an inevitable factor that influences the function analysis, design, and safe operation in engineering systems. Due to the complexity property and unclear failure mechanism, uncertainty is an intrinsic property of slope engineering. Hence, stability analysis and design cannot meet the demands of slope engineering based on the traditional deterministic method, which cannot deal with uncertainty. In this study, a practical reliability approach was developed to consider the uncertainty factor in slope stability analysis by combining the multiplicative dimensional reduction method (MDRM) and first-order second moment (FOSM). MDRM was used to approximate the complex, nonlinear, high-dimensional, and implicit limit state function. The statistical moment of safety factor was estimated based on the moment method using MDRM. FOSM is adopted to compute the reliability index based on the statistical moment of the safety factor. The proposed method was illustrated and verified by an infinite slope with an analytical solution. The reliability index and failure probability were compared with Monte Carlo simulations (MCS) in various cases. Then, it was applied to a slope based on numerical solutions. The results show that the proposed method is feasible and effective for probabilistic slope stability analysis. The reliability index obtained from the proposed method shows high consensus with the traditional response surface method (RSM). It shows that the proposed method is effective, efficient, and accurate. MDRM provides a practical, simple, and efficient probabilistic slope stability analysis approach.

1. Introduction

Stability analysis and design are essential to safety in slope construction. Various traditional methods have been applied to slope stability analysis, such as limit equilibrium [1], limit analysis [2], numerical method [3], and intelligent method [4]. A field-testing program investigated five expansive soil slopes with different inclinations subjected to artificial rainfalls and calibrated based on a numerical model [5]. The characteristics and prevention mechanisms of artificial slope instability were explored with field investigation in a typical watershed using a neural network [6]. The soilbag-protected slopes in expansive soils were designed to consider the swelling pressure based on the balance between the soilbag friction and the active lateral earth pressure [7]. A limit analysis was used to evaluate the stability of expansive soil slopes stabilized by anchor cables based on the kinematic limit analysis theorem [8]. The uncoupled and hydro-mechanical coupled analyses were conducted to deal with the hydraulic and hydro-mechanical responses of the surficial layer of soil slopes [9]. However, the traditional slope stability analysis does not deal with uncertainty. Obviously, this does not conform to the reality of slope engineering. Uncertainty is the intrinsic feature of slope engineering due to the complex property of geomaterials, complicated and changeable geological conditions, unclear failure mechanisms, etc. How the uncertainty to deal with is one of the biggest challenges in slope engineering.

Recently, many researchers have paid more attention to the uncertainty analysis of slope [10]. The reliability analysis method has been widely used in slope stability analysis for considering the uncertainty in the past decades [11,12,13,14,15,16,17]. Li et al. integrated the random finite element method (RFEM) with an advanced Monte Carlo Simulation and developed an efficient RFEM for the reliability analysis and risk assessment of soil slopes [18]. Various reliability methods have been developed for slope reliability analysis such as first order second moment (FOSM) [19,20], first-order reliability method (FORM) [19,20,21,22,23], and second-order reliability methods (SORM) [21,24]. A Bayesian approach was developed to characterize the soil–water retention curve and hydraulic conductivity and was illustrated through a slope example [25]. The above methods need the gradient of the limit state function. However, it is difficult to obtain the explicit limit state function for practical slope engineering. To overcome this problem, the response surface method (RSM) has been developed to estimate the reliability of slopes by combining it with stability analysis methods such as the limited equilibrium method, or the numerical method [23,26,27,28,29]. A genetic algorithm optimized Taylor Kriging surrogate model was developed for the system reliability analysis of soil slopes [30]. Li et al. reviewed the application of RSM in slope reliability analysis [31]. Polynomial-based RSM was commonly used in slope reliability analysis which is time-consuming when practicing engineering problems dealing with a high-order polynomial. Other methods, such as artificial neural networks (ANN), support vector machines (SVM), and Relevance vector machine (RVM) overcome this problem [20,24,32,33,34]. Those methods have the advantage of providing high-order approximations with fewer samples than polynomial functions of comparable order; however, they have some inherent drawbacks, such as their slow convergence, a less generalized performance, arriving at a local minimum, over-fitting problems, and the selection of a suitable kernel function. The limits of the above reliability methods hindered the application of the reliability method to practical geotechnical engineering.

The moment methods have been the most popular method to find an approximate solution in uncertainty analysis [35]. The idea is to calculate the first four moments of the response to back calculate the parameters of the distribution [35,36,37]. Discovering what is the moment computation of response is not an easy task due to the distribution type assumed and the lack of a unique solution [38]. To overcome this problem, the dimensional reduction method was adopted to compute the statistical moments [39]. MDRM provides an excellent way to determine the function moment based on the multiplicative form of the dimensional reduction method. FOSM is a commonly used reliability method based on the first and second moment of the limit state function, which can be obtained based on MDRM.

This study proposes a new reliability analysis approach that combines the merits of the MDRM and of FOSM. MDRM is used to approximate the limit state function. The statistical moment was estimated based on an MDRM model. FOSM was adopted to compute the reliability index of a slope. The remainder of this study is structured as follows. In Section 2, the FOSM algorithm was reviewed. Section 3 introduces the basic theory of MDRM- and MDRM-based moment computations, and the MDRM-based reliability analysis method was developed, and the procedure was presented in detail. Some applications of the proposed method for reliability analysis of slopes were presented in Section 4. Some conclusions were given in Section 5.

2. First Order Second Moment (FOSM)

The limit state function of slopes may be established as follows:

$$\mathrm{Z}=\mathrm{g}\left(X_1,X_1,\dots ,X_n\right)=F\left(X_1,X_1,\dots ,X_n\right)-1$$

(1)

where n is the number of random variables; X_i (i = 1, 2, …, n) are the random variables in the slope reliability analysis; g(X₁, X₂, X₃, …, X_n) is the limit state function; Z > 0 indicates that the slope is stable, Z < 0 indicates that it has failed, and Z = 0 means that the boundary is hovering between stable and unstable. F(X₁, X₂, X₃, …, X_n) is the safety factor of slope.

The mean and variance of the limit state function using the first-order approximation can be calculated using

$${\mu }_z=\mathrm{g}\left({\mu }_{X1},{\mu }_{X2},\dots ,{\mu }_{Xn}\right)$$

(2)

$${\sigma }_z^2={{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^n\frac{\partial \mathrm{g}}{\partial X_i}\frac{\partial \mathrm{g}}{\partial X_j}cov\left(X_i,X_j\right)$$

(3)

where cov(X_i, X_j) is the covariance of X_i and X_j, μ_z is the mean value of the limit state function Z, and σ²_z is the variance of Z (σ_z is the standard deviation of Z). Consequently, the reliability index in slope safety analysis was evaluated as follows based on FOSM:

$$\beta =\frac{{\mu }_z}{{\sigma }_z}$$

(4)

where β is the reliability index in slope stability analysis. The key step is to calculate the statistical moments of the limit state function, i.e., the mean value μ_z and the standard deviation σ_z. In the calculation of μ_z and σ_z, the values of the safety factor of slope and the corresponding first-order partial derivatives are needed according to Equations (2) and (3). However, it is difficult to obtain it in the practical slope engineering. Based on the reliability index, the probability of failure can be evaluated from

$$p_f\approx 1-\mathsf{\Phi }(\beta )$$

(5)

where Φ is the cumulative distribution function of the standard normal variable.

For most stability analysis methods for slopes, the factor of safety will be calculated using a numerical method and cannot be represented as an explicit function of the random variables. It is difficult to calculate the partial derivatives of the limit state function in slope reliability analysis. However, the partial derivatives are indispensable for the FOSM method in reliability analysis. To overcome the above difficulty, MDRM, which avoids determining the limit state function and their partial derivatives, was adopted to determine the moment of the slope safety factor. Once the first and second moment of the limit state function was determined, FOSM could be utilized to evaluate the slope reliability based on Equation (4) using MDRM.

3. Dimensional Reduction Method and Moment

The safety factor of a slope can be evaluated as a function of input variables, such as rock mechanical parameters, in situ stress, etc., which is denoted as

y = g(X)

(6)

where y is the safety factor of slope and X is the vector of input random variables. According to the MDRM algorithm, Equation (6) can be represented by a multiplicative of the low dimensional function [40]. Based on the FOSM, the reliability index can be obtained based on the first and second moments. In this study, the moment of Equation (6) could be calculated using the MDRM. The primary idea of MDRM could be presented in the following.

3.1. Multiplicative Dimensional Reduction Method

For MDRM, the response function y = g(X) is evaluated with respect to a reference fixed input point, known as the cut point, with coordinates c.

c = (c₁, c₂, …, c_n)

(7)

where c₁, c₂, …, c_n corresponds to the mean value of each random variables x₁, x₂, …, x_n. Thus, an ith cut function is obtained by fixing all the point random variables, except x_i, at their respective cut point coordinates, which are generally chosen as the mean values (c₁, c₂, …, c_n) such that

g_i(x_i) = g(c₁, c₂, …, c_i−1, x_i, c_i+1, …, c_n)

(8)

According to the MDRM method [41], the response function is approximated in a multiplicative form as

$$y=\mathrm{g}\left(X\right)\approx {\mathrm{g}}_0^{\left(1-n\right)}\times {{\displaystyle \prod }}_{i=1}^n{\mathrm{g}}_i\left(x_i\right)$$

(9)

where g_i(·) is called the cut component function. For the detailed explanations, algorithm, and procedure of MDRM, some literature [39,40,41] can be referenced.

3.2. Evaluate the Statistics Moment Based on MDRM

Based on the MDRM model, a kth statistics moment of response can be approximated as

$$E\left[y^k\left]\approx E\right[{\left({\mathrm{g}}_0^{\left(1-n\right)}\times {{\displaystyle \prod }}_{i=1}^n{\mathrm{g}}_i\left(x_i\right)\right)}^k\right]$$

(10)

where the mathematical exception operation is denoted as E[ ] and for k = 1, E[y^k] = E[y] is the mean value of y. Assuming that all input random variables are independent, the above equation can be written as

$$E\left[y^k\right]\approx {\mathrm{g}}_0^{k\left(1-n\right)}{{\displaystyle \prod }}_{i=1}^{n}E\left[{\left({\mathrm{g}}_i\left(x_i\right)\right)}^k\right]$$

(11)

Based on the Equation (10), the first and second moment of response can be approximated as

$${\mu }_y=E\left[\mathrm{y}\right]\approx {\mathrm{g}}_0^{\left(1-n\right)}{{\displaystyle \prod }}_{i=1}^{n}E\left[{\mathrm{g}}_i\left(x_i\right)\right]$$

(12)

$${\mu }_{2y}=E\left[y^2\right]\approx {\mathrm{g}}_0^{2\left(1-n\right)}{{\displaystyle \prod }}_{i=1}^{n}E\left[{\left({\mathrm{g}}_i\left(x_i\right)\right)}^2\right]$$

(13)

Then, the standard deviation of response can be obtained as

$${\sigma }_y=\sqrt{{\mu }_{2y}-{\mu }_y{}^2}$$

(14)

where σ_y is the standard deviation of the response such as the safety factor of slope. The computation of the mean and any other kth moment of response requires the calculation of a kth moment of all the cut functions through one-dimensional integration. The numerical integration can be significantly optimized using the Gauss quadrature formulas. A kth moment of an ith cut function can be approximated as a weighted sum.

$$E\left[{\left({\mathrm{g}}_i\left(x_i\right)\right)}^k\right]={{\displaystyle \int }}_{X_i}^{}{\left[{\mathrm{g}}_i\left(x_i\right)\right]}^k{f}_i\left(x_i\right)d{x}_i\approx {{\displaystyle \sum }}_{j=1}^L{w}_j{\left[{\mathrm{g}}_i\left(x_j\right)\right]}^k$$

(15)

where L is the number of the Gauss quadrature points, x_j and w_j are the coordinates and weights, respectively, of the Gauss quadrature points (j = 1, …, L) and h_i (i = 1, 2,…, n) is the response when ith cut function is set at jth Gauss quadrature point.

Obviously, MDRM could determine the moment of the response function and avoid determining the response function and its partial derivatives, which is a challenging task for the traditional response surface method using FOSM.

4. MDRM-Based Reliability Analyses

In this study, MDRM was adopted to represent the implicit, high-dimensional, and nonlinear relationship between random variables and safety factors of a slope to improve the efficiency. The statistics moment of safety factor was estimated based on MDRM. The mean and standard variation of the safety factor was computed based on the statistics moment. FOSM is used to determine the reliability index of the slope. To the practical slope engineering, the slope stability model was built based on numerical methods such as limit equilibrium theory, finite element method, discrete element method, etc. Then, the following contents was used to determine the moment of slope safety factor and compute the reliability index.

4.1. Determine the Input Grid

It is difficult to approximate the relationship between the safety factor and its influence factor (random variables) because the limit state function is a nonlinear, high-dimensional, and implicit function. In this study, we used MDRM to approximate the limit state function. To determine the MDRM model, the cut component function needs to be computed based on some known safety factors of a slope. The known safety factors were created for this work by using numerical or analytical analysis, which is used to obtain the safety factor of slope according to the input grid (random variable combinations). For this study, the Gauss quadrature was adopted to construct the input grid.

Table 1. Some commonly used Gauss points and its weight for Gauss quadrature.

Gauss Rule	k	1	2	3	4	5
Gauss-Legendre	wk	0.2369	0.47863	0.5689	0.4786	0.2369
	xk	−0.9062	−0.5385	0	0.5385	0.9062
Gauss-Hermite	wk	1.13 × 10−2	0.2221	0.5333	0.2221	1.13 × 10−2
	xk	−2.8570	−1.3556	0	1.3556	2.8570
Gauss-Laguerre	wk	0.5218	0.39867	7.59 × 10−2	3.61 × 10−3	2.34 × 10−5
	xk	0.2636	1.4134	3.5864	7.0858	12.641

has listed the Gauss point and Gauss weights of five-order rules of Gauss quadrature.

4.2. Determine the MDRM Model and Statistics Moment

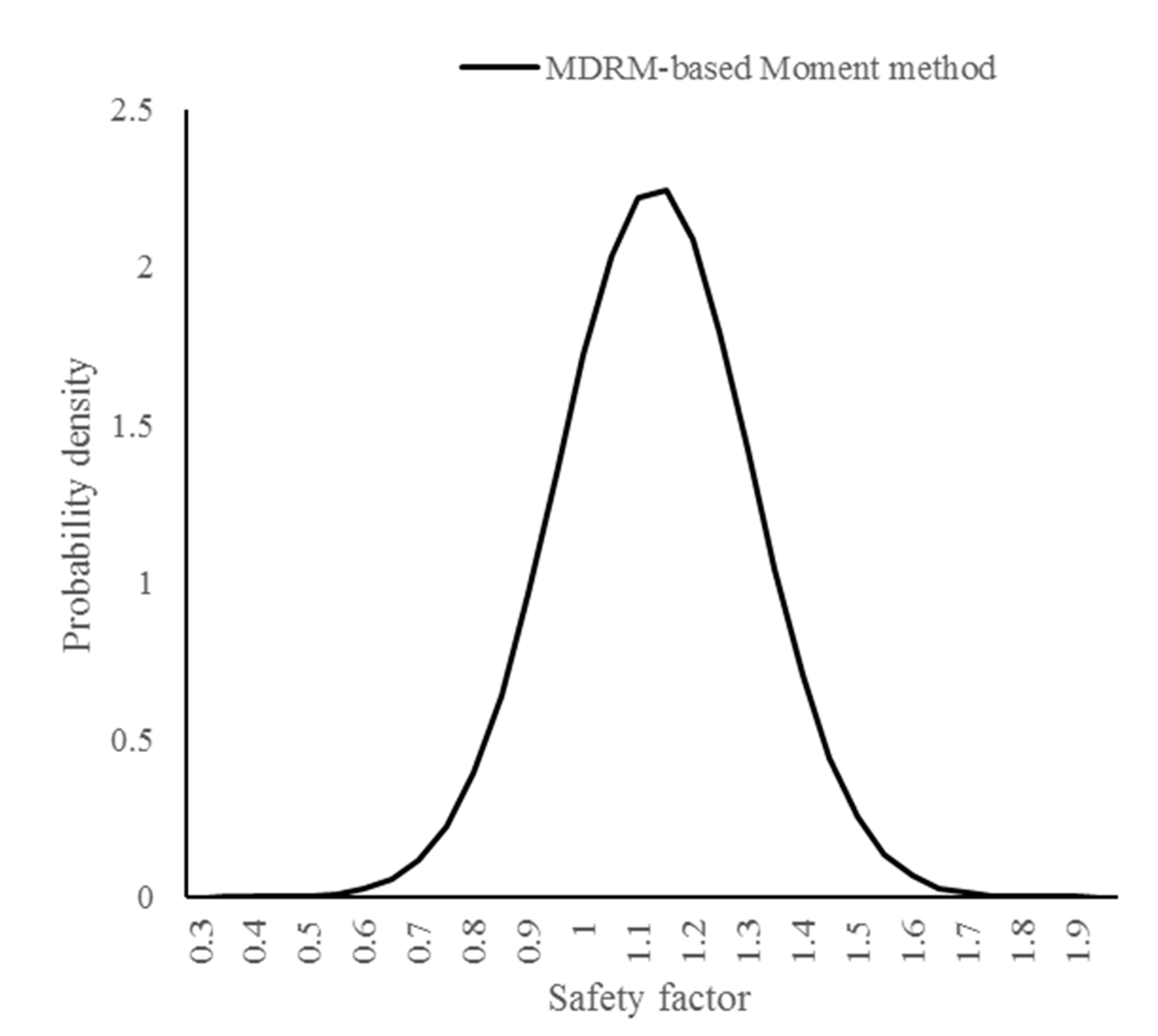
Once the input grid was determined, the numerical method was used to compute the safety factor of a slope at each point in the input grid. Each of the cut component functions can be determined based on the input grid and corresponding safety factor. The MDRM model of limit state function can be represented by Equation (9). Once the MDRM model of a limit state function has been obtained, the statistics moment of safety factor can be calculated by Equation (15). The numerical integration procedure for the kth order moment can be calculated using the Gauss quadrature scheme.

4.3. Determining the Reliability Index and Failure Probability

According to FOSM, the reliability of the slope can be determined based on the mean value and standard deviation of the safety factor. Through combining FOSM and MDRM models, the reliability index can be expressed in the following form.

$$\beta =\frac{{\mu }_y}{{\sigma }_y}=\frac{{\mathrm{g}}_0^{\left(1-n\right)}{{\displaystyle \prod }}_{i=1}^{n}E\left[g_i\left(x_i\right)\right]}{\sqrt{{\mathrm{g}}_0^{2\left(1-n\right)}{{\displaystyle \prod }}_{i=1}^{n}E\left[{\left({\mathrm{g}}_i\left(x_i\right)\right)}^2\right]-{\left({\mathrm{g}}_0^{2\left(1-n\right)}{{\displaystyle \prod }}_{i=1}^{n}E\left[{\left({\mathrm{g}}_i\left(x_i\right)\right)}^2\right]\right)}^2}}$$

(16)

Once the reliability index has been obtained, the failure probability of slope can be estimated using Equation (5).

4.4. The Procedure of Reliability Analysis for Slope

The reliability index and probability failure of the slope was determined through combining MDRM and FOSM. MDRM is adopted to approximate the high dimensional and implicit limit state function. FOSM is used to estimate the reliability index and probability failure of slope. In this process, the Gauss quadrature scheme was used to build the input integration grid and compute the statistics moment. The procedure was shown in Figure 1 and is explained below.

Step 1: Collect the slope engineering information, such as geological conditions, project scale, geomaterial mechanical parameters, in situ stress, etc.; determine the numerical or analytical model of slope stability analysis.

Step 2: According to the information collected in Step 1, determine the random variables and their statistics property.

Step 3: Construct the input integration grid for MDRM based on Gauss point and compute the corresponding safety factor of a slope using a numerical or analytical method.

Step 4: Compute the statistics moment of safety factor based on the MDRM model.

Step 5: Determine the reliability index and probability failure of a slope using FOSM.

The above procedure includes slope stability analysis (computing slope safety factor, determining the input grid, constructing MDRM model, computing moment based on MDRM and computing the reliability index. Obviously, input grid can be easily obtained based on Table 1. Then, the MDRM and moment can be obtained through repeating slope stability analysis. Finally, Equation (16) was used to determine the reliability index. The proposed method is perfectly consistent with slope stability analysis in practice.

5. Applications

In this section, the proposed method was applied to two slopes. The first slope is an infinite soil slope with an analytical solution [42]. The limited equilibrium method was used to compute the factor of safety. Reliability index and failure probability were estimated using MDRM and FOSM. The results were compared with the results of MCS. In general, it is difficult to obtain an analytical solution for practical slopes. Therefore, the second slope is a soil slope with no analytical solution. The strength reduction method was adopted to compute the factor of safety [43]. The reliability index was computed by the proposed method.

5.1. Example 1: Infinite Soil Slope

A typical slice of the infinite slope was shown in Figure 2. The safety factor of the infinite slope is given by the following equation [42].

$$\mathrm{FOS}=\frac{\left(H\gamma co{s}^2\beta -u\right)tan{\phi }^{\prime }+c^{\prime }}{H\gamma sin\beta cos\beta }$$

(17)

where FOS is the safety factor of a slope, H is the depth of the soil layer to the potential failure surface, β is the slope inclination, γ is the total unit weight of soil, u is the pore pressure at the base of the slice, φ′ is the effective soil friction angle at the base of the slice and c′ is the effective cohesion at the base of the slice.

To the infinite slope, there are six influence factors for the safety factor of slope. To illustrate the proposed method, two cases of slope stability were evaluated, i.e., frictional/cohesion soil (2 random variables) and frictional soil with pore pressures (4 random variables) to verify the proposed method.

5.1.1. Frictional/Cohesion Soil

Now, we consider an effective stress analysis of the infinite slope with shear strength parameters (c′ and tanφ′) and no pore pressure. In this case, the safety factor of the slope can be estimated by the following equation.

$$\mathrm{FOS}=\frac{c^{\prime }}{\gamma Hsin\beta cos\beta }+\frac{tan{\phi }^{\prime }}{tan\beta }$$

(18)

Soil strength parameters (c′ and tanφ′) were regarded as random variables with a normal distribution. The statistical parameters of random variables were listed in

Table 2. The statistical parameters of random variables for infinite slope without pore pressure.

Random Variable	Distribution	Mean	Standard Deviation
c′	Normal	10	3
tan(φ′)	Normal	0.5774	0.1732

. The other parameters were determinative. The proposed method was adopted to estimate the reliability index of the slope. The input integration grid and cut component function value were listed in

Table 3. Input grid and corresponding safety factor.

Random Variables	Trial	C′	tan(φ′)	FOS
c′	1	1.42909	0.5774	0.860396
	2	5.93311	0.5774	0.973175
	3	10	0.5774	1.075007
	4	14.06689	0.5774	1.17684
	5	18.57091	0.5774	1.289619
tan(φ′)	1	10	0.082573	0.368321
	2	10	0.342605	0.739685
	3	10	0.5774	1.075007
	4	10	0.812195	1.41033
	5	10	1.072227	1.781694
Fixed mean value		10	0.5774	1.075007

. To H = 5 m, β = 30, and γ = 17 kN/m³, the mean value and standard deviation of safety factors are 1.2718 and 0.3114, respectively. MCS, which was implement 10,000 times, was used to verify the proposed method. The probability distributions are shown in Figure 3. It shows the probability distribution of safety factor is in excellent agreement with MCS’s results. The proposed method obtained the exact result with nine times computation which is far less than the 10,000 times of MCS. It shows the proposed method can improve efficiency dramatically.

To further verify the proposed method, the reliability of slope was estimated in different depths of potential failure surface and slope inclination.

Table 4. Reliability index and failure probability of slope in different H.

H (m)	MDRM Based Reliability Analysis				FORM
	Mean	Standard Deviation	β	pf	β	pf
3	1.4529	0.3305	1.3706	0.0852	1.3753	0.0845
5	1.2718	0.3114	0.8728	0.1914	0.8743	0.1910
7	1.1942	0.3059	0.6348	0.2628	0.6353	0.2626

listed the reliability index and failure probability of slope in different H. The values of the proposed method are in good agreement with the values based on FORM. The maximum relative error of the reliability index is less than 0.3%. Table 4 listed the results of reliability analysis in different slope inclination using the proposed method and FORM. The results are similar to the results in different H. The maximum relative error of the reliability index is less than 0.18%. The above results show the proposed method has good accuracy and performance.

To evaluate the uncertainty of slope, the probability distribution was shown in Figure 4 in different H. Figure 4 shows the mean value of the safety factor will decrease with the increasing of H. Table 4 also shows the mean value, standard deviation, and reliability index all decrease with the increasing of H, and the failure probability increase with the increasing of H. There shows the failure risk of slope will increase with the increasing of H. This is consistent with the theory and practice of slope engineering.

Table 5. Reliability index and failure probability of slope in different θ.

θ (°)	MDRM Based Reliability Analysis				FORM
	Mean	Standard Deviation	β	pf	β	pf
25	1.5454	0.3833	1.4230	0.0774	1.4252	0.0771
30	1.2718	0.3114	0.8728	0.1914	0.8743	0.1910
35	1.0750	0.2591	0.2896	0.3861	0.2902	0.3858

also shows similar results.

The goal of reliability analysis is for guiding the design and construction of slope. Figure 5 and Figure 6 show the accumulative density and failure probability of safety factor. The results of the proposed method are very close to the results of MCS. It shows the proposed method can bring out the character of the uncertainty of slope with high accuracy and efficiency. This is very useful for reliability-based design optimization in slope engineering.

5.1.2. Frictional Soil with Pore Pressure

To further verify the proposed method, we assume tanφ′, tanβ, γ, and u are the random variables. The other two parameters (c′ and H) are determinative. To simplify computation, let c′ = 0 and H = 5 m. The statistical parameters of random variables are listed in

Table 6. The statistical parameters of random variable for infinite slope with pore pressure.

Random Variable	Distribution	Mean	Standard Deviation
tanβ	Normal	0.3250	0.0325
tanφ	Normal	0.5770	0.1732
γ	Normal	18.0000	0.5000
u	Normal	12.0000	1.2000

. In this case, the safety factor of slope can be estimated by the following equation.

$$\mathrm{FOS}=\frac{tan{\phi }^{\prime }}{tan\beta }\left(1-\frac{u\left(1+ta{n}^2\beta \right)}{\gamma H}\right)$$

(19)

The proposed method was adopted to estimate the reliability of the slope in this case. The input integration grid and cut component function value were listed in

Table 7. Input grid and corresponding safety factor.

Random Variables	Trial	tanβ	tanφ	γ	u	FOS
tanβ	1	0.2321	0.577	18	12	2.1362212
	2	0.2809	0.577	18	12	1.7583501
	3	0.3250	0.577	18	12	1.5136633
	4	0.3691	0.577	18	12	1.3265885
	5	0.4179	0.577	18	12	1.1646101
tanφ	1	0.325	0.0822	18	12	0.2155666
	2	0.325	0.3422	18	12	0.8977175
	3	0.325	0.5770	18	12	1.5136633
	4	0.325	0.8118	18	12	2.1296092
	5	0.325	1.0718	18	12	2.81176
γ	1	0.325	0.577	16.5715	12	1.4911026
	2	0.325	0.577	17.3222	12	1.5034222
	3	0.325	0.577	18.0000	12	1.5136633
	4	0.325	0.577	18.6778	12	1.5231612
	5	0.325	0.577	19.4285	12	1.5329065
u	1	0.325	0.577	18	8.5716	1.5884363
	2	0.325	0.577	18	10.3732	1.5491431
	3	0.325	0.577	18	12.0000	1.5136633
	4	0.325	0.577	18	13.6268	1.4781836
	5	0.325	0.577	18	15.4284	1.4388903
fixed mean value		0.325	0.577	18	12.0000	1.5136633

. The mean value and standard deviation of the safety factor are 1.5294 and 0.4903, respectively. The reliability index and failure probability of slope are 1.0796 and 0.1401 and are very close to the value 1.1014 and 0.1354 based on FORM. The maximum relative error of reliability index and failure probability is less than 2% and 3.5%, respectively. It shows MDRM can represent well the high-dimensional, nonlinear, complex, and implicit relationship between the safety factor and its influence factors. It is feasible to approximate the limit state function using the MDRM model. MCS, which may be implemented 10,000 times, was used to compare with the proposed method. The probability distributions are listed in Figure 7. It shows the probability distribution of the safety factor to be in good agreement with MCS’s results. The proposed method obtained the exact result with 17 times computation which is far less than the 10,000 times of MCS. It shows the proposed method can improve efficiency dramatically. MDRM provides a good way to approximate the limit state function and reliability analysis of practical slope engineering.

5.2. Example 2: Soil Slope

This example compares the proposed method to the traditional polynomial response surface method. The problem set is a homogeneous slope. The strength parameters of soil (cohesion c and friction angle φ) are the random variables with a normal distribution. The statistical parameters of random variables are listed in

Table 8. The statistical parameter of soil strength for soil slope.

Random Variables	Distribution	Mean	Standard Deviation
Cohesion c	Normal	13,000	2600
Friction angle φ	Normal	25	5

. Other parameters of the slope are the determinate and the following value are specified, i.e., height of slope H = 10 m, slope angle β = 45°, unit weight of soil γ = 20 kN/m³, and a gravitational acceleration g = 9.81 m/s². The numerical model was shown in Figure 8. Mohr–Coulomb yield criterion was adopted in this numerical model. There are 1130 nodes and 1024 elements. The safety factor was computed using the strength reduction method.

The proposed method was used to estimate the reliability of the slope. The mean value and standard deviation of the safety factor are 1.1304 and 0.1768, respectively. The mean value is very close to the safety factor (1.13) by numerical solution using the mean point of random variables. Figure 9 shows the failure mode at the mean point, and failure is also indicated by shear strain rate contours. It shows it is feasible and accurate to estimate the statistical moment using MDRM. The probability distribution of the safety factor was shown in Figure 10 using MDRM based reliability analysis. For sake of comparison, the traditional RSM was adopted to compute the reliability index and failure probability. The comparisons of reliability index and failure probability are shown in Figure 11 based on a different method. The results are in excellent agreement with the traditional response surface method. The maximum relative error of reliability index and failure probability is less than 1.5% and 1.6%, respectively. It shows MDRM can represent well the implicit limit state function, which is a complex, and nonlinear relationship between safety factors. It is feasible to approximate the limit state function using MDRM in slope engineering. In practical slopes, a numerical model was commonly adopted to determine the safety factor. Once the slope stability model is built, it is convenient to determine the MDRM and moment through a repeating calling slope stability analysis model. Therefore, the proposed method provides a practical approach to deal with the uncertainty.

5.3. Slope with Multiple Soil Layers

In this section, a classical complex slope was utilized to verify and illustrate the proposed method [23]. The slope consists of three soil layers.

Table 9. The statistics property of random variables.

Soil Layer	c (kN/m2)		φ (°)
	Mean	Standard Deviation	Mean	Standard Deviation
I	0	0	38	5
II	5.3	0.7	23	3
III	7.2	0.2	20	3

lists the soil property and their uncertainty for each layer. Similar to Section 5.2, a numerical method was used to evaluate slope stability based on the strength reduction method. The numerical model was built first, and the geometry and numerical mesh are shown in Figure 12.

In order to verify the proposed method, the traditional RSM was utilized to evaluate the slope reliability, and the reliability index is 2.97. The proposed method was also used to determine the reliability index. It is 2.91 and is close to the reliability index obtained by RSM. The result is in excellent agreement with the traditional response surface method. The relative error of the reliability index is less than 2%. The comparisons of the reliability index are shown in Figure 13. The proposed method can be applied to the practical slope, which includes multiple soil layers and has a complex soil layer.

6. Conclusions

In this study, a practical reliability analysis approach was developed to estimate the stability of slope under uncertainties through combining MDRM and FOSM. MDRM was used to approximate the limit state function. The mean value and standard deviation of the safety factor were estimated by numerical quadrature based on the MDRM model. FOSM was adopted to compute the reliability index and failure probability. The proposed method was applied to two slopes, one with an analytical solution and one with a numerical solution. The proposed method improved the efficiency of reliability analysis with higher accuracy. It provided a practical way to estimate and qualify the uncertainty of slope.

(1)

MDRM model approximated the complexity, nonlinearity, and high dimensional relationship between the safety factor and its influence factor using low dimension function. MDRM can characterize the mechanical behavior of slope well.

(2)

It is simple and practical to estimate the statistics moment based on MDRM without any gradient information of limit state function. The MDRM based reliability analysis does not need iteration to obtain the reliability index in contrast to the response surface method. This is important to reliability-based design optimization of a slope.

(3)

The probability distribution of the safety factor was estimated based on the MDRM model. It was in good agreement with the results of MCS. It showed that MDRM-based reliability analysis can represent the uncertainty of slope well. It is feasible to deal with uncertainty using the MDRM model.

(4)

The reliability index obtained by the proposed method showed excellent agreement with those obtained by FORM and the traditional RSM methods when used for reliability analysis in slope engineering. The proposed method can also be applied in other rock engineering contexts.