Numerical Investigation of the Hydrodynamic Characteristics of 3-Fin Surfboard Configurations
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Fin Design
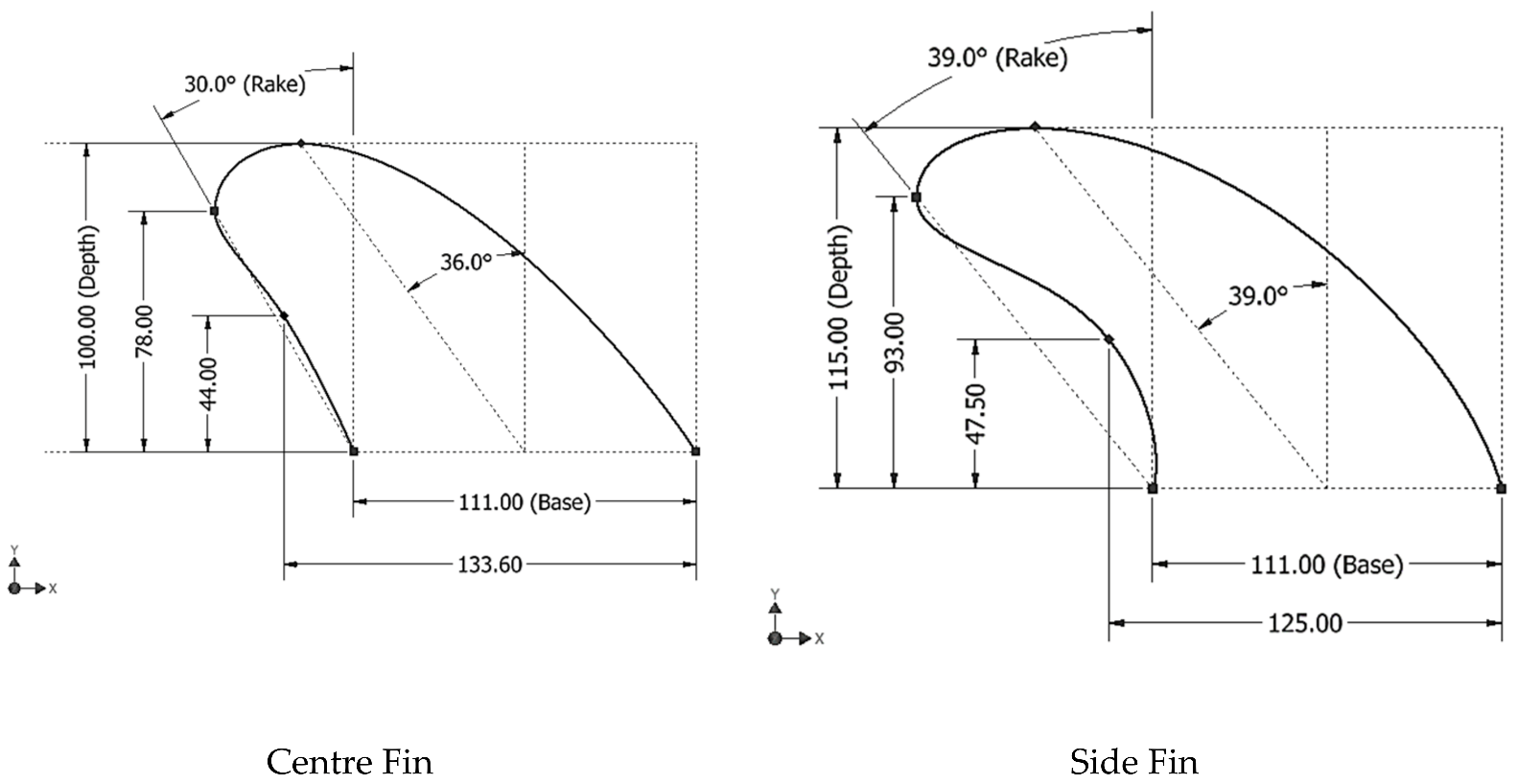
2.2. Optimised Design (Wave Condition)
2.3. Numerical Methods
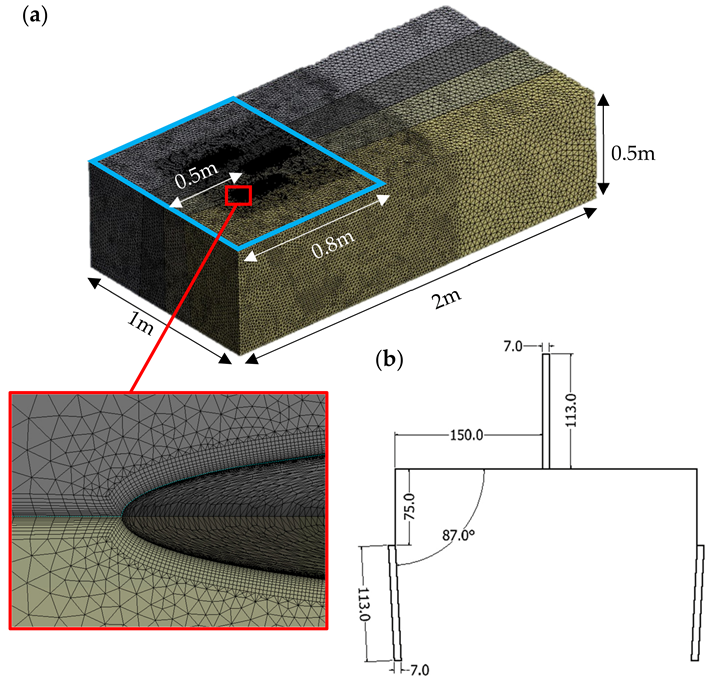
2.4. Fluid Domain
2.5. Mesh Generation
2.6. Numerical Error and Uncertainty Estimation
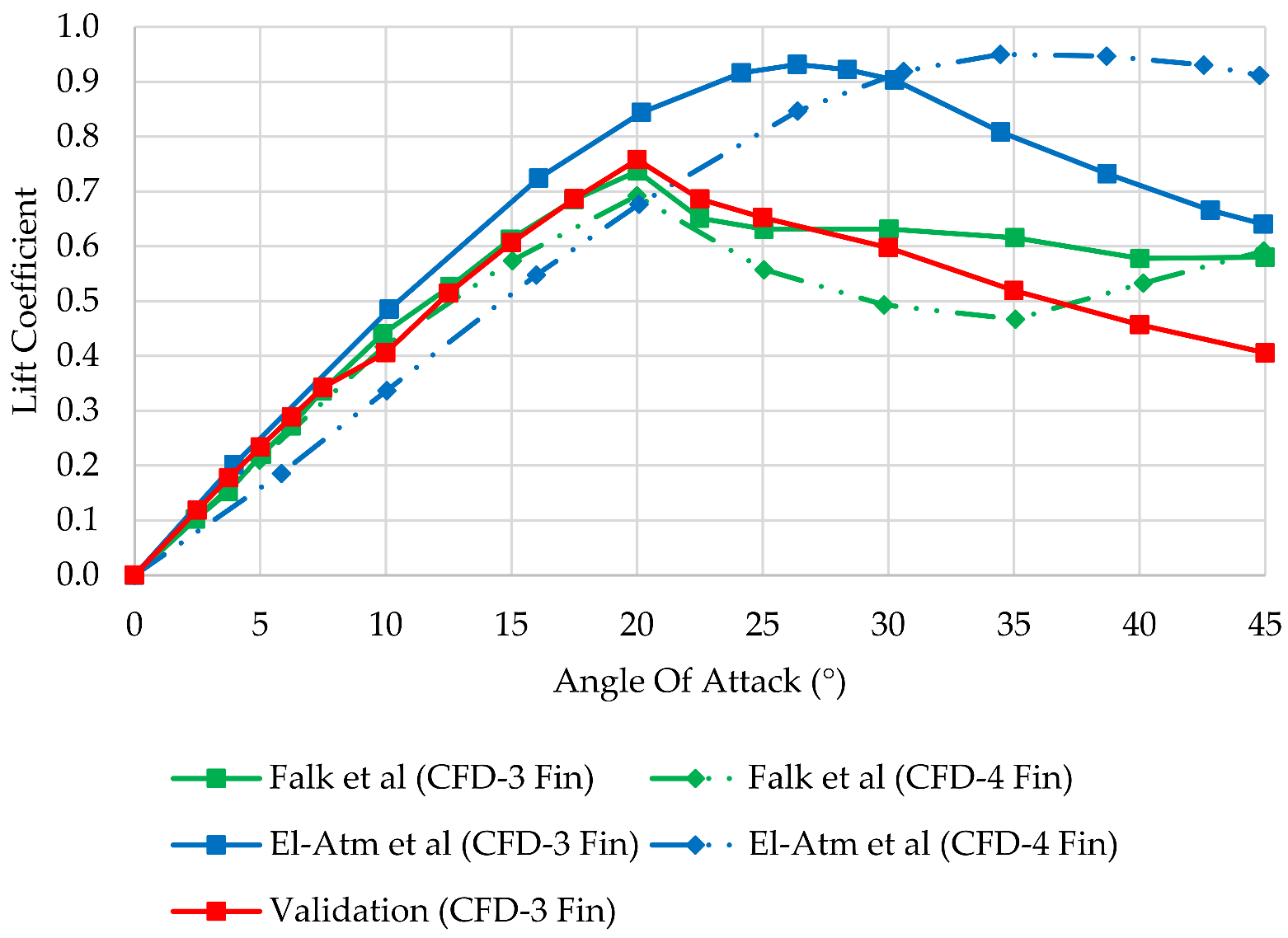
2.7. Validation
3. Results and Discussion
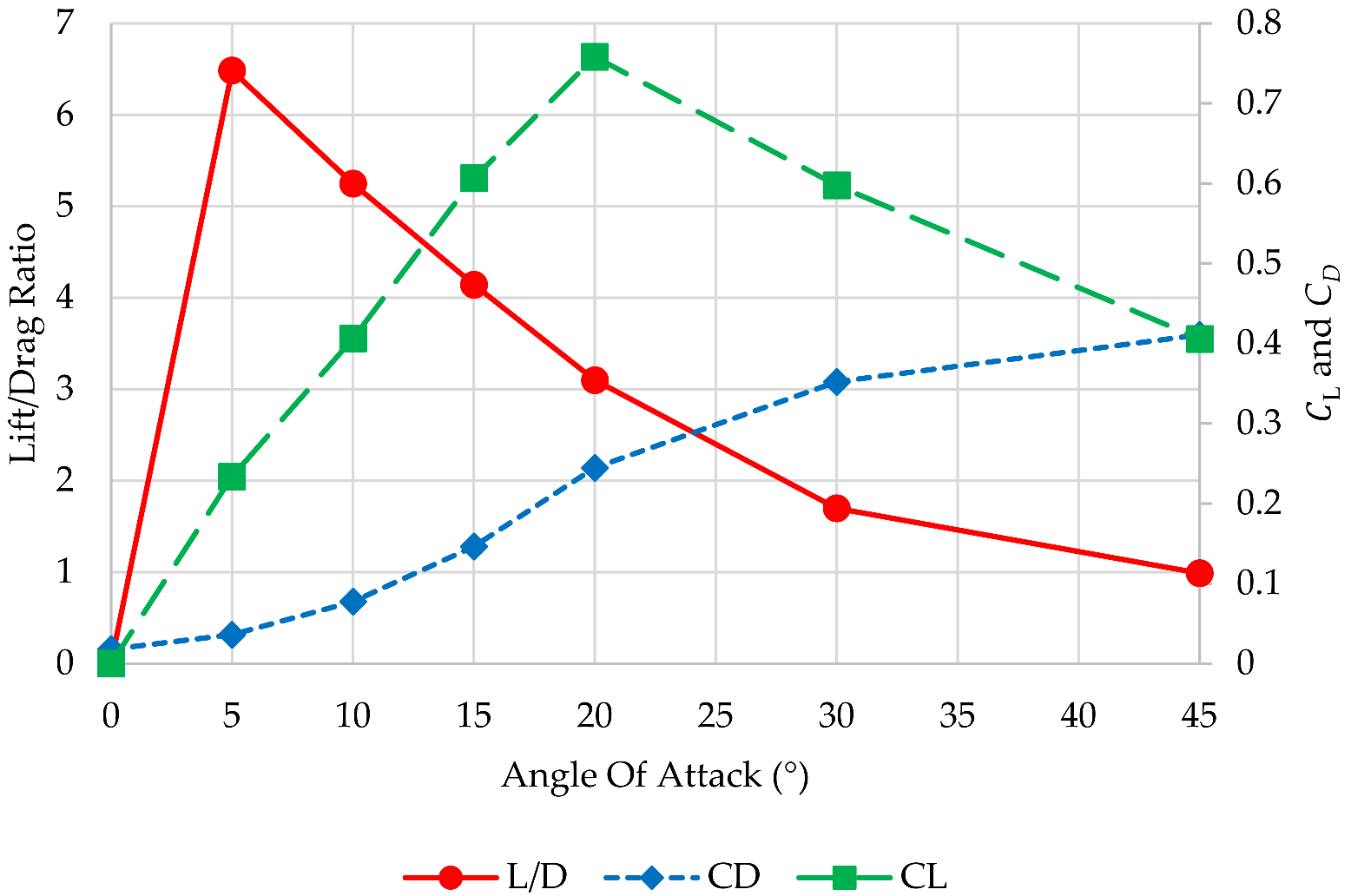
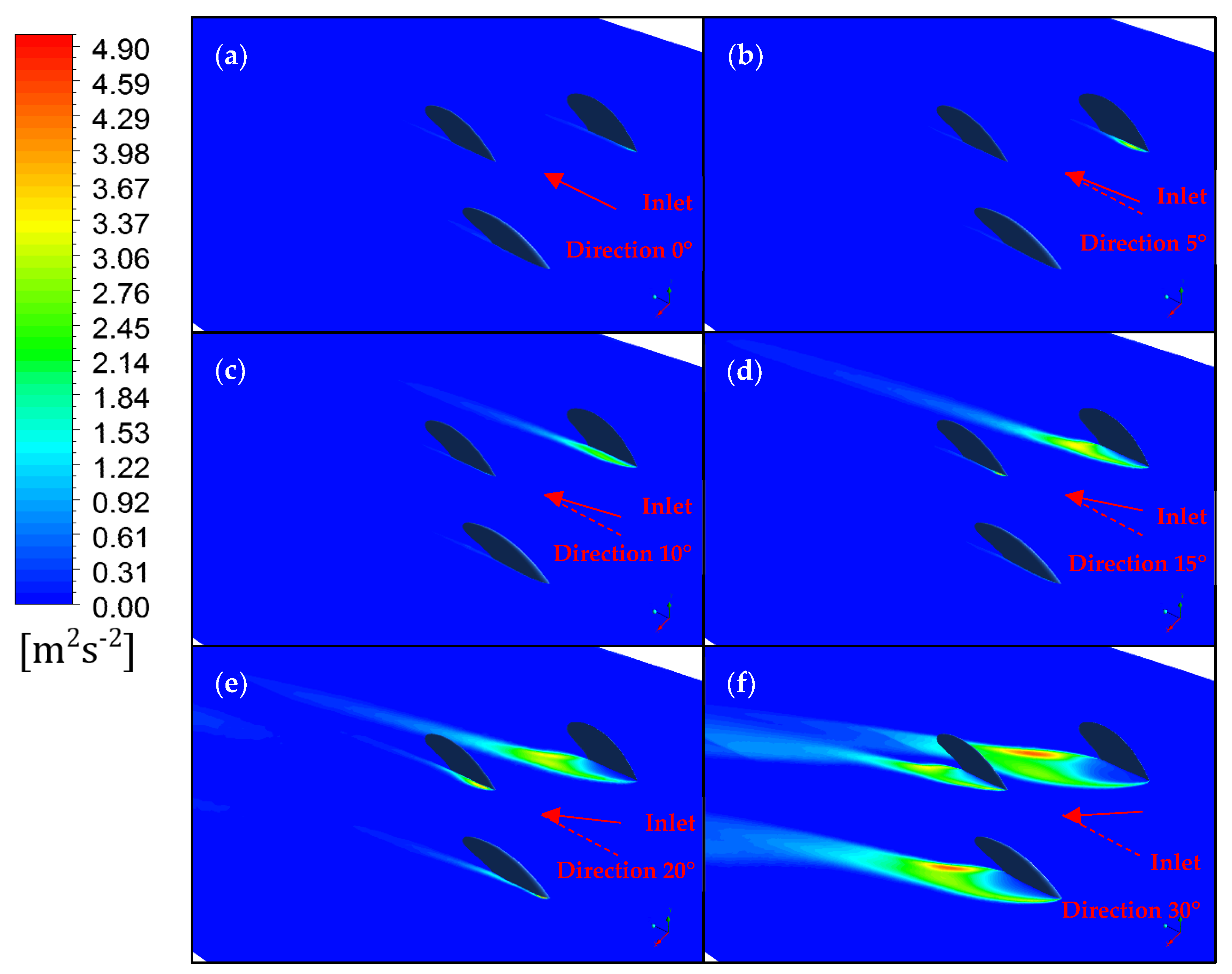
3.1. Baseline Fin
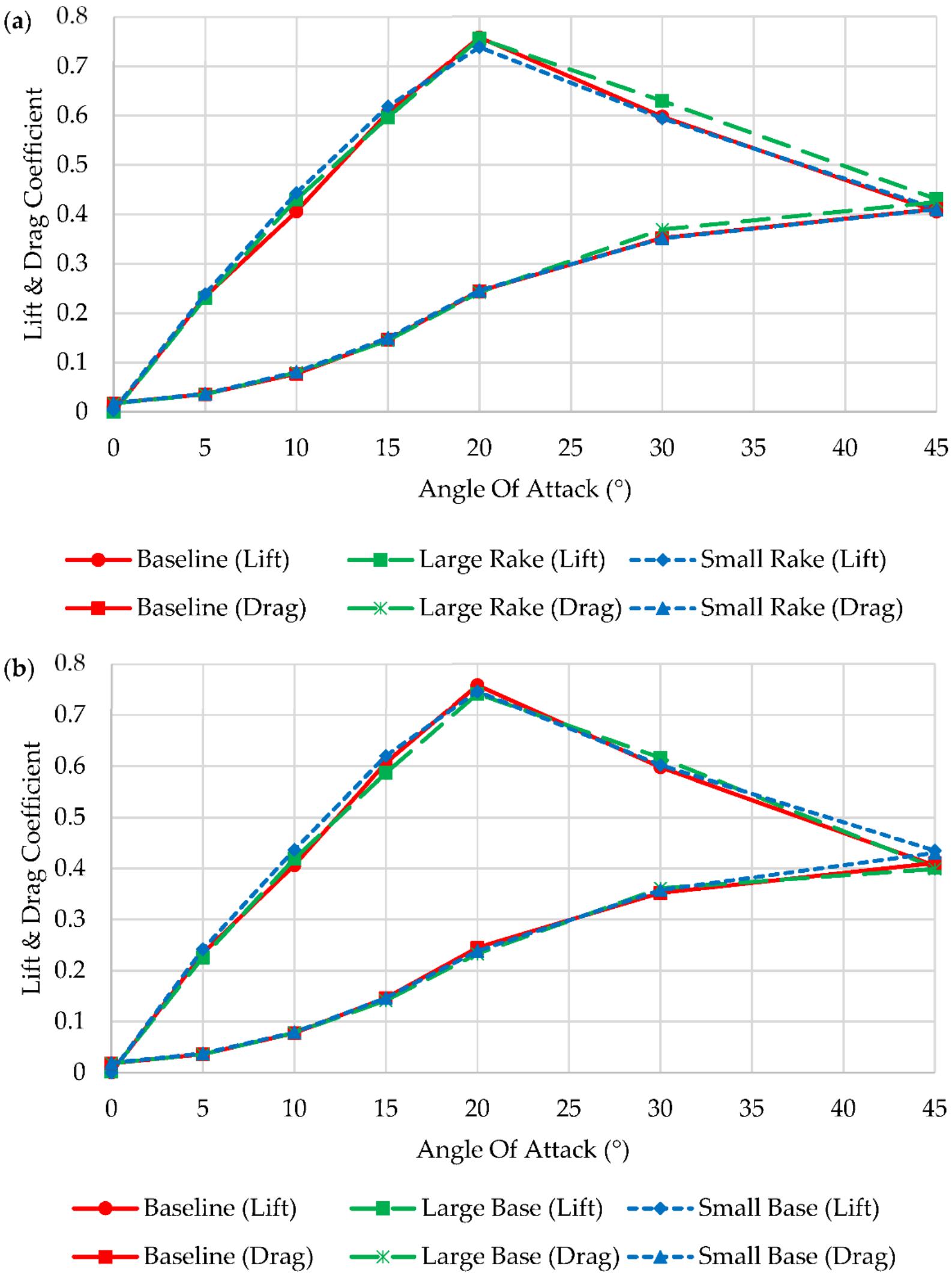
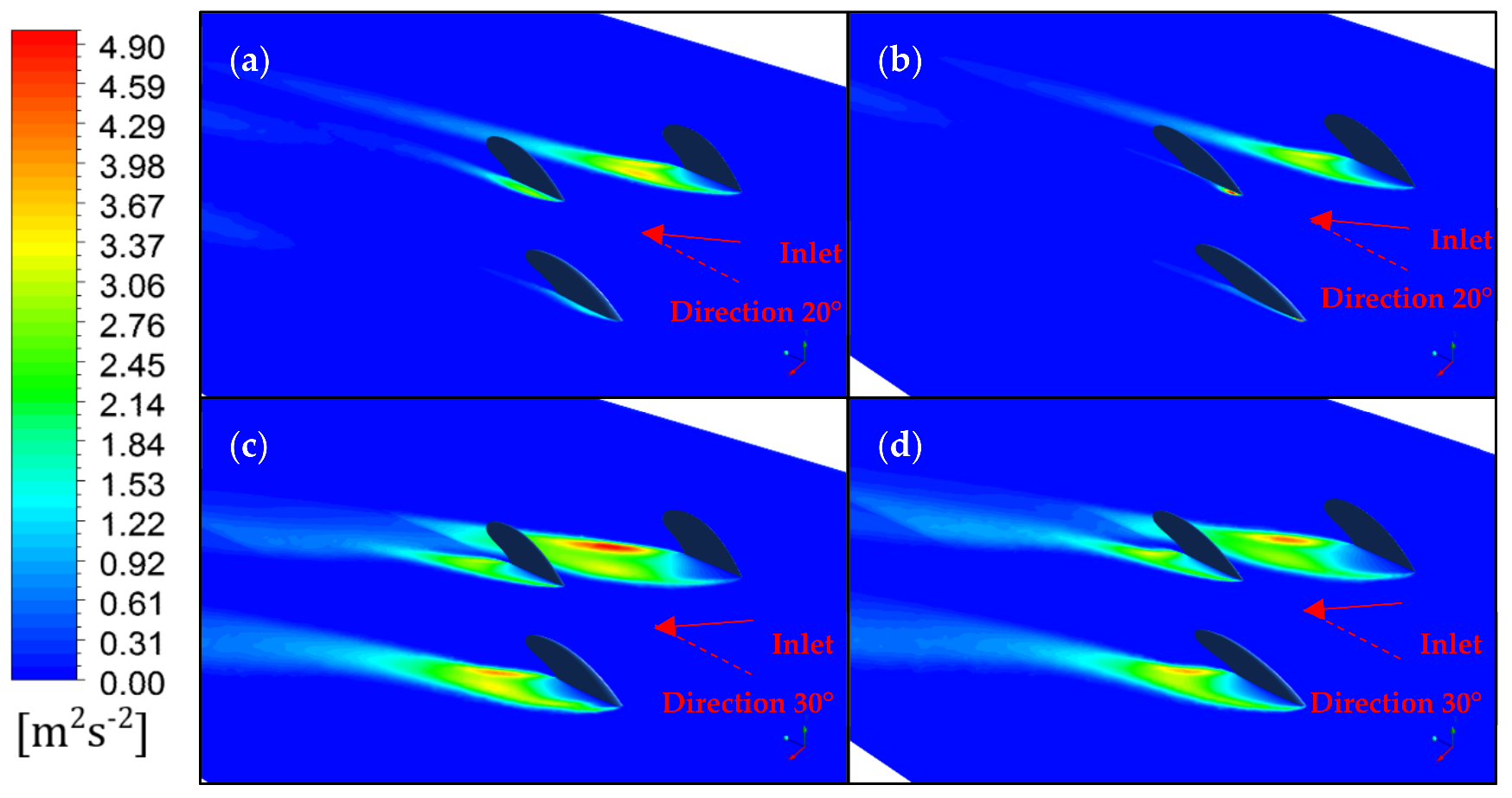
3.2. Template Comparison
3.3. Optimisation Results
3.4. Shortcoming
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lavery, N.; Foster, G.; Carswell, D.; Brown, S. CFD modeling of the effect of fillets on fin drag. Reef J. 2009, 1, 93–111. [Google Scholar]
- El-Atm, B.; Kelson, N.; Gudimetla, P. A finite element analysis of the hydrodynamic performance of 3- and 4- fin surfboard configurations. In Proceedings of the 9th Global Congress on Manufacturing & Management, Gold Coast, Australia, 12–14 November 2008; pp. 1–6. [Google Scholar]
- Falk, S.; Kniesburges, S.; Janka, R.; Grosso, R.; Becker, S.; Semmler, M.; Döllinger, M. Computational hydrodynamics of a typical 3-fin surfboard setup. J. Fluids Struct. 2019, 90, 297–314. [Google Scholar] [CrossRef]
- Falk, S.; Kniesburges, S.; Janka, R.; O’Keefe, T.; Grosso, R.; Döllinger, M. Numerical Investigation of the Hydrodynamics of Changing Fin Positions within a 4-Fin Surfboard Configuration. Appl. Sci. 2020, 10, 816. [Google Scholar] [CrossRef] [Green Version]
- MacNeill, M.S. Bio-Inspired Optimal fin Shape and Angle for Maximum Surfboard Stability. Master’s Thesis, Michigan Technological University, Civil and Environmental Engineering Commons, Houghton, MI, USA, 2015. [Google Scholar]
- Brandner, P.A.; Walker, G.J. Hydrodynamic performance of a surfboard fin. In Proceedings of the 15th Australasian Fluid Mechanics Conference, Sydney, Australia, 13–17 December 2004; p. 4. [Google Scholar]
- Sakellariou, K.; Rana, Z.A.; Jenkins, K.W. Optimisation of the surfboard fin shape using computational fluid dynamics and genetic algorithms. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2017, 231, 344–354. [Google Scholar]
- FCS Fin Data. Fin Control Systems. 2020. Available online: https://www.surffcs.com.au/pages/fcs-fin-data (accessed on 6 October 2020).
- Gately, R.D.; Beirne, S.; Latimer, G.; Shirlaw, M.; Kosasih, B.; Warren, A.; Steele, J.R.; in het Panhuis, M. Additive Manufacturing, Modeling and Performance Evaluation of 3D Printed Fins for Surfboards. MRS Adv. 2017, 2, 913–920. [Google Scholar] [CrossRef]
- Forbes, S.M., Jr.; Sweeney, B. Global Surfaris; Running Press Book Publishers: Philadelphia, PA, USA, 2007. [Google Scholar]
- Glauert, H. The Elements of Aerofoil and Airscrew Theory; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Oggiano, L. Numerical Comparison between a Modern Surfboard and an Alaia Board using Computational Fluid Dynamics (CFD). In Proceedings of the 5th International Congress on Sport Sciences Research and Technology Support, Funchal, Portugal, 30–31 October 2017. [Google Scholar]
- Oggiano, L.; Pierella, F. CFD for Surfboards: Comparison between Three Different Designs in Static and Maneuvering Conditions. Proceedings 2018, 2, 309. [Google Scholar] [CrossRef] [Green Version]
- Ngo, C.; Gramoll, K. Boundary Layer Theory-Flow Past a Flat Plate. Multimedia Engineering Fluid Mechanics. Available online: https://ecourses.ou.edu/cgi-bin/eBook.cgi?topic=fl&chap_sec=09.3&page=theory (accessed on 25 March 2021).
- Phillips, T.S.; Roy, C.J. Richardson Extrapolation-Based Discretization Uncertainty Estimation for Computational Fluid Dynamics. J. Fluids Eng. 2014, 136, 121401. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef] [Green Version]
- Shormann, D.; Oggiano, L.; Panhuis, M.I.H. Numerical CFD Investigation of Shortboard Surfing: Fin Design vs. Cutback Turn Performance. Proceedings 2020, 49, 132. [Google Scholar] [CrossRef]
- Shormann, D.; Panhuis, M.I.H.; Oggiano, L. Field Research and Numerical CFD Analysis of Humpback Whale-Inspired Shortboard Fins. Proceedings 2020, 49, 158. [Google Scholar]
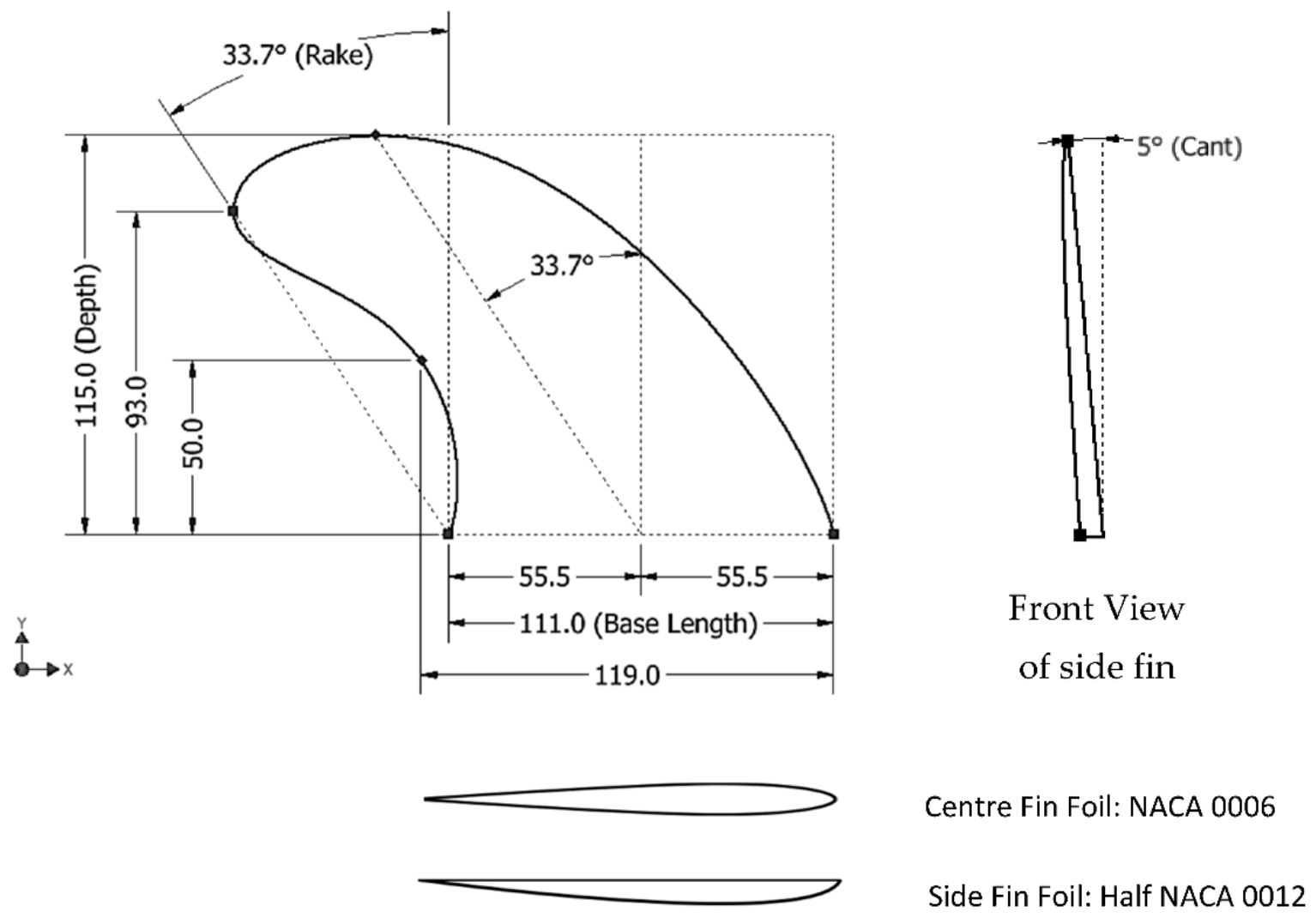


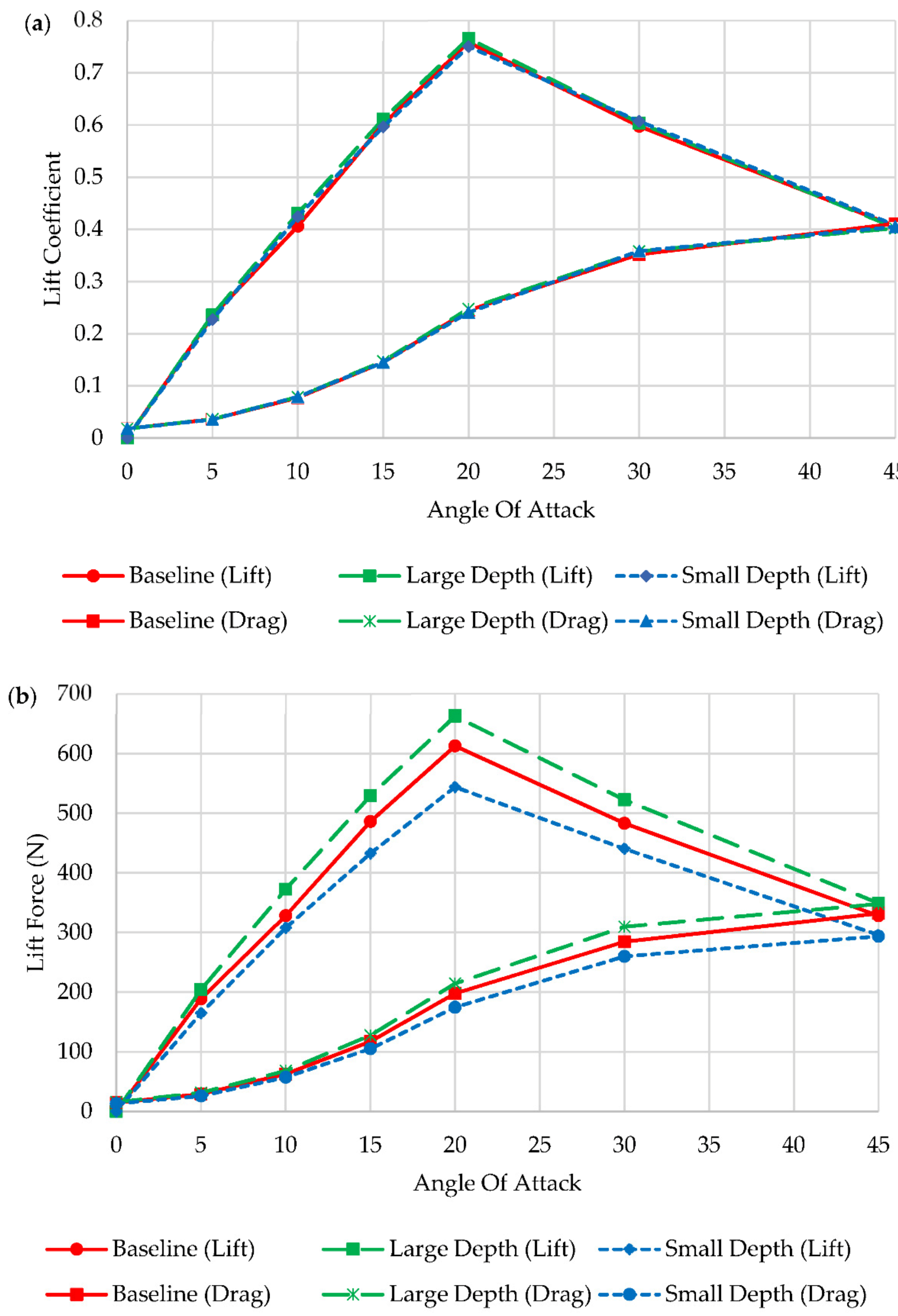
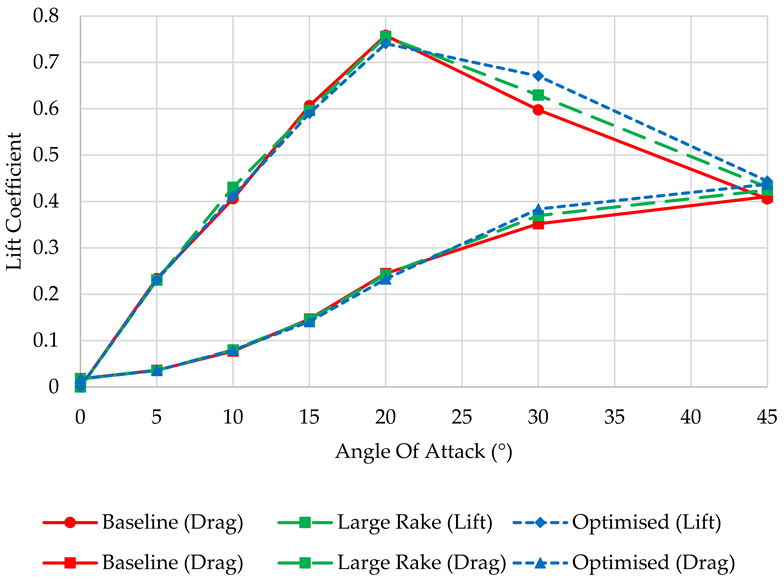
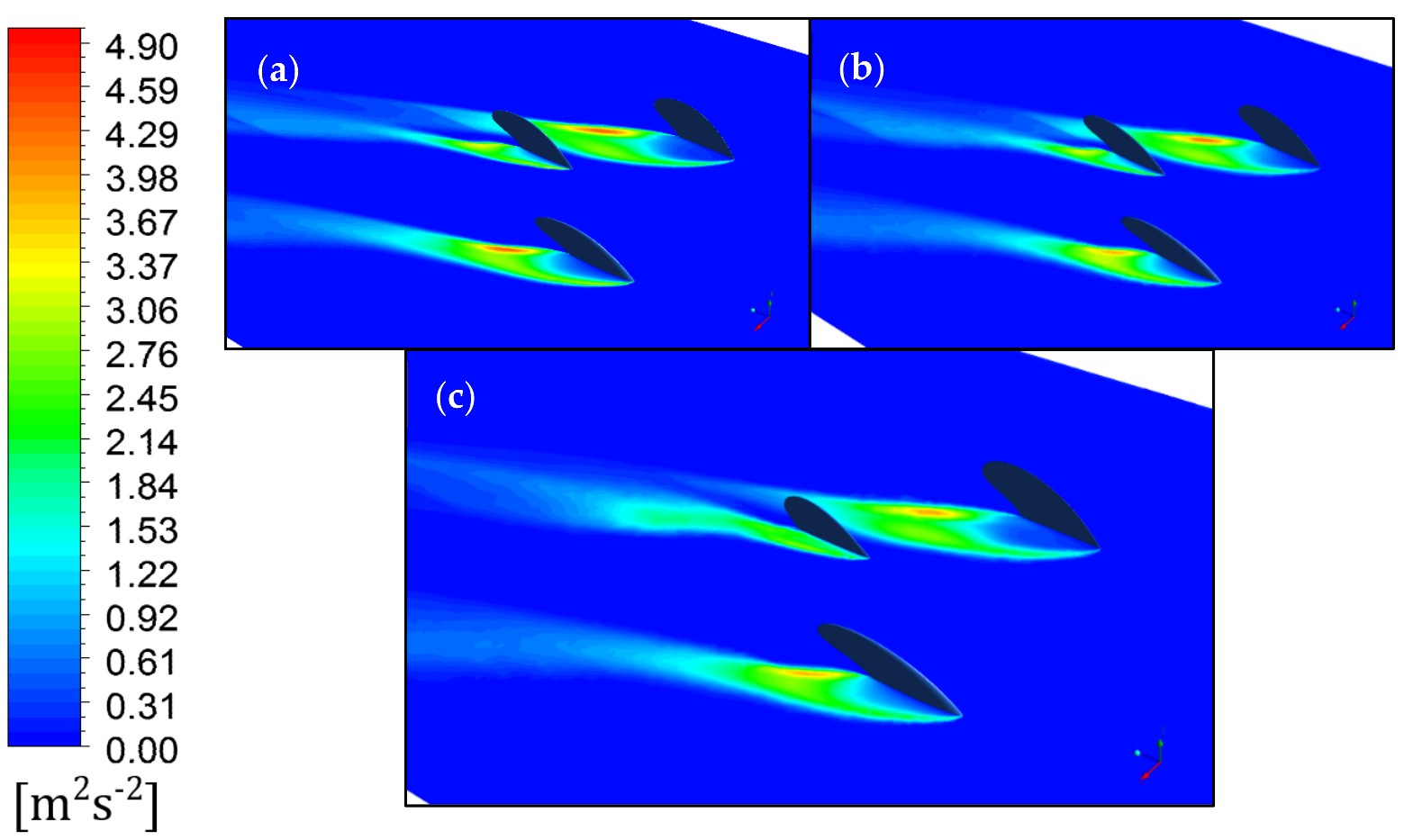
| Template Name | Rake (°) | Base Length (mm) | Depth (mm) | Foil Centre | Foil Side | 3-Fin Reference Area (mm2) |
|---|---|---|---|---|---|---|
| Baseline | 33.7 | 111 | 115 | NACA 0006 | Half NACA 0012 | 21,994.9 |
| Large-Rake | 37 | 111 | 115 | NACA 0006 | Half NACA 0012 | 22,804.8 |
| Small-Rake | 28 | 111 | 115 | NACA 0006 | Half NACA 0012 | 21,268.3 |
| Large-Base | 33.7 | 119 | 115 | NACA 0005 * | Half NACA 0005 * | 23,453.7 |
| Small-Base | 33.7 | 100 | 115 | NACA 0014 * | Half NACA 0014 * | 20,039.9 |
| Large-Depth | 33.7 | 111 | 121 | NACA 0006 | Half NACA 0012 | 23,617.5 |
| Small-Depth | 33.7 | 111 | 105 | NACA 0006 | Half NACA 0012 | 19,788.5 |
| Optimised | (Side: 39) (Centre: 30) | 111 | (Side: 115) (Centre: 100) | NACA 0006 | Half NACA 0012 | 20,388.2 |
| Mesh | Number of Elements | Time (h) | Lift Force (N) | |
|---|---|---|---|---|
| Coarse (M5) | 1,164,030 | 0.19 | 501.1528 | 0.6200 |
| M4 | 2,500,329 | 0.60 | 496.0812 | 0.6137 |
| Medium (M3) | 6,284,662 | 2.55 | 489.3098 | 0.6054 |
| M2 | 11,720,165 | 4.96 | 485.0050 | 0.6000 |
| Fine (M1) | 18,296,932 | 7.93 | 484.2851 | 0.5991 |
| Mesh | GCI | |
|---|---|---|
| M3 | 6.40 × 10−3 | 7.99 × 10−3 |
| M2 | 1.07 × 10−3 | 1.34 × 10−3 |
| M1 | 1.79 × 10−4 | 2.24 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crameri, S.; Collins, P.K.; Gharaie, S. Numerical Investigation of the Hydrodynamic Characteristics of 3-Fin Surfboard Configurations. Appl. Sci. 2022, 12, 3297. https://doi.org/10.3390/app12073297
Crameri S, Collins PK, Gharaie S. Numerical Investigation of the Hydrodynamic Characteristics of 3-Fin Surfboard Configurations. Applied Sciences. 2022; 12(7):3297. https://doi.org/10.3390/app12073297
Chicago/Turabian StyleCrameri, Sam, Paul K. Collins, and Saleh Gharaie. 2022. "Numerical Investigation of the Hydrodynamic Characteristics of 3-Fin Surfboard Configurations" Applied Sciences 12, no. 7: 3297. https://doi.org/10.3390/app12073297
APA StyleCrameri, S., Collins, P. K., & Gharaie, S. (2022). Numerical Investigation of the Hydrodynamic Characteristics of 3-Fin Surfboard Configurations. Applied Sciences, 12(7), 3297. https://doi.org/10.3390/app12073297







