A Robust Scheduling Framework for Re-Manufacturing Activities of Turbine Blades
Abstract
:1. Introduction and Industrial Motivation
2. Literature Review
3. Re-Manufacturing of Turbine Blades
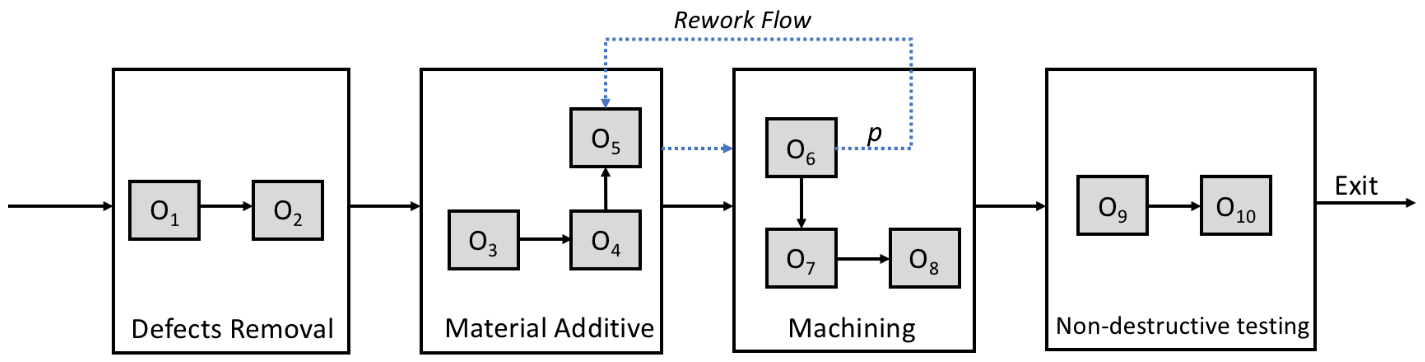
3.1. Re-Manufacturing Processes
- 1.
- Blades are disassembled at the production site and shipped to the OEM to be refurbished/renewed.
- 2.
- Upon arrival at the OEM, blades are inspected to assess the severity of wear and damages. Blades that cannot be repaired are discarded and the supply/production of new blades is issued. On the contrary, for reparable blades, the re-manufacturing process starts, whose process parameters depends on the assessed damage level.
- 3.
- The re-manufacturing process consists of removing the damaged (e.g., cracked) parts of the blades, restore the removed material through welding/additive technologies, machining/grinding the blade to reconstruct the desired shape. During the material removal phase, as well as at the end of the processing, non-destructive tests are operated to verify the complete removal of the defects.
- 4.
- The blades undergo the definition of small-size features (e.g., internal cooling ducts, specific shapes in the terminal side or in the coupling with the rotor) and are successively coated with high-resistance materials.
- 5.
- Finally, the blades belonging to the same stage are assembled together and balanced. Hence they are shipped back to the operating site of the turbine where they will be re-assembled and be ready to go into production again.
3.2. Uncertainty in Re-Manufacturing Processes
- 1.
- A major source of uncertainty is embedded in the characteristics and volumes of the parts to be processed. Used parts arrives from different use-phase conditions and, thus, could be worn differently. Moreover, grounding on their characteristics, the number of parts whose re-manufacturing is feasible or attractive could be different, thus impacting on the actual volumes of parts to be re-manufactured.
- 2.
- The re-manufacturing process plan could vary for different specimens of the same products. Thus, according to the characteristic of the item (wear, presence of damages, etc), different process steps arranged in different sequences could be needed. This impact on the management of the re-manufacturing system due to the need of implementing different routines among the available resources.
- 3.
- Grounding on the characteristics of each specific part, re-manufacturing process can differ in terms of the characteristics and parameters of re-manufacturing operations. This a clear impact on the execution of the processes (forces, velocity, processing times, etc.)
4. Robust Scheduling Framework
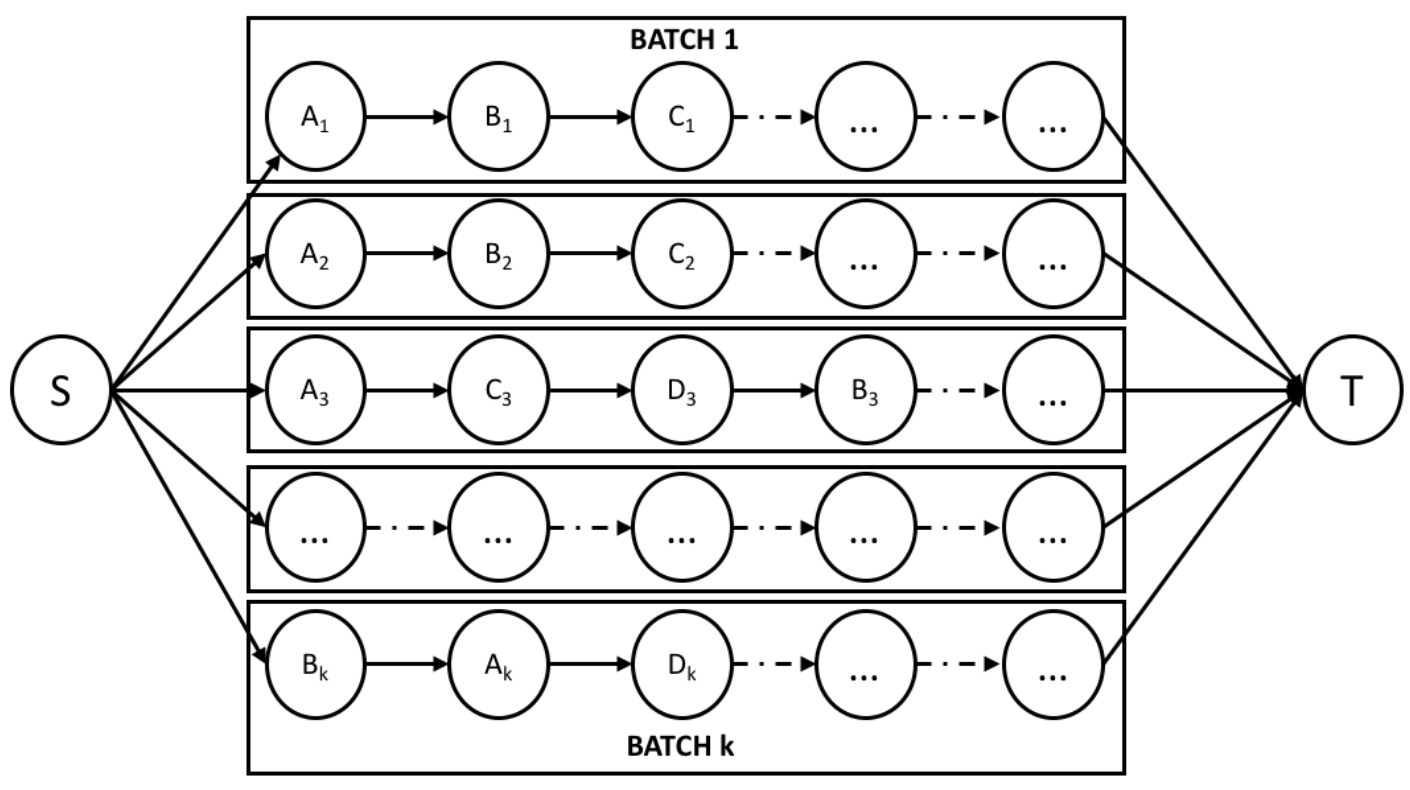
4.1. Shop Scheduling Model
4.2. Modeling Uncertainty
4.2.1. Uncertainty Affecting Processing Times
- 1.
- The number of blades in a batch depends on their level of damage. Extremely worn blades cannot be refurbished and must be discarded. A rejection rate table based on the damage level of each type of blade is defined. Thus, each batch of blades to be processed is assigned a level of damage (high, medium, low) sampled from a discrete distribution. Hence, the rejection rate is modeled as an uniform distribution defined by a lowest and highest rejection rates for that class of blades.
- 2.
- The processing time of an operation on a single blade is modeled as an interval whose boundaries can be determined grounding on historical data. Thus, the distribution of the processing time of a batch of blades can be obtained through a convolution operation between the distribution of the number of blades in the batch to be re-manufactured and the distribution of the processing time of a single blade.
4.2.2. Uncertainty Affecting the Process Steps
- 1.
- A RCPSP model is defined considering both work and rework activities.
- 2.
- The processing time of rework activities is obtained through the convolution of the occurrence and processing time distributions described above.
4.3. Robustness Measures
4.3.1. Minimizing the Maximum Regret of the Objective Function
4.3.2. Minimizing the Value-at-Risk/Conditional Value-at-Risk of the Objective Function
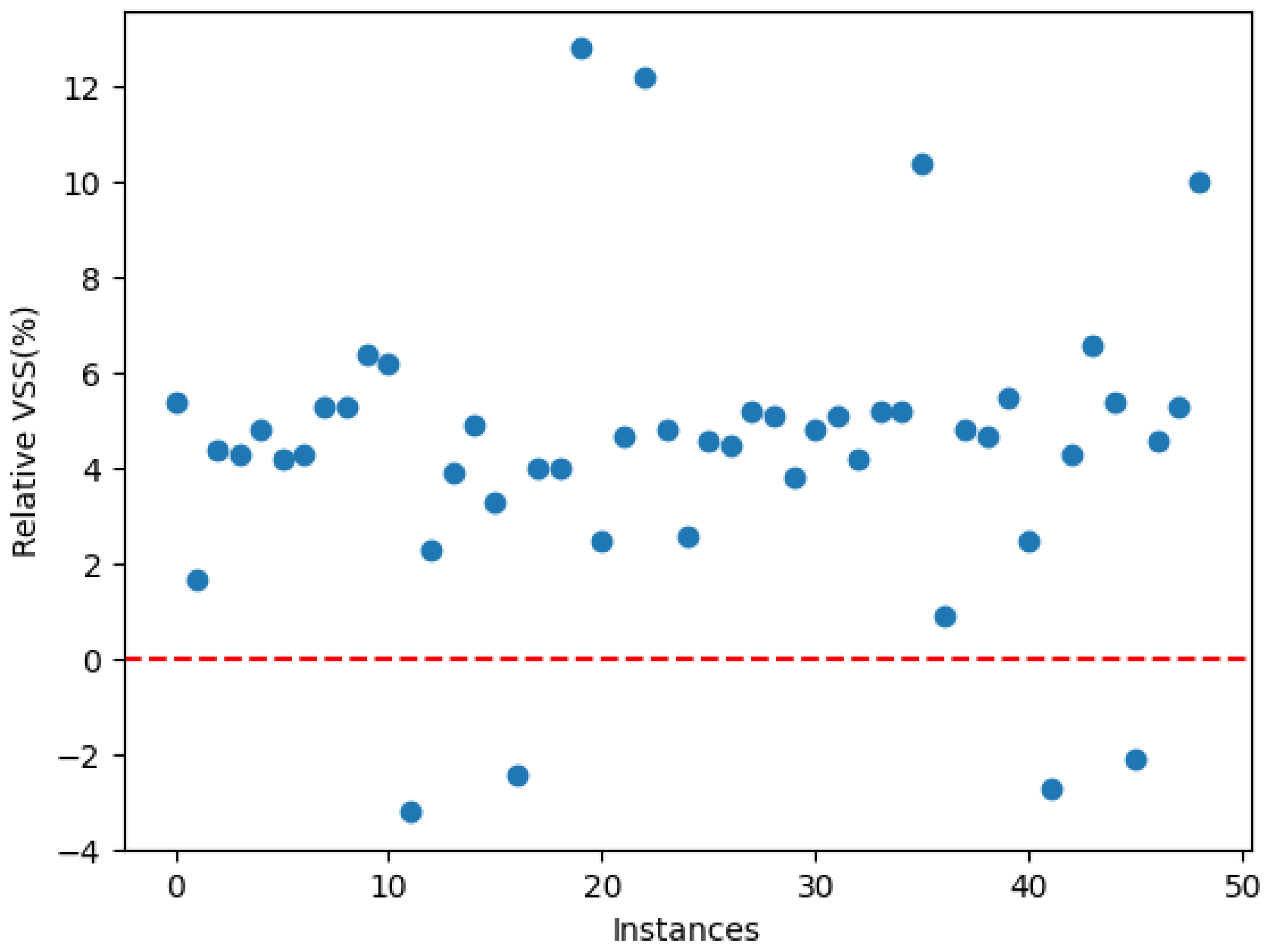
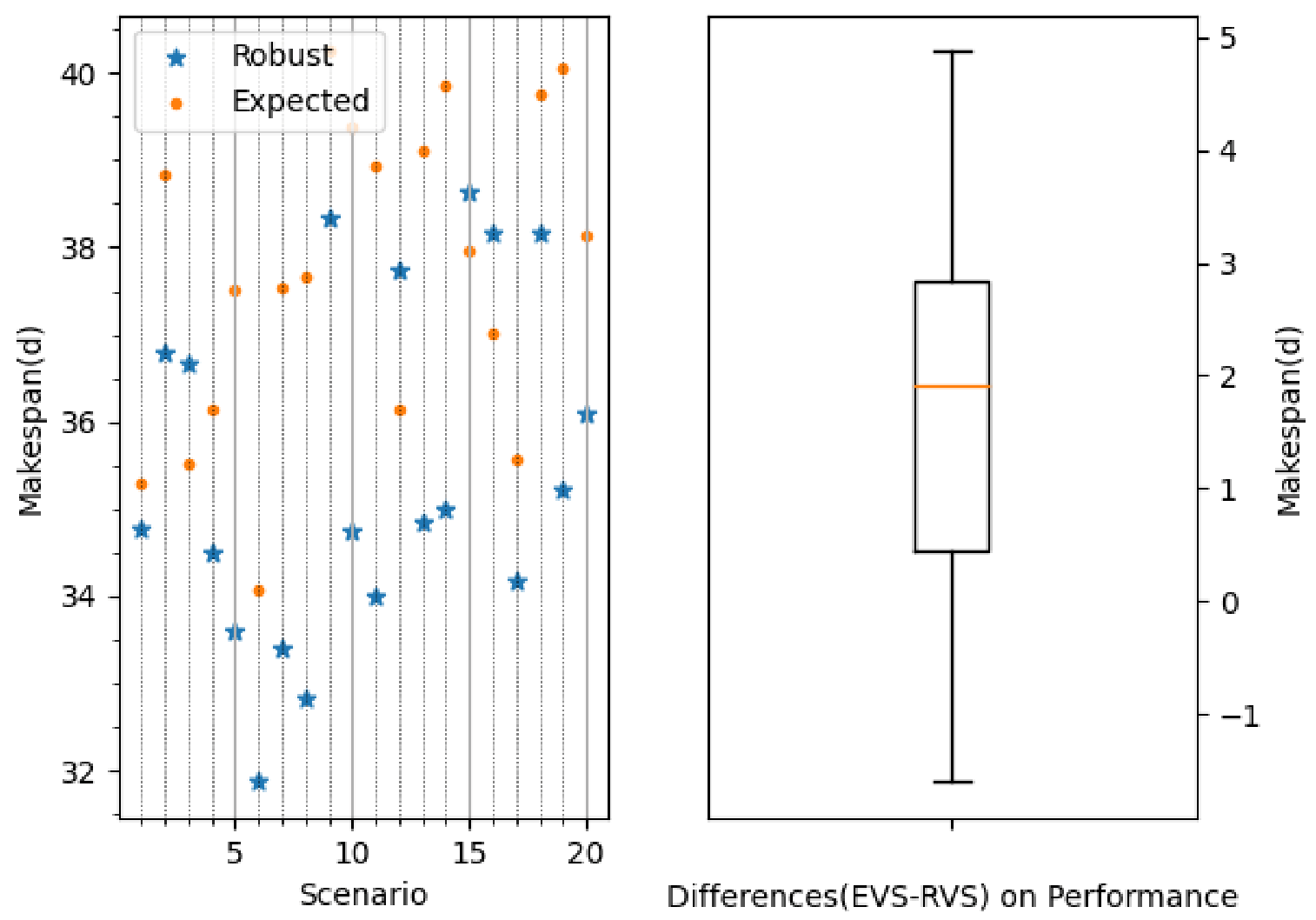
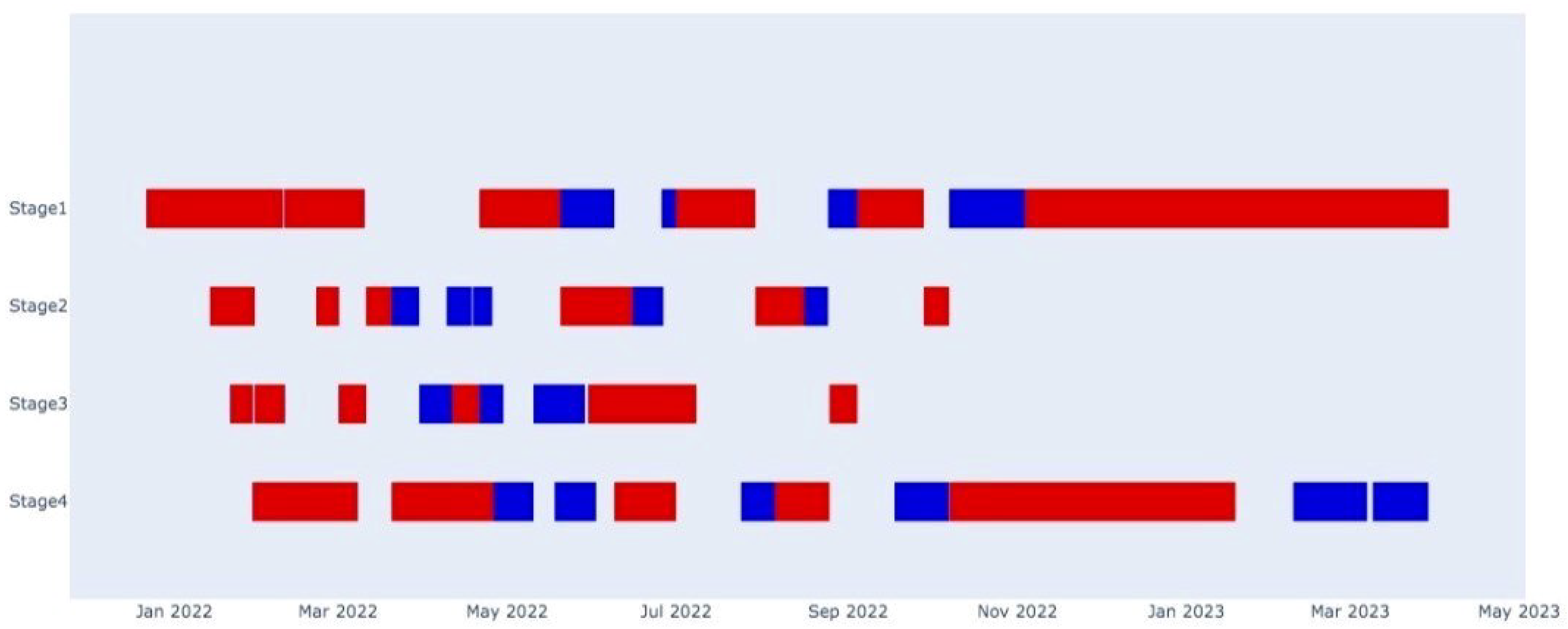
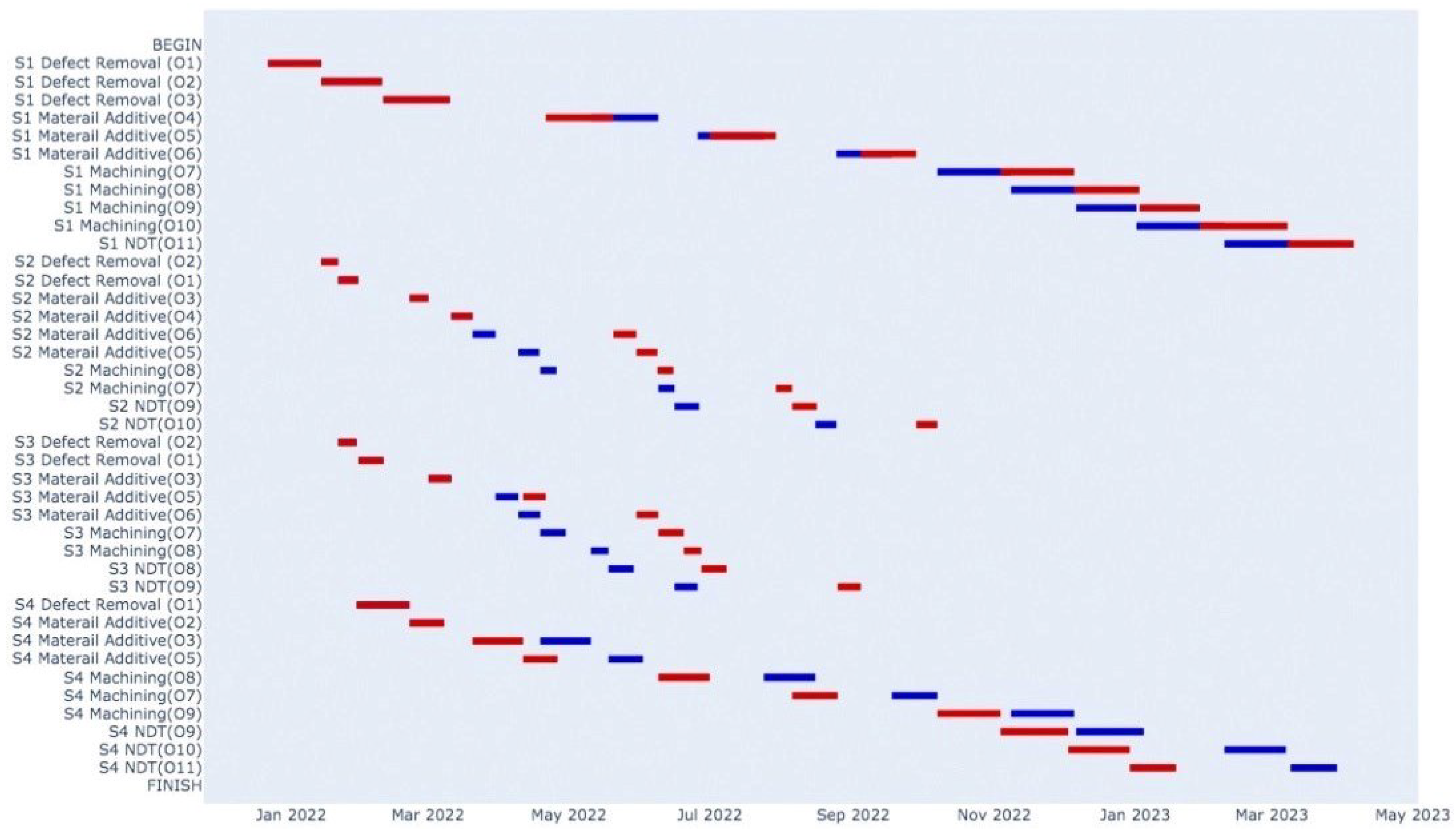
5. Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, M.R.; McCarthy, I.P. Product recovery decisions within the context of extended producer responsibility. J. Eng. Technol. Manag. 2014, 34, 9–28. [Google Scholar] [CrossRef]
- Tolio, T.; Bernard, A.; Colledani, M.; Kara, S.; Seliger, G.; Duflou, J.; Battaia, O.; Takata, S. Design, management and control of demanufacturing and remanufacturing systems. CIRP Ann. 2017, 66, 585–609. [Google Scholar] [CrossRef]
- Liu, C.; He, K.; Zhang, Y.; Liu, C. Research on data mining technology for the connotation and measurement of uncertainty for reassembly dimensions. Int. J. High Perform. Syst. Archit. 2018, 8, 13–21. [Google Scholar] [CrossRef]
- Frank, A.G.; Dalenogare, L.S.; Ayala, N.F. Industry 4.0 technologies: Implementation patterns in manufacturing companies. Int. J. Prod. Econ. 2019, 210, 15–26. [Google Scholar] [CrossRef]
- Magruk, A. Analysis of Uncertainties and Levels of Foreknowledge in Relation to Major Features of Emerging Technologies—The Context of Foresight Research for the Fourth Industrial Revolution. Sustainability 2021, 13, 9890. [Google Scholar] [CrossRef]
- Goodall, P.; Rosamond, E.; Harding, J. A review of the state of the art in tools and techniques used to evaluate remanufacturing feasibility. J. Clean. Prod. 2014, 81, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Rickli, J.L.; Dasgupta, A.K.; Dinda, G.P. A descriptive framework for additive remanufacturing systems. Int. J. Rapid Manuf. 2014, 4, 199–218. [Google Scholar] [CrossRef]
- Huang, W.; Jiang, Z.; Wang, T.; Wang, Y.; Hu, X. Remanufacturing scheme design for used parts based on incomplete information reconstruction. Chin. J. Mech. Eng. 2020, 33, 1–14. [Google Scholar] [CrossRef]
- Liu, L.; Urgo, M. Scheduling Remanufacturing Activities for the Repair of Turbine Blades: An Approximate Branch and Bound Approach to Minimize a Risk Measure. In Selected Topics in Manufacturing; Springer: Berlin/Heidelberg, Germany, 2022; pp. 41–59. [Google Scholar]
- Rizova, M.I.; Wong, T.; Ijomah, W. A systematic review of decision-making in remanufacturing. Comput. Ind. Eng. 2020, 147, 106681. [Google Scholar] [CrossRef]
- Guide, V.D.R., Jr. Production planning and control for remanufacturing: Industry practice and research needs. J. Oper. Manag. 2000, 18, 467–483. [Google Scholar] [CrossRef]
- Morgan, S.D.; Gagnon, R.J. A systematic literature review of remanufacturing scheduling. Int. J. Prod. Res. 2013, 51, 4853–4879. [Google Scholar] [CrossRef]
- Kin, S.T.M.; Ong, S.; Nee, A. Remanufacturing process planning. Procedia Cirp 2014, 15, 189–194. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Ong, S.; Nee, A.Y. A simulation-based genetic algorithm approach for remanufacturing process planning and scheduling. Appl. Soft Comput. 2015, 37, 521–532. [Google Scholar] [CrossRef]
- Ducker, M. The Fall of the F-Class Turbine. 2015. Available online: https://www.power-eng.com/emissions/policy-regulations/the-fall-of-the-f-class-turbine/#gref (accessed on 19 January 2022).
- GE H Series Power Generation Gas Turbine. Available online: https://en.wikipedia.org/wiki/Gas_turbine (accessed on 8 March 2022).
- Wikipedia. Turbine Blade. 2009. Available online: https://en.wikipedia.org/wiki/Turbine_blade (accessed on 19 December 2021).
- Behdad, S.; Williams, A.S.; Thurston, D. End-of-Life Decision Making with Uncertain Product Return Quantity. J. Mech. Des. 2012, 134, 100902. [Google Scholar] [CrossRef]
- Bermejo, J.; Calinescu, A.; Efstathiou, J.; Schirn, J. Dealing with uncertainty in manufacturing: The impact on scheduling. In Proceedings of the Thirty-Second International Matador Conference, Manchester, UK, 10–11 July 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 149–154. [Google Scholar]
- Jorge Leon, V.; David Wu, S.; Storer, R.H. Robustness measures and robust scheduling for job shops. IIE Trans. 1994, 26, 32–43. [Google Scholar] [CrossRef]
- Urgo, M.; Váncza, J. A branch-and-bound approach for the single machine maximum lateness stochastic scheduling problem to minimize the value-at-risk. Flex. Serv. Manuf. J. 2019, 31, 472–496. [Google Scholar] [CrossRef] [Green Version]
- Nudtasomboon, N.; Randhawa, S.U. Resource-constrained project scheduling with renewable and non-renewable resources and time-resource tradeoffs. Comput. Ind. Eng. 1997, 32, 227–242. [Google Scholar] [CrossRef]
- Artigues, C.; Demassey, S.; Neron, E. Resource-Constrained Project Scheduling: Models, Algorithms, Extensions and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sotskov, Y.N.; Lai, T.C.; Werner, F. Measures of problem uncertainty for scheduling with interval processing times. OR Spectr. 2013, 35, 659–689. [Google Scholar] [CrossRef]
- Liao, W.; Fu, Y. Min–max regret criterion-based robust model for the permutation flow-shop scheduling problem. Eng. Optim. 2019, 52, 687–700. [Google Scholar] [CrossRef]
- Paprocka, I. The model of maintenance planning and production scheduling for maximising robustness. Int. J. Prod. Res. 2019, 57, 4480–4501. [Google Scholar] [CrossRef]
- Law, A.M.; Kelton, W.D.; Kelton, W.D. Simulation Modeling and Analysis; McGraw-Hill: New York, NY, USA, 2000; Volume 3. [Google Scholar]
- Tolio, T.; Urgo, M.; Váncza, J. Robust production control against propagation of disruptions. CIRP Ann. 2011, 60, 489–492. [Google Scholar] [CrossRef]
- Aissi, H.; Bazgan, C.; Vanderpooten, D. Min–max and min–max regret versions of combinatorial optimization problems: A survey. Eur. J. Oper. Res. 2009, 197, 427–438. [Google Scholar] [CrossRef] [Green Version]
- Averbakh, I. Computing and minimizing the relative regret in combinatorial optimization with interval data. Discret. Optim. 2005, 2, 273–287. [Google Scholar] [CrossRef] [Green Version]
- Artigues, C.; Leus, R.; Nobibon, F.T. Robust optimization for resource-constrained project scheduling with uncertain activity durations. Flex. Serv. Manuf. J. 2013, 25, 175–205. [Google Scholar] [CrossRef] [Green Version]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef]
- Atakan, S.; Bülbül, K.; Noyan, N. Minimizing value-at-risk in single-machine scheduling. Ann. Oper. Res. 2017, 248, 25–73. [Google Scholar] [CrossRef] [Green Version]
- Urgo, M. A branch-and-bound approach to schedule a no-wait flow shop to minimize the CVaR of the residual work content. Comput. Ind. Eng. 2019, 129, 67–75. [Google Scholar] [CrossRef]
- Sarykalin, S.; Serraino, G.; Uryasev, S. Value-at-risk vs. conditional value-at-risk in risk management and optimization. In State-of-the-art Decision-Making Tools in the Information-Intensive Age; Informs: Catonsville, MD, USA, 2008; pp. 270–294. [Google Scholar] [CrossRef] [Green Version]
- Dixit, V.; Tiwari, M.K. Project portfolio selection and scheduling optimization based on risk measure: A conditional value at risk approach. Ann. Oper. Res. 2020, 285, 9–33. [Google Scholar] [CrossRef]
- Dodin, B. Bounding the project completion time distribution in PERT networks. Oper. Res. 1985, 33, 862–881. [Google Scholar] [CrossRef]
- Dodin, B. Determining the optimal sequences and the distributional properties of their completion times in stochastic flow shops. Comput. Oper. Res. 1996, 23, 829–843. [Google Scholar] [CrossRef]
- Kulkarni, V.G.; Adlakha, V. Markov and Markov-regenerative PERT networks. Oper. Res. 1986, 34, 769–781. [Google Scholar] [CrossRef]
- Angius, A.; Horváth, A.; Urgo, M. A Kronecker Algebra Formulation for Markov Activity Networks with Phase-Type Distributions. Mathematics 2021, 9, 1404. [Google Scholar] [CrossRef]
- Felberbauer, T.; Gutjahr, W.J.; Doerner, K.F. Stochastic project management: Multiple projects with multi-skilled human resources. J. Sched. 2019, 22, 271–288. [Google Scholar] [CrossRef] [Green Version]
- Manzini, M.; Demeulemeester, E.; Urgo, M. A predictive–reactive approach for the sequencing of assembly operations in an automated assembly line. Robot. Comput.-Integr. Manuf. 2022, 73, 102201. [Google Scholar] [CrossRef]




| Damage Level | Rejection Rate LB (%) | Rejection Rate UB (%) |
|---|---|---|
| Heavy | 60 | 90 |
| Medium | 30 | 60 |
| Light | 0 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Urgo, M. A Robust Scheduling Framework for Re-Manufacturing Activities of Turbine Blades. Appl. Sci. 2022, 12, 3034. https://doi.org/10.3390/app12063034
Liu L, Urgo M. A Robust Scheduling Framework for Re-Manufacturing Activities of Turbine Blades. Applied Sciences. 2022; 12(6):3034. https://doi.org/10.3390/app12063034
Chicago/Turabian StyleLiu, Lei, and Marcello Urgo. 2022. "A Robust Scheduling Framework for Re-Manufacturing Activities of Turbine Blades" Applied Sciences 12, no. 6: 3034. https://doi.org/10.3390/app12063034
APA StyleLiu, L., & Urgo, M. (2022). A Robust Scheduling Framework for Re-Manufacturing Activities of Turbine Blades. Applied Sciences, 12(6), 3034. https://doi.org/10.3390/app12063034






