1. Introduction
Mobile robots have a huge range of potential applications in industrial, office and home environments. Autonomous mobile robots must be able to perform localization, mapping and navigation with reasonable levels of accuracy in order to successfully develop and complete their tasks. Localization methods consist of absolute or relative positioning methods [
1,
2]. Borenstein et al. [
2] reviewed the most relevant mobile robot relative positioning methods based on internal data gathered by the mobile robot: odometry and inertial navigation, and the most relevant absolute positioning methods based on gathering external surrounding data.
Odometry is usually defined as a relative positioning method that uses the measures of the velocities of the wheels to estimate the position of the robot. Compared to other techniques, odometry is simple, affordable, and can be used in real-time, but as a relative positioning method it cumulates errors that may lead to inaccurate results. The improvement of odometry through proper calibration reduces the position errors and can contribute to lowering the costs of mobile robots by avoiding the use of precise external sensors.
In 1996, Borenstein et al. [
3] introduced a benchmark test to measure the odometric accuracy of a mobile robot. This test, called University of Michigan Benchmark (UMBmark), consists on a bidirectional square path experiment in which a differential drive mobile robot performs a squared path in the clockwise and counterclockwise directions to avoid the compensation of odometry errors that might occur in unidirectional squared path experiments. The method first computes the contribution of errors caused by incorrect wheelbase (distance from the wheel to the center of the mobile robot) and by unequal wheel diameters. These errors are evaluated separately and then superimposed. In the case of a differential drive mobile robot, a wheelbase error causes pure rotation errors, which can be corrected by applying a correction factor to the wheelbase distances. The unequal wheel diameters error causes the robot to move on curved paths instead of straight trajectories. The radius of curvature of the real path can be computed to determine the ratio between the two-wheel diameters and compensate this systematic error. The application of the UMBmark provides a quantitative measure and corrects the systematic odometry errors, which allows comparison between different mobile robots. In summary, the results presented by Borenstein et al. [
3] allowed an improvement of one order of magnitude in odometry accuracy.
An alternative to direct odometry calibration from the information gathered from the wheels is the application of data fusion from different sensors. Gargiulo et al. [
4] estimated the mobile robot position and orientation by fusing information gathered from the wheels and an Inertial Measurement Unit (IMU). Zwierzchowski et al. [
5] used a similar approach and included the information gathered from a vision system that measures the distance between the robot and custom markers located in the surrounding space. Xue et al. [
6] fuses the information gathered from the wheels, an IMU and a 2D LIDAR in order to operate in diverse outdoor environments without any prior information. In a different approach, Palacin et al. [
7] directly estimates the position and orientation of the mobile robot using the information provided by an onboard precise 2D LIDAR processed with simultaneous location and mapping (SLAM) [
8]. In this case, the odometry was used as an initial estimation of the relative motion in order to improve the computational efficiency of SLAM. More recently, Xiao et al. [
9] fused the information gathered from one IMU and two low-precision 2D LIDARs placed transversally to estimate the position and orientation of a mobile robot. However, the main disadvantage of using LIDARs is the cost of the sensor that is proportional to its measurement accuracy.
In the specific case of omnidirectional mobile robots, the determination of the odometry from the velocity gathered from the wheels has similar error sources but more complexity because of having more degrees of freedom in the motion [
10]. In this direction, Maddahi et al. [
11] proposed a method for the calibration of small three-wheeled omnidirectional mobile robots in order to reduce positioning errors. The procedure was based on the determination of two corrective indices for the inverse kinematic matrix used by the odometry to estimate the position of the robot. This method consists of: (1) determining the kinematic equations of the robot; (2) registering of the motion of the non-calibrated robot moving along a straight line; (3) evaluating the longitudinal error (
), lateral error (
) and angular error (
) between the target and real trajectory positions; and (4) the computation of some corrective indices. This method corrects the longitudinal (
) and lateral (
) errors separately. First, a lateral corrective matrix, which compensates the lateral position error of the robot (
), is computed from the angular error of the robot (
). Secondly, a longitudinal corrective factor used to eliminate the longitudinal position error (
) is computed from the longitudinal (
) and lateral errors (
). Finally, both indices are multiplied with the Jacobian matrix used by the odometry to estimate the velocities of the wheels. The corrected Jacobian matrix is then used to compute the corrected angular velocities of the wheels. This proposal was experimentally validated with different trajectories, comparing the positioning errors before and after calibration. Results showed significant improvements: the root mean square (RMS) of the positioning error was reduced between 68% and 91% in double-squared, double-triangle and circular paths. In this case, the analysis of the trajectories and positioning errors evidenced that the improvement depends on the type of trajectory being accurate in straight trajectories and less accurate in the case of combined straight and curved trajectories.
Similarly, Lin et al. [
12] presented an odometry calibration method for medium-size three-wheeled omnidirectional mobile robots based on the correction of its kinematic model. The method consists on gathering discrete position and orientation data and estimating the kinematic parameters by a least square method. The information required by this process is the initial and final positions of the mobile robot through N experiments (multiple data sets). This proposal is not limited by the relationship between the parameters used in the kinematic equations, so the obtained kinematic model may better describe the odometry of the mobile robot. Lin et al. [
12] verify their calibration method by comparing the ideal trajectory and the trajectories before and after calibration.
In a similar direction, Li et al. [
13] presented a method for the reduction of positioning errors of four-wheel omnidirectional mobile robots using Mecanum wheels. The main problem of four-wheel omnidirectional mobile robots is wheel slippage, so this method analyzed the kinematic model of the mobile robot and provides a velocity compensation matrix to reduce the errors of the robot motion caused by wheel slippage. This compensation matrix was validated using virtual simulations and experimental tests. Results showed that the compensation matrix reduces the errors of robot motions caused by wheel slippage, improving the motion accuracy of the system. However, Li et al. [
13] concluded that this velocity compensation matrix must be adjusted according to the velocity of the mobile robot. Alternatively, Lu et al. [
14] fused the information gathered from an IMU, a gyroscope and encoders to estimate the odometry of a mobile robot using four Mechanum wheels to estimate the estimated odometry on a floating ground.
More recently, Savaee et al. [
15] proposed a simplification of the method presented by Maddahi et al. [
11]. The new method uses the kinematic model of a three-wheeled mobile robot and computed a corrected Jacobian matrix to reduce the effects of systematic errors in the odometry. This method used a genetic algorithm to find the matrix elements of a corrected Jacobian matrix, which are called Effective Kinematic Parameters (EPKs). This new method consists of: (1) creating a model of the virtual robot and of the systematic errors; (2) performing simulation tests with the virtual robot; (3) performing experimental tests with a real robot; (4) comparing both results to estimate the EPKs and redefine the Jacobian matrix of the mobile robot. In this case, the simulation and experimental tests consist of two robot translations along straight paths and one rotation about itself, and the calculated EPKs are used to correct the angular velocities of the wheels. This procedure was verified with a three-wheeled omnidirectional mobile robot performing different paths. In general, the evaluation of tracking errors in offline analysis has the advantage of avoiding local minimum in complex parametric nonlinear systems [
16].
New Contribution
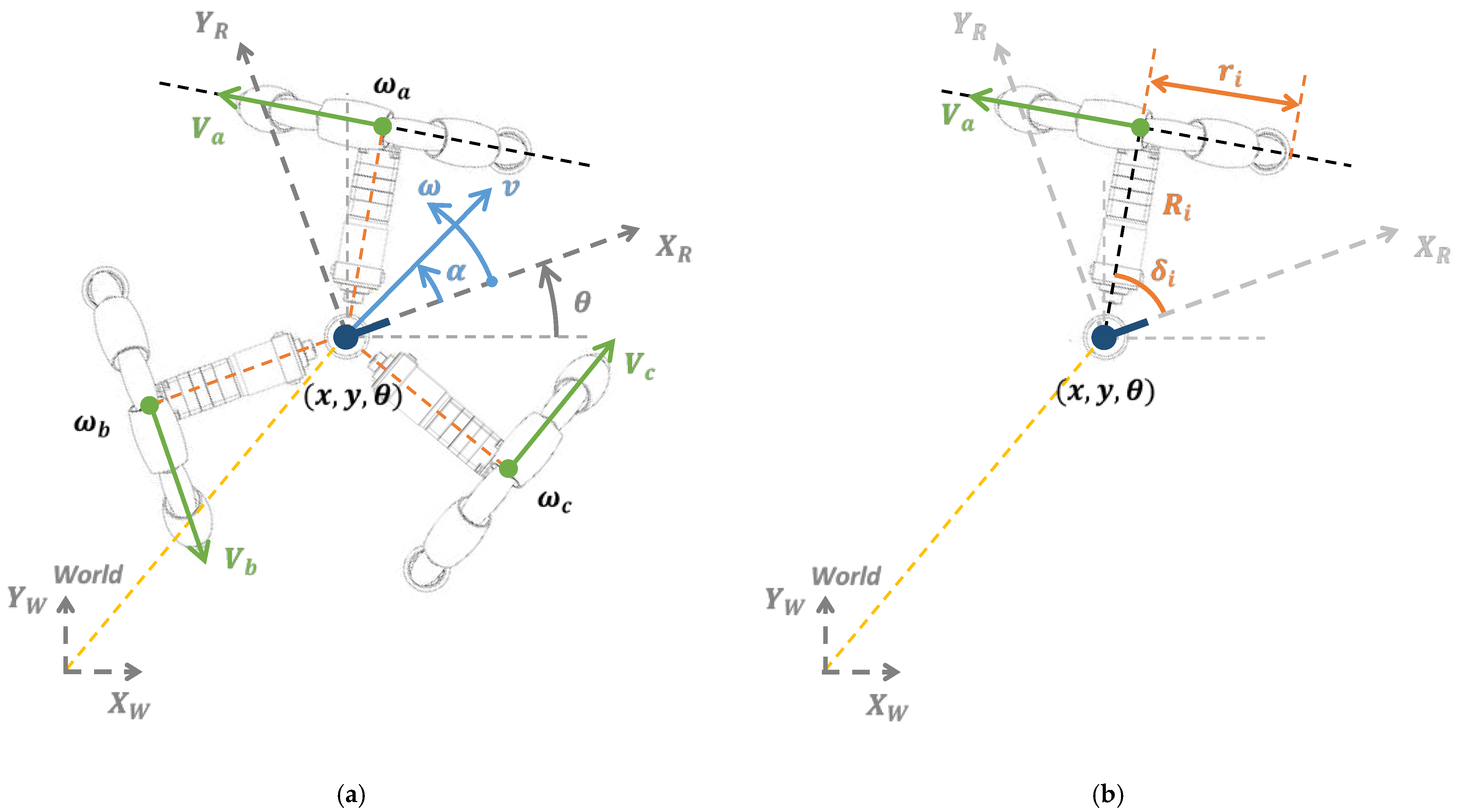
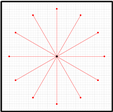
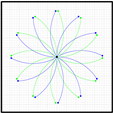
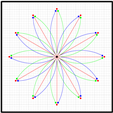
The new contribution of this paper is the proposal of a combination of 36 straight and curved calibration trajectories for systematic odometry error evaluation and correction in a three-wheeled omnidirectional mobile robot. This procedure has been empirically applied and validated in a real human-sized three-wheeled omnidirectional mobile robot of 1.760 m and 30 Kg (
Figure 1). These 36 calibration trajectories have been proposed as a representative test-bench of the infinite trajectories that can be performed by an omnidirectional mobile robot, which together depict a characteristic flower-shaped figure. The calibration procedure implemented requires the registering of the real odometry and ground truth trajectories generated while performing each calibration trajectory. Finally, the odometry of each calibration trajectory is recomputed offline to iteratively adjust the effective values of the kinematic parameters of the mobile robot in order to match the odometry with the ground truth trajectory. This paper has evaluated different matching strategies using different sets of calibration trajectories. The best matching between the odometry and ground truth trajectories has been obtained using genetic algorithms and 5 repetitions of each one of the proposed 36 calibration trajectories. The fitting results of the kinematic parameters have been validated by performing 5 additional repetitions of the 36 calibration trajectories.
This new contribution was inspired in Batlle et al. [
17], who proposed the use of four curved calibration trajectories, and in Maddahi et al. [
11], who calibrated the odometry with straight paths but concluded that the percentage of error correction depends on the type of the path. The new contribution is the proposal of a complete set of straight and curved calibration trajectories which together depict a characteristic flower-shaped figure. This new contribution is also inspired in the work of Savaee et al. [
15] that used genetic algorithms to adjust the kinematic matrix of a three-wheeled mobile robot although without comparing the results obtained with other minimization alternatives. This proposal will apply the same methodology proposed by Lin et al. [
12], based on the comparison of the initial and final positions of the mobile robot through N experiments to directly evaluate the odometry improvement achieved. Finally, as an alternative to Savaee et al. [
15] and Lin et al. [
12], this new proposal adjusts the value of the kinematic parameters of the mobile robot (radii of the wheels, distance from the wheel to the center of the mobile robot and angular orientation of the wheels) instead of directly adjusting the values of the kinematic matrix, allowing a direct physical interpretation of the fitting results obtained.
3. Systematic Odometry Error Evaluation and Correction
The procedure proposed in this paper to systematically evaluate and correct the systematic odometry errors of the omnidirectional mobile robot APR-02 is based on the definition of 36 individual calibration trajectories which together depict a flower-shaped figure, on the measurement of the odometry and ground truth trajectory in each calibration trajectory, and on the application of several strategies to iterative adjustment of the effective value of the kinematic parameters to match the odometry and the ground truth trajectories registered in these 36 calibration trajectories. The implementation of the 36 trajectories that define the flower-shaped figure is proposed as a representative test-bench of the infinite trajectories that can perform this omnidirectional mobile robot. In this paper, each calibration trajectory has been repeated 10 times; with a total of 360 registered trajectories. Five repetitions will be used to calibrate the effective value of the kinematic parameters and Five repetitions will be used to validate the results.
3.1. Calibration Trajectories Depicting a Characteristic Flower-Shaped Figure
This paper proposes the improvement of the odometry of the omnidirectional mobile robot APR-02 using a set of specific individual calibration trajectories that globally depict a characteristic flower-shaped figure.
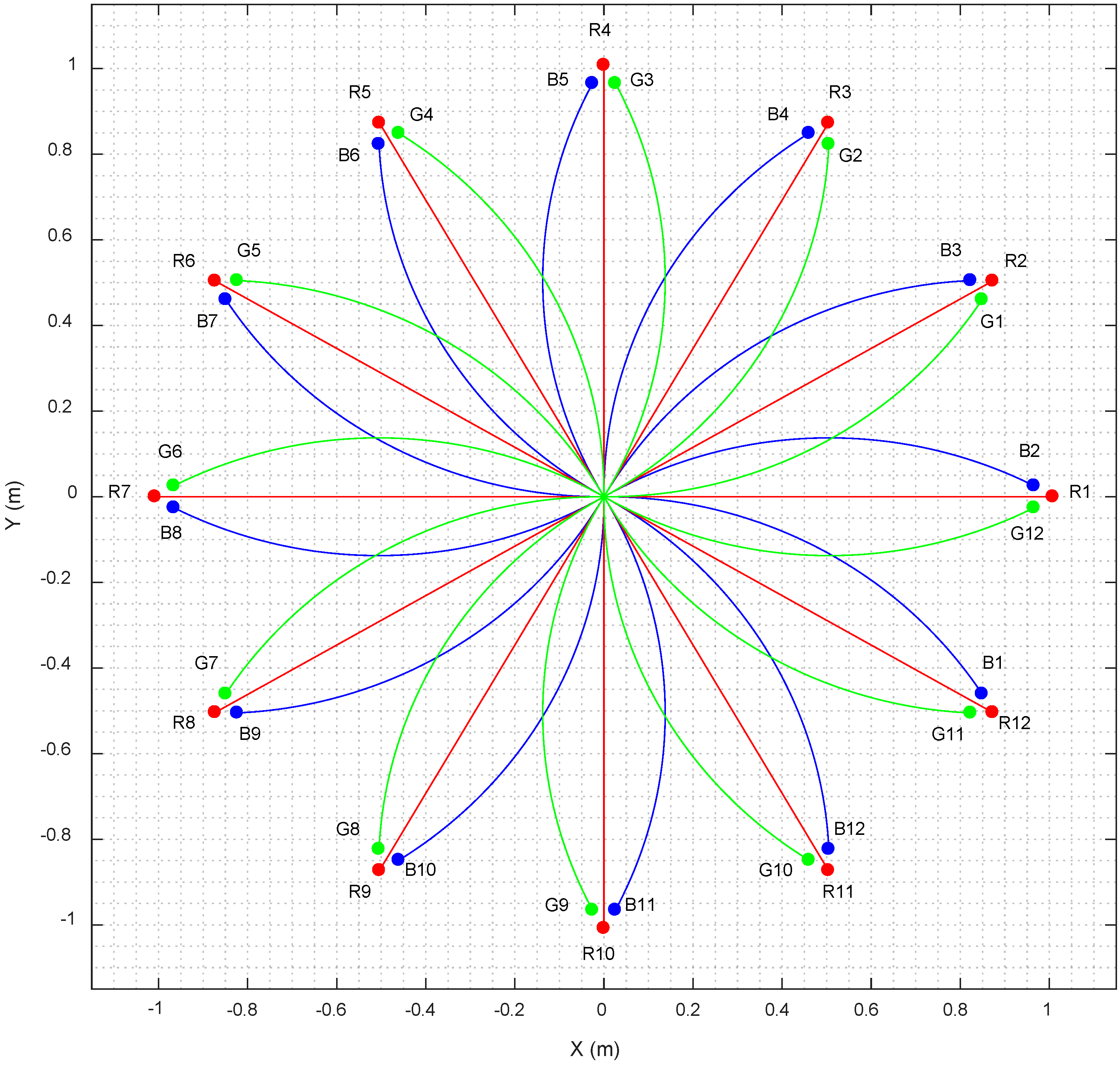
Figure 9 shows the proposed trajectories and
Table A1 (listed in
Appendix A) presents the motion command required to implement each calibration trajectory and the values of the corresponding target angular rotational velocities of the wheels required to implement each trajectory that will be specific for each mobile robot type.
The target angular velocities of the wheels shown in
Table A1 (
Appendix A) are in revolutions per minute (rpm) because this unit is normally used by the PIDs controlling the angular rotational velocity of the motors of the mobile robot. The calibration trajectories comprise straight displacements (
Figure 9, red line labeled with an R followed with a number), clockwise displacements (blue line labeled with a B followed with a number), and counterclockwise displacements (green line labeled with a G followed with a number). These 36 combinations of angular rotational velocities of the wheels are a short representation of the infinite set of possible motion combinations. The linear displacement of all trajectories has been limited to 1 m in order to generate a characteristic and easy to remember flower-shaped figure. In this paper, each trajectory has been repeated and registered 10 times in a total of 360 trajectory experiments. Each trajectory register contains the sequence of instantaneous angular velocities of the three wheels
, where
is the number of samples available; the vector containing the position of the mobile robot estimated by the odometry
; and the vector containing the ground truth position
estimated by the SLAM procedure.
The adequacy of the trajectories proposed in
Figure 9 to the calibration of the odometry mobile robot APR-02 will be evaluated in the following section.
3.2. Odometry Calibration Strategies and Results
The odometry calibration strategies tested in this paper are based on analysis of the calibration trajectories proposed in
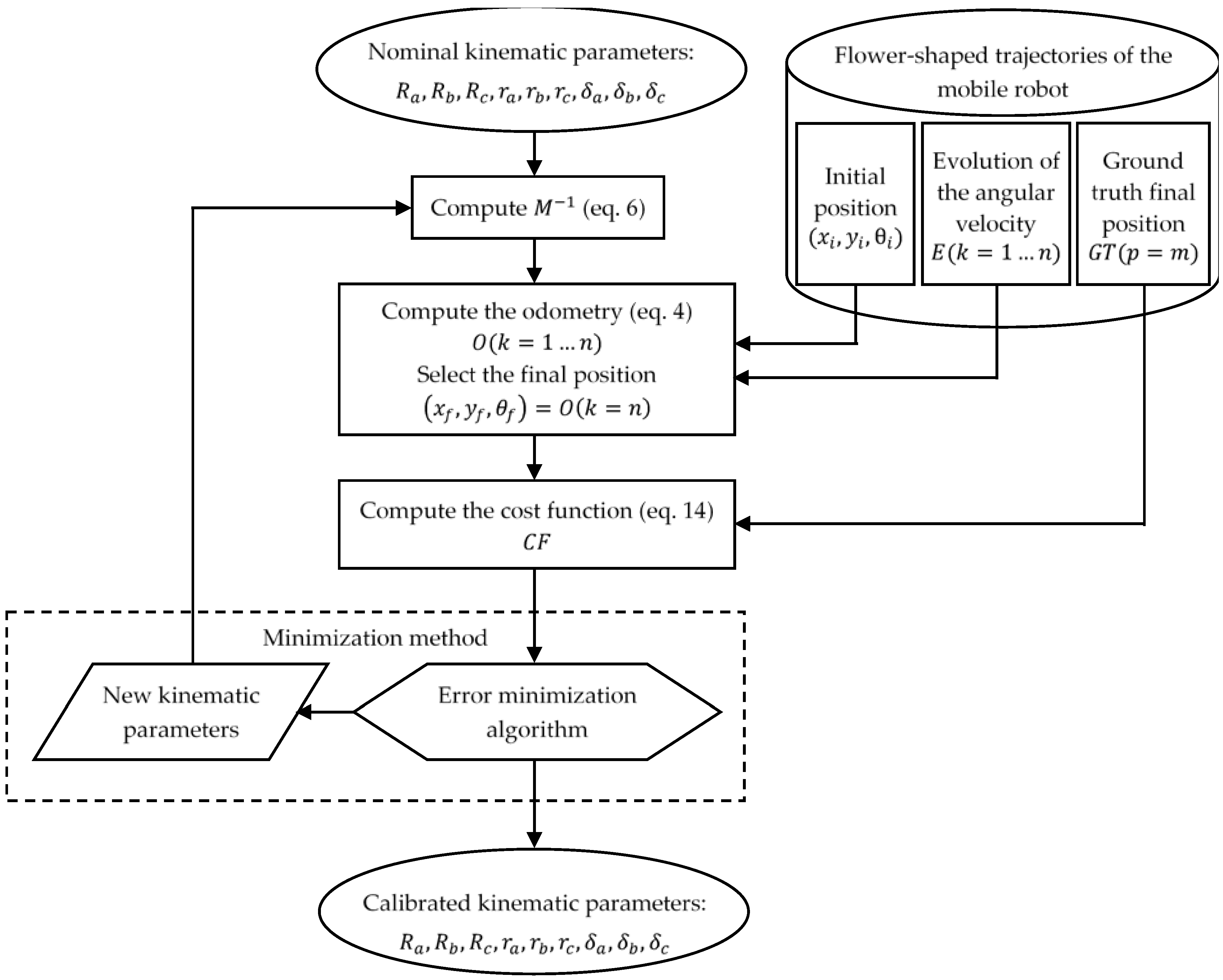
Figure 9. The iterative calibration procedure used has been previously described in
Section 2.6. In summary, this iterative calibration gets the registered calibration trajectories and iteratively adjusts the values of the effective kinematic parameters to globally match the odometry and ground truth trajectories.
Table 4 presents the results obtained:
Trajectories depicts which trajectories have been used in the iterative search;
Strategy shows the acronym of the calibration strategy applied;
Method describes the iterative function used (GA or fmin) and the number of trajectory repetitions used in the iterative search: (1) one or (5) five repetitions;
shows the value of the kinematic matrix obtained as a result of the iterative search;
is the value of the average cost function obtained during the iterative search or training;
is the average value of the cost function obtained with five additional calibration trajectories (the complete flower-shape);
Improvement depicts the relative improvement of
relative to the uncalibrated case (
None strategy).
The calibration strategies shown in
Table 4 have been generally labeled as
STX-GAZ and
STX-FminZ, where
X describes the group of trajectories considered (from
A to
E);
GA refers to the use of the
ga.m iterative function and
Fmin to the
fmincon.m iterative function; and
Z is the number of repetitions of each calibration trajectory considered, a value that can be 1 or 5. The evaluation of each calibration strategy with one or five repetitions was proposed to compare the achievements obtained relative to the additional effort required to obtain 5 repetitions of each calibration trajectory. The calibration strategies evaluated in
Table 4 are:
None. This strategy provides a reference evaluation result of the cost function using the uncalibrated kinematic parameters to compute the odometry of the 5 repetitions of all calibration trajectories registered to validate the results.
STA. This strategy uses only the straight calibration trajectories corresponding to a forward motion and two additional motions at ±120° (
Figure 9, trajectories: R1, R5 and R9). For example, STA-GA1 uses one repetition of the straight calibration trajectories and genetic algorithms, whereas STA-Fmin5 uses five repetitions of the straight calibration trajectories evaluated with the nonlinear multivariable function.
STB. This strategy uses only the curved clockwise and counterclockwise trajectories corresponding to a forward motion and two additional motions at ±120° (
Figure 9, trajectories: B2, B6, B10, G12, G4 and G8).
STC. This strategy uses only the straight trajectories corresponding to a forward motion and eleven additional motions at ±30° (
Figure 9, trajectories from R1 to R12).
STD. This strategy uses only the curved clockwise and counterclockwise trajectories corresponding to a forward motion and eleven additional motions at ±30° (
Figure 9, trajectories from B1 to B12 and from G1 to G12).
STE. This strategy uses all the straight and curved paths that depict the characteristic flower-shaped figure (
Figure 9, all calibration trajectories).
3.3. Discussion of the Results Obtained with the Odometry Calibration Strategies
The results of the calibration strategies evaluated in
Table 4 show that the evaluation of straight trajectories usually generates worse validation results than curved trajectories. It is likely that straight target trajectories (
Table A1: R1…R12) are less representative of the motion because they only use three different angular rotational velocities: ±11.291, ±19.557 and ±22.583 rpm, while the curved trajectories cover six angular velocities (
Table A1). In general, the best results of the iterative search are obtained with GA, probably because GA is less prone to local minimum converge.
The best calibration result ( was obtained with the strategy STB-GA5, using GA and five repetitions of only six curved calibration trajectories, also with very good validation results . A similar result was obtained with the strategy STB-GA1, using only one repetition of these six curved calibration trajectories (), confirming the representativeness of the curved calibration trajectories. The strategies STB-GA1 and STB-GA5 represent a huge improvement of 73.1 % and 81.3 % in the average validation of relative to the uncalibrated case.
The best validation result was obtained with the strategy STE-GA5, using GA and 5 repetitions of all 36 calibration trajectories (180 training experiments). However, a very similar result was also obtained using GA and with only 1 repetition of all training trajectories (STE-GA1, 36 experiments, ). The improvements obtained in the validation of STE-GA1 and STE-GA5 were 81.8 % and 82.1 % respectively, so the conclusion is that both strategies are valid to calibrate the kinematic parameters of the mobile robot APR-02.
Table 5 compares the differences between the nominal and calibrated kinematic parameters obtained with STE-GA5. Unexpectedly, the differences between the nominal and calibrated values of the distance from the wheels to the center of the mobile robot
are higher than 10%, likely caused by the bending of the structure that supports the wheels (wheelbase). The differences in the effective values of the radii of the wheels
are in a range from 2 to 5%, probably caused by the complex assembly of the wheels. Finally, the values of the angular orientation of the wheels
vary within a very small range (0.18% and 0.52%), confirming the good alignment of the wheels and DC motors during the assembly of the mobile robot.
The exact value of the best inverse of the compact kinematic matrix
computed from the effective value of the kinematic parameters obtained with STE-GA5 is:
Finally,
Table 6 summarizes the average RMS errors and average maximum errors obtained with the uncalibrated and calibrated kinematic parameters. These validation results have been obtained with the five repetitions of the 36 calibration trajectories registered for validation (180 validation experiments).
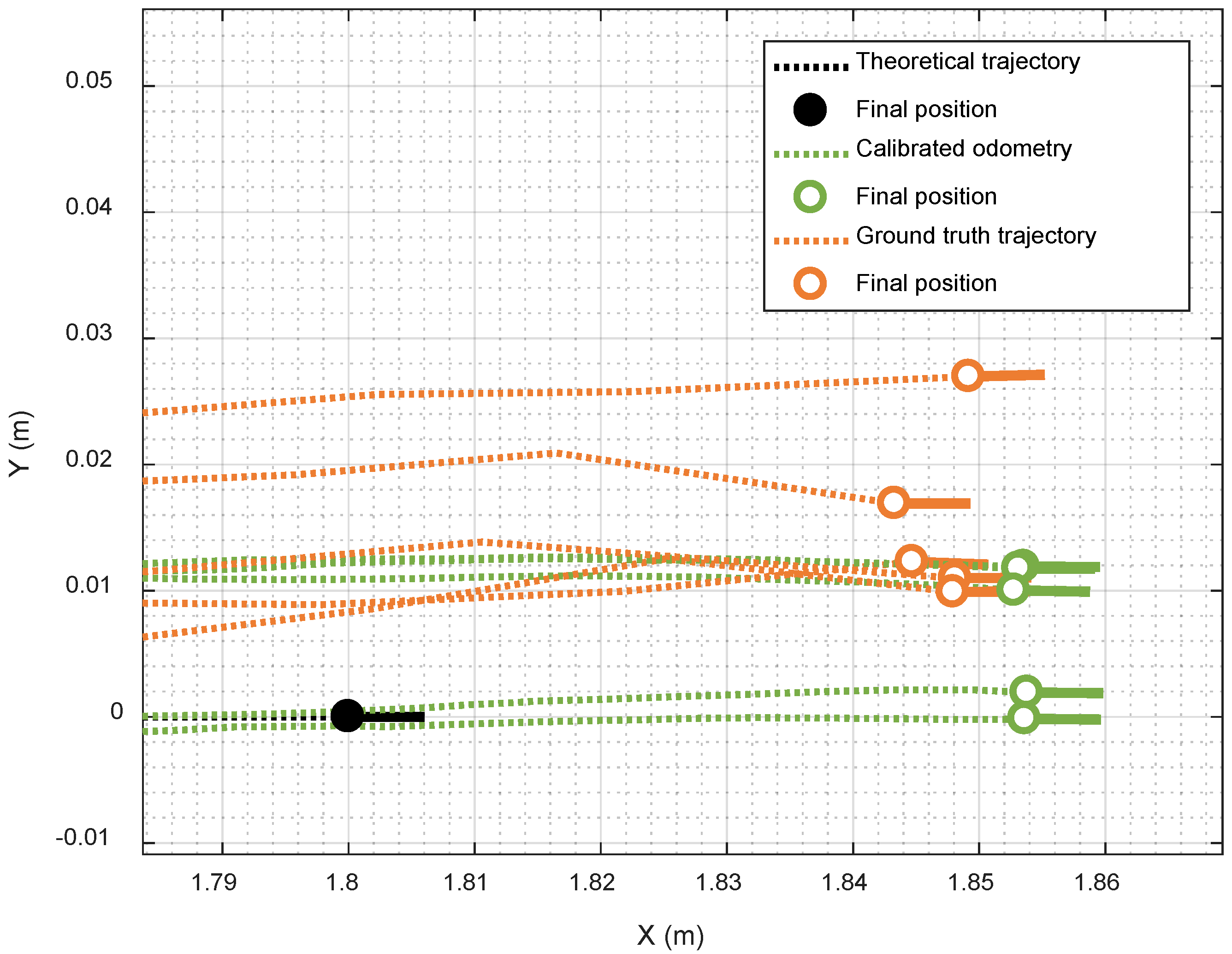
Table 6 shows that the improvement computed from the validation value of the cost function (82.1%) is representative of the trajectory improvements achieved. The application of the calibrated kinematic parameters showed an improvement of 67 % in the evaluation of the RMS error distance between the odometry trajectory and the ground truth trajectory, and an improvement of 71% in the RMS error evaluation of the absolute difference between the angular orientation of the mobile robot during these trajectories. The application of the calibrated kinematic parameters also showed a reduction in the maximum absolute differences between the odometry and ground truth trajectories, which have been reduced from 76 mm to 23 mm and from 5.86° to 1.77°. Similar improvements have been obtained in the error in the determination of the final location and angular orientation of the mobile robot that has been reduced from 74 mm to 16 mm and from and from 5.32° to 0.73°.
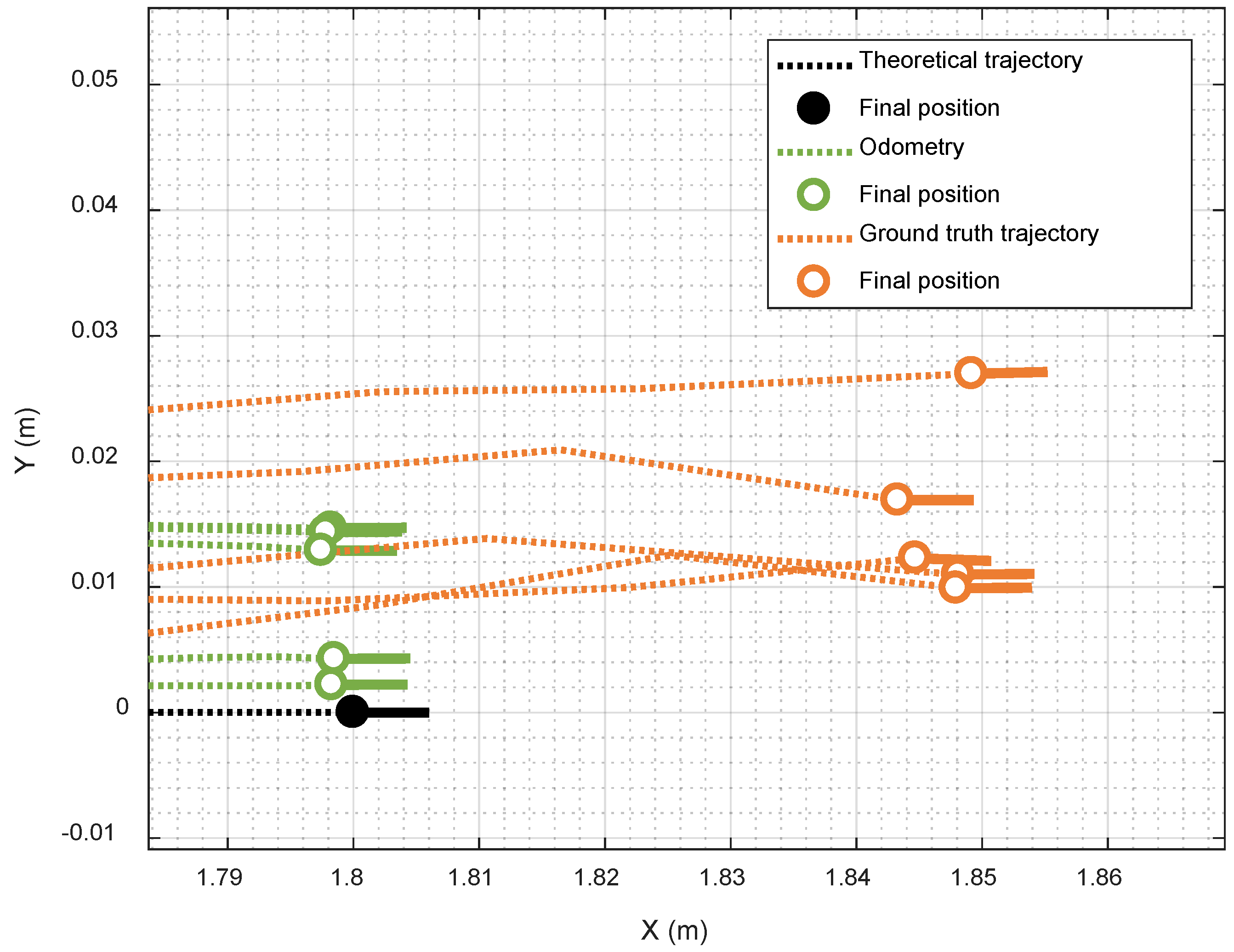
Figure 10 shows the application of the calibrated odometry to the trajectories shown previously in
Figure 7, which correspond to five repetitions of the R1 calibration trajectory.
4. Discussion and Conclusions
This paper proposes a general procedure to evaluate and correct the systematic odometry errors of a real three-wheeled omnidirectional mobile robot (1.760 m, 30 Kg) designed as a versatile personal assistant tool. This procedure is based on the definition of 36 representative straight and curved calibration trajectories which together depict a characteristic flower-shaped figure.
The odometry and ground truth trajectories measured while performing each one of these calibration trajectories are measured and registered for later offline fitting of the kinematic parameters of the mobile robot in order to match these two trajectories. This paper has evaluated the use of different trajectory subsets and the use of two iterative matching strategies based on gradient search minimization and genetic algorithms. The best matching between odometry and ground truth trajectories has been obtained using genetic algorithms and five repetitions of all calibration trajectories. The fitting of the kinematic parameters has shown differences higher than 10% in the distance from the wheels to the center of the mobile robot and between 2 and 5% in the radii of the wheels . This approach has the advantage of the feasible physical interpretation of the fitting results in the omnidirectional mobile robot.
The fitting results have been validated with five new additional repetitions of all these measured trajectories, providing an average improvement of 82% in the evaluation of the multivariable cost function that compares the final position and orientation of the mobile robot. The best performances of the genetic algorithm agree with the results of Savaee et al. [
15], and confirm that the mutation and combinations generated during the search based on genetic algorithms has the best chance to detect the global minimum of the multivariate function that summarizes the differences between the odometry and ground truth trajectories of the mobile robot. In this case, the genetic algorithm search (strategy STE-GA5) required 187 iterations and 37.545 function counts to meet the stopping criteria.
The final conclusion of the comparative calibration analysis performed in this work is that the use of curved calibration trajectories is more representative to calibrate the kinematic parameters of an omnidirectional mobile robot. This conclusion agrees with Batlle et al. [
17], who proposed the use of four curved trajectories for general omnidirectional mobile robot calibration, and with Maddahi et al. [
11], who concluded that the performance of a calibration procedure depends on the type of trajectory analyzed.
Future works will analyze the application of this procedure to different units of the same mobile robot type in order to validate its application in a general manufacturing stage.