Interactions of Self-Localised Optical Wavepackets in Reorientational Soft Matter
Abstract
:1. Introduction
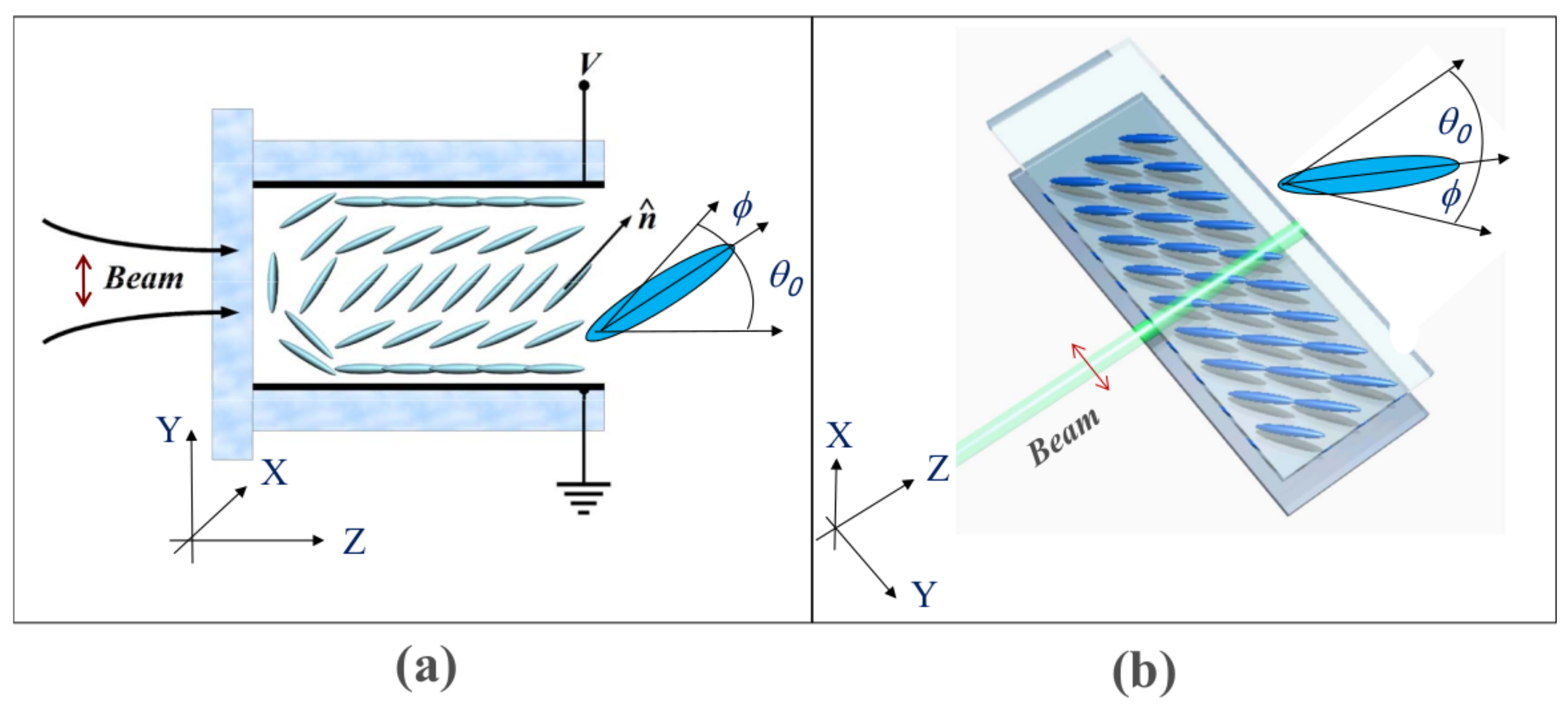
2. NLC Equations
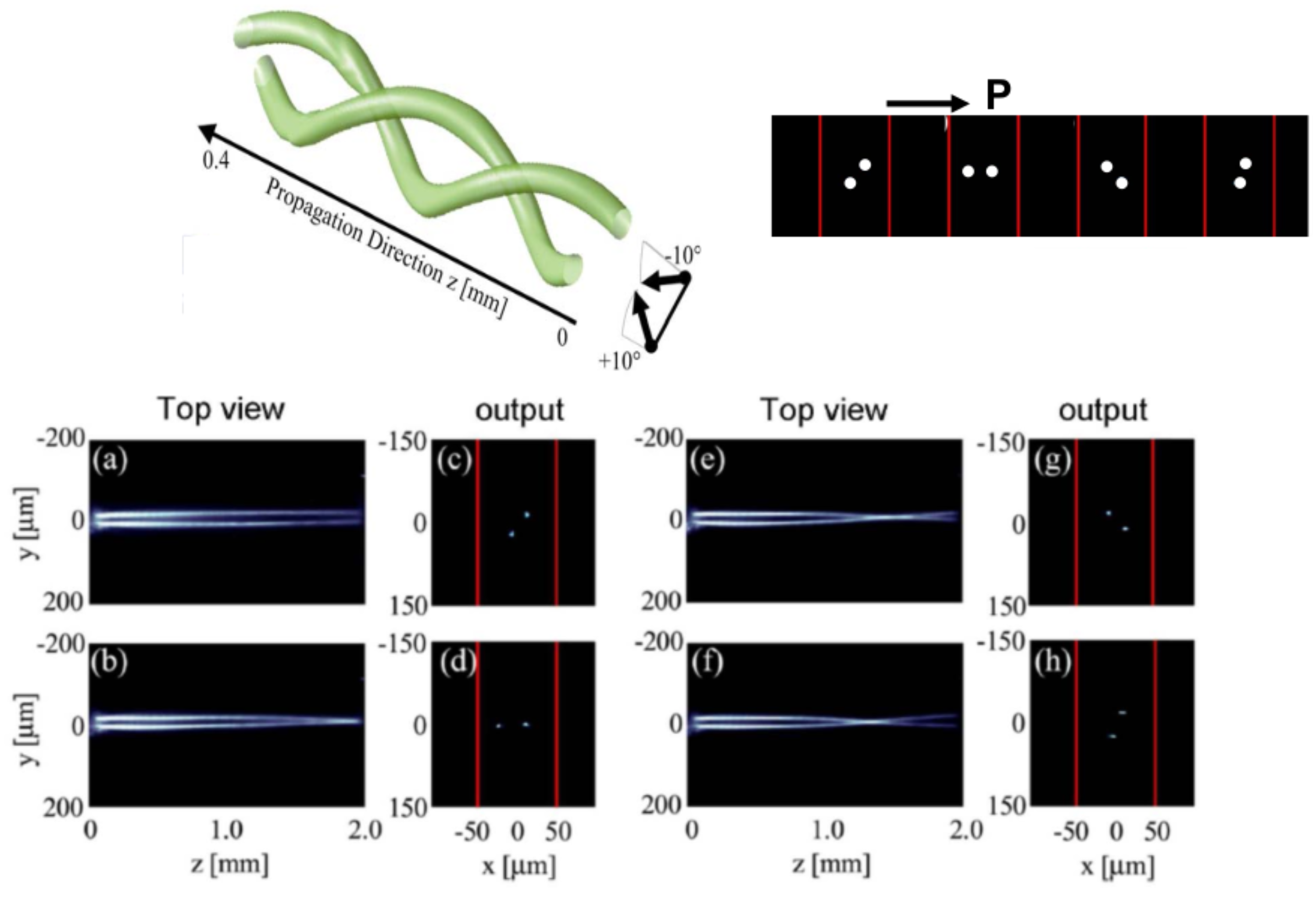
3. Interacting Beams
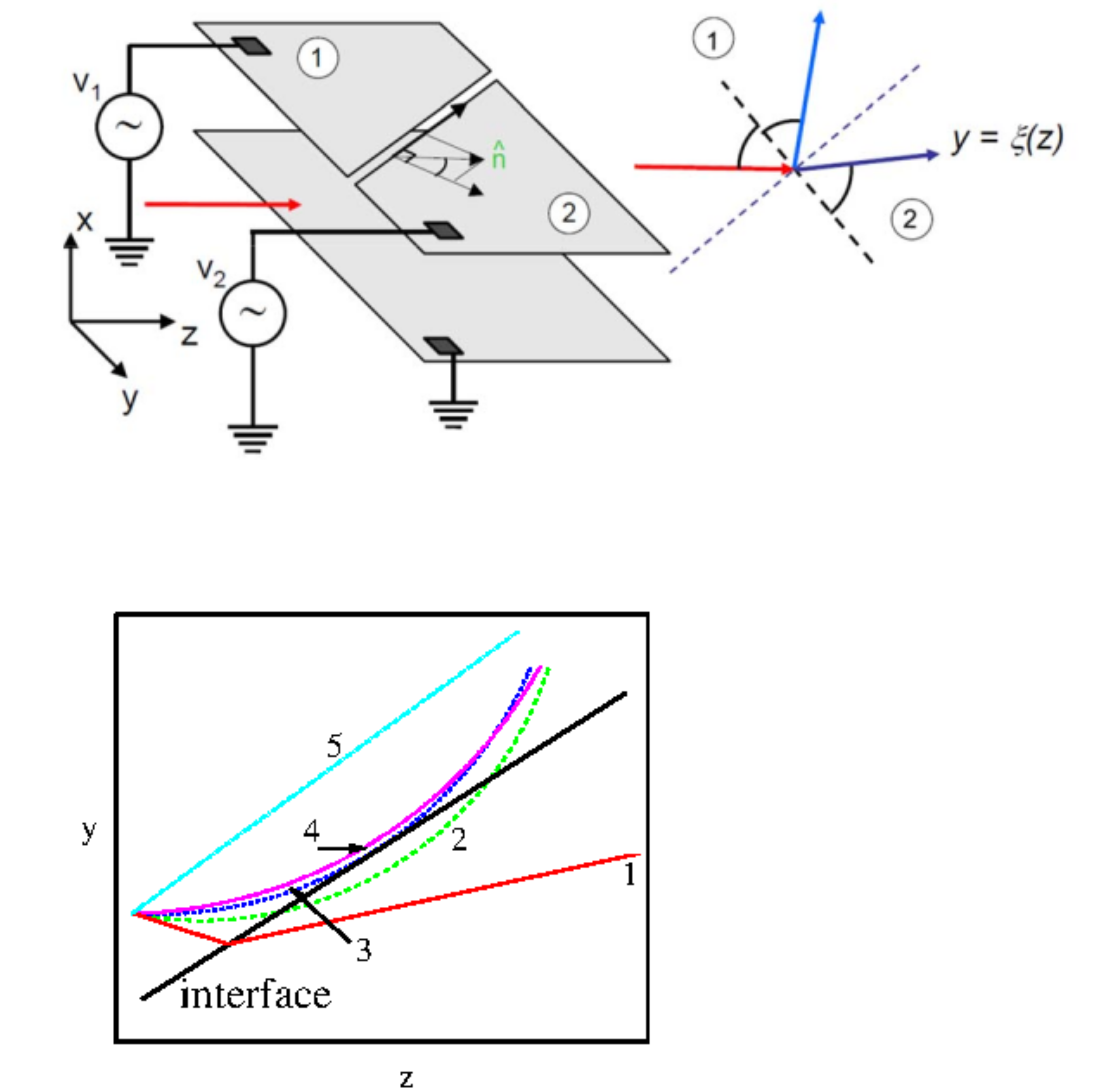
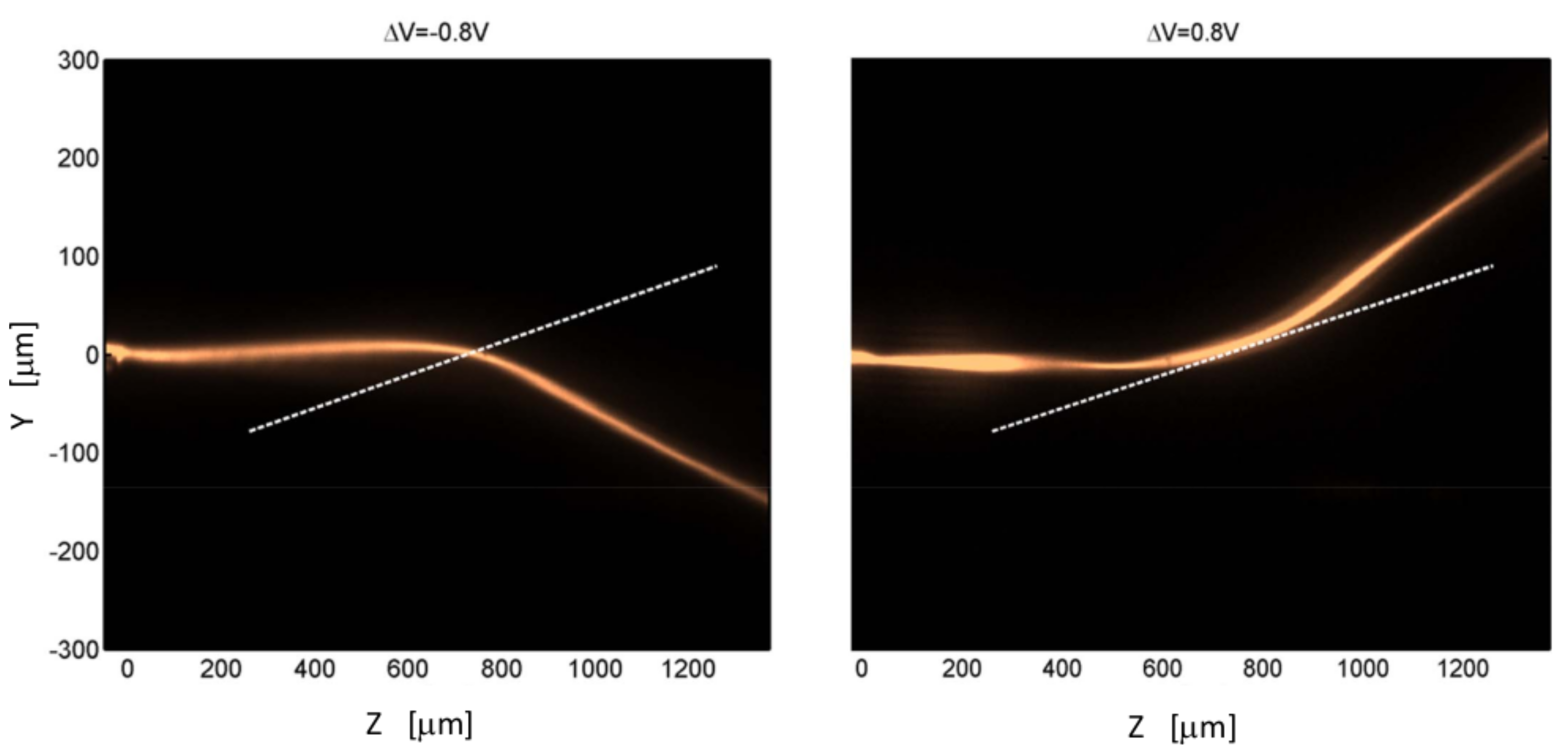
4. Refraction and Reflection of Self-Guided Beams at Interfaces
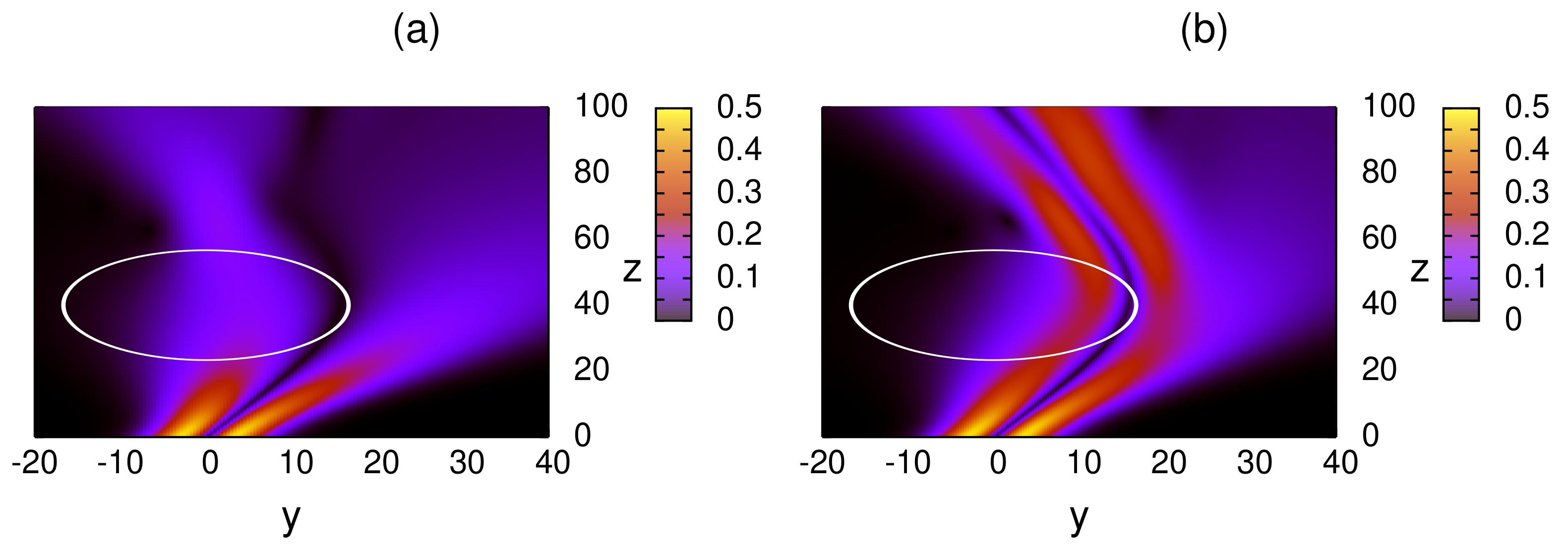
5. Interaction of Localised Beams with Dielectric Perturbations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Russell, J.S. Report on waves. In Proceedings of the 14th Meeting of the British Association for the Advancement of Science; John Murray: London, UK, 1845; pp. 311–390. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; J. Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Ablowitz, M.J. Nonlinear Dispersive Waves. Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Stegeman, G.I.; Christodoulides, D.N.; Segev, M. Optical spatial solitons: Historical perspectives. IEEE J. Sel. Top. Quantum Electron. 2000, 5, 1419–1427. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons. From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Peccianti, M.; Assanto, G. Nematicons. Phys. Rep. 2012, 516, 147–208. [Google Scholar] [CrossRef]
- Assanto, G.; Smyth, N.F. Self-confined light waves in nematic liquid crystals. Phys. D 2020, 402, 132182. [Google Scholar] [CrossRef]
- Jeffrey, A. Role of the Korteweg-de Vries equation in plasma physics. Q. J. R. Astron. Soc. 1973, 14, 183–189. [Google Scholar]
- Davydov, A.S. Solitons in Molecular Systems, 2nd ed.; Kluwer Academic: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Tlidi, M.; Staliunas, K.; Panajotov, K.; Vladimirov, A.G.; Clerc, M.G. Localized structures in dissipative media: From optics to plant ecology. Phil. Trans. R. Soc. A 2014, 372, 20140101. [Google Scholar] [CrossRef] [PubMed]
- Kaup, D.J.; Newell, A.C. Solitons as particles, oscillators, and in slowly changing media: A singular perturbation theory. Proc. R. Soc. Lond. A Math. Phys. Sci. 1978, 361, 413–446. [Google Scholar]
- Khoo, I.C. Liquid Crystals; Wiley: New York, NY, USA, 2022. [Google Scholar]
- Peccianti, M.; Assanto, G.; De Luca, A.; Umeton, C.; Khoo, I.C. Electrically assisted self-confinement and waveguiding in planar nematic liquid crystal cells. Appl. Phys. Lett. 2000, 77, 7–9. [Google Scholar] [CrossRef]
- Assanto, G.; Karpierz, M. Nematicons: Self-localized beams in nematic liquid crystals. Liq. Cryst. 2009, 36, 1161–1172. [Google Scholar] [CrossRef]
- Assanto, G. Nematicons: Reorientational solitons from optics to photonics. Liq. Cryst. Rev. 2018, 6, 170–194. [Google Scholar] [CrossRef]
- Assanto, G.; Peccianti, M. Spatial solitons in nematic liquid crystals. IEEE J. Quantum Electron. 2003, 39, 13–21. [Google Scholar] [CrossRef]
- Assanto, G.; Minzoni, A.A.; Smyth, N.F. Light self-localization in nematic liquid crystals: Modelling solitons in nonlocal reorientational media. J. Nonlinear Opt. Phys. Mater. 2009, 18, 657–691. [Google Scholar] [CrossRef]
- Alberucci, A.; Assanto, G.; MacNeil, J.M.L.; Smyth, N.F. Nematic liquid crystals: An excellent playground for nonlocal nonlinear light localization in soft matter. J. Nonlinear Opt. Phys. Mater. 2014, 23, 1450046. [Google Scholar] [CrossRef]
- Peccianti, M.; Conti, C.; Assanto, G.; de Luca, A.; Umeton, C. All-optical switching and logic gating with spatial solitons in liquid crystals. Appl. Phys. Lett. 2002, 81, 3335–3337. [Google Scholar] [CrossRef]
- Peccianti, M.; Conti, C.; Assanto, G.; de Luca, A.; Umeton, C. Routing of anisotropic spatial solitons and modulational instability in liquid crystals. Nature 2004, 432, 733–737. [Google Scholar] [CrossRef] [PubMed]
- Serak, S.V.; Tabiryan, N.V.; Peccianti, M.; Assanto, G. Spatial soliton all-optical logic gates. IEEE Photonics Technol. Lett. 2006, 18, 1287–1289. [Google Scholar] [CrossRef]
- Peccianti, M.; Dyadyusha, A.; Kaczmarek, M.; Assanto, G. Escaping solitons from a trapping potential. Phys. Rev. Lett. 2008, 101, 153902. [Google Scholar] [CrossRef] [Green Version]
- Piccardi, A.; Assanto, G.; Lucchetti, L.; Simoni, F. All-optical steering of soliton waveguides in dye-doped liquid crystals. Appl. Phys. Lett. 2008, 93, 171104. [Google Scholar] [CrossRef]
- Alberucci, A.; Piccardi, A.; Bortolozzo, U.; Residori, S.; Assanto, G. Nematicon all-optical control in liquid crystal light valves. Opt. Lett. 2010, 35, 390–392. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Bortolozzo, U.; Residori, S.; Assanto, G. Soliton gating and switching in liquid crystal light valve. Appl. Phys. Lett. 2010, 96, 071104. [Google Scholar] [CrossRef]
- Assanto, G.; Minzoni, A.A.; Smyth, N.F.; Worthy, A.L. Refraction of nonlinear beams by localised refractive index changes in nematic liquid crystals. Phys. Rev. A 2010, 82, 053843. [Google Scholar] [CrossRef] [Green Version]
- Peccianti, M.; Dyadyusha, A.; Kaczmarek, M.; Assanto, G. Tunable refraction and reflection of self-confined light beams. Nat. Phys. 2006, 2, 737–742. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Kravets, N.; Buchnev, O.; Assanto, G. Power controlled transition from standard to negative refraction in reorientational soft matter. Nat. Commun. 2014, 5, 5533–5541. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perumbilavil, S.; Piccardi, A.; Barboza, R.; Buchnev, O.; Strangi, G.; Kauranen, M.; Assanto, G. Beaming random lasers with soliton control. Nat. Commun. 2018, 9, 3863. [Google Scholar] [CrossRef]
- MacNeil, J.M.L.; Smyth, N.F.; Assanto, G. Exact and approximate solutions for solitary waves in nematic liquid crystals. Phys. D 2014, 284, 1–15. [Google Scholar] [CrossRef]
- Malomed, B. Variational methods in nonlinear fiber optics and related fields. Prog. Opt. 2002, 43, 71–193. [Google Scholar]
- Conti, C.; Peccianti, M.; Assanto, G. Route to nonlocality and observation of accessible solitons. Phys. Rev. Lett. 2003, 91, 073901. [Google Scholar] [CrossRef] [Green Version]
- García-Reimbert, C.; Minzoni, A.A.; Smyth, N.F.; Worthy, A.L. Large-amplitude nematicon propagation in a liquid crystal with local response. J. Opt. Soc. Am. B 2006, 23, 2551–2558. [Google Scholar] [CrossRef] [Green Version]
- Assanto, G.; Minzoni, A.A.; Peccianti, M.; Smyth, N.F. Optical solitary waves escaping a wide trapping potential in nematic liquid crystals: Modulation theory. Phys. Rev. A 2009, 79, 033837. [Google Scholar] [CrossRef] [Green Version]
- Izdebskaya, Y.; Krolikowski, W.; Smyth, N.F.; Assanto, G. Vortex stabilization by means of spatial solitons in nonlocal media. J. Opt. 2016, 18, 054006. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsov, E.A.; Rubenchik, A.M. Soliton stabilization in plasmas and hydrodynamics. Phys. Rep. 1986, 142, 103–165. [Google Scholar] [CrossRef] [Green Version]
- Dabby, F.W.; Whinnery, J.R. Thermal self-focusing of laser beams in lead glasses. Appl. Phys. Lett. 1968, 13, 284–286. [Google Scholar] [CrossRef]
- Rotschild, C.; Alfassi, B.; Cohen, O.; Segev, M. Long-range interactions between optical solitons. Nat. Phys. 2006, 2, 769–774. [Google Scholar] [CrossRef]
- Salazar-Romero, M.Y.; Ayala, Y.A.; Brambila, E.; Lopez-Peña, L.A.; Sciberras, L.; Minzoni, A.A.; Terborg, R.A.; Torres, J.P.; Volke-Sepúlveda, K. Steering and switching of soliton-like beams via interaction in a nanocolloid with positive polarizability. Opt. Lett. 2017, 42, 2487–2490. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. Quantum computation, entanglement and state reduction. Phil. Trans. R. Soc. Lond. A 1998, 356, 1927–1939. [Google Scholar] [CrossRef]
- Moroz, I.M.; Penrose, R.; Tod, P. Spherically-symmetric solutions of the Schrödinger-Newton equations. Class. Quantum Gravity 1998, 15, 2733–2742. [Google Scholar] [CrossRef]
- Paredes, A.; Olivieri, D.N.; Michinel, H. From optics to dark matter: A review on nonlinear Schrödinger–Poisson systems. Phys. D 2020, 403, 132301. [Google Scholar] [CrossRef]
- Guth, A.H.; Hertzberg, M.P.; Prescod-Weinstein, C. Do dark matter axions form a condensate with long-range correlation? Phys. Rev. D 2015, 92, 103513. [Google Scholar] [CrossRef] [Green Version]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef] [Green Version]
- Paredes, A.; Michinel, H. Interference of dark matter solitons and galactic offsets. Phys. Dark Universe 2016, 12, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Navarrete, A.; Paredes, A.; Salgueiro, J.R.; Michinel, H. Spatial solitons in thermo-optical media from the nonlinear Schrödinger-Poisson equation and dark-matter analogues. Phys. Rev. A 2017, 95, 013844. [Google Scholar] [CrossRef] [Green Version]
- Davey, A.; Stewartson, K. On three-dimensional packets of surface waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1974, 338, 101–110. [Google Scholar]
- Freeman, N.; Davey, A. On the evolution of packets of long surface waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1975, 344, 427–433. [Google Scholar]
- Ioannou-Sougleridis, I.; Frantzeskakis, D.J.; Horikis, T.P. A Davey-Stewartson description of two-dimensional solitons in nonlocal media. Stud. Appl. Math. 2019, 144, 3–17. [Google Scholar] [CrossRef]
- Skuse, B.D.; Smyth, N.F. Interaction of two colour solitary waves in a liquid crystal in the nonlocal regime. Phys. Rev. A 2009, 79, 063806. [Google Scholar] [CrossRef] [Green Version]
- Peccianti, M.; Brzdia̧kiewicz, K.A.; Assanto, G. Nonlocal spatial soliton interactions in nematic liquid crystals. Opt. Lett. 2002, 27, 1460–1462. [Google Scholar] [CrossRef]
- Alberucci, A.; Peccianti, M.; Assanto, G.; Dyadyusha, A.; Kaczmarek, M. Two-color vector solitons in nonlocal media. Phys. Rev. Lett. 2006, 97, 153903. [Google Scholar] [CrossRef] [PubMed]
- Fratalocchi, A.; Peccianti, M.; Conti, C.; Assanto, G. Spiralling and cyclic dynamics of nematicons. Mol. Cryst. Liq. Cryst. 2004, 421, 197–207. [Google Scholar] [CrossRef]
- Desyatnikov, A.S.; Sukhorukov, A.A.; Kivshar, Y.S. Azimuthons: Spatially modulated vortex solitons. Phys. Rev. Lett. 2005, 95, 203904. [Google Scholar] [CrossRef] [Green Version]
- Kartashov, Y.V.; Torner, L.; Vysloukh, V.A.; Mihalache, D. Multipole vector solitons in nonlocal nonlinear media. Opt. Lett. 2006, 31, 1483–1485. [Google Scholar] [CrossRef] [Green Version]
- Skuse, B.D.; Smyth, N.F. Two-colour vector soliton interactions in nematic liquid crystals in the local response regime. Phys. Rev. A 2008, 77, 013817. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Zhang, T.; Guo, Q.; Xuan, L.; Lan, S. Nonlocality-controlled interactions of spatial solitons in nematic liquid crystals. Appl. Phys. Lett. 2006, 89, 071111. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.G.; Zheng, Y.J.; Hu, W.; Yang, P.B.; Guo, Q. Long-range interactions between nematicons. Chin. Phys. Lett. 2009, 26, 064209. [Google Scholar]
- Izdebskaya, Y.; Shvedov, V.; Desyatnikov, A.S.; Kivshar, Y.S.; Krolikowski, W.; Assanto, G. Incoherent interaction of nematicons in bias-free liquid crystal cells. J. Eur. Opt. Soc. 2008, 5, 10008. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Ouyang, S.; Yang, P.; Guo, Q.; Lan, S. Short-range interactions between strongly nonlocal spatial solitons. Phys. Rev. A 2008, 77, 033842. [Google Scholar] [CrossRef] [Green Version]
- Minzoni, A.A.; Smyth, N.F.; Worthy, A.L. Modulation solutions for nematicon propagation in non-local liquid crystals. J. Opt. Soc. Am. B 2007, 24, 1549–1556. [Google Scholar] [CrossRef] [Green Version]
- Smyth, N.F.; Tope, B. Beam on beam control: Beyond the particle approximation. J. Nonlinear Opt. Phys. Mater. 2016, 25, 1650046. [Google Scholar] [CrossRef] [Green Version]
- Fratalocchi, A.; Piccardi, A.; Peccianti, M.; Assanto, G. Nonlinear management of the angular momentum of soliton clusters: Theory and experiments. Phys. Rev. A 2007, 75, 063835. [Google Scholar] [CrossRef] [Green Version]
- Skupin, S.; Grech, M.; Krolikowski, W. Rotating soliton solutions in nonlocal nonlinear media. Opt. Express 2008, 16, 9118–9131. [Google Scholar] [CrossRef] [Green Version]
- Assanto, G.; Smyth, N.F.; Worthy, A.L. Two colour, nonlocal vector solitary waves with angular momentum in nematic liquid crystals. Phys. Rev. A 2008, 78, 013832. [Google Scholar] [CrossRef] [Green Version]
- Minzoni, A.A.; Smyth, N.F. Theoretical Approaches to Nonlinear Wave Evolution in Higher Dimensions. In Nematicons: Spatial Optical Solitons in Nematic Liquid Crystals; Assanto, G., Ed.; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Shen, M.; Chen, X.; Shi, J.; Wang, Q.; Krolikowski, W. Incoherently coupled vector dipole soliton pairs in nonlocal media. Opt. Commun. 2009, 282, 4805–4809. [Google Scholar] [CrossRef]
- Shen, M.; Kong, Q.; Shi, J.; Wang, Q. Incoherently coupled two-color Manakov vector solitons in nonlocal media. Phys. Rev. A 2008, 77, 015811. [Google Scholar] [CrossRef]
- Wang, X.H.; Wang, Q.; Yang, J.R.; Mao, J.J. Scalar and vector Hermite–Gaussian soliton in strong nonlocal media with exponential-decay response. Opt. Commun. 2017, 402, 20–25. [Google Scholar] [CrossRef]
- Lopez-Aguayo, S.; Desyatnikov, A.S.; Kivshar, Y.S.; Skupin, S.; Krolikowski, W.; Bang, O. Stable rotating dipole solitons in nonlocal optical media. Opt. Lett. 2006, 31, 1100–1102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeng, S.; Chen, M.; Zhang, T.; Hu, W.; Guo, Q.; Lu, D. Analytical modeling of soliton interactions in a nonlocal nonlinear medium analogous to gravitational force. Phys. Rev. A 2018, 97, 013817. [Google Scholar] [CrossRef]
- Rotschild, C.; Cohen, O.; Manela, O.; Segev, M. Solitons in nonlinear media with an infinite range of nonlocality: First observation of coherent elliptic solitons and of vortex-ring solitons. Phys. Rev. Lett. 2005, 95, 213904. [Google Scholar] [CrossRef] [Green Version]
- Alberucci, A.; Piccardi, A.; Barboza, R.; Buchnev, O.; Kaczmarek, M.; Assanto, G. Interactions of accessible solitons with interfaces in anisotropic media: The case of uniaxial nematic liquid crystals. New J. Phys. 2013, 15, 043011. [Google Scholar] [CrossRef] [Green Version]
- Assanto, G.; Smyth, N.F.; Xia, W. Modulation analysis of nonlinear beam refraction at an interface in liquid crystals. Phys. Rev. A 2011, 84, 033818. [Google Scholar] [CrossRef] [Green Version]
- Goos, F.; Hänchen, H. Ein neuer und fundamentaler Versuch zur Totalreflexion. Ann. Phys. 1947, 436, 333–346. [Google Scholar] [CrossRef] [Green Version]
- Assanto, G.; Smyth, N.F.; Xia, W. Refraction of nonlinear light beams in nematic liquid crystals. J. Nonlinear Opt. Phys. Mater. 2012, 21, 1250033. [Google Scholar] [CrossRef] [Green Version]
- Aceves, A.B.; Moloney, J.V.; Newell, A.C. Theory of light-beam propagation at nonlinear interfaces: I. Equivalent-particle theory for a single interface. Phys. Rev. A 1989, 39, 1809–1827. [Google Scholar] [CrossRef]
- Barboza, R.; Bortolozzo, U.; Assanto, G.; Vidal-Henriquez, E.; Clerc, M.G.; Residori, S. Vortex induction via anisotropy self-stabilized light-matter interaction. Phys. Rev. Lett. 2012, 109, 143901. [Google Scholar] [CrossRef] [PubMed]
- Smyth, N.F.; Xia, W. Refraction and instability of optical vortices at an interface in a liquid crystal. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 165403. [Google Scholar] [CrossRef] [Green Version]
- Yakimenko, A.I.; Zaliznyak, Y.A.; Kivshar, Y. Stable vortex solitons in nonlocal self-focusing nonlinear media. Phys. Rev. E 2005, 71, 065603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Izdebskaya, Y.V.; Shvedov, V.G.; Jung, P.S.; Krolikowski, W. Stable vortex soliton in nonlocal media with orientational nonlinearity. Opt. Lett. 2018, 43, 66–69. [Google Scholar] [CrossRef]
- Laudyn, U.A.; Kwasny, M.; Karpierz, M.A.; Assanto, G. Vortex nematicons in planar cells. Opt. Express 2020, 28, 8282–8290. [Google Scholar] [CrossRef]
- Kwasny, M.; Karpierz, M.A.; Assanto, G.; Laudyn, U.A. Optothermal vortex solitons in liquid crystals. Opt. Lett. 2020, 45, 2451–2454. [Google Scholar] [CrossRef]
- Assanto, G.; Smyth, N.F. Soliton aided propagation and routing of vortex beams in nonlocal media. J. Las. Opt. Photon 2014, 1, 105. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Weng, Z.; Yuan, J. Vector vortex breathers in thermal nonlocal media. Opt. Comm. 2021, 492, 126978. [Google Scholar] [CrossRef]
- Zhang, H.; Weng, Z.; Yuan, J. Stabilization of vector vortex beams in thermal nonlinear media. Optik 2021, 238, 166686. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, T.; Dai, C. Stabilization of higher-order vortex solitons by means of nonlocal nonlinearity. Phys. Rev. A 2022, 105, 013520. [Google Scholar] [CrossRef]
- Pasquazi, A.; Alberucci, A.; Peccianti, M.; Assanto, G. Signal processing by opto-optical interactions between self-localized and free propagating beams in liquid crystals. Appl. Phys. Lett. 2005, 87, 261104. [Google Scholar] [CrossRef] [Green Version]
- Izdebskaya, Y.V.; Desyatnikov, A.S.; Assanto, G.; Kivshar, Y.S. Deflection of nematicons through interaction with dielectric particles. J. Opt. Soc. Am. B 2013, 30, 1432–1437. [Google Scholar] [CrossRef] [Green Version]
- Piccardi, A.; Peccianti, M.; Assanto, G.; Dyadyusha, A.; Kaczmarek, M. Voltage-driven in-plane steering of nematicons. Appl. Phys. Lett. 2009, 94, 091106. [Google Scholar] [CrossRef] [Green Version]
- Izdebskaya, Y.V. Routing of spatial solitons by interaction with rod microelectrodes. Opt. Lett. 2014, 39, 1681–1684. [Google Scholar] [CrossRef] [PubMed]
- Derrien, F.; Henninot, J.F.; Warenghem, M.; Abbate, G. A thermal (2D+1) spatial optical soliton in a dye doped liquid crystal. J. Opt. A Pure Appl. Opt. 2000, 2, 332–337. [Google Scholar] [CrossRef]
- Simoni, F.; Lucchetti, L.; Lucchetta, D.; Francescangeli, O. On the origin of the huge nonlinear response of dye-doped liquid crystals. Opt. Express 2001, 9, 85–90. [Google Scholar] [CrossRef]
- Lucchetti, L.; Gentili, M.; Simoni, F. Colossal optical nonlinearity induced by a low frequency external electric fields in dye-doped liquid crystals. Opt. Express 2006, 14, 2236–2241. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Assanto, G. Self-turning self-confined light beams in guest-host media. Phys. Rev. Lett. 2010, 104, 213904. [Google Scholar] [CrossRef]
- Blach, J.F.; Henninot, J.F.; Petit, M.; Daoudi, A.; Warenghem, M. Observation of spatial optical solitons launched in biased and bias-free polymer-stabilized nematics. J. Opt. Soc. Am. B 2007, 24, 1122–1129. [Google Scholar] [CrossRef]
- Karimi, N.; Virkki, M.; Alberucci, A.; Buchnev, O.; Kauranen, M.; Priimagi, A.; Assanto, G. Molding optical waveguides with nematicons. Adv. Opt. Mater. Commun. 2017, 5, 1700199. [Google Scholar] [CrossRef] [Green Version]
- Izdebskaya, Y.V.; Shvedov, V.G.; Assanto, G.; Krolikowski, W. Magnetic routing of light-induced waveguides. Nat. Commun. 2017, 8, 14452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shvedov, V.G.; Izdebskaya, Y.V.; Sheng, Y.; Krolikowski, W. Magnetically controlled negative refraction of solitons in liquid crystals. Appl. Phys. Lett. 2017, 110, 091107. [Google Scholar] [CrossRef]
- Perumbilavil, S.; Kauranen, M.; Assanto, G. Magnetic steering of beam-confined random laser in liquid crystals. Appl. Phys. Lett. 2018, 110, 121107. [Google Scholar] [CrossRef]
- Kwaśny, M.; Laudyn, U.A.; Rutkowska, K.A.; Karpierz, M.A. Nematicons routing through two types of disclination lines in chiral nematic liquid crystals. J. Nonlinear Opt. Phys. Mater. 2014, 23, 1450042. [Google Scholar] [CrossRef]
- Hess, A.J.; Poy, G.; Tai, J.-S.B.; Zumer, S.; Smalyukh, I.I. Control of light by topological solitons in soft chiral birefringent media. Phys. Rev. X 2020, 10, 031042. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Bortolozzo, U.; Residori, S.; Assanto, G. Readdressable interconnects with spatial soliton waveguides in liquid crystal light valves. IEEE Photonics Technol. Lett. 2010, 22, 694–696. [Google Scholar] [CrossRef]
- Alberucci, A.; Assanto, G.; Minzoni, A.A.; Smyth, N.F. Scattering of reorientational optical solitary waves at dielectric perturbations. Phys. Rev. A 2012, 85, 013804. [Google Scholar] [CrossRef] [Green Version]
- Laudyn, U.A.; Kwaśny, M.; Sala, F.A.; Karpierz, M.A.; Smyth, N.F.; Assanto, G. Curved optical solitons subject to transverse acceleration in reorientational soft matter. Nat. Sci. Rep. 2017, 7, 12385. [Google Scholar] [CrossRef] [Green Version]
- Sala, F.A.; Smyth, N.F.; Laudyn, U.A.; Karpierz, M.A.; Minzoni, A.A.; Assanto, G. Bending reorientational solitons with modulated alignment. J. Opt. Soc. Am. B 2017, 34, 2459–2466. [Google Scholar] [CrossRef]
- Laudyn, U.A.; Kwaśny, M.; Karpierz, M.; Smyth, N.F.; Assanto, G. Accelerated optical solitons in reorientational media with transverse invariance and longitudinally modulated birefringence. Phys. Rev. A 2018, 98, 023810. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Smyth, N.F.; Minzoni, A.A.; Kivshar, Y.S. Vector vortex solitons in nematic liquid crystals. Opt. Lett. 2009, 34, 1414–1416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minzoni, A.A.; Smyth, N.F.; Worthy, A.L.; Kivshar, Y.S. Stabilization of vortex solitons in nonlocal nonlinear media. Phys. Rev. A 2009, 76, 063803. [Google Scholar] [CrossRef] [Green Version]
- Assanto, G.; Minzoni, A.A.; Smyth, N.F. Deflection of nematicon-vortex vector solitons in liquid crystals. Phys. Rev. A 2014, 89, 013827. [Google Scholar] [CrossRef]
- Assanto, G.; Minzoni, A.A.; Smyth, N.F. Vortex confinement and bending with nonlocal solitons. Opt. Lett. 2014, 39, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Karpierz, M.A.; Sierakowski, M.; Swillo, M.; Wolinski, T. Self focusing in liquid crystalline waveguides. Mol. Cryst. Liq. Cryst. 1998, 320, 157–163. [Google Scholar] [CrossRef]
- Karpierz, M.A. Solitary waves in liquid crystalline waveguides. Phys. Rev. E 2002, 66, 036603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Assanto, G.; Smyth, N.F. Spin-optical solitons in liquid crystals. Phys. Rev. A 2020, 102, 033501. [Google Scholar] [CrossRef]
- Poy, G.; Hess, A.J.; Smalyukh, I.I.; Zumer, S. Chirality-enhanced periodic self-focusing of light in soft birefringent media. Phys. Rev. Lett. 2020, 125, 077801. [Google Scholar] [CrossRef]
- Warenghem, M.; Blach, J.F.; Henninot, J.F. Thermo-nematicon: An unnatural coexistence of solitons in liquid crystals? J. Opt. Soc. Am. B 2008, 25, 1882–1887. [Google Scholar] [CrossRef]
- Laudyn, U.A.; Kwasny, M.; Piccardi, A.; Karpierz, M.A.; Dabrowski, R.; Chojnowska, O.; Alberucci, A.; Assanto, G. Nonlinear competition in nematicon propagation. Opt. Lett. 2015, 40, 5235–5238. [Google Scholar] [CrossRef]
- Laudyn, U.A.; Piccardi, A.; Kwasny, M.; Karpierz, M.A.; Assanto, G. Thermo-optic soliton routing in nematic liquid crystals. Opt. Lett. 2018, 43, 2296–2299. [Google Scholar] [CrossRef] [PubMed]
- Cyprych, K.; Jung, P.S.; Izdebskaya, Y.; Shvedov, V.; Christodouliles, D.N.; Krolikowski, W. Anomalous interaction of spatial solitons in nematic liquid crystals. Opt. Lett. 2019, 44, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Alberucci, A.; Laudyn, U.A.; Piccardi, A.; Kwasny, M.; Klus, B.; Karpierz, M.A.; Assanto, G. Nonlinear continuous-wave optical propagation in nematic liquid crystals: Interplay between reorientational and thermal effects. Phys. Rev. E 2017, 96, 012703. [Google Scholar] [CrossRef] [Green Version]
- Jung, P.S.; Krolikowski, W.; Laudyn, U.A.; Karpierz, M.A.; Trippenbach, M. Semi-analytical approach to supermode spatial solitons formation in nematic liquid crystals. Opt. Express 2017, 25, 23893. [Google Scholar] [CrossRef]
- Jung, P.S.; Krolikowski, W.; Laudyn, U.A.; Trippenbach, M.; Karpierz, M.A. Supermode spatial optical solitons in liquid crystals with competing nonlinearities. Phys. Rev. A 2017, 95, 023820. [Google Scholar] [CrossRef] [Green Version]
- Ramaniuk, A.; Trippenbach, M.; Jung, P.S.; Christodoulides, D.N.; Krolikowski, W.; Assanto, G. Scalar and vector supermode solitons owing to competing nonlocal nonlinearities. Opt. Express 2021, 29, 8015–8023. [Google Scholar] [CrossRef] [PubMed]
- Assanto, G.; Khan, C.; Smyth, N.F. Multihump thermo-reorientational solitary waves in nematic liquid crystals: Modulation theory solutions. Phys. Rev. A 2021, 104, 013526. [Google Scholar] [CrossRef]
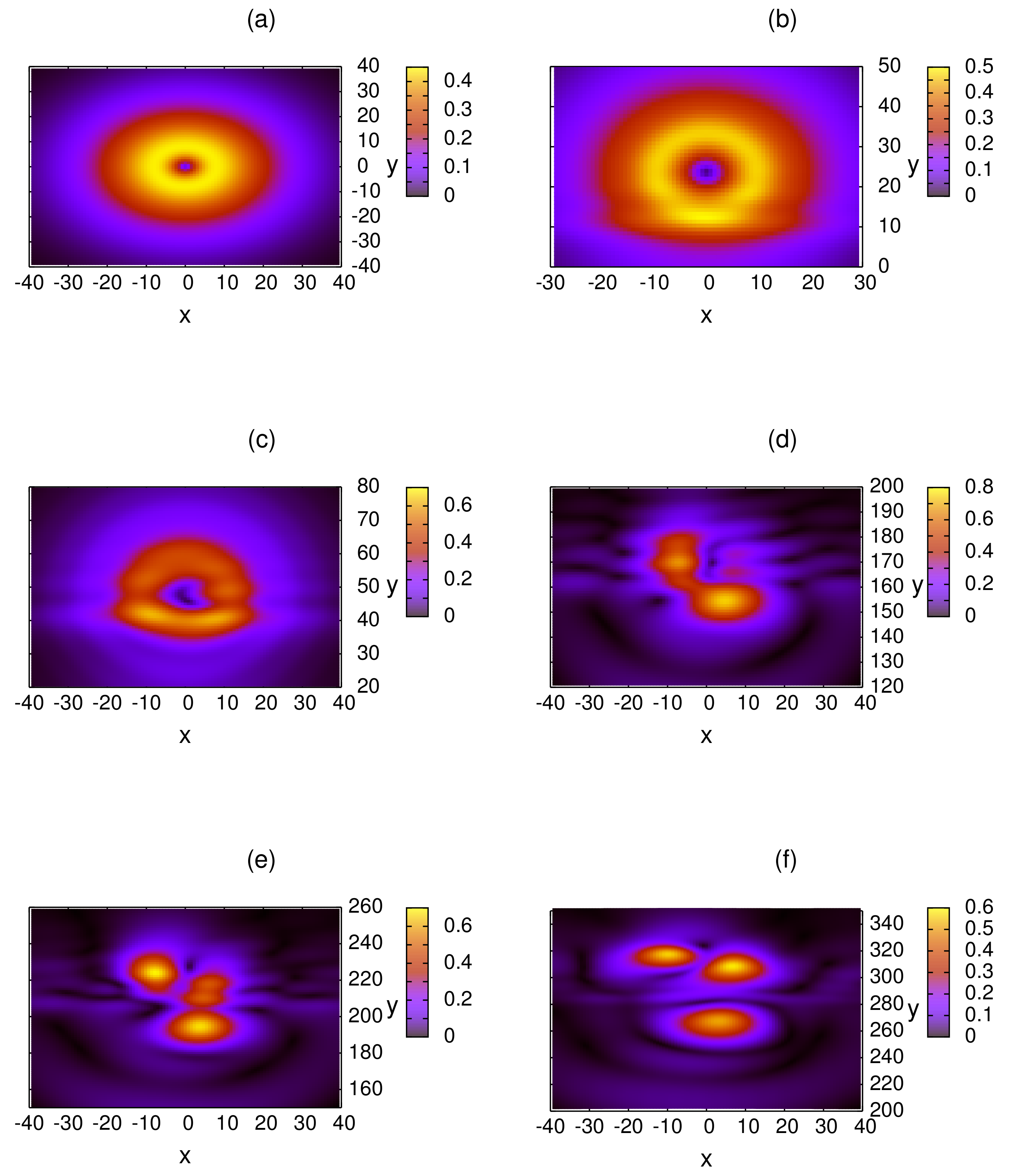
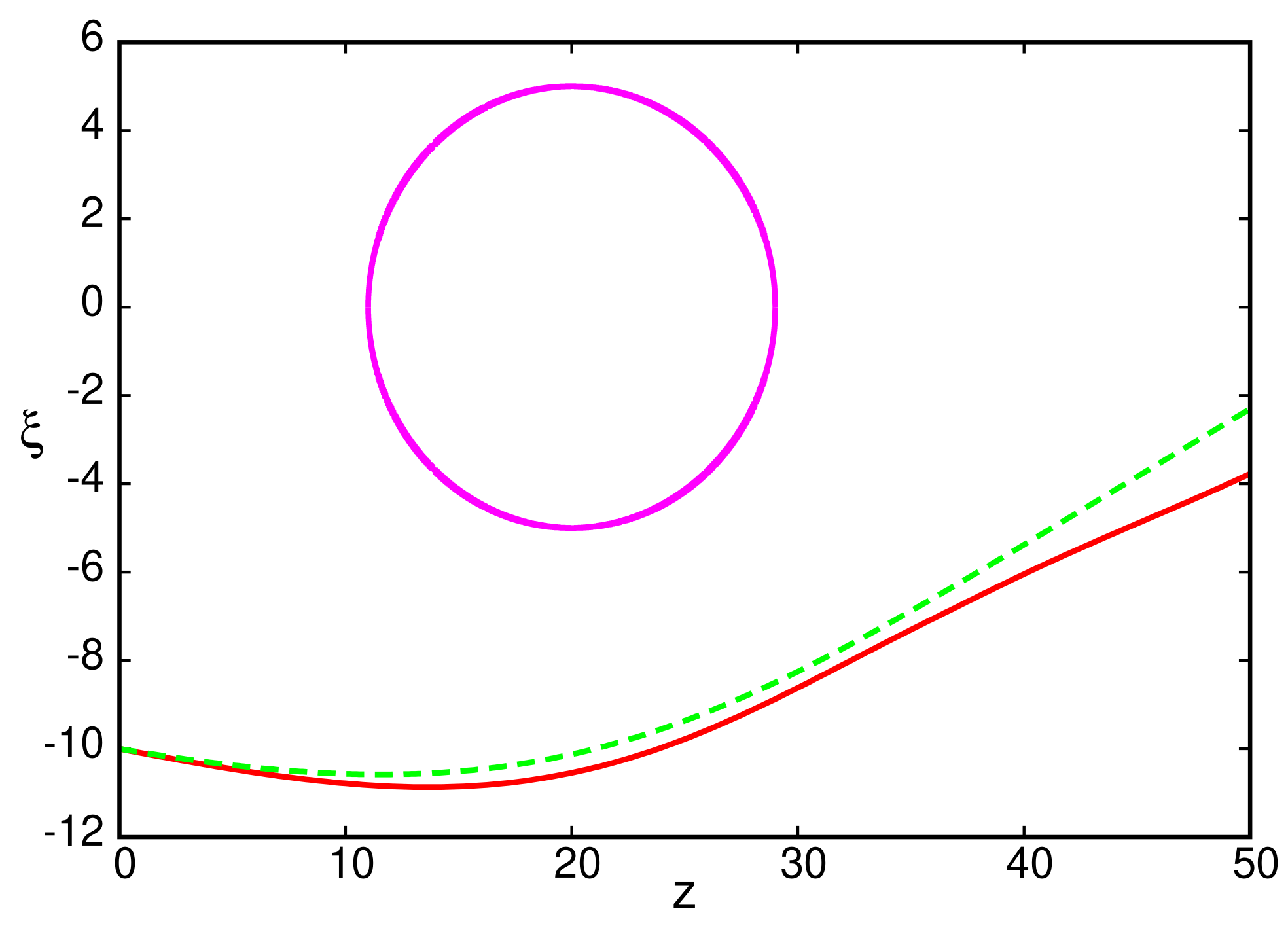
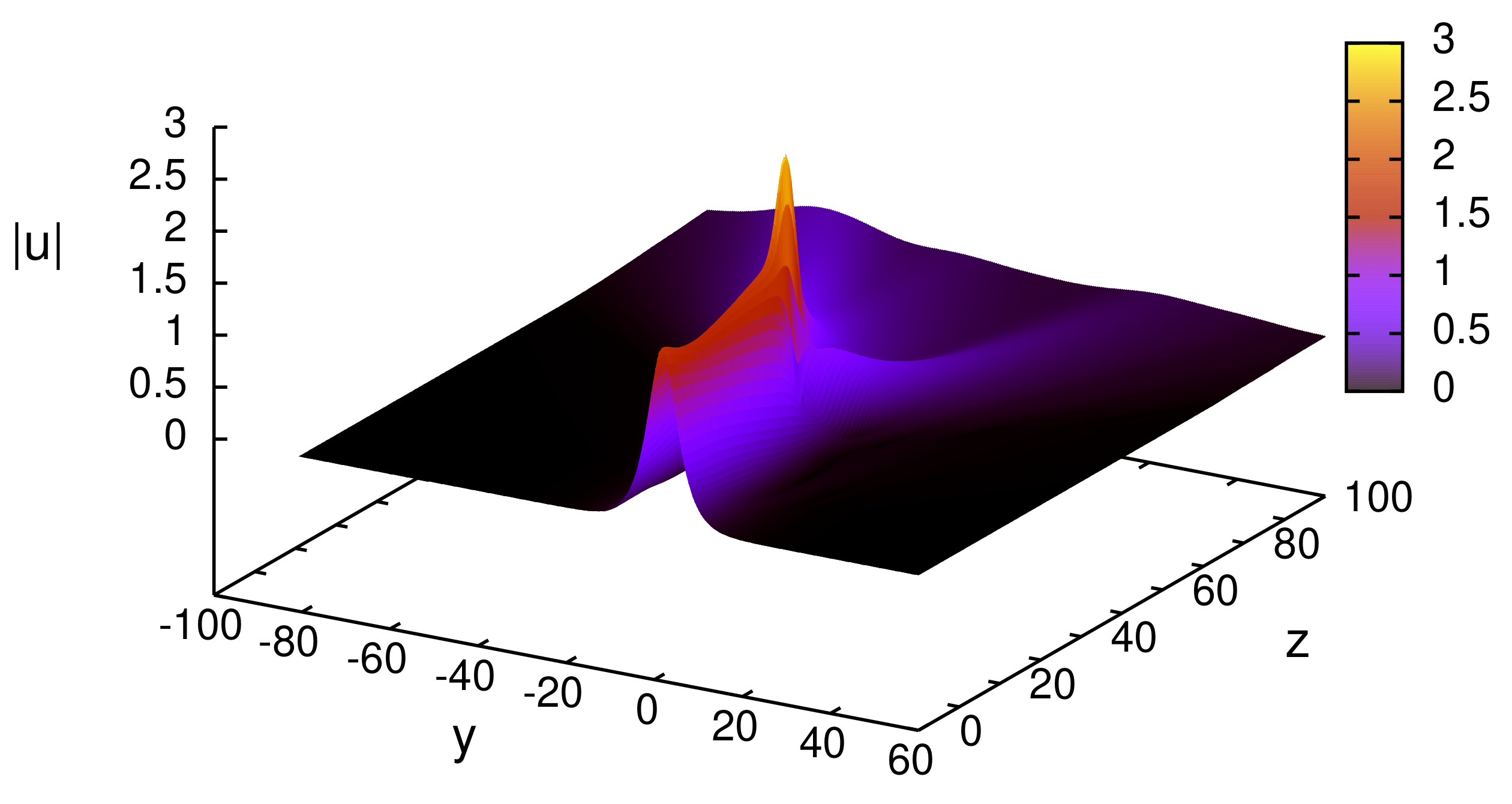
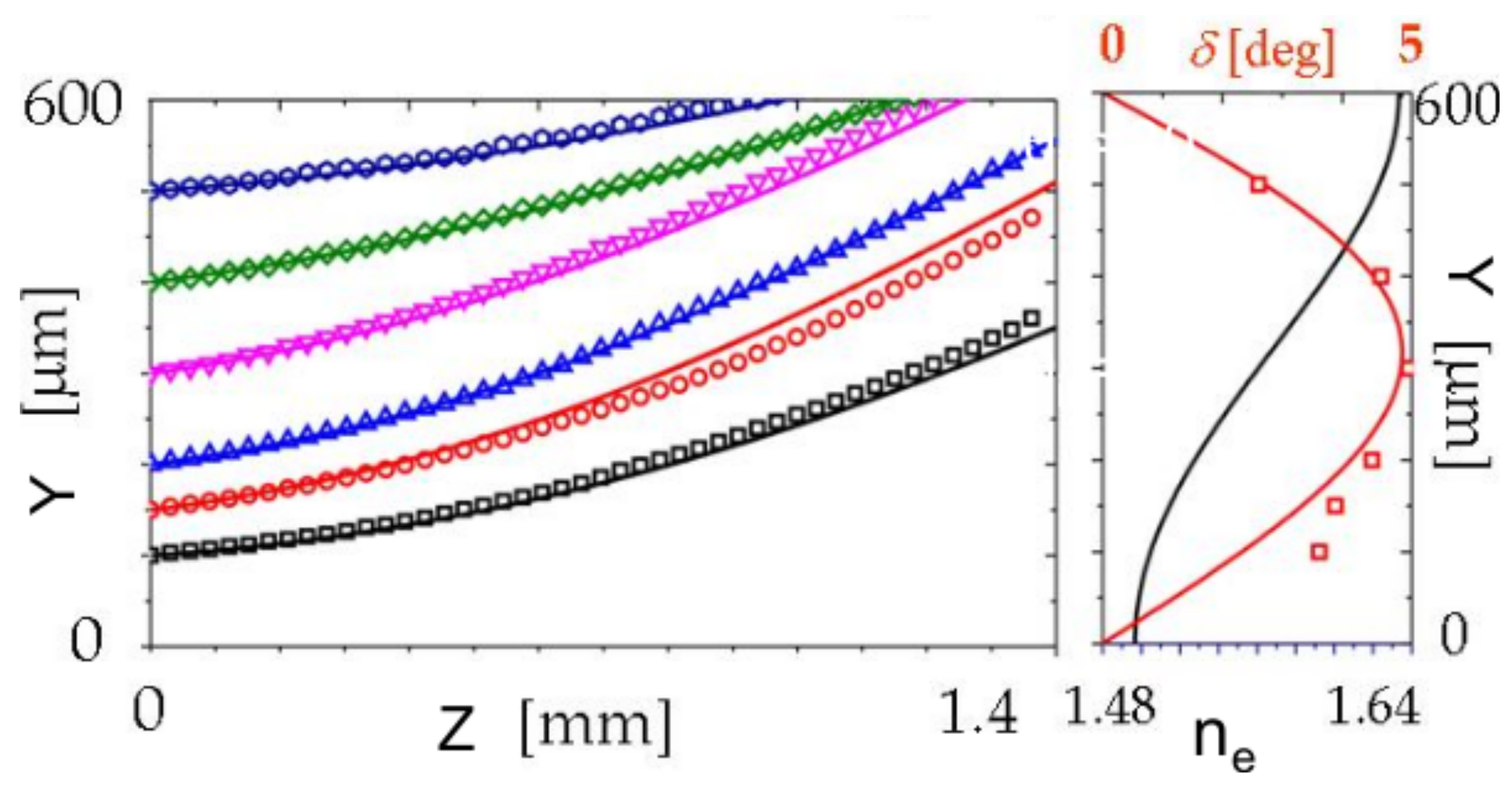
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Assanto, G.; Marchant, T.R.; Smyth, N.F. Interactions of Self-Localised Optical Wavepackets in Reorientational Soft Matter. Appl. Sci. 2022, 12, 2607. https://doi.org/10.3390/app12052607
Assanto G, Marchant TR, Smyth NF. Interactions of Self-Localised Optical Wavepackets in Reorientational Soft Matter. Applied Sciences. 2022; 12(5):2607. https://doi.org/10.3390/app12052607
Chicago/Turabian StyleAssanto, Gaetano, Timothy R. Marchant, and Noel F. Smyth. 2022. "Interactions of Self-Localised Optical Wavepackets in Reorientational Soft Matter" Applied Sciences 12, no. 5: 2607. https://doi.org/10.3390/app12052607
APA StyleAssanto, G., Marchant, T. R., & Smyth, N. F. (2022). Interactions of Self-Localised Optical Wavepackets in Reorientational Soft Matter. Applied Sciences, 12(5), 2607. https://doi.org/10.3390/app12052607






