One-Dimensional Convolutional Neural Network for Pipe Jacking EPB TBM Cutter Wear Prediction
Abstract
:1. Introduction
2. Literature Review
3. EPB Machine Specifications
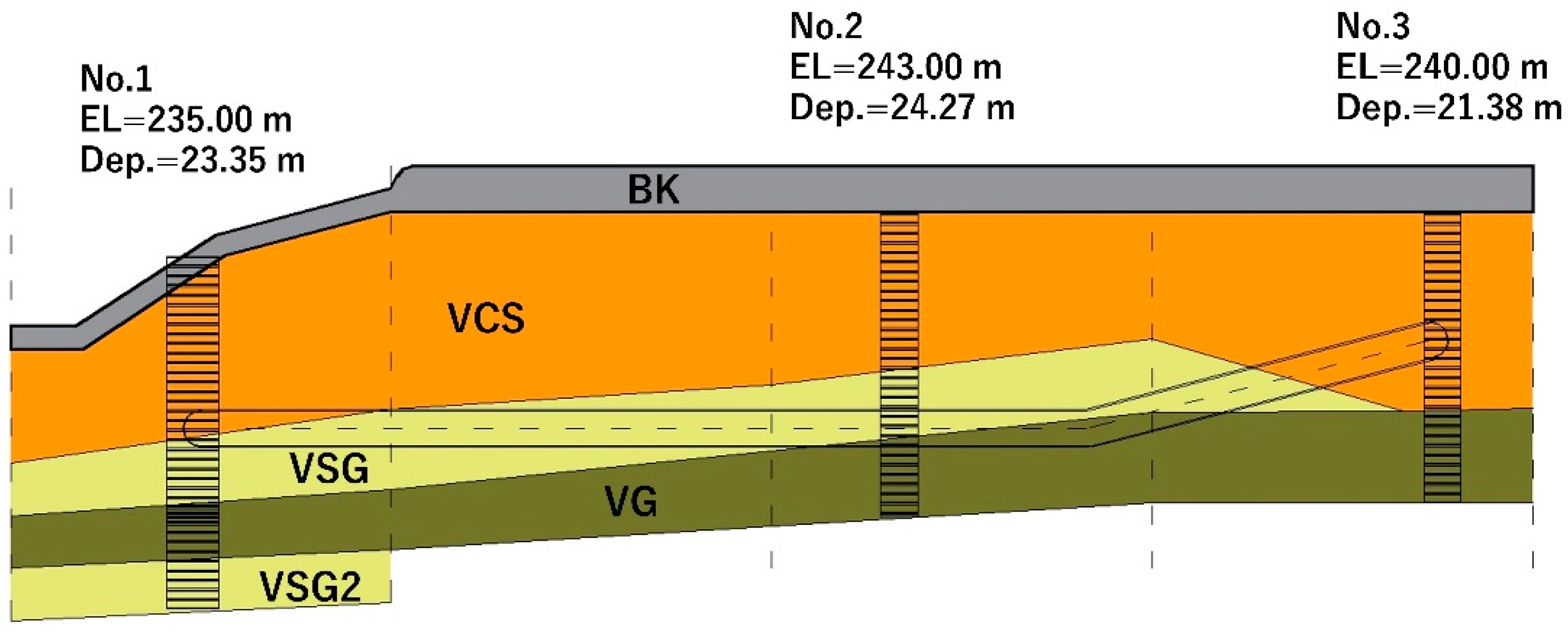
4. Engineering Geology
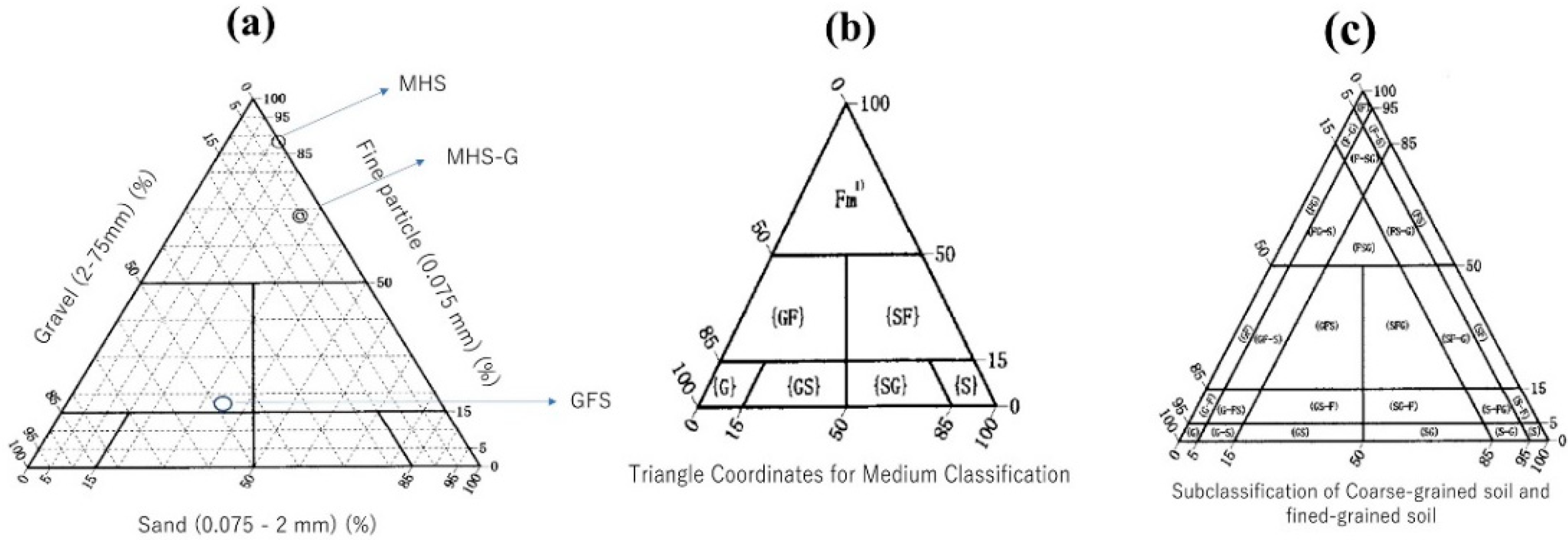
4.1. Grain Size Distribution and Characteristics
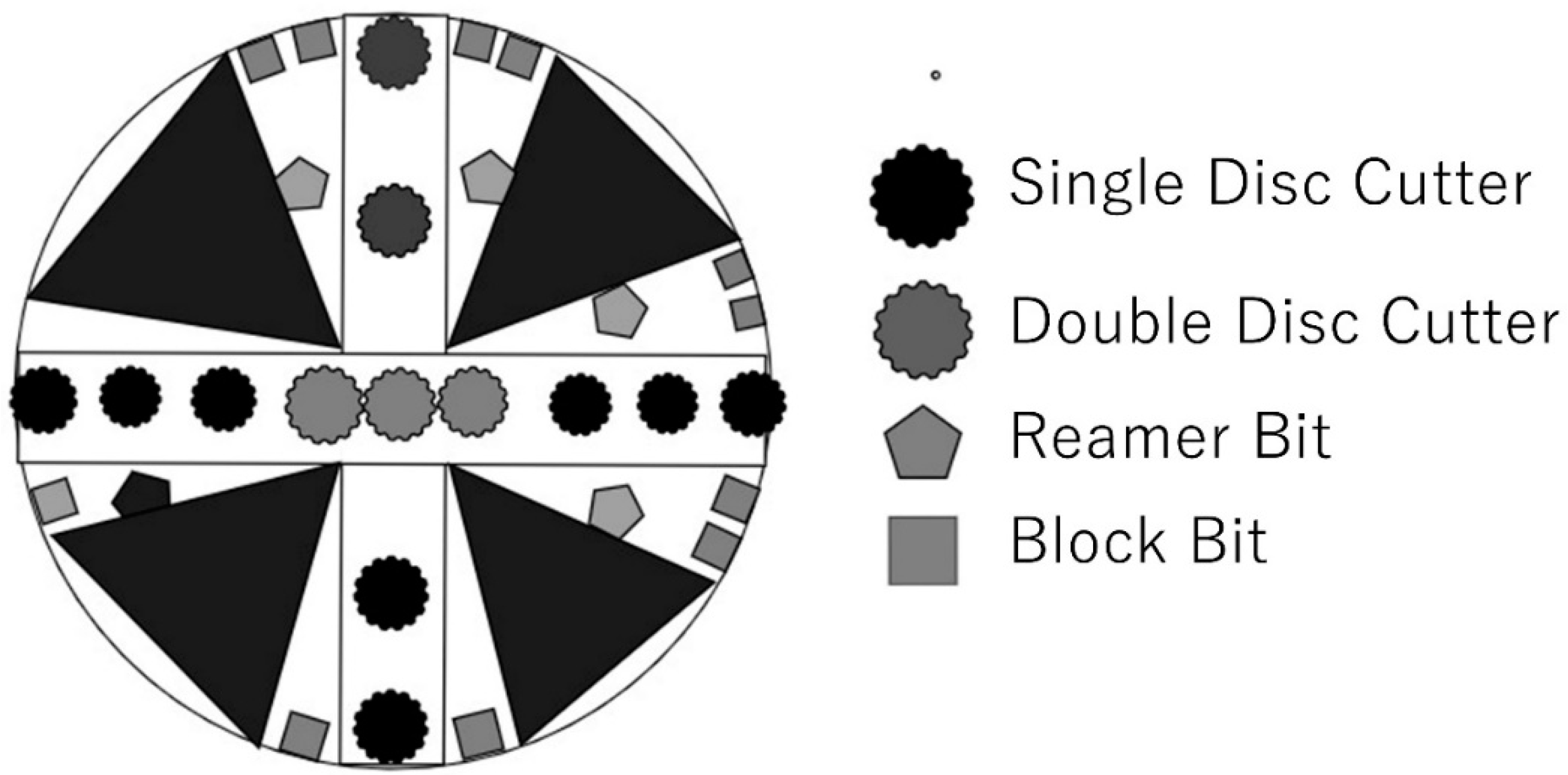
5. EPB Cutting Tool Wear and Machine Parameters
Machine Parameters and Tool Wear Evaluation
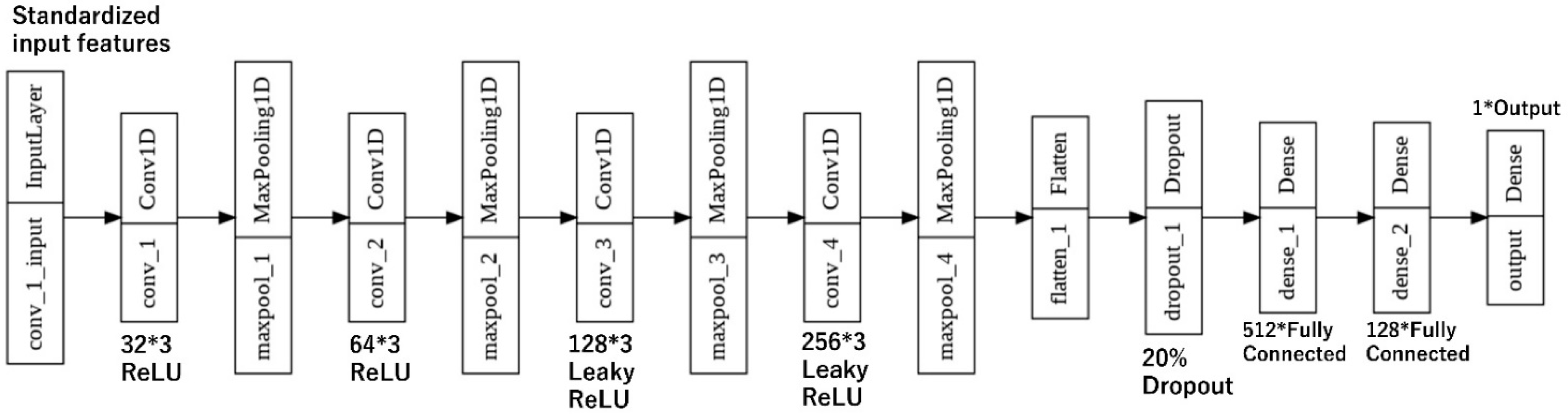
6. Explanation of CNN
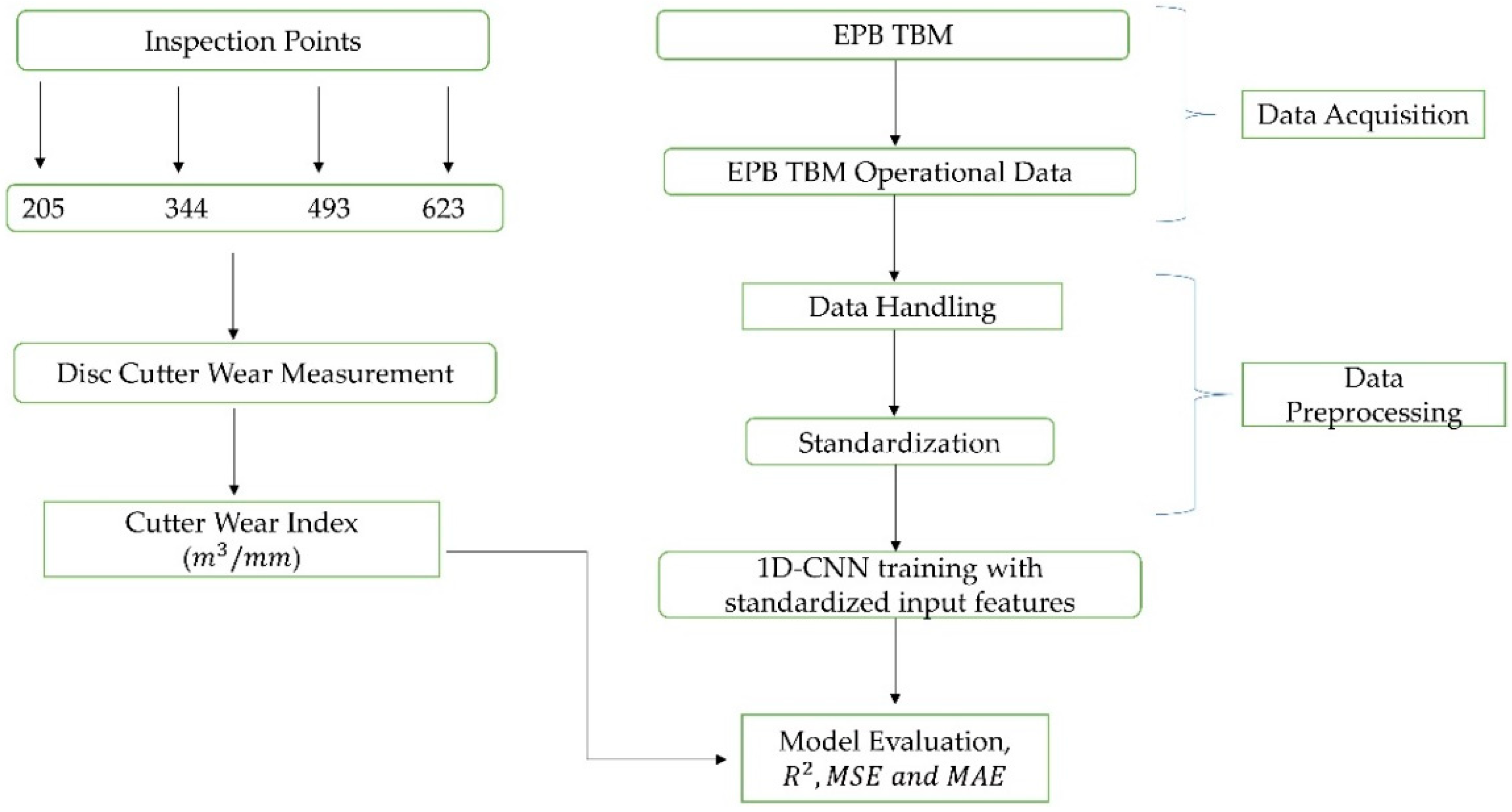
7. Proposed 1D CNN Regression for Cutter Wear Prediction
7.1. Data Preprocessing
7.2. ReLU Function
7.3. Leaky ReLU
7.4. Mean Squared Error (MSE)
7.5. Mean Absolute Error (MAE)
7.6. Regularization
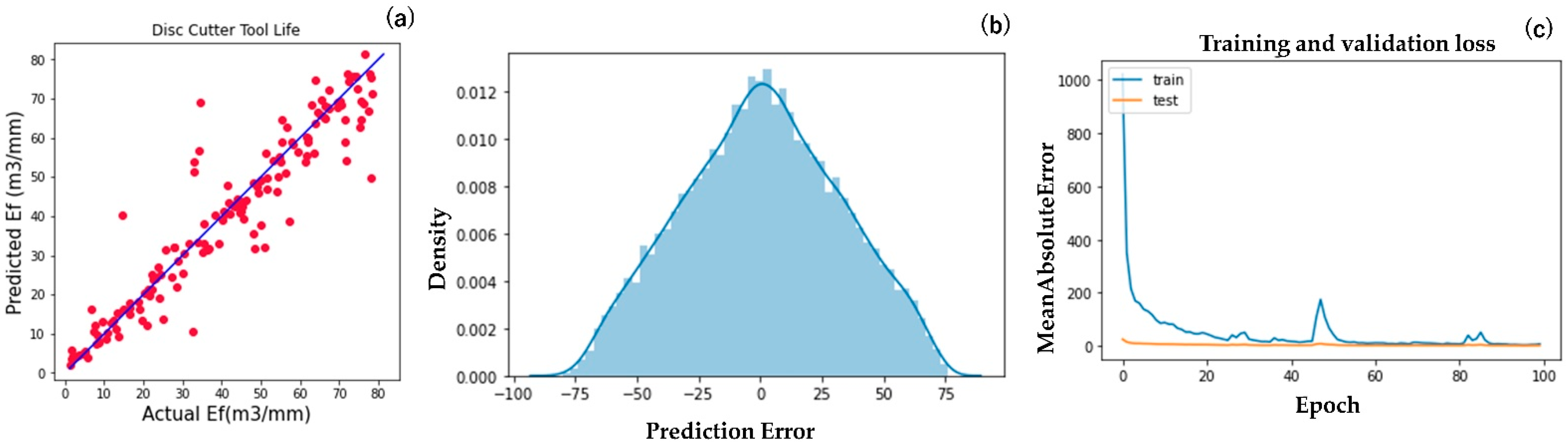
8. Model Comparison
9. Discussion
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, S.; Chen, Z.; Luo, H.; Wang, S.; Zhao, Y.; Liu, L.; Ling, D.; Jing, L. Tunnel Boring Machines (TBM) Performance Prediction: A Case Study Using Big Data and Deep Learning. Tunn. Undergr. Space Technol. 2021, 110, 103636. [Google Scholar] [CrossRef]
- Hartlieb, P.; Grafe, B.; Shepel, T.; Malovyk, A.; Akbari, B. Experimental Study on Artificially Induced Crack Patterns and Their Consequences on Mechanical Excavation Processes. Int. J. Rock Mech. Min. Sci. 2017, 100, 160–169. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, Y.; Zhang, Y.; Tan, Q.; Zhu, Z.; Lin, L. Experimental Study on Wear Behaviors of TBM Disc Cutter Ring under Drying, Water and Seawater Conditions. Wear 2017, 392–393, 109–117. [Google Scholar] [CrossRef]
- Ren, D.-J.; Shen, S.-L.; Arulrajah, A.; Cheng, W.-C. Prediction Model of TBM Disc Cutter Wear during Tunnelling in Heterogeneous Ground. Rock Mech. Rock Eng. 2018, 51, 3599–3611. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Tarigh Azali, S.; Zhao, J. Introduction of an Empirical TBM Cutter Wear Prediction Model for Pyroclastic and Mafic Igneous Rocks; a Case History of Karaj Water Conveyance Tunnel, Iran. Tunn. Undergr. Space Technol. 2014, 43, 222–231. [Google Scholar] [CrossRef]
- Barzegari, G.; Khodayari, J.; Rostami, J. Evaluation of TBM Cutter Wear in Naghadeh Water Conveyance Tunnel and Developing a New Prediction Model. Rock Mech. Rock Eng. 2021, 54, 6281–6297. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Y.; Li, J.; Jing, L.; Zhao, G.; Nie, L. A TBM Cutter Life Prediction Method Based on Rock Mass Classification. KSCE J. Civ. Eng. 2020, 24, 2794–2807. [Google Scholar] [CrossRef]
- Rong, X.; Lu, H.; Wang, M.; Wen, Z.; Rong, X. Cutter Wear Evaluation from Operational Parameters in EPB Tunneling of Chengdu Metro. Tunn. Undergr. Space Technol. 2019, 93, 103043. [Google Scholar] [CrossRef]
- Su, W.; Li, X.; Jin, D.; Yang, Y.; Qin, R.; Wang, X. Analysis and Prediction of TBM Disc Cutter Wear When Tunneling in Hard Rock Strata: A Case Study of a Metro Tunnel Excavation in Shenzhen, China. Wear 2020, 446–447, 203190. [Google Scholar] [CrossRef]
- Jamal, R.; Ozdemir, L. New model for performance production of hard rock TBMs. In Proceedings of the Rapid Excavation and Tunneling Conference, Boston, MA, USA, 1 January 1993; pp. 793–809. [Google Scholar]
- Bruland, A. Hard Rock Tunnel Boring; Norwegian University of Science and Technology: Trondheim, Norway, 2000. [Google Scholar]
- Roxborough, F.F.; Phillips, H.R. Rock Excavation by Disc Cutter. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1975, 12, 361–366. [Google Scholar] [CrossRef]
- Wijk, G. A Model of Tunnel Boring Machine Performance. Geotech. Geol. Eng. 1992, 10, 19–40. [Google Scholar] [CrossRef]
- Barton, N.R. TBM Tunnelling in Jointed and Faulted Rock; CRC Press: Boca Raton, FL, USA, 2000; p. 184. [Google Scholar]
- Cardu, M.; Iabichino, G.; Oreste, P.; Rispoli, A. Experimental and Analytical Studies of the Parameters Influencing the Action of TBM Disc Tools in Tunnelling. Acta Geotech. 2017, 12, 293–304. [Google Scholar] [CrossRef]
- Zare, S.; Bruland, A. Applications of NTNU/SINTEF Drillability Indices in Hard Rock Tunneling. Rock Mech. Rock Eng. 2013, 46, 179–187. [Google Scholar] [CrossRef]
- Macias, F.J.; Dahl, F.; Bruland, A. New Rock Abrasivity Test Method for Tool Life Assessments on Hard Rock Tunnel Boring: The Rolling Indentation Abrasion Test (RIAT). Rock Mech. Rock Eng. 2016, 49, 1679–1693. [Google Scholar] [CrossRef]
- Ko, T.Y.; Lee, S.S. Effect of Rock Abrasiveness on Wear of Shield Tunnelling in Bukit Timah Granite. Appl. Sci. 2020, 10, 3231. [Google Scholar] [CrossRef]
- Farrokh, E. Primary and Secondary Tools’ Life Evaluation for Soft Ground TBMs. Bull. Eng. Geol. Environ. 2021, 80, 4909–4927. [Google Scholar] [CrossRef]
- Alvarez Grima, M.; Bruines, P.A.; Verhoef, P.N.W. Modeling Tunnel Boring Machine Performance by Neuro-Fuzzy Methods. Tunn. Undergr. Space Technol. 2000, 15, 259–269. [Google Scholar] [CrossRef]
- Benardos, A.G.; Kaliampakos, D.C. Modelling TBM Performance with Artificial Neural Networks. Tunn. Undergr. Space Technol. 2004, 19, 597–605. [Google Scholar] [CrossRef]
- Yagiz, S.; Gokceoglu, C.; Sezer, E.; Iplikci, S. Application of Two Non-Linear Prediction Tools to the Estimation of Tunnel Boring Machine Performance. Eng. Appl. Artif. Intell. 2009, 22, 808–814. [Google Scholar] [CrossRef]
- Ghasemi, E.; Yagiz, S.; Ataei, M. Predicting Penetration Rate of Hard Rock Tunnel Boring Machine Using Fuzzy Logic. Bull. Eng. Geol. Environ. 2014, 73, 23–35. [Google Scholar] [CrossRef]
- Mahdevari, S.; Shahriar, K.; Yagiz, S.; Akbarpour Shirazi, M. A Support Vector Regression Model for Predicting Tunnel Boring Machine Penetration Rates. Int. J. Rock Mech. Min. Sci. 2014, 72, 214–229. [Google Scholar] [CrossRef]
- Mahdevari, S.; Torabi, S.R.; Monjezi, M. Application of Artificial Intelligence Algorithms in Predicting Tunnel Convergence to Avoid TBM Jamming Phenomenon. Int. J. Rock Mech. Min. Sci. 2012, 55, 33–44. [Google Scholar] [CrossRef]
- Shao, C.; Li, X.; Su, H. Performance Prediction of Hard Rock TBM Based on Extreme Learning Machine. In Proceedings of the International Conference on Intelligent Robotics and Applications, Busan, Korea, 25–28 September 2013; Lee, J., Lee, M.C., Liu, H., Ryu, J.-H., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2013; pp. 409–416. [Google Scholar] [CrossRef]
- Salimi, A.; Faradonbeh, R.S.; Monjezi, M.; Moormann, C. TBM Performance Estimation Using a Classification and Regression Tree (CART) Technique. Bull. Eng. Geol. Environ. 2018, 77, 429–440. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Nikouei, S.S.; Marto, A.; Fahimifar, A.; Jahed Armaghani, D.; Mohamad, E.T. Predicting Tunnel Boring Machine Performance through a New Model Based on the Group Method of Data Handling. Bull. Eng. Geol. Environ. 2019, 78, 3799–3813. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Tootoonchi, H.; Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hedayat, A. Application of Deep Neural Networks in Predicting the Penetration Rate of Tunnel Boring Machines. Bull. Eng. Geol. Environ. 2019, 78, 6347–6360. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Faradonbeh, R.S.; Momeni, E.; Fahimifar, A.; Tahir, M.M. Performance Prediction of Tunnel Boring Machine through Developing a Gene Expression Programming Equation. Eng. Comput. 2018, 34, 129–141. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Song, K. A New Hybrid Grey Wolf Optimizer-Feature Weighted-Multiple Kernel-Support Vector Regression Technique to Predict TBM Performance. Eng. Comput. 2020, 1–17. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Guo, D.; Li, X.; Chen, Z. Advanced Prediction of Tunnel Boring Machine Performance Based on Big Data. Geosci. Front. 2021, 12, 331–338. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.-L.; Zhou, A.; Yuan, D.-J.; Xu, Y.-S. Optimization of EPB Shield Performance with Adaptive Neuro-Fuzzy Inference System and Genetic Algorithm. Appl. Sci. 2019, 9, 780. [Google Scholar] [CrossRef] [Green Version]
- Mahmoodzadeh, A.; Mohammadi, M.; Hashim Ibrahim, H.; Nariman Abdulhamid, S.; Farid Hama Ali, H.; Mohammed Hasan, A.; Khishe, M.; Mahmud, H. Machine Learning Forecasting Models of Disc Cutters Life of Tunnel Boring Machine. Autom. Constr. 2021, 128, 103779. [Google Scholar] [CrossRef]
- Massalov, T.; Yagiz, S.; Adoko, A.C. Application of Soft Computing Techniques to Estimate Cutter Life Index Using Mechanical Properties of Rocks. Appl. Sci. 2022, 12, 1446. [Google Scholar] [CrossRef]
- Yu, H.; Tao, J.; Huang, S.; Qin, C.; Xiao, D.; Liu, C. A Field Parameters-Based Method for Real-Time Wear Estimation of Disc Cutter on TBM Cutterhead. Autom. Constr. 2021, 124, 103603. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.-L.; Zhou, A.; Yin, Z.-Y.; Lyu, H.-M. Prediction of Disc Cutter Life during Shield Tunneling with AI via the Incorporation of a Genetic Algorithm into a GMDH-Type Neural Network. Engineering 2021, 7, 238–251. [Google Scholar] [CrossRef]
- Obara, H.; Maejima, Y.; Kohyama, K.; Ohkura, T.; Takata, Y. Outline of the Comprehensive Soil Classification System of Japan–First Approximation. Jpn. Agric. Res. Q. 2015, 49, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Hirai, H.; Hamazaki, T. Historical Aspects of Soil Classification in Japan. Soil Sci. Plant 2004, 50, 611–622. [Google Scholar] [CrossRef]
- Park, J.; Santamarina, J.C. Revised Soil Classification System for Coarse-Fine Mixtures. J. Geotech. Geoenviron. 2017, 143, 04017039. [Google Scholar] [CrossRef] [Green Version]
- Amoun, S.; Sharifzadeh, M.; Shahriar, K.; Rostami, J.; Tarigh Azali, S. Evaluation of Tool Wear in EPB Tunneling of Tehran Metro, Line 7 Expansion. Tunn. Undergr. Space Technol. 2017, 61, 233–246. [Google Scholar] [CrossRef]
- O’Carroll, J.B. A Guide to Planning, Constructing, and Supervising Earth Pressure Balance TBM Tunneling; Parsons Brinckerhoff: New York, NY, USA, 2005. [Google Scholar]
- Bilgin, N.; Copur, H.; Balci, C. Mechanical Excavation in Mining and Civil Industries; CRC Press: Boca Raton, FL, USA, 2013; pp. 49–120. [Google Scholar]
- Hassanpour, J.; Rostami, J.; Zhao, J.; Azali, S.T. TBM Performance and Disc Cutter Wear Prediction Based on Ten Years Experience of TBM Tunnelling in Iran. Geomech. Tunn. 2015, 8, 239–247. [Google Scholar] [CrossRef]
- Bruland, A. Hard rock tunnel boring: Drillability test methods. In Project Report 13A-98, NTNU Trondheim 21; Academia: San Francisco, CA, USA, 1998. [Google Scholar]
- Liu, Q.; Liu, J.; Pan, Y.; Zhang, X.; Peng, X.; Gong, Q.; Du, L. A Wear Rule and Cutter Life Prediction Model of a 20-in. TBM Cutter for Granite: A Case Study of a Water Conveyance Tunnel in China. Rock Mech. Rock Eng. 2017, 50, 1303–1320. [Google Scholar] [CrossRef]
- Jakobsen, P.D.; Lohne, J. Challenges of Methods and Approaches for Estimating Soil Abrasivity in Soft Ground TBM Tunnelling. Wear 2013, 308, 166–173. [Google Scholar] [CrossRef]
- Köppl, F.; Thuro, K.; Thewes, M. Suggestion of an Empirical Prognosis Model for Cutting Tool Wear of Hydroshield TBM. Tunn. Undergr. Space Technol. 2015, 49, 287–294. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a Convolutional Neural Network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Aloysius, N.; Geetha, M. A Review on Deep Convolutional Neural Networks. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP), Tamilnadu, India, 6–8 April 2017; pp. 0588–0592. [Google Scholar] [CrossRef]
- Dhillon, A.; Verma, G.K. Convolutional Neural Network: A Review of Models, Methodologies and Applications to Object Detection. Prog. Artif. Intell. 2020, 9, 85–112. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, C.; Peng, X.; Jian, L.; Liu, Z. Towards End-to-End Pulsed Eddy Current Classification and Regression with CNN. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Khan, Z.A.; Hussain, T.; Ullah, A.; Rho, S.; Lee, M.; Baik, S.W. Towards Efficient Electricity Forecasting in Residential and Commercial Buildings: A Novel Hybrid CNN with a LSTM-AE Based Framework. Sensors 2020, 20, 1399. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]







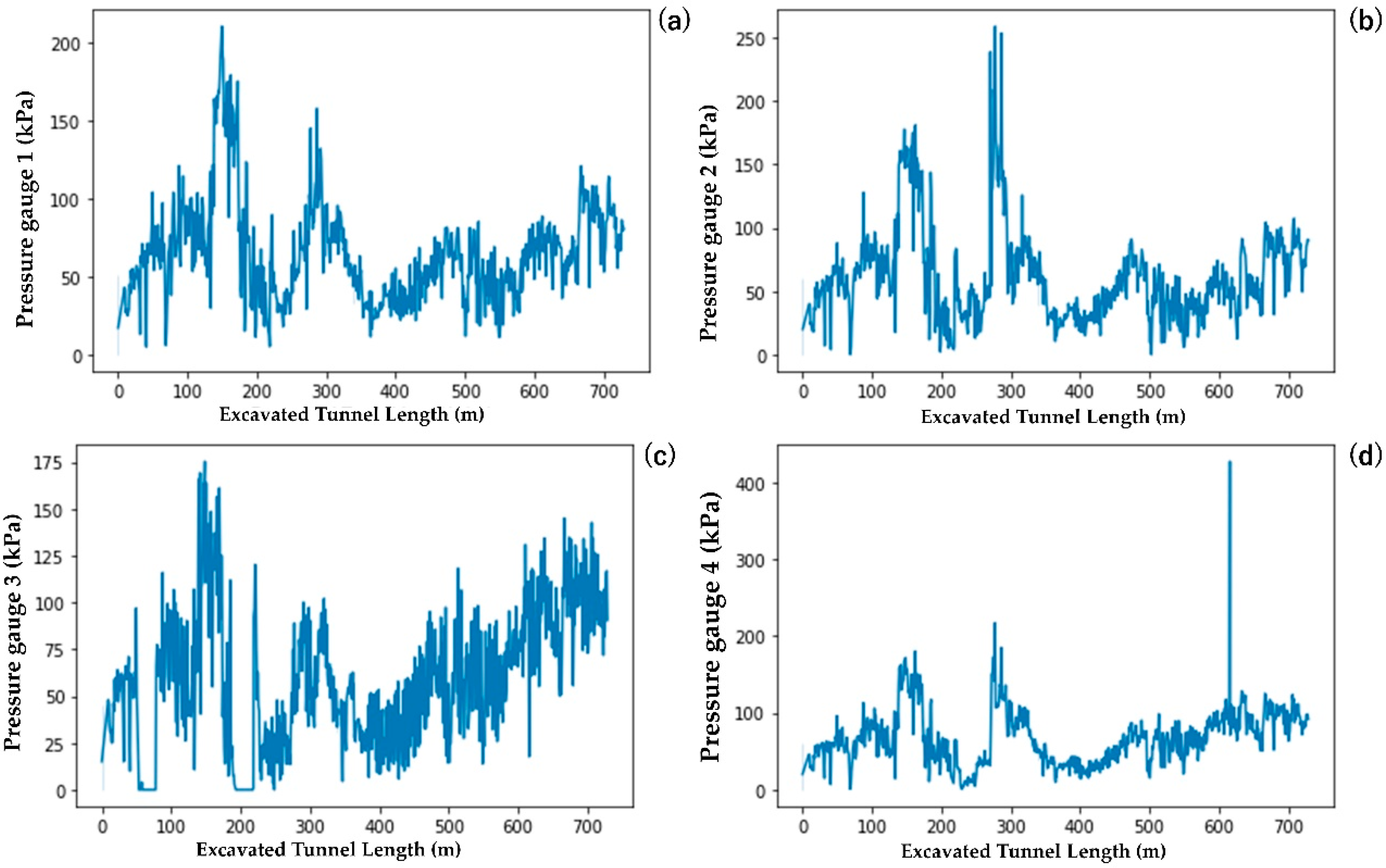
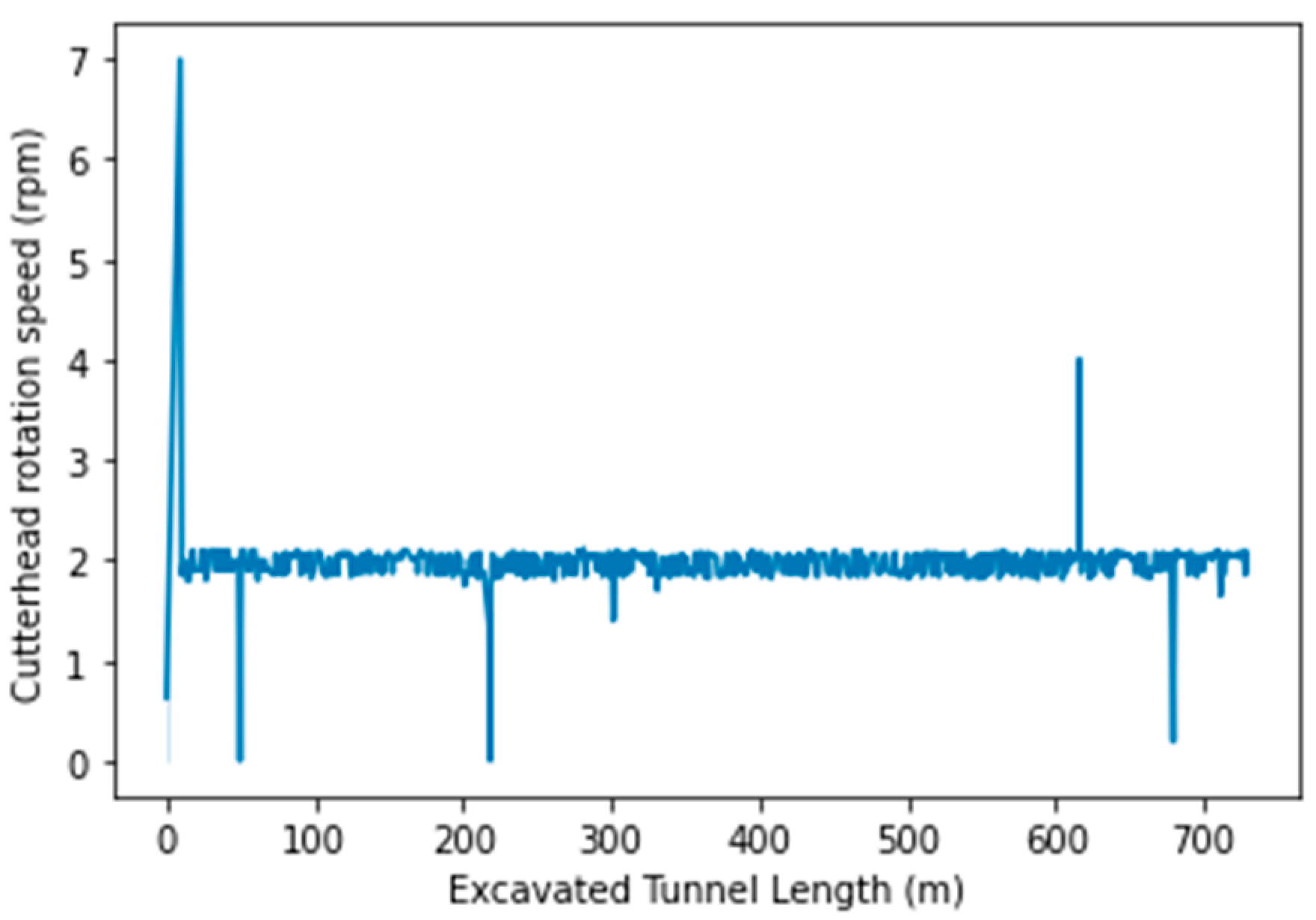
| Machine Specifications | |
|---|---|
| Shield outer diameter (m) | 3.12 |
| Shield length (m) | 7.42 |
| Thrust force (kN/m2) | 1342 |
| Shield jack speed (mm/min) | 63 |
| Torque (kN.m) | 886 |
| Borehole Number | Depth (m) | Soil Layers | Soil Layers | Test Points | Elastic Module (MN/m2) | Consolidated Undrained Triaxial Test | |
|---|---|---|---|---|---|---|---|
| Cohesion | Friction Angle | ||||||
| No. 1 | 7.50 | Silty clay | Vcs | 6 | 15.97 | 16.4 | 31.04 |
| 10 | Sandy silt mixed with gravel | Vcs | 5 | 14.76 | 21.4 | 41.37 | |
| No. 2 | 16 | Sandy clay | Vsg | 50 | 83.45 | 92.1 | 31.27 |
| 19.50 | Silty sand | Vsg | 18 | 45.20 | 60.5 | 23.33 | |
| No. 3 | 11 | Silty clay | Vcs | 4 | 4.37 | 19.7 | 27.25 |
| 14.50 | Silty gravel | Vg | 34 | 62.37 | 2.7 | 40.44 | |
| Descriptive | Pressure Gauge (kPa) | Digging Velocity (mm/min) | Shield Jack Stroke (mm) | Propulsion Pressure (MPa) | Total Thrust (kN) | Cutter Torque (kN.m) | Cutter Rolling Velocity (rpm) | Screw Pressure (MPa) | Screw Rotation Speed (rpm) | Gate Opening (%) | Mud Injection Pressure (MPa) | Add MudFlow (L/min) | Back in injection rate (%) | Ef (m3/mm) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | Left | Right | Left | Right | ||||||||||||
| Count | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 | 726 |
| Mean | 64.95 | 60.85 | 58.51 | 67.22 | 13.74 | 13.27 | 694.17 | 696.96 | 15.75 | 3459 | 482 | 1.96 | 2.85 | 0.90 | 29.40 | 0.18 | 16.33 | 96.9 | 39.79 |
| Std | 32.64 | 36.99 | 36.26 | 36.88 | 14.14 | 10.71 | 137.75 | 213.39 | 5.82 | 1268 | 69 | 0.27 | 5.42 | 2.96 | 12.16 | 0.08 | 8.24 | 37.71 | 22.6 |
| Min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −114 | −1.21 | 0 | 0 | 0 | 0 | 0 |
| 25% | 42.43 | 35.90 | 31.63 | 39.75 | 8.18 | 8 | 692.27 | 689.31 | 11.36 | 2517 | 449 | 1.87 | 2.66 | 0.30 | 22.72 | 0.14 | 10.2 | 79.54 | 30.15 |
| 50% | 60.45 | 53.90 | 56.13 | 64.19 | 12 | 12 | 700.5 | 699 | 14.90 | 3290 | 478 | 2 | 2.93 | 0.55 | 27.09 | 0.17 | 15.56 | 91.36 | 39.81 |
| 75% | 80.79 | 76.81 | 84.38 | 88.43 | 17.34 | 16.90 | 706.63 | 707.15 | 19.97 | 4335 | 515 | 2.06 | 3.35 | 1.1 | 35.63 | 0.22 | 21.48 | 110.2 | 59.39 |
| Max | 210.27 | 259 | 175.36 | 426.93 | 336 | 239 | 3504.2 | 5946 | 31.54 | 7160 | 694 | 7 | 7.69 | 78.25 | 67.27 | 1.6 | 58.31 | 560 | 78.7 |
| Inspection Points | Total Wear (mm) |
|---|---|
| 205 | 76 |
| 344 | 33 |
| 493 | 41 |
| 623 | 103 |
| Total | 253 |
| M (arithmetic average) | 63.3 |
| Layer | Output Shape | Parameters |
|---|---|---|
| Conv_1 (1D) | (None, 1532) | 128 |
| MaxPooling1D | (None, 1532) | 0 |
| Conv_2 (1D) | (None, 1364) | 6208 |
| MaxPooling1D | (None, 1364) | 0 |
| Conv_3 (1D) | (None, 11,128) | 24,704 |
| MaxPooling1D | (None, 11,128) | 0 |
| Conv_4 (1D) | (None, 9256) | 98,560 |
| MaxPooling1D | (None, 9256) | 0 |
| Flatten | (None, 2304) | 0 |
| Dense_1 | (None, 512) | 1,180,160 |
| Dense_2 | (None, 128) | 65,664 |
| Output (Dense) | (None, 1) | 129 |
| Trainable Params | 1,375,553 |
| Model | MSE | MAE | Time | |
|---|---|---|---|---|
| Proposed 1D CNN | 89.6 | 57.5 | 1.6 | 3 min 22 s |
| MLPRegressor | 77.8 | 107 | 5.93 | 3 min 26 s |
| LSTMRegressor | 39 | 326.3 | 11.12 | 12 min 38 s |
| Extratree regression | 77.90 | 111.16 | 7.31 | 0.497 s |
| Light gradient boosting machine | 73.98 | 130.19 | 8.04 | 0.101 s |
| Gradient boosting machine | 71.81 | 141.01 | 8.71 | 0.182 s |
| Random forest regression | 70.72 | 147.54 | 8.35 | 0.671 s |
| AdaBoost regressor | 59.12 | 202.48 | 11.84 | 0.127 s |
| k-NN regression | 19.04 | 452.03 | 15.47 | 0.062 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kilic, K.; Toriya, H.; Kosugi, Y.; Adachi, T.; Kawamura, Y. One-Dimensional Convolutional Neural Network for Pipe Jacking EPB TBM Cutter Wear Prediction. Appl. Sci. 2022, 12, 2410. https://doi.org/10.3390/app12052410
Kilic K, Toriya H, Kosugi Y, Adachi T, Kawamura Y. One-Dimensional Convolutional Neural Network for Pipe Jacking EPB TBM Cutter Wear Prediction. Applied Sciences. 2022; 12(5):2410. https://doi.org/10.3390/app12052410
Chicago/Turabian StyleKilic, Kursat, Hisatoshi Toriya, Yoshino Kosugi, Tsuyoshi Adachi, and Youhei Kawamura. 2022. "One-Dimensional Convolutional Neural Network for Pipe Jacking EPB TBM Cutter Wear Prediction" Applied Sciences 12, no. 5: 2410. https://doi.org/10.3390/app12052410
APA StyleKilic, K., Toriya, H., Kosugi, Y., Adachi, T., & Kawamura, Y. (2022). One-Dimensional Convolutional Neural Network for Pipe Jacking EPB TBM Cutter Wear Prediction. Applied Sciences, 12(5), 2410. https://doi.org/10.3390/app12052410






