Modelling of Static Liquefaction of Partially Saturated Non-Cohesive Soils
Abstract
:1. Introduction
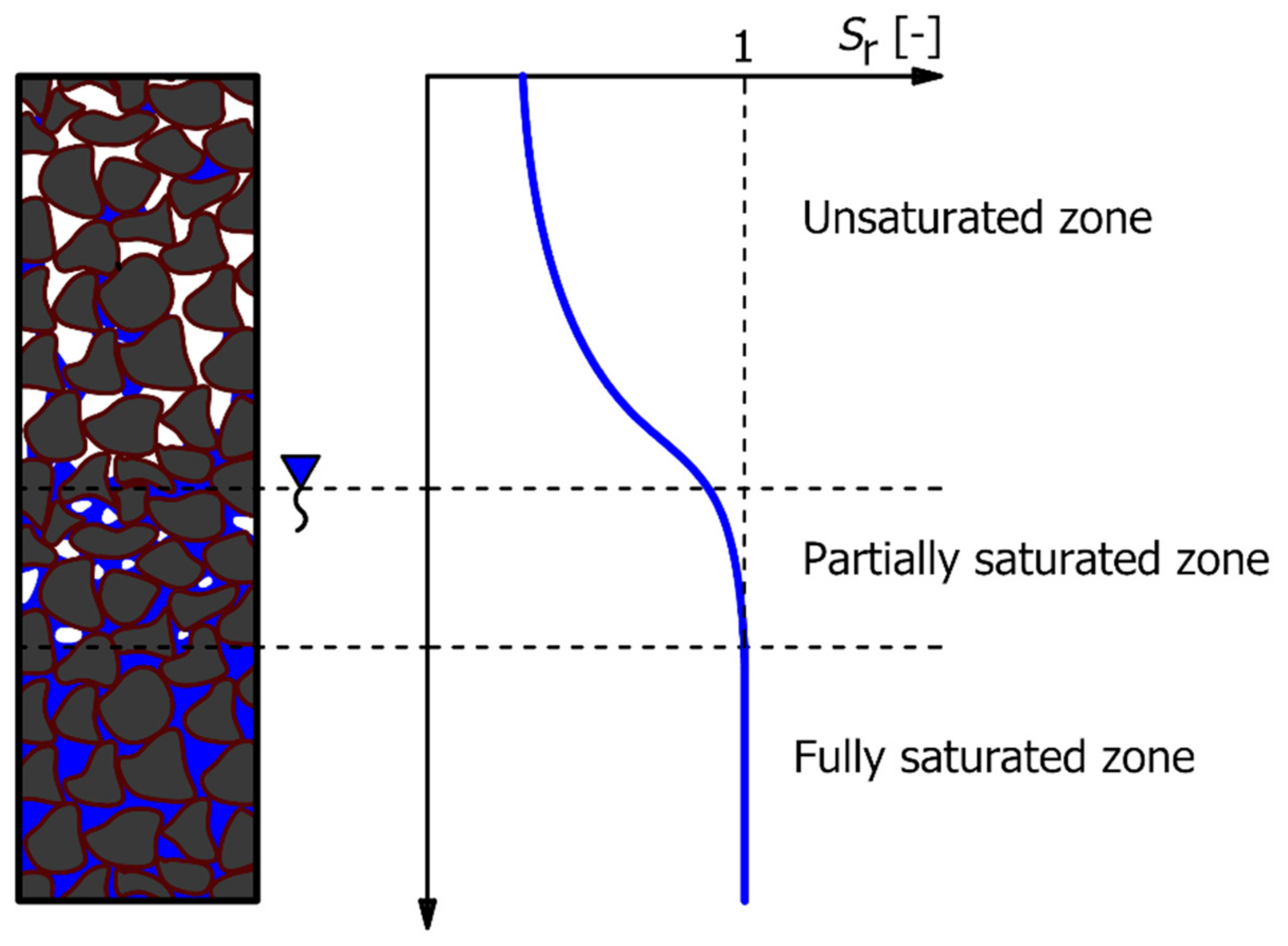
2. Generation of Pore Pressure in Partially Saturated Soils
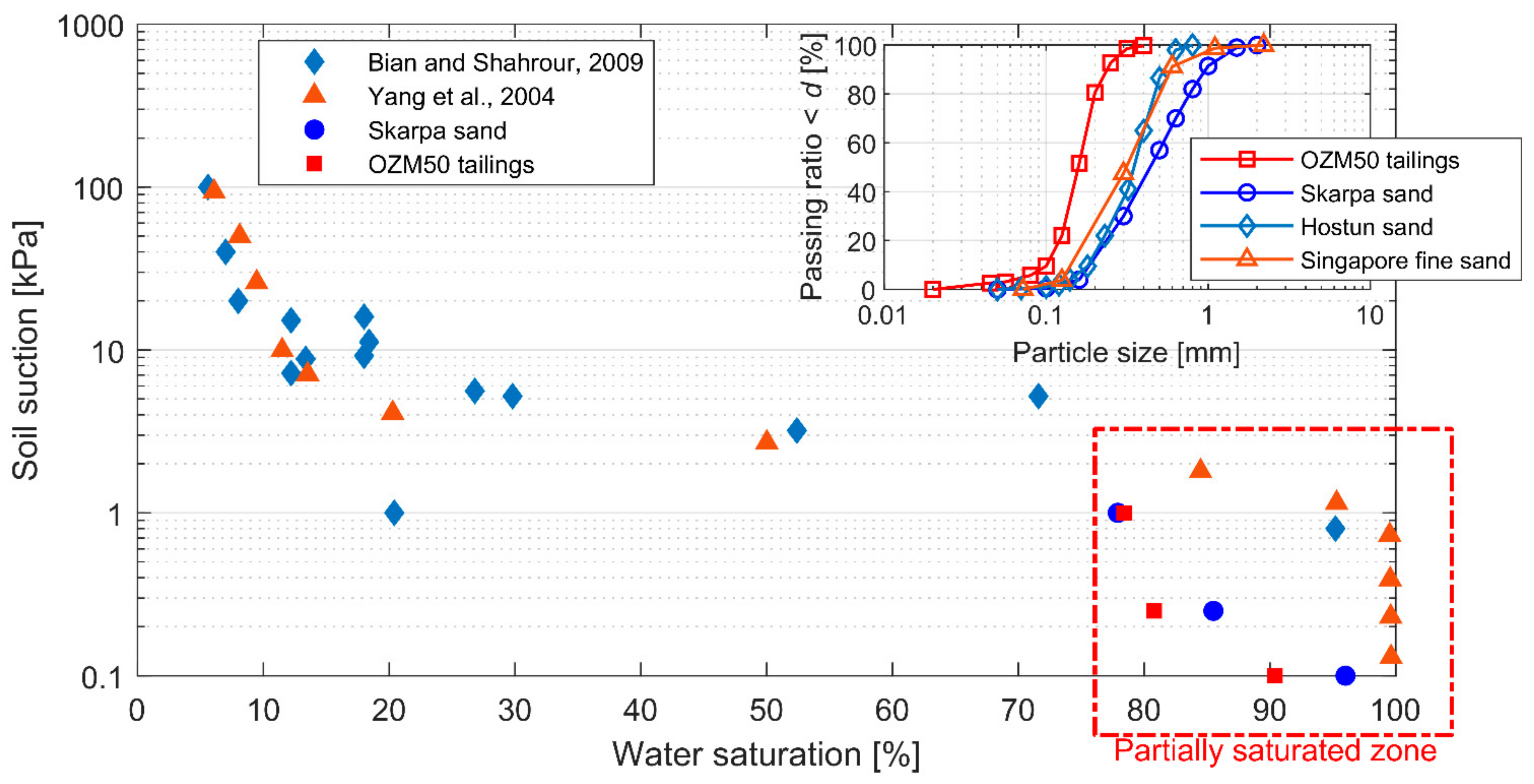
2.1. Materials and Methods
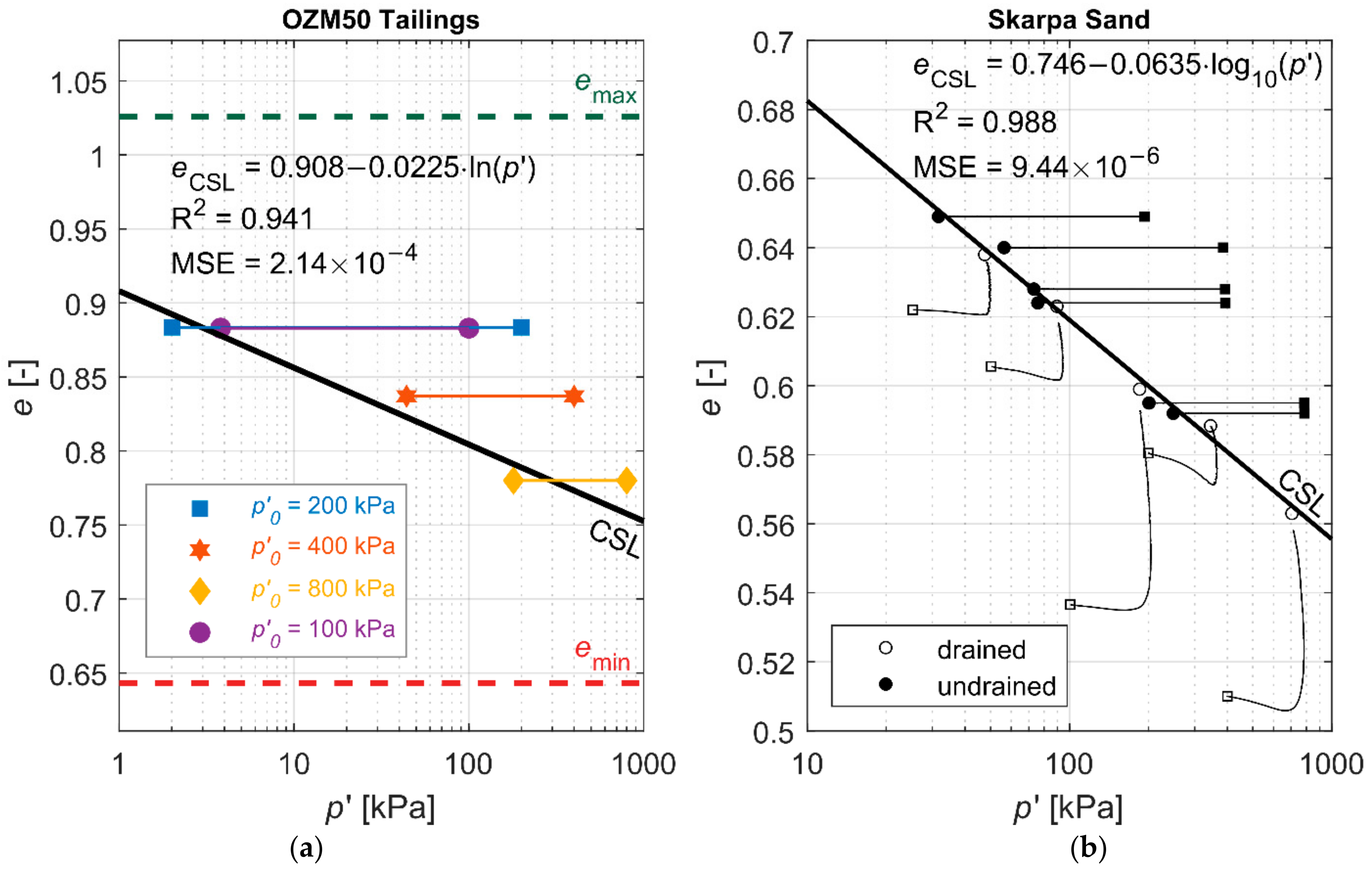
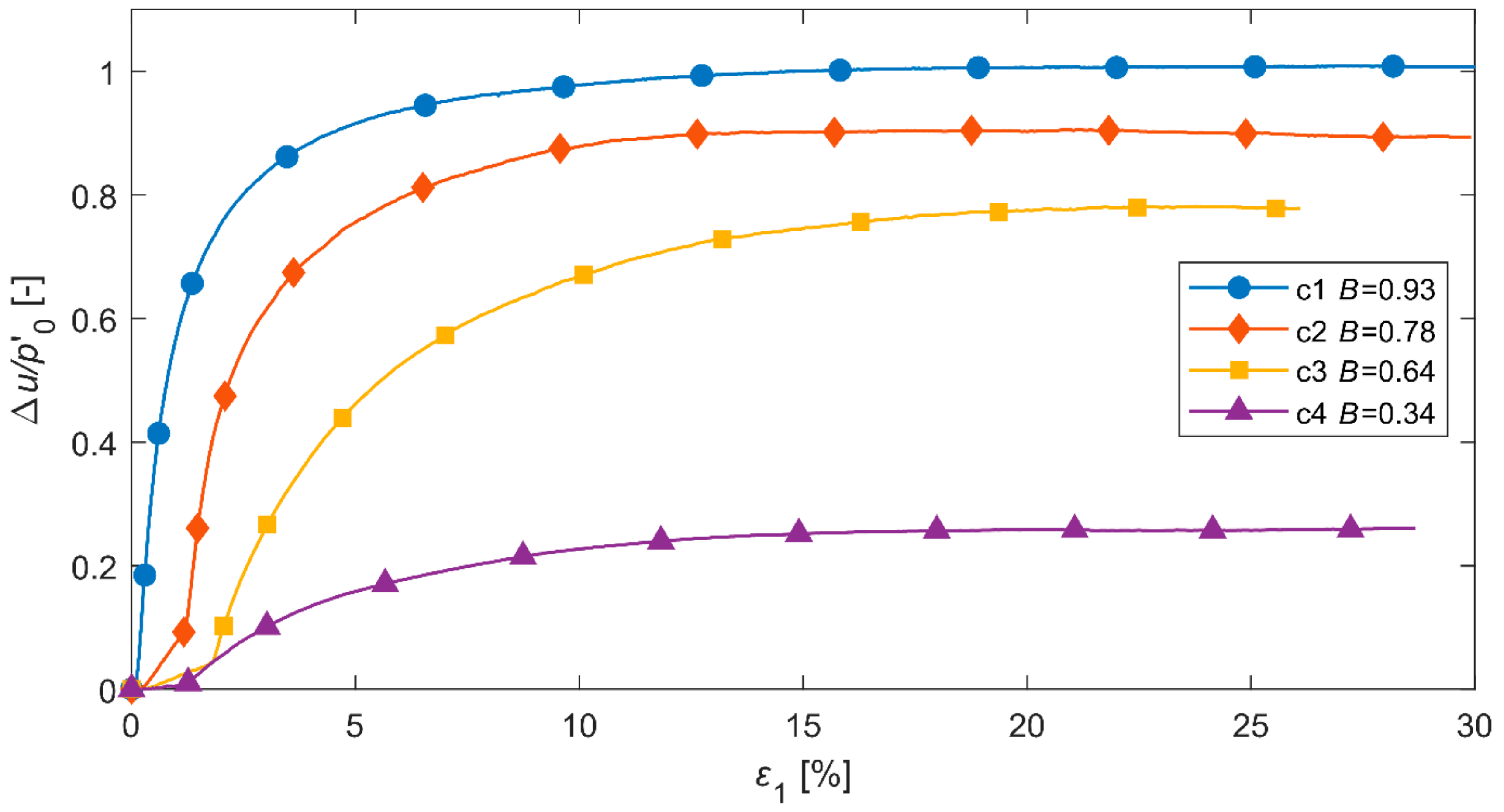
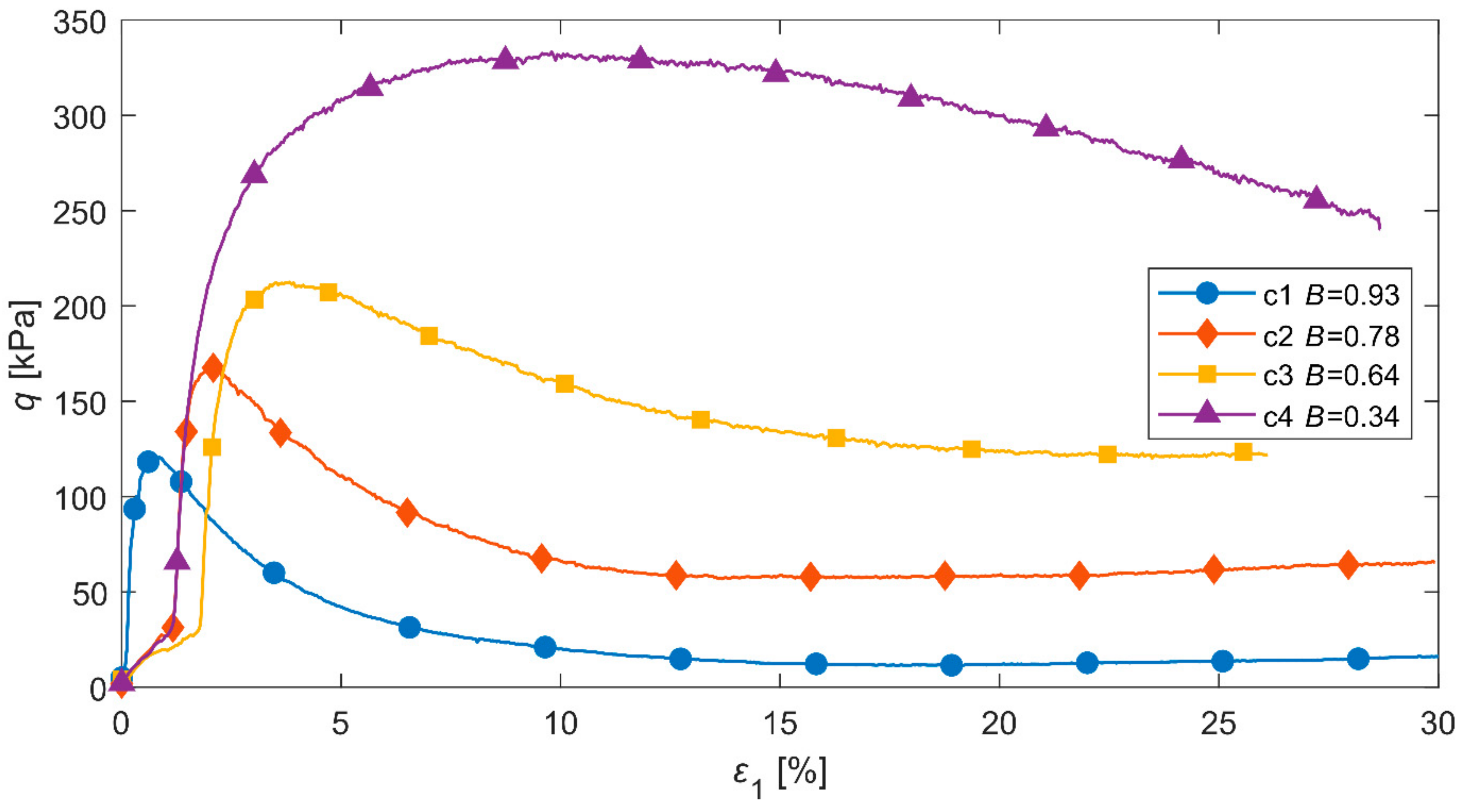
2.2. Experimental Results
3. Theoretical Model
3.1. Governing Equations
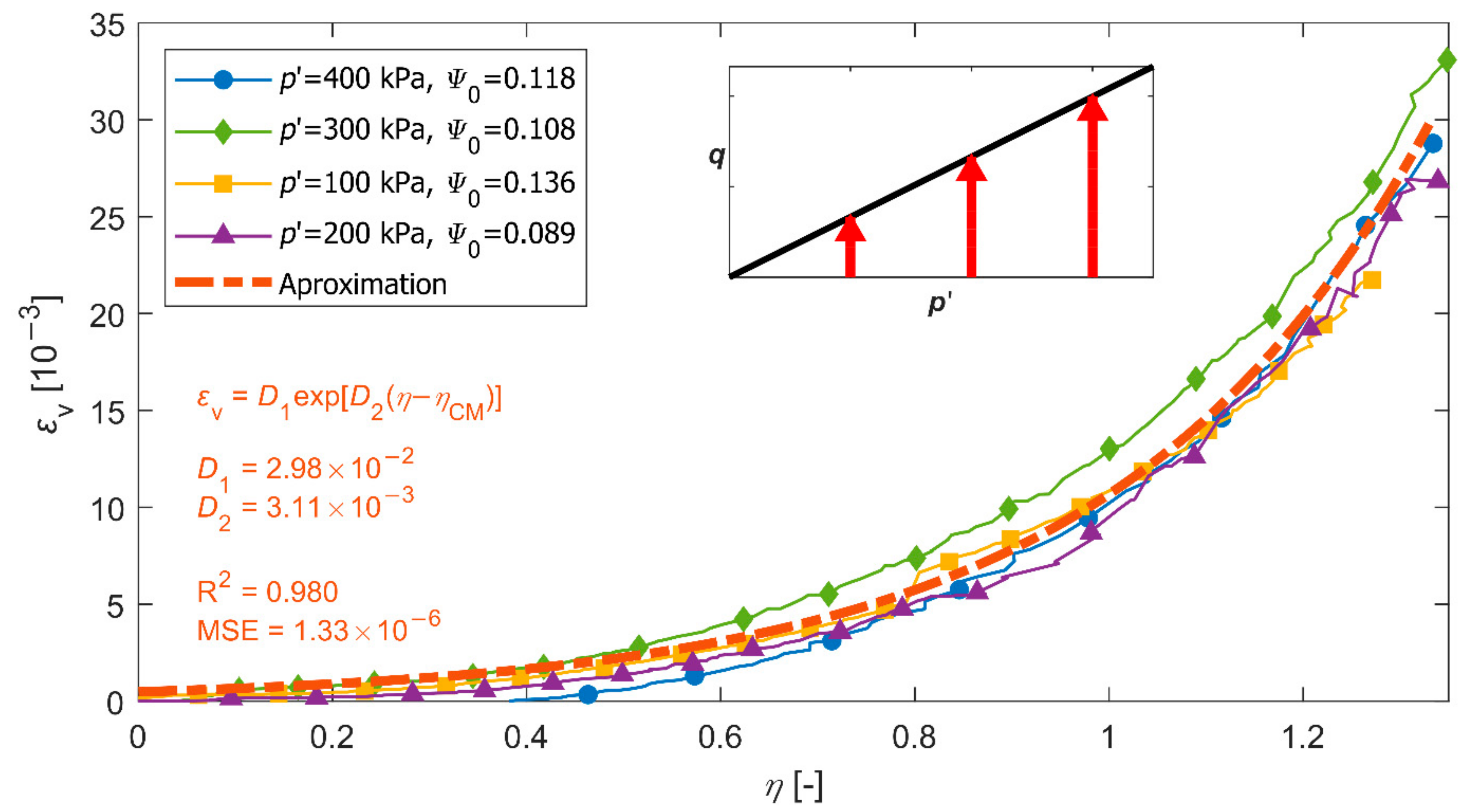
3.2. Pore Fluid Compressibility Function, κƒ
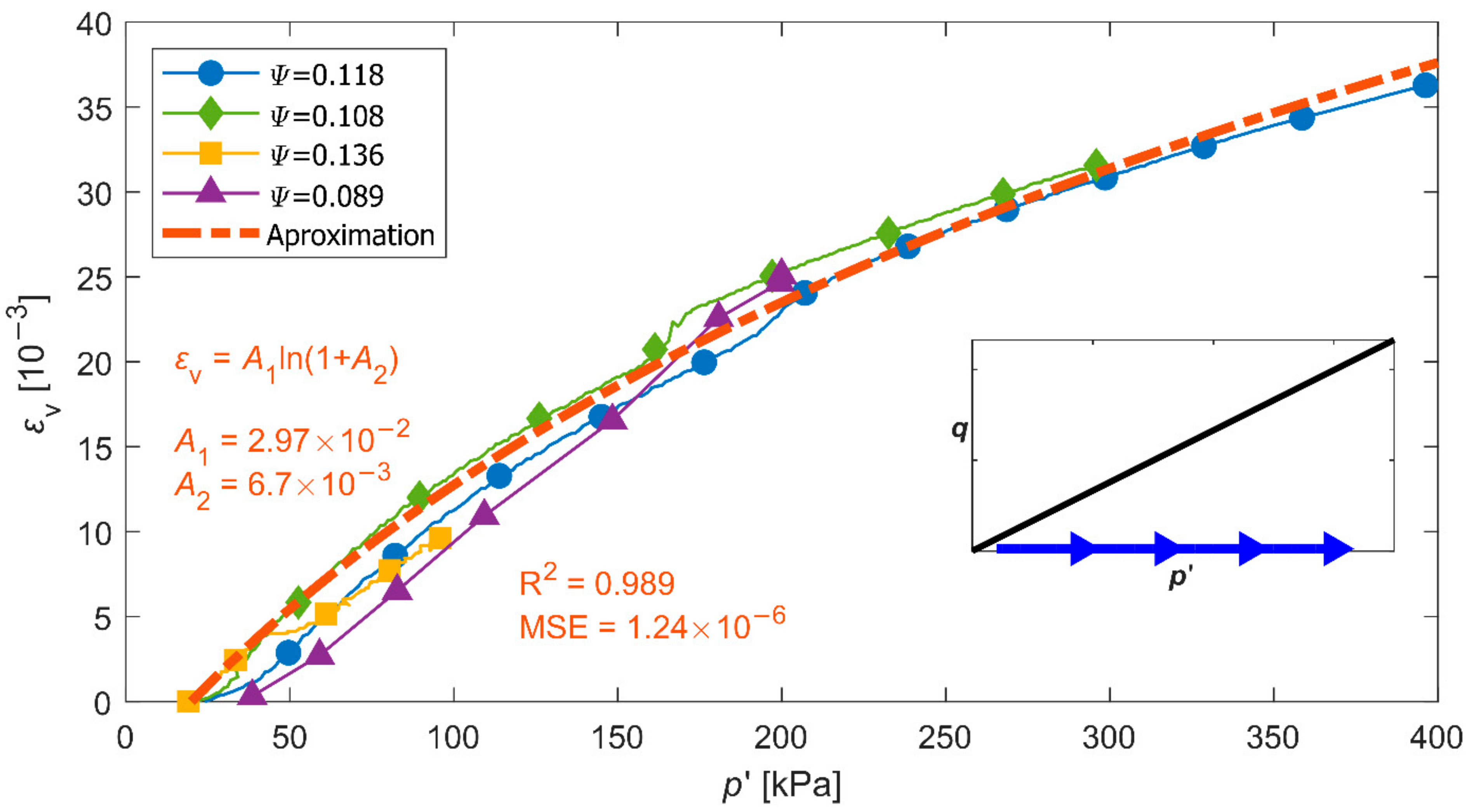
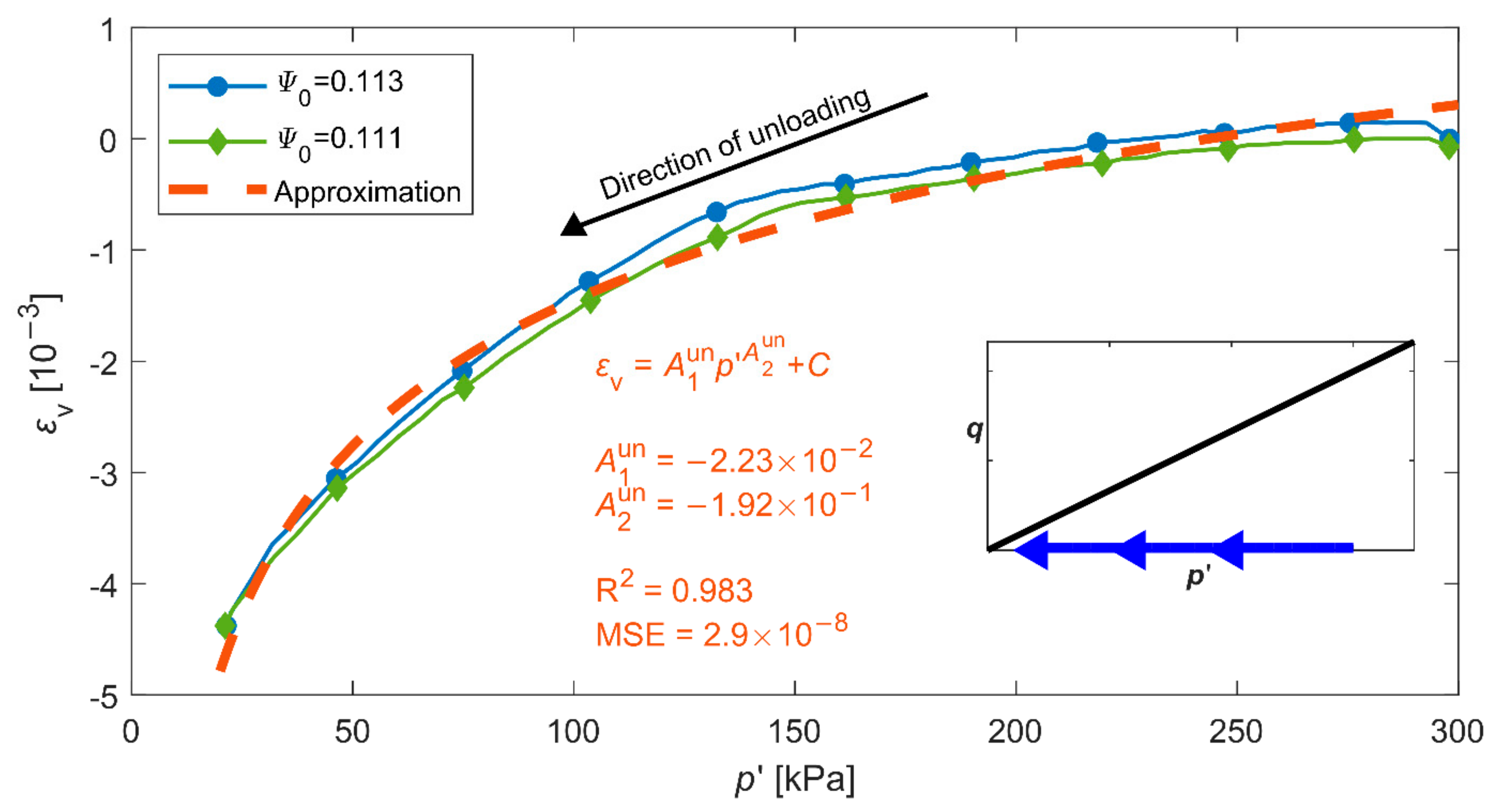
3.3. Soil Skeleton Compressibility Functions
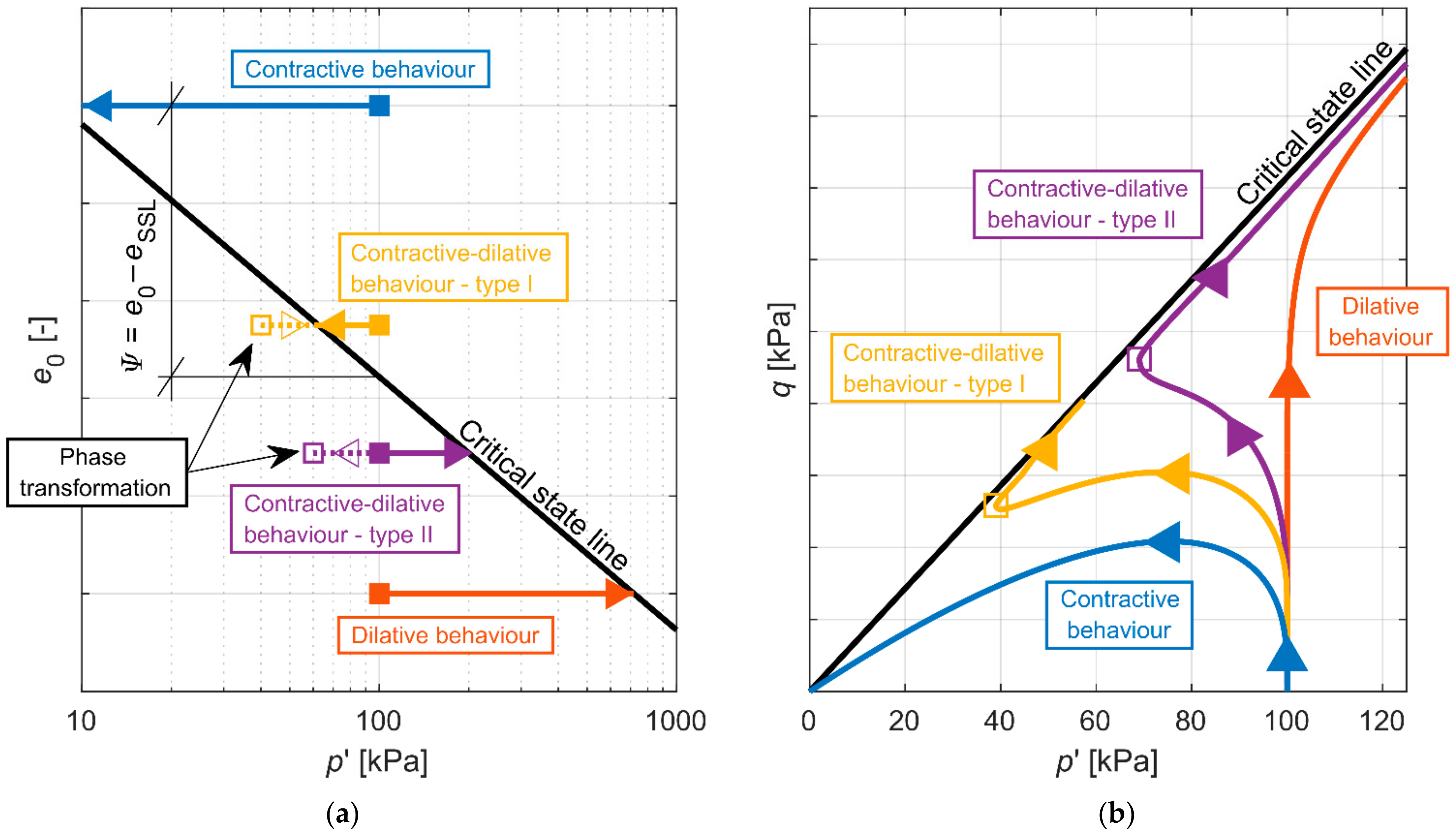
3.4. Predicted Stress Paths
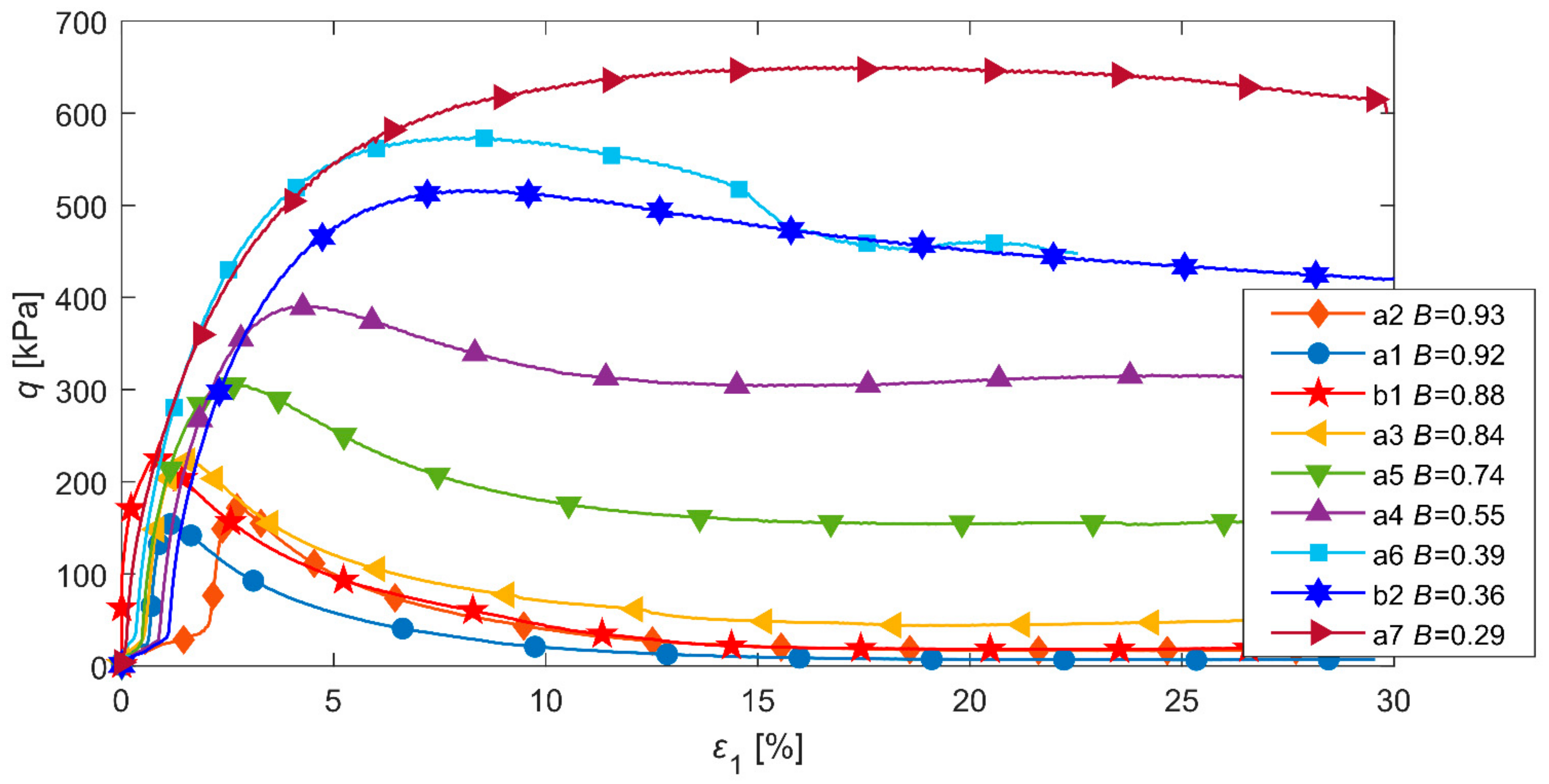
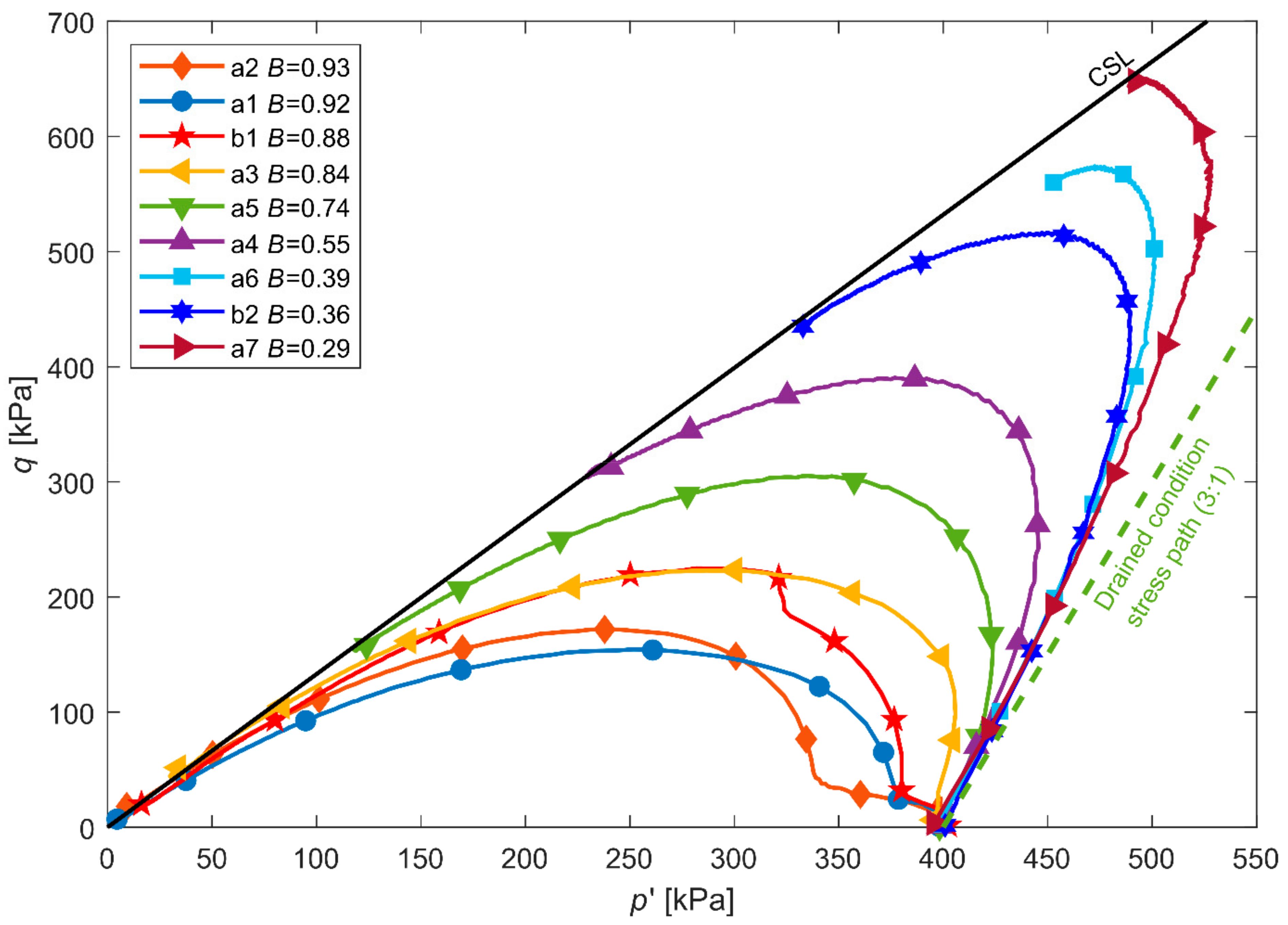
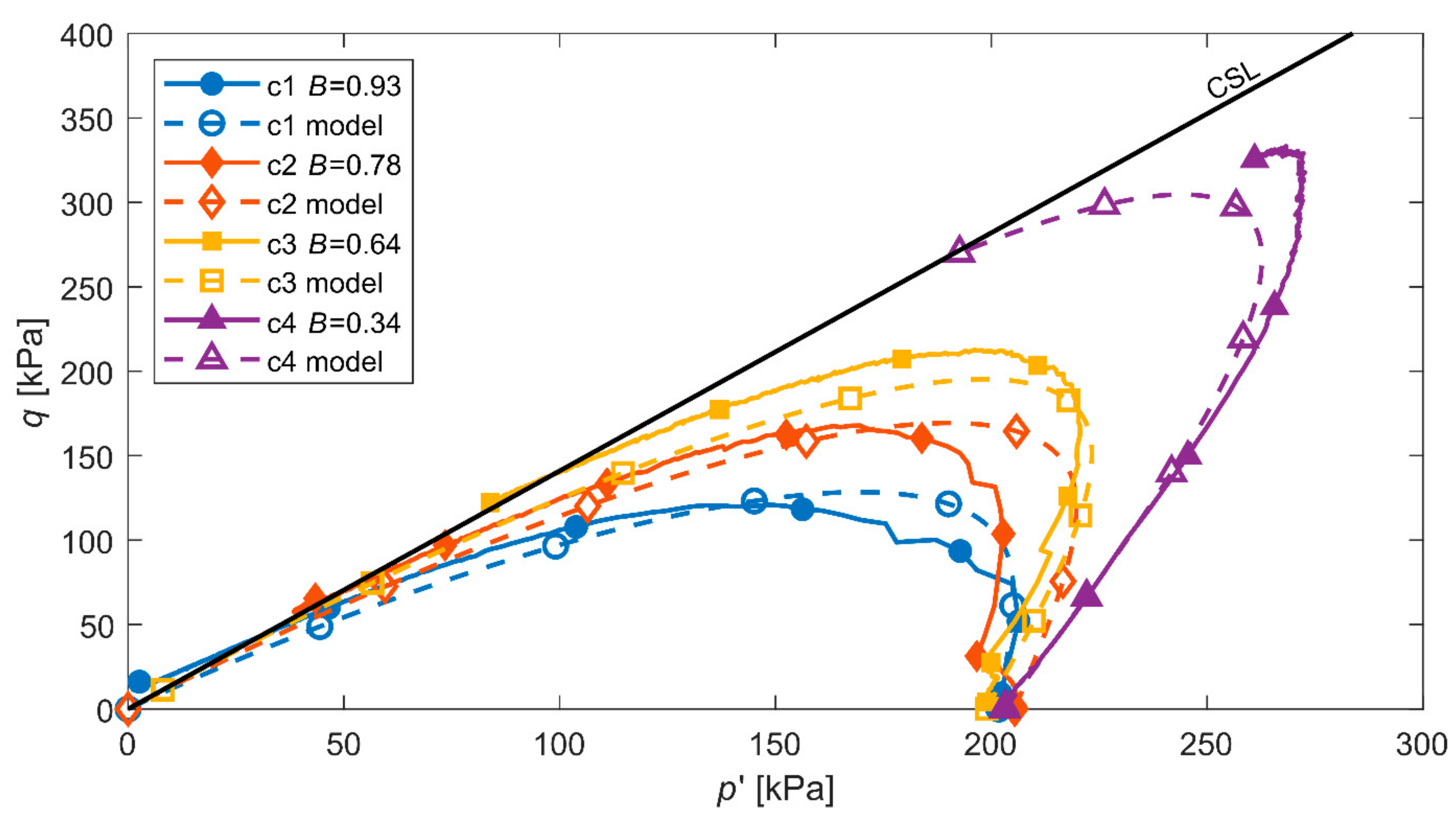
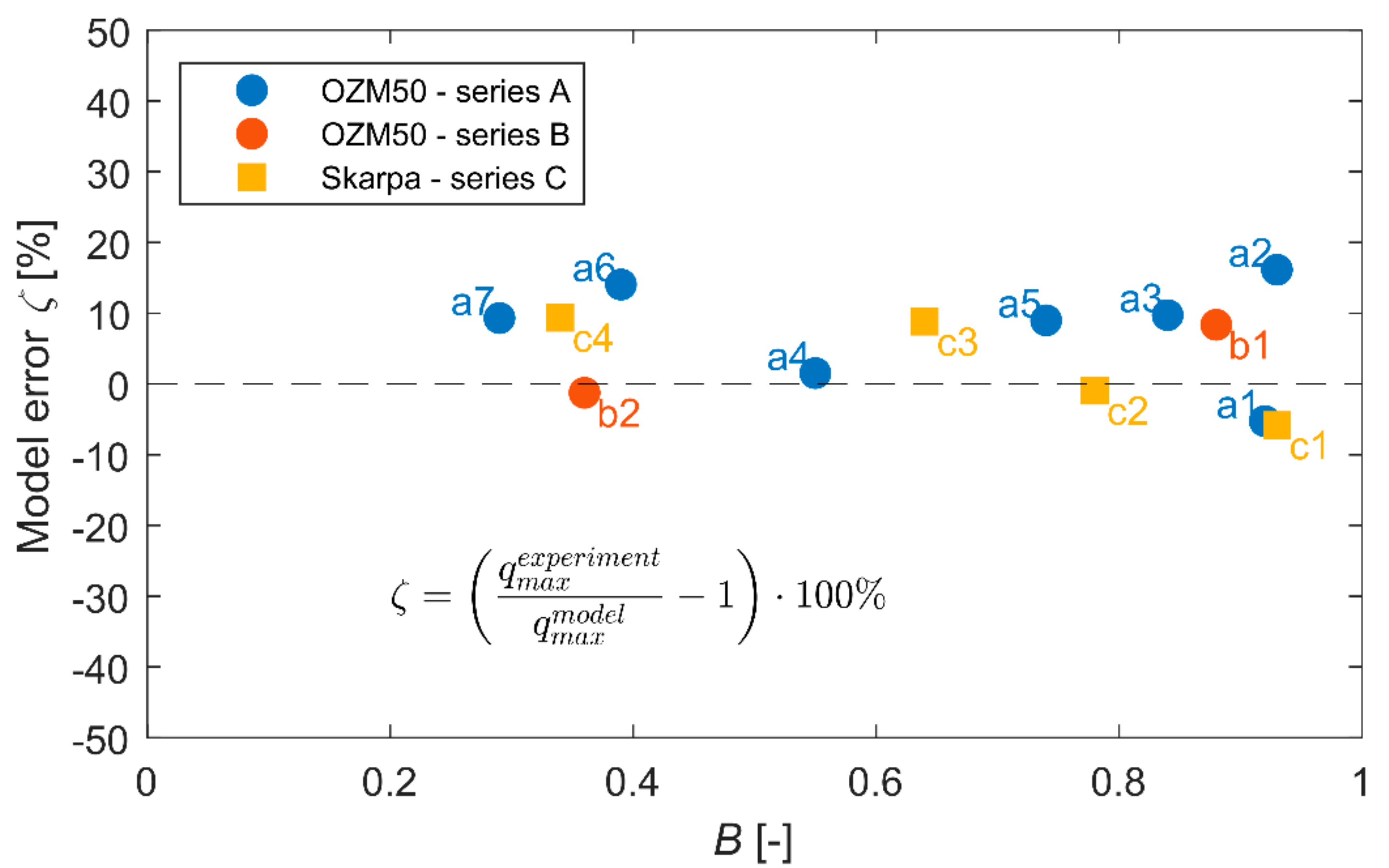
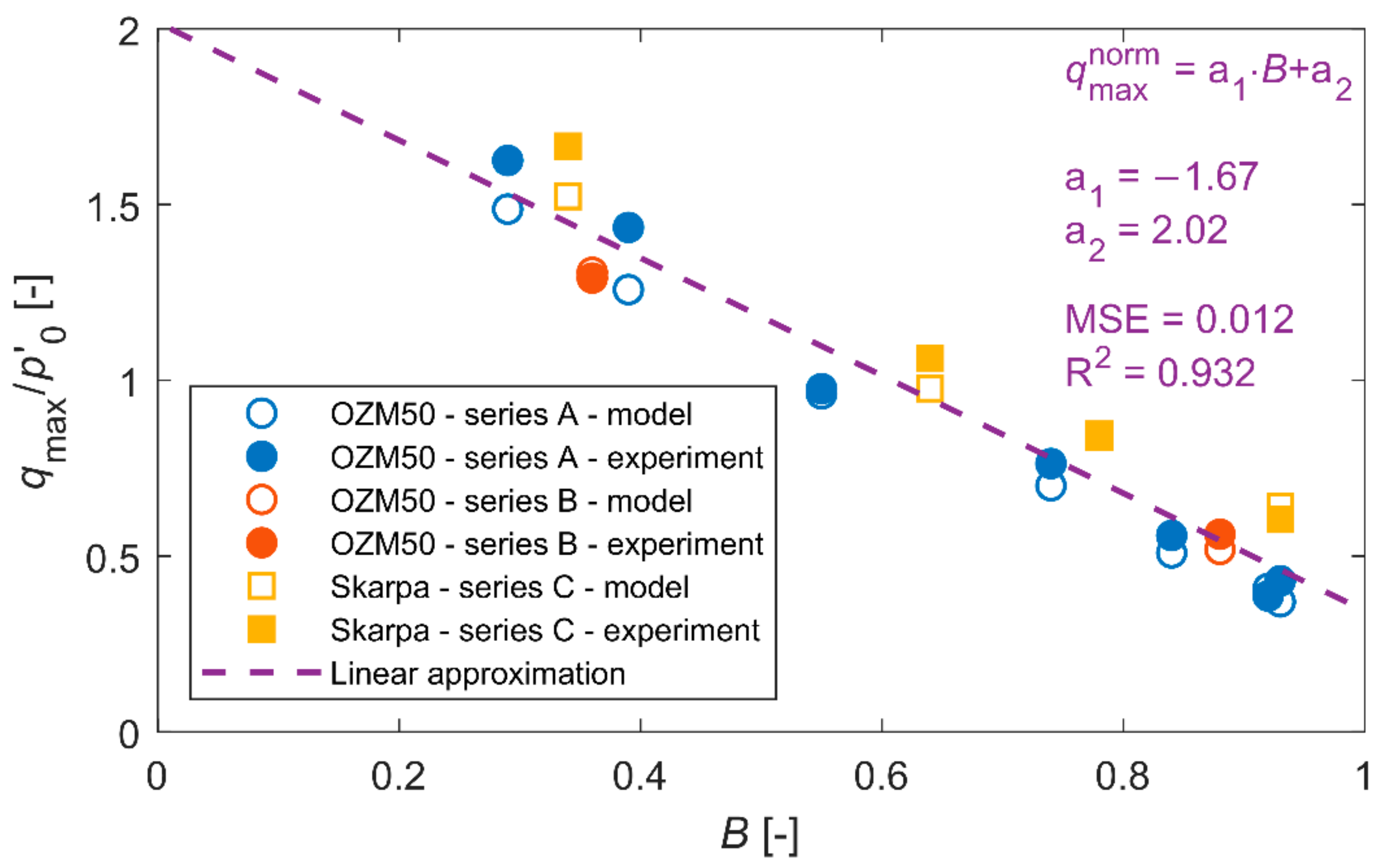
4. Verification of the Model
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fourie, A.B.; Tshabalala, L. Initiation of static liquefaction and the role of K0 consolidation. Can. Geotech. J. 2005, 42, 892–906. [Google Scholar] [CrossRef]
- Mele, L.; Tian, J.T.; Lirer, S.; Flora, A.; Koseki, J. Liquefaction resistance of unsaturated sands: Experimental evidence and theoretical interpretation. Géotechnique 2019, 69, 541–553. [Google Scholar] [CrossRef]
- Mele, L.; Flora, A. On the prediction of liquefaction resistance of unsaturated sands. Soil Dyn. Earthq. Eng. 2019, 125, 105689. [Google Scholar] [CrossRef]
- Marinelli, F.; Buscarnera, G. Instability criteria for quasi-saturated viscous soils. Int. J. Numer. Anal. Methods Géoméch. 2018, 42, 379–400. [Google Scholar] [CrossRef]
- Sherif, M.; Ashibashi, I.; Tsuchiya, C. Saturation effect on initial soil liquefaction. J. Geotech. Eng. Div. 1977, 103, 914–917. [Google Scholar] [CrossRef]
- Yoshimi, Y.; Tanaka, K.; Tokimatsu, K. Liquefaction Resistance of a Partially Saturated Sand. Soils Found. 1989, 29, 157–162. [Google Scholar] [CrossRef] [Green Version]
- Arab, A.; Shahrour, I.; Lancelot, L. A laboratory study of liquefaction of partially saturated sand. J. Iber. Geol. 2011, 37, 29–36. [Google Scholar]
- Ishihara, K.; Tsuchiya, H.; Huang, Y.; Kamada, K. Recent studies on liquefaction resistance of sand-effect of saturation. In Proceedings of the 4th International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, San Diego, CA, USA, 26–31 March 2001. [Google Scholar]
- Okamura, M.; Soga, Y. Effects of Pore Fluid Compressibility on Liquefaction Resistance of Partially Saturated Sand. Soils Found. 2006, 46, 695–700. [Google Scholar] [CrossRef] [Green Version]
- Tsukamoto, Y.; Kawabe, S.; Matsumoto, J.; Hagiwara, S. Cyclic resistance of two unsaturated silty sands against soil liquefaction. Soil Found. 2014, 54, 1094–1103. [Google Scholar] [CrossRef] [Green Version]
- Unno, T.; Kazama, M.; Uzuoka, R.; Sento, N. Liquefaction of Unsaturated Sand Considering the Pore Air Pressure and Volume Compressibility of the Soil Particle Skeleton. Soils Found. 2008, 48, 87–99. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Koseki, J.; Sato, T.; Chiaro, G.; Tian, J.T. Effect of saturation on liquefaction resistance of iron ore fines and two sandy soils. Soils Found. 2016, 56, 732–744. [Google Scholar] [CrossRef]
- Xia, H.; Hu, T. Effects of Saturation and Back Pressure on Sand Liquefaction. J. Geotech. Eng. 1991, 117, 1347–1362. [Google Scholar] [CrossRef]
- Arab, A.; Belkhatir, M.; Sadek, M. Saturation effect on behaviour of sandy soil under monotonic and cyclic loading: A laboratory investigation. Geotech. Geol. Eng. 2016, 34, 347–358. [Google Scholar] [CrossRef]
- Della, N.; Arab, A. Laboratory investigation on the saturation and initial structure effects on the undrained behavior of granular soil under static loading. Acta Polytech. Hung. 2010, 7, 143–160. [Google Scholar]
- He, J.; Chu, J.; Liu, H. Undrained shear strength of desaturated loose sand under monotonic shearing. Soils Found. 2014, 54, 910–916. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, K.; Tsukamoto, Y.; Kamada, K. Undrained behaviour of near-saturated sand in cyclic and monotonic loading. In Cyclic Behaviour of Soils and Liquefaction Phenomena, 1st ed.; Triantafyllidis, T., Ed.; CRC Press: New York, NY, USA, 2004; pp. 27–39. [Google Scholar]
- Kamata, T.; Tsukamoto, Y.; Ishihara, K. Undrained shear strength of partially saturated sand in triaxial tests. Bull. N. Z. Soc. Earthq. Eng. 2009, 42, 57–62. [Google Scholar] [CrossRef]
- Maleki, M.; Bayat, M. Experimental evaluation of mechanical behavior of unsaturated silty sand under constant water content condition. Eng. Geol. 2012, 141–142, 45–56. [Google Scholar] [CrossRef]
- Bian, H.; Shahrour, I. Numerical model for unsaturated sandy soils under cyclic loading: Application to liquefaction. Soil Dyn. Earthq. Eng. 2009, 29, 237–244. [Google Scholar] [CrossRef]
- Kimoto, S.; Ishikawa, R.; Akaki, T. Behavior of unsaturated sandy soil during triaxial compression tests under fully undrained conditions and its modelling. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Korea, 17–22 September 2017; pp. 1187–1190. [Google Scholar]
- Duan, X.; Zeng, L.; Sun, X. Generalized stress framework for unsaturated soil: Demonstration and discussion. Acta Geotech. 2018, 14, 1459–1481. [Google Scholar] [CrossRef]
- Gens, A.; Sánchez, M.; Sheng, D. On constitutive modelling of unsaturated soils. Acta Geotech. 2006, 1, 137–147. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Zhou, C.; Chiu, C.F. Constitutive modelling of state-dependent behaviour of unsaturated soils: An overview. Acta Geotech. 2020, 15, 2705–2725. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Y.; Zhang, X.; Kong, L.; Xu, G. Numerical modelling of gassy sand behaviour under monotonic loading. Acta Geotech. 2021, 1–14. [Google Scholar] [CrossRef]
- Lü, X.; Huang, M.; Andrade, J.E. Modeling the static liquefaction of unsaturated sand containing gas bubbles. Soils Found. 2018, 58, 122–133. [Google Scholar] [CrossRef]
- Yang, G.; Bai, B. A thermodynamic model to simulate the thermomechanical behaviour of fine-grained gassy soil. Bull. Eng. Geol. Environ. 2020, 79, 2325–2339. [Google Scholar] [CrossRef]
- Yang, G.; Bai, B.; Liu, Y.; Chen, P. Constitutive modelling for undrained shear behaviour of gassy sand considering energy dissipation at the mesoscopic scale. Ocean. Eng. 2021, 219, 108307. [Google Scholar]
- Zapata-Medina, D.; Vergara, C.Y.; Vega-Posada, C.A.; Arboleda-Monsalve, L.G. On the use of Fredlund gas–fluid compressibility relationship to model medium-dense gassy sand behavior. Can. Geotech. J. 2019, 56, 1070–1079. [Google Scholar] [CrossRef]
- Mihalache, C.; Buscarnera, G. Controllability Criteria for Soils Saturated by a Compressible Fluid. J. Eng. Mech. 2016, 142, 4016076. [Google Scholar] [CrossRef]
- Shi, Z.; Tong, S.; Huang, M. Evaluation of instability of quasi saturated sand with entrapped gas due to decreasing total confining stress. Eng. Geol. 2021, 293, 106296. [Google Scholar] [CrossRef]
- Zhou, M.-Z.; Jeng, D.-S.; Qi, W.-G. A new model for wave-induced instantaneous liquefaction in a non-cohesive seabed with dynamic permeability. Ocean Eng. 2020, 213, 107597. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Jeng, D.S.; Lee, C.P. Oscillatory soil response and liquefaction in an unsaturated layered seabed. Int. J. Numer. Anal. Methods Géoméch. 1995, 19, 825–849. [Google Scholar] [CrossRef]
- Gallant, A.P.; Finno, R.J. Measurement of Gas Released during Blast Densification. Geotech. Test. J. 2017, 40, 1011–1025. [Google Scholar] [CrossRef]
- Gudehus, G. Mechanisms of partly flooded loose sand deposits. Acta Geotech. 2016, 11, 505–517. [Google Scholar] [CrossRef]
- Kido, R.; Higo, Y.; Takamura, F.; Morishita, R.; Khaddour, G.; Salager, S. Morphological transitions for pore water and pore air during drying and wetting processes in partially saturated sand. Acta Geotech. 2020, 15, 1745–1761. [Google Scholar] [CrossRef]
- Świdziński, W.; Mierczyński, J.; Mikos, A. Response of partially saturated non-cohesive soils. Arch. Hydro-Eng. Environ. Mech. 2017, 64, 187–207. [Google Scholar] [CrossRef] [Green Version]
- Świdziński, W.; Mierczyński, J.; Smyczyński, M. Modelling of the response of partially saturated non-cohesive soil subjected to undrained loading. Arch. Hydro-Eng. Environ. Mech. 2018, 65, 11–29. [Google Scholar] [CrossRef] [Green Version]
- Jefferies, M.; Been, K. Soil Liquefaction: A Critical State Approach, 2nd ed.; CRC Press: New York, NY, USA, 2015. [Google Scholar]
- Been, K.; Jefferies, M.G. A state parameter for sands. Géotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
- Lashkari, A. A simple critical state interface model and its application in prediction of shaft resistance of non-displacement piles in sand. Comput. Geotech. 2017, 88, 95–110. [Google Scholar] [CrossRef]
- Gao, Z.; Zhao, J. Constitutive Modeling of Anisotropic Sand Behavior in Monotonic and Cyclic Loading. J. Eng. Mech. 2015, 141, 4015017. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.B.K.; Rahman, M.; Fourie, A. The critical state behaviour of granular material in triaxial and direct simple shear condition: A DEM approach. Comput. Geotech. 2021, 138, 104325. [Google Scholar] [CrossRef]
- Wood, M. Soil Behaviour and Critical State Soil Mechanics; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Poulos, S.J. The Steady State of Deformation. J. Geotech. Geoenvironmental Eng. 1981, 107, 501–516. [Google Scholar] [CrossRef]
- Woo, S.I.; Salgado, R. Bounding surface modeling of sand with consideration of fabric and its evolution during monotonic shearing. Int. J. Solids Struct. 2015, 63, 277–288. [Google Scholar] [CrossRef]
- Nguyen, H.; Rahman, M.; Fourie, A. How particle shape affects the critical state and instability triggering of granular material: Results from a DEM study. Geotéchnique 2021, 71, 749–764. [Google Scholar] [CrossRef]
- Castro, G.; Poulos, S.J. Factors Affecting Liquefaction and Cyclic Mobility. J. Geotech. Eng. Div. 1977, 103, 501–516. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Moscariello, M.; Cuomo, S.; Salager, S. Capillary collapse of loose pyroclastic unsaturated sands characterized at grain scale. Acta Geotech. 2017, 13, 117–133. [Google Scholar] [CrossRef]
- Yang, H.; Rahardjo, H.; Leong, E.; Fredlund, D.G. Factors affecting drying and wetting soil-water characteristic curves of sandy soils. Can. Geotech. J. 2004, 41, 908–920. [Google Scholar] [CrossRef]
- Finno, R.J.; Zhang, Y.; Buscarnera, G. Experimental Validation of Terzaghi’s Effective Stress Principle for Gassy Sand. J. Geotech. Geoenvironmental Eng. 2017, 143, 4017092. [Google Scholar] [CrossRef]
- Skempton, A.W. The Pore-Pressure Coefficients A and B. Géotechnique 1954, 4, 143–147. [Google Scholar] [CrossRef]
- Smyczyński, M. Reakcje nawodnionych gruntów niespoistych o niepełnym nasyceniu w warunkach bez odpływu wody z porów. Responses of Partially Saturated Non-Cohesive Soils under Undrained Conditions. Ph.D. Thesis, Institute of Hydro-Engineering of Polish Academy of Sciences, Gdańsk, Poland, 2019. (In Polish). [Google Scholar]
- Świdziński, W.; Mierczyński, J. Instability line as a basic characteristic of non-cohesive soils. Arch. Hydro-Eng. Environ. Mech. 2005, 52, 59–85. [Google Scholar]
- Świdziński, W. Instability of Post-Flotation Tailing Ponds due to Static Liquefaction; Internal Report Falling into Commercial Restrictions; Institute of Hydro-Engineering of Polish Academy of Sciences: Gdańsk, Poland, 2011. (In Polish) [Google Scholar]
- Sawicki, A.; Świdziński, W. Stress-Strain Relations for Dry and Saturated Sands. Part I: Incremental Model. J. Theor. Appl. Mech. 2010, 48, 309–328. [Google Scholar]
- Świdziński, W. Teoretyczny opis Reakcji Nawodnionego Piasku Poddanego Ścinaniu w Warunkach Częściowego Nasycenia. Theoretical Description of the Reaction of Sand Exposed on Sheared in Partial Saturation Conditions; Institute of Hydro-Engineering of Polish Academy of Sciences: Gdańsk, Poland, 2015. (In Polish) [Google Scholar]
- Sawicki, A. 3D and 2D formulations of incremental stress-strain relations for granular soils. Arch. Hydro-Eng. Environ. Mech. 2008, 55, 45–53. [Google Scholar]
- Verruijt, A. Elastic storage of aquifers. In Flow through Porous Media; De Wiest, R.J.M., Ed.; Academic Press: New York, NY, USA, 1969; pp. 331–376. [Google Scholar]
- He, J.; Chu, J. Undrained Responses of Microbially Desaturated Sand under Monotonic Loading. J. Geotech. Geoenvironmental Eng. 2014, 140, 4014003. [Google Scholar] [CrossRef]
- Lade, P.V.; Hermamdez, S.B. Membrane Penetration Effects in Undrained Tests. J. Geotech. Eng. Div. 1977, 103, 109–125. [Google Scholar] [CrossRef]
- Yang, J. Liquefaction resistance of sand in relation to P-wave velocity. Géotechnique 2002, 52, 295–298. [Google Scholar] [CrossRef]
- Sławińska-Budzich, J.; Mierczyński, J. Deformations and stability of granular soils: Classical triaxial tests and numerical results from an incremental model. Studia Geotech. Et Mech. 2020, 42, 137–150. [Google Scholar] [CrossRef]

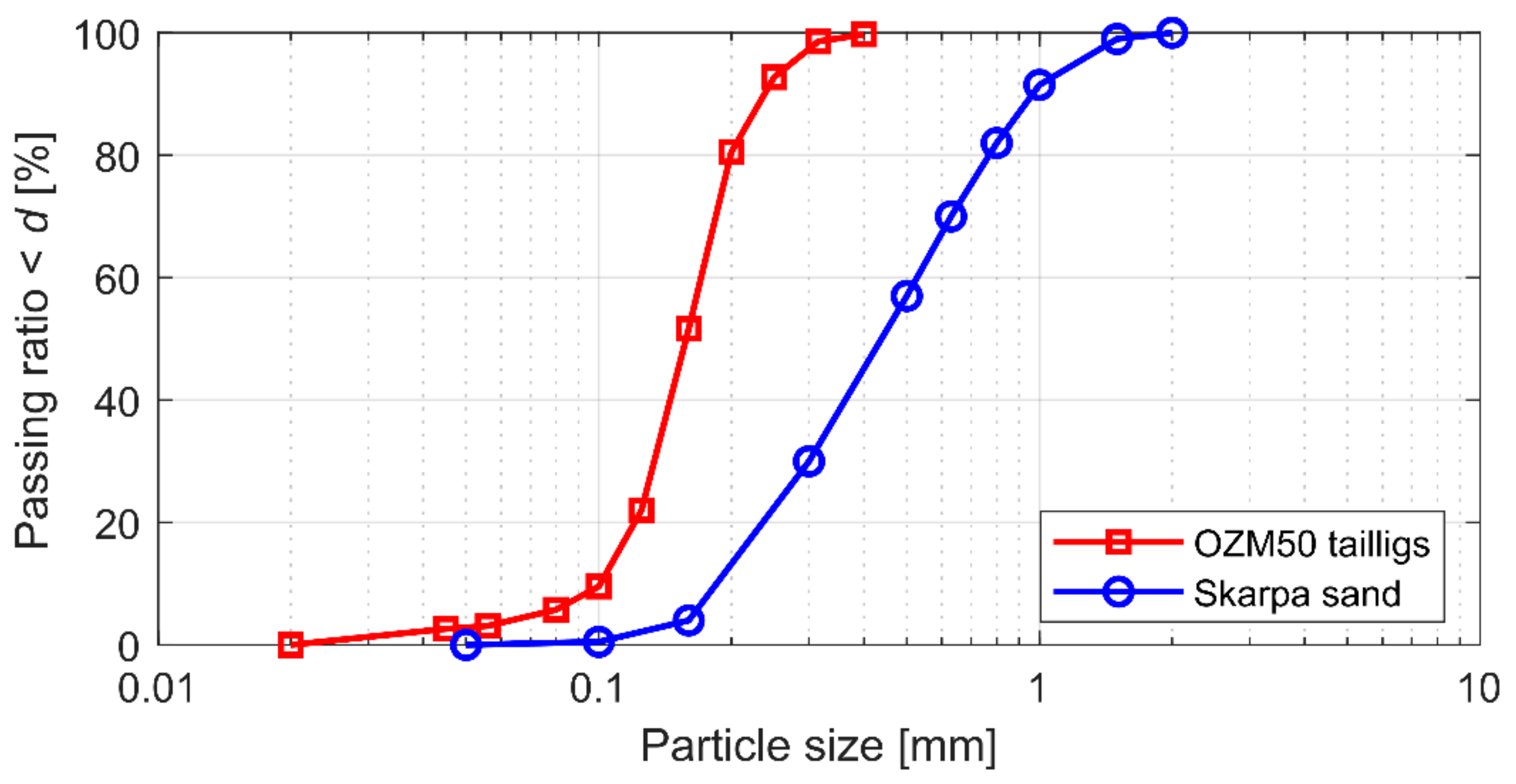
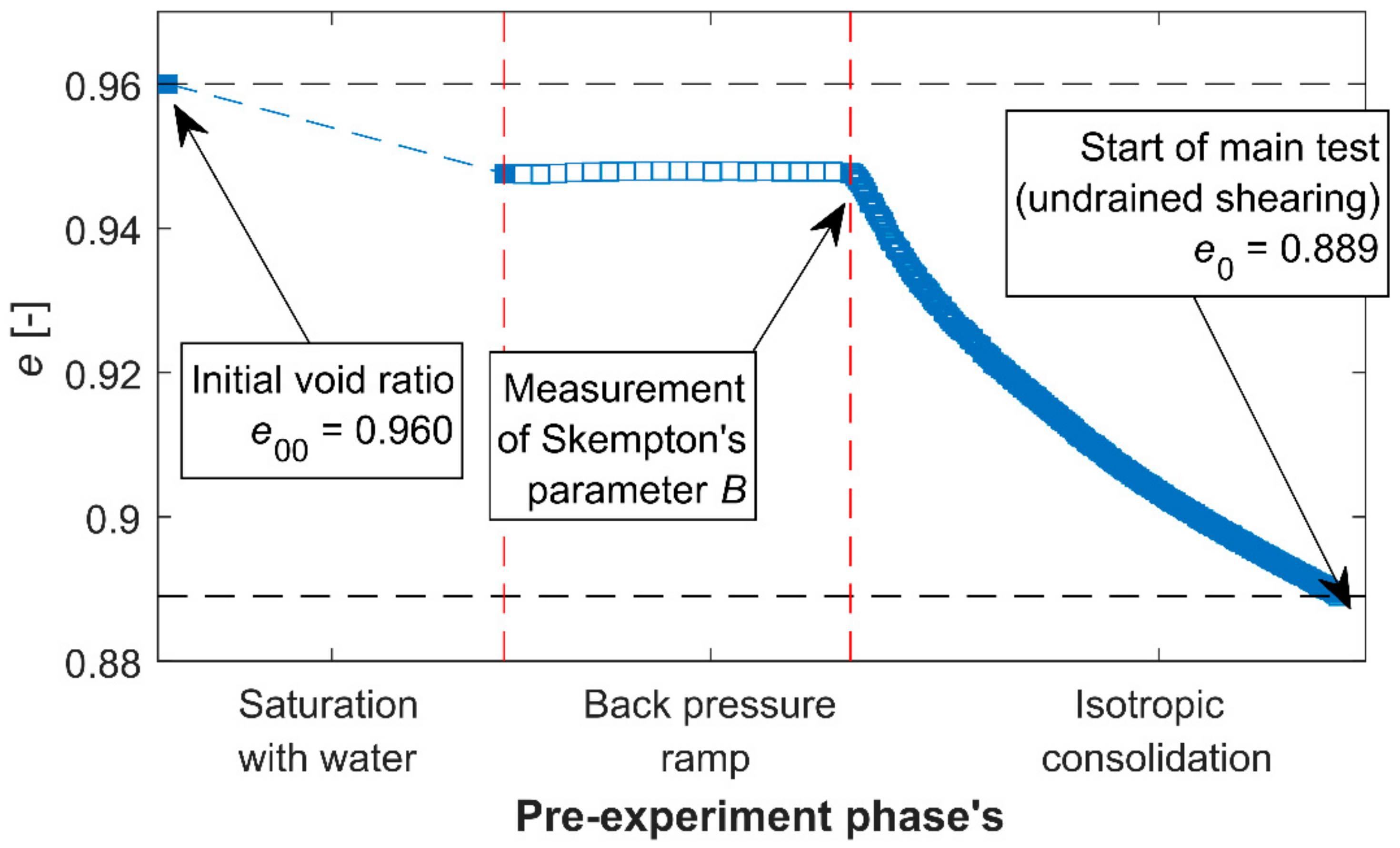
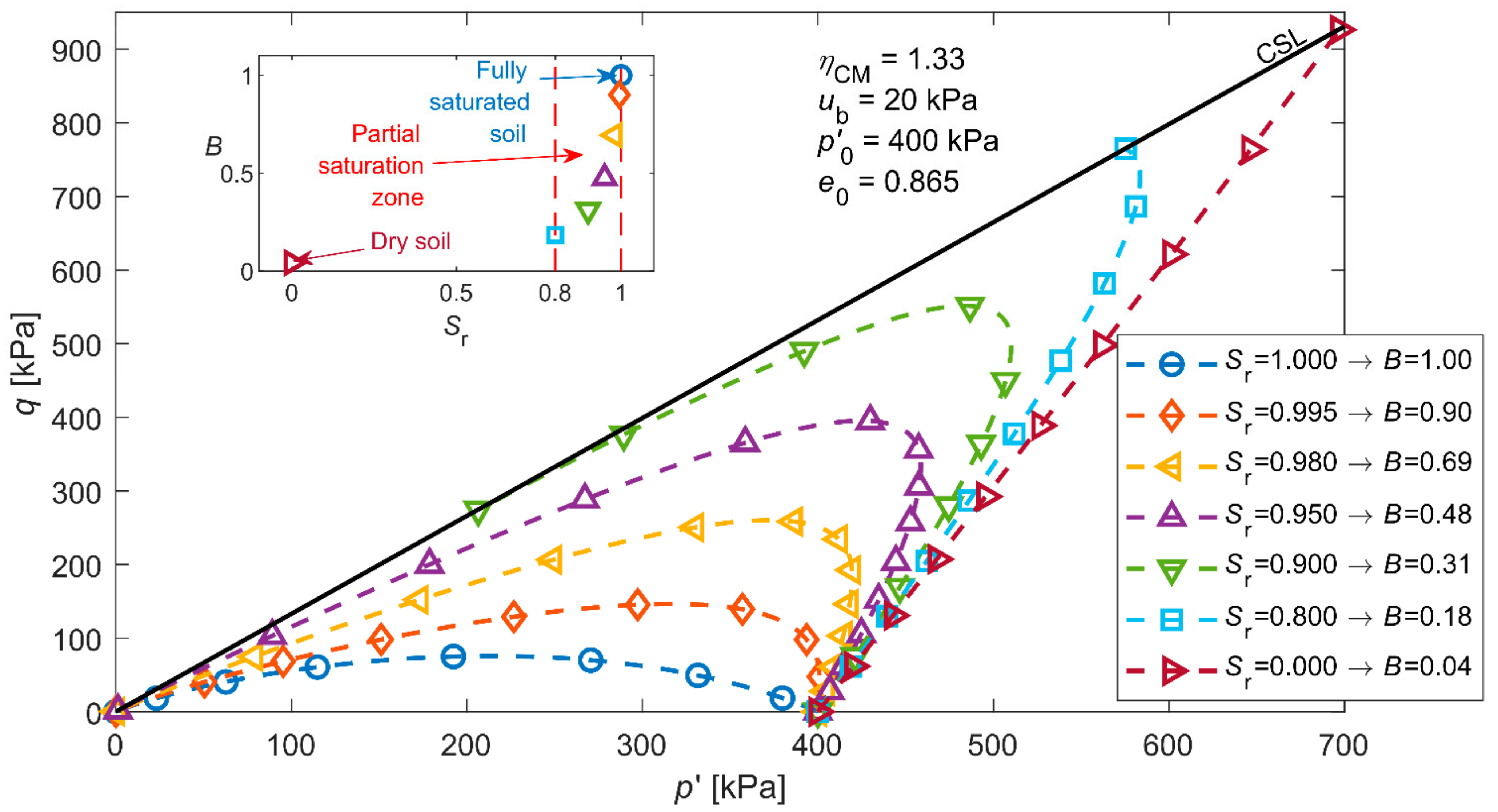
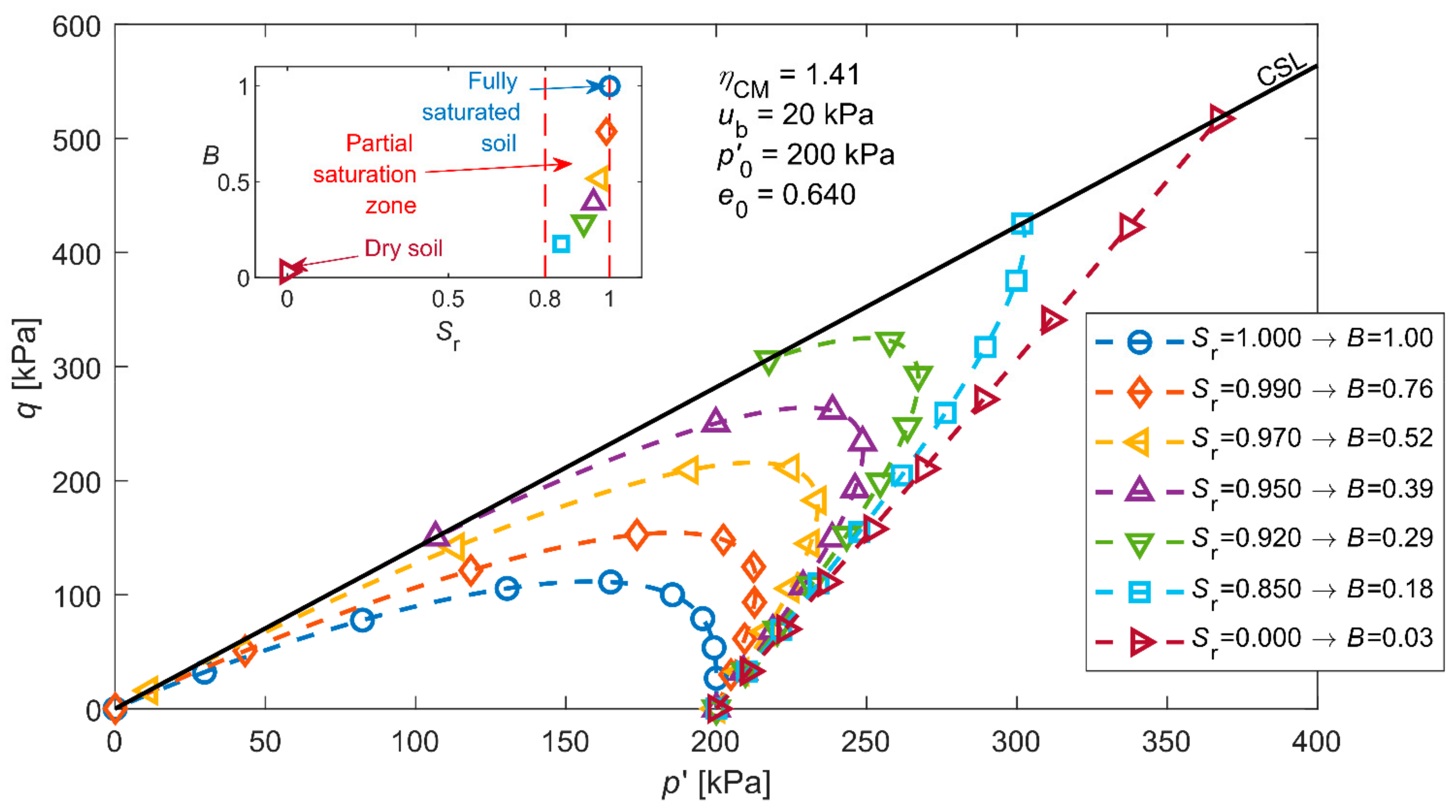

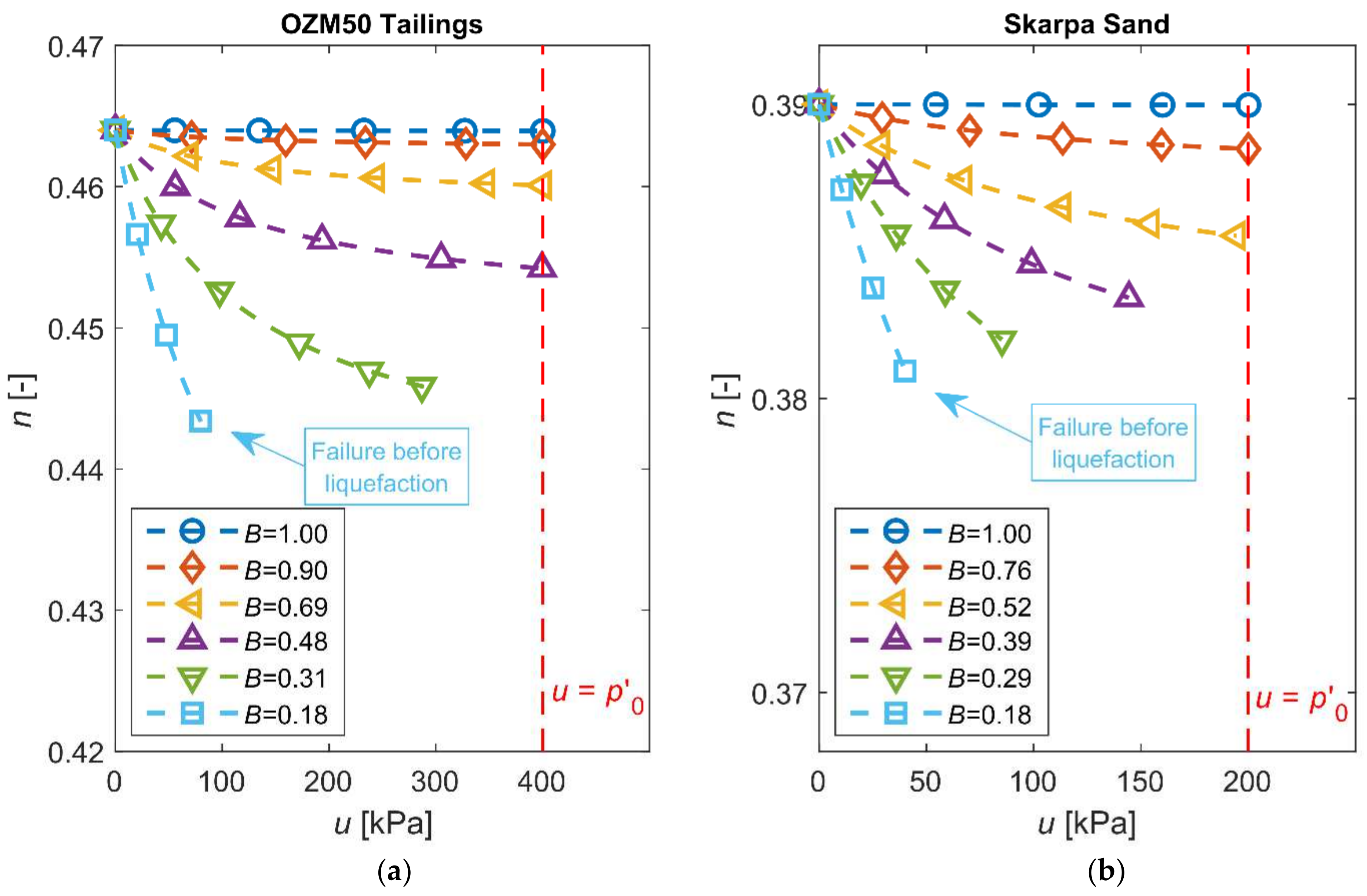
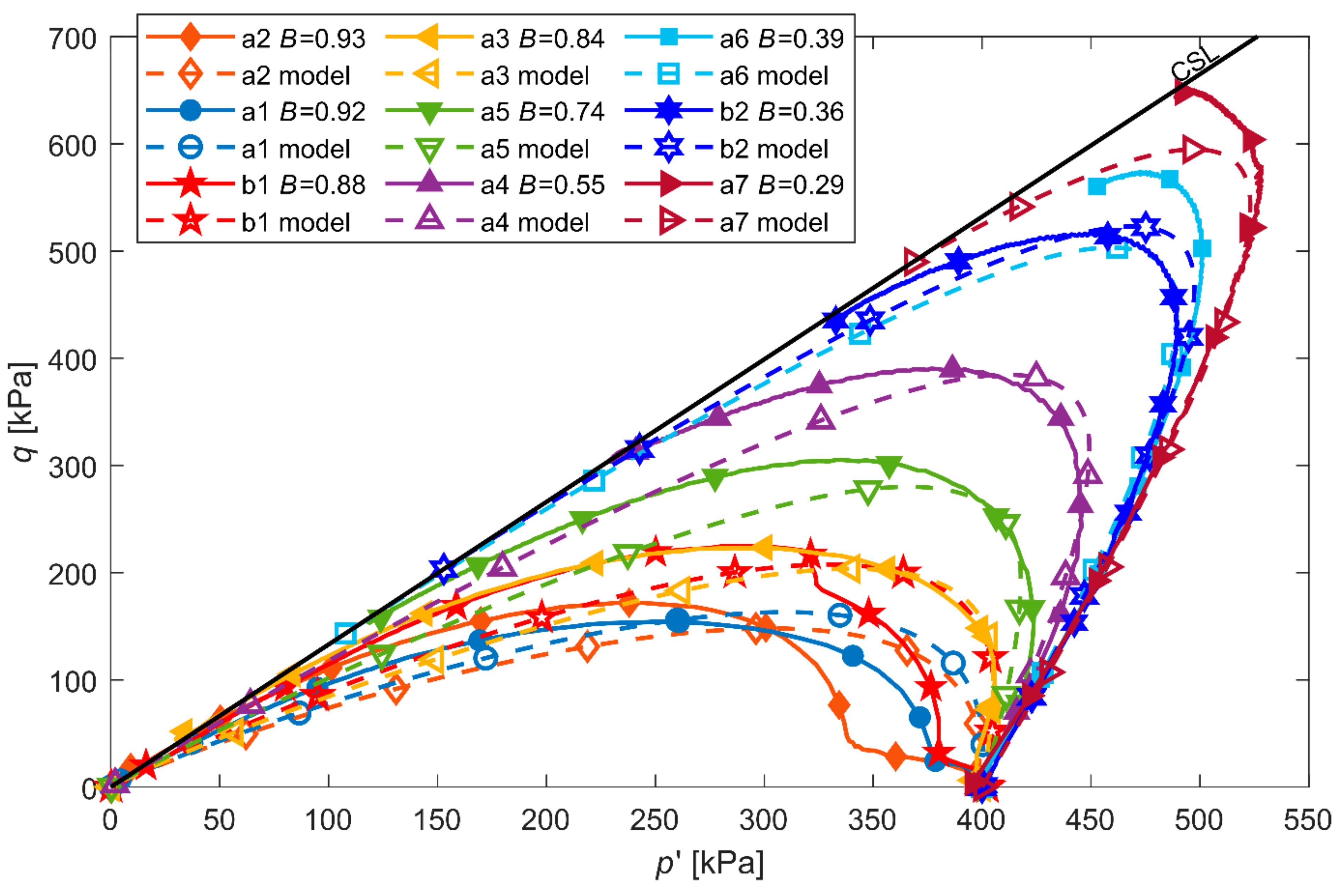
| Soil Type | (g/cm3) | (mm) | (%) | (−) | (−) | (°) |
|---|---|---|---|---|---|---|
| Skarpa | 2.650 | 0.420 | 0.25 | 0.432 | 0.677 | 34.8 |
| OZM50 | 2.675 | 0.157 | 5.8 | 0.643 | 1.026 | 33.0 |
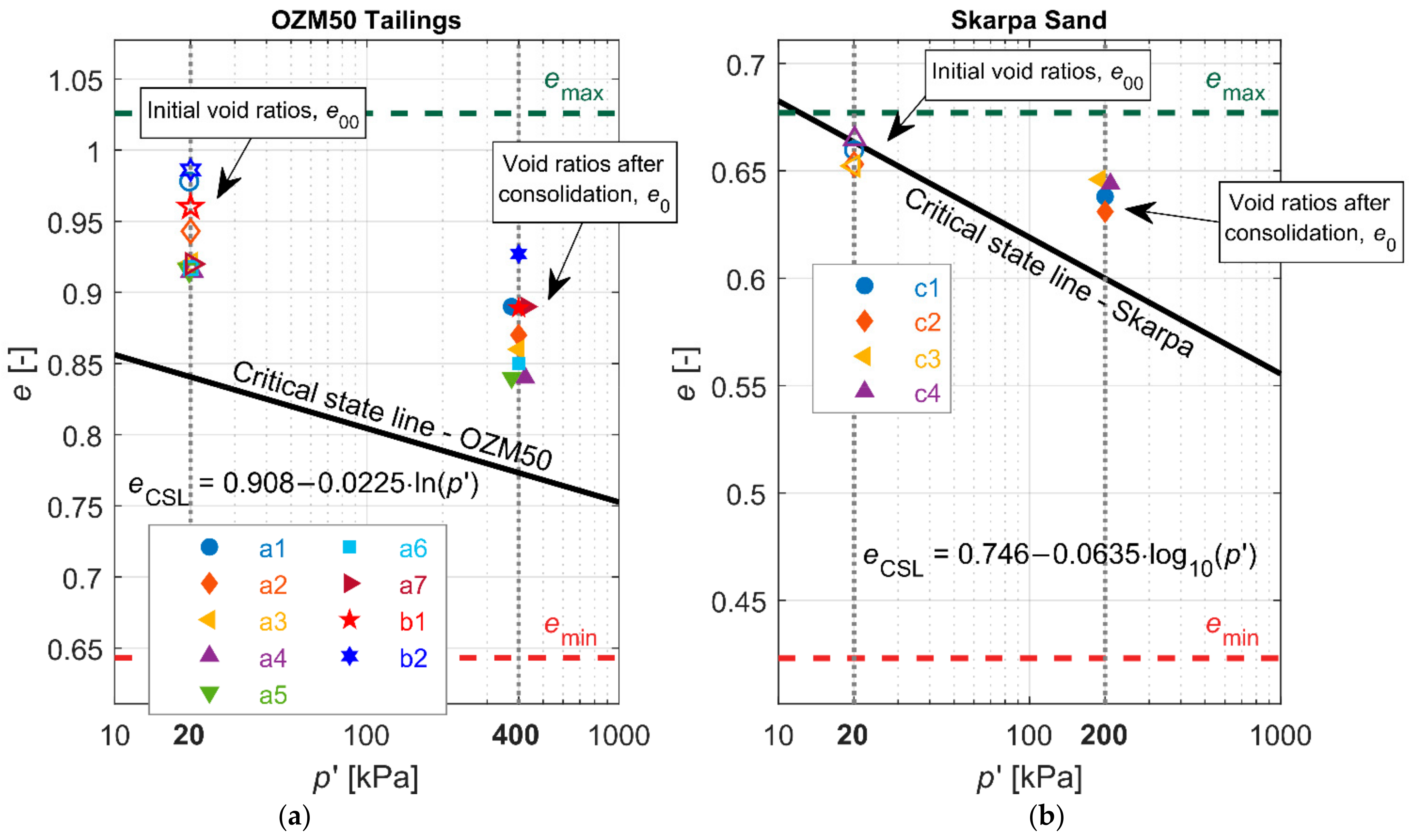
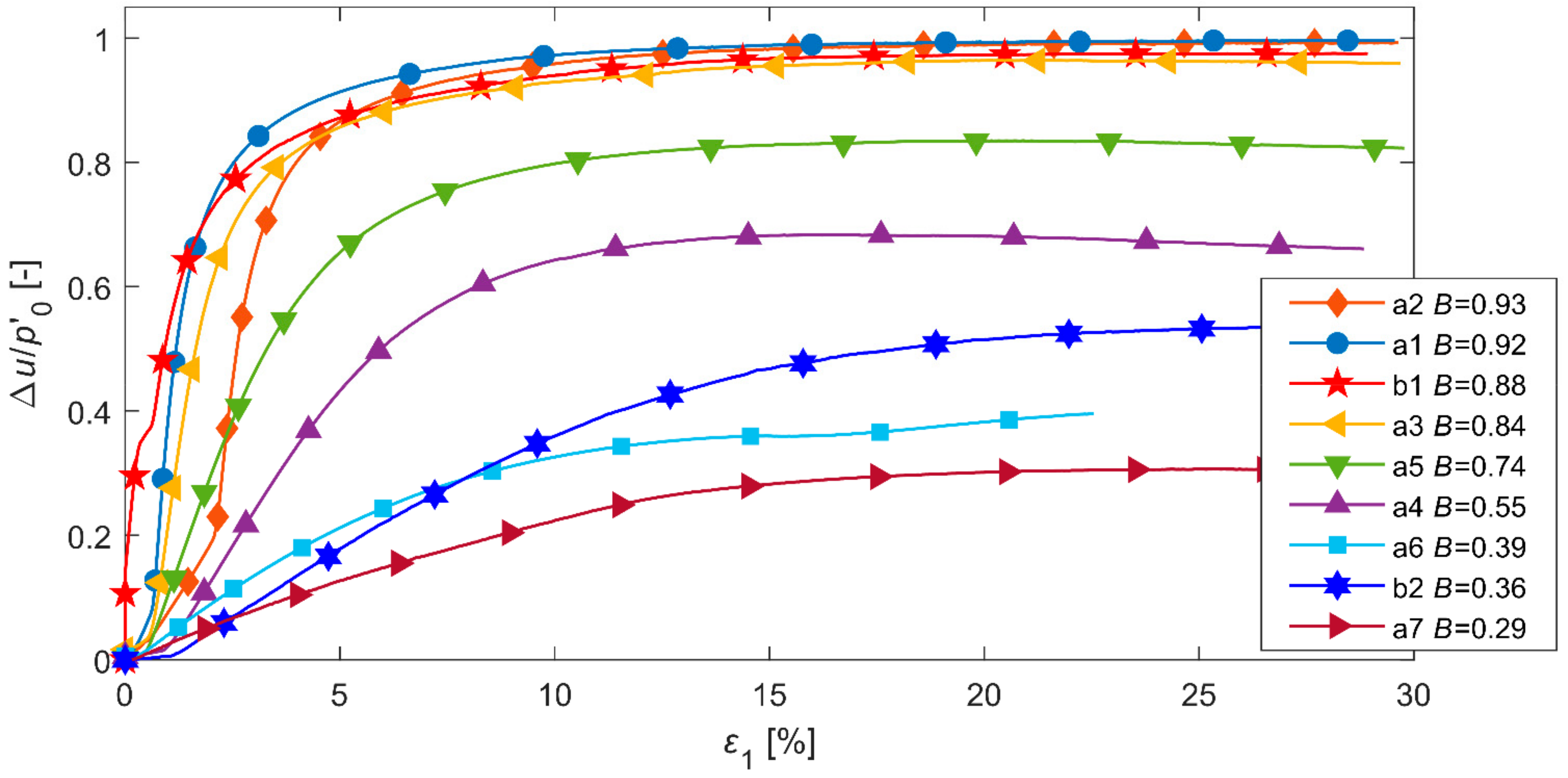
| Sample | B (−) | (kPa) | (kPa) | (−) | (−) | (−) | (−) |
|---|---|---|---|---|---|---|---|
| OZM50 tailings—series A [37] | |||||||
| a1 | 0.92 | 300 | 400 | 0.36 | 0.12 | 0.978 | 0.887 |
| a2 | 0.93 | 200 | 400 | 0.41 | 0.10 | 0.943 | 0.873 |
| a3 | 0.84 | 100 | 400 | 0.43 | 0.09 | 0.920 | 0.864 |
| a4 | 0.55 | 100 | 400 | 0.49 | 0.07 | 0.915 | 0.839 |
| a5 | 0.74 | 180 | 400 | 0.49 | 0.07 | 0.916 | 0.836 |
| a6 | 0.39 | 68 | 400 | 0.46 | 0.08 | 0.917 | 0.846 |
| a7 | 0.29 | 34 | 400 | 0.36 | 0.12 | 0.920 | 0.890 |
| OZM50 tailings—series B | |||||||
| b1 | 0.88 | 499 | 400 | 0.36 | 0.12 | 0.960 | 0.889 |
| b2 | 0.36 | 51 | 400 | 0.26 | 0.15 | 0.986 | 0.927 |
| Skarpa sand—series C | |||||||
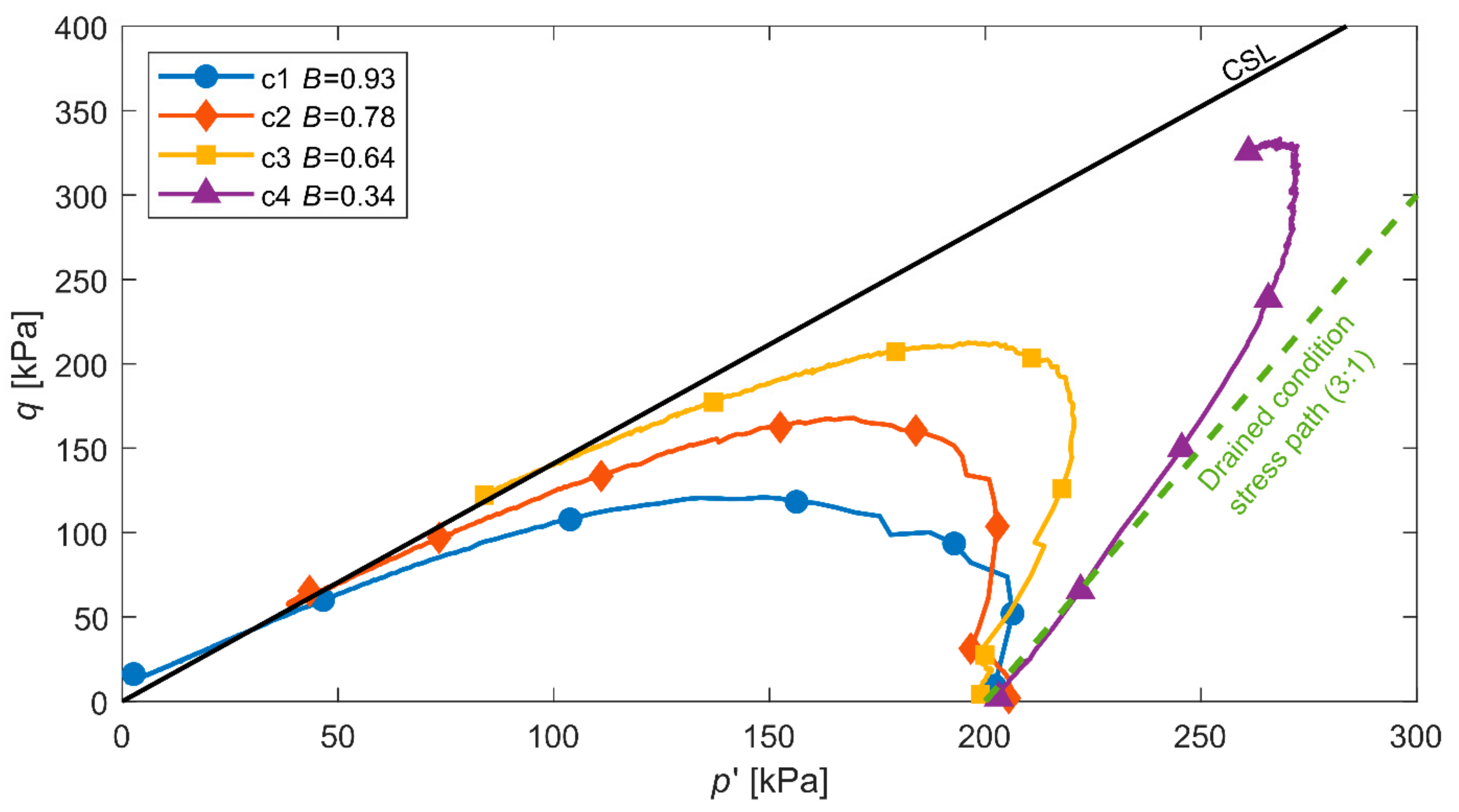
| c1 | 0.93 | 251 | 200 | 0.15 | 0.038 | 0.660 | 0.638 |
| c2 | 0.78 | 396 | 200 | 0.18 | 0.031 | 0.653 | 0.631 |
| c3 | 0.64 | 203 | 200 | 0.12 | 0.046 | 0.652 | 0.646 |
| c4 | 0.34 | 48 | 200 | 0.13 | 0.044 | 0.665 | 0.644 |
| Soil | Isotropic Load | Isotropic Unload | Deviatoric Load |
|---|---|---|---|
| Skarpa sand | |||
| OZM50 tailings | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Świdziński, W.; Smyczyński, M. Modelling of Static Liquefaction of Partially Saturated Non-Cohesive Soils. Appl. Sci. 2022, 12, 2076. https://doi.org/10.3390/app12042076
Świdziński W, Smyczyński M. Modelling of Static Liquefaction of Partially Saturated Non-Cohesive Soils. Applied Sciences. 2022; 12(4):2076. https://doi.org/10.3390/app12042076
Chicago/Turabian StyleŚwidziński, Waldemar, and Marcin Smyczyński. 2022. "Modelling of Static Liquefaction of Partially Saturated Non-Cohesive Soils" Applied Sciences 12, no. 4: 2076. https://doi.org/10.3390/app12042076
APA StyleŚwidziński, W., & Smyczyński, M. (2022). Modelling of Static Liquefaction of Partially Saturated Non-Cohesive Soils. Applied Sciences, 12(4), 2076. https://doi.org/10.3390/app12042076