Structural Assessment under Uncertain Parameters via the Interval Optimization Method Using the Slime Mold Algorithm

Abstract

Damage detection of civil and mechanical structures based on measured modal parameters using model updating schemes has received increasing attention in recent years. In this study, for uncertainty-oriented damage identification, a non-probabilistic structural damage identification (NSDI) technique based on an optimization algorithm and interval mathematics is proposed. In order to take into account the uncertainty quantification, the elastic modulus is described as unknown-but-bounded interval values and the proposed new scheme determines the upper and lower bounds of the damage index. In this method, the interval bounds can provide supports for structural health diagnosis under uncertain conditions by considering the uncertainties in the variables of optimization algorithm. The model updating scheme is subsequently used to predict the interval-bound of the Elemental Stiffness Parameter (ESP). The slime mold algorithm (SMA) is used as the main algorithm for model updating. In addition, in this study, an enhanced variant of SMA (ESMA) is developed, which removes unchanged variables after a defined number of iterations. The method is implemented on three well-known numerical examples in the domain of structural health monitoring under single damage and multi-damage scenarios with different degrees of uncertainty. The results show that the proposed NSDI methodology has reduced computation time, by at least 30%, in comparison with the probabilistic methods. Furthermore, ESMA has the capability to detect damaged elements with higher certainty and lower computation cost in comparison with the original SMA.

1. Introduction

Structural systems in civil and mechanical engineering are subjected to damage and deterioration during their service life. Damage is defined as a weakening of a structure that may result in undesired displacements, stresses, strains, or vibrations, resulting in unexpected and catastrophic consequences. Therefore, early detection of damage can improve safety and extend serviceability of infrastructures [1].

Modal parameters of a structure are usually used to detect structural damages [2,3,4,5,6,7,8,9,10], since modal parameters (modal frequencies and mode shapes) are functions of the physical parameters (mass and stiffness). As a result, the presence of damage causes changes in the structure’s modal characteristics. Modal parameters can also be monitored conveniently and precisely. The experimentally obtained modal parameters are considered accurate and deterministic in conventional applications of model updating for damage detection [11,12,13,14,15,16,17,18]. However, there are always uncertainties in the recorded modal parameters in real applications, which can lead to unreliable and inaccurate structural damage assessments. As a result, uncertainties in structural damage detection must be considered [19,20].

In the domain of damage detection, research addressing uncertainty has been conducted utilizing probability analysis and fuzzy theory [21]. The randomness of the structural finite element (FE) model and the test data were employed by Xia et al. [22]. The probability distribution characteristics of the FE model were determined using the Monte Carlo technique and data perturbation. The structural damage probability was then calculated using the interval estimation approach. Despite extensive studies that have been performed, some problems have been identified by other scholars in the study of uncertain damage identification. One major difficulty is that the existing uncertain damage detection methods based on probability analysis and fuzzy theory typically require a large quantity of sample data to explain the source of uncertainty [23]. However, the probability model is commonly used to follow specific distributions in engineering practice because of insufficient experimental information and limited cost [24].

As a result, the accuracy and reliability of approaches based on probability and fuzzy theory cannot be guaranteed [25]. In interval analysis, uncertain parameters are represented as interval numbers that only require the uncertainty parameters’ boundaries [26]. As a result of its convenience and feasibility, the interval analysis approach is extensively used in damage identification and other domains [27,28]. The interval optimization technique, which combines interval analysis with an intelligent algorithm, is a new way to handle interval problems [29]. Based on an auto-regressive model and interval optimization, Liu and Mao [30] presented a non-probabilistic damage detection approach. To determine interval bounds of uncertain variables, Ghiasi et al. [31] suggested a non-probabilistic Least Square Support Vector Machine (LS-SVM) approach. The results show that the proposed method can successfully identify the structural damage elements. However, the interval optimization method is still immature and suffers from the problem of high computational cost, especially when handling a large-scale structure.

In comparison with probabilistic methods, research on non-probabilistic uncertain damage identification has been relatively limited. Scholars have used various algorithms to raise the calculation precision of interval methods, but interval expansion is still a severe problem [32]. Therefore, in this study, a non-probabilistic structural damage identification (NSDI) approach based on a model updating scheme and interval mathematics is proposed in order to address the aforementioned shortcomings.

Damage estimation strategies using modal data are mainly based on model updating methods. These methods rely on a structure’s parametric model and the optimization of the designated objective functions based on the differences between measured data and model predictions [33,34]. The accuracy of the FE model, the quality of the modal tests, the formulation of the optimization problem, and the capabilities of the optimization algorithm all play a role in the success of the finite element (FE) model updating process. In this paper, a new optimization algorithm is proposed.

Li et al. [35] recently developed SMA, a simple and effective continuous optimization technique for optimization problems. The performance of SMA is improved in this study by deleting unchanging variables after a certain number of iterations. This aspect increases the approach’s adaptability for a larger range of practical applications while retaining the fundamental SMA’s attractive features.

Based on the aforementioned discussion and in order to tackle the shortcomings of non-probabilistic based schemes, the objective of this paper is to investigate the influence of uncertainty on damage identification of civil and mechanical structures. To consider the uncertainties in the measurement data, a novel non-probabilistic approach is introduced. Using this method, Young’s modulus, which acts as an elemental stiffness parameter (ESP), is defined as a variable of the SMA algorithm. Moreover, damage indexes are defined by utilizing the natural frequencies and mode shapes of the structure. Furthermore, measurement noise of the structural responses is assumed to be coupled rather than statistically distributed using the interval analysis approach [21]. It is worth noting that, in previous work of the authors [31], LS-SVM acts as a non-probabilistic surrogate model for damage detection of structures, whereas the exact FE model is implemented in this work. Furthermore, ESMA acts as a metaheuristic search algorithm and is used as the main algorithm of the model updating process.

A 31-bar planar truss, a 120-bar dome truss, and a four-story building of Phase II of the IASC-ASCE SHM benchmark are used to demonstrate the robustness of the developed procedure. The impact of various noise levels and damage severity levels on the damage detection results are also investigated using parametric computations. The study’s main contribution is to provide an effective strategy for implementing a damage detection procedure that takes uncertainty into account, based on the interval optimization method and ESMA.

The article is structured as follows. Section 2 presents the process of damage detection using a correlation index. Interval analysis method is described in Section 3. The fundamental basis of SMA and proposed enhanced version are described in Section 4 and Section 5. Section 6 presents the main steps for the proposed damage detection method. In Section 7, the merits of the algorithms are assessed by solving NSDI problems. Some concluding remarks are provided in Section 8.

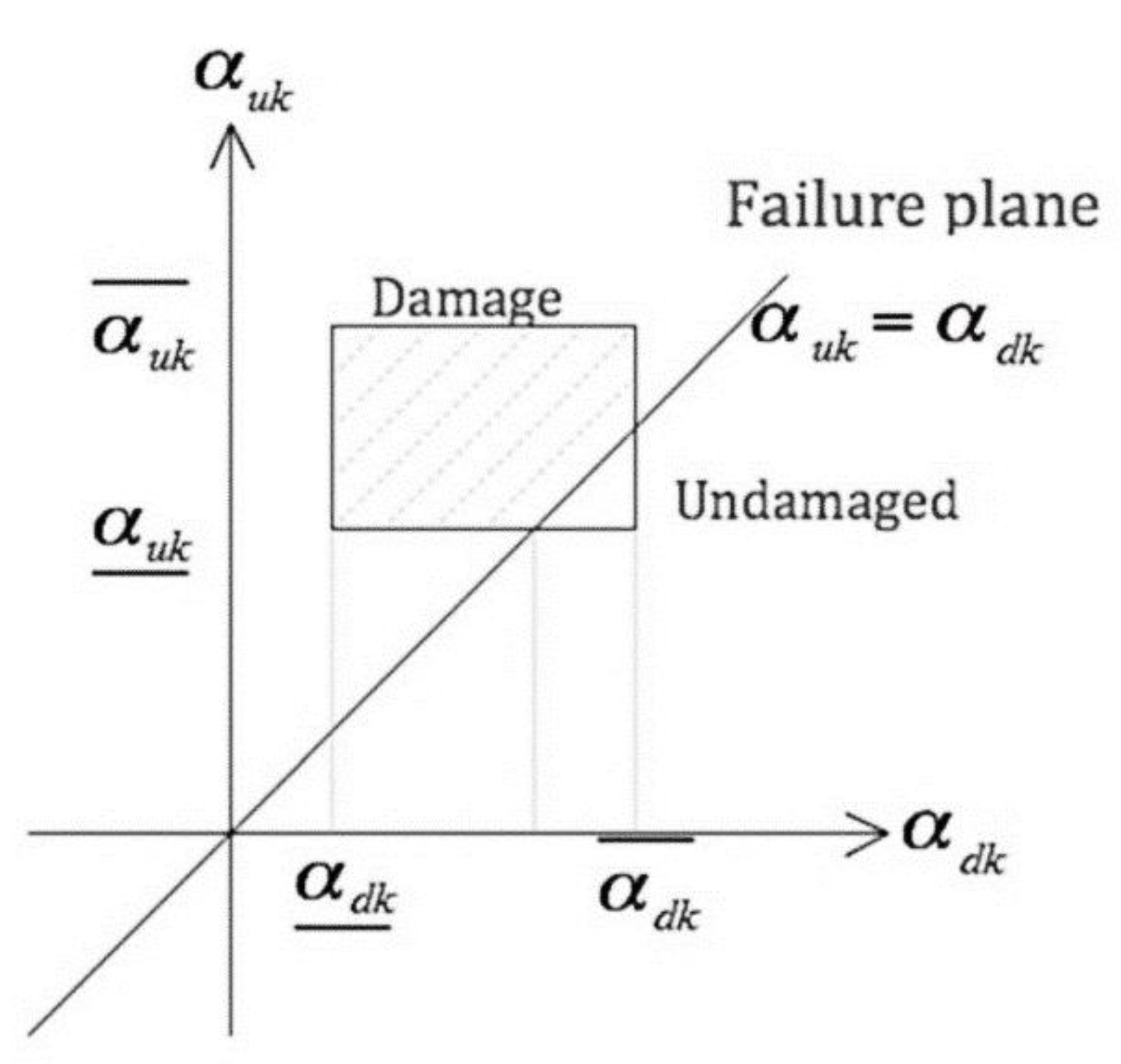
2. Multiple Damage Location Assurance Criterion (MDLAC)

Structural damage detection (SDD) techniques are generally classified into two main categories. They are the dynamic and static identification techniques, which, respectively, need dynamic and static test data. Furthermore, compared with static identification approaches, dynamic identification methods have proven to be superior [36]. Among the dynamic data, the modal analysis information of a structure such as the natural frequencies and mode shapes have been widely used for SDD [36,37]. The level of correlation between measured and estimated natural frequencies and/or mode shapes can be used to locate and evaluate structural damage. When the natural frequencies are employed to identify the damage, two parameter vectors are defined. One parameter vector consists of the ratios of the first $n_f$ natural frequency changes $\Delta F$ due to structural damage, i.e.:

$$\Delta F=\frac{F_h-F_d}{F_h},$$

(1)

where $F_h$ and $F_d$ denote the natural frequency vectors of the healthy and damaged structure, respectively. Another parameter vector can be defined similarly as:

$$\delta F\left(ESP\right)=\frac{F_h-F\left(ESP\right)}{F_h},$$

(2)

where $F\left(ESP\right)$ is a natural frequency vector that can be predicted from an analytic model and elemental stiffness parameters (ESPs) $ESP={\left[E_1,\dots ,E_i,\dots ,E_n\right]}^T$, which represents a damage variable vector containing the elasticity modulus of structural elements $\left(E_i,i=1,\dots ,n\right)$ of all $n$ structural elements.

There are numerous approaches to evaluate the level of correlation given a pair of parameter vectors. The multiple damage location assurance criterion (MDLAC), which is presented in the following form, is an effective technique to analyze a correlation index [38]:

$$MDLAC{\left(ESP\right)}_F=\frac{{\left|\Delta F^T\delta F\left(ESP\right)\right|}^2}{\left(\Delta F^T\Delta F\right)\left(\delta F^T\left(ESP\right)\delta F\left(ESP\right)\right)},$$

(3)

The MDLAC analyzes two frequency change vectors, one from the inspected structure and the other from the analytical model. The MDLAC ranges from 0 to 1. It will be at its maximum when the analytical frequency vector equals the frequency vector of the damaged structure, i.e.:

$$F\left(ESP\right)=F_d,$$

(4)

In addition to using the natural frequencies to identify structural damage, the mode shape vectors have been used in several studies. [39,40]. In this case, the correlation coefficient of Equation (3) can be expressed as:

$$MDLAC{\left(ESP\right)}_{\phi }=\frac{{\left|\Delta {\phi }^T\delta \phi \left(ESP\right)\right|}^2}{\left(\Delta {\phi }^T\Delta \phi \right)\left(\delta {\phi }^T\left(ESP\right)\delta \phi \left(ESP\right)\right)},$$

(5)

where $\Delta \phi$ is the vector of the measured mode shape changes that have a dimension equal to the product of the number of measured modes and sensor locations; and $\delta \phi$ is the vector of the analytical mode shape changes with the same dimension as $\Delta \phi$. In this paper, an objective function is defined based on a combination of $MDLAC{\left(ESP\right)}_{\phi }$ and $MDLAC{\left(ESP\right)}_F$.

3. Interval Analysis Method for Consideration of Uncertainties

The updated ESP is prone to uncertainty since uncertainties (noises) in the obtained vibration data are unavoidable. The uncertainties in the measured modal data are considered to be independent, normally distributed random variables with zero means and a particular covariance, as indicated in [19]. As a result, the eigenvalues and mode shapes may be written in the following [19]:

$${\lambda }_i^E={\lambda }_{i,0}^E\left(1+X_{\lambda i}\right), i=1,2,\dots ,n_m,$$

(6)

$${\varphi }_i^E={\varphi }_{i,0}^E\left(1+X_{\varphi i}\right), i=1,2,\dots ,n_m,$$

(7)

where the subscript $0$ represents the true values, $X_{\lambda i}$ and $X_{\varphi i}$ indicate relative random noises in the measured frequencies and mode shapes, respectively. The mean value of vector $X$ is zero and the standard deviation indicates the noise level.

The interval bounds can provide supports for structural health monitoring under uncertain conditions [41]. To account for epistemic and aleatory uncertainties, the main concept of interval mathematics is implemented by providing the upper and lower boundaries of input parameters to generate the upper and lower boundaries of the output parameters. The stiffness reduction factor (SRF) represents the changes in the stiffness parameter for each element of the structure, as given in:

$$SRF=1-\frac{{\alpha }_d}{{\alpha }_u},$$

(8)

where ${\alpha }_d$ is ESP value of the damaged state and ${\alpha }_u$ is ESP value of the undamaged state. The intervals of the ESPs, including the natural frequencies and mode shapes, for the undamaged and damaged state, can be formulated as follows [42]:

$$\left[\underset{¯}{\alpha }\right]\approx \left[\underset{¯}{\lambda };\underset{¯}{\varphi }\right]=\mathrm{ESP} \mathrm{value} \mathrm{lower} \mathrm{bound},$$

(9)

$$\left[\overline{\alpha }\right]\approx \left[\overline{\lambda };\overline{\varphi }\right]=\mathrm{ESP} \mathrm{value} \mathrm{upper} \mathrm{bound},$$

(10)

Therefore, the interval bounds for each parameter can be derived as:

$${\lambda }_c^I=\left[\underset{¯}{{\lambda }_c^I},\overline{{\lambda }_c^I}\right]={\left\{{\lambda }_{c1}^I,{\lambda }_{c2}^I,\cdots ,{\lambda }_{ci}^I\right\}}^T,{\lambda }_{ci}^I=\left[\underset{¯}{{\lambda }_{ci}^I},\overline{{\lambda }_{ci}^I}\right],$$

(11)

$${\varphi }_c^I=\left[\underset{¯}{{\varphi }_c^I},\overline{{\varphi }_c^I}\right]={\left\{{({\varphi }_{c1}^I)}^T,{({\varphi }_{c2}^I)}^T,\cdots ,{({\varphi }_{cj}^I)}^T\right\}}^T,{\varphi }_{cij}^I=\left[\underset{¯}{{\varphi }_{cij}^I},\overline{{\varphi }_{cij}^I}\right],$$

(12)

$${\alpha }_c^I=\left[\underset{¯}{{\alpha }_c^I},\overline{{\alpha }_c^I}\right]={\left\{{\alpha }_{c1}^I,{\alpha }_{c2}^I,\cdots ,{\alpha }_{ck}^I\right\}}^T,{\alpha }_{ck}^I=\left[\underset{¯}{{\alpha }_{ck}^I},\overline{{\alpha }_{ck}^I}\right]$$

(13)

where the subscript $c$ is the index of damage cases, the subscripts $i, j$ and $k$ are the number of modes, the number of structural nodes, and the number of segments of structures, respectively. The middle values of the parameters are denoted as:

$$x^c=m\left(x\right)=\frac{\left(\underset{¯}{x}+\overline{x}\right)}{2},$$

(14)

where $x$ denotes the exact values of the modal parameters (frequencies and mode shapes) and the output parameters (ESPs). The upper and lower bars, respectively, represent the upper and lower boundaries of $x$.

The uncertainties are coupled with the natural frequencies ($\lambda$) and mode shapes ($\varphi$) in terms of the interval bounds. The ESPs are used as variables of the optimization algorithm, and natural frequencies and mode shapes are used as in MDLAC as damage indexes. Thus, two ESMA models, which include the lower bound and upper bound analyses, are provided. The expressions are summarized in

Table 1. Model input and output variables.

Model	Model Input	Output
ESMA 1 (Lower Bounds)	$\underset{¯}{{\lambda }_{ci}}={\lambda }_{ci}-{\lambda }_{ci}\left({\omega }_{\lambda }\right)$	$\underset{¯}{{\alpha }_{ck}}$
	$\underset{¯}{{\varphi }_{cij}}={\varphi }_{cij}-{\varphi }_{cij}\left({\omega }_{\varphi }\right)$
ESMA 2 (Upper Bounds)	$\overline{{\lambda }_{ci}}={\lambda }_{ci}+{\lambda }_{ci}\left({\omega }_{\lambda }\right)$	$\overline{{\alpha }_{ck}}$
	$\overline{{\varphi }_{cij}}={\varphi }_{cij}+{\varphi }_{cij}\left({\omega }_{\varphi }\right)$

.

The variable $\omega$ represents the modal data’s level of uncertainty, with varying values for natural frequencies and mode shapes. The + and − values of the uncertainty in two separate ESMA models—ESMA 1 and ESMA 2—are used to apply the boundaries (lower and upper bounds) of the input parameters of MDLAC. $\underset{¯}{\alpha }$ and $\overline{\alpha }$ are the values of the variables of the optimization algorithm after its execution and represent the lower and upper bounds of the predicted ESPs of damage case c.

After determining the lower and upper bounds of the ESPs, the possibility of damage existence (PoDE) is computed, and the damage severity is determined using the damage measure index (DMI).

$${\alpha }_u^I={\left\{{\alpha }_{u1}^I,{\alpha }_{u2}^I,\dots ,{\alpha }_{uk}^I\right\}}^T,$$

(15)

$${\alpha }_d^I={\left\{{\alpha }_{d1}^I,{\alpha }_{d2}^I,\dots ,{\alpha }_{dk}^I\right\}}^T,$$

(16)

where ${\alpha }_u^I$ shows the interval bound for the undamaged ESP $\left(\left[\overline{{\alpha }_{uk}},\underset{¯}{{\alpha }_{uk}}\right]\right)$ and ${\alpha }_d^I$ shows the interval bound for the damaged ESP $\left(\left[\overline{{\alpha }_{dk}},\underset{¯}{{\alpha }_{dk}}\right]\right)$. A detailed explanation of these indexes is presented in the next section.

The intersection of the intervals of the damaged and undamaged ESPs on the same axis is depicted in Figure 1, with the shaded region indicating the PoDE. The PoDE ranges from 0 to 100%, with 100% indicating a relatively high possibility of damage to that particular element and 0% indicating no damage.

Figure 2 depicts the regions of damaged and undamaged ESP on two different axes. A single rectangle depicts the probable damage region, with the failure plane for both states being equal. The shaded region reflects the ESP damage. Since the ESP damage is greater than that of the undamaged ESP, the PoDE is defined as the ratio of the area of damage region to the total area of the entire region. As a result, the quantitative measurement of the PoDE can be described as below [43]:

$$PoDE=\frac{A_{damage}}{A_{total}}\times 100\%,$$

(17)

The interval value of damaged and undamaged ESP will have large variances in reality. As a result, relying just on PoDE will not give an accurate estimation of the damage. As a result, the damage measure index (DMI) is developed [26]:

$$DMI=SRF\times PoDE$$

(18)

4. Brief Description of the Slime Mold Algorithm

Chen et al. [35] presented the slime mold algorithm (SMA) based on the oscillation mode of slime mold in nature. The suggested SMA contains a number of unique features, including a mathematical model that uses adaptive weights to simulate the process of producing positive and negative feedback in slime mold propagation waves. These characteristics are based on a bio-oscillator, which creates the best path for connecting food with high exploring ability and exploitation tendency. For complete details, please refer to the paper published by [35]. An overview of the slime mold algorithm is provided below.

4.1. Approach Food

The following rule is given to represent the approaching behavior of slime mold as a mathematical equation to replicate the contraction mode:

$$\overrightarrow{X\left(t+1\right)}=\left\{\begin{array}{c}\overrightarrow{X_b\left(t\right)}+\overrightarrow{vb}·\left(\overrightarrow{W}·\overrightarrow{X_A\left(t\right)}-\overrightarrow{X_B\left(t\right)}\right), r<p\\ \overrightarrow{vc}·\overrightarrow{X\left(t\right)}, r\ge p\end{array}\right.$$

(19)

where $\overrightarrow{W}$ is the weight of slime mold,$\overrightarrow{ vb}$ is a parameter with a range of $\left[-a,a\right]$, $\overrightarrow{vc}$ decreases linearly from one to zero. $t$ represents the current iteration, $\overrightarrow{X_b}$ represents the individual location with the highest odor concentration currently found, $\overrightarrow{X}$ represents the location of slime mold, $\overrightarrow{X_A}$ and $\overrightarrow{X_B}$ represent two individuals randomly selected from the swarm, $\overrightarrow{W}$ represents the weight of slime mold. The formula of $p$ is as follows:

$$p=\tanh \left|S\left(i\right)-DF\right|$$

(20)

where $i\in 1,2,\dots ,n$, $S\left(i\right)$ represents the fitness of $\overrightarrow{X}$. The best fitness acquired in all iterations is denoted by the $DF$. The $\overrightarrow{vb}$ formula is as follows:

$$\overrightarrow{vb}=\left[-a,a\right],$$

(21)

$$a=\mathrm{arctanh}\left(-\left(\frac{t}{\max \_t}\right)+1\right),$$

(22)

The formula of $\overrightarrow{W}$ is organized as follows:

$$\overrightarrow{W\left(SmellIndex\left(i\right)\right)}=\left\{\begin{array}{l}1+r·\log \left(\frac{bF-S\left(i\right)}{bF-wF}+1\right),condition \\ 1-r·\log \left(\frac{bF-S\left(i\right)}{bF-wF}+1\right), others\end{array}\right.$$

(23)

$$SmellIndex=sort\left(S\right),$$

(24)

where $condition$ represents that $S\left(i\right)$ ranks first half of the population, $r$ denotes the random value in the interval of $\left[0,1\right]$, $bF$ and $wF$ denotes the optimal and worst fitness obtained in the current iterative process, respectively. $SmellIndex$ represents the sequence of fitness values sorted (ascends in the minimum value problem).

4.2. Wrap Food

The following describes the updating position of slime mold:

$$\overrightarrow{X^{*}}=\left\{\begin{array}{c}rand·\left(UB-LB\right)+LB,rand<z\\ \overrightarrow{X_b\left(t\right)}+\overrightarrow{vb}·\left(W·\overrightarrow{X_A\left(t\right)}-\overrightarrow{X_B\left(t\right)}\right),r<p\\ \overrightarrow{vc}·\overrightarrow{X\left(t\right)}, r\ge p\end{array}\right.$$

(25)

where $LB$ and $UB$ represents the lower and upper boundaries of the searching range, $rand$ and $r$ denote the random value in [0, 1].

4.3. Grabble Food

As the number of iterations increases, the value of $\overrightarrow{vb}$ oscillates randomly between $\left[-a,a\right]$ and gradually approaches zero. The value of $\overrightarrow{vc}$ oscillates between $\left[-1,1\right]$ and eventually tends to zero.

The logic of SMA is shown in Figure 3 and its pseudo-code is presented in Algorithm 1.

Algorithm 1. Pseudo-code of SMA.

Initialize the parameters popsize, $Max\_iteraition$; Initialize the positions of slime mould $X_i\left(i=1,2,\dots ,n\right)$; While ($t\le Max\_iteraition)$      Calculate the fitness of all slime mould; $Update bestFitness, X_b$      Calculate the W by Equation (23);      For $each search portion$      $Update p,vb, vc$;      $Update positions by Equation \left(25\right)$;      End For      $t=t+1$; End While      Return $bestFitness, X_b$;

5. Enhanced Slime Mold Algorithm

This paper proposes an enhanced version of SMA to improve its capability to handle problems with a large array of variables. For structural damage evaluation, there may be a large number of variables to consider. Damaged elements and damage extents are evaluated by an optimization procedure in an optimization-based SDD problem, such that the response of a hypothesized damaged structure equals that of an actual damaged structure. The number of elements (variables) in a real structure increases when a large-scale structure such as bridge or space structure is considered. [44]. As a result, when the optimization technique seeks to minimize the objective function, it must be able to handle a large number of variables, which may slow down the convergence speed of the algorithm. To resolve this issue, this study presents a strategy as presented in the following.

When the initial population is generated, each slime mold has a location vector that reflects its position in an n-dimensional space. The elasticity modulus of the structural components is represented by each variable in this vector. The number of variables in initial stage of the SMA algorithm is considered as the total number of elements. Then, the algorithm will converge to the exact locations and severity of damages by eliminating all intact elements at each stage. A non-zero value for a variable indicates that the $i-\mathrm{th}$ element of the structure is damaged, whereas a zero value indicates that the $i-\mathrm{th}$ element of the structure is intact. If the variables with near zero values ($SR{F}_i\le 0.05$) remain the same for 10 iterations, it can be concluded that these variables belong to the intact elements set and therefore these near-zero variables will be eliminated in the next iteration of the SMA.

The objective function is defined as an unconstrained optimization problem, as follows:

$$\left\{\begin{array}{c}Find:ES{P}_i=\left\{E_1,E_2,E_3,\dots .,E_n\right\} \\ Minimize:F\left(ESP\right)=\Vert 1-MDLAC{\Vert }^2 \\ Where E_{min}\le E\le E_{max} \end{array}\right.$$

(26)

$F\left(ESP\right)$ is the minimization problem, whereas $E_{min}$ and $E_{max}$ are the damage vector’s lower and upper limits, respectively. The structure’s physical behavior necessitates the use of boundaries. The damage variables are estimated using an optimization approach and by solving Equation (26).

6. Main Steps of the Proposed NSDI Method

The following are the main steps in the suggested NSDI approach utilizing the ESMA algorithm:

(a)

Create two parallel ESMA model based on Table 1 and set the initial number of variables equal to the total number of elements in structure.

(b)

Employ the ESMA to determine the optimal solution.

(c)

Determine the total number of intact elements using finding $i$ as $X_i\cong 0$ for all components of the damage vector.

(d)

Reduce the number of variables from the optimization problem by removing the intact elements from the damage vector.

(e)

Run ESMA again, this time using the revised optimization size from d.

(e)

Check the convergence by computing $1-MDLAC$ based on Equation (26). If the two response vectors are almost identical, save the results and end the optimization process; otherwise, go to the step c.

(g)

Based on determined damage variables, calculate PoDE and DMI based on Equations (17) and (18).

7. Numerical Results of NSDI

Three structures are used as numerical examples in this work to illustrate the robustness and accuracy of the proposed NSDI approach. These structures are:

• 31-bar planer truss,
• 120-bar dome truss, and
• four-story steel structure model.

Damage to the structure is modeled as a relative reduction in the elasticity modulus of each individual element, with the mass matrix assumed to remain constant. For the optimization process, the number of slime molds for ESMA was fixed to 20 for each run along a maximum of 100 iterations. The fit-test design in the current iteration is compared to that of 20 prior iterations as a measure of convergence for engineering optimization problems. As a result, if the difference between these two results is smaller than a certain tolerance value, it is recorded as converged. The desired value for this example is set as ${10}^{-3}$. If the converge does not occur, the algorithm will be terminated by implementing a fixed maximum number of iterations.

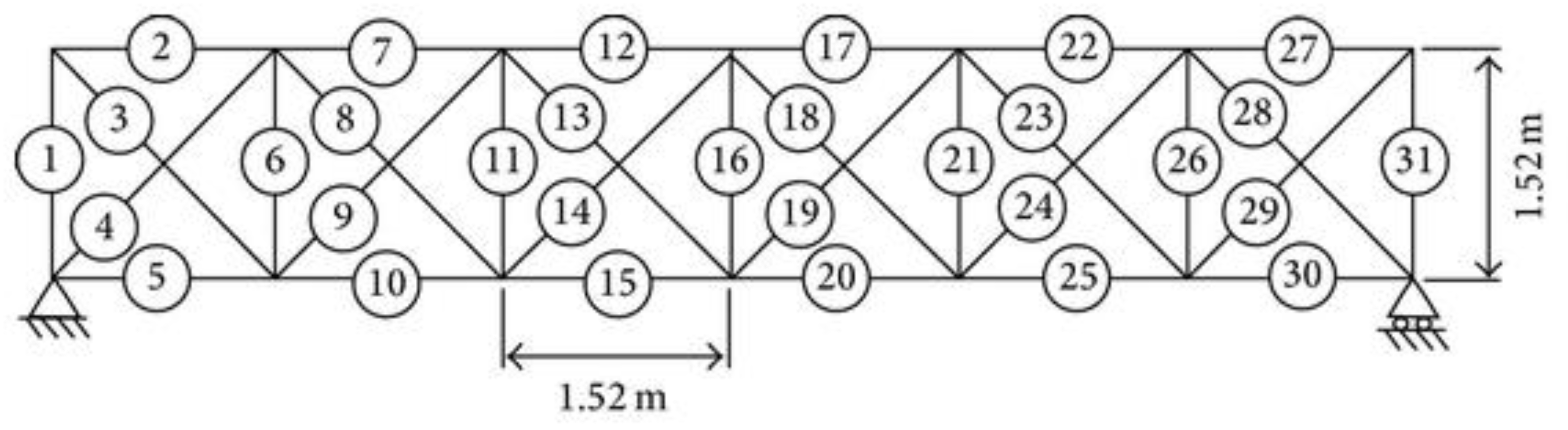
7.1. 31-Bar Planar Truss

The standard finite element (FE) approach is used to model the 31-bar planar truss in Figure 4 without internal nodes, resulting in 25 degrees of freedom [45]. The first five vibrating modes are used for NSDI in this case. The elasticity modulus and density of the material are 70 GPa and 2770 kg/m, respectively. Two distinct damage scenarios are implemented in the structure, as shown in

Table 2. Damage scenarios of the planar truss.

Case 2		Case 1
Element Number	SRF	Element Number	SRF
11	0.25	1	0.30
25	0.15	2	0.20

, and the suggested approach is evaluated in each case.

The impact of noise on the accuracy of NSDI based on modal data is studied in this section. The uncertainties of the measured mode shapes of structures are typically larger than the uncertainties of the frequencies in modal testing [1]. In this study, uncertain frequencies and mode shapes are considered as the normal distributed random variables defined in Equations (6) and (7). The mean values of the relative random noises $X_{\lambda i}$ are zeros, and standard deviations ${\xi }_{\lambda }$ indicate the noise level.

Table 3. PoDEs and DMIs of case 1 for the 31-bar planar truss.

Element Number	ESMA (PoDE) %	ESMA (DMI) %
1	100.00	30.00
2	96.00	19.10
10	0.00	0.00
18	7.00	1.00
Total time (s)	195	-
Root Mean Square Error (RMSE)	$1.1\times {10}^{-3}$	-

and

Table 4. PoDEs and DMIs of case 2 for the 31-bar planar truss.

Element Number	ESMA (PoDE) %	ESMA (DMI) %
10	0.00	0.00
11	100.00	25.00
12	8.00	0.80
14	2.00	0.50
25	95.00	14.20
Total time (s)	175	-
RMSE	$1.2\times {10}^{-3}$	-

show PODEs and DMIs of the damage scenarios 1 and 2, respectively. The noise level is set as 2% and 5% in the frequencies and mode shapes, respectively. In scenario 1, higher PoDE values are obtained at element numbers 1 and 2 compared to the undamaged elements. Moreover, the PoDE values of elements 1 and 2 are higher than those of the undamaged elements. The DMI value of element 1 is similarly higher than that of element 2; both of these elements are correct damage locations with varying severity conditions. The same condition can be seen for scenario 2, where higher PoDE values observed at segments 11 and 25 and the DMI values are also higher at the elements with higher severity.

To further prove the capability of the proposed method,

Table 5. PoDEs and PDEs of case 1 for the 31-bar planar truss.

Element Number	ESMA (PoDE) %	ESMA (PDE) %
1	100.00	98.00
2	96.00	96.00
10	0.00	7.00
11	0.00	0.00
12	0.00	1.00
18	7.00	0.00
19	0.00	5.00
22	0.00	10.00
26	0.00	3.00
Total time (s)	195	313
RMSE	$1.1\times {10}^{-3}$	$1.2\times {10}^{-2}$

and

Table 6. PoDEs and PDEs of case 2 for the 31-bar planar truss.

Element Number	ESMA (PoDE) %	ESMA (PDE) %
10	0.00	7.00
11	100.00	96.00
12	8.00	20.00
13	0.00	0.00
14	2.00	0.00
24	0.00	5.00
25	95.00	92.30
26	0.00	12.00
Total time (s)	175	301
RMSE	$1.2\times {10}^{-3}$	$1.0\times {10}^{-2}$

compare the PoDE values obtained by the proposed method with the PDE values for the same damage cases calculated using a probability-based method developed by Ghiasi et al. [33,46].

Ghiasi et al. [33] uses the probability density function of the existence of undamaged and damaged states to determine the probability of damage existence (PDE). The main algorithm consists of three interconnected loops based on coupling metamodeling techniques with a metaheuristic optimization algorithm for probability-based damage detection (PBDD) of structures.

These results show that the proposed technique outperforms the PBDD method by providing a more meaningful damage severity indicator than the statistical surrogate model method, which simply displays damage severity in terms of the probabilities. [21,26]. Furthermore, compared to the aforementioned surrogate methods [33,47], the proposed non-probabilistic method provides an advantage since it does not require surrogate models to predict the upper and lower boundaries of the ESP values. Surrogate models impose some uncertainties on the process, which increase the prediction error. The standard deviation of the probability density function (PDF) used to calculate the probability of damage existence is typically increased by the prediction error in the statistical surrogate model (PDE) [47]. This higher standard deviation may result in lower probability values when detecting damage in structures.

On other hand, in both scenarios, the PoDE is demonstrated to be a more accurate damage index and results in smaller errors. For example, in scenario 1, the suggested approach reveals a 0% PoDE value in element 10, which is undamaged, compared to a 7% PDE value. In scenario 2, the undamaged element 26 shows 0% damage, whereas the probability-based technique predicts 12% damage. It is also observed that for both scenarios, the proposed method provides higher PoDE values at the damaged elements compared to the PDE value. The main reason is that the proposed non-probabilistic method utilizes only two models to predict the upper and lower boundaries of the ESP values. Furthermore, it implemented the exact FE model. In comparison, the probabilistic method for the same example needs four surrogate models to calculate the probability density function of the damage [47], which leads to greater prediction errors. Furthermore, as can be seen in Table 5 and Table 6, the proposed methodology reduces the computation time by at least 37%.

7.2. 120-Bar Dome Truss

The second example is a 120-bar dome truss, as illustrated in Figure 5 [48].

The dome’s diameter and height are 31.78 m and 7 m, respectively. A seamless steel pipe with a modulus of elasticity of 30,450 ksi (210,000 MPa) and material density of 0.288 $\frac{lb}{i{n}^3}$ (7971.810 $\frac{kg}{m^3}$) is used. The pipes have an external diameter of 0.2 m and a thickness of 0.006 m. For FE modeling and analysis, OpenSees software [42] was used. As described in

Table 7. Damage scenarios for the 120-bar dome truss.

Case 1		Case 2
Element Number	SRF	Element Number	SRF
12	0.30	4	0.35
38	0.20	30	0.20
53	0.25	51	0.35
79	0.2	58	0.25
-	-	89	0.2
-	-	105	0.40

, two damage scenarios are considered. Figure 6 and Figure 7a and

Table 8. PoDE for damage case 1 of the dome truss.

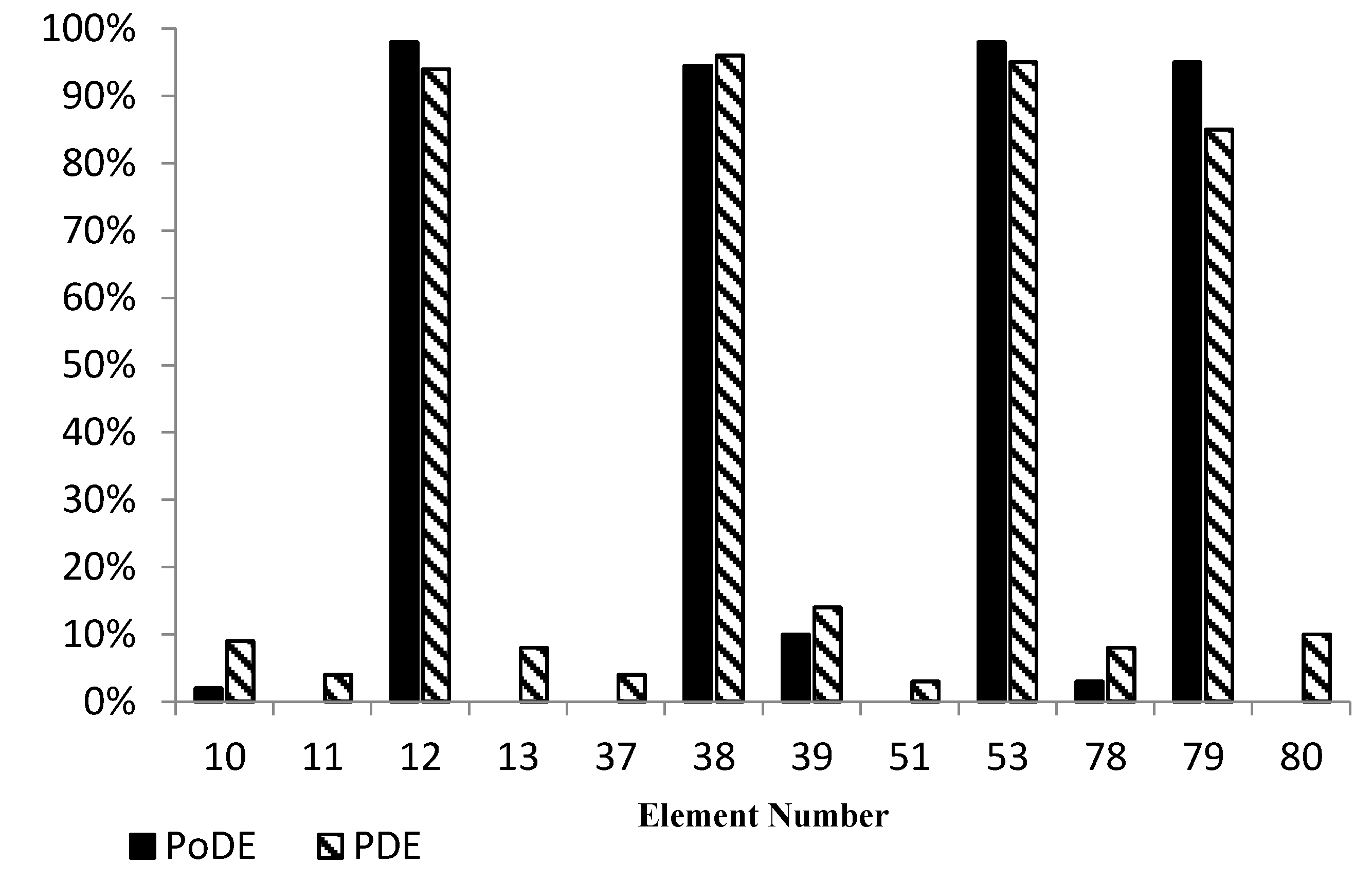
Element Number	PoDE	PDE
10	2%	9%
11	0%	4%
12	98%	94%
13	0%	8%
37	0%	4%
38	95%	96%
39	10%	14%
51	0%	3%
53	98%	95%
78	3%	8%
79	95%	85%
80	0%	10%

and

Table 9. PoDE for damage case 2 of the dome truss.

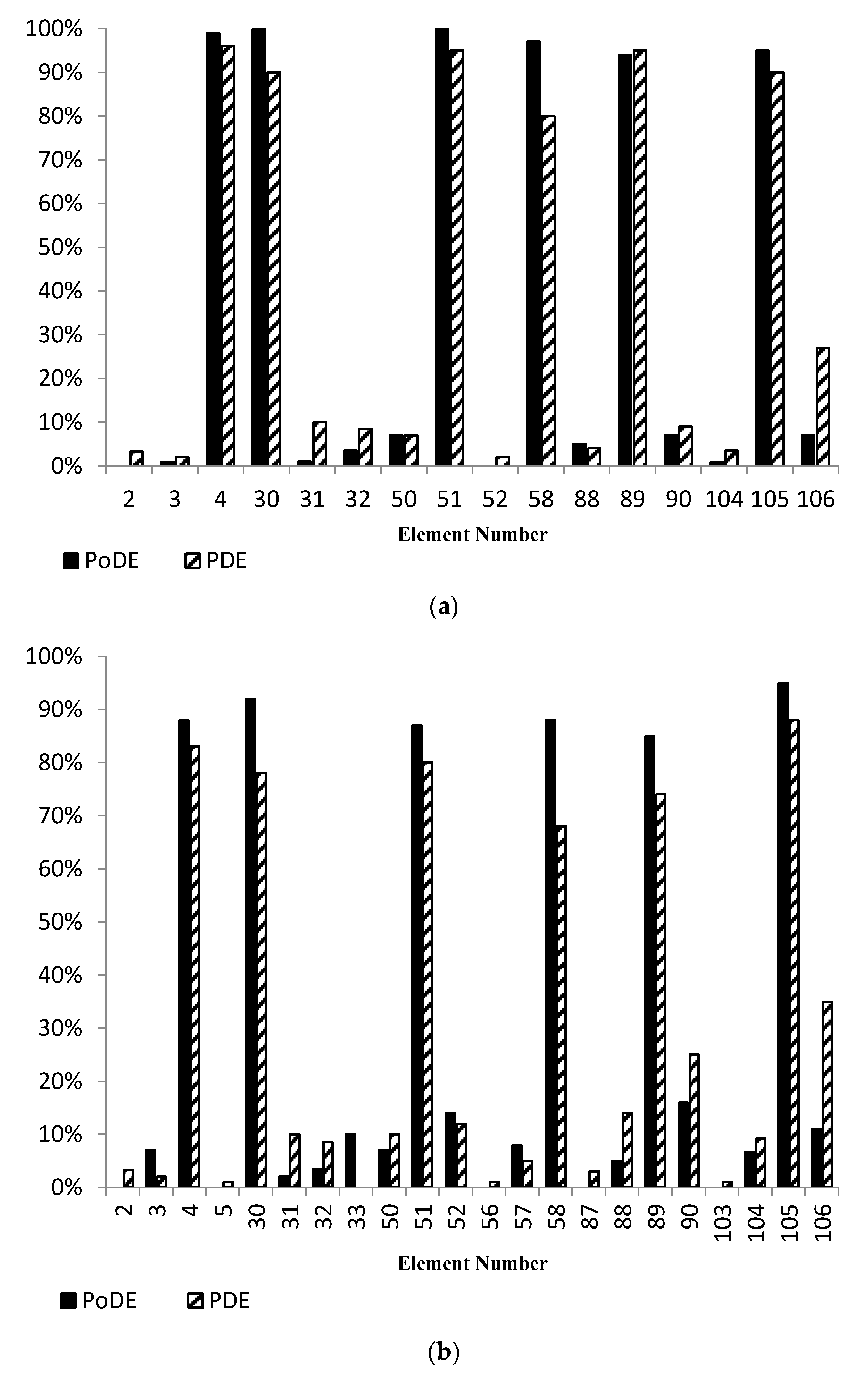
Element Number	PoDE	PDE
2	0%	3%
3	1%	2%
4	99%	96%
30	100%	90%
31	1%	10%
32	4%	9%
50	7%	7%
51	100%	95%
52	0%	2%
58	97%	80%
88	5%	4%
89	94%	95%
90	7%	9%
104	1%	4%
105	95%	90%
106	7%	27%

show the performance of the proposed method. It is worth noting that the noise level is set as 2% and 5% in the frequencies and mode shapes, respectively.

The results show that although the measured modal data were noise corrupted, the proposed approach provides a reliable prediction of damage occurrence. Furthermore, ESMA can effectively find the correct locations and severity of the damage. For a larger noise level, that is ${\xi }_{\lambda }=10\%$, the resultant PoDE values of damage scenario 2 are shown in Figure 7b and

Table 10. PoDE for damage case 2 of the dome truss with ${\xi }_{\lambda }=10\%$.

Element Number	PoDE	PDE
2	0%	3%
3	7%	2%
4	88%	83%
5	0%	1%
30	92%	78%
31	2%	10%
32	4%	9%
33	10%	0%
50	7%	10%
51	87%	80%
52	14%	12%
56	0%	1%
57	8%	5%
58	88%	68%
87	0%	3%
88	5%	14%
89	85%	74%
90	16%	25%
103	0%	1%
104	7%	9%
105	95%	88%
106	11%	35%

.

The numerical results show that the proposed method performs well in detecting the location and severity of the damage scenarios even with a large noise level. The PoDE values of the damaged elements are higher in NSDI approaches, whereas the PoDE values of the undamaged elements are lower.

7.3. 4 Story Steel Structure Model

The third example is a 3D modular structure based on Phase II of the IASC–ASCE SHM benchmark four-story building [49,50]. As illustrated in Figure 8, the model is built without side braces along the four floors. The structure has 12 degrees of freedom (DOFs) and 84 members. This structure has a base plan of 2.5$\times$2.5 m and height of 3.6 m. The members are hot rolled grade 300 W steel with a nominal yield stress 300 MPa (42.6 kpsi).

This complex model can effectively illustrate the efficiency of structural damage tracking using the proposed non-probabilistic method. As indicated in Figure 9, one damage situation is considered by replicating the damage in element 7 by reducing its Young’s modulus by 25%.

Table 11. PoDEs, PDEs, and DMIs for the four-story steel structure.

Element Number	ESMA (PoDE) %	ESMA (PDE) %	ESMA (DMI) %	SMA (PoDE) %	SMA (PDE) %	SMA (DMI) %
1	2.00	4.00	0.24	0.00	5.00	0.00
7	100.00	99.00	25.00	100.00	98.00	25.00
12	0.00	0.00	0.00	4.00	0.00	0.32
13	8.00	14.00	0.96	10.00	14.00	1.2
18	10.00	10.00	1.00	16.00	17.00	2.50
28	0.00	0.00	0.00	3.00	9.00	0.15
39	0.00	9.00	0.00	13.00	5.00	2.60
Total time (s)	202	612	-	370	815	-
NFEs	1250	1800	-	1730	2000	-
RMSE	6.00 $\times {10}^{-3}$	7.00 $\times {10}^{-2}$	-	8.11 $\times {10}^{-2}$	9.21 $\times {10}^{-2}$	-

show PODEs, DMIs, and PDEs for the damage scenario. Furthermore, a comparison between the proposed ESMA and the original SMA is shown. Herein, the simulated mode shapes and frequencies consist of 5% and 2% measurement noise, respectively.

The maximum numbers of function evaluations (NFEs) shown in Table 11 indicate that determining the global optimum with ESMA is substantially less computationally costly than with SMA.

Based on the results displayed in Table 11, it can be determined that SMA has the ability to detect damaged elements with high certainty, whereas the resulting PDE, PoDE, and DMI for the undamaged elements is higher in comparison with ESMA. Furthermore, as can be seen in Table 11, the proposed methodology reduces the computation time by at least 30%.

8. Conclusions

Using the most recently introduced optimization algorithm (SMA), a unique approach for NSDI was proposed in this study as a one-stage procedure. There are always uncertainties in the measured modal parameters in typical applications of health monitoring approaches, which can lead to unreliable and inaccurate structural damage prediction. As a result, uncertainties are included in the developed NSDI process. An SMA method is updated to increase its performance in dealing with problems involving a large number of variables. An interval analysis is adopted for use with the ESMA to consider the uncertainties using the interval bounds of the uncertainties in the damage variables of the metaheuristic optimization model.

The numerical results demonstrate that the proposed approach is capable of accurately detecting the location and severity of various damage scenarios. Based on the results it can be concluded that the proposed interval optimization method procedure can obtain accurate PoDE and DMI and can provide robust damage identification results. In summary, the proposed non-probabilistic method is able to provide accurate damage detection results and has a small prediction cost since it does not require the utilization of surrogate models. Despite these advantages, this approach may need further improvements to be implemented in the real-time recorded response of a structure, such as adding the structural identification (SI) stage, in order to convert the acceleration response to the frequency response. Consideration of uncertainty in loadings will be pursued in our upcoming papers.